Piotr Koprowicz

Algorytmy i struktury danych 1

Projekt 2 - Problemu wie Hanoi dla k wie

Wst p

“W wielkiej wi tyni Benares w Hanoi, pod kopuł , która zaznacza rodek wiata,

znajduje si płytka z br zu, na której umocowane s trzy diamentowe igły, wysokie na łokie

i cienkie jak talia osy. Na jednej z tych igieł, w momencie stworzenia wiata, Bóg umie cił 64

kr ki ze szczerego złota. Najwi kszy z nich le y na płytce z br zu, a pozostałe jeden na

drugim, id c malej co od najwi kszego do najmniejszego. Jest to wie a Brahma. Bez

przerwy, we dnie i w nocy, kapłani przekładaj kr ki z jednej diamentowej igły na drug

przestrzegaj c niewzruszonych praw Brahma. Prawa te chc , aby kapłan na słu bie brał tylko

jeden kr ek na raz i aby umieszczał go na jednej z igieł w ten sposób, by nigdy nie znalazł

si pod nim kr ek mniejszy. Wówczas, gdy 64 kr ki zostan przeło one z igły, na której

umie cił je Bóg w momencie stworzenia wiata, na jedn z dwóch pozostałych igieł, wie a,

wi tynia, bramini rozsypi si w proch i w jednym oka mgnieniu nast pi koniec wiata.”

W standardowym algorytmie rozwi zuj cym problem wie Hanoi do przeło enia

wszystkich kr ków potrzebna jest 2

n

-1 ilo kroków, gdzie n to ilo kr ków.

Rozwa my, co by si stało, gdyby my mieli do dyspozycji k wie .

Opis algorytmu dla k wie

Rozwa my algorytm dla liczby wie wi kszej lub równej 3.

Niech n b dzie ilo ci kr ków, a k ilo ci wie .

Dla 3 kr ków wykonujemy tradycyjny algorytm wie Hanoi.

Załó my teraz, i liczba wie jest wi ksza od 3. Wówczas wprowadzamy logiczny podział

liczby wie na dwie cz ci:

1.

Pierwsze 3 wie e

2.

Liczba wie równa k-3

Do póki n>= k wtedy stosujemy nast puj c sekwencj :

Przekładamy tradycyjnym algorytmem n-k+3 kr ków, a te, które zostały przekładamy na

wie e z drugiej cz ci logicznej, w nast puj cym porz dku: najwi kszy na czwarty i nastepne

kolejno na odpowiadaj ce im wie e, przy czym na ka dej b dzie co najwy ej jeden kr ek

Po tej czynno ci kr ki z kolejnych wie , zaczynaj c od wie y 5, przekładamy na 4.

Kiedy n<k wtedy stosujemy nast puj ce kroki:

1.

Wszystkie kr ki, poza najwi kszym przesuwamy na inne wie e w ustalonym

porz dku, przy czym na ka dej wie y b dzie co najwy ej 1 kr ek.

2.

Przesuwamy ostatni na czwart wie

3.

Pozostałe kr ki przekładamy na t wie , na której jest najwi kszy zaczynaj c od

kr ka o 1 mniejszego od najwi kszego i na kr ku najmniejszym ko cz c.

W ten sposób wszystkie kr ki zostan przeło one na pierwsz wie z drugiej cz ci

logicznej.

Badanie działania algorytmu

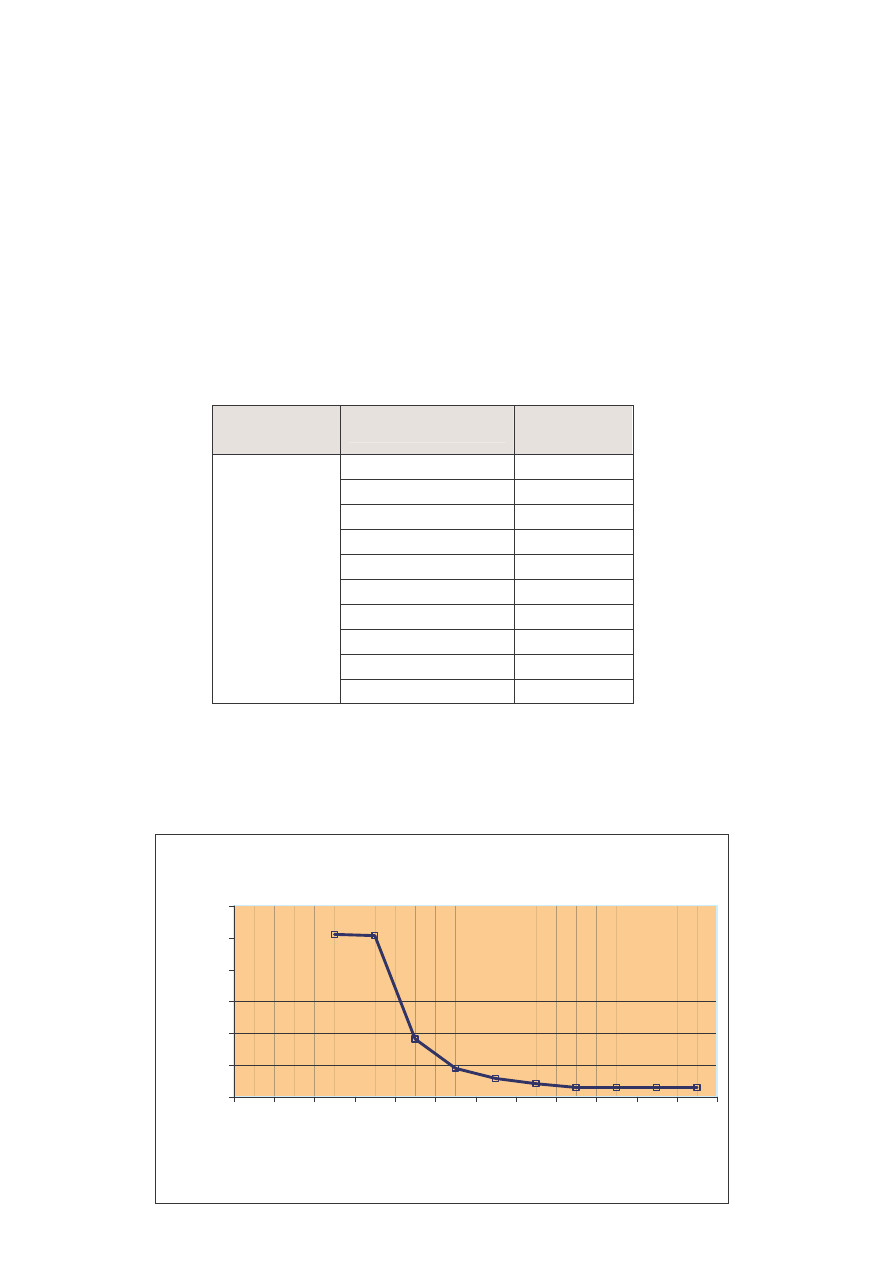
Zbadajmy algorytm dla ustalonej liczby kr ków:

Ilo kr ków – 8

Ilo

kr ków

Ilo wie

Ilo

kroków

1

Niemo liwe

2

Niemo liwe

3

255

4

253

5

91

6

45

7

29

8

21

9

15

8

10

15

Z powy szych rozwa a wynika, i zwi kszenie liczby wie zdecydowanie wpływa na ilo

potrzebnych kroków do przeniesienia wszystkich kr ków, co obrazuje poni szy wykres (

1

):

ilosc kroków przy ustalonej liczbie kr ków - 8

0

50

100

150

200

250

300

1

2

3

4

5

6

7

8

9

10

11

12

ilosc wie

ilo

sc

k

ro

ko

w

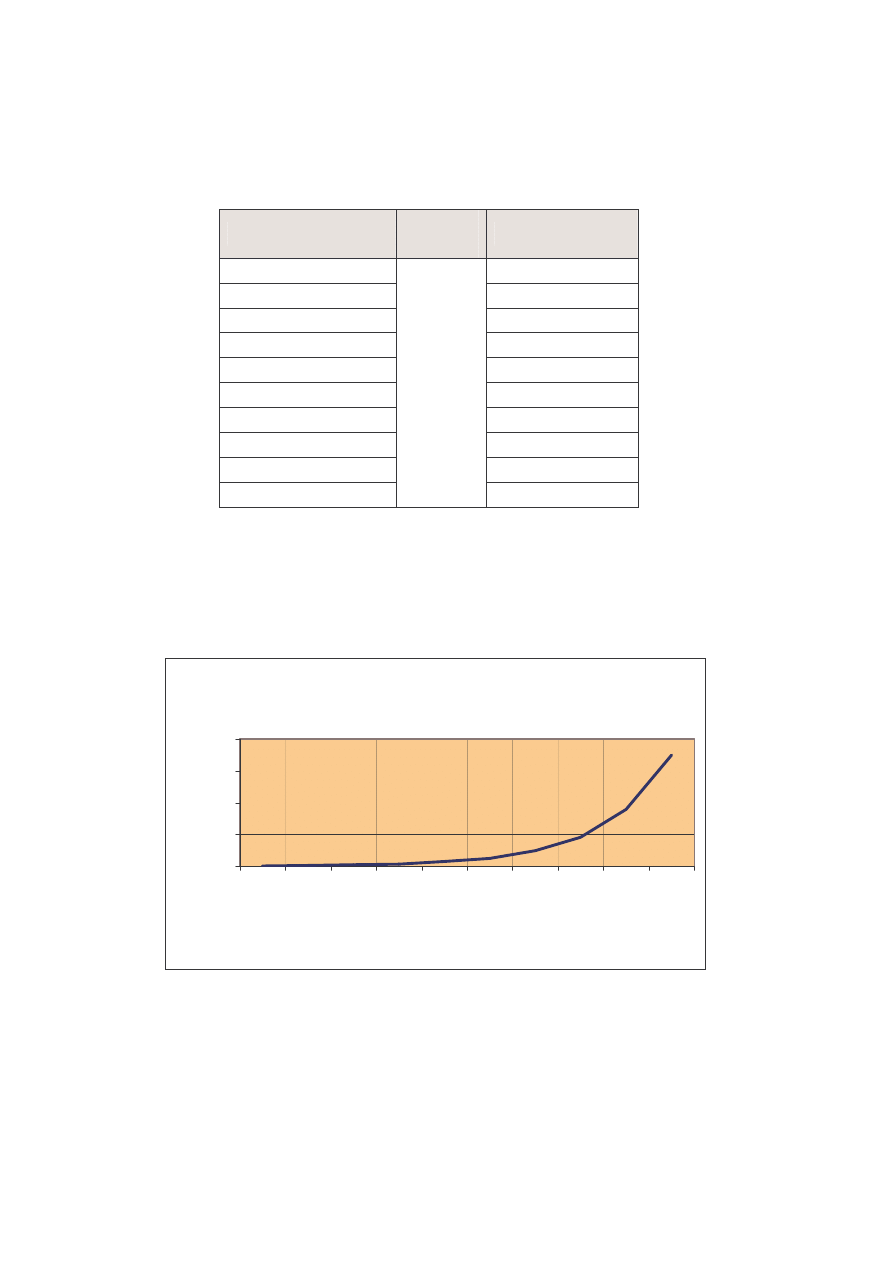
Zobaczmy co si dzieje, gdy ilo wie jest ustalona, a zwi kszamy ilo kr ków:

Ilo wie – 5

Ilo kr ków

Ilo

wie

Ilo kroków

1

1

2

3

3

5

4

7

5

15

6

25

7

49

8

91

9

179

10

5

349

Wida wyra nie, i przy ustalonej liczbie wie , dodanie do liczby kr ków nast pnego

wydłu a ilo potrzebnych kroków. Zale no t ilustruje poni szy wykres(

2

):

ilo kroków przy ustalonej liczbie wie - 5

0

100

200

300

400

1

2

3

4

5

6

7

8

9

10

ilosc kr kow

ilo

sc

k

ro

ko

w

Wnioski cz ciowe: Zwi kszanie ilo ci kr ków zwi ksza ilo kroków, natomiast

zwi kszanie liczby wie zmniejsza ilo kroków,ale tylko dopóki ilo

wie nie b dzie równa k

0 ,

gdzie k

0

>=n+1. Po osi gni ciu liczby n

0

ilo

kroków b dzie stała.

Analiza algorytmu dla 3 słupków

Wie Hanoi z n kr kami oznaczmy przez h

n

. Z przeprowadzonych testów

mo na zauwa y , e: h

1

=2

1

−1 ; h

2

=2

2

−1 ; h

3

=2

3

−1 ; ... , gdzie pot ga jest równa

indeksowi liczby h . Na tej podstawie mo na przypuszcza , e h

n

=2n−1 dla dowolnej

liczby kr ków n. Z rekurencyjnego algorytmu rozwi zywania problemu wie Hanoi

wynika nast puj ca zale no rekurencyjna mi dzy liczbami:

h

n =

>

+

=

1

dla

,

1

2h

1

n

dla

,

1

1

-

n

Powy sz zale no mo emy sprawdzi indukcyjnie.

Wiemy, e: h1 = 2

1

−1 = 1 ,

załó my, e h

n

= 2

n

−1 ,

a zatem

h

n+1

= 2(h

n

) + 1 = 2(2

n

−1) + 1 =2

n+1

−1

Udowodnili my zatem, e zło ono algorytmu wynosi O(2

n

)

Analiza algorytmu dla 4 słupków

Ilo przeło e dla 4 słupków wyra a si wzorem:

>

+

=

=

−

=

+

4

,

3

2

,

3

..

1

,

1

2

1

n

a

a

n

n

a

n

n

n

sprawd my wzór dla 5 kr ków:

29 = h

5

= 2h

4

+ 3 = 2(2h

3

+ 3) + 3 = 2 ( 2 (2*3 - 1) + 3) + 3 = 2 (2*5 + 3) + 3 = 29

Powy sz zale no mo emy sprawdzi indukcyjnie.

Wiemy, e:

h

5

= 2h

4

+ 3 = 29

Załó my, e

h

n

= 2

n

- 3,

a zatem

h

n+1

= 2h

n

+ 3 = 2 (2

n

- 3) + 3 = 2

n+1

- 3.

Udowodnili my zatem, e zło ono algorytmu wynosi O(2

n

), dla n>4

Analiza algorytmu dla 5 słupków

Ilo przeło e dla 5 słupków wyra a si wzorem:

−

>

+

−

=

−

>

+

−

=

=

−

=

−

−

)

(

4

,

1

2

)

(

4

,

6

2

,

4

..

1

,

1

2

1

1

parzyste

n

n

n

a

a

e

nieparzyst

n

n

n

a

a

n

n

a

n

n

n

n

n

sprawd my wzór dla 6 kr ków:

25 = h

6

= 2*h

5

– 6+1 = 2*(2*h

4

- 5 + 6) - 6 + 1 = 2*(2*(2*4-1)

- 5 + 6) - 6 + 1 =

= 2*(2*(7) + 1) -5 =2*(15) – 5 = 25

a wi c powy sza zale no jest prawdziwa, co mo na udowodni indukcyjnie.

Wnioski ko cowe:

„Tradycyjny” algorytm wie Hanoi, a wi c dla 3 słupków jest algorytmem

optymalnym i ma zło ono O

(2

n

).

Zwi kszanie ilo ci kr ków zwi ksza ilo kroków (wykres

2

), natomiast

zwi kszanie liczby wie zmniejsza ilo kroków ,ale tylko dopóki ilo wie nie b dzie równa

k

0 ,

gdzie k

0

>=n+1. (wykres

1

). Po osi gni ciu liczby k

0

ilo kroków b dzie stała.

Prezentowane rozwi zanie nie nale y do optymalnych, jednak nie znaleziono

algorytmu, który dokonałby przeło enia wszystkich kr ków w minimalnej liczbie ruchów.

Akceptowane b d wszystkie rozwi zania, które dadz wynik nie gorszy od naszego i b d

miały nie gorsz zło ono .