Projekt współfinansowany przez

Unię Europejską w ramach

Europejskiego Funduszu Społecznego

Materiały dydaktyczne opracowano do realizacji projektu

”Program Rozwojowy Potencjału Dydaktycznego Politechniki Świętokrzyskiej w Kielcach: kształcenie na miarę sukcesu’’

Umowa UDA-POKL.04.01.01-00-175/08-00

Maszyny elektryczne – wykład multimedialny

Autorzy:

Prof. dr hab. inż. Roman Nadolski

Dr inż. Jan Staszak

Dr inż. Krzysztof Ludwinek

Mgr inż. Zbigniew Gawęcki

Lata realizacji 2008-2011

SPIS TREŚCI

1.

Ogólne

wiadomości

o

maszynach

elektrycznych,

podstawy

elektromagnetyzmu

1.1 Pole magnetyczne

1.2 Indukcja magnetyczna, strumień magnetyczny, natężenie pola magnetycznego

1.3 Materiały magnetyczne

1.4 Podstawowe prawa obwodu magnetycznego

1.5 Indukcyjność własna i wzajemna

1.6 Indukcja elektromagnetyczna

1.7 Energia pola magnetycznego

LITERATURA

1.

Ogólne

wiadomości

o

maszynach

elektrycznych,

podstawy

elektromagnetyzmu

1.1

Pole magnetyczne

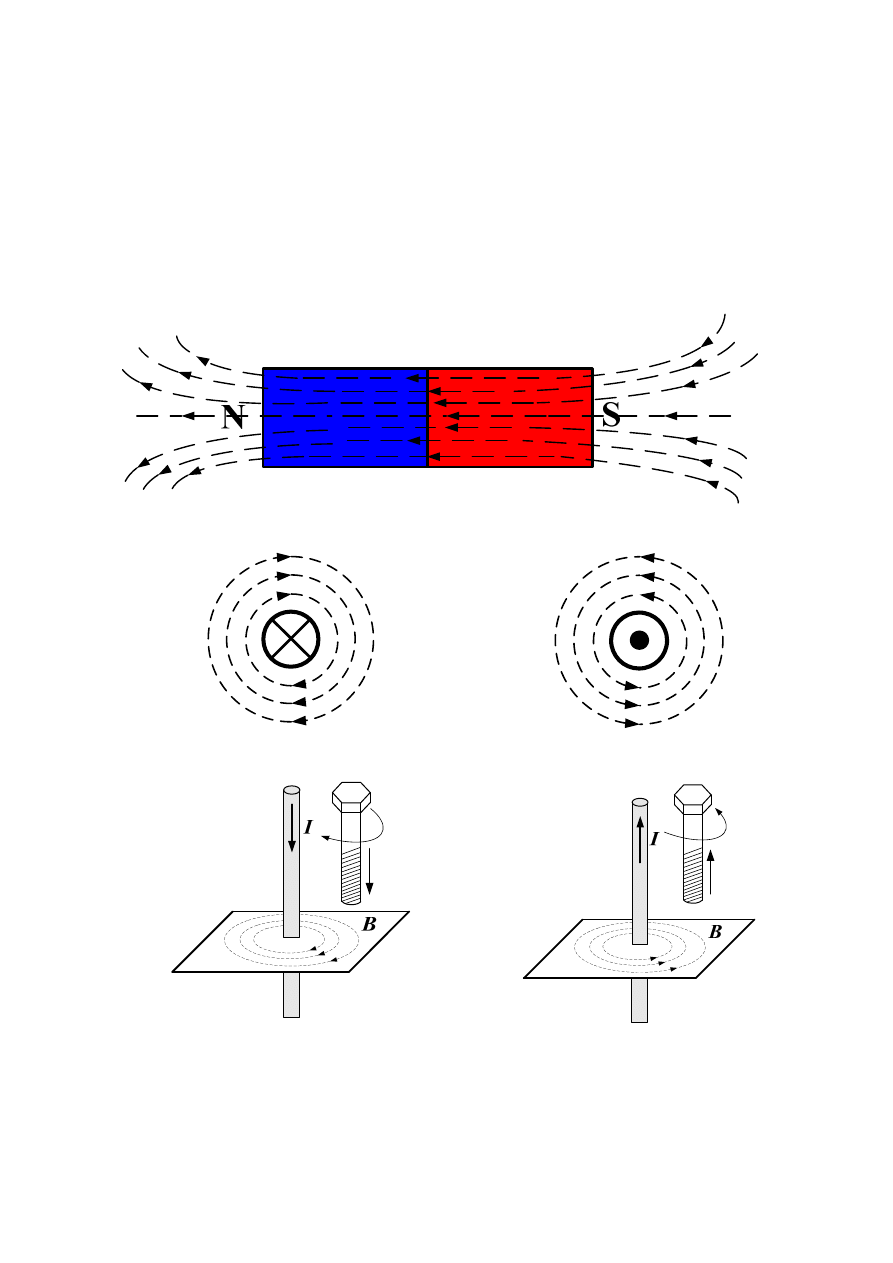
Zasada działania maszyn elektrycznych i transformatorów opiera się na istnieniu pola
magnetycznego. Pole magnetyczne może być wytworzone za pomocą magnesów trwałych
(rys.1a) lub za pośrednictwem prądu elektrycznego płynącego w przewodniku (rys.1b).

a)

b)

Rys.1. Pole magnetyczne: a) magnesu trwałego, b) przewodu prostoliniowego.

Zwrot linii pola magnetycznego wokół przewodnika prostoliniowego zależy od zwrotu
płynącego prądu i określamy go za pomocą reguły śruby prawoskrętnej.

Zgodnie z tą regułą, jeżeli zwrot prądu płynącego w przewodniku prostoliniowym jest zgodny
z posuwem śruby to kierunek obrotu śruby wyznacza zwrot linii pola magnetycznego.


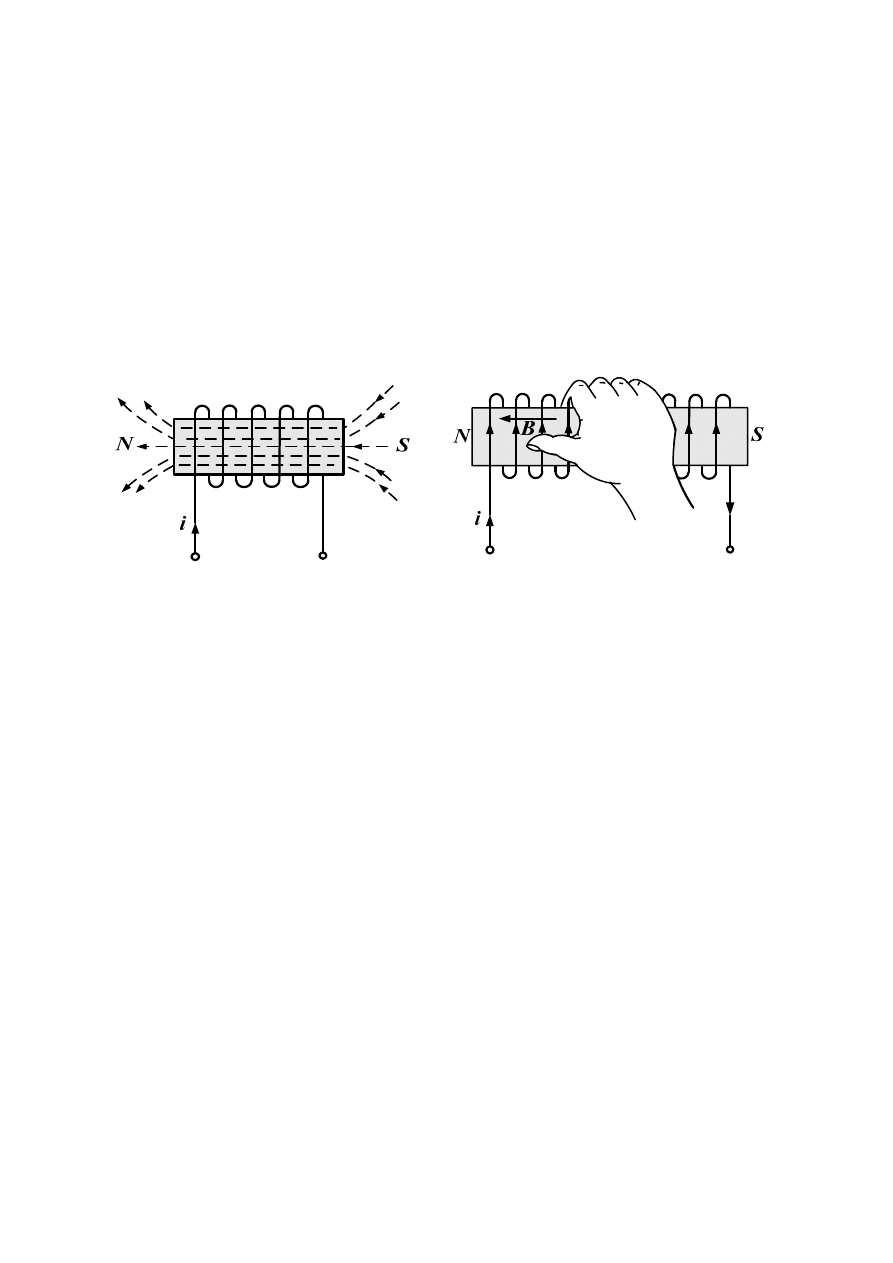
Na rys.2a przedstawiono obraz linii pola magnetycznego wytworzony przez prąd elektryczny
płynący w cewce (solenoidzie).

a)

b)

Rys. 2. Obraz linii pola magnetycznego wytworzony przez prąd elektryczny płynący w

cewce (solenoidzie).

Ten koniec cewki z którego linie pola magnetycznego wychodzą na zewnątrz, stanowi biegun
północny N, natomiast koniec cewki do którego linie wchodzą jest biegunem południowym S.
Linie pola magnetycznego wewnątrz cewki są skierowane od bieguna S do bieguna N. Zwrot
linii pola wewnątrz cewki określa się za pomocą reguły prawej ręki (rys. 2b).
Zgodnie z tą regułą prawą rękę należy położyć na cewce tak, aby cztery palce obejmujące
cewkę były skierowane zgodnie z prądem to odchylony duży palec wskazuje zwrot linii pola
magnetycznego wewnątrz cewki.

1.2 Indukcja magnetyczna, strumień magnetyczny, natężenie pola magnetycznego

Podstawową wielkością charakteryzującą pole magnetyczne jest strumień magnetyczny.
Miarą strumienia jest liczba linii pola przenikająca określoną powierzchnię. Natomiast liczbę
linii pola magnetycznego przypadającą na jednostkę powierzchni prostopadłą do tych linii
nazywamy indukcją magnetyczną. Wartość strumienia magnetycznego przenikającego
powierzchnię S określa zależność

∫

=

Φ

S

BdS

(1)

gdzie: B – wektor indukcji magnetycznej, S – powierzchnia całkowania

Jednostką strumienia jest weber (1Wb = 1Vs), natomiast jednostką indukcji jest tesla
(1T=1Wb/m

2

). Do opisu pola magnetycznego oprócz wektora indukcji magnetycznej B

wprowadza się pojęcie wektora natężenia pola magnetycznego H. Jednostką natężenia pola

magnetycznego jest A/m. Związek między natężeniem pola magnetycznego a indukcją
magnetyczną określa zależność

H

B

µ

=

(2)

gdzie:

µ

jest przenikalnością magnetyczną, przy czym

r

µ

µ

µ

0

=

(3)

We wzorze (3)

µ

0

jest przenikalnością magnetyczną bezwzględną próżni a

µ

r

jest

przenikalnością względną zależną od rodzaju środowiska. Przenikalność magnetyczna próżni
wynosi:

µ

0

= 4

π⋅

10

-7

H/m.

1.3 Materiały magnetyczne

Materiały magnetyczne charakteryzują się zdolnością do porządkowania ich cząsteczek lub w
przypadku czystych stopów atomów (tzw. drobin lub domen) pod wpływem zewnętrznego
pola magnetycznego.

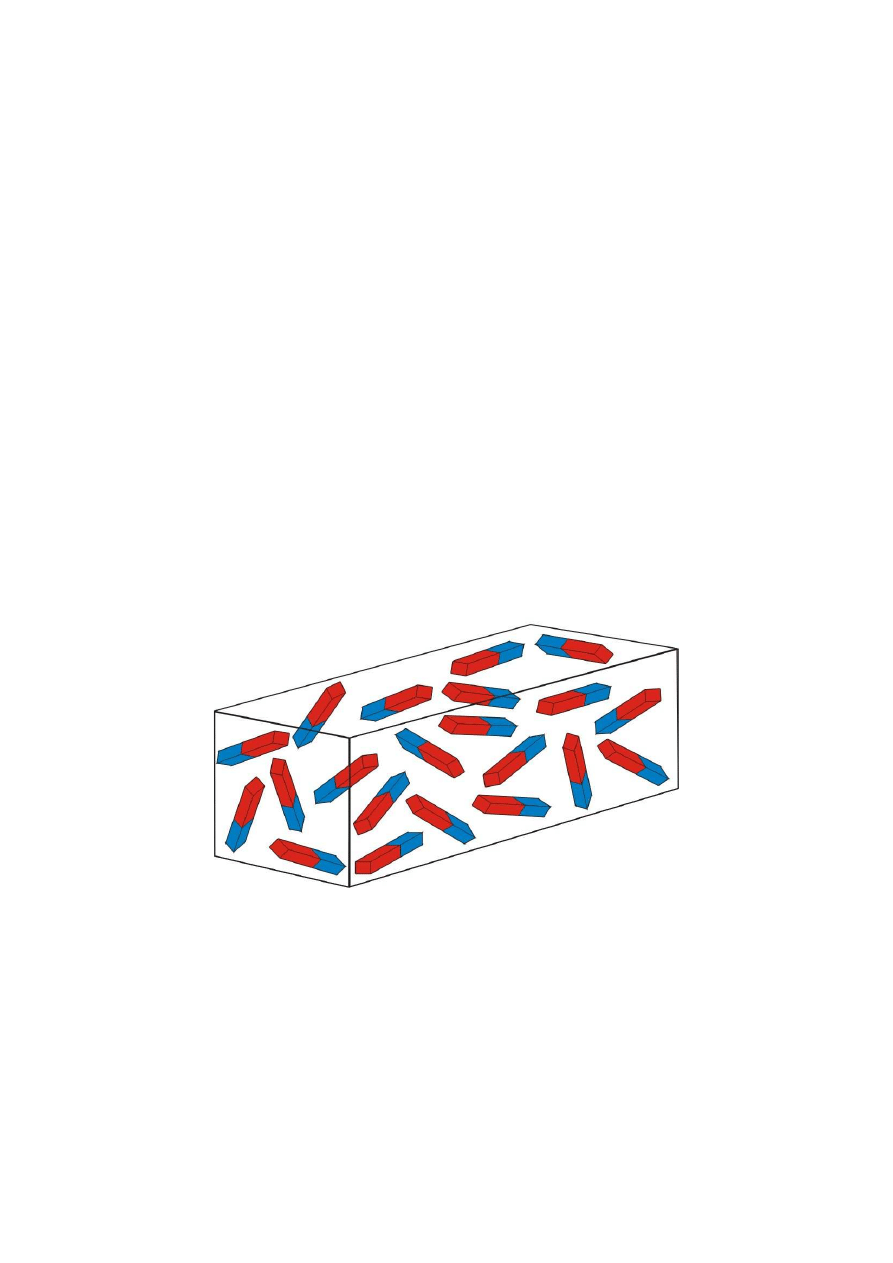
Domeny w materiałach magnetycznych przed działaniem zewnętrznego pola magnetycznego
charakteryzują się nieuporządkowaną strukturą, co obrazuje rys. 3.

Rys. 3. Rozkład domen w materiałach magnetycznych.

Stopniowa zmiana kierunku namagnesowania w granicach domen nieuporządkowanych
widoczna jest na rys. 4. Granica domen jest to taki obszar o szerokości około 100 średnic
atomowych, w którym kierunek namagnesowania zmienia się stopniowo aż do 180°.

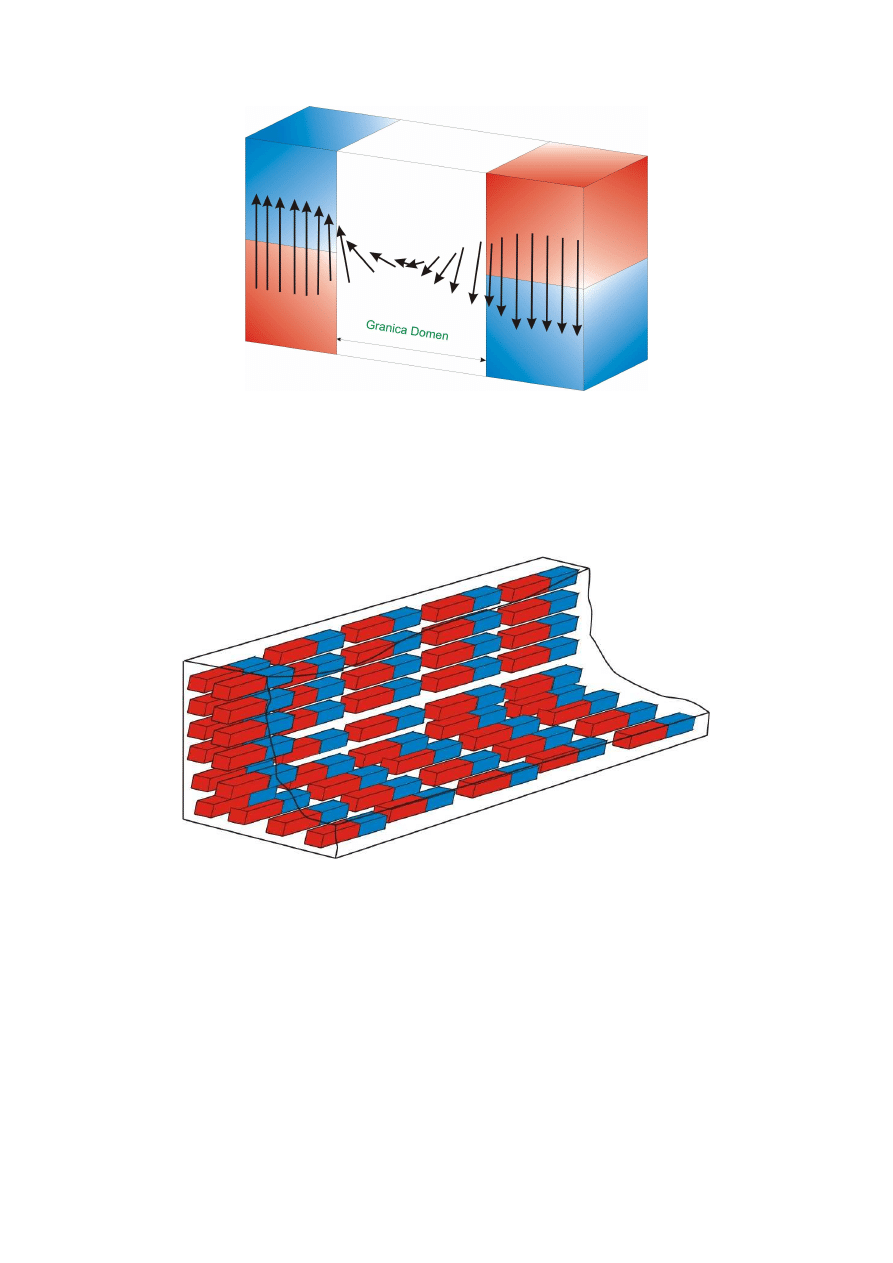
Rys. 4. Stopniowa zmiana kierunku namagnesowania w granicach domen

.

Pod wpływem silnego pola magnetycznego (natężenia pola H) domeny te ulegają
uporządkowaniu. Przy natężeniu zwanym natężeniem nasycenia już wszystkie domeny
ulegają uporządkowaniu co obrazuje rys. 5. Dalsze zwiększanie pola magnetycznego już nic
nie zmienia w strukturze wewnętrznej. Stan taki nosi nazwę nasycenia.

Rys. 5. Wpływ silnego pola magnetycznego- stan nasycenia.

Materiały magnetyczne często opisuje się za pomocą szeregu parametrów, które widoczne są
na rys. 6 przedstawiającym charakterystykę magnesowania B=f(H):

•

µ

max

– maksymalna przenikalność magnetyczna,

•

µ

i

– początkowa przenikalność magnetyczna,

•

Natężenie pola powściągające powodujące nasycenie (saturację)H

c

,

•

Indukcja nasycenia pola B

s

,

•

Remanencję (pozostałość szczątkową po zewnętrznych zmianach pola magnetycznego)
B

r

.

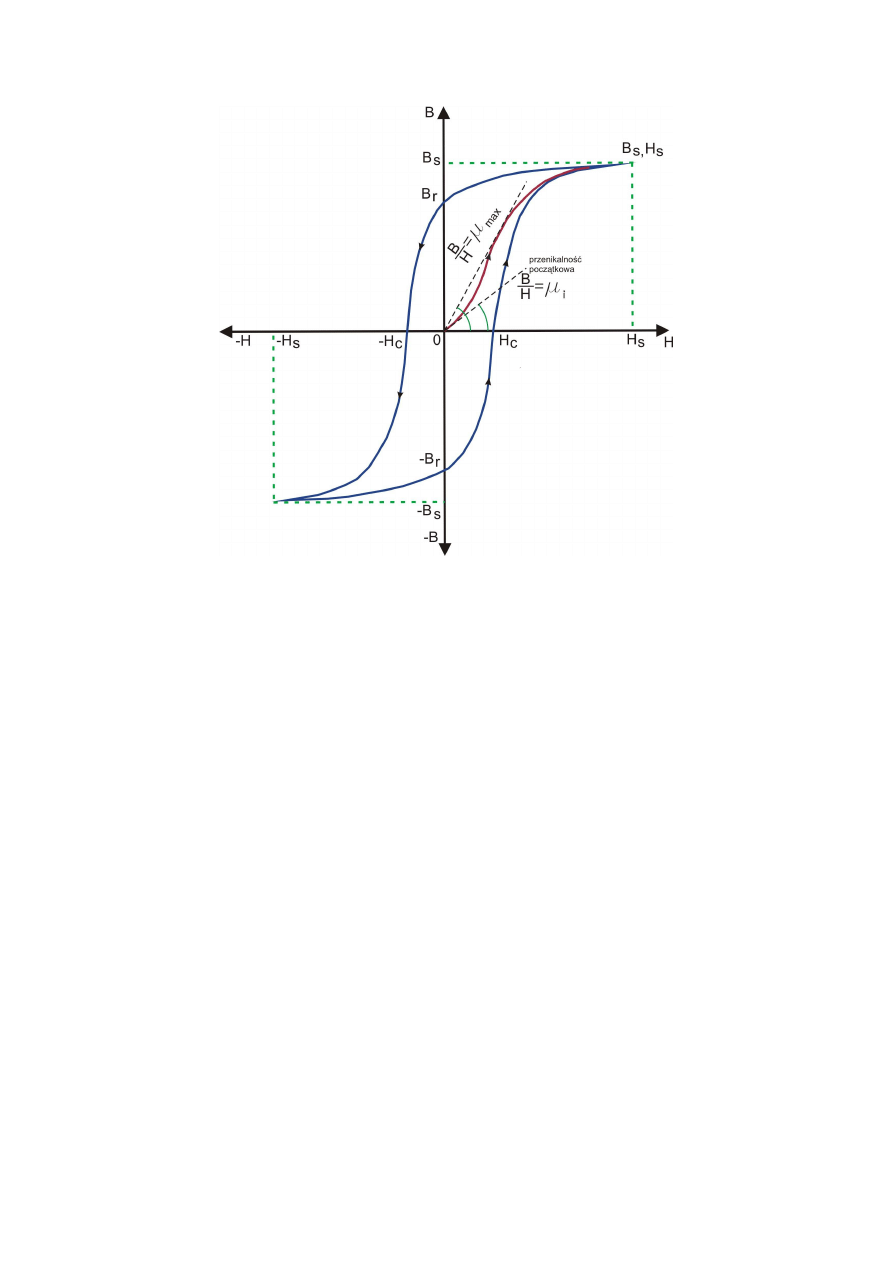
Rys. 6. Charakterystyka magnesowania

.

Materiały magnetyczne wykazują tzw. zjawisko histerezy. Histereza to zjawisko

nieodwracalne, polegające na:

•

łatwych i nietrwałych zmianach indukcji magnetycznej pod wpływem zewnętrznego

pola magnetycznego i charakteryzujące się wąską pętlą histerezy – takie materiały

nazywa się magnetycznie miękkie,

•

trudnych i trwałych zmianach indukcji magnetycznej pod wpływem zewnętrznego

pola magnetycznego i charakteryzujące się szeroką pętlą histerezy – takie materiały

nazywa się magnetycznie twarde.

Blacha elektrotechniczna to taki rodzaj blachy, który posiada właściwości materiału
magnetycznie miękkiego.

W elektrotechnice blachy produkuje się w różnych grubościach od 0.7 mm (blachy
izotropowe) do 0.23 mm (blachy anizotropowe).

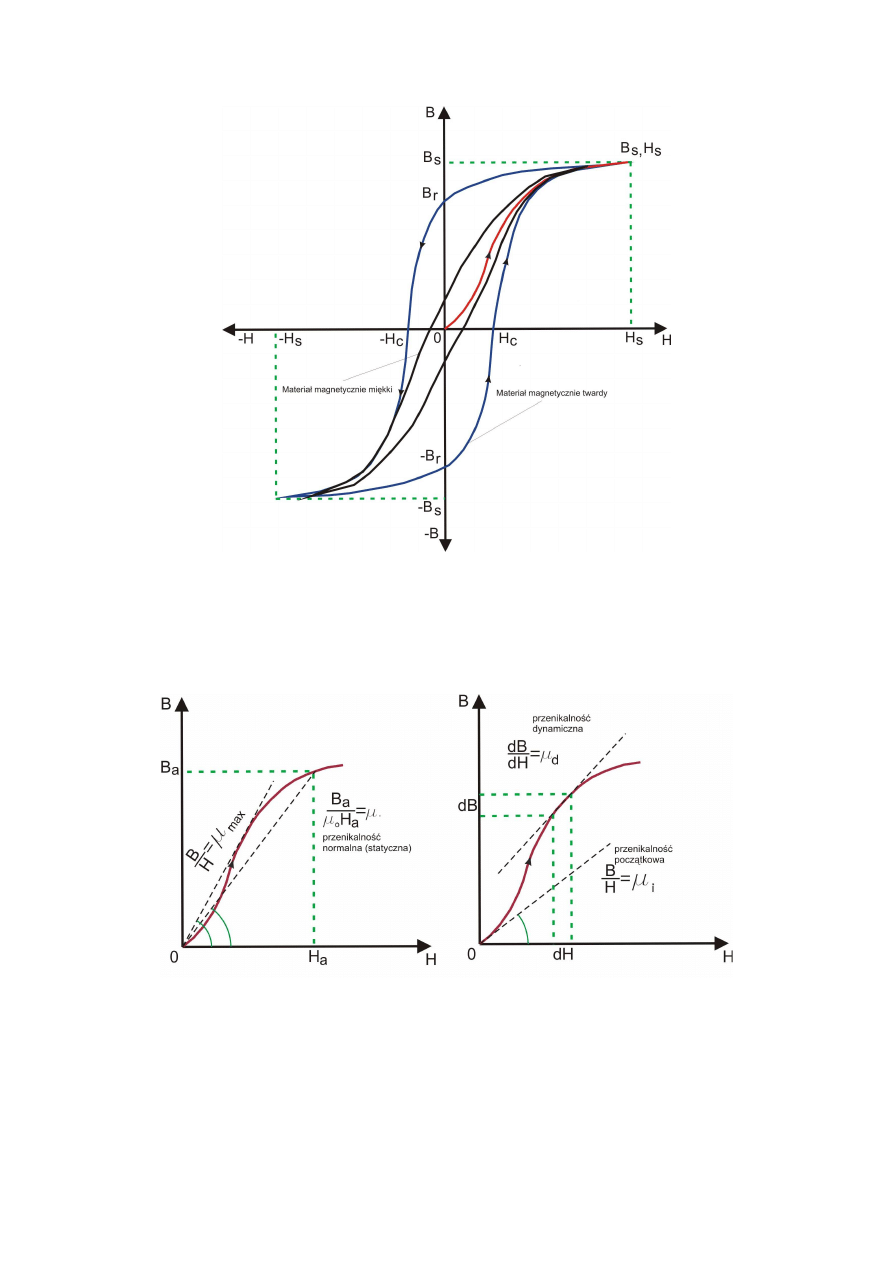
Rys. 7. Charakterystyki magnesowania dla materiałów magnetycznie miękkich i twardych.

W praktyce własności magnetyczne materiałów ferromagnetycznych określa się za pomocą
przenikalności magnetycznej maksymalnej i początkowej. Ponadto w danym punkcie można
wyznaczyć przenikalność statyczną oraz w każdym przedziale zmian natężenia pola można
wyznaczyć przenikalność dynamiczną. Powyższe przenikalności zilustrowane są na
wykresach.

Rys. 8. Przenikalność magnetyczna początkowa, maksymalna, statyczna i dynamiczna

.

Przebieg zmian indukcji dla różnych wymuszeń zmian natężenia pola obrazuje
charakterystyka normalna magnesowania (inna nazwa – komutacyjna)

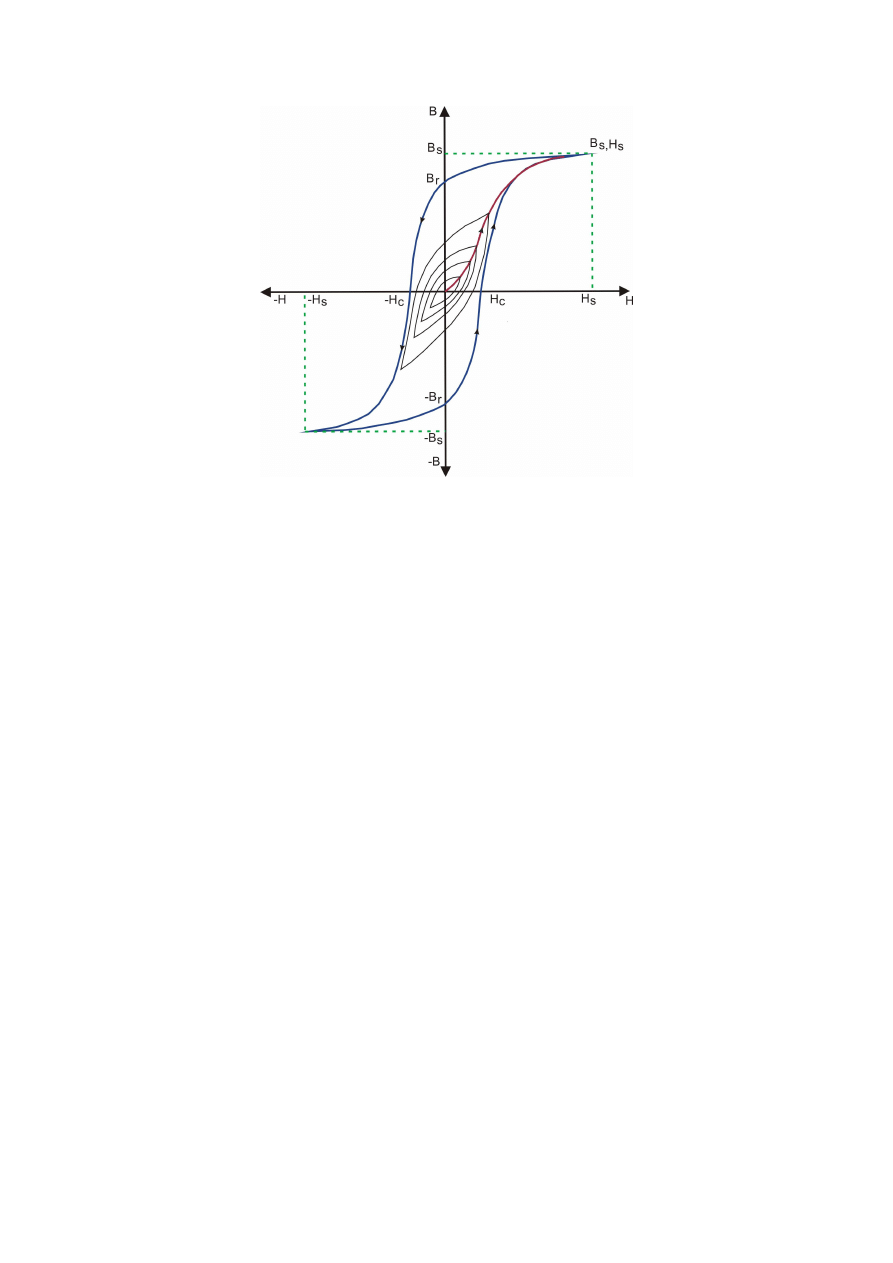
Rys. 9. Charakterystyka magnesowania komutacyjna.

Materiały magnetycznie miękkie

Blacha elektrotechniczna jest to specjalny rodzaj blachy zoptymalizowanej tak, aby osiągnąć
jak najlepsze własności magnetyczne. Stąd jej głównym składnikiem jest żelazo (powyżej
93%) z dodatkami taki jak, krzem, który zwiększa rezystywność blachy elektrotechnicznej, a
więc po złożeniu dowolnej maszyny elektrycznej z takich blach znacznie ograniczy się prądy
wirowe (w przeciwieństwie do stali konstrukcyjnych, węgiel w stopach wykorzystywanych w
elektrotechnice jest dodatkiem niepożądanym i jego zawartość jest znacznie redukowana do
możliwie najniższych wartości). Ponadto krzem ułatwia wytwarzanie struktury
polikrystalicznej - zorientowanej, która znacznie poprawia anizotropowe własności
magnetyczne blachy. W zależności od ilości krzemu wytwarza się blachy elektrotechniczne
izotropowe (tanie), gdzie zawartość krzemu jest zazwyczaj niewielka (mniej niż 1 %)
natomiast w blachach anizotropowych (droższych) najczęściej jest to około 3 %. Wzrost
zawartości krzemu w blachach elektrotechnicznych spowoduje nieznaczny spadek wartości
nasycenia magnetycznego B

s

ale znacznie wzrosta twardości i kruchość takiej blachy, co

wiąże się z trudnościami w obróbce mechanicznej. Duże wartości krzemu np. 6.5 % są
niepożądane z uwagi na niemal zerową magnetostrykcję blachy czyli wydłużenia blachy w
kierunku ustawiania się domen, co jest głównym powodem tzw. buczenia wszystkich
transformatorów szczególnie w energetyce.

Diamagnetyk – materiał w którym występuje zjawisko polegające na osłabianiu indukcji pola
magnetycznego, znajdującym się w zewnętrznym polu magnetycznym. Zjawisko odwrotne do
diamagnetyzmu to paramagnetyzm. Dla tych ciał względna przenikalność magnetyczna µ w
materiale jest niewiele mniejsza od jedności (przenikalność względna dla próżni =1). Wynika
stąd, że diamagnetyki osłabiają pole magnetyczne. Do diamagnetyków zalicza się: gazy
szlachetne, prawie wszystkie metale nie wykazujące własności para- lub ferromagnetycznych
(np: złoto, miedź, krzem, bizmut, cynk, magnez), ale również woda, fosfor, grafit. Zjawisko
diamagnetyzmu zostało opisano po raz pierwszy przez holenderskiego przyrodnika i lekarza
S.J. Burgmansa w 1778 roku. Nazwę "diamagnetyzm" rozpowszechnił Michael Faraday w
1846 r

Paramagnetyk – materiał w którym występuje zjawisko magnesowania się makroskopowego
(nieznacznym wzmacnianiu pola w materiale) w zewnętrznym polu magnetycznym w
kierunku zgodnym z kierunkiem przyłożonego zewnętrznego pola magnetycznego.
Paramagnetykiem są substancje o tzw. niesparowanych elektronach. Paramagnetyki mają
przenikalność magnetyczną µ niewiele większą od jedności, tj. (przenikalność względna dla
próżni =1). Przykłady paramagnetyków: Pt, O

2

, Al. Paramagnetyk jest słabo przyciągany

przez magnes, w odróżnieniu od ferromagnetyka. Wzmacnianie pola nazywa się podatnością.
Podatność magnetyczna zależy od temperatury, zjawisko to ujmuje prawo Curie. Niektóre
materiały paramagnetyczne poniżej pewnej temperatury stają się ferromagnetykami. W
niskich temperaturach lub w silnych polach magnetycznych dochodzi do uporządkowania
niemal wszystkich dipoli magnetycznych elektronów w wyniku czego dochodzi do nasycenia.

Ferromagnetyk – materiał w którym występuje zjawisko które wykazuje własności
magnetyczne silnie wzmacniające pole wewnątrz materiału. Materiał taki posiada obszary
stałego namagnesowania (tzw. uporządkowane domeny magnetyczne), wytwarzające wokół
siebie pole magnetyczne w danym kierunku podobnie jak małe magnesy. Ferromagnetykiem
są niektóre pierwiastki z okresu 4 (patrz tabela) żelazo, kobalt, nikiel i niektóre stopy oraz
metale z grupy żelaza i tzw. metali ziem rzadkich. Ferromagnetyki posiadają właściwości
magnetyczne poniżej temperatury Curie. W ferromagnetykach występuje zjawisko nasycenia
magnetycznego B

s

(patrz rys.) gdzie wszystkie elementarne drobiny czyli dipole magnetyczne

ustawiają się zgodnie z kierunkiem działania zewnętrznego pola magnetycznego.
Ferromagnetyki dzieli się na:

•

miękkie – po usunięciu zewnętrznego pola magnetycznego tracą namagnesowanie
zachowując jedynie namagnesowanie resztkowe B

r

, które jest znacznie mniejsze od

maksymalnego B

s

,

•

twarde - po usunięciu zewnętrznego pola magnetycznego zachowują stan
namagnesowania B

r

•

półtwarde - po usunięciu zewnętrznego pola magnetycznego zachowują stan
namagnesowania, ale jest on łatwy do usunięcia (nietrwały).

Magnesy trwałe stanowią ferromagnetyki twarde, które stosuje się do wyrobu elementów
wzbudzenia w maszynach elektrycznych. Natomiast stojan, wirnik, kolumny i jarzma
stanowią obwody magnetyczne maszyn elektrycznych prądu przemiennego.

Ferromagnetyki półtwarde używane są np. do zapisu danych cyfrowych: FDD, HDD.

Ważnym parametrem dla ferromagnetyków jest temperatura Curie Tc. Jest to taka
temperatura przy której µi =1 (przenikalność początkowa) materiał nie jest ferromagnetykiem

Ferrimagnetyk - materiał w którym występuje zjawisko polegająca na tym, że w
temperaturach poniżej tzw. temperatury Néela pojawia się spontaniczne antyrównoległe
uporządkowanie elementarnych momentów magnetycznych, które to momenty nie
kompensują się wzajemnie do zera w odróżnieniu od antyferromagnetyków.

C

zołowym

przedstawicielem Ferrimagnetyków jest magnetyt (Fe

3

O

4

), a są to związki o ogólnym wzorze

MeO · Fe

2

O

3

.

Antyferromagnetyk - materiał w którym występuje zjawisko polegająca na początkowym
wzroście z temperaturą, a po osiągnięciu punktu krytycznego (tzw. punktu Neela) podatność
magnetyczna maleje. Antyferromagnetykiem mogą być: Cr, Pt, Pd, Mn.

Związki żelaza używane w elektrotechnice przemysłowej

CZYSTE śELAZO charakteryzuje się dużą przewodnością magnetyczną i średnią
elektryczną materiału, dużą indukcją nasycenia do 2T i polem tzw. koercji około 1,2A/m.

•

Dla pól magnetycznych przemiennych charakteryzuje się dużymi stratami
wynikającymi z braku ograniczenia czystej powierzchni żelaza dla prądów wirowych.

•

Dla pól magnetycznych stałych charakteryzuje się bardzo dobrymi własnościami, stąd
wykorzystuje się czyste żelazo do budowy elementów magnetycznych maszyn prądu
stałego stojan, nabiegunniki ale również jako rdzenie przekaźników i
elektromagnesów pracujących przy prądach stałych.

Materiały magnetyczne wykonane z czystego żelaza stosuje się w elektrotechnice na elementy
zasilane bardzo niskimi częstotliwościami lub najczęściej w obwodach prądu stałego.

ś

ELAZO z DOMIESZKIAMI (Si - krzem, C - węgiel, Mg - magnez) charakteryzuje mniejsza

przewodność magnetyczna i elektryczna materiału niż w/w czystego żelaza, również mniejszą
indukcją nasycenia poniżej 2T, większe pole koercji (20 - 40A/m) wynikającą dodatkowych
domieszek.

•

Dla pól magnetycznych przemiennych charakteryzuje się znacznie mniejszymi stratami
wynikającymi z izolacyjnych własności domieszek szczególnie dodawanych przy
powierzchni np. blach co powoduje ograniczenie prądów wirowych. Stąd wykorzystuje
się żelazo z domieszkami (na powierzchni blach) w postaci blach (pakietu) do budowy
elementów magnetycznych rdzeni maszyn wirujących (stojan, wirnik) i transformatorów
(jarzma i kolumny).

•

Dla pól magnetycznych stałych charakteryzuje się również bardzo dobrymi własnościami,
jednak nieco gorszymi ze względu zmniejszenie udziału czystego żelaza przy tej samej
objętości co czyste żelazo. Stąd dla maszyn elektrycznych pracujących przy prądach
stałych wykorzystuje się raczej czyste żelazo, natomiast wykonuje się tylko niewielkie
wstawki z blach z domieszkami w miejscu gdzie obwód magnetyczny styka się ze
zmiennym polem magnetycznym.

W tabeli podano przykładowe parametry magnetyczne dla stopu żelaza z krzemem zwanej
często stalą krzemową.

Tabela 1. Parametry magnetyczne dla stopu żelaza z krzemem

Rodzaj

Zawartość Si

[%]

Indukcja max.

[T]

Względna

przenikalność

magnetyczna

[-]

Stratność

[W/kg]

1

2.1

14000

3

3

2.0

9000

2.3

Stal krzemowa

4.5

1.96

7000

1.7

Materiały magnetyczne wykonane z żelaza z domieszkami (Si, C, Mg) stosuje się na
częstotliwości nie przekraczające 1000Hz

STOPY śELAZA i NIKLU (30 – 80%), znane pod nazwą PERMALOJ, HYPERM,
SUPERMAALOJ, charakteryzują małe straty wynikające z prądów wirowych szczególnie dla
częstotliwości f > 10 kHz, indukcja nasycenia od 0,8 T do 1,5 T, pole koercji 0,2 – 50A/m,
duża przenikalność magnetyczna.

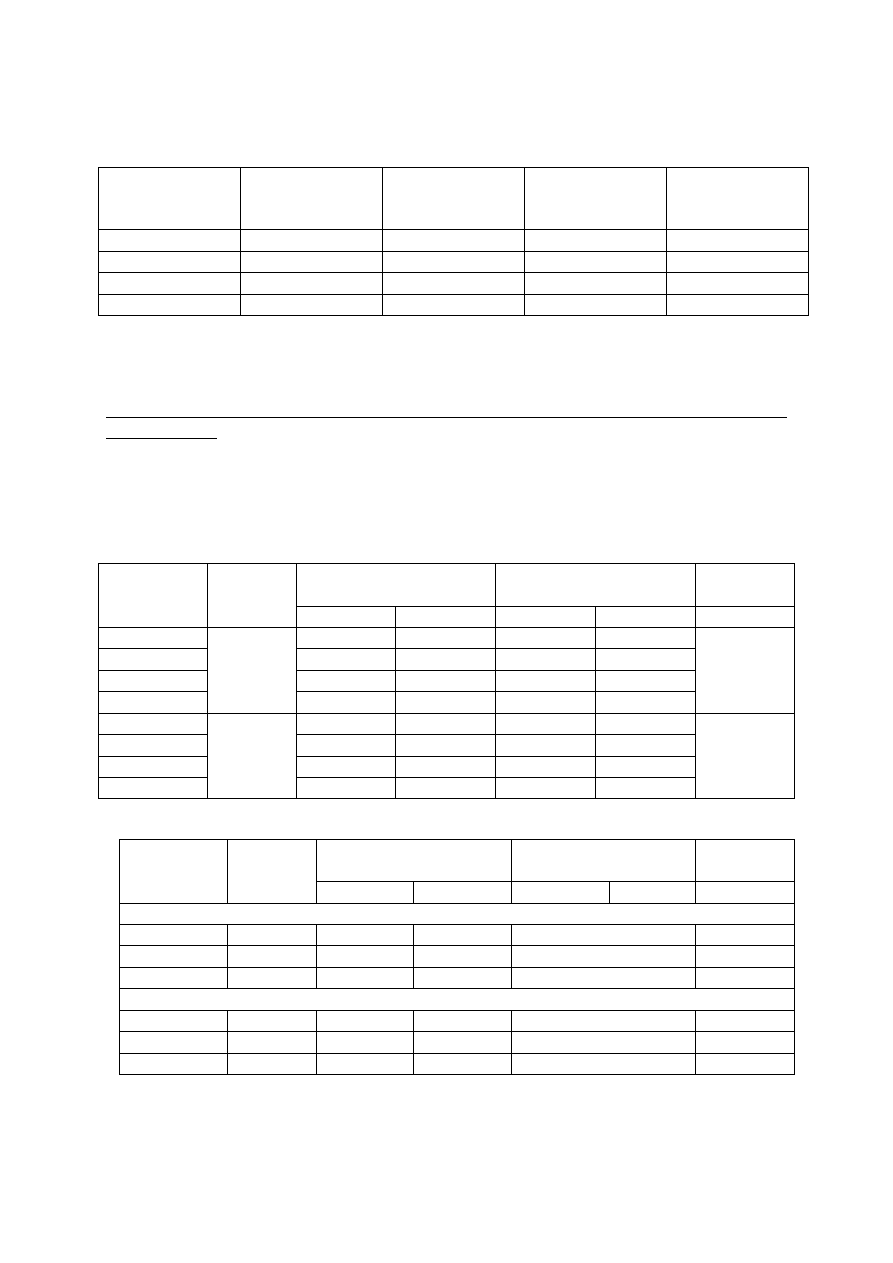
W tabeli 2 podano przykładowe parametry magnetyczne dla stopu żelaza z niklem

Tabela 2. Parametry magnetyczne dla stopu żelaza z niklem

Zawartość Ni

[%]

Indukcja max.

[T]

Względna

przenikalność

magnetyczna

Anizotropia

Nazwa stopu

36

1.3

14000

Nie

Hyperm

50

1.5

28000

Nie

Hyperm

70

0.8

120000

Tak

Permaloj

80

0.82

1000000

Tak

Suprmaloj

Materiały magnetyczne wykonane z stopów żelaza i niklu stosuje się w technice dużych
częstotliwości powyżej 100 kHz, jako: cienkie warstwy elementów pamięciowych, głowice
do zapisu magnetycznego, blachy transformatorowe, ekrany magnetyczne.

STOPY śELAZA I KOBALTU (35 – 50%) + V - Vanad, Cr - Chrom, znane pod nazwą
PERMENDUR charakteryzuje duża wartość indukcji nasycenia (2,4T), mała rezystywność,
duże straty z prądów wirowych, wykorzystuje się je w obwodach prądu stałego i
przemiennego jako: elementy konstrukcyjne maszyn elektrycznych wirujących i
transformatorów AC.

Tabela 3. Parametry wybranych gatunków blach produkowanych w Polsce

Stratność

[W/kg]

B[T] przy H=800A/m

k

Fe

Gatunek

Grubość

[mm]

1.5T

1T

2500

5000

min

EP 330-50A

3.3

1.35

1.49

1.60

EP 400-50A

4.0

1.70

1.51

1.61

EP 470-50A

4.7

2

1.52

1.62

EP 600-50A

0.5

6.0

2.60

1.55

1.65

0.97

EP 530-65A

5.3

2.30

1.52

1.62

EP 600-65A

6.0

2.60

1.54

1.64

EP 700-65A

7.0

3

1.55

1.65

EP 800-65A

0.65

8.0

3.60

1.58

1.68

0.97

Tabela 4. Blachy i taśmy stalowe magnetyczne o ziarnie zorientowanym wg PN-IEC 404-8-7:1996

Stratność

[W/kg]

B[T] przy H[A/m]

k

Fe

Gatunek

wg PN-IEC

404-4-7

1

Grubość

[mm]

1.5T

1.7T

2500

5000

min

Materiały o normalnych właściwościach

089-27-N5

0.27

0.89

1.40

1.75

0.95

097-30-N5

0.30

0.97

1.50

1.75

0.955

111-35-N5

0.35

1.11

1.65

1.75

0.96

Materiały o obniżonych stratnościach

130-27-S5

0.27

1.30

1.78

0.95

140-30-S5

0.30

1.40

1.78

0.955

155-35-S5

0.35

1.55

1.78

0.96

1

PN-IEC 404-8-7:1996 Materiały magnetyczne – Blachy i taśmy stalowe magnetyczne o

ziarnie zorientowanym

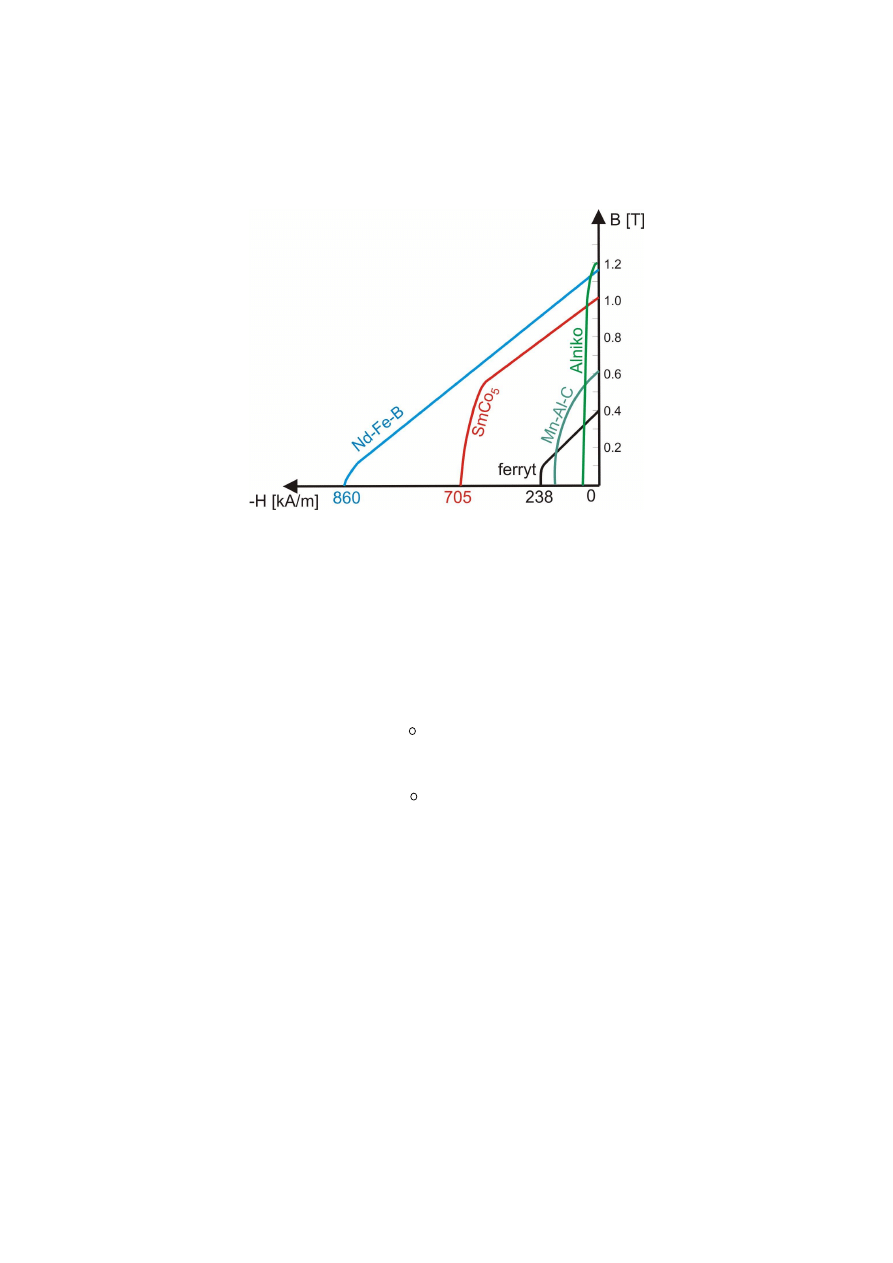
Charakterystyki odmagnesowania magnesów trwałych stosowanych w maszynach
elektrycznych przedstawiono na rys 10.

Rys.10. Charakterystyki odmagnesowania magnesów trwałych

1.4

Podstawowe prawa obwodu magnetycznego

Podstawą do obliczania obwodów magnetycznych są zależności

Θ

=

∫

C

Hdl

(4)

0

=

∫

S

BdS

(5)

Równanie (5) jest postacią całkową I-go równania Maxwella i znane jest pod nazwą prawa
przepływu Ampera. Natomiast równanie (6) wynika z bezźródłowości pola magnetycznego.
Całka liniowa wektora natężenia pola magnetycznego H po krzywej zamkniętej C jest równa
przepływowi prądu

Θ

przenikającemu przez powierzchnię ograniczoną tą linią. Przepływ

Θ

jest równy całkowitemu prądowi przenikającemu przez daną powierzchnię.

∫

=

Θ

S

JdS

(6)

W obwodach maszyn elektrycznych i transformatorów rozkład gęstości prądu jest nieciągły,
gdyż przepływ prądu jest wytworzony przez uzwojenia umieszczone w żłobkach maszyn
elektrycznych lub przez uzwojenia w postaci skupione (cewki) transformatorów lub
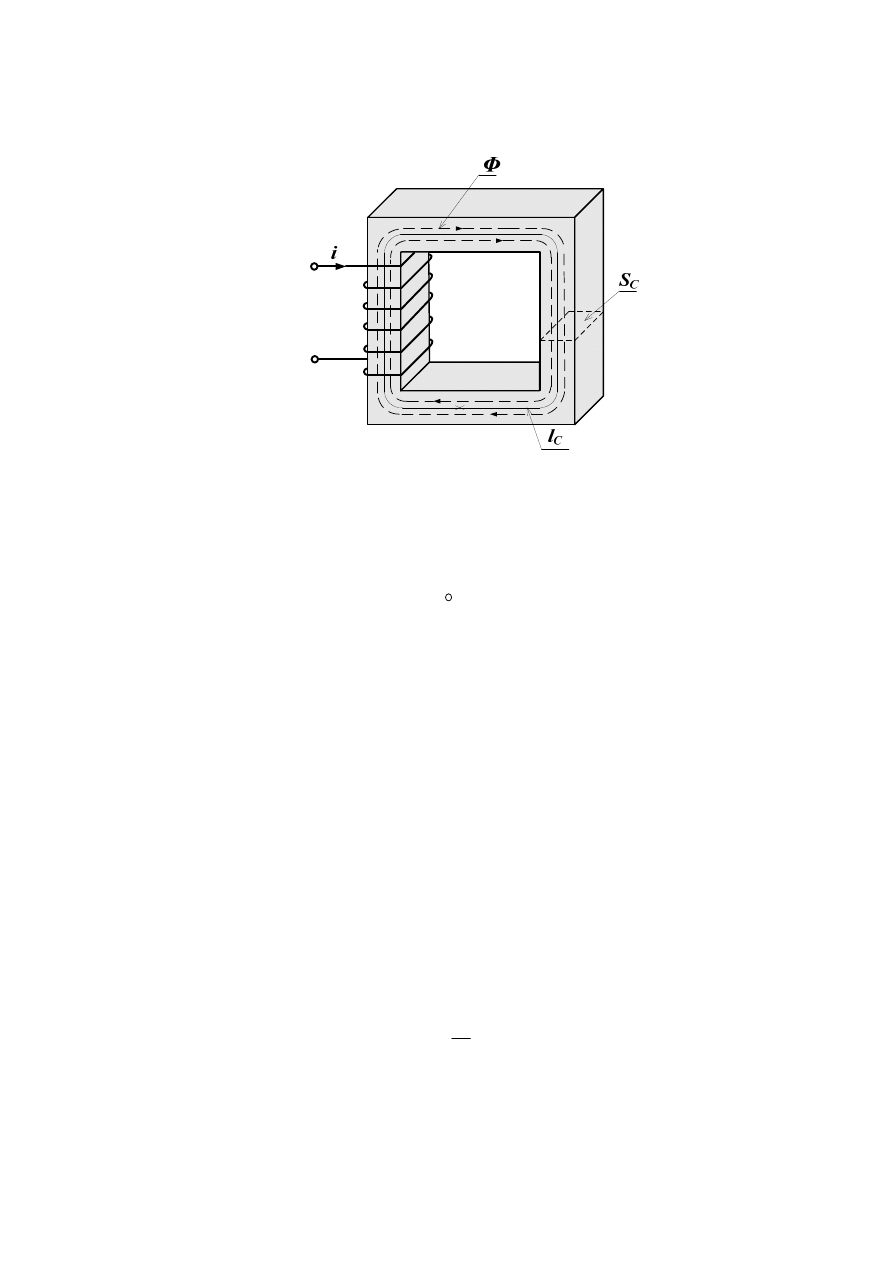
dławików. Jeżeli przez cewkę o liczbie zwojów N (rys.11) przepływa prąd i to przepływ
uzwojenia wynosi:

i

N

=

Θ

(7)

Rys.11. Obwód magnetyczny nierozgałęziony.

Całka liniowa po prawej stronie równania (4) nazywa się napięciem magnetycznym

U

m

∫

=

C

m

Hdl

U

(8)

Jeżeli obwód magnetyczny można podzielić na n odcinków i w każdym z tych odcinków
wektor natężenia pola magnetycznego posiada stałą wartość i jest styczny do tych odcinków,
to napięcie magnetyczne może być wyrażone zależnością

∑

=

=

n

k

k

k

m

l

H

U

1

(9)

Dla obwodu magnetycznego przedstawionego na rys. 11 równanie wektorowe (5) można
zapisać w postaci skalarnej

c

c

l

H

i

N

=

=

Θ

(10)

gdzie: H

c

– średnia wartość natężenia pola magnetycznego w rdzeniu, l

c

– średnia długość

obwodu magnetycznego

Ś

rednią wartość indukcji magnetycznej w rdzeniu obliczamy z zależności

c

c

S

B

Φ

=

(11)

Podstawiając zależność (1) do równania (2) oraz wykorzystując zależność (2), otrzymujemy

c

c

c

c

R

S

l

i

N

Φ

=

Φ

=

=

Θ

µ

(12)

gdzie: R

c

– reluktancja obwodu magnetycznego, przy czym

c

c

c

c

S

l

R

µ

=

(13)

Równanie można zapisać w postaci

c

c

R

ΘΛ

=

Θ

=

Φ

(14)

gdzie:

Λ

c

– permeancja (przewodność magnetyczna) obwodu magnetycznego, przy czym

c

c

c

c

l

S

µ

=

Λ

(15)

Równanie (3) przez analogię do obwodów elektrycznych jest nazywane prawem Ohma dla
obwodu magnetycznego, przy czym odpowiednikiem prądu elektrycznego jest strumienia
magnetyczny, odpowiednikiem napięcia elektrycznego jest przepływ zaś odpowiednikiem
rezystancji jest reluktancja obwodu magnetycznego.
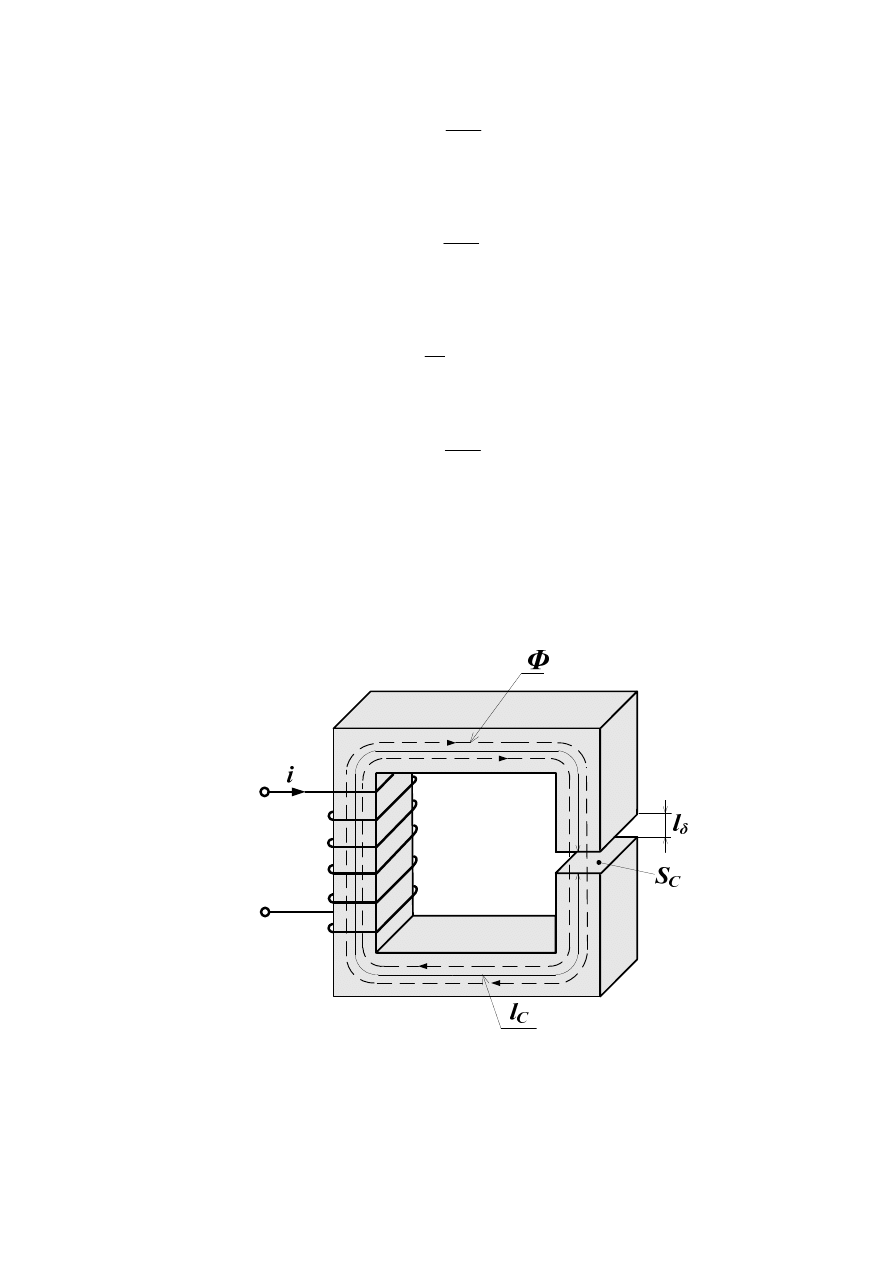
Obwody magnetyczne maszyn elektrycznych zawierają szczeliny powietrzne. Na rys.12
przedstawiono obwód magnetyczny ze szczeliną powietrzną.

Rys.12. Obwód magnetyczny nierozgałęziony ze szczeliną powietrzną.

Zakładając, że przez rdzeń o długości l

c

i szczelinę powietrzną o długości l

δ

przepływa ten

sam strumień

Φ

, wartości indukcji magnetycznej wyniosą odpowiednio

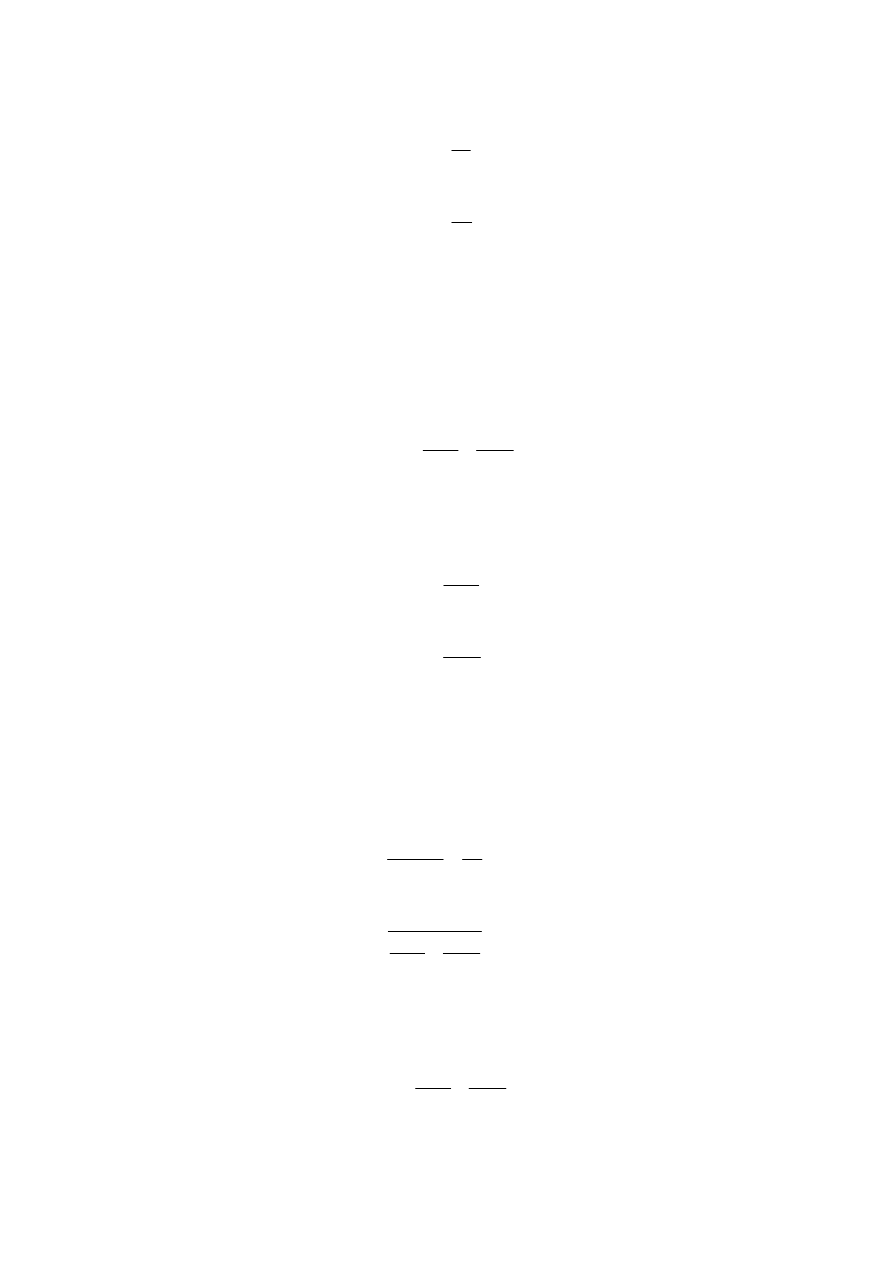
c

c

S

B

Φ

=

(16)

δ

δ

S

B

Φ

=

(17)

Stosując prawo przepływu do obwodu magnetycznego, otrzymujemy

δ

δ

l

H

l

H

c

c

+

=

Θ

(18)

Podstawiając zależności (16) i (17) do równania (18) oraz wykorzystując zależność ()
otrzymujemy













+

Φ

=

Θ

δ

δ

µ

µ

S

l

S

l

c

c

c

0

(19)

Wprowadzając oznaczenia

c

c

c

c

S

l

R

µ

=

(20)

δ

δ

δ

µ

S

l

R

0

=

(21)

zależność (19) przyjmie postać

)

(

δ

R

R

c

+

Φ

=

Θ

(22)

stąd

e

e

c

R

R

R

ΘΛ

=

Θ

=

+

Θ

=

Φ

δ

(23)

lub

e

c

c

c

S

l

S

l

ΘΛ

=

+

Θ

=

Φ

δ

δ

µ

µ

0

(24)

gdzie: R

e

– zastępcza reluktancja obwodu magnetycznego,

Λ

e

– zastępcza permeancja

obwodu magnetycznego, przy czym

δ

δ

µ

µ

S

l

S

l

R

c

c

c

e

0

+

=

(25)

δ

δ

µ

µ

S

l

S

l

c

c

c

e

0

1

+

=

Λ

(26)

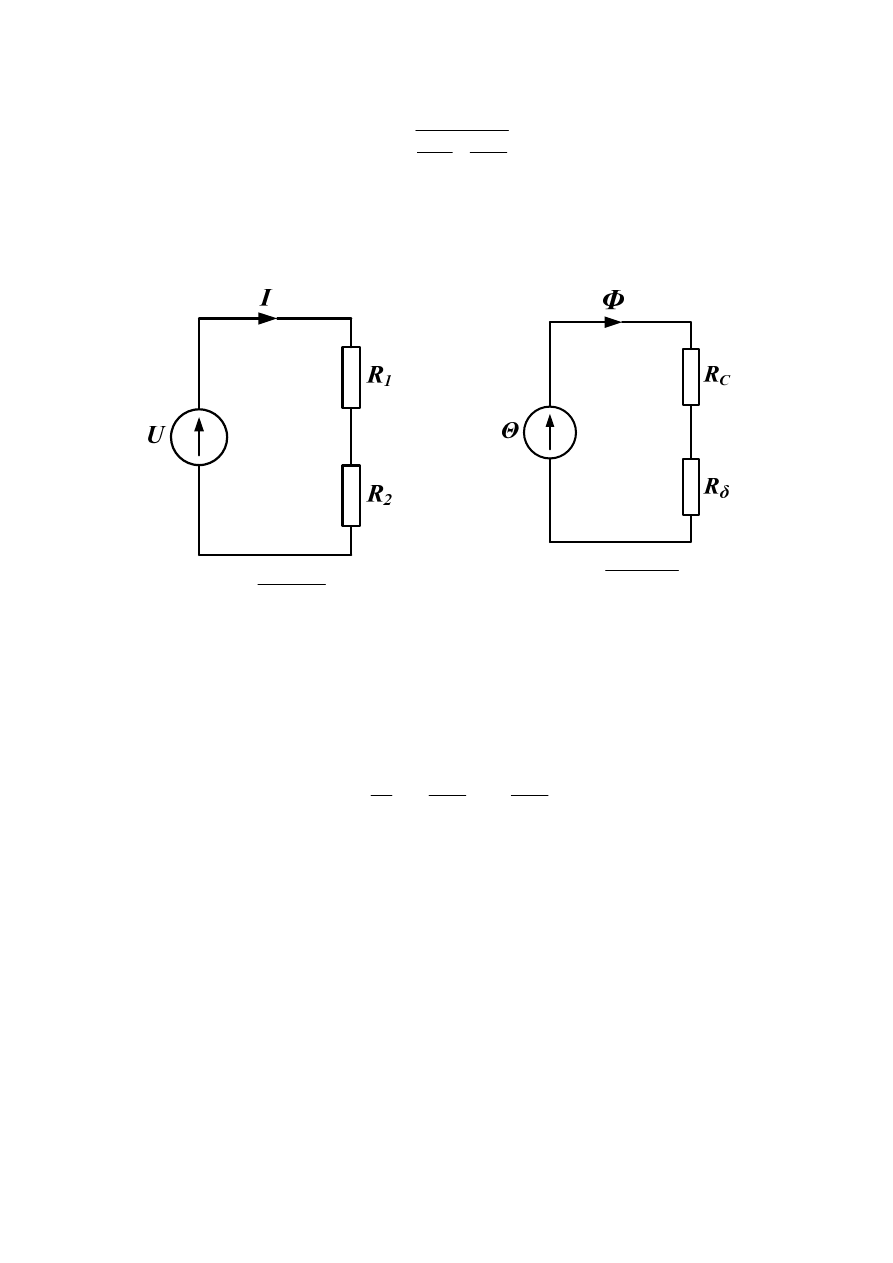
Korzystając z analogii do obwodu elektrycznego, zależność (22) można przedstawić w
postaci schematu elektrycznego (rys.13)

2

1

R

R

U

I

+

=

δ

C

R

R

Φ

Θ

+

=

Rys. 13. Analogia pomiędzy obwodem elektrycznym a magnetycznym: a) schemat obwodu

elektrycznego, b) schemat obwodu magnetycznego

.

Jeżeli

µ

c

S

c

/l

c

>>

µ

0

S

δ

/l

δ

, co jest często słuszne w obwodach maszyn elektrycznych i

transformatorów, równanie (24) można napisać w postaci

δ

δ

δ

δ

δ

µ

µ

l

S

i

N

l

S

R

0

0

=

Θ

=

Θ

≈

Φ

(27)

Obwody magnetyczne transformatorów są obwodami rozgałęzionymi (rys poniżej).
W poszczególnych gałęziach obwodów rozgałęzionych występują na ogół różne strumienie.
Między tymi strumieniami zachodzą zależności wynikające z warunku bezźródłowości pola
magnetycznego danego równaniem (5)

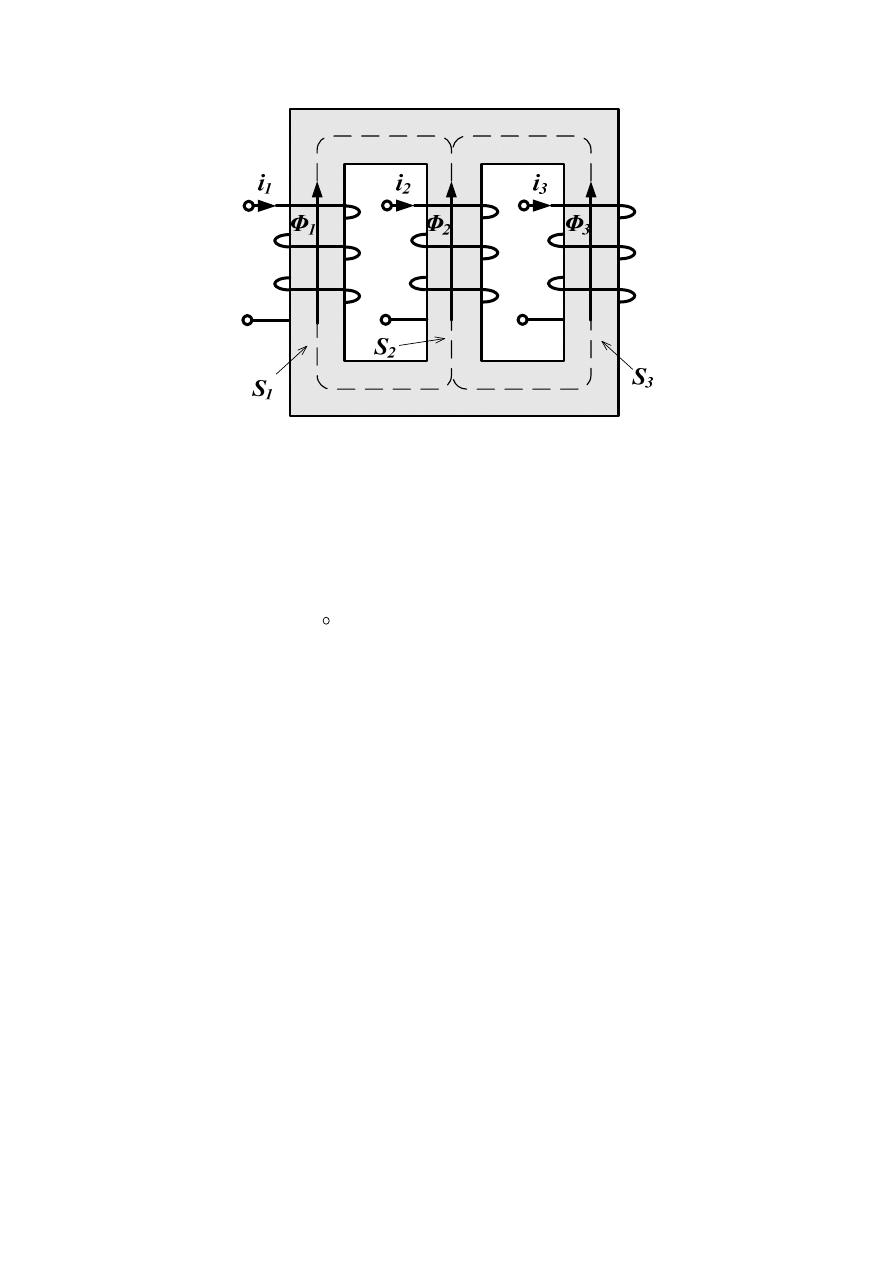
Rys. 14. Obwód magnetyczny rozgałęziony.

Zamkniętą powierzchnię dobiera się tak, aby przecinała ona tylko te gałęzie obwodu
magnetycznego, które połączone są z rozpatrywanym węzłem. Zakładając, że strumień
magnetyczny przechodzi wyłącznie przez rdzenie i szczeliny robocze obwodu (rys.14), a
indukcja B poza rdzeniem jest znikomo mała, można przeprowadzić całkowanie tylko po
powierzchniach przekrojów rdzeni lub szczelin roboczych. Dla trzech gałęzi o przekrojach S

1

,

S

2

, S

3

otrzymuje się

∫

∫

∫

∫

=

+

+

=

1

1

1

0

S

S

S

S

BdS

BdS

BdS

BdS

(28)

Ponieważ poszczególne całki we wzorze przedstawiają strumienie magnetyczne

Φ

1

,

Φ

2

,

Φ

3

,

wzór ten można przedstawić w ogólnej postaci

∑

=

=

Φ

n

k

k

1

0

(29)

Wzór ten przez analogię do obwodu elektrycznego nosi nazwę pierwszego prawa Kirchhoffa
dla obwodu magnetycznego

1.5

Indukcyjność własna i wzajemna

W rdzeniach ferromagnetycznych strumień magnetyczny wytworzony przez uzwojenie
zamyka się głównie w rdzeniu, gdyż przenikalność magnetyczna rdzenia jest dużo większa od
przenikalności powietrza. Jednak pewna część strumienia wychodzi na zewnątrz rdzenia i
zamyka się w powietrzu tworząc strumień rozproszenia. Na rys.15 przedstawiono obwód
magnetyczny składający się z rdzenia ferromagnetycznego oraz szczeliny powietrznej.

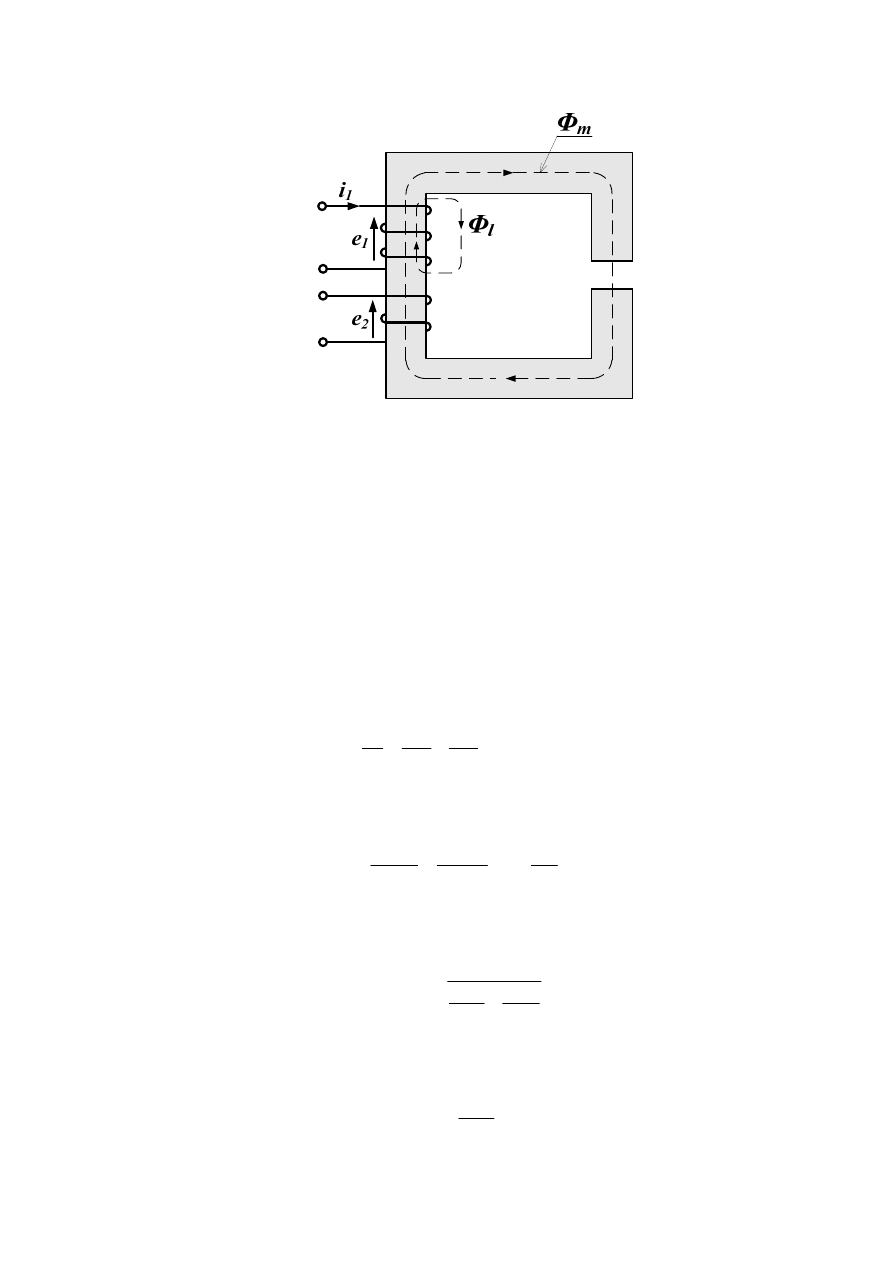
Rys. 15. Obwód magnetyczny ze szczeliną powietrzną- indukcyjność własna i wzajemna

uzwojeń.

Na rdzeniu nawinięte są dwa uzwojenia: pierwotne (wzbudzające) o liczbie zwojów N

1

i

wtórne o liczbie zwojów N

2

. Strumień

Φ

1

wytworzony przez uzwojenie wzbudzające dzieli

się na strumień główny

Φ

m

zamykający się w rdzeniu i strumień rozproszenia

Φ

σ

zamykający

się poza rdzeniem (w powietrzu).

σ

Φ

+

Φ

=

Φ

m

1

(30)

Strumień sprzężony z uzwojeniem pierwotnym wynosi

σ

σ

1

1

1

1

1

1

1

1

Ψ

+

Ψ

=

Φ

+

Φ

=

Φ

=

Ψ

m

m

N

N

N

(31)

Natomiast indukcyjność własną uzwojenia pierwotnego wyznaczamy z zależności

σ

σ

1

1

1

1

1

1

1

1

1

L

L

i

i

i

L

m

m

+

=

Ψ

+

Ψ

=

Ψ

=

(32)

gdzie: L

1

σ

- indukcyjność rozproszenia uzwojenia pierwotnego, L

1m

– indukcyjność główna

(magnesowania) uzwojenia pierwotnego, przy czym

1

2

1

1

1

2

1

1

1

1

Θ

Φ

=

Φ

=

Φ

=

m

m

m

m

N

i

N

N

i

N

L

(33)

Uwzględniając zależności (23) otrzymujemy

δ

δ

µ

µ

S

l

S

l

N

N

L

c

c

c

e

m

0

2

1

2

1

1

+

=

Λ

=

(34)

dla l

δ

= 0, indukcyjność magnesowania wynosi

c

c

c

m

l

S

N

L

µ

2

1

1

=

(35)

natomiast dla

µ

c

S

c

/l

c

>>

µ

0

S

δ

/l

δ

, zależność na indukcyjność magnesowania upraszcza się do

postaci

δ

µ

l

S

N

L

c

m

0

2

1

1

=

(36)

Z uzwojeniem wtórnym sprzęga się strumień główny

Φ

m

i strumień skojarzony z uzwojeniem

wtórnym wyniesie

m

N

Φ

=

Ψ

2

2

(37)

Natomiast indukcyjność wzajemną między uzwojeniem pierwotnym a wtórnym określamy z
zależności

1

2

1

1

1

2

1

1

2

1

2

21

Θ

Φ

=

Φ

=

Φ

=

Ψ

=

m

m

m

N

N

i

N

N

N

i

N

i

L

(38)

m

m

m

L

N

N

N

N

N

N

N

L

1

1

2

1

2

1

1

2

1

2

1

21

=

Θ

Φ

=

Θ

Φ

=

(39)

Uwzględniając zależność (34) otrzymujemy

δ

δ

µ

µ

S

l

S

l

N

N

N

N

L

c

c

c

e

0

2

1

2

1

21

+

=

Λ

=

(40)

dla l

δ

= 0 oraz

µ

c

S

c

/l

c

>>

µ

0

S

δ

/l

δ

, zależność na indukcyjność wzajemną wyniesie

odpowiednio

c

c

c

l

S

N

N

L

µ

2

1

21

=

(41)

natomiast dla

µ

c

S

c

/l

c

>>

µ

0

S

δ

/l

δ

, zależność na indukcyjność magnesowania upraszcza się do

postaci

δ

µ

l

S

N

N

L

c

0

2

1

21

=

(42)

1.6 Indukcja elektromagnetyczna

Zjawisko indukowania się napięcia w obwodzie elektrycznym pod wpływem zmian
strumienia objętego przez ten obwód nazywa się indukcją elektromagnetyczną. Wartość tego
napięcia określamy na podstawie prawa Faraday’a.

∫

∫

−

=

=

S

C

BdS

dt

d

Edl

e

(43)

Uwzględniając zależność () otrzymujemy

dt

d

Edl

e

C

Φ

−

=

=

∫

(44)

przym znak (

−

) odnosi się do obiegu drogi całkowania zgodnie z regułą śruby prawoskrętnej

w stosunku do strumienia magnetycznego.

W przypadku szczególnym, w którym ten sam strumień magnetyczny sprzęga się z N
zwojami cewki, zależność możemy napisać w postaci

dt

d

dt

d

N

e

Ψ

±

=

Φ

±

=

(45)

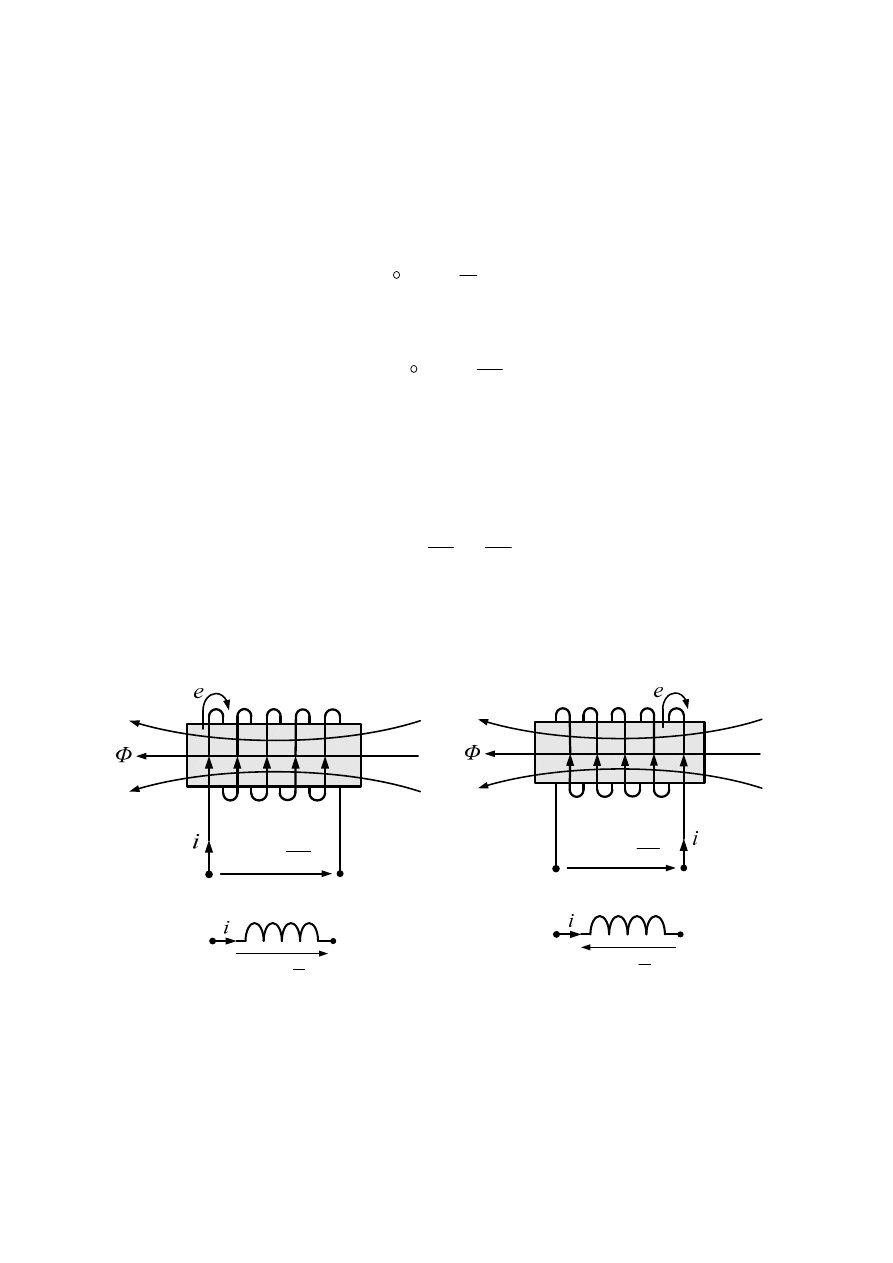
We wzorze (45) należy brać znak (+) jeżeli strzałka e jest przyjęta niezgodnie z regułą śruby
prawoskrętnej w stosunku do strumienia, natomiast znak (

−

) należy brać wtedy gdy strzałka e

jest przyjęta zgodnie z regułą śruby prawoskrętnej w stosunku do strumienia (rys.16).
a)

dt

dΦ

z

e

−

=

dt

di

L

u

−

=

b)

dt

dΦ

z

e

+

=

dt

di

L

u

=

Rys. 16. Sposoby strzałkowania napięć indukowanych w cewce.

Dla układu elektromagnetycznego przedstawionego na rys. 17 napięcia indukowane w
poszczególnych uzwojeniach wyniosą

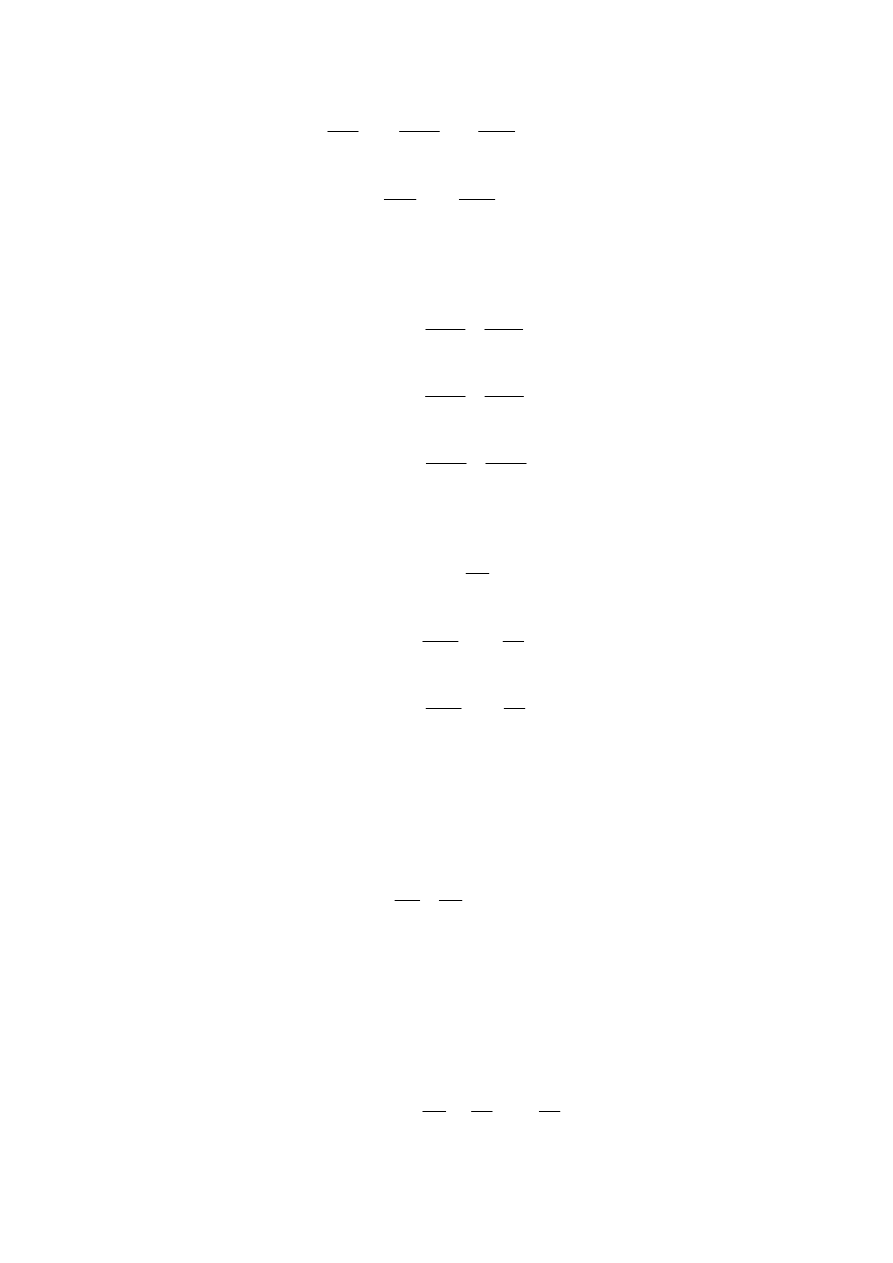
m

m

e

e

dt

d

N

dt

d

N

dt

d

e

1

1

1

1

1

1

1

+

=

Φ

+

Φ

=

Ψ

=

σ

σ

(46)

m

m

e

dt

d

N

dt

d

e

2

2

2

2

=

Φ

=

Ψ

=

(47)

gdzie:

Ψ

1

,

Ψ

2

– strumień skojarzony z uzwojeniem pierwotnym i wtórnym, Φ

m

, Φ

1σ

–

strumień magnesowania oraz strumień rozproszenia, przy czym

dt

d

dt

d

N

e

σ

σ

σ

1

1

1

1

Ψ

=

Φ

=

(48)

dt

d

dt

d

N

e

m

m

m

1

1

1

1

Ψ

=

Φ

=

(49)

dt

d

dt

d

N

e

m

m

m

2

1

2

2

Ψ

=

Φ

=

(50)

Uwzględniając zależność (32) otrzymujemy

dt

di

L

e

1

1

1

σ

σ

=

(51)

dt

di

L

dt

d

N

e

m

m

m

1

1

1

1

=

Φ

=

(52)

dt

di

L

dt

d

N

e

m

m

1

21

2

2

=

Φ

=

(53)

gdzie: L

1σ

– indukcyjność rozproszenia uzwojenia pierwotnego, L

1m

– indukcyjność główna

(magnesowania) uzwojenia pierwotnego, L

21

– indukcyjność wzajemna między uzwojeniem

pierwotnym a uzwojeniem wtórnym.
Stosunek napięć indukowanych w uzwojeniu pierwotnym i wtórnym przez strumień główny
Φ

m

nazywamy przekładnią zwojową

ϑ

ϑ

=

=

2

1

2

1

N

N

e

e

m

m

(54)

stąd

'

2

2

1

m

m

m

e

e

e

=

=

ϑ

(55)

gdzie:

'

2m

e

- napięcie indukowane w uzwojeniu wtórnym sprowadzone na stronę uzwojenia

pierwotnego, przy czym

dt

di

L

dt

di

L

N

N

e

e

m

m

m

1

'

2

1

12

2

1

2

'

2

=

=

=

ϑ

(56)

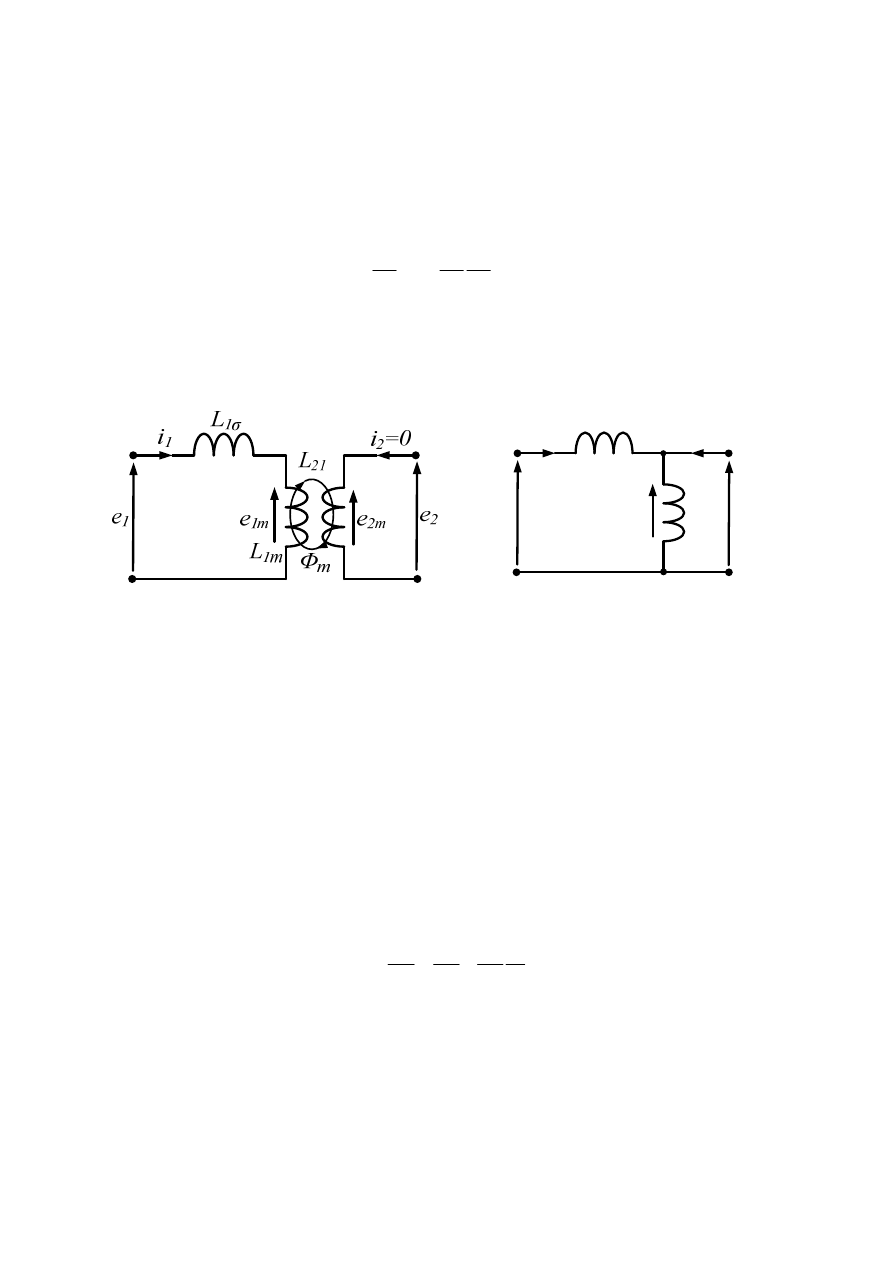
gdzie:

'

2m

L

- indukcyjność magnesowania uzwojenia wtórnego sprowadzona na stronę

uzwojenia pierwotnego.

Uwzględniając zależność (39) indukcyjność magnesowania

'

2m

L

można zapisać w postaci

m

m

m

L

L

N

N

N

N

L

N

N

L

1

1

1

2

2

1

12

2

1

'

2

=

=

=

(57)

Zależnością (46 i 47) odpowiada schemat elektryczny:

a)

b)

i

1

i

2

=0

e

1

e

2

L

1

σ

e

1m

=e

’

2m

Rys 17. Schemat elektryczny obwodu magnetycznego przedstawionego na rys.15:

a)w

układzie rzeczywistym, b) w układzie sprowadzonym.

Uwzględniając zależności (56 i 57) schemat zastępczy (rys. 17a) można przedstawić w
układzie sprowadzonym (rys. 17b).



Przyczyną indukowania się napięcia może być zmiana strumienia magnetycznego w czasie
lub ruch względny przewodnika względem stałego pola. W przypadku ogólnym strumień

Ψ

skojarzony z uzwojeniem może być funkcją czasu t i położenia x uzwojenia względem pola,
czyli

Ψ

=

Ψ

(x,t) oraz x=x(t).

W tych warunkach (rys.18) prawo indukcji elektromagnetycznej można zapisać w postaci

t

x

x

t

dt

d

e

∂

∂

∂

Ψ

∂

+

∂

Ψ

∂

=

Ψ

=

(58)

Z równania (58), wynika że napięcie w przewodniku może się indukować w następujących
przypadkach:

•

Nieruchomy przewodnik znajduje się w zmiennym polu magnetycznym,

Ψ

=

Ψ

(t)=var.,

v=dx/dt=0, wówczas wzór (58) przyjmie postać

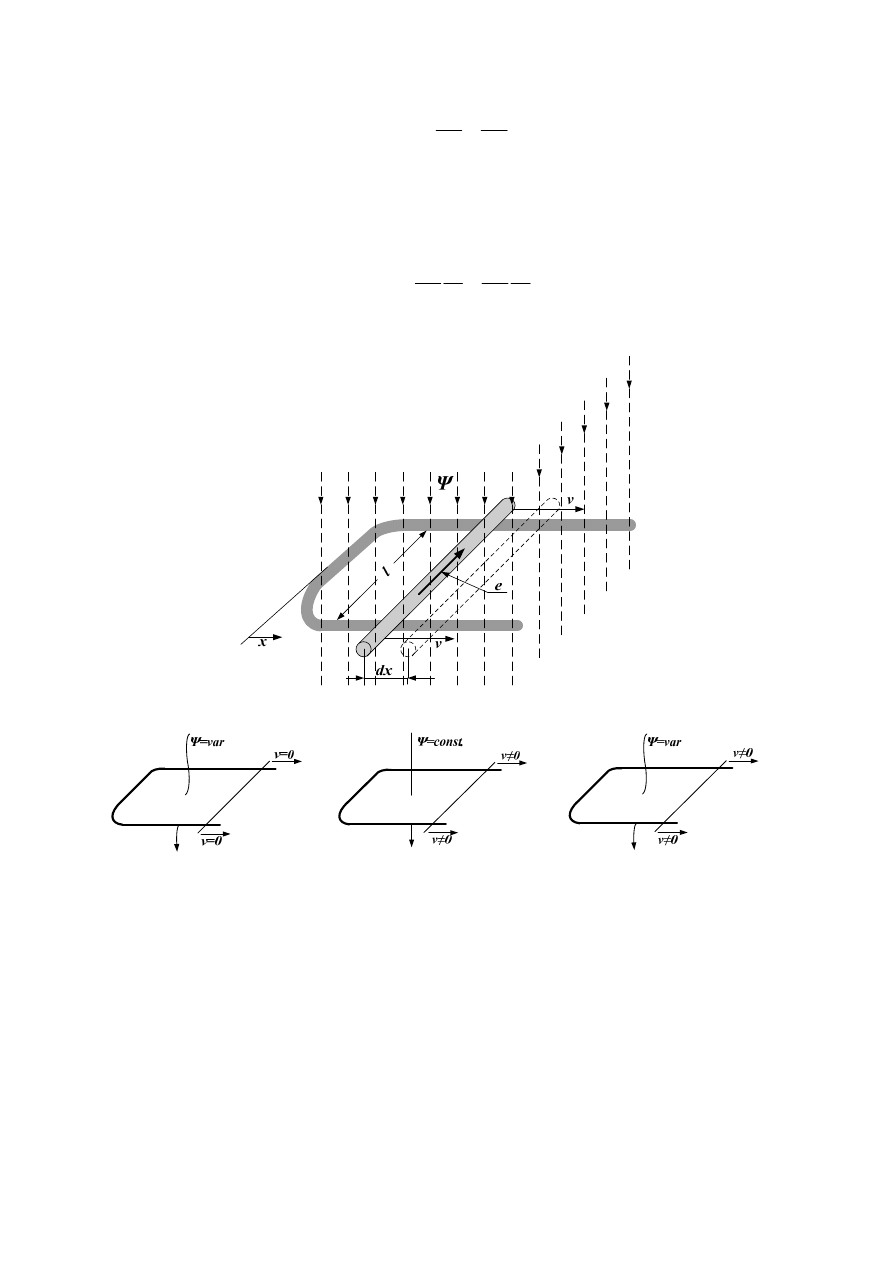
dt

d

t

e

e

t

Ψ

=

∂

Ψ

∂

=

=

(59)

Napięcie indukowane w wyniku zmiennego pola magnetycznego nazywamy napięciem
transformacji e

t

.

•

Ruchomy przewodnik przemieszcza się w stałym polu magnetycznym,

Ψ

=const.,

v=dx/dt

≠

0, wówczas

dt

dx

dx

d

t

x

x

e

e

r

Ψ

=

∂

∂

∂

Ψ

∂

=

=

(60)

a)

b)

c)

d)

Rys. 18. Zjawisko indukcji elektromagnetycznej: a) model fizyczny, b)napięcie indukowane

transformacji, c) napięcie indukowane rotacji, d)napięcie indukowane transformacji i rotacji.

Zmiana strumienia d

ψ

sprzężonego ze zwojem o długości l (rys.19), poruszającym się w

stałym polu magnetycznym wynosi

Bldx

d

=

Ψ

(61)

podstawiając powyższą zależność do wzoru (60) otrzymujemy

Blv

e

e

r

=

=

(62)

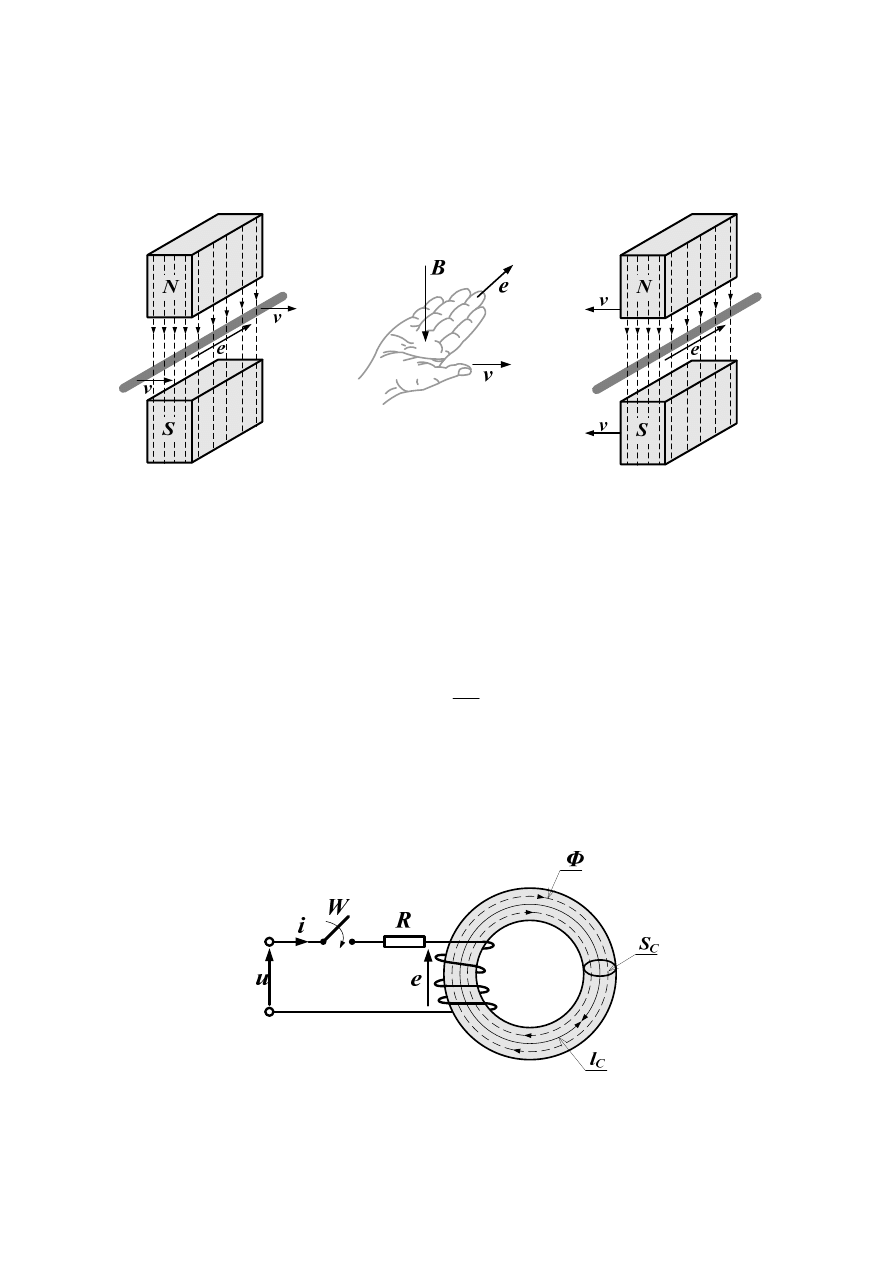
Napięcie indukowane w wyniku ruchu przewodnika w polu magnetycznym nazywamy
napięciem rotacji e

r

. Do wyznaczania zwrotu indukowanego napięcia stosujemy regułę

prawej dłoni (rys.19)

a)

b)

Rys.19. Zjawisko indukcji elektromagnetycznej – reguła prawej dłoni

Reguła ta brzmi: jeżeli prawą dłoń ułożymy tak, aby linie strumienia magnetycznego były
zwrócone ku dłoni, a odchylony duży palec (kciuk) wskazywał kierunek prędkości względnej
przewodu, to pozostałe cztery palce ułożone wzdłuż przewodu, wskażą zwrot indukowanego
napięcia.

W ogólnym przypadku przewodnik może poruszać się w zmienym polu magnetycznym,

ψ

=var, v=var., wówczas napięcie indukowane można zapisać w ogólnej postaci

Blv

dt

d

e

e

e

r

t

+

Ψ

=

+

=

(63)

1.7

Energia pola magnetycznego

Rozpatrzone zostaną zjawiska energetyczne w cewce zasilanej z idealnego źródła napięcia
stałego u (rys.20). Po zamknięciu wyłącznika W w obwodzie zaczyna płynąć prąd i a w
cewce indukuje się napięcie e.

Rys.20. Schemat zastępczy obwodu elektromagnetycznego cewki zasilanej ze źródła napięcia

stałego.

Dla rozpatrywanego obwodu obowiązuje równanie napięciowe

e

Ri

u

+

=

(64)

Mnożąc obustronnie równanie (64) przez idt i wykonując całkowanie w czasie od 0 do t,
otrzymujemy bilans energii

∫

∫

∫

+

=

t

t

t

eidt

dt

Ri

uidt

0

0

2

0

(65)

Pierwszy składnik równania (65) przedstawia energię traconą na rezystancji R, natomiast
drugi składnik przedstawia energię W zgromadzoną w cewce

∫

=

t

eidt

W

0

(66)

Podstawiając równanie (65) do równania (66), wyrażenie na energię pola magnetycznego
można zapisać w postaci

∫

Ψ

Ψ

=

0

id

W

(67)

Podstawiając w równaniu za d

Ψ

=Ldi, otrzymujemy wyrażenie na koenergię pola

magnetycznego

∫

∫

Ψ

=

=

i

i

c

di

Lidi

W

0

0

(68)

Dla układów liniowych indukcyjność jest stała i nie zależy od przepływającego przez nią
prądu, czyli L=const. Wówczas wyrażenie na energię i koenergię pola magnetycznego
przyjmie postać

L

d

L

id

W

2

1

2

0

0

Ψ

=

Ψ

Ψ

=

Ψ

=

∫

∫

Ψ

Ψ

(69)

2

0

2

1

Li

Lidi

W

i

c

=

=

∫

(70)

Ze wzorów (69) i (70) wynika, że dla układów liniowych energia magnetyczna jest równa
koenergii magnetycznej. Graficzną interpretację energii oraz koenergii magnetycznej
przedstawiono na rys 21.

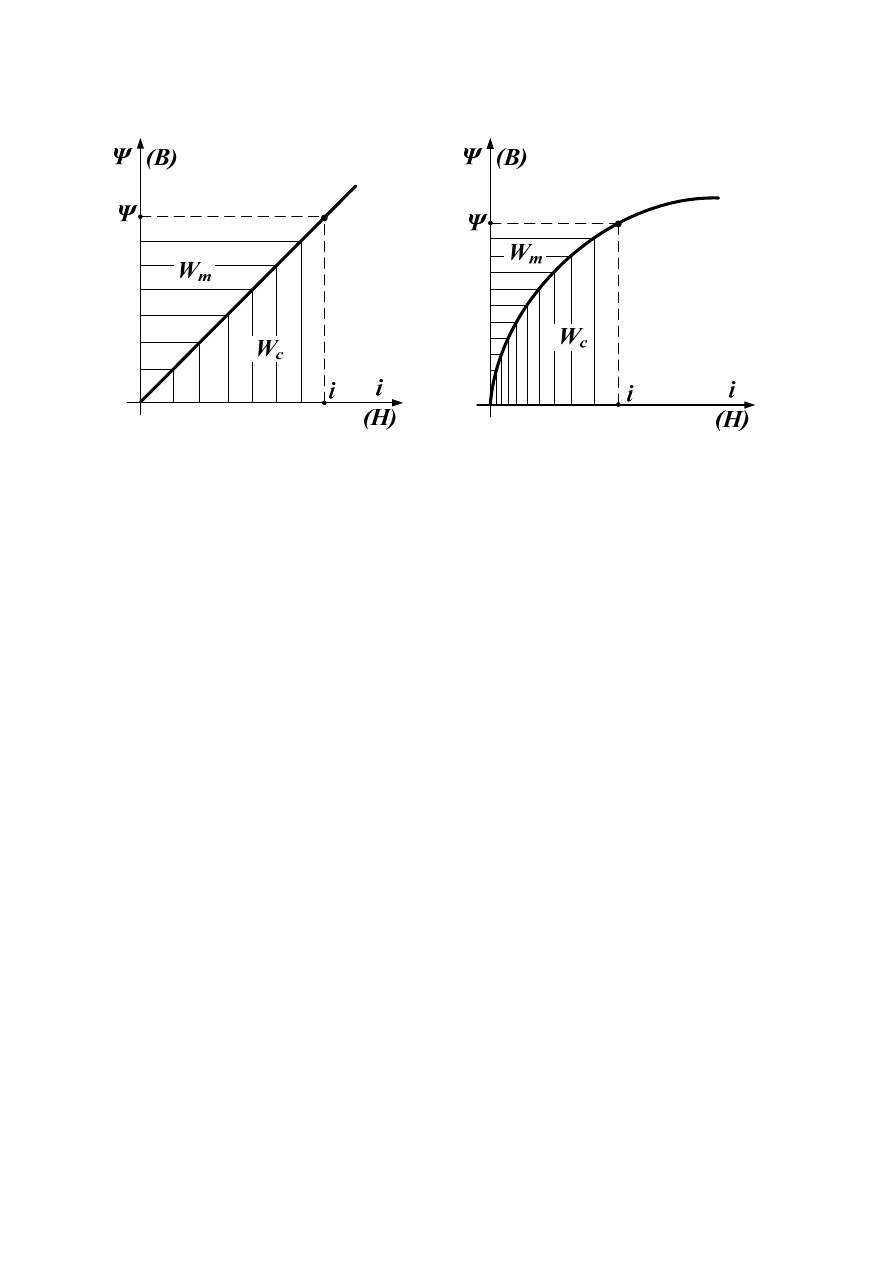
a)

b)

Rys. 21. Energia i koenergia magnetyczna zawarta w polu magnetycznym: a) w środowisku liniowym,

b) nieliniowym.

LITERATURA

[1]

Bajorek Z.: Maszyny elektryczne

, WNT, Warszawa 1983

[2]

Chapman S.J.: Electric machinery fundamentals, Third Edition, McGraw-Hill Book

Company, Singapore 1999.

[3]

Fitzgerald A. E., Kingsley Ch. Jr., Stephen D. Umans S.D.: Electric machinery, Sixth

edition, McGraw-Hill, USA, New York, 2003.

[4]

Gieras J.F., Wing M.: Permanent magnet motor technology. Design and Application,

Second Edition, Marcel Dekker Inc., New York 2002.

[5]

Krause P.C.: Analysis of electric machinery, McGraw-Hill Book Company, New York

1986.

[6]

Kurdziel R.: Podstawy elektrotechniki, WNT, Warszawa 1975

[7]

Latek W.: Teoria maszyn elektrycznych, WNT, Warszawa 1987

[8]

Plamitzer A.: Maszyny elektryczne

, WNT, Warszawa 1982