Tylko dla celów dydaktycznych

ĆWICZENIE

pt.

KONCENTRACJA NAPRĘśEŃ W ELEMENTACH

KONSTRUKCJI STALOWEJ

Instrukcja

Opracował:

mgr inż. Konstanty Chochoł

mgr inż. Łukasz Wojsław

INSTYTUT MASZYN ROBOCZYCH CIĘśKICH

POLITECHNIKA WARSZAWSKA

Wrzesień 2003

2

Spis treści

1.

Podstawy teorii koncentracji naprężeń

................................................................. 1

1.1

Przyczyny powstawania koncentracji naprężeń ............................................................. 1

1.2

Podstawowe rodzaje koncentracji naprężeń ................................................................... 2

1.3

Określenie wielkości koncentracji naprężeń .................................................................. 2

2.

Metody stosowane w badaniach koncentracji naprężeń ................................ 3

2.1

Metoda kruchych pokryć ................................................................................................ 3

2.2

Badania modelowe ......................................................................................................... 4

2.3

Metoda elastooptyczna ................................................................................................... 4

2.4

Metoda tensometryczna.................................................................................................. 4

2.4.1

Budowa tensometrów rezystancyjnych .......................................................................................4

2.4.2

Budowa tensometrów rezystancyjnych .......................................................................................6

2.5

Metody numeryczne ....................................................................................................... 7

2.5.1

Metoda elementów skończonych (MES).....................................................................................7

2.5.2

Metoda elementów brzegowych (MEB

).............................................................................. 7

3.

Wykonanie ćwiczenia......................................................................................... 8

3.1

Teoretyczne określenie wielkości naprężeń ................................................................... 8

3.2

Doświadczalne określenie wielkości naprężeń ............................................................ 10

3.3

Stanowisko badawcze................................................................................................... 11

3.3.1

Element badany .........................................................................................................................12

3.3.1.1 Parametry belki dwuteowej stanowiącej element badany

...............................................................12

3.3.1.2

Rozkład tensometrów

...........................................................................................................................12

3.3.1.3

Zastosowane czujniki

...........................................................................................................................12

3.3.2

Układ napinający .......................................................................................................................12

3.4

Aparatura pomiarowa ................................................................................................... 15

3

Koncentracja naprężeń w elementach konstrukcji stalowej

Celem ćwiczenia jest zapoznanie się ze zjawiskiem koncentracji naprężeń w

elementach konstrukcyjnych, przyczynami występowania koncentracji, podstawami
teoretycznymi oraz praktycznymi metodami określania miejsc i wielkości występujących
naprężeń.

1.

Podstawy teorii koncentracji naprężeń

1.1

Przyczyny powstawania koncentracji naprężeń

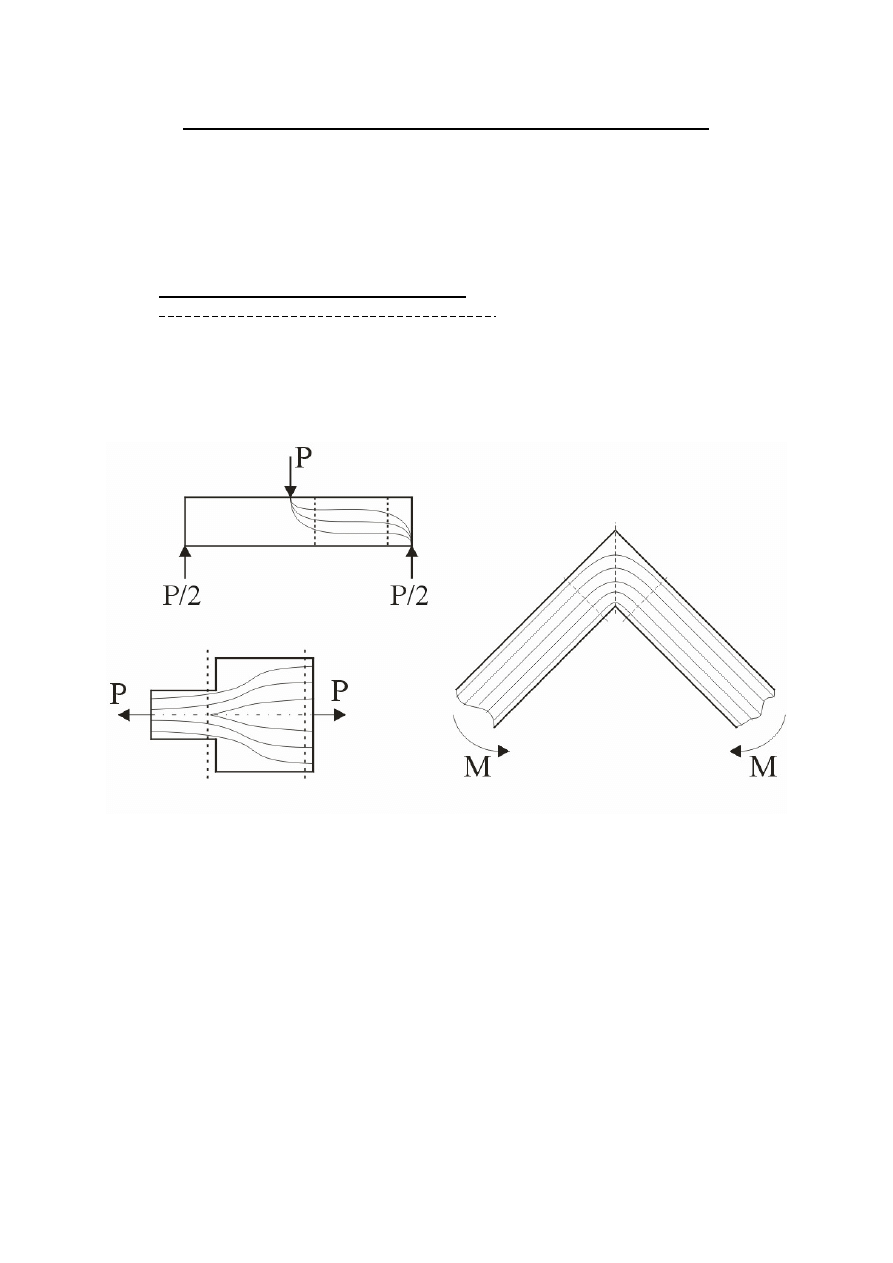
W teorii koncentracji naprężeń posługujemy się pojęciami: „linia sił” i „potok sił”. Są

to umowne linie poprowadzone wewnątrz ciała sprężystego w przewidywanym kierunku
przekazywania oddziaływania sił (rys. 1). Przy wejściu i wyjściu z ciała linie sił odpowiadają
(pokrywają się) kierunkom oddziaływania sił zewnętrznych.

Rysunek 1

Całokształt linii sił, zwany „potokiem sił” rozkłada się w ciele sprężystym, w

miejscach odpowiednio oddalonych od miejsc przyłożenia obciążeń skupionych,
równomiernie w całym przekroju prostopadłym do osi. Tę niezwykle istotną dla celów
praktycznych prawidłowość określa zasada de Saint Venanta (rys. 2):
„Jeżeli na pewien niewielki obszar ciała sprężystego w równowadze działają kolejno
rozmaicie umieszczone ale statycznie równoważne obciążenia, to w odległości od tego
obszaru, przewyższającej wyraźnie jego rozmiary, powstają jednakowe stany naprężenia i
odkształcenia.”

4

Rysunek 2

Wszelkie szczegóły kształtu elementu, wywołujące zmianę potoku sił, stają się

przyczyną powstawania koncentracji naprężeń wewnątrz elementu. Przy gwałtownych
(skokowych) zmianach przekroju belki, występują rozszerzenia lub zwężenia potoku sił, a
przy załamanej osi belki, występują skrzywienia osi „potoku sił” (przypadek analizowany w
niniejszym ćwiczeniu) – (rys.1). Przyczyną powstawania koncentracji, poza szczegółami
kształtu, mogą być również niejednorodne własności sprężyste materiałów, wynikające z
niejednorodności jego struktury, wad lub uszkodzeń materiału w rodzaju porowatości czy
pęknięć.

1.2

Podstawowe rodzaje koncentracji naprężeń

Koncentracja pierwotna – występuje w miejscach przyłożenia obciążenia zewnętrznego (w
większości przypadków wielkość ta jest znana i możliwa do ścisłego określenia).
Koncentracja wtórna – występuje w rezultacie przeciwstawiania się ciała sprężystego
oddziaływaniom zewnętrznym (zarówno wielkość jest i miejsce występowania nie są znane).

1.3

Określenie wielkości koncentracji naprężeń

Wielkość koncentracji naprężeń jest stosunkiem największego rzeczywistego

naprężenia, działającego w danym przekroju (punkcie) do średniego, określonego
teoretycznie za pomocą metod wytrzymałości materiałów. Wielkość ta charakteryzuje się
współczynnikiem koncentracji naprężeń K

T

określanym wzorem:

st

me

T

K

σ

σ

=

gdzie:

σ

me

–

największe, określone eksperymentalnie naprężenie w rozpatrywanym

przekroju,

σ

st

–

średnie, teoretyczne określone naprężenie, w punkcie działania największego

naprężenia rzeczywistego

)

1

(

A

P

=

δ

A

P

=

δ

A

P

=

δ

A

P

=

δ

A

P

=

δ

2

P

2

P

2

P

2

P

P

P

5

2.

Metody stosowane w badaniach koncentracji naprężeń

Możliwe miejsca lub strefy występowania wtórnych koncentracji naprężeń, określa się

wstępnie na podstawie analizy „potoku sił”. Można tu też posłużyć się metodą analogii,
wykorzystując rezultaty wcześniej wykonanych badań przy rozwiązywaniu podobnych zadań.
Dzięki tym wstępnym ustaleniom badania eksperymentalne (np. tensometryczne)
przeprowadzone są tylko dla określonego przekroju (strefy), gdzie spodziewać się należy
wystąpienia koncentracji. Powyższa kolejność określania koncentracji naprężeń pozwala
skrócić do minimum kosztowne i pracochłonne badania eksperymentalne.

2.1

Metoda kruchych pokryć

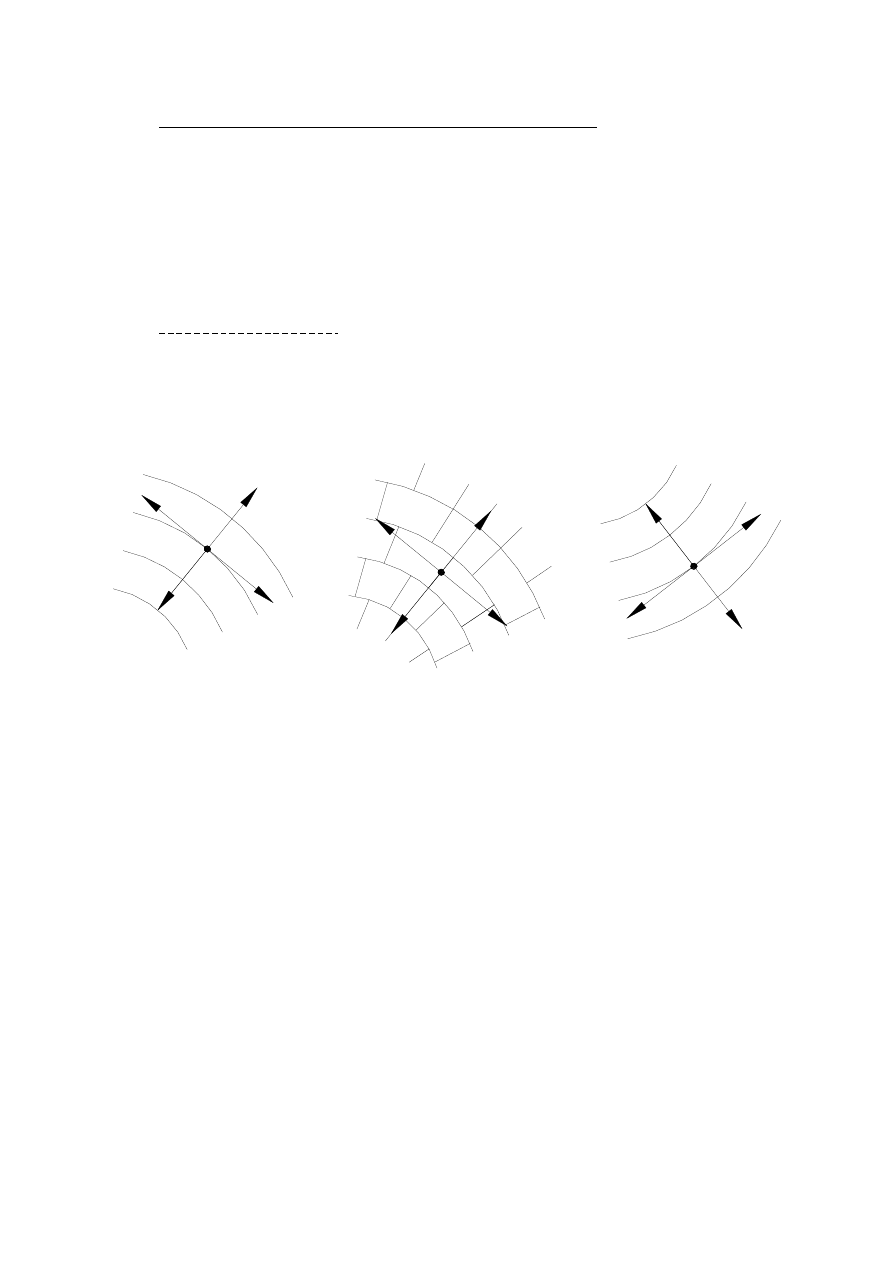
Powierzchnię elementu konstrukcyjnego lub jego modelu pokrywa się warstwą

kruchej substancji, ściśle przylegającej do powierzchni. W wyniku obciążenia elementu w
warstwie kruchej pokrycia pojawiają się układy pęknięć w kierunkach prostopadłych do
kierunków maksymalnych naprężeń rozciągających (rys. 3).

Rysunek 3

Zasadnicze typy pęknięć kruchego pokrycia: a) pęknięcia prostopadłe do kierunku naprężenia δ

1k

przy

obciążeniu elementu, b) pęknięcia prostopadłe do kierunku naprężenia δ

2k

przy obciążaniu elementu po

uprzednim uzyskaniu pęknięć typu a, c) pęknięcia prostopadłe do kierunku naprężenia, uzyskane przy
odciążeniu elementu

Badając pręty pryzmatyczne poddawane rozciąganiu względnie zginaniu, wzrasta

liczba pęknięć, przypadająca na jednostkę długości wzdłuż osi pręta. Można zatem, określić
związek empiryczny między gęstością pęknięć a odkształceniem. Związek ten jest podstawą
oszacowania wartości odkształceń głównych na powierzchni obiektu pokrytego układami
pęknięć kruchego pokrycia. Znając odkształcenia główne oraz stałe E,ν danego materiału,
wyznacza się odpowiednie wartości naprężeń głównych. Bezpośrednia obserwacja kolejności
pojawiania się pęknięć kruchego pokrycia, w miarę obciążania elementu oraz końcowej
gęstości pęknięć, umożliwia ustalenie miejsc spiętrzeń naprężeń. Ze względu na pewien
rozrzut wyników pomiarów gęstości pęknięć, wartości odkształceń naprężeń wyznaczone tą
metodą mają charakter orientacyjny.

k

1

δ

k

1

δ

k

1

δ

k

1

δ

k

1

δ

k

1

δ

k

2

δ

k

2

δ

k

2

δ

k

2

δ

k

2

δ

k

2

δ

6

2.2

Badania modelowe

W badaniach modelowych wyniki pomiarów na modelach są podstawą określenia

wartości odpowiednich wielkości dotyczących rzeczywistego elementu konstrukcyjnego
(obiektu). Do interpretacji wyników badań modelowych stosuje się kryteria podobieństwa
modelowego, wynikające z zasad teorii podobieństwa modelowego. W badaniach modeli
mechanicznych stosuje się na ogół modele geometryczne podobne do obiektu, zachowując
określoną skalę K

l

wymiarów liniowych i skalę K

P

obciążeń. Skale te określamy wzorami:

m

l

l

l

K

=

m

P

P

P

K

=

gdzie:

l, l

m

–

odpowiadające sobie wymiary liniowe obiektu i modelu,

P, P

m

–

odpowiadające sobie wartości obciążeń obiektu i modelu.

W badaniach w zakresie odkształceń liniowo – sprężystych jednym z warunków, tak

zwanego, ścisłego podobieństwa jest równość współczynnika Poissona dla modelu i obiektu.
W przypadku ogólnym, badania układów liniowo – sprężystych do obliczania wartości
naprężeń (σ) w obiekcie stosuje się wzór:

m

l

P

K

K

σ

σ

⋅

=

2

2.3

Metoda elastooptyczna

Przy metodzie elastooptycznej badania przeprowadza się na modelach mechanicznych

rzeczywistych elementów konstrukcyjnych. Modele te wykonywane są z przezroczystych,
optycznie czułych materiałów (żywice poliestrowe, epoksydowe, fenolowo-formaldehydowe,
polimetakrynowe, rzadziej szkło, celuloid, żelatyna). Wymienione materiały w stanie wolnym
od naprężeń i odkształceń są optycznie izotropowe. W stanie naprężenia materiały te przestają
być izotropowe i wykazują dwójłomność wymuszoną, która umożliwia badanie tego stanu
metodą optyczną w świetle spolaryzowanym. W wyniku wystąpienia dwójłomności,
przechodzący przez model promień spolaryzowanego światła ulega rozproszeniu na dwa
promienie składowe, których płaszczyzny drgań pokrywają się z kierunkami naprężeń
(odkształceń) głównych, a wzajemne przesunięcie (opóźnienie) w fazie jest proporcjonalne do
różnicy naprężeń (odkształceń) głównych modelu. Po przejściu tych promieni przez filtr
polaryzacyjny, można uzyskać interferencję odpowiednich składowych promieni, a w
rezultacie – obraz pokryty układem ciemnych prążków interferencyjnych. Znajomość
rozkładu tych prążków umożliwia wyznaczenie składowych stanu naprężenia w modelu.

2.4

Metoda tensometryczna

2.4.1

Budowa tensometrów rezystancyjnych

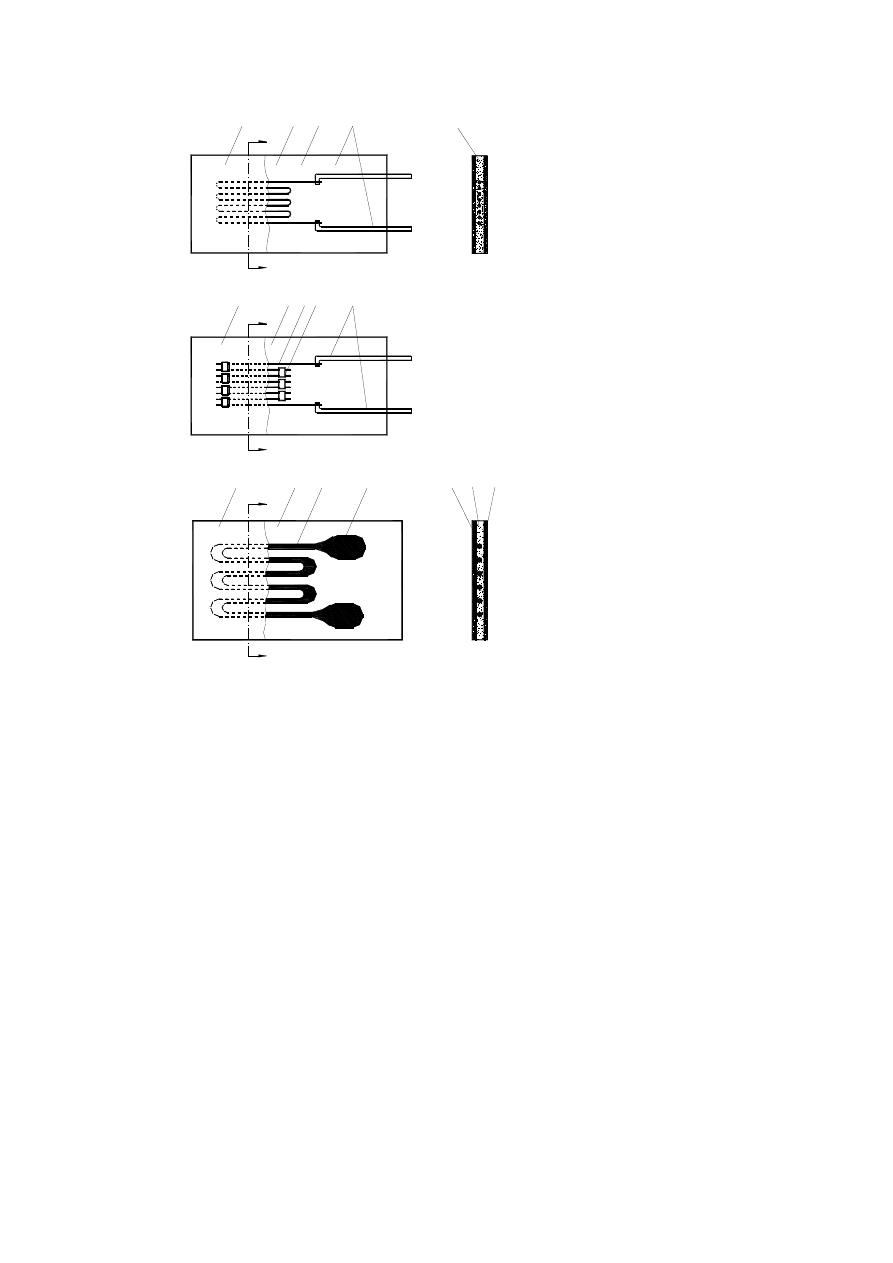
Są dwa rodzaje tensometrów rezystancyjnych: drucikowi i foliowe. W pierwszych na

element przewodzący prąd bierze się cienki drucik metalowy o znacznej rezystywności, w
drugim – zamiast drucików używa się cienkich i wąskich tasiemek metalowych. Tensometry
drucikowe dzielą się na wężykowe i kratowe.

)

2

(

)

3

(

7

Tensometr drucikowy-wężykowy (rys. 4) utworzony jest z bardzo cienkiego drutu

rezystancyjnego 1 w kształcie wielokrotnego wężyka, przyklejonego specjalnym klejem 2 do
podkładki nośnej 3 papierowej lub z folii z tworzywa sztucznego. Do końców drutu
rezystancyjnego przymocowane są druty 4 o większych przekrojach, służące za przewody dla
połączeń z układem pomiarowym. Zarówno wężyk oporowy, jak i zakończenia przewodów
łączących, przykrywa się paskiem papieru lub cienką folią z tworzywa sztucznego 5, po
uprzednim powleczeniu klejem powierzchni styku. Tensometr wężykowy wykazuje znaczną
czułość na odkształcenia w kierunku poprzecznym, o czym decydują połączenia w kształcie
łuku poszczególnych drucików siatki.

Tensometr drucikowy-kratowy (rys. 5) jest pozbawiony czułości w kierunku

poprzecznym i składa się on z szeregu drucików z cienkiego drutu rezystancyjnego 1
ułożonych równolegle i połączonych między sobą za pomocą znacznie grubszych odcinków
taśmy miedzianej 2, lutowanych lub zgrzewanych. Taśmy z obu stron przecinane są w ten
sposób, że otrzymuje się rezystor z drucików ułożonych wzajemnie szeregowo.

Tensometr foliowy (rys. 6) składa się z siatki rezystancyjnej 1 w postaci wężykowatej,

wykonanej z cienkiej folii metalowej, sklejonej pod naciskiem z podkładką nośną 2. Część
pomiarowa wężyka przykryta jest nakładką ochronną 3, wykonaną podobnie jak w przypadku
tensometrów drucikowych.

Rysunek 4
1 – siatka rezystancyjna w kształcie wężyka
2 – klej
3 – podkładka nośna
4 – przewody doprowadzające
5 – nakładka nośna

5

3

1

4

2

4

3

1 2

5

Rysunek 5
1 – drut rezystancyjny
2 – tasiemka Cu
3 – podkładka nośna
4 – zakładka
5 – przewody doprowadzające

Rysunek 6
1 – siatka rezystancyjna
2 – podkładka nośna
3 – nakładka ochronna
4 – zakończenia
5 – klej

3

2 1

4

2

5

3

8

2.4.2 Podstawowe równanie tensometryczne

Metoda tensometryczna jest uniwersalną metodą elektryczną do pomiaru parametrów

mechanicznych. Z uwagi na jej szereg zalet jest obecnie szeroko stosowaną zarówno do
pomiarów statycznych jak i dynamicznych.
Załóżmy, że przewodnik w postaci drutu o polu przekroju S stałym na długości l i średnicy d
oraz rezystywności (oporze właściwym) materiału ρ, ma rezystancję R. Wzajemny związek
między tymi wielkościami wyraża wzór:

S

l

R

⋅

=

ρ

Prawidłowo zaprojektowane i wykonane przetworniki są niewrażliwe na zmiany

warunków otoczenia (temperatura, wilgotność) oraz pozwalają na eliminowanie
niepożądanych wpływów mechanicznych (np. układ reagujący na zginanie i eliminujący
wpływ rozciągania). Spełnienie podstawowego warunku metody tensometrycznej, praca w
granicach proporcjonalności odkształceń, zapewnia liniowość charakterystyki przetwornika
tensometrycznego i pozwala na uzyskanie dużej dokładności wyników pomiarów. Naprężenie
panujące w badanym elemencie, na który został naklejony tensometr, jest funkcją odkształceń
i własności fizycznych materiału (moduł Younga). Dla jednowymiarowego stanu:

ε

σ

⋅

= E

Zasadnicze równanie w zakresie tensometrii, wiążące podstawowe mechaniczne i elektryczne
parametry pracy tensometru wygląda następująco:

ε

⋅

=

∆

K

R

R

gdzie:

R

R

∆

–

sygnał elektryczny

K –

stała tensometru (wsp. tensoczułości)

K = 1.9 – 6.0 zależnie od materiału tensometru

Znając opór i stałą tensometru, odczytujemy przyrost oporu na aparaturze i znajdujemy:

R

R

R 1

⋅

∆

=

ε

2.5

Metody numeryczne

W ostatnich latach coraz większą popularność zdobywają metody numeryczne do

wyznaczania koncentracji naprężeń w konstrukcjach. Dzieje się tak ze względu na bardzo
szybki rozwój technologii mikroprocesorowej, która umożliwia zarówno łatwe modelowanie
rzeczywistego obiektu, jak i przeprowadzenie na nim obliczeń.

2.5.1

Metoda elementów skończonych (MES)

Metoda elementów skończonych (MES) należy do najbardziej popularnych metod

komputerowych służących do rozwiązań zagadnień brzegowych mechaniki. Jej istota polega
na zastąpieniu ciągłego modelu układu mechanicznego modelem dyskretnym, który
elementów opisie matematycznym przyjmuje postać układu równań algebraicznych.

)

4

(

)

5

(

)

6

(

)

7

(

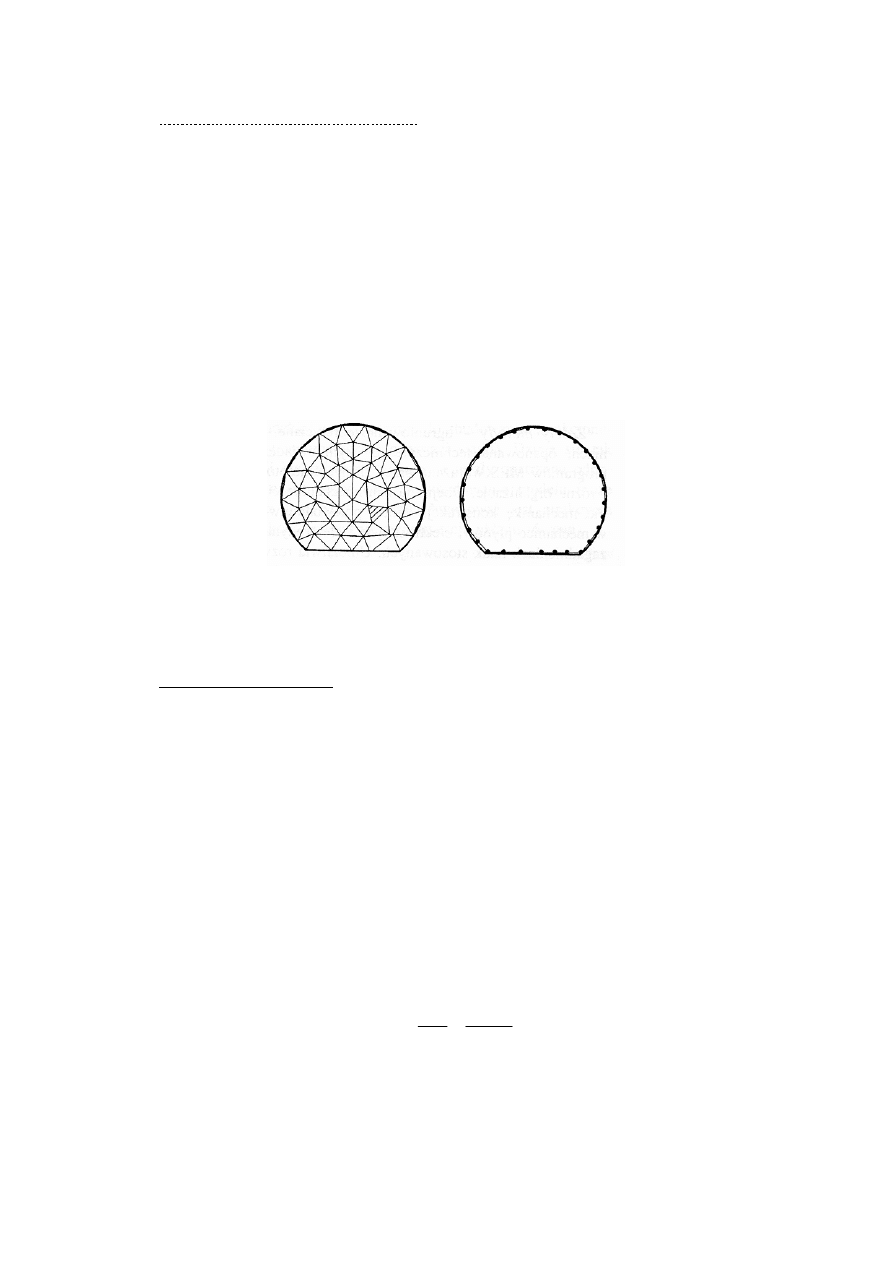
9

2.5.2 Metoda elementów brzegowych (MEB

)

Metoda elementów brzegowych (MEB) jest metodą komputerową, która dzięki

intensywnemu rozwojowi stała się w ostatnich latach atrakcyjną i stosowaną metodą
numeryczną mechaniki.

Główną zaletą tej metody jest zmniejszenie o jeden rząd, w porównaniu z MES,

wymiaru geometrycznego rozwiązywanego zagadnienia, dzięki czemu dyskretyzacji podlega
tylko powierzchnia ciała w przypadku zagadnień przestrzennych lub brzegu obszaru
dwuwymiarowego w przypadku zagadnień płaskich, bez ingerencji w obszar wewnętrzny.
Jednak uzyskane rozwiązanie nie ogranicza się wyłącznie do brzegów, lecz ważne jest
również wewnątrz modelowanego obszaru. Metoda ta przy tym samym stopniu dyskretyzacji
daje zwykle równie dokładne wyniki jak metody, które wymagają dyskretyzacji całego
obszaru zajmowanego przez ciało.

MES MEB

Rysunek 7

3.

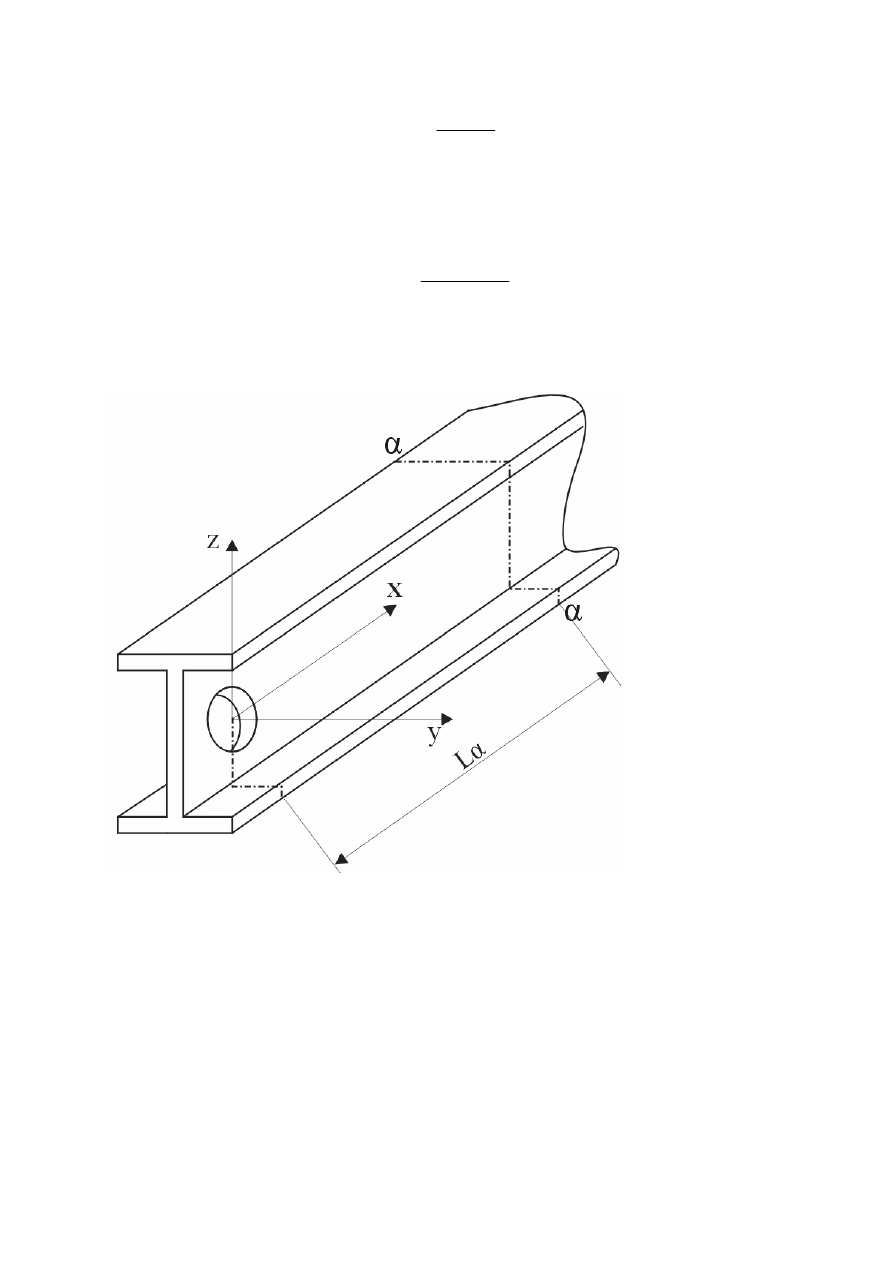
Wykonanie ćwiczenia

Doświadczalna część niniejszego ćwiczenia ma na celu określenie metodą

doświadczalną (tensometryczną) naprężeń rzeczywistych występujących w strefie załamania
belki (stanowiącej model wygiętego wysięgnika żurawia) oraz określenie współczynnika
koncentracji naprężeń przez porównanie wartości rzeczywistych z wykonanym teoretycznie.

3.1

Teoretyczne określenie wielkości naprężeń

Przy zginani dźwigara o dowolnym przekroju, obciążonego siłą skupioną, występują

w nim naprężenia główne σ

x

, poprzeczne τ

xz

oraz ściskające σ

z

od ściskania międzypasowego.

Układ tensometrów pozwoli na wyznaczenie rzeczywistych wartości naprężeń w

danym przekroju, zatem dla wyznaczenia współczynnika koncentracji potrzebna jest
znajomość ich wartości wyznaczonych teoretycznie, bez uwzględnienia spiętrzenia naprężeń.
naprężeń teorii wytrzymałości materiałów naprężenia te określane są odpowiednio:

y

y

y

y

x

I

z

M

W

M

⋅

=

=

σ

gdzie:

M

y

–

moment gnący w przekroju prostopadłym do osi `x`

W

y

–

wskaźnik przekroju

)

8

(

10

)

(

)

(

z

b

I

z

S

T

y

xz

⋅

⋅

=

τ

gdzie: T – siła tnąca

S(z) – statyczny moment odciętej części przekroju, względem osi `z`

b(z) – szerokość ścianki na wysokości `z`

)

(

)

(

2

2

z

b

I

E

z

S

M

y

y

z

⋅

⋅

⋅

=

σ

gdzie:

I

y

–

moment bezwładności przekroju.

Rysunek 8

Łatwo sprawdzić, że w naszym przypadku (I

y

=171 cm

4

, S(z)=19.9 cm

3

(dla połowy

przekroju), b=0.45 cm (dla środnika)) naprężenia σ

z

w przekroju E przy sile obciążającej do

6000 N nie przekroczą na środniku wartości 0.1 MPa. Są zatem one pomijalnie małe,
możemy więc przyjąć, że naprężenia normalne na półce i środniku występują tylko w
kierunku osi wzdłużnej `x`. Ewentualne empiryczne stwierdzenie naprężeń normalnych
poprzecznych świadczyć może o niesymetrycznym odkształceniu belki, wystąpieniu
spiętrzenia naprężeń lub błędzie zastosowanej metody pomiarowej. Pomijając niewielkie
odkształcenia półek w płaszczyźnie yz możemy przyjąć naprężenia normalne σ

x

na

zewnętrznych powierzchniach półek jako naprężenia główne – występuje tu zatem
jednoosiowy stan naprężeń. Ich wielkość wyznaczymy na drodze teoretycznej ze wzoru (8),

)

9

(

)

10

(

11

uwzględniając dodatkowo stałe naprężenia pochodzące od ściskania składową siłą P. Mamy
zatem w dowolnym przekroju α na ramieniu L

α

dla półki górnej i dolnej:

A

P

L

W

P

A

N

W

M

y

y

g

d

g

x

°

−

⋅

°

±

=

−

±

=

−

±

=

45

cos

45

sin

α

α

α

α

σ

σ

σ

[MPa]

Porównanie tych wielkości z wyznaczonymi empirycznie pozwoli na określenie

współczynnika koncentracji na półce, co jest sprawą oczywistą z uwagi na jednoosiowy stan
naprężeń. Określenie współczynnika koncentracji naprężeń na środniku jest sprawą bardziej
skomplikowaną. Złożony stan naprężeń występujący na środniku wymaga określenia dla
danego punktu pewnej wielkości charakteryzującej ten stan, Posłużymy się tu hipotezą
energetyczną Hubera wyznaczając dla danego punktu σ

red

według wzoru dla płaskiego stanu

naprężenia:

xz

z

x

z

x

red

2

2

2

3

τ

σ

σ

σ

σ

σ

+

−

+

=

Ponieważ w naszym przypadku σ

z

=0, teoretyczną wartość σ

red

obliczymy ze wzoru:

xz

x

red

2

2

3

τ

σ

σ

+

=

Współczynnik koncentracji dla środnika wyrazi się więc jako stosunek σ

red

e

określonego z

naprężeń rzeczywistych do σ

red

t

określonego z naprężeń teoretycznych wg wzoru (12).

Wartości we wzorze (13) wyznaczamy z zależności (8) i (9) (uwzględniając odpowiednio
wpływ ściskania – patrz 11), korzystając z danych wyjściowych i parametrów stanowiska. Z
uwagi na możność określenia σ

red

e

tylko dla jednego punktu (rozetka tensometryczna), σ

red

t

wyliczymy tylko dla tego jednego punktu (E

6,16

), zaś w pozostałych interesować nas będą

tylko składowe stanu naprężeń.

3.2

Doświadczalne określenie wielkości naprężeń

Zgodnie z zasadą pomiaru tensometrycznego uzyskane wyniki (różnice odczytu z

mostka dla stanu obciążonego i nieobciążonego) są względnymi wydłużeniami `ε` w danym
przekroju. Dla znalezienia odpowiednich naprężeń korzystamy z prawa Hooke`a:

ε

σ

⋅

⋅

=

E

k

k

t

m

gdzie:

k

m

–

współczynnik czułości mostka (stała mostka) = 2.0

k

t

–

współczynnik tensoczułości (stała tensometru) = 2.7

Dla punktów, których występuje płaski stan naprężeń (środnik) wartość ich

wyznaczymy z uogólnionego prawa Hooke`a:

(

)

z

x

x

E

kt

km

νε

ε

ν

σ

±

−

⋅

=

2

1

Dla wyznaczenia σ

red

e

wg wzoru (12) dla rzeczywistego stanu naprężeń, nie wystarczy

znajomość rzeczywistych wartości naprężeń normalnych σ

x

i σ

z

wyznaczonych wg wzorów

(15). Naprężeń stycznych τ

xz

nie określimy bezpośrednio przez pomiar tensometrem.

)

11

(

)

12

(

)

13

(

)

14

(

)

15

(

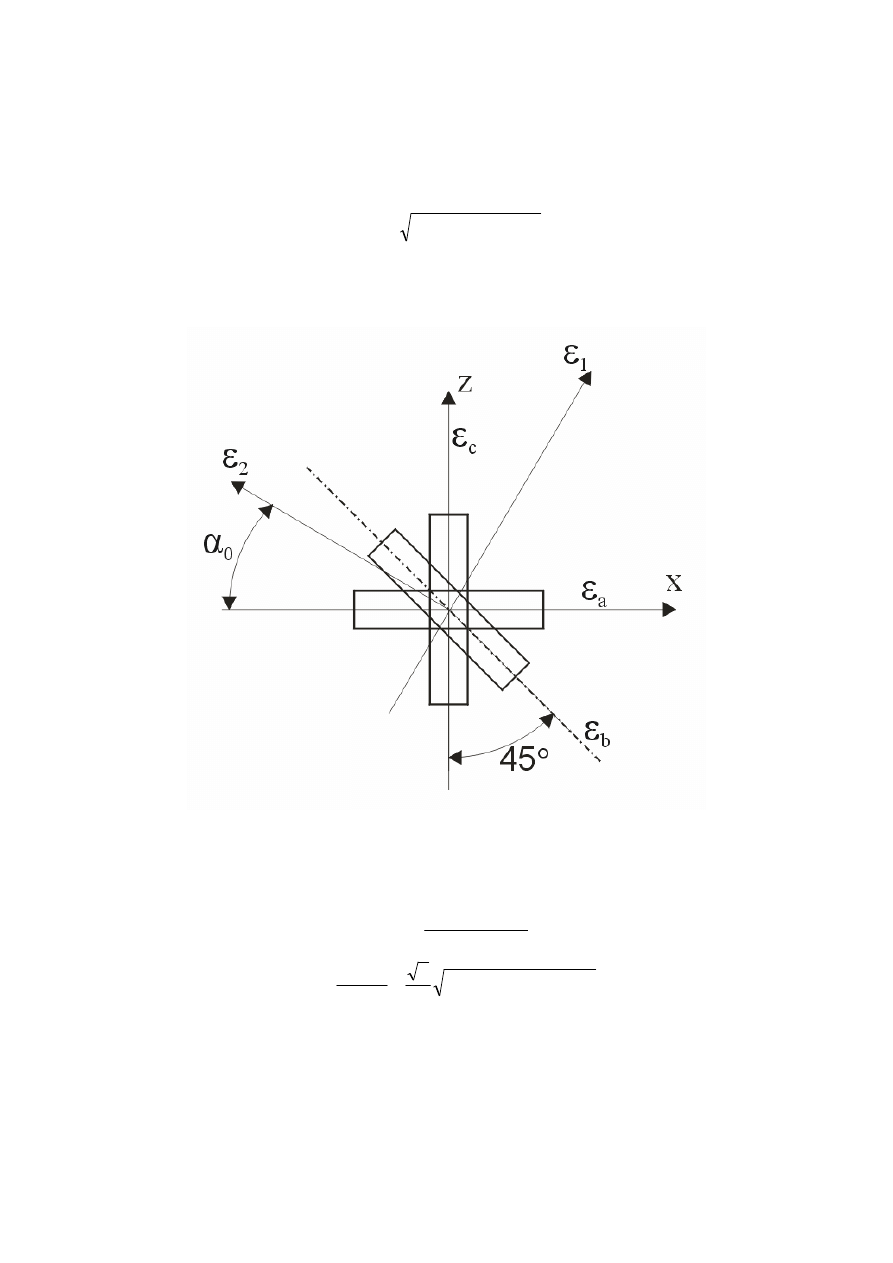
12

Naprężenie σ

red

e

dla stanu rzeczywistego określimy przy pomocy układu trzech tensometrów

– rozetka tensometryczna. Na podstawie wzorów otrzymać możemy z wielkości
pomiarowych kierunki i odkształcenia główne, a co za tym idzie i naprężenia główne (15).
Znając naprężenia główne określamy σ

red

e

dla stanu rzeczywistego:

2

1

2

2

2

1

σ

σ

σ

σ

σ

−

+

=

red

Rozetka umieszczona jest w przekroju E w punkcie 6.16, dla którego z=3.2 cm, a

zatem dla tego punktu określić możemy współczynnik koncentracji. Rozetka naklejona jest w
następujący sposób:

Rysunek 9

Kierunki i odkształcenia główne wyznaczamy wg wzorów:

(

)

c

a

c

a

b

tg

ε

ε

ε

ε

ε

α

−

+

−

=

2

2

0

(

)

(

)

2

2

2

,

1

2

2

2

c

b

b

a

c

a

ε

ε

ε

ε

ε

ε

ε

−

+

−

+

=

m

Poza wyznaczeniem naprężeń głównych w punkcie E

6,.16.6

i określeniem dla tego

punktu współczynnika koncentracji, interesować nas będzie przebieg naprężeń rzeczywistych
σ

x

i σ

z

na środniku w badanych przekrojach.

)

16

(

)

17

(

)

18

(

13

3.3

Stanowisko badawcze

Podstawowe zespoły stanowiska przedstawione są na rys. 10 to:

-

rama (1),

-

element badany (2) z naklejoną siatką tensometrów,

-

układ napinający (3), w skład którego wchodzi element pomiarowy – dynamometr

tensometryczny,

-

aparatura pomiarowa.

3.3.1

Element badany

3.3.1.1 Parametry belki dwuteowej stanowiącej element badany:

-

wysokość h=100 mm

-

szerokość półki a=50 mm

-

grubość ścianki środnika g=4.5 mm

-

powierzchnia przekroju A=10.6 cm

2

-

moment bezwładności I

y

=170 cm

4

-

moment statyczny połowy przekroju S

y

=19.9 cm

3

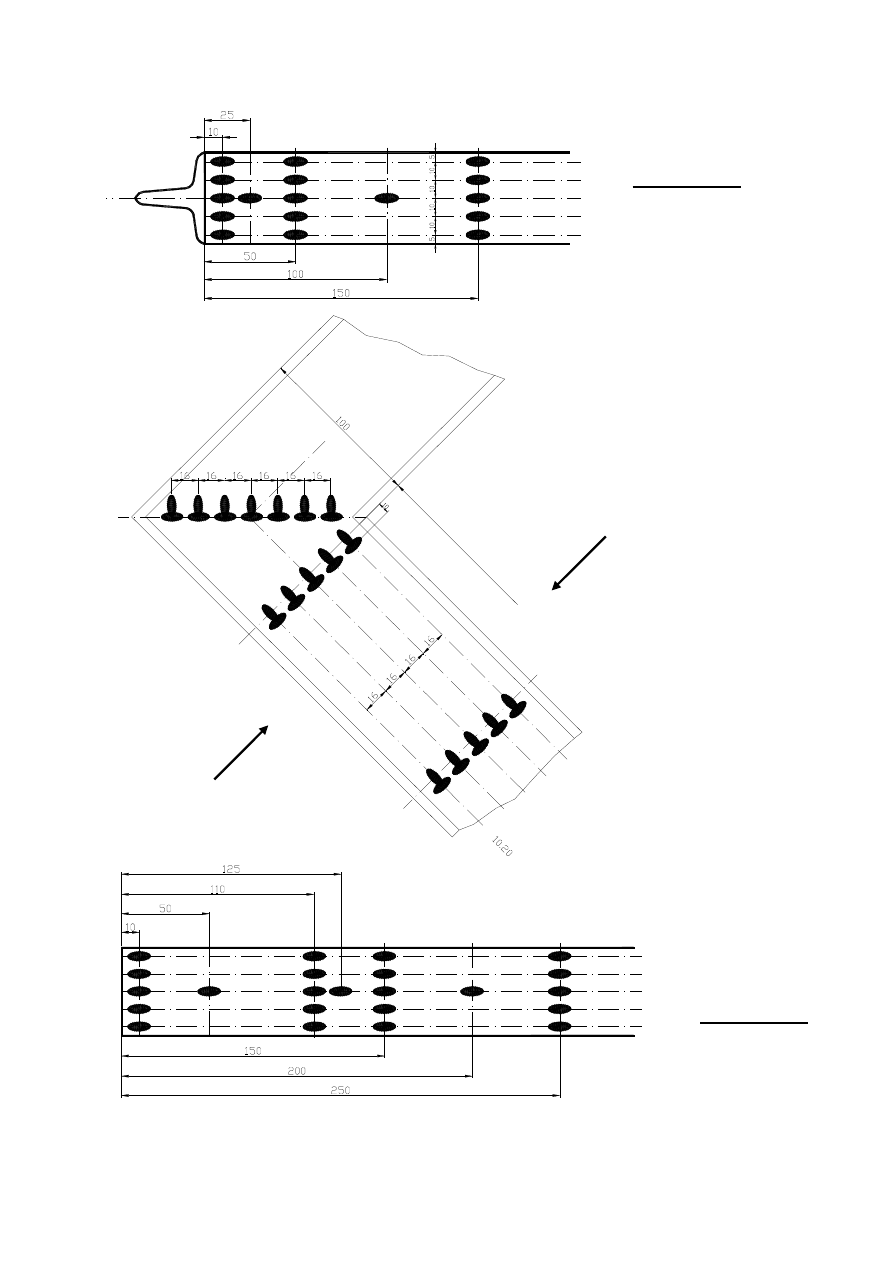
3.3.1.2 Rozkład tensometrów

Siatka tensometrów na elemencie badanym (rys. 14) pozwala na określenie

następujących przebiegów naprężeń:
-

przebieg naprężeń wzdłużnych σ

x

na półkach w miarę zbliżania się do strefy

koncentracji (naroża),

-

rozkład naprężeń wzdłużnych σ

x

na półkach w przekrojach prostopadłych do osi

wzdłużnej A, C, E, G,

-

rozkład naprężeń σ

x

i σ

z

na środniku w przekrojach A, E,

-

rozkład naprężeń głównych w przekroju H,

-

określenie naprężeń głównych w punkcie E

6,16.6

(rozetka tensometryczna).

3.3.1.3 Zastosowane czujniki

W ćwiczeniu zastosowano czujniki tensometryczne wężykowe typu PbKn 6/130, dla

których stałą tensometru wynosi kt

w

=2.7 oraz kratowe typu RL10/120 o stałej kt

k

=2.15. Na

półkach naklejone są tensometry wężykowe, zaś na środniku wężykowe i kratowe, w tych
samych miejscach po obu stronach ścianki (te same oznaczenia), dla porównania wskazań obu
rodzajów tensometrów przy dwuosiowym stanie naprężeń. Końcówki wyprowadzeń
tensometrów znajdują się na oznakowanej tabliczce (rys. 12), zamocowanej na badanym
elemencie. Opis łączenia – patrz punkt 3.4.

3.3.2

Układ napinający

Schemat układu napinającego przedstawia rys 11. Pokręcając pokrętłem (5)

powodujemy przesuw tulei (6) w ucho (2). Tuleja pociąga pręt połączony z drugiej strony z
dynamometrem, zaś dynamometr (1) połączony jest z drugim uchem (3).

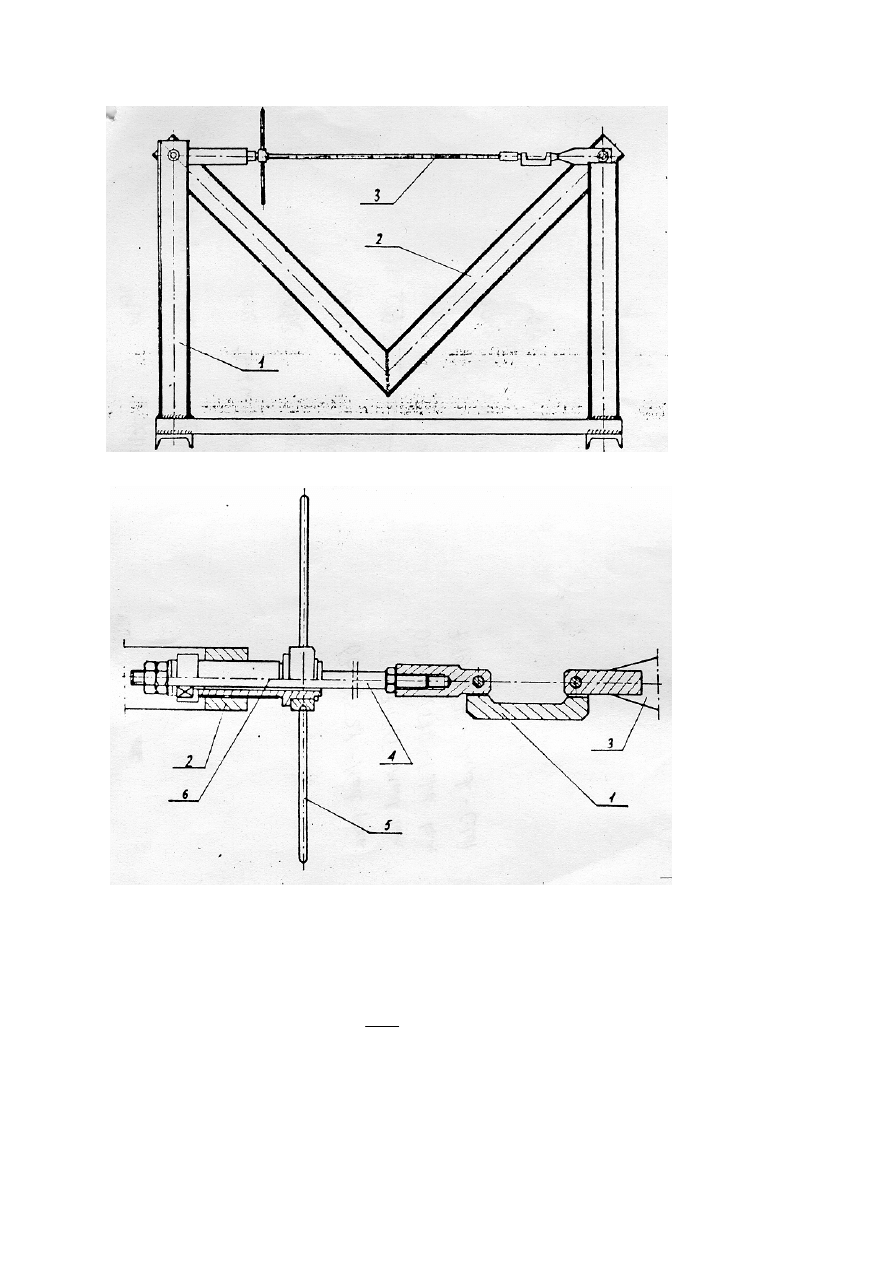
14

Rysunek 10

Rysunek 11

Na dynamometrze (element zginany) naklejone są dwa tensometry połączone w układzie
połowy mostka. Jest to układ reagujący na zginanie i eliminujący wpływ rozciągania – daje
też kompensację wpływu temperatury. Dynamometr ma liniową charakterystykę określoną
stałą:

o

o

/

2400

°

=

N

A

dla `k

m

`=2.0

Zatem siła w układzie napinającym określona jest liniową zależnością:

d

A

P

ε

⋅

=

[N]

gdzie: ε

d

= b – a [‰]

)

19

(

15

jako różnicę odczytów dla dynamometru w stanie obciążonym (b) i nieobciążonym (a). Dla
uzyskania żądanej siły P należy wyznaczyć ze wzoru (19)

ε

d

i układem napinającym uzyskać

wskazanie mostka dla dynamometru odpowiadające tej sile uzyskać wartość odczytu (b).

3.4

Aparatura pomiarowa

Pomiarów naprężeń naprężeń wyznaczonych przekrojach przy obciążeniach

statycznych dokonujemy na mostku tensometrycznym typu T2 produkcji ZBMM PW,
przystosowanym głównie do pomiarów statycznych metodą zerową. Zmiany liniowe ∆l/l
tensometru mierzone są pośrednio jako zmiany jego względnej oporności ∆R/R. Regulacja
stanu równowagi mostka zgrubsza w zakresie 0 – 25 ‰ skokowo co 1 ‰ odkształcenia
precyzyjnego za pomocą potencjometru ślizgowego. Najmniejsza wartość przyrostowa
ε=0.005‰

odpowiada najmniejszej działce potencjometru ślizgowego. Mostek posiada

ponadto możliwość regulacji stałej mostka `km` skokowo w zakresie 1.75 –2.4. Schemat
blokowy aparatury przedstawia rys. 14. Odpowiednie parametry badanego przekroju łączymy
z mostkiem poprzez skrzynkę rozdzielczą, Umożliwiająca podłączenie 24 tensometrów.
Wyjścia tensometrów z oznakowanej tablicy zamocowanej na elemencie badanym łączymy
kolejno z zaciskami kolumny A, przewód zerowy (czarny) z dowolnym zaciskiem kolumny B,
zaś kompensacyjny (czerwony) z dowolnym zaciskiem kolumny C zwartej odpowiednią
listwą.

1

2

3

4

5

6

7

8

9

10 11 12 13 14 15 16 17 18 19 20

A

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

B

x

x

C

x

x

x

x

x

x

x

x

x

x

D

x

x

E

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

F

x

0

K

G

x

x

x

x

x

H

x

x

x

x

x

x

x

x

x

x

x

x

x

x

Rysunek 12

Skokowe pokrętło skrzyni rozdzielczej służy do kolejno łączenia tensometrów (numer

z kolumny A) z mostkiem tensometrycznym.

Rysunek 13

zasilacz

generator

mostek

wzmacniacz

małej częst.

detektor

fazoczuły

galwanometr

skrzynka

rozdzielcza

czujniki

tensometryczne

16

A

B

C

D

E

2

4

3

5

1

1

3

4

5

6

7

2

1

1

1

2

1

3

1

4

1

5

1

6

1

7

A

L=

95

0

E

E

A

6.1

6

7.1

7

8.1

8

9.1

9

A

B

C

D

E

F

G

11

12

15
14

13

Rysunek 14

W

Widok W

Widok Z

Z

H

H

17

4.

Spis literatury

1.

Jakubowicz – Orłoś „Wytrzymałoś materiałów” roz. 1, 5, 6, 10, 11, 12, 18

2.

J. Rutecki „Cienkościenne konstrukcje nośne” WNT 1966, roz. VII, §60

3.

Instrukcja obsługi mostka T2

4.

W. Styburski „Przetworniki tensometryczne” WNT 1971, roz. 4, 6

5.

Z Soliński „Zarys tensometrii elektrooporowej” roz. 7, 8

6.

Z. Orłoś „Doświadczalna analiza odkształceń odkształceń naprężeń” PWN, roz. 2, 3

7.

„Poradnik mechanika”