Wykład 1
Wykład 1
Formalne Podstawy Informatyki
I rok MSIB, 2009/2010

Zakres materiału
Zakres materiału
1.
Maszyna Turinga
2.
Architektura komputerów
3.
Logika
4.
Rachunek zdań
5.
Działania na zbiorach
Maszyna Turinga
Maszyna Turinga
W roku 1937 angielski matematyk Alan Turing pracując
nad koncepcją obliczalności funkcji matematycznych
opisuje bardzo prostą maszynę logiczną, która dziś nosi
nazwę Maszyny Turinga. Pomimo swej prostoty
posiada ona obecnie olbrzymie znaczenie teoretyczne,
ponieważ wszystkie współczesne komputery dają się
do niej sprowadzić. Problem jest rozwiązalny na
komputerze, jeśli da się zdefiniować rozwiązującą go
maszynę Turinga.
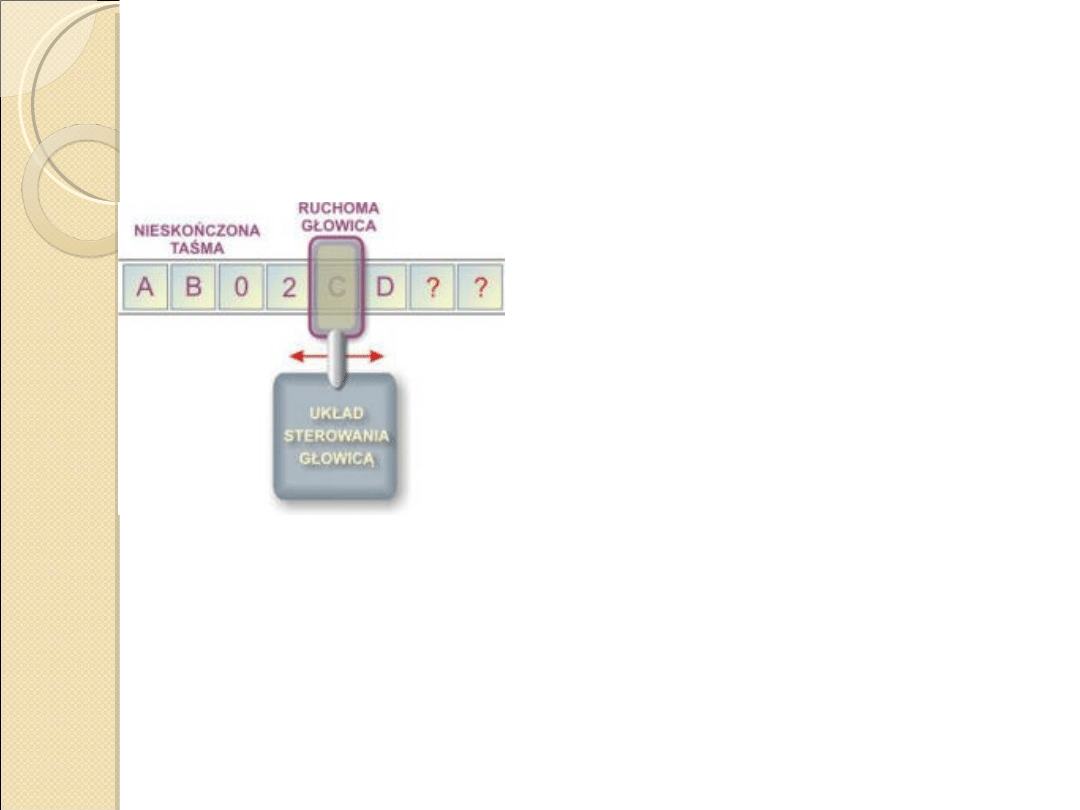
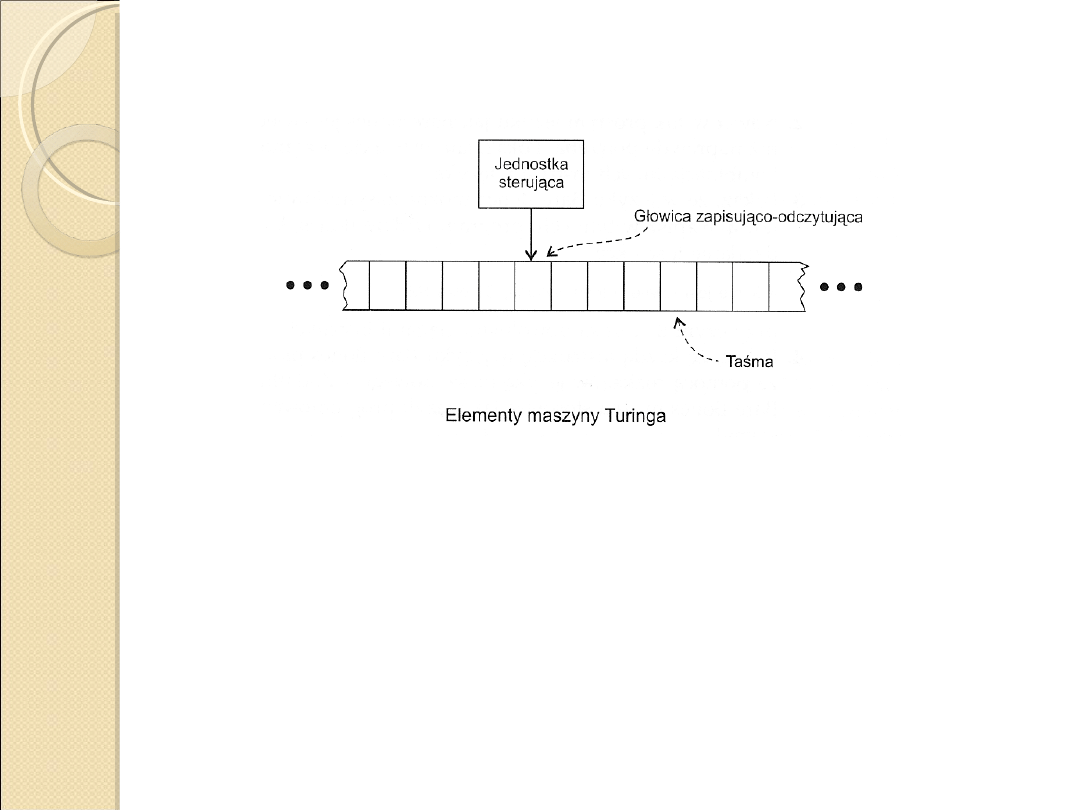
Maszyna zbudowana jest z
trzech głównych elementów:
◦
Nieskończonej taśmy zawierającej komórki z
przetwarzanymi symbolami
◦
Ruchomej głowicy zapisująco-odczytującej.
◦
Układu sterowania głowicą.
Maszyna Turinga
Maszyna Turinga
Działanie
•obliczenia rozpoczynają się i kończą w wyróżnionych komórkach taśmy
pamięci
• akcja maszyny jest zdeterminowana zawartością bieżącej komórki i
stanem maszyny
• program maszyny definiuje jej akcję: zapis i odczyt wartości, zmianę
stanu i kierunek ruchu głowicy
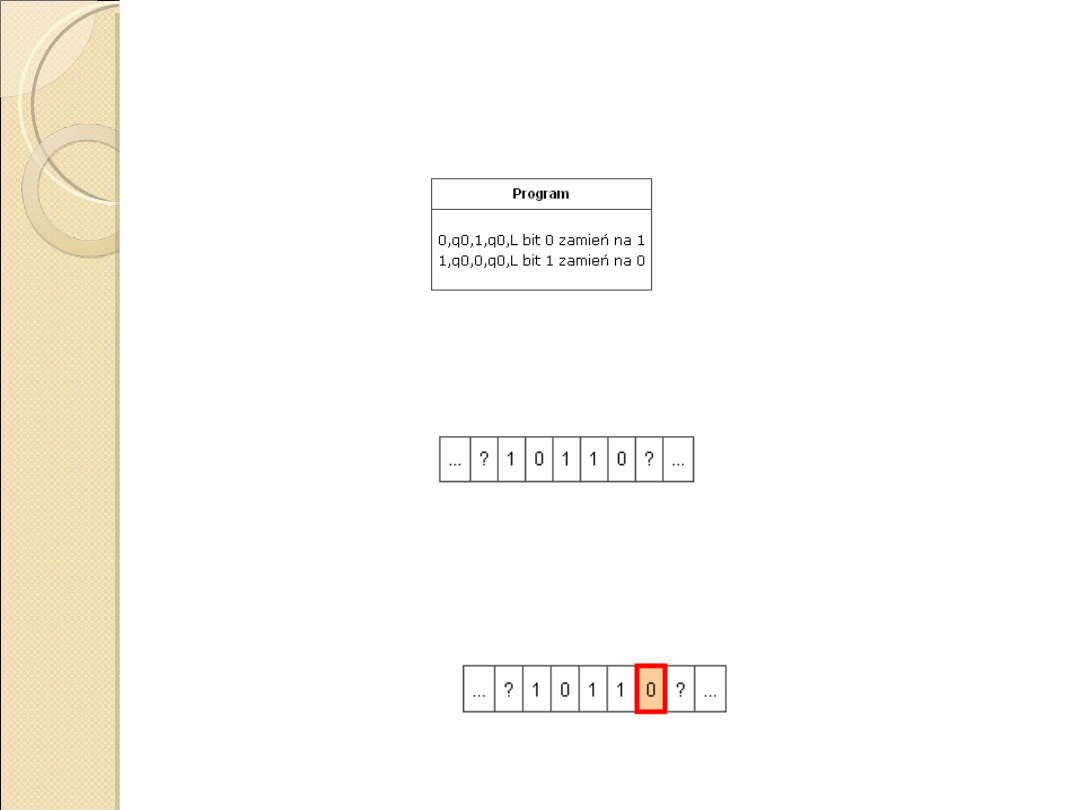
Załóżmy, że taśma zawiera ciąg symboli:
Ustawiamy głowicę:
Maszyna Turinga-jak działa?
Maszyna Turinga-jak działa?
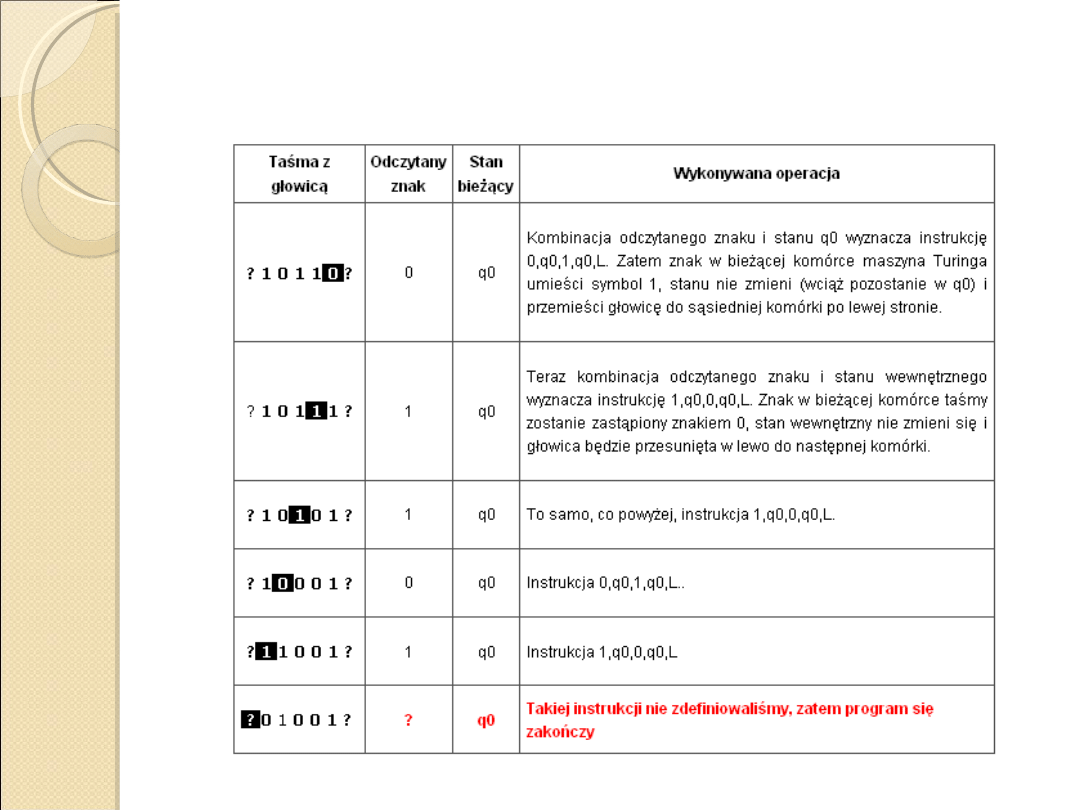
Maszyna Turinga-jak działa?
Maszyna Turinga-jak działa?
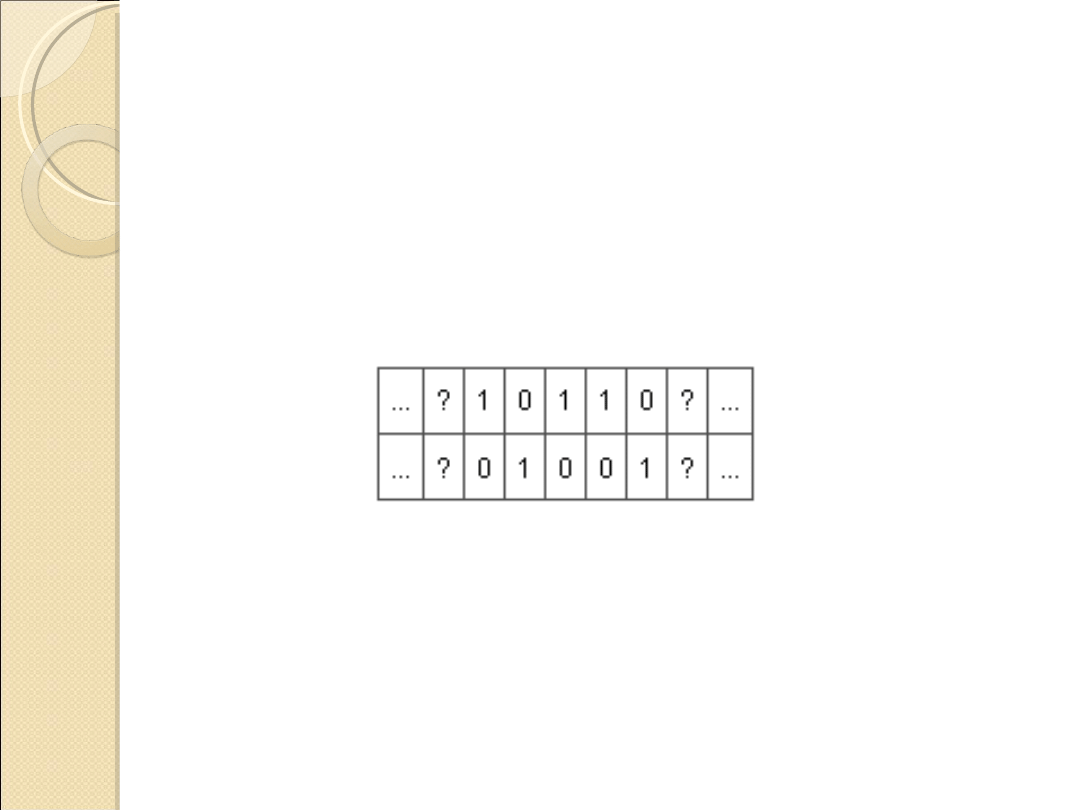
Porównajmy stan taśmy przed i po
wykonaniu programu:
Czego dokonuje podany program?
Maszyna Turinga-jak działa?
Maszyna Turinga-jak działa?

Architektura komputerów
Architektura komputerów
Architektura wg von Neumann’a
Procesor
Pamięć operacyjna
Urządzenia wejścia/wyjścia
Ze względu na sposób organizacji pamięci i wykonywania
programu dzielimy na:
•architektura von Neumanna
•Architektura harwardzka
•architektura mieszana

Architektura komputerów
Architektura komputerów
Założenia logiczne komputera:
◦
Pamięć jest uporządkowana w sposób
jednowymiarowy (komórka pamięci ma adres,
wyrażony liczbą).
◦
Instrukcje i dane są przechowywane w pamięci
(w postaci liczb - nierozróżnialne).
◦
Interpretacja (znaczenie) danych nie jest
przechowywane wraz z nimi.
◦
Instrukcje są wykonywane sekwencyjnie.

Nomenklatura
Nomenklatura
Procesor – Central Processing Unit (CPU)
= Arithmetic/Logic Unit (ALU) + Control Unit
Pamięć operacyjna – Random Access Memory
(RAM)
Urządzenia wejścia/wyjścia – Input/Output (I/O)
Płyta główna – Motherboard (MB)
Układ sterowania – Chipset
Jednostka zmiennoprzecinkowa – Floating Point
Unit (FPU)
Pamięć stała (tylko do odczytu) – Read-Only
Memory (ROM)

Modularna budowa komputera PC
Modularna budowa komputera PC
Standaryzacja elementów w oparciu o
publicznie dostępne specyfikacje
Otwarta architektura urządzeń
wejścia/wyjścia

Modularna budowa komputera PC
Modularna budowa komputera PC
Płyta główna - tablica obwodów drukowanych
łączących wszystkie elementy komputera wraz ze
sterującymi układami elektronicznymi i standardowymi
gniazdami I/O.
µ
-procesor - układ scalony b. wysokiej skali integracji.
Chipset - układy sterujące połączeniami płyty głównej.
Pamięć RAM - w postaci modułów dołączanych do płyty
głównej.
Urządzenia wejścia/wyjścia - np. klawiatura, dysk twardy
(pamięć masowa), karta graficzna, mysz, itp. - dołączane
do płyty głównej poprzez gniazda (porty) I/O.

Uzupełnienie tematu
Uzupełnienie tematu
1. Rodziny procesorów
2. Pamięć RAM-rodzaje.
3. Magistrale wejścia/wyjścia
4. Urządzenia I/O –rodzaje,, przykłady
producentów
5. Dyski twarde/optyczne- opis, producenci
6. Karty graficzne-rodzaje

Zarys działania komputera PC
Zarys działania komputera PC
Inicjalizacja systemu – BIOS (Basic
Input/Output System) umieszczony w ROM
◦
testowanie podstawowych elementów
komputera (POST- Power On Self Test),
◦
rozpoznanie konfiguracji sprzętowej,
◦
odnalezienie urządzenia startowego (boot device)
◦
załadowanie programu ładującego (loader) z
pierwszego sektora urządzenia (boot sector),
◦
ładowanie systemu operacyjnego przez loader.

Zadania systemu operacyjnego
Zadania systemu operacyjnego
Zadania systemu operacyjnego:
◦
ponowne rozpoznanie konfiguracji sprzętowej
(załadowanie programowych sterowników urządzeń),
◦
uruchomienie domyślnej konfiguracji programowej,
◦
obsługa zadań generowanych przez urządzenia I/O (tzw.
przerwań – interrupts),
◦
ładowanie programów użytkowych do pamięci,
◦
udostępnianie zasobów sprzętowych programom
użytkowym – pamięć wirtualna, wielozadaniowość,
obsługa komunikacji z urządzeniami I/O,
◦
usuwanie programów z pamięci.

Logika
Logika

Logika klasyczna zajmuje się tylko niektórymi zdaniami, które można
wypowiedzieć w języku polskim
Zdaniami podmiotowymi orzekającymi, o których można jednoznacznie
stwierdzić, czy są prawdziwe, czy fałszywe.
Przykłady:
Warszawa jest stolicą Polski.
3*5 = 15
Warszawa jest stolicą Norwegii. (to akurat zdanie jest fałszywe)
Słońce krąży dookoła Ziemi.
Nie są zaś zdaniami w sensie logicznym:
Wiele jarzyn jest paskudnych. (co to znaczy "wiele"? tego nie można stwierdzić
jednoznacznie)
Która godzina?
Kończ waść, wstydu oszczędź.
x > 4 (nie wiemy, co to jest "x")
Hurra!
itd.
Jeśli zdanie jest prawdziwe, mówimy, że ma wartość logiczną 1, jeśli fałszywe - 0.

Wstęp
Wstęp
Logika (gr.
, logos - rozum) nauka normatywna, analizująca źródła
λόγος
poznania pod względem prawomocności czynności poznawczych z nimi
związanych. Zajmuje się badaniem ogólnych praw, według których przebiegają
wszelkie poprawne rozumowania w szczególności wnioskowania. Logika, jako
dyscyplina normatywna, nie tylko opisuje jak faktycznie przebiegają rozumowania,
ale także formułuje twierdzenia normatywne, mówiące o tym, jak rozumowania
powinny przebiegać.
Logika matematyczna, to dział matematyki, który wyodrębnił się jako samodzielna
dziedzina na przełomie XIX i XX wieku, wraz z dążeniem do dogłębnego zbadania
podstaw matematyki. Koncentruje się on na analizowaniu zasad rozumowania
oraz pojęć z nim związanych z wykorzystaniem sformalizowanych oraz
uściślonych metod i narzędzi matematyki

Zdania w sensie logicznym
Zdania w sensie logicznym
— DEFINICJA
Zdanie w sensie logicznym
- zdanie oznajmujące, któremu
można przypisać jedną z dwóch wartości -prawda lub fałsz. Przyjmujemy, że
symbolem prawdy jest 1, a 0 jest symbolem fałszu.
— DEFINICJA
Zmienną logiczną
nazywamy zmiennaą w miejsce której
wstawiamy zdania (prawdziwe lub fałszywe), otrzymując zdania w sensie
logicznym. Najczęściej zmienne zdaniowe oznaczamy małymi literami: p, q,
r, . . . .
— Wartość logiczną zdania p oznaczamy symbolem w(p):
w(p) = 0 – p jest zdaniem fałszywym
w(p) = 1 – p jest zdaniem prawdziwym
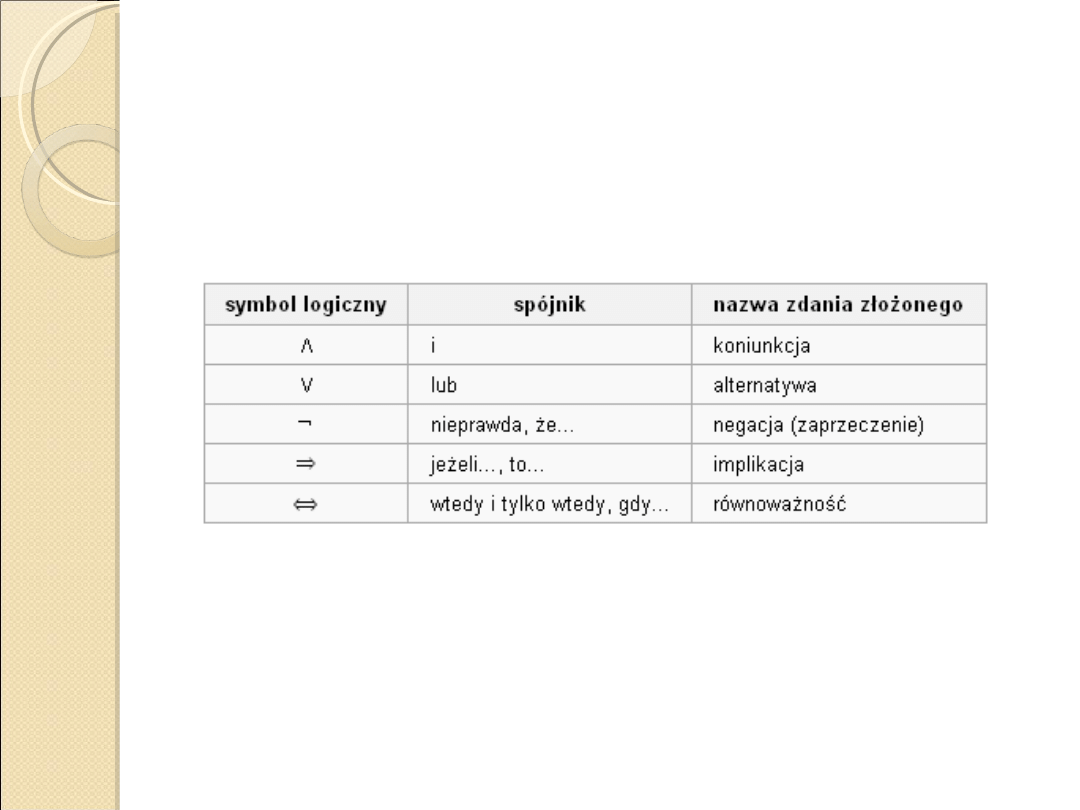
Funktory zdaniotwórcze
Funktory zdaniotwórcze
Ze zdań logicznych możemy tworzyć zdania złożone przy pomocy spójników
logicznych (funktorów zdaniotwórczych) oraz nawiasów.
Zastanów się teraz, które z poniższych zdań może być prawdziwe?
„Księżyc krąży wokół Ziemi i pies ma osiem łap”.
„Księżyc krąży wokół Ziemi lub pies ma osiem łap”.
„Księżyc krąży wokół Ziemi wtedy i tylko wtedy, gdy pies ma osiem łap”.
„Jeśli pies ma osiem łap, to Księżyc krąży wokół Ziemi”.
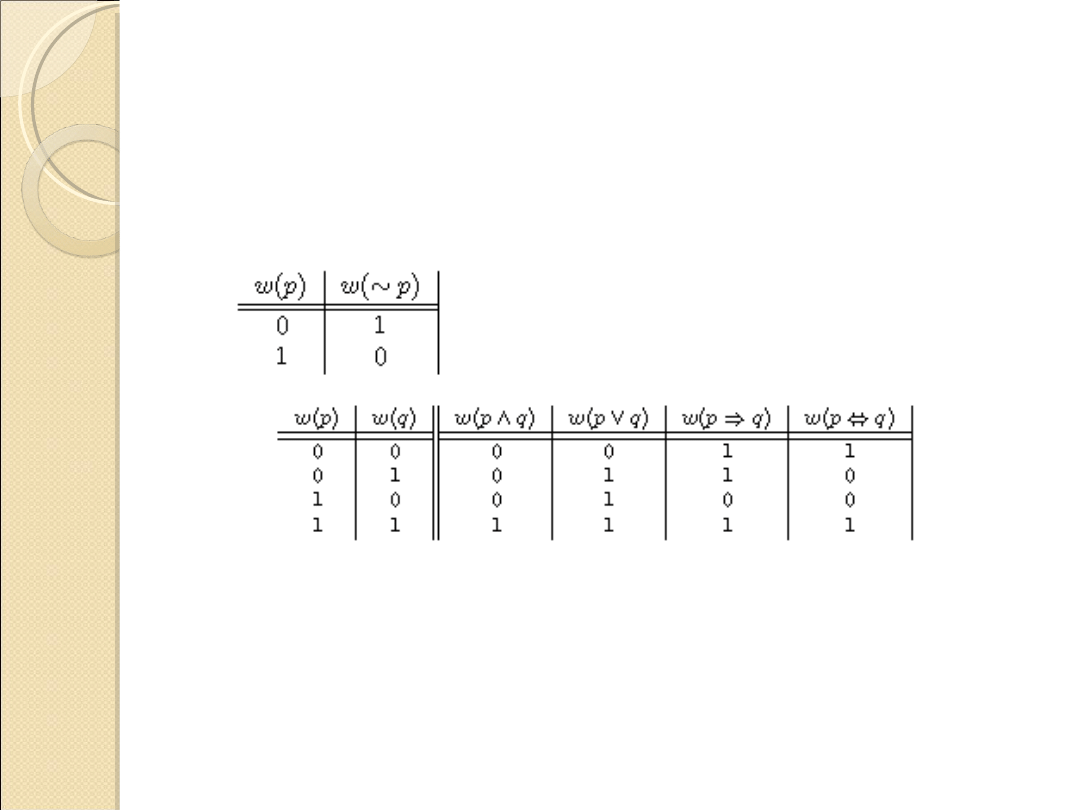
Definicja spójników logicznych
Definicja spójników logicznych

Tautologie
Tautologie
DEFINICJA
Tautologia
lub prawem rachunku zdań nazywamy formułę
logiczna, która jest prawdziwa bez względu na wartość logiczna
występujących w niej zmiennych zdaniowych. Ozn. t.
DEFINICJA Zdaniem sprzecznym
nazywamy formułę logiczna, która jest
fałszywa bez względu na wartość logiczna występujących w niej zmiennych
zdaniowych. Ozn. f.
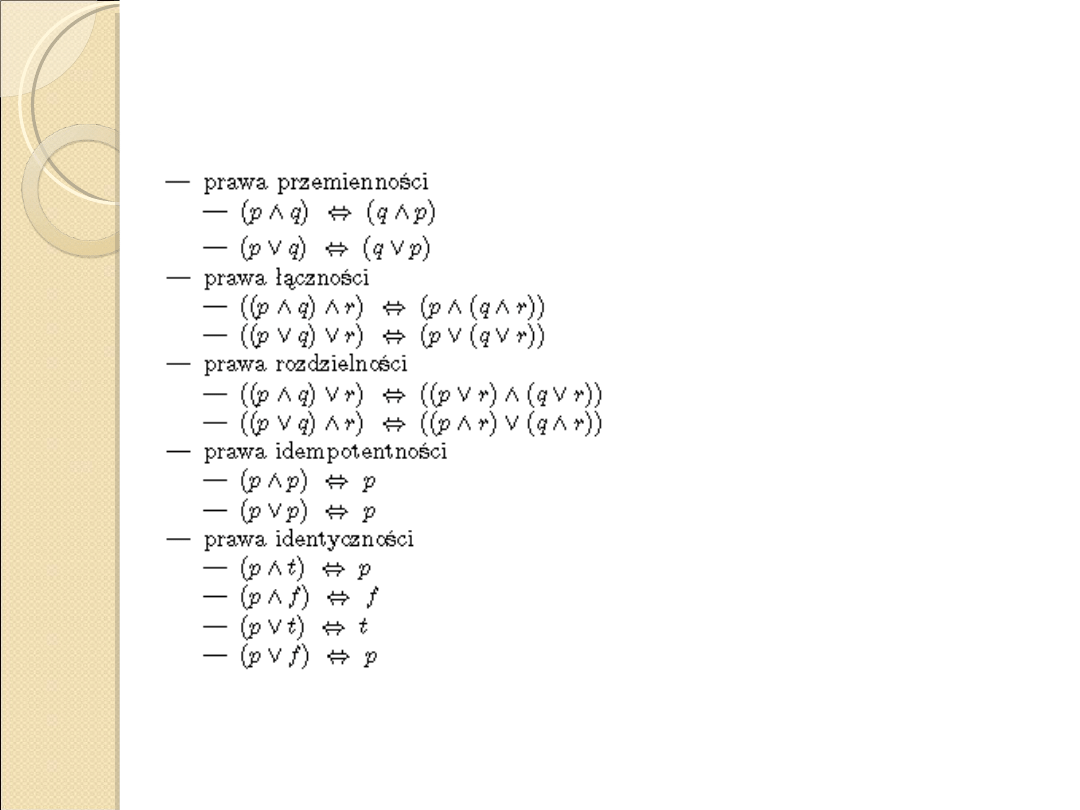
Prawa rachunku zdań cz.1
Prawa rachunku zdań cz.1

Prawa rachunku zdań cz.II
Prawa rachunku zdań cz.II

Działania na zbiorach
Działania na zbiorach

Zbiory
Zbiory

Suma zbiorów
Suma zbiorów

Iloczyn zbiorów
Iloczyn zbiorów

Różnica zbiorów
Różnica zbiorów

Różnica symetryczna
Różnica symetryczna

Dopełnienie zbiorów
Dopełnienie zbiorów

Własności działań na zbiorach
Własności działań na zbiorach

Własności działań na zbiorach
Własności działań na zbiorach
Document Outline
- Slajd 1
- Slajd 2
- Slajd 3
- Slajd 4
- Slajd 5
- Slajd 6
- Slajd 7
- Slajd 8
- Slajd 9
- Slajd 10
- Slajd 11
- Slajd 12
- Slajd 13
- Slajd 14
- Slajd 15
- Slajd 16
- Slajd 17
- Slajd 18
- Slajd 19
- Slajd 20
- Slajd 21
- Slajd 22
- Slajd 23
- Slajd 24
- Slajd 25
- Slajd 26
- Slajd 27
- Slajd 28
- Slajd 29
- Slajd 30
- Slajd 31
- Slajd 32
- Slajd 33
Wyszukiwarka
Podobne podstrony:
fetch datenblatt attiny26
fetch datenblatt 24c64
fetch datenblatt cny70
fetch datenblatt lm358
Fetch 5 5 1 SN
fetch datenblatt ntc02
więcej podobnych podstron