1
Fizyka
promieniowania
jonizującego
Zygmunt Szefliński
1
Fizyka
promieniowania
jonizującego
Zygmunt Szefliński
Wykład 3
2
Ogólne własności jąder atomowych
(masy ładunki, izotopy, izobary, izotony izomery).
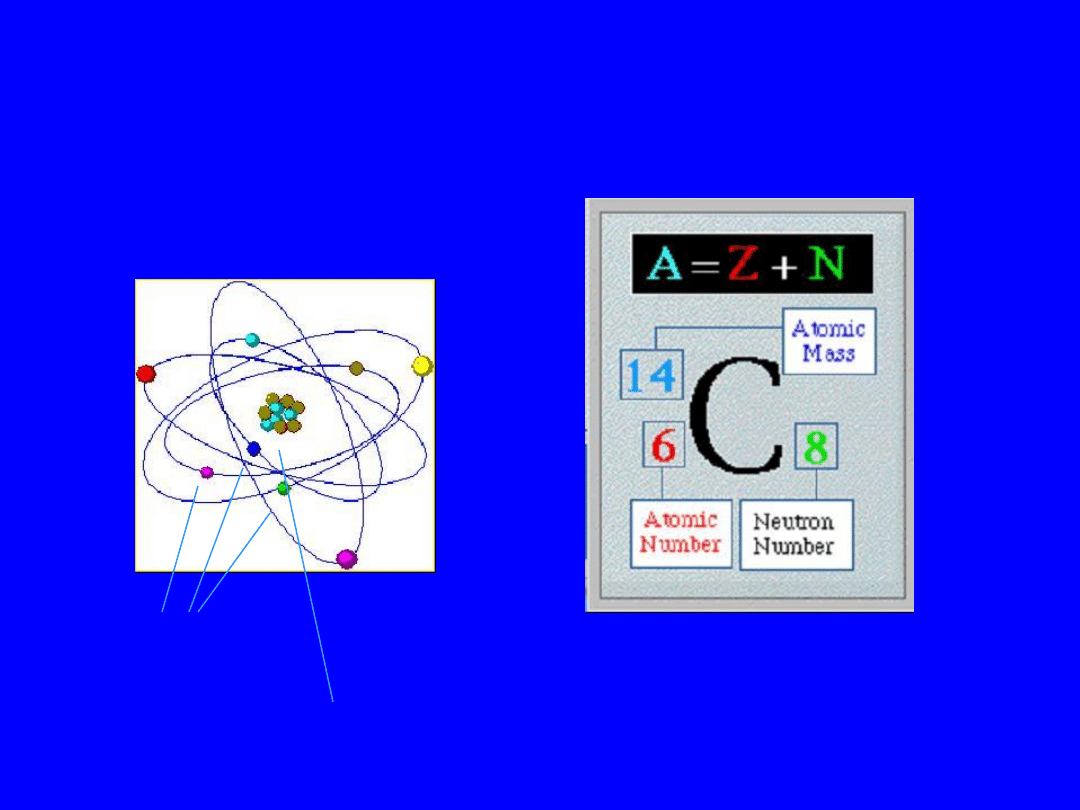
Liczba atomowa i masowa
Liczba nukleonów (protonów i neutronów) w jądrze to liczba
masowa (A), która jest liczbą całkowitą, zbliżoną do masy atomowej
pierwiastka.
Liczba atomowa, decydująca o właściwościach chemicznych
pierwiastka, to liczba protonów w jądrze, decyduje ona o ładunku jądra i
jednocześnie o liczbie elektronów w powłoce atomowej, a jest oznaczana
symbolem Z. Liczba neutronów jest oznaczana symbolem N.
Liczba masowa, A=N+Z wskazuje ile razy atom cięższy jest od
atomu wodoru.
Tylko nieliczne substancje
chemiczne składają się tylko z
jednego rodzaju atomów.
3
Budowa jader (A, Z)
4
C
12
6
He
4
2
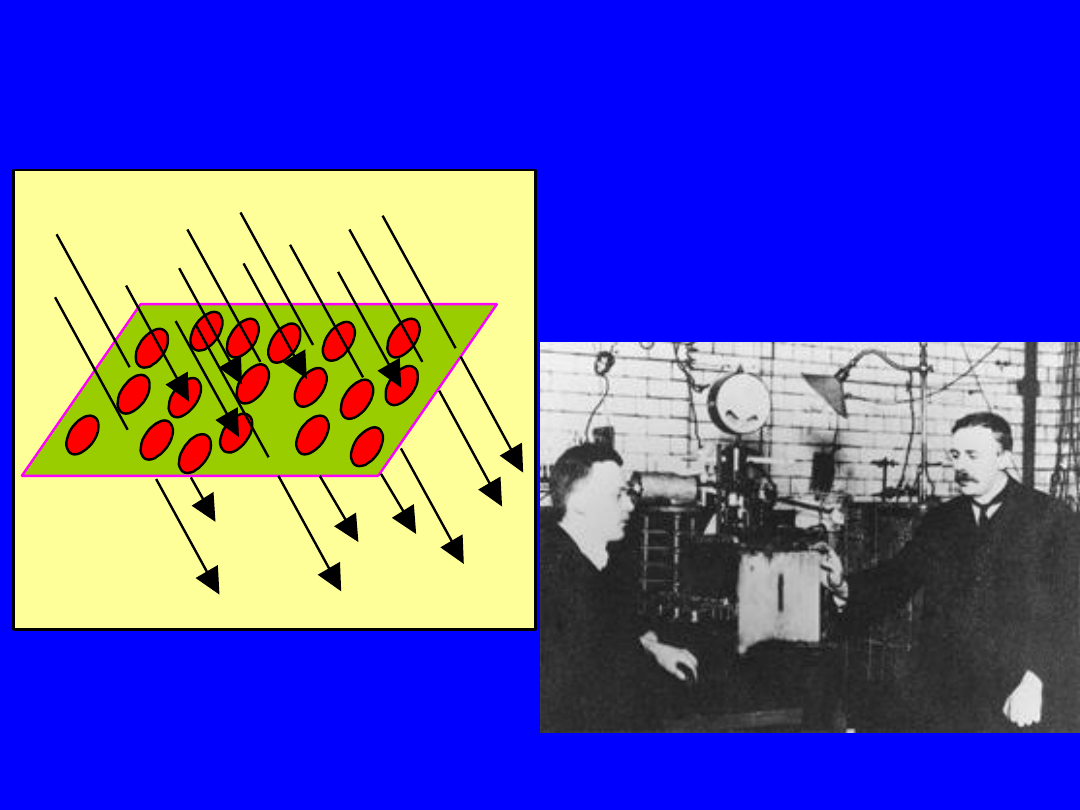
5
Odkrycie jądra atomowego
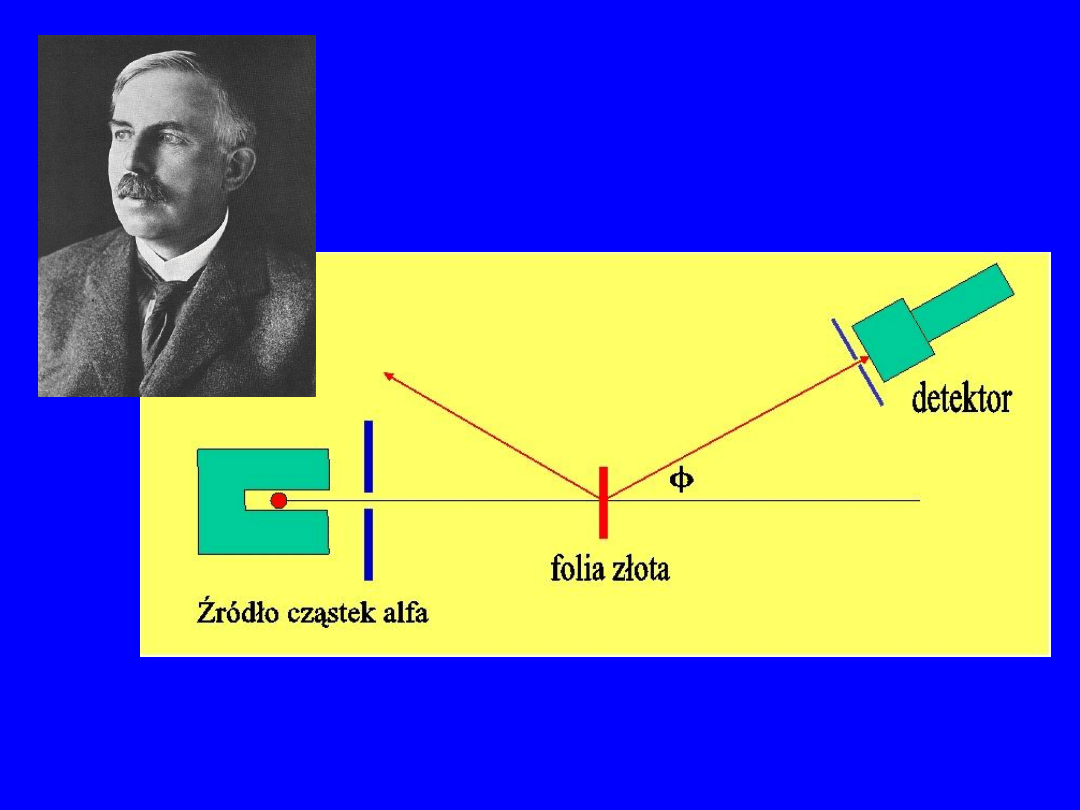
6
Odkrycie jądra
atomowego
Przykładowe bezwzględne wartości promieni jader atomowych to: R
(He)=2 fm, R(Mg)= 4 fm, , R( U ) = 7,5 fm, fm=10
-15
m).
Przedstawienie modelowe
m
r
jadra
15
10
4
m
r
atomu
11
10
5
Mała moneta, d=1cm
Wysoka wieża, h=10
4
cm = 100m
7
Rozmiary atomów i jąder
8
m
10
10
~
m
14
10
~
m
2
10
~
m
2
10
~
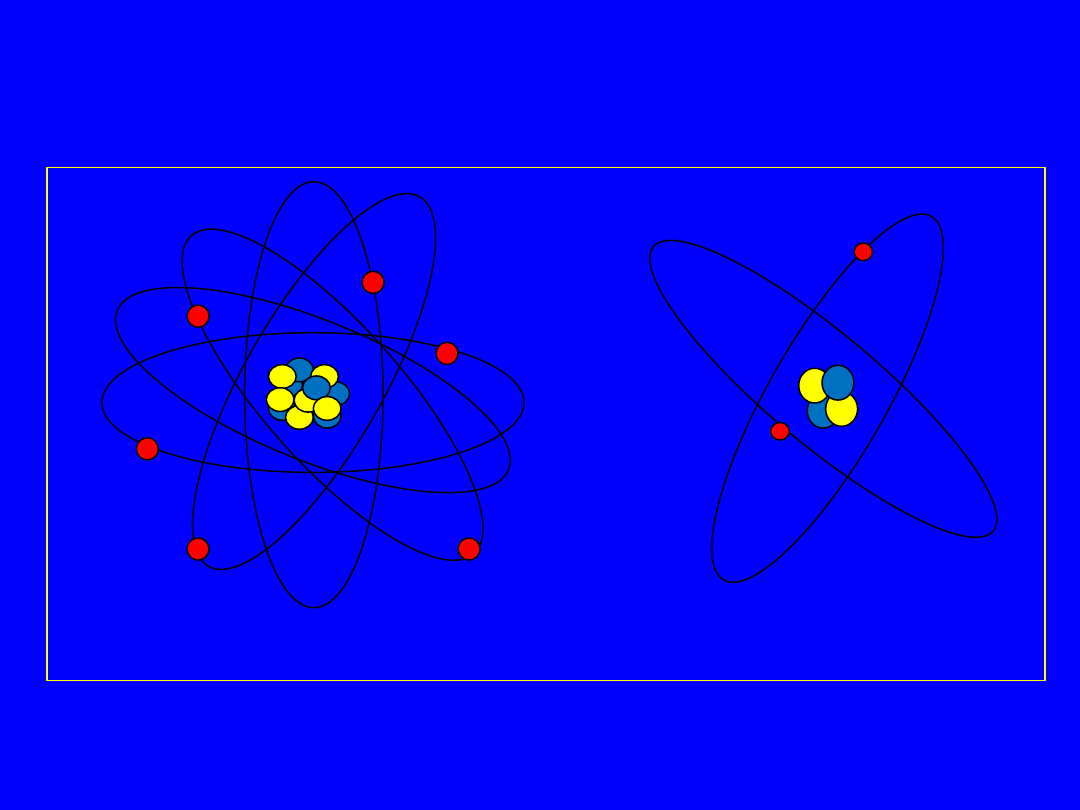
Przykładowe atomy -schemat
9
helu
Atom
wegla
Atom
10
Składniki jądra protony i neutrony
nuklid - jądro o określonej liczbie masowej (A)
i ładunku (Ze ) a symbol X określa atom
pierwiastka chemicznego o liczbie atomowej Z.
Jednocześnie Z określa liczbę protonów w
nuklidzie, A - liczbę nukleonów (protonów i
neutronów). Wszędzie, gdzie nie budzi to
nieporozumień, terminu nuklid będziemy
używać zarówno dla określenia atomu, jak i
odpowiedniego jądra. W przypadku, gdy
rozważania mają charakter ilościowy,
wymagający uwzględnienia mas, przez masę
nuklidu będziemy rozumieć masę neutralnego
atomu.
X
A
Z
Masy nuklidów
11
Praktycznie masę atomową Aw danego pierwiastka wyraża
liczba określająca, ile razy masa atomu jest większa od 1/12
masy nuklidu
12
C
Z podanej zależności wynika, że znając masę atomową
pierwiastka można obliczyć masę jego atomu wyrażoną w kg.
ma(kg) = Aw*1,6605*10
-27
Przykład obliczenia masy atomu wapnia mCa =
40,08*1,6605*10
-27
= 6,65*10
-26
kg
Wartości mas atomowych Aw wyrażone w jednostkach mas
atomowych (u) odczytujemy z układu okresowego
pierwiastków
Przykład dla helu (He) Hel(He) - 4,003u.
12
Pojęcia fizyki jądrowej
•izotopy – to nuklidy o tym samym Z, lecz różnej
liczbie neutronów, a zatem o różnej liczbie
masowej A
•izobary -nuklidy o tej samej liczbie masowej A,
lecz różnych liczbach atomowych, Z
•izotony - nuklidy o tej samej liczbie neutronów
(A-Z), lecz różnych wartościach A i Z,
•izomery - nuklidy o tej samej liczbie masowej A
i atomowej, Z, lecz różniące się masą (energią)
jądra. Są to stosunkowo długo żyjące stany
wzbudzone nuklidów
,
,
,
3
1
2
1
1
1
H
H
H
6
14
7
14
8
14
C
N
O
,
,
B
Be
Li
He
9
5
8
4
7
3
6
2
,
,
,
*
X
A
Z
13
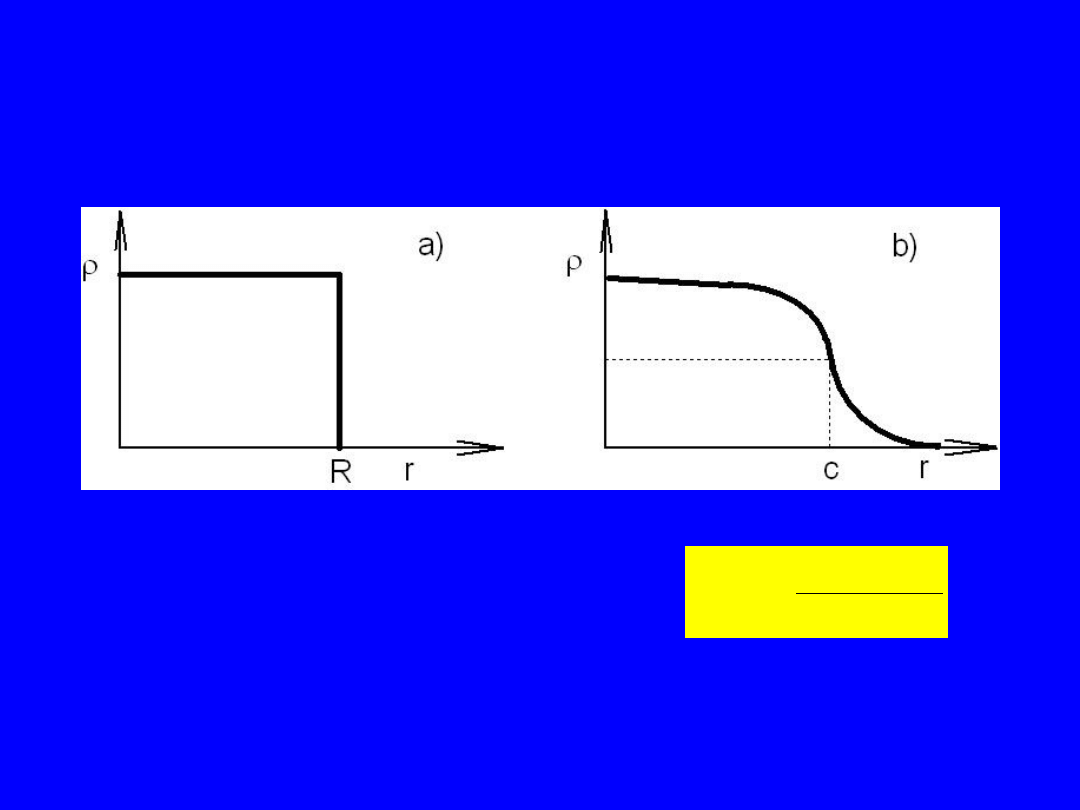
Rozmiary i kształty jąder
( )
(
)/
r
e
r c a
1
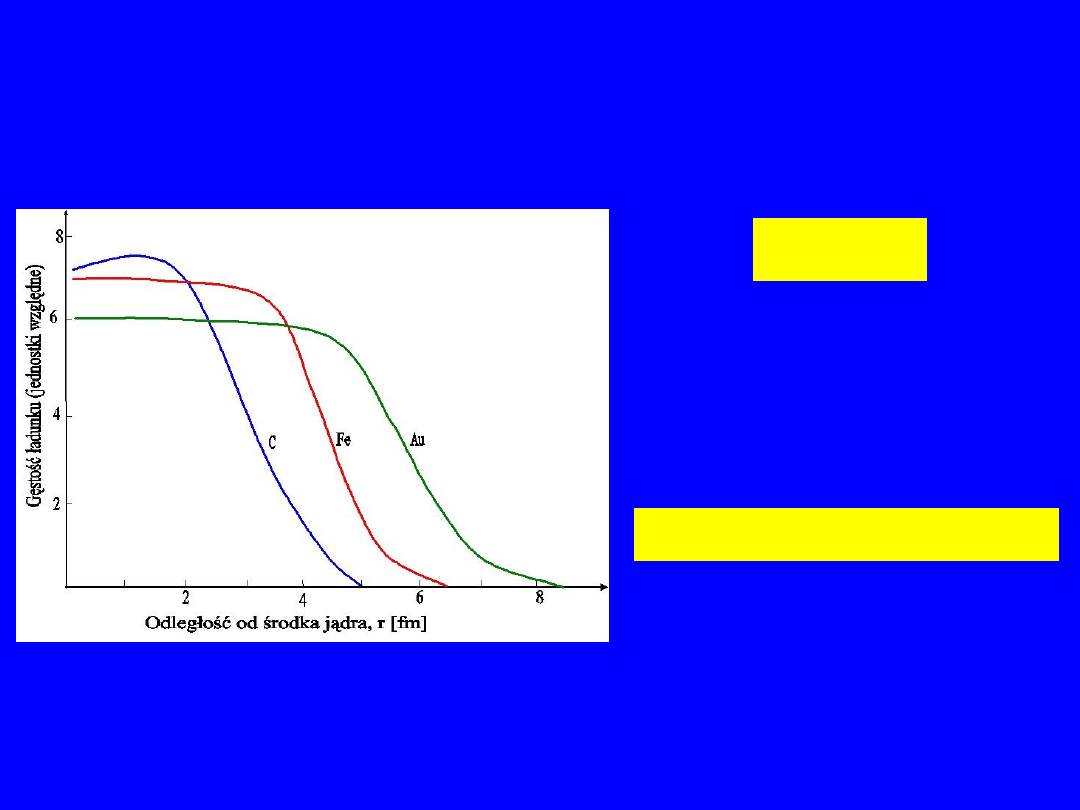
14
Rozkłady ładunku
3
/
1
0
A
r
R
Gdzie r
0
jest
parametrem o
przybliżonej wartości
ok 1.2 fm.
fm
fm
R
Sn
6
5
2
,
1
125
50
15
Przykład rozmiarów
16
Kształty jąder
• Jądra, zwane magicznymi są sferyczne
• Liczby nukleonów tworzące zamknięte powłoki nazywamy liczbami
magicznymi. Liczby magiczne są różne dla protonów i neutronów, a liczby
definiujące zamknięte powłoki protonowe i neutronowe to:
• 2, 8, 20 (28)., 50, 82, 126, (184) dla neutronów,
• 2, 8, 20 (28)., 50, 82, (114) dla protonów.
• Jądra, dalekie od liczb magicznymi są niesferycne
Ca
O
Sn
48
20
16
8
132
50
,
,
Wykład 4.
17
Ogólne własności jąder atomowych
(masy ładunki, izotopy, izobary, izotony izomery).
18
Identifikacja izotopów
Jądro
Atom
Elektrony
Energia wiązania jąder
19
A
Z
M
Z
m
N
m
B
p
n
,
Pomiary mas jąder M (Z,A) prowadzą do stwierdzenia, że
różnica między sumą mas składników a masą złożonego z
nich jądra jest wielkością różną od zera, dodatnią, różną dla
różnych jąder.
Energię wiązania można określić jako ilość energii, koniecznej
do pełnego rozbicia jądra na wszystkie jego składniki. Np.
energia wiązania deuteronu (jądra ) wynosi 2.224 MeV
n
p
H
2
1
Energia wiązania cząstki alfa (jądra He) wynosi około 27 MeV.
Energia wiązania He
20
A
Z
M
Z
m
N
m
B
p
n
,
M
p
M
n
= 931,494 MeV/c
2
M
= 4.00150
2,0146+2,0173=4,0319
4,0319-4,0015=0,0304
0,0304*931,5
28 MeV
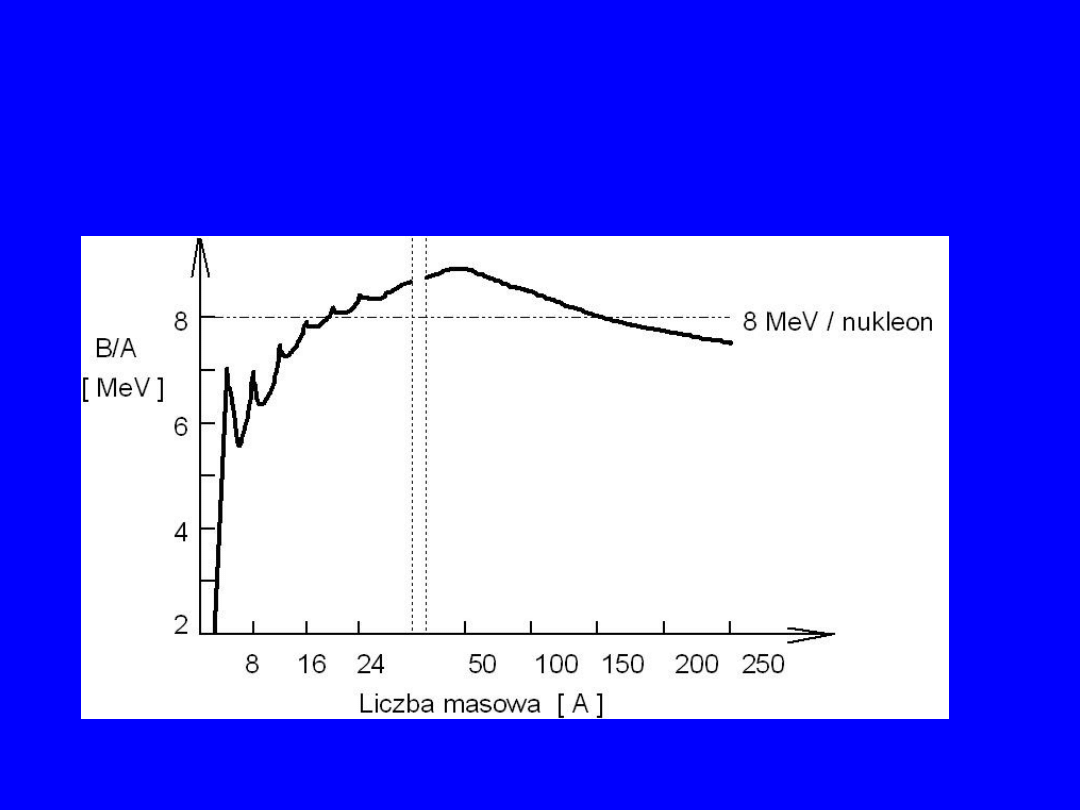
Energia wiązania nukleonu
21
Często rozważa się wartość energii wiązania przypadającej -
średnio - na jeden nukleon, B/A
Przebieg energii wiązania B/A
22
Mimo pewnych nieregularności, można sformułować następujące wnioski z
przebiegu zależności B/A w funkcji A:
1.
fakt, że energie wiązania są dodatnie - (mimo odpychania kolumbowskiego
między protonami) świadczy o istnieniu silnych oddziaływań
przyciągających, działających między nukleonami,
2.
dla małych liczb masowych wartość B/A rośnie szybko z liczbą nukleonów
A (każdy "nowododany" nukleon wzmacnia wiązanie),
3.
dla średnich liczb masowych wzrost staje się coraz wolniejszy aż do
szerokiego maksimum (średnio ciężkie jądra z obszaru A~60, mają tę samą
energię wiązania przypadającą na jeden nukleon). Świadczy to o krótkim
zasięgu sił oddziaływania nukleon-nukleon (N-N) gdyż "nowo-dodane"
nukleony nie oddziaływają już praktycznie z odległymi nukleonami w
centrum. Efekt ten nazywamy "wysycaniem sił jądrowych",
4.
dla ciężkich jąder wartość B/A powoli maleje, co świadczy o wzmagającej
się roli kulombowskiego odpychania między coraz liczniejszymi protonami.
Energia separacji
23
Energię niezbędną dla oderwania od jądra jednego nukleonu
(neutron, proton), z reguły różniącą się od wielkości B/A,
nazywamy energią separacji neutronu (Sn) czy protonu (Sp).
Energię separacji definiuje się jako różnicę między sumą masy
"odrywanej" cząstki i pozostałego jądra, a masą jądra
początkowego.
Energia separacji neutronu i protonu to:
A
Z
M
A
Z
M
m
S
n
n
,
)
1
,
(
A
Z
M
A
Z
M
m
S
p
p
,
)
1
,
1
(
24
Radioaktywność
• Radioaktywność to własność jąder atomowych
• Dzięki tej własności jądro może być niestabilne i
podlegać przemianom jądrowym. Ten proces może
być szybki (krótki czas życia) lub wolny (długi czas
życia).
• Nigdy, czas przemiany nie może być przewidziany
dla danego jądra – to zdarzenie przypadkowe
opisywane prawami statystycznymi.
XI-2010
25
Przemiany spontaniczne
Spontanicznymi nazywamy procesy realizowane
samorzutnie, w odróżnieniu od reakcji, dla których niezbędne jest
oddziaływanie między "pociskiem" a "tarczą". Mówimy wówczas
o przemianie spontanicznej, bądź o rozpadzie.
Podstawową charakterystyką przemiany spontanicznej jest
prawdopodobieństwo jej realizacji. Miarą jego jest stała zaniku
,
lub jej odwrotność,
=1/
, czyli średni czas życia .
W fizyce jądrowej, rozważając przemiany
promieniotwórcze, często używa się innej wielkości okres
połowicznego zaniku, T
1/2
=
ln 2.
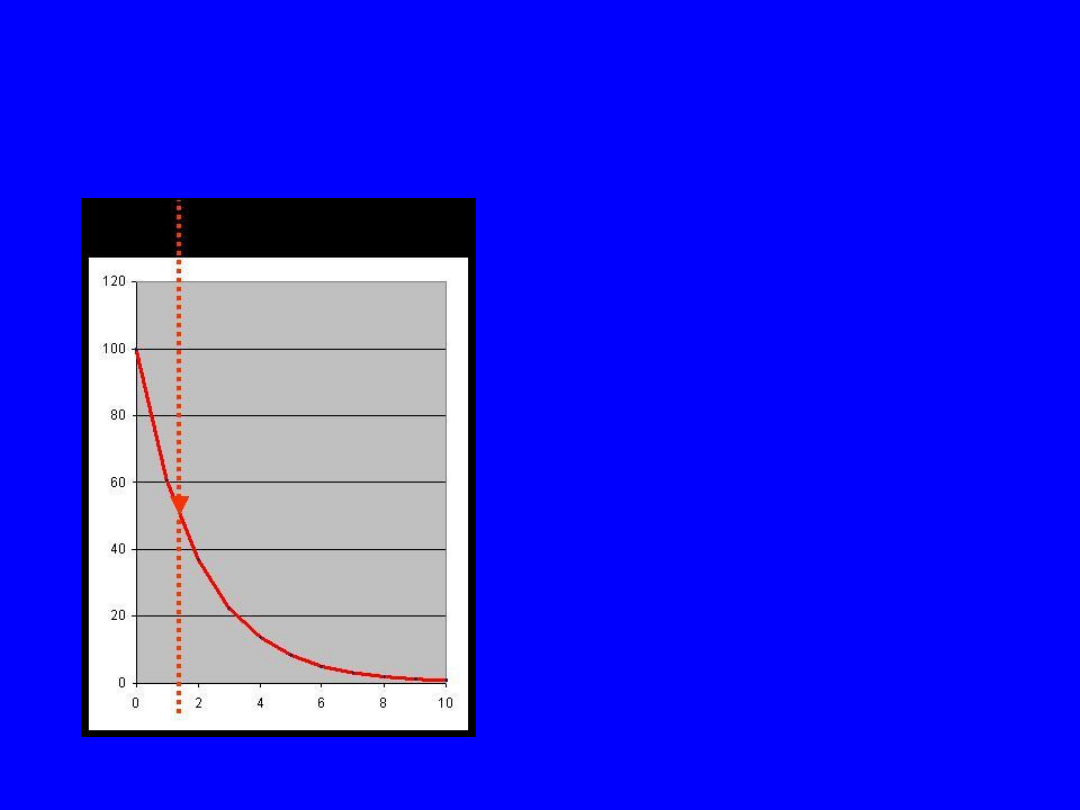
26
Czas połowicznego zaniku T
1/2
• Opisuje jak szybko
zachodzi proces
przemiany jadrowej
• T
1/2
to czas przemiany
połowy materiału
radioaktywnego
(liczba rozpadów w
jednostce czasu maleje
do połowy)
27
A(t) = A(0) exp(-t ln2 / t
1/2
)
• A(t)
aktywność w czasie t
• A(0)
poczatkowa aktywność w czasie 0
• t
czas
• t
1/2
czas połowicznego zaniku
XI-2010
28
Prawo rozpadu promieniotwórczego
Rozpady obiektów nietrwałych podlegają
statystycznemu prawu, które można zapisać w
postaci;
N
N t
N
dt
dN
Rozwiązanie:
t
e
N
N
0
Rozwiązanie po zlogarytmowaniu:
t
N
N
0
ln
ln
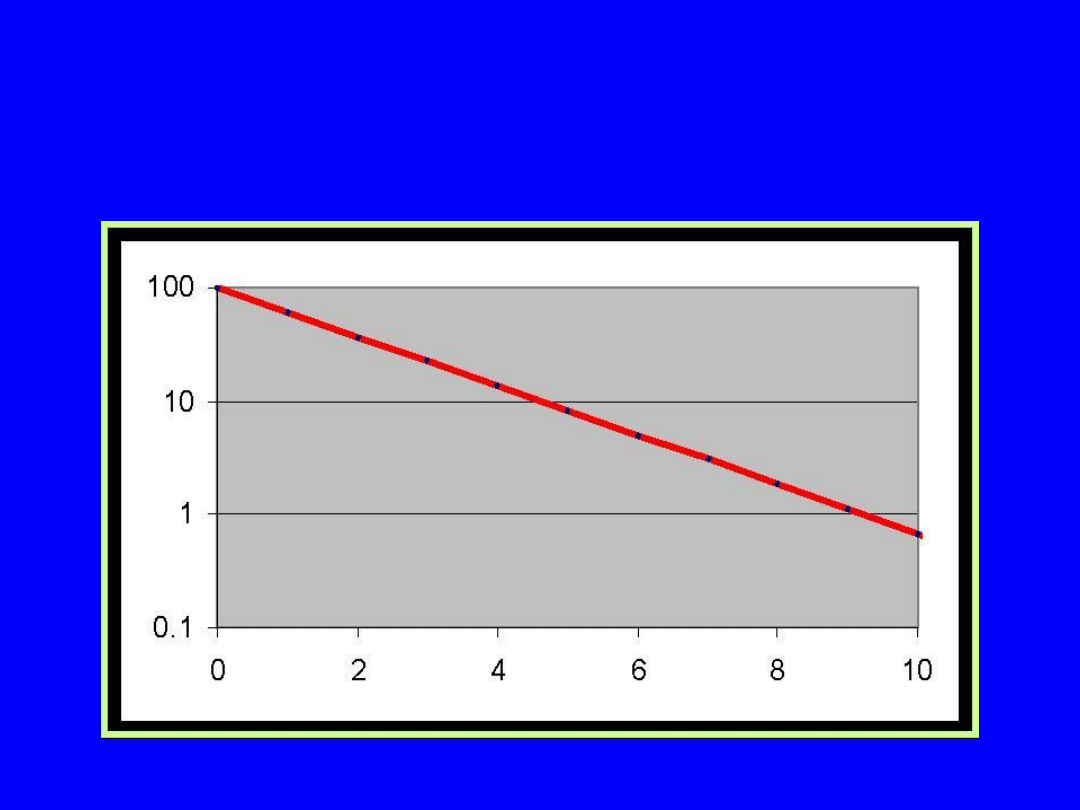
29
Czas zaniku – wykres logarytmiczny
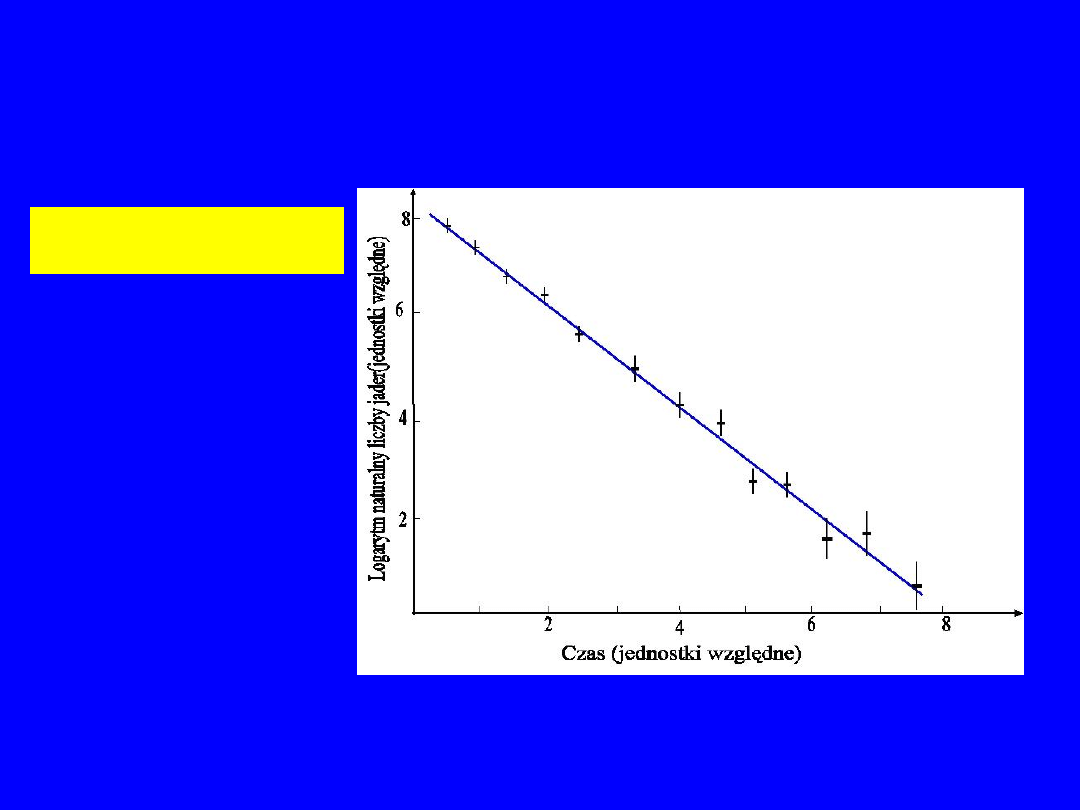
XI-2010
30
Prawo rozpadu promieniotwórczego
t
N
N
0
ln
ln
Krzywa rozpadu promieniotwórczego w skali logarytmicznej
XI-2010
31
Aktywność źródła
Aktywnością promieniotwórczej próbki
nazywamy liczbę rozpadów, zachodzących w
jednostce czasu.
Jednostki aktywności to:1Ci - 1 kiur
1 Ci=3.7
10
10
rozpadów na sekundę,
oraz znacznie mniejsza jednostka:
1Bq = 1bekerel = 1 rozpad na sekundę.
32
Typy radioaktywności
(rozpadów)
• Rozpad alfa (jądra Helu) - “ciężka”,
ładunek +2e, silnie oddziałująca z materią
• Rozpad beta, promieniowanie beta
(elektrony) – lekkie cząstki, słabo
oddziałująca z materią, skończony zasięg.
• Promieniowanie gamma (fotony)
Wykład 5
33
Promieniowanie elektromagnetyczne
atomów – promieniowanie X
(widmo liniowe, promieniowanie charakterystyczne,
układ okresowy pierwiastków).
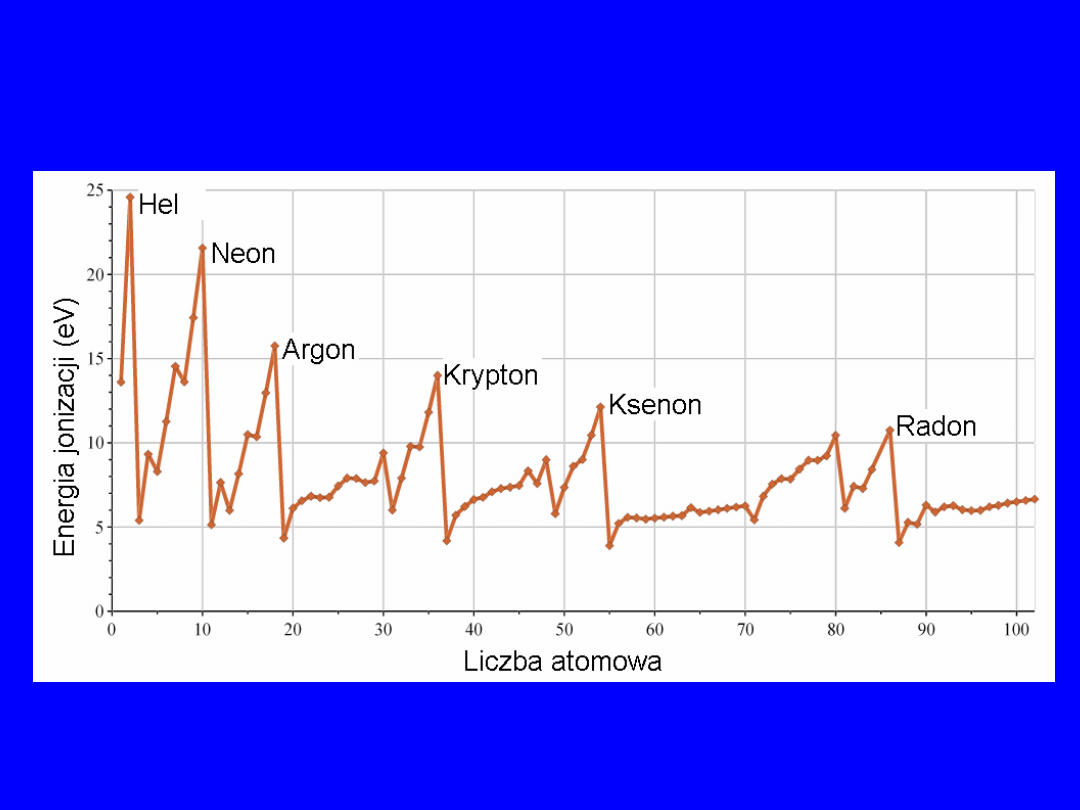
Potencjały jonizacyjne
34
Podpowłoki
Tab. Oznaczenia literowe podpowłok
l
0
1
2
3
4
5
Oznaczenie
s
p
d
f
g
h
Już w roku 1915 Sommerfeld wprowadził kolejną
liczbę kwantową l, zwaną orbitalna liczbą kwantową,
charakteryzującą moment pędu, pozostawiając
główną liczbę kwantową n charakteryzującą średnią
odległość elektronu od jądra. Okazało się, że orbitalna
liczba kwantowa może przyjmować wartości od zera
do n-1
35
Inne liczby kwantowe
Z orbitalnym momentem pędu związany jest moment
magnetyczny, co oznacza, że w polu magnetycznym, na każdą orbitę
działa moment siły dążący do ustawienia wektora momentu
magnetycznego wzdłuż pola. Taki moment siły wywołuje precesję
Larmora, co wprowadza dodatkowe stany energetyczne układu,
opisywane kolejną liczba kwantową m, zwaną magnetyczną liczba
kwantową.
Magnetyczna liczba kwantowa może przyjmować całkowite
wartości od –l do l , co oznacza że dla każdego stanu o momencie
pędu l istnieje 2l+1 podstanów, różniących się magnetyczną liczba
kwantową.
Dla wyjaśnienia struktury subtelnej linii widmowych
Uhlenbeck i Goudsmit wprowadzili spinowa liczbę kwantową
elektronu, s. Spin elektronu, który znalazł się w rozwiązaniu
równania Diraca, może przyjmować dwie wartości,-1/2 i +1/2 .
36
Budowa powłok elektronowych
Właściwości pierwiastka
Liczby kwantowe
Konfiguracja elektronów
Pier-
wiastek
Z
Pierwszy potencjał
jonizacji (eV)
n
l
m
s
K
L
M
N
H
He
1
2
13,6
24,6
1
1
0
0
0
0
-1/2
+1/2
1
2
Li
Be
B
C
N
O
F
Ne
3
4
5
6
7
8
9
10
5,4
9,3
8,3
11,3
14,5
13,6
17,4
21,6
2
2
2
2
2
2
2
2
0
0
1
1
1
1
1
1
0
0
-1
-1
0
0
+1
+1
-1/2
+1/2
-1/2
+1/2
-1/2
+1/2
-1/2
+1/2
2
2
2
2
2
2
2
2
1
2
3
4
5
6
7
8
Na
Mg
Al.
Si
P
S
Cl
Ar
11
12
13
14
15
16
17
18
5,1
7,6
6,0
8,2
10,6
10,4
13,0
15,8
3
3
3
3
3
3
3
3
0
0
1
1
1
1
1
1
0
0
-1
-1
0
0
+1
+1
-1/2
+1/2
-1/2
+1/2
-1/2
+1/2
-1/2
+1/2
2
2
2
2
2
2
2
2
8
8
8
8
8
8
8
8
1
2
3
4
5
6
7
8
K
19
4,3
4
0
0
-1/2
2
8
8
1
37
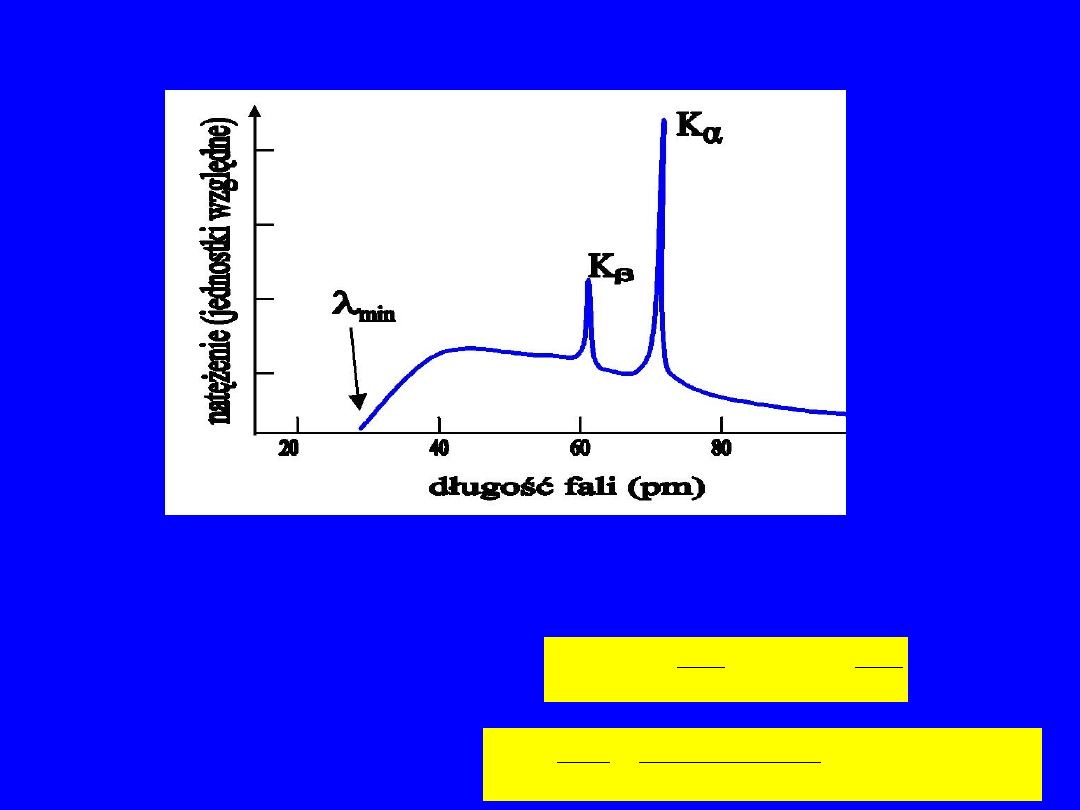
Promieniowanie X
e
e
E
c
c
h
E
2
2
min
min
max
Granica krótkofalowa jest zdefiniowana przez energię kinetyczną elektronów
padających na tarczę, gdyż maksymalna energia promieniowania hamowania nie
może przekroczyć energii kinetycznej elektronu. Dla energii kinetycznej E
e
,
możemy wyliczyć granicę krótkofalową
pm
fm
MeV
fm
MeV
E
c
e
31
10
31
10
40
197
2
2
3
3
min
Dla E
e
=40 keV mamy:
38
Energie rentgenowskie
39
Energia wiązania elektronu ciężkich pierwiastków jest znacznie wyższa
niż wyliczyliśmy dla atomu wodoru .Ponieważ energia ta jest
proporcjonalna do Z
2
, możemy oczekiwać, że np. dla miedzi może ona
osiągnąć wartości prawie trzy rzędy wyższe niż obserwowaliśmy w
atomie wodoru i odpowiednio krótsze długości fal. Poziomy dla powłok
wyższych niż K, są w rzeczywistości grupami poziomów, opisanymi
różnymi liczbami kwantowymi l, m i s.
Jeśli napięcie przyłożone do antykatody przewyższa istotnie wartość energii
powłoki K (n=0), to elektrony będą traciły energie na kilka sposobów:
• na ogrzewanie antykatody,
• na emisję ciągłego promieniowania hamowania,
• na wybicie elektronu z wewnętrznej powłoki antykatody, co wiąże się
z emisją promieniowania charakterystycznego.
40
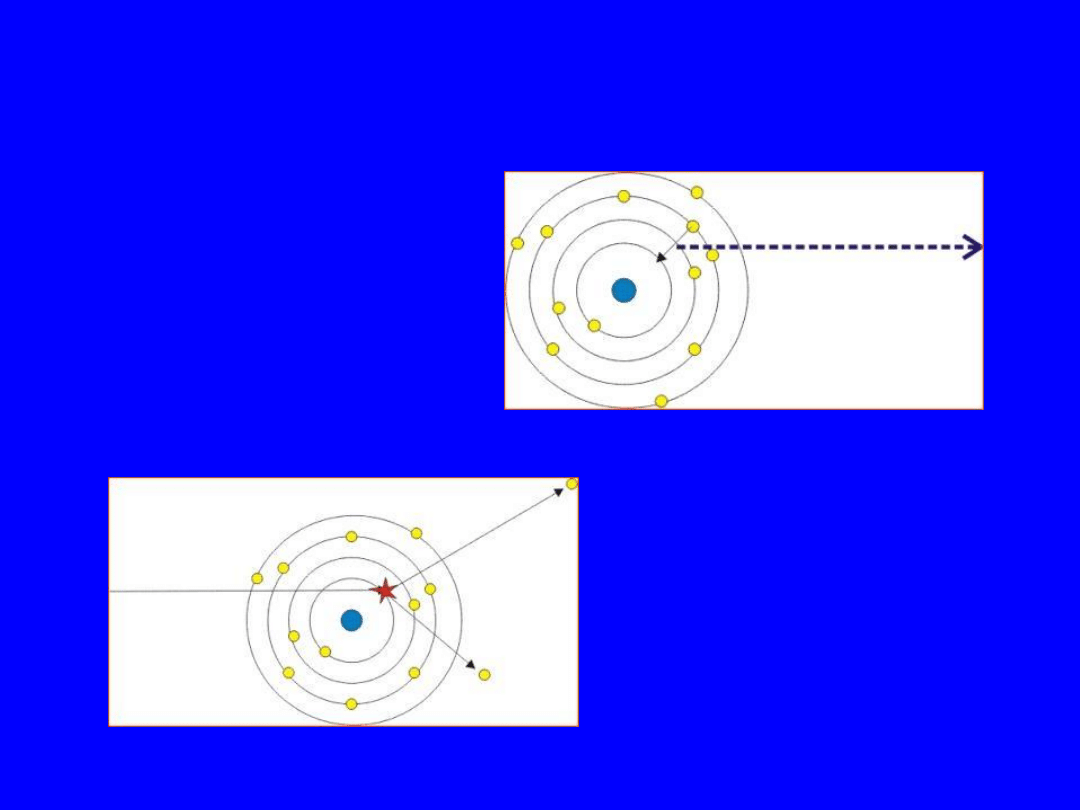
Promieniowanie charakterystyczne
– padajacy elekrton
wybija elektron z
wewnętrznej powłoki
– elektron z wyższej
powłoki zapełnia dziurę,
a różnica energii jest
emitowana jako foton
promieniowania X
1
2
1
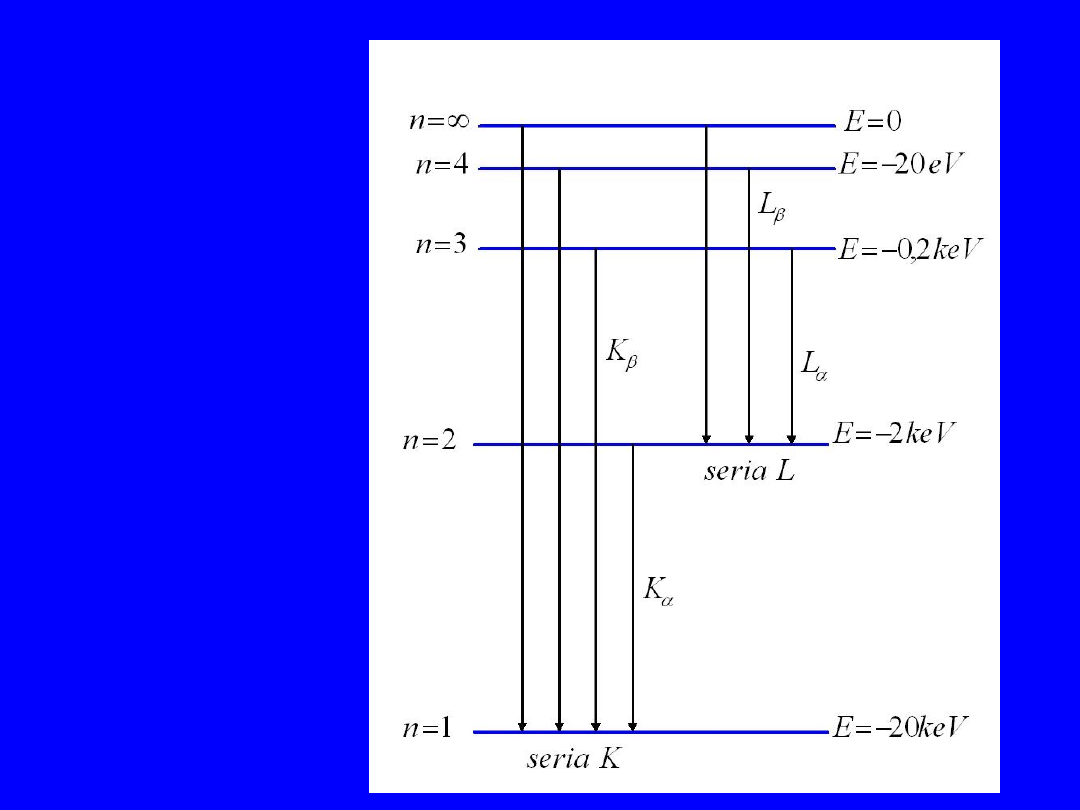
Diagram
przejść X
41
Widmo atomu wodoru –
( z wykł. 2)
Energia całkowita elektronu w atomie wodoru
2
2
4
2
2
2
2
n
e
mZ
r
Ze
E
2
2
2
2
2
2
4
2
2
2
2
4
2
6
,
13
137
2
511
2
2
n
eV
n
keV
c
n
e
Z
mc
n
e
mZ
E
Wartość liczbowa
42
Prawo Mosley’a
Rozważmy jeden z dwu elektronów na powłoce K(n=1). Ze względu na
obecność drugiego elektronu (na powłoce K mogą znaleźć się tylko dwa
elektrony nasz elektron widzi efektywny ładunek jądra, Z-1. W modelu Bohra
energia elektronu atomu wieloelektronowego na tej powłoce będzie dana:
2
2
2
2
4
2
1
6
,
13
2
1
n
Z
eV
n
e
Z
m
E
Dla emisji fotonu promieniowania rentgenowskiego Kα mamy przejście między
powłokami n=2 i n=1 co daje energię przejścia elektromagnetycznego:
2
2
2
2
1
2
1
2
,
10
1
1
2
1
1
6
,
13
Z
eV
Z
eV
E
E
E
Po podstawieniu:
h
eV
a
2
,
10
2
a
aZ
Dzięki liniowej zależności Mosleya, częstość promieniowania rentgenowskiej linii
Kα można wykorzystać do przypisania pierwiastkom właściwego miejsca w
układzie okresowym.
43
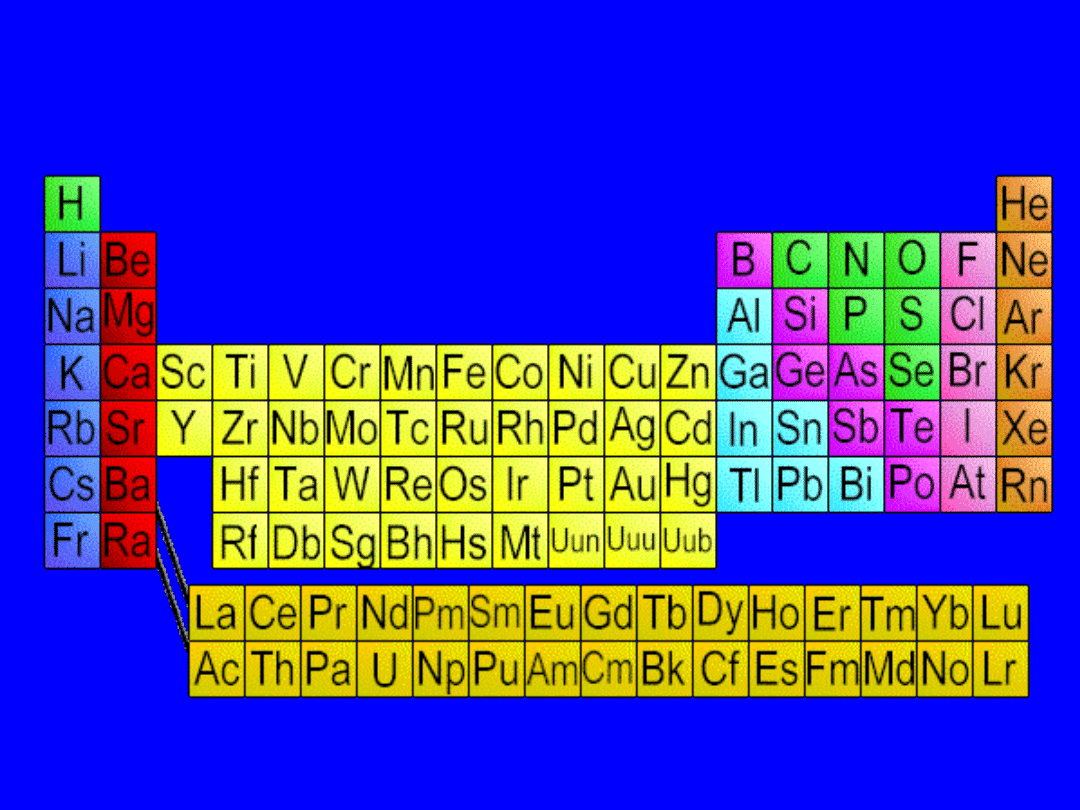
Układ okresowy
44
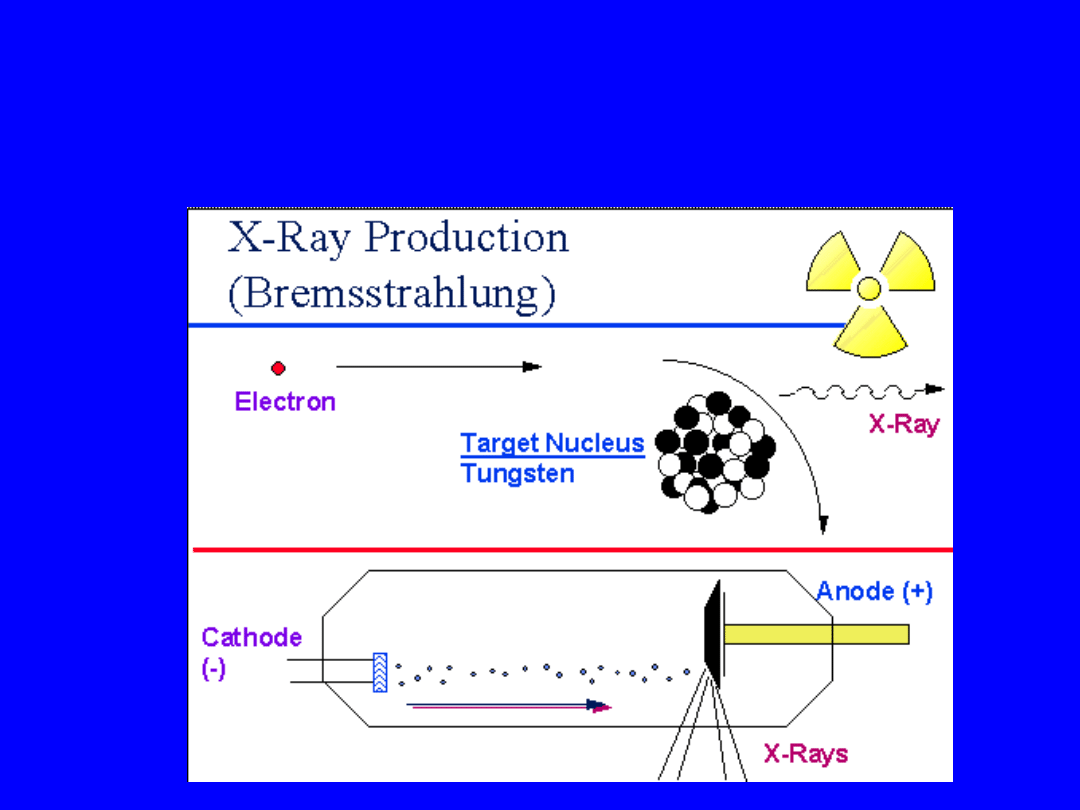
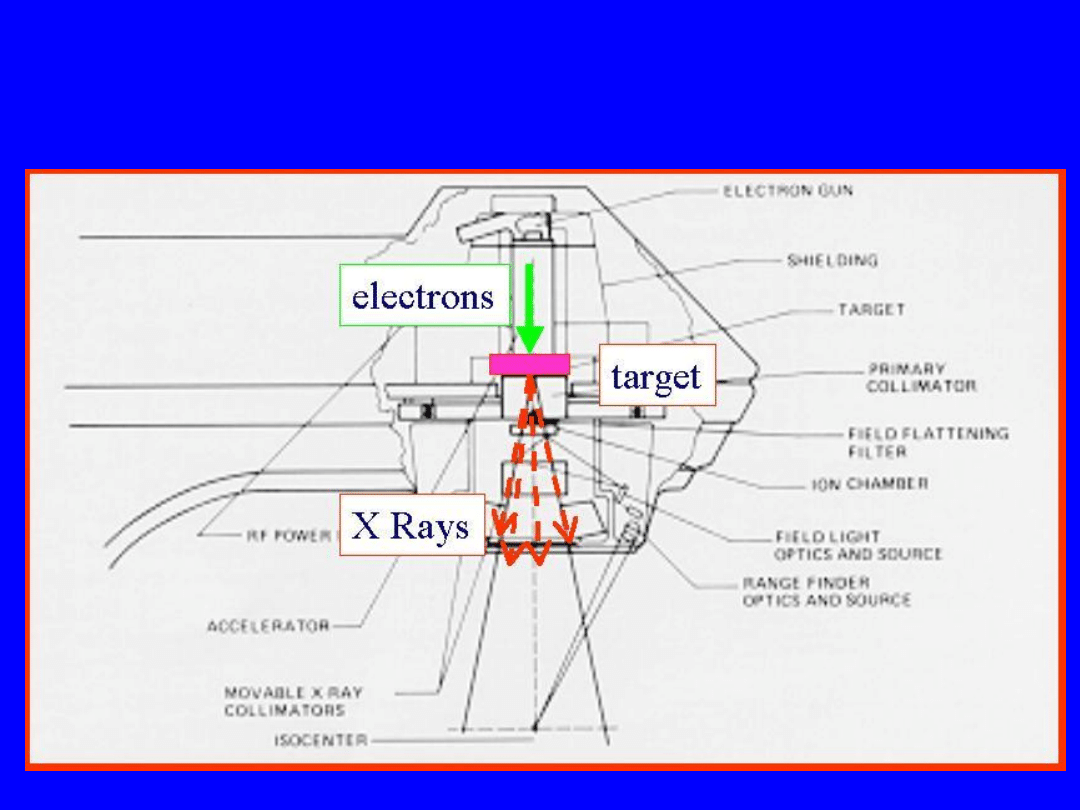
Produkcja promieni X
45
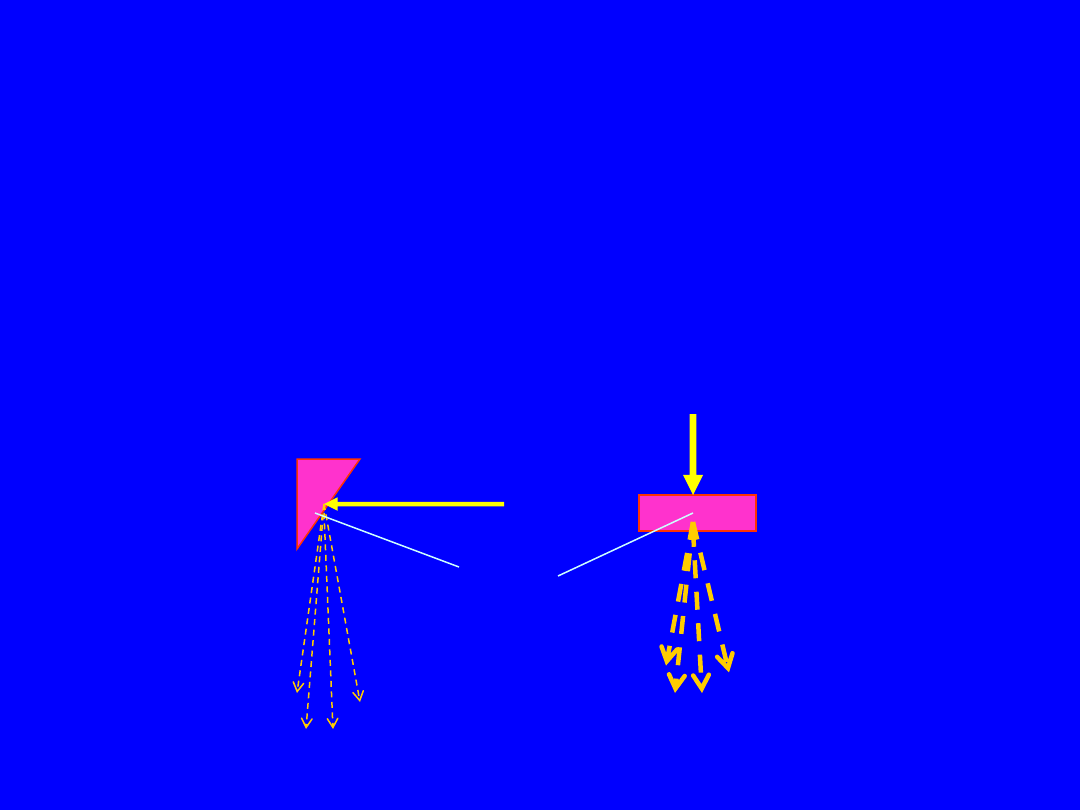
46
Produkcja promieniowania X
• Elektrony wysokiej energii uderzają w
tarczę (metal) gdzie część ich energii jest
przekształcana w promieniowanie
target
electrons
Niskie i
Średnie
energie
(10-400keV)
Wysokie
> 1MeV
energie
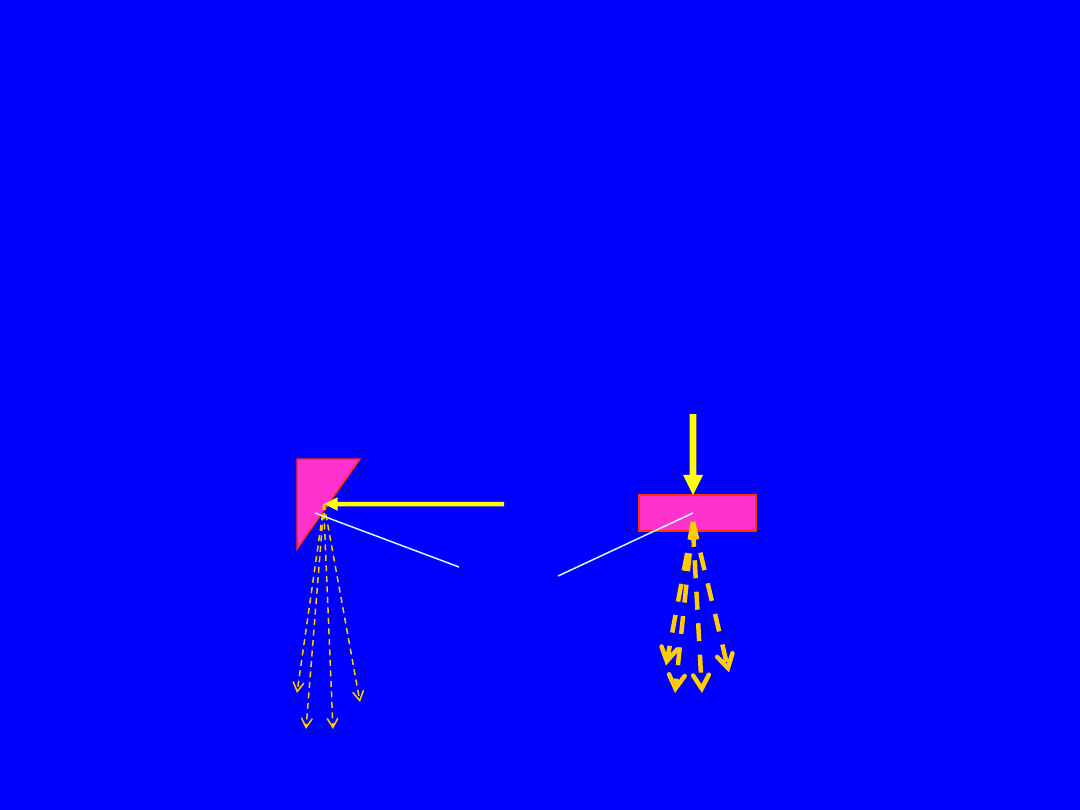
47
Własności promieniowania X
• Rozkłady kątowe: Promieniowanie X wysokich
energii jest skierowane głownie do przodu, a
promieniowanie X niskich energii jest emitowane
głównie prostopadle do kierunku wiązki
elektronów – stąd odbicie od tarczy
target
Niskie i
Średnie
energie
(10-400keV)
Wysokie
> 1MeV
energie
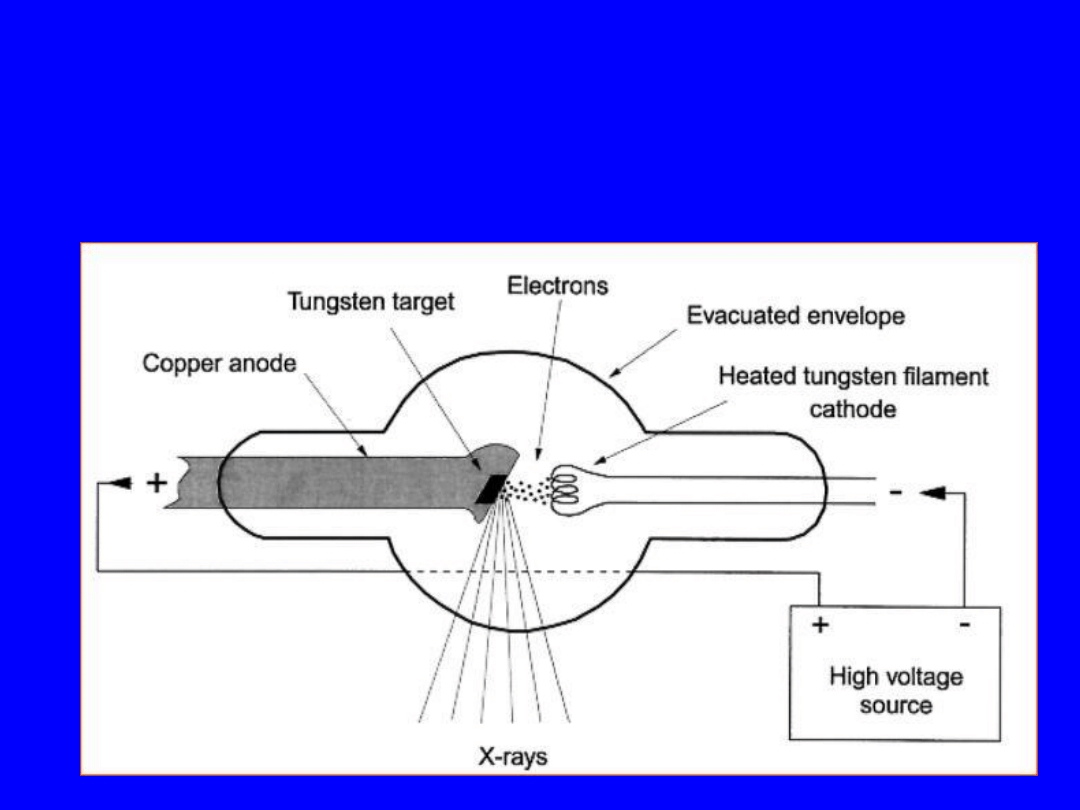
48
Lampa rentgenowska dla promieniowania
niskich i średnich energii
49
Liniak Megavoltowy
Parametry aparatów rentgenowskich
50
1. Napięcie (w kV) określa maksimum widma
rentgenowskiego.
2. Strumień elektronów (w mA) definiuje natężenie.
generowanego promieniowania (jest proporcjonalne).
3. Zwiększenie napięcia również skutkuje wzrostem natężenia.
promieniowania X. Wyższe energie – wyższa wydajność
produkcji .
4. Kształt widma i położenie maksimum zależy od:
•
rodzaju katody
•
napięcia
•
dodanych filtrów
5. Produkcja promieniowania X jest mało wydajna. Znaczna
część energii jest konwertowana na ciepło, nawet > 98%.
51
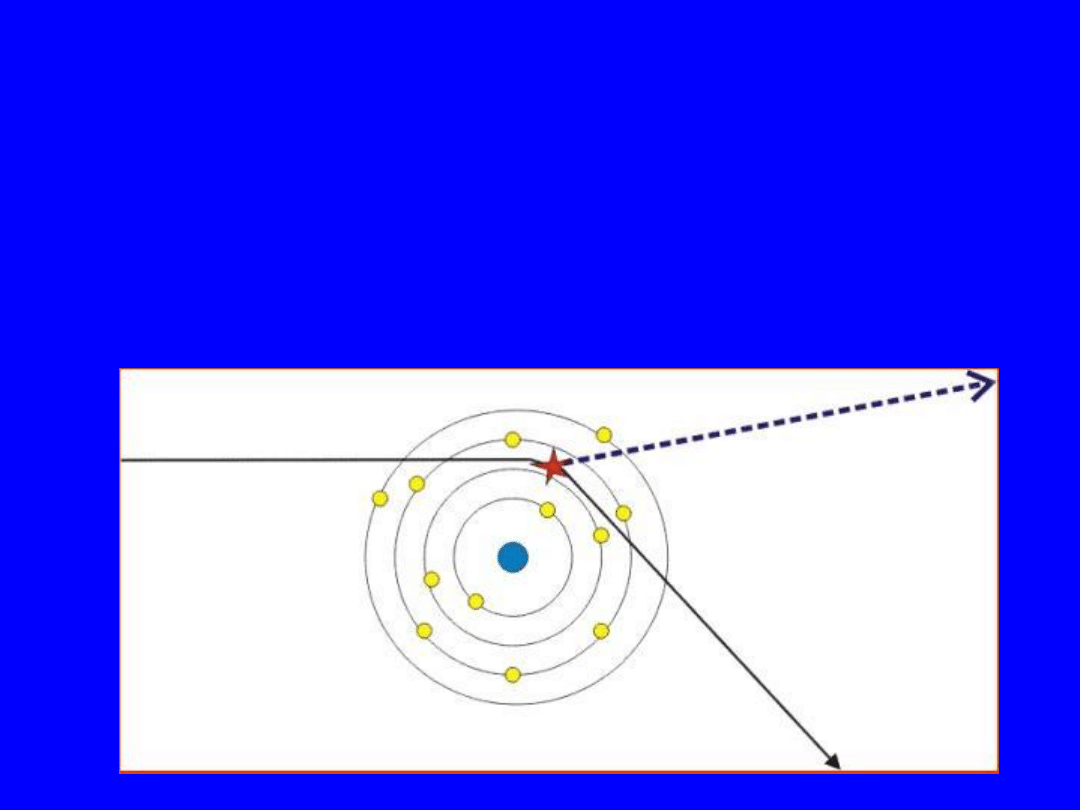
Promieniowanie hamowania
• Padający elektron jest odchylony przez pole
elektryczne jądra (atomu) i hamowany. Róznica
energii jest emitowana jako foton X.
52
Własności produkcji
promieniowania hamowania
• Produkcja X wzrasta wraz z liczbą atomową
tatgetu
• Produkcja X wzrasta z energią padajacych
elektronów
• Dla kazdej energii elektronów produkcja X
maleje ze wzrostem energii promienowania
X (rentgenowskiego)
53
The resulting X Ray spectrum
Unfiltered radiation (in vacuum)
20
40
60
80
100 120
INTENSITY
PHOTON ENERGY (keV)
Characteristic
X Rays
Bremsstrahlung
Spectrum after
filtration
Maximum electron energy
54
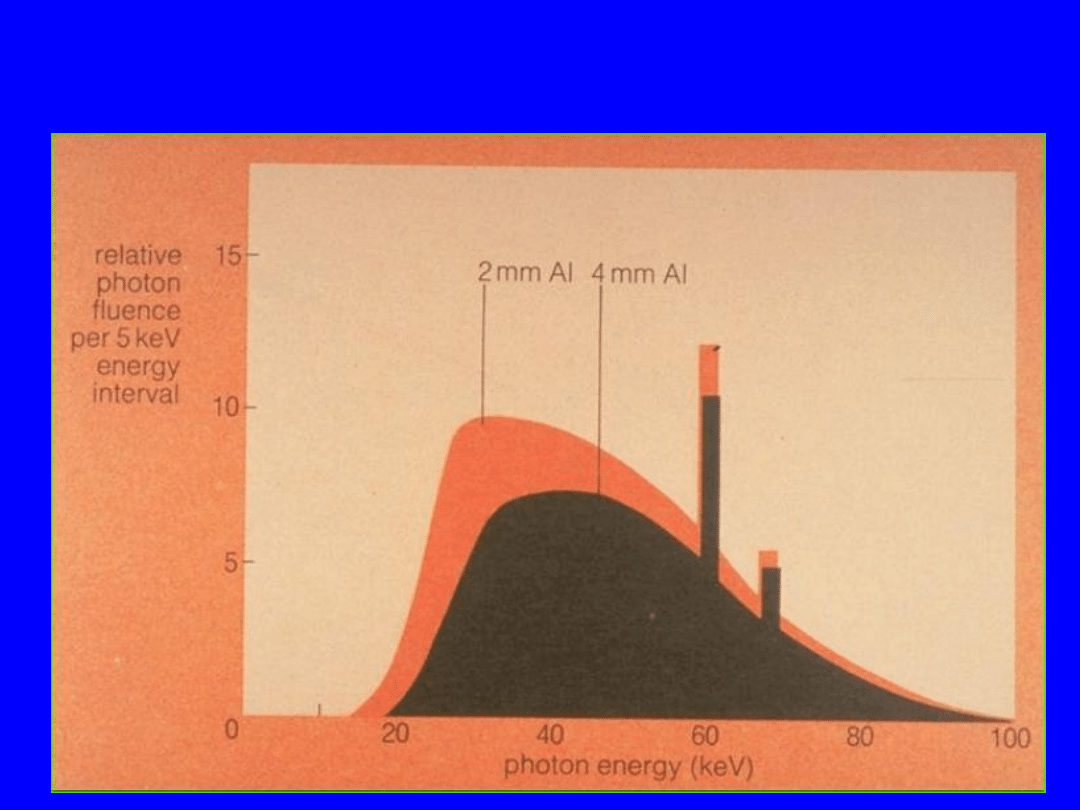
Efekt dodatkowej filtracji
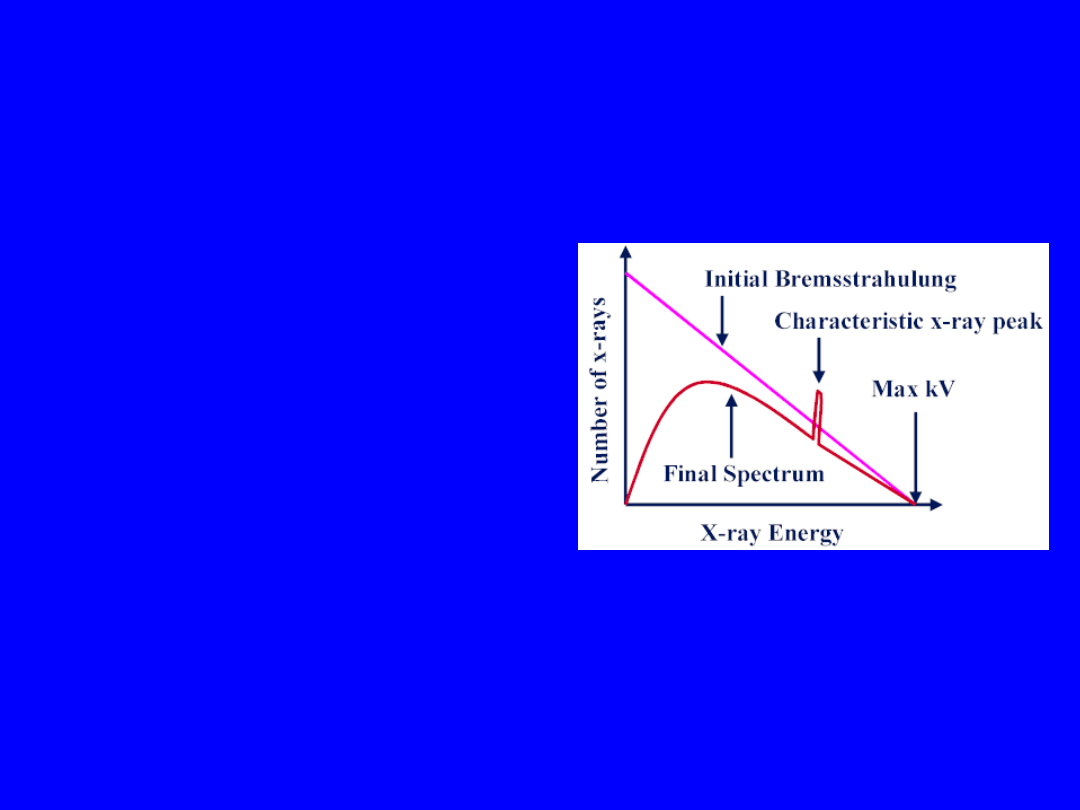
Widmo promieniowania hamowania
55
1. Hamowanie elektronów jest różne,
więc widmo promieniowania
hamowania jest ciągłe.
2. Promieniowanie
charakterystyczne powstaje po
wybiciu elektronów z
wewnętrznych powłok atomów
tarczy
3. Promieniowanie X o niskich
energiach jest absorbowane w
obudowie aparatu (lub filtrach)
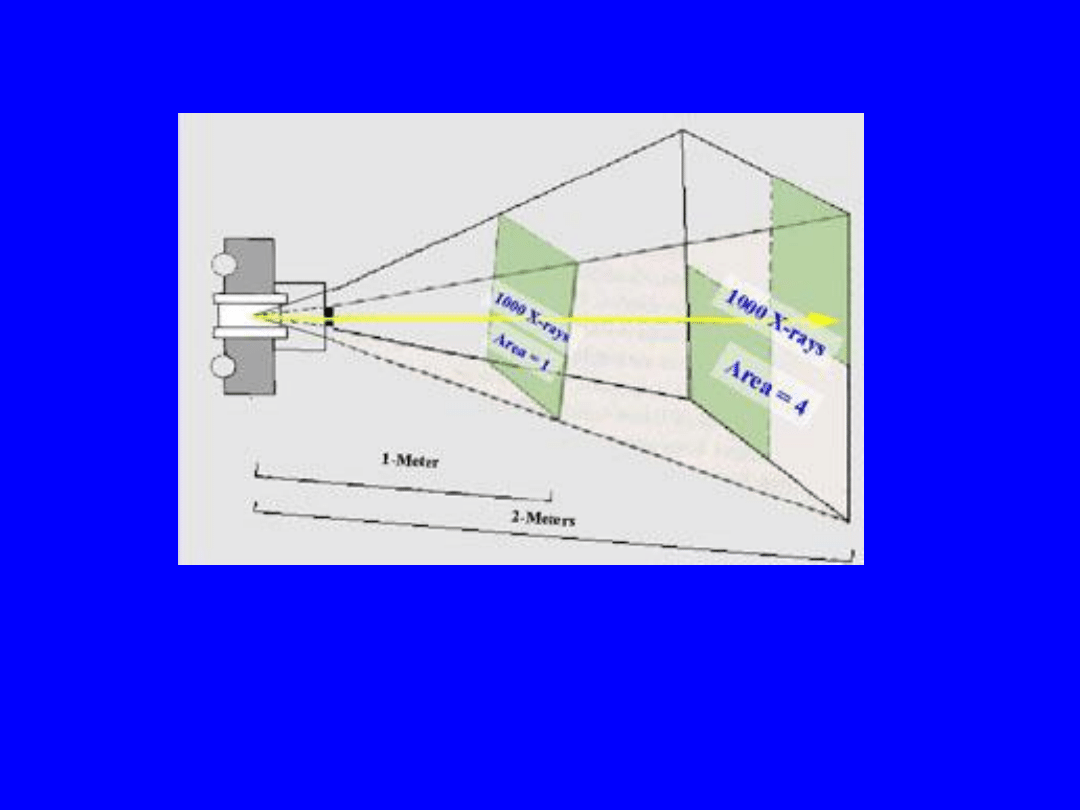
Prawo odwrotnych kwadratów
56
Odległość 1m – 1000 fotonów /jednostkę powierzchni
Odległość 2m – 1000 fotonów / 4 jednostki powierzchni
= 250 fotonów /jednostkę powierzchni