1
Pole elektrostatyczne - Zadanie 1
Treść:
O ile więcej ładunków elementarnych ujemnych niż dodatnich zawiera kula
naładowana ładunkiem Q=-1.6
.
10
-2
C?
Dane:
Q= -1.6
.
10
-2
C
e = 1.6
.
10
-19
C
Szukane:
n = ?
Wzory:
Rozwiązanie:
Szukamy liczby ładunków elementarnych. Znamy wartość pojedynczego ładunku
elementarnego, która wynosi
W celu rozróżnienia, czy mamy do czynienia z ładunkiem ujemnym, czy ładunkiem
dodatnim, możemy dodać odpowiedni znak przed tą wartością. Ponieważ szukamy liczby
ładunków ujemnych, zatem:
Zanim podamy rozwiązanie, pomyślmy, co oznacza liczba Q.
Jeżeli jakieś ciało ma tyle samo ładunków ujemnych i ładunków dodatnich, wtedy Q = 0.
Oznacza to, że gdy Q < 0, to wtedy w danym ciele jest przewaga ładunków ujemnych, a jeśli
Q > 0, to wtedy owe ciało posiada więcej ładunków dodatnich.
W naszym zadaniu wartość Q jest wartością ujemną, zatem kula zawiera więcej ładunków
ujemnych i wartość różnicy ładunków ujemnych i ładunków dodatnich wynosi Q = -1.6
.
10
-2
C. Oznacza to, że jeżeli chcemy obliczyć liczbę ładunków ujemnych, to wartość Q musimy
podzielić przez ładunek elementarny e. To tak, jakbyśmy chcieli obliczyć, ile jabłek po 0.50
zł za sztukę możemy kupić za 200 zł. Zatem:
Kula posiada 10
17
więcej ładunków ujemnych niż dodatnich.
2
Pole elektrostatyczne - Zadanie 2
Treść:
Dwa różnoimienne ładunki punktowe o wartości 1C każdy, znajdujące się w
ośrodku o stałej dielektrycznej 2, umieszczone są w odległości 1m. Jaką siłą
przyciągają się te ładunki?
Dane:
q = 1 C
r = 1 m
ε
R
= 2
Szukane:
F = ?
Wzory:
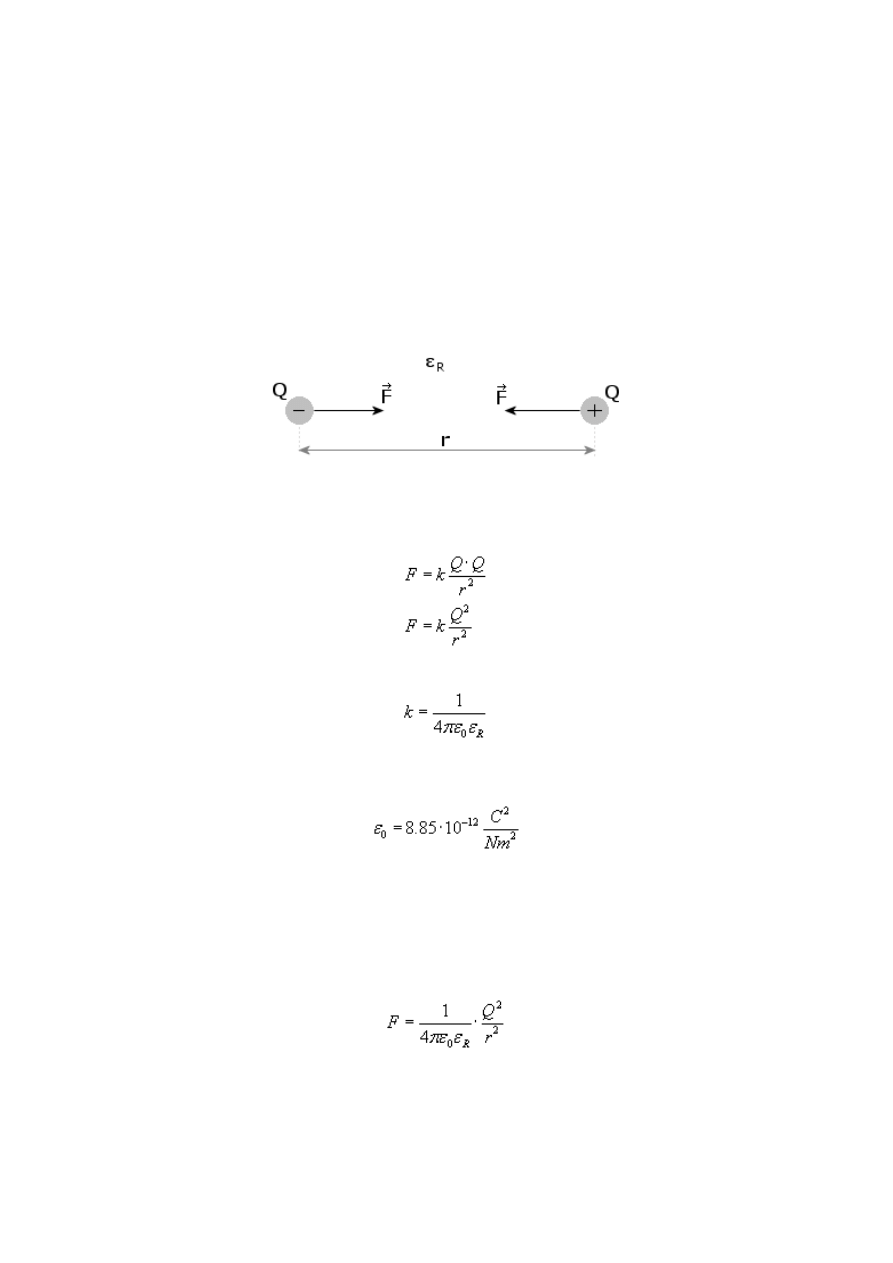
Rysunek:
Rozwiązanie:
Dwa ładunki różnoimienne o wartości Q każdy zgodnie z prawem Coulomba przyciągają się
tymi samymi co do wartości siłami F. Zależność tę wyrażamy wzorem
k to współczynnik proporcjonalności, który wyrażamy wzorem:
Wartość ε
0
to przenikalność dielektryczna próżni, która zawsze wynosi (wartości tej szukaj
zawsze w tablicach fizycznych):
a wartość ε
R
to przenikalność dielektryczna danego środowiska (liczba niemianowana, w
próżni wynosi 1 - czyli jest to jakaś wielokrotność wartości ε
0
).
Po uwzględnieniu tego wszystkiego wzór wynikający z prawa Coulomba przybiera
następującą postać:
Możemy więc obliczyć szukaną wartość siły
3
Sprawdzamy jednostkę:
Ładunki punktowe przyciągają się siłą równą około 4.5
.
10
9
N.
Pole elektrostatyczne - Zadanie 3
Treść:
Dwa ładunki punktowe znajdowały się w pewnej odległości od siebie.
Zmniejszenie odległości o 10cm spowodowało czterokrotny wzrost siły
wzajemnego oddziaływania. Ile wynosiła początkowa odległość między
ładunkami?
Dane:
d = 10 cm = 0.1 m
4 F
1
= F
2
Szukane:
x = ?
Wzory:
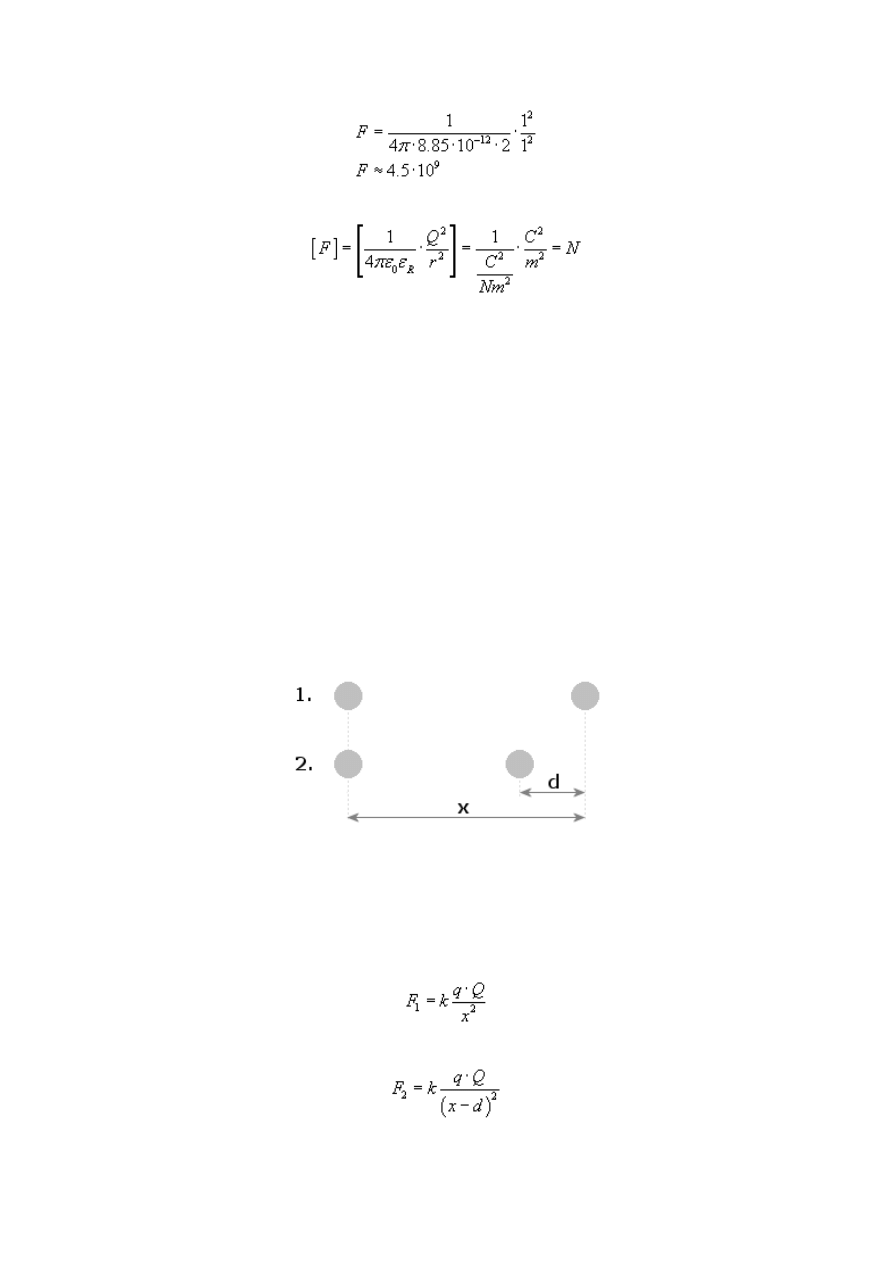
Rysunek:
Rozwiązanie:
Dwa ładunki elektryczne (załóżmy, że znajdują się w szarych kulach) działają na siebie
zgodnie z prawem Coulomba jakąś siłą F. Zauważcie, że nie wiemy nic o znakach ładunków -
przyjmijmy więc, że jeden ma wartość Q, a drugi wartość q.
Oba ładunki na początku (1) znajdowały się w szukanej odległości x. Wtedy siła
oddziaływania ładunków miała wartość zgodnie z prawem Coulomba
Potem (2) zmniejszamy odległość o d = 10 cm i wtedy siła oddziaływania ładunków wynosi
4
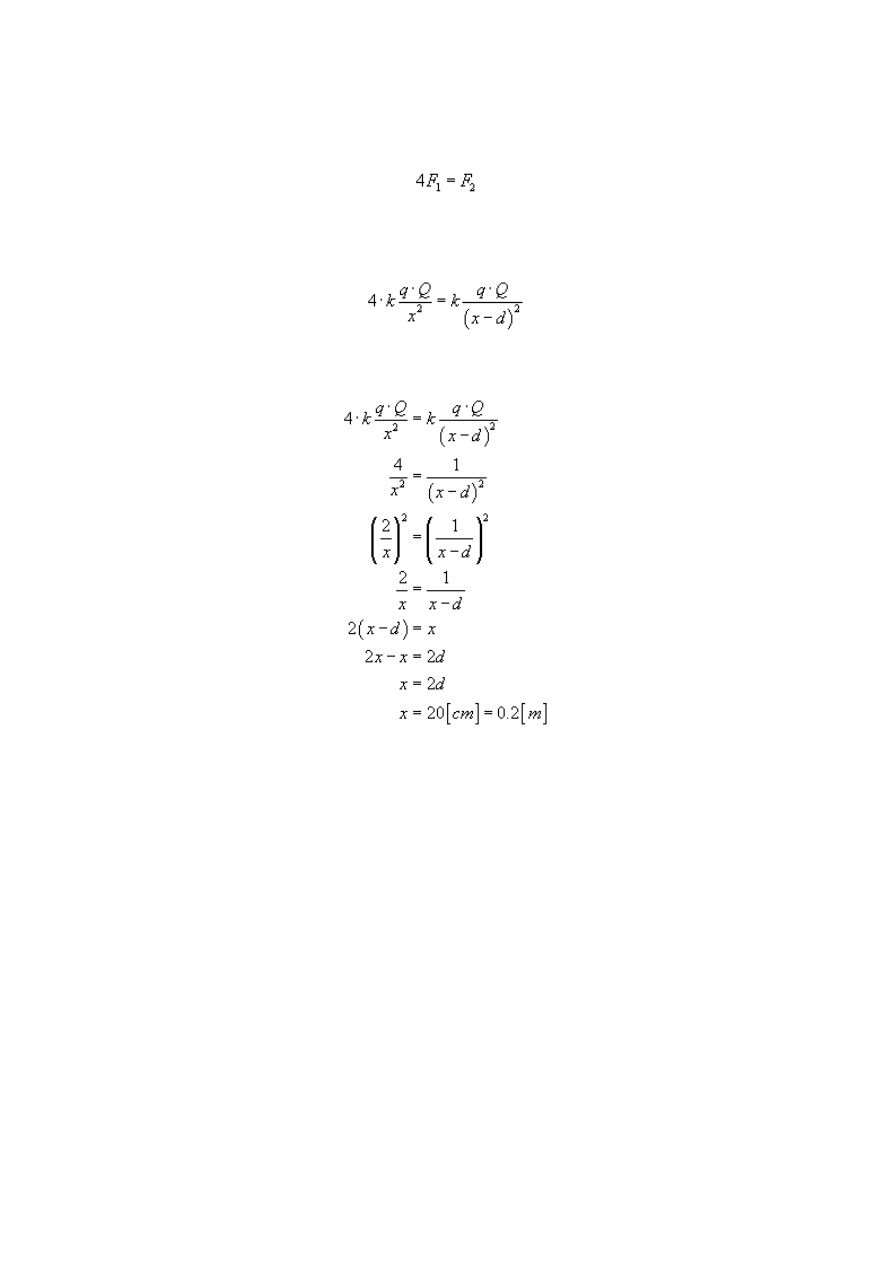
Z treści zadania wiemy jeszcze, że po zbliżeniu ładunków odnotowano czterokrotny wzrost
siły wzajemnego oddziaływania
Podstawiamy wartości sił wyliczone wcześniej:
Wartość ładunków oczywiście się nie zmienia, współczynnik proporcjonalności k również jest
stały, bo nie zależy od odległości. Wyliczamy więc szukaną wartość x:
Początkowa odległość między ładunkami wynosiła 20 cm.
5
Pole elektrostatyczne - Zadanie 4
Treść:
Dwa ładunki elektryczne działają na siebie w próżni siłą F. Jak należy zmienić
odległość między tymi ładunkami, by po zanurzeniu ich w cieczy o stałej
dielektrycznej ε
R
=81, siła ich wzajemnego oddziaływania nie zmieniła się?
Dane:
F
ε
R
= 81
Szukane:
r
2
= ?
Wzory:
Rozwiązanie:
Mamy dwa ładunki - przyjmijmy, że jeden z nich ma wartość q, a drugi wartość Q.
Na początku ładunki te znajdują się w próżni (w próżni ε
R
= 1) i oddziałują na siebie siłą
wynikającą z prawa Coulomba:
Współczynnik k
1
dla próżni wynosi:
Zatem
Potem umieszczamy ładunki w cieczy o stałej dielektrycznej ε
R
= 81. Wtedy siła wzajemnego
oddziaływania wynosi...
...a współczynnik k
2
...
...więc:
Chcemy, aby siły oddziaływania nie zmieniły się, czyli:
Stąd możemy wyrazić szukaną odległość r
2
.
6
Po zanurzeniu odległość między ładunkami należy zmniejszyć 9 razy.
Pole elektrostatyczne - Zadanie 5
Treść:
Dwie jednakowe przewodzące kulki oddalone od siebie o r, naładowane
ładunkami 2q i 6q, odpychają się siłą F
1
. Jak zmieni się siła F
2
w stosunku do siły
F
1
, jeżeli kulki ze sobą zetkniemy i rozsuniemy na taką samą odległość r?
Dane:
r
F
1
q
1
= 2q
q
2
= 6q
Szukane:
F
1
/ F
2
= ?
Wzory:
Rozwiązanie:
Na początku mamy dwie kulki naładowane ładunkiem 2q i 6q. Siła wzajemnego
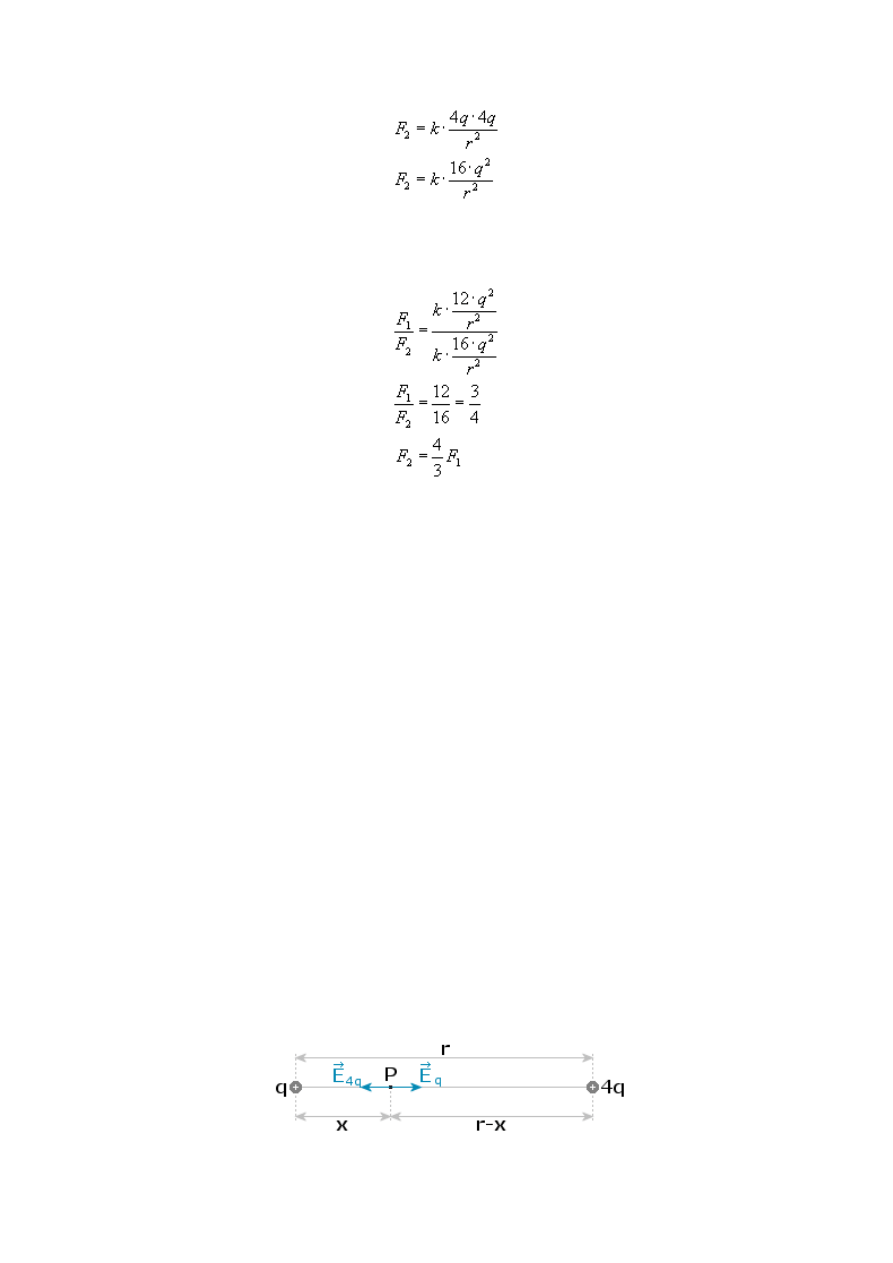
oddziaływania pomiędzy tymi kulkami, zgodnie z prawem Coulomba, wynosi
Potem kulki ze sobą stykamy. Ponieważ kulki dążą do równowagi elektrostatycznej, ładunki
w obu kulkach wyrównają się i zgodnie z zasadą zachowania ładunku będą wynosić po 4q.
Wtedy siła wzajemnego oddziaływania wynosić będzie
7
Pamiętajmy, że odległość r nie zmienia się, a współczynnik k jest stały, gdyż nie zmieniamy
środowiska, w którym znajdują się kulki.
Obliczmy szukany stosunek sił:
Po zetknięciu kulek i rozsunięciu ich na odległość r, siła wzajemnego oddziaływania wzrośnie
4/3 razy (czyli o 1/3).
Pole elektrostatyczne - Zadanie 6
Treść:
Dwa dodatnie ładunki punktowe q i 4q znajdują się w odległości r od siebie. W
jakiej najbliższej odległości od ładunku q znajduje się punkt, w którym natężenie
pola elektrostatycznego równa się zeru? Oblicz potencjał w tym punkcie.
Dane:
q
4q
r
Szukane:
x = ? V = ?
Wzory:
Rysunek:
8
Rozwiązanie:
Mamy znaleźć punkt, położony jak najbliżej ładunku q, w którym natężenie pola
elektrostatycznego będzie równe zeru; punkt ten oznaczamy literą P.
Oba ładunki wytwarzają dookoła siebie pole elektrostatyczne. Tak więc działają tutaj dwa
pola, korzystamy więc z zasady superpozycji, która mówi że natężenie pola w danym punkcie
jest sumą wektorową natężeń pól wytwarzanych przez każdy z tych ładunków niezależnie.
Szukany punkt znajduje się na linii prostej łączącej oba ładunki (patrz rysunek). Jest wiele
takich punktów, w których natężenie równa się zeru, znajdują się one jednak w
nieskończoności.
Przyjmijmy oznaczenia odległości, jakie są na rysunku. Pamiętajmy że wektor natężenia ma
zawsze zwrot skierowany od ładunku dodatniego. Korzystając z zasady superpozycji oraz
tego, że w punkcie P natężenie jest równe zeru, mamy:
Tak więc wartości wektorów
Korzystamy teraz ze wzoru na natężenie pola:
gdzie k jest stałe.
Możemy już wyliczyć szukaną odległość x, upraszczając na samym początku wzór:
Zatem punkt ten znajduje się w odległości r/3 od ładunku q.
Czas zająć się potencjałem. Potencjał ten będzie dodatni, ponieważ znajdujemy się w polu
ładunków dodatnich.
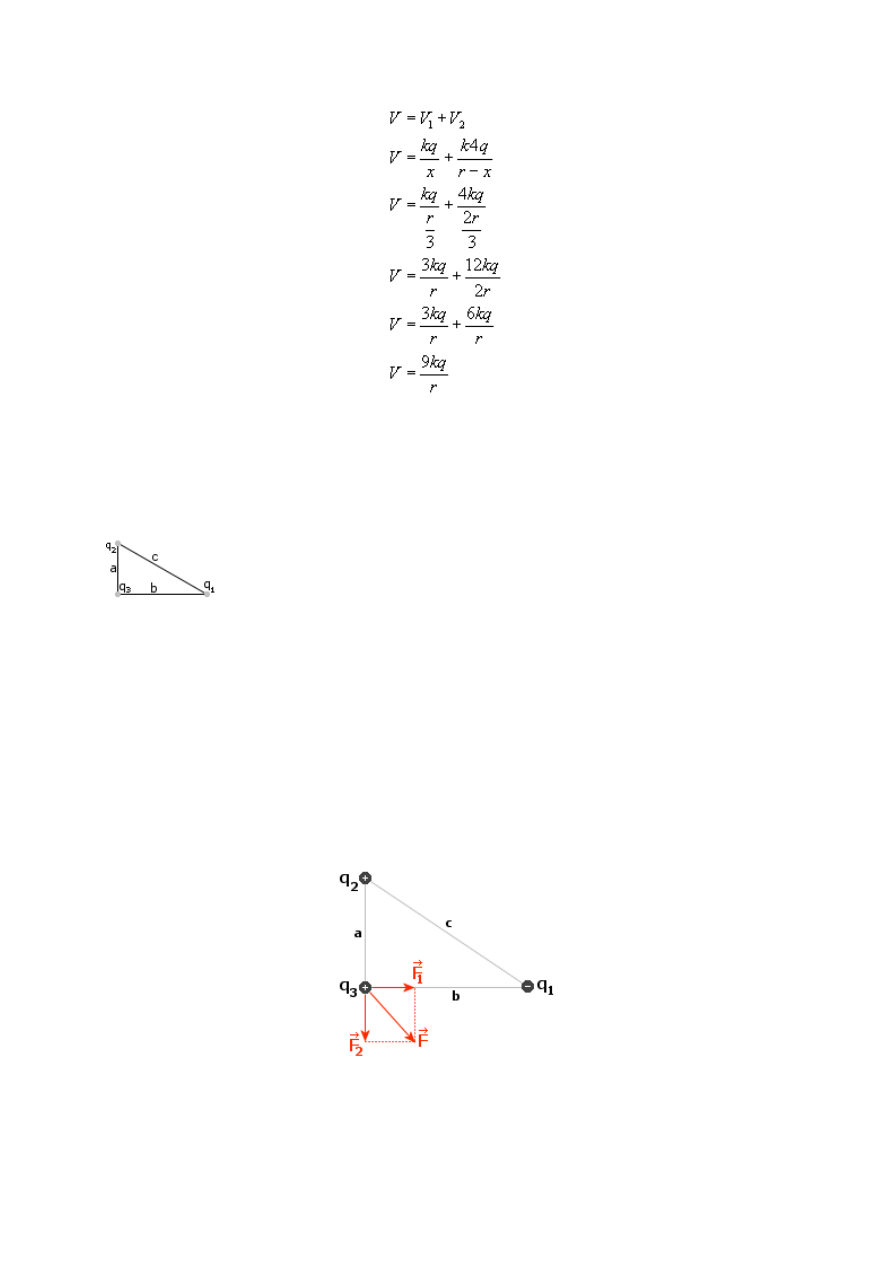
Zgodnie z zasadą nakładania się pól potencjał w punkcie P jest sumą algebraiczną:
Podstawiamy dane:
9
Jamnik
Pole elektrostatyczne - Zadanie 7
Treść:
Trzy ładunki q
1
=-5
.
10
-4
C, q
2
=5
.
10
-4
C i q
3
=10
-4
C umieszczono we
wierzchołkach trójkąta o bokach równych a=3m, b=4m i c=5m,
tak jak na rysunku. Ile wynosi siła działająca na ładunek q
3
?
Dane:
q
1
= -5
.
10
-4
C
q
2
= 5
.
10
-4
C
q
3
= 10
-4
C
a = 3 m
b = 4 m
c = 5 m
Szukane:
F = ?
Wzory:
Rozwiązanie:
Ponieważ a
2
+ b
2
= c
2
, to mamy do czynienia z trójkątem prostokątnym.
Zastanówmy się, jakie siły działają na ładunek q
3
.
Pamiętajmy, że ładunki jednoimienne odpychają się, zaś różnoimienne przyciągają. Siłą
działającą na ładunek q
3
jest siła wypadkowa F powstała z sił F
1
i F
2
i wyliczyć ją można z
twierdzenia Pitagorasa:
10
Korzystamy z prawa Coulomba, by podać wartości składowych sił:
Sprowadzamy dwa ułamki pod pierwiastkiem do mianownika
gdzie:
Ze wzoru wyprowadziliśmy spod pierwiastka co się dało, mimo to otrzymany wzór jest mało
przyjemny. Możecie się pokusić o wyliczenie dokładnej wartości siły. :)
Pole elektrostatyczne - Zadanie 8
Treść:
Dwa ładunki punktowe q
1
=2
.
10
-4
C i q
2
=-2
.
10
-4
C umieszczono w odległości
r
1
=1m. Jaką pracę należy wykonać aby zwiększyć ich odległość do r
2
=2m?
Dane:
q
1
= 2
.
10
-4
C
q
2
= -2
.
10
-4
C
r
1
= 1 m
r
2
= 2m
Szukane:
W = ?
Wzory:
Rozwiązanie:
Energia potencjalna dwóch ładunków q
1
i q
2
, umieszczonych w odległości r jest równa
11
Szukana praca jest równa przyrostowi energii potencjalnej układu:
Pamiętaj, że k to stała (zakładamy, że ładunki znajdują się w próżni):
Zatem możemy podać wartość wykonanej pracy
Sprawdźmy jeszcze jednostkę:
Wykonana praca równa się 180 J.
12
Pole elektrostatyczne - Zadanie 9
Treść:
Mamy dipol elektryczny, w którym dwa ładunki wynoszą Q=(+/-)2
.
10
-4
C, a
odległość pomiędzy ładunkami r=12m. Jaką należy wykonać pracę, aby przenieść
ładunek q=10
-5
C z punktu A, odległego o x=10m od każdego z ładunków Q, do
punktu B odległego o y=8m od każdego z ładunków Q?
Dane:
Q = 2
.
10
-4
C
r = 12 m
q = 10
-5
C
x = 10 m
y = 8 m
Szukane:
W = ?
Wzory:
Rysunek:
Rozwiązanie:
Na początku trzeba dowiedzieć się, czym jest dipol elektryczny.
Dipol składa się z dwóch jednakowych ładunków (Q) o przeciwnych znakach, umieszczonych
w odległości r (patrz rysunek).
Zgodnie z treścią zadania umieszczamy jakiś ładunek q w odległości x od każdego z naszych
ładunków Q (punkt A). Potem przesuwamy ten ładunek do punktu, w którym odległość od
każdego z ładunków Q wynosi y. Takie punkty możliwe są dwa, oznaczyłem je przez B i B'.
Zauważmy że punkty te tworzą prostą, która jest symetralną odcinka o długości r (przerywana
linia).
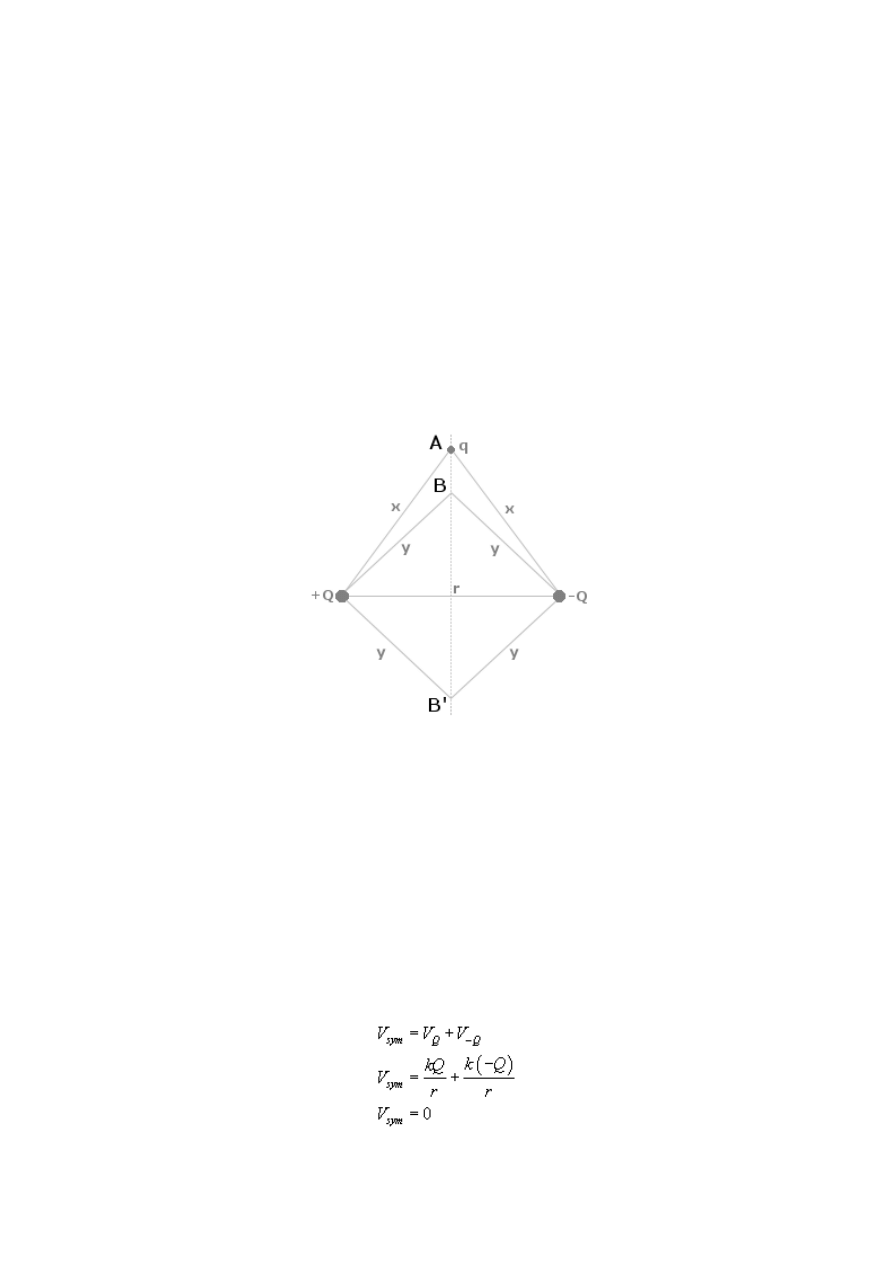
Ponieważ każdy punkt na symetralnej odcinka jest równo odległy od ładunków Q, to zgodnie
z zasadą superpozycji pól potencjał V na symetralnej jest stały i wynosi zero:
13
Zamiast odległości r możemy wstawić dowolną inną odległość, ale zawsze wyjdzie zero. Tak
więc potencjał w punkcie A, B oraz B' równy jest zeru.
Ale zaraz! My mieliśmy obliczyć pracę.
Przypomnijmy sobie jednak jeden ze wzorów na pracę w polu elektrostatycznym, w którym
występuje potencjał
A ponieważ...
...to:
Praca W jest równa zeru.
Pole elektrostatyczne - Zadanie 10
Treść:
Proton o ładunku e i masie m, mający prędkość v, zbliża się do nieruchomego
ładunku dodatniego Q. Ile wynosi minimalna odległość r
min
, na którą zbliży się
proton do ładunku Q?
Dane:
e
m
v
Q
Szukane:
r
min
= ?
Wzory:
Rozwiązanie:
Proton ma ładunek dodatni.
Zgodnie z zasadą zachowania energii całkowitej początkowa energia kinetyczna protonu (bo
gdzieś w nieskończoności nie ma energii potencjalnej pola elektrostatycznego) zostanie
zamieniona na energię potencjalną w punkcie największego zbliżenia ładunków (ponieważ
dwa ładunki dodatnie się odpychają, to siła coulombowska, powodująca to odpychanie,
zahamuje proton, czyli wtedy energia kinetyczna będzie równa zeru).
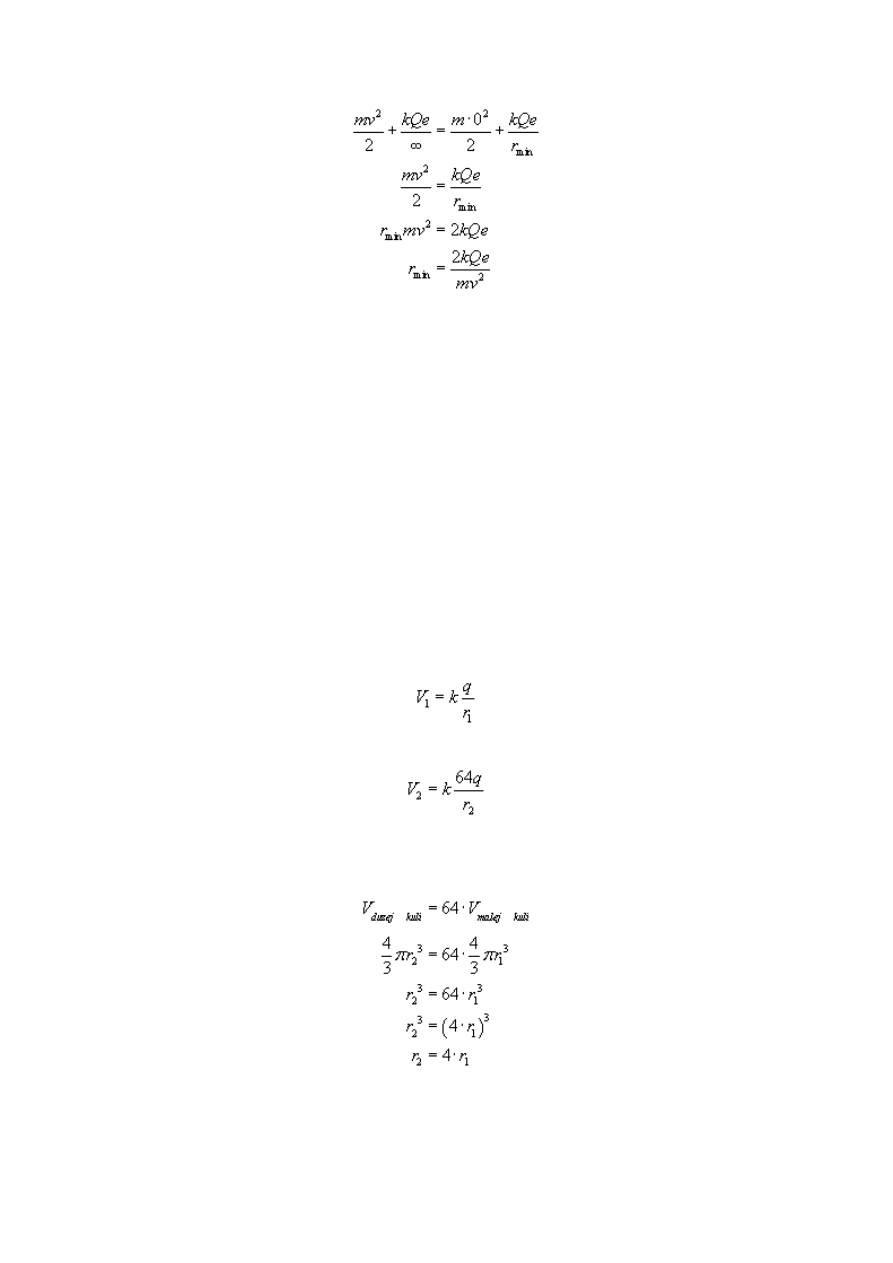
Zapiszmy zasadę zachowania energii (pamiętajmy, że dla ładunków jednoimiennych energia
potencjalna ma wartość dodatnią):
14
Otrzymany wzór wyraża minimalną odległość, na jaką zbliży się proton do ładunku Q.
Pole elektrostatyczne - Zadanie 11
Treść:
64 krople rtęci, o równych promieniach, naładowane takimi samymi ładunkami,
łączą się w jedną dużą kroplę. Jeżeli V
1
oznacza potencjał przy powierzchni małej
kropli, a V
2
przy powierzchni dużej kropli, to oblicz stosunek V
2
/ V
1
.
Dane:
64 małe krople
1 duża kropla
q - ładunek małej kropli
Szukane:
V
2
/ V
1
= ?
Wzory:
Rozwiązanie:
Potencjał przy powierzchni małej kropli o promieniu r
1
, naładowanej ładunkiem q, jest równy
Analogicznie dla dużej kropli o promieniu r
2
mamy
Możemy znaleźć również zależność promieni małej i dużej kropli. Ponieważ objętość dużej
kropli równa jest łącznej objętości małych kropel więc
Ponieważ potencjał i objętość oznacza się w fizyce zwyczajowo literą V, nie pomylcie tych
wielkości fizycznych!
Ostatecznie szukany stosunek wynosi:
15
Szukany stosunek potencjałów wynosi więc 16.
Pole elektrostatyczne - Zadanie 12
Treść:
Potencjał w punkcie P pola elektrycznego trzech
ładunków punktowych q
1
=q, q
2
=2q, q
3
jest równy
zeru. Ile wynosi ładunek q
3
?
Dane:
q
1
= q
q
2
= 2q
Szukane:
q
3
= ?
Wzory:
Rozwiązanie:
Obiecuję, że zadanie nie jest trudne.
Przede wszystkim trzeba znać zasadę składania potencjałów, jeżeli mamy kilka ładunków w
polu. Zasada ta mówi, że potencjał w danym punkcie pola jest równy sumie algebraicznej
potencjałów pochodzących od każdego ładunku. A więc potencjał V w punkcie P wynosi
gdzie V
i
oznacza potencjał w punkcie P liczony dla i-tego ładunku (i = 1, 2, 3).
Z zadania wiemy, że potencjał w punkcie P jest równy zeru.
Za każdy potencjał podstawiamy wartość zgodną ze wzorem i rysunkiem
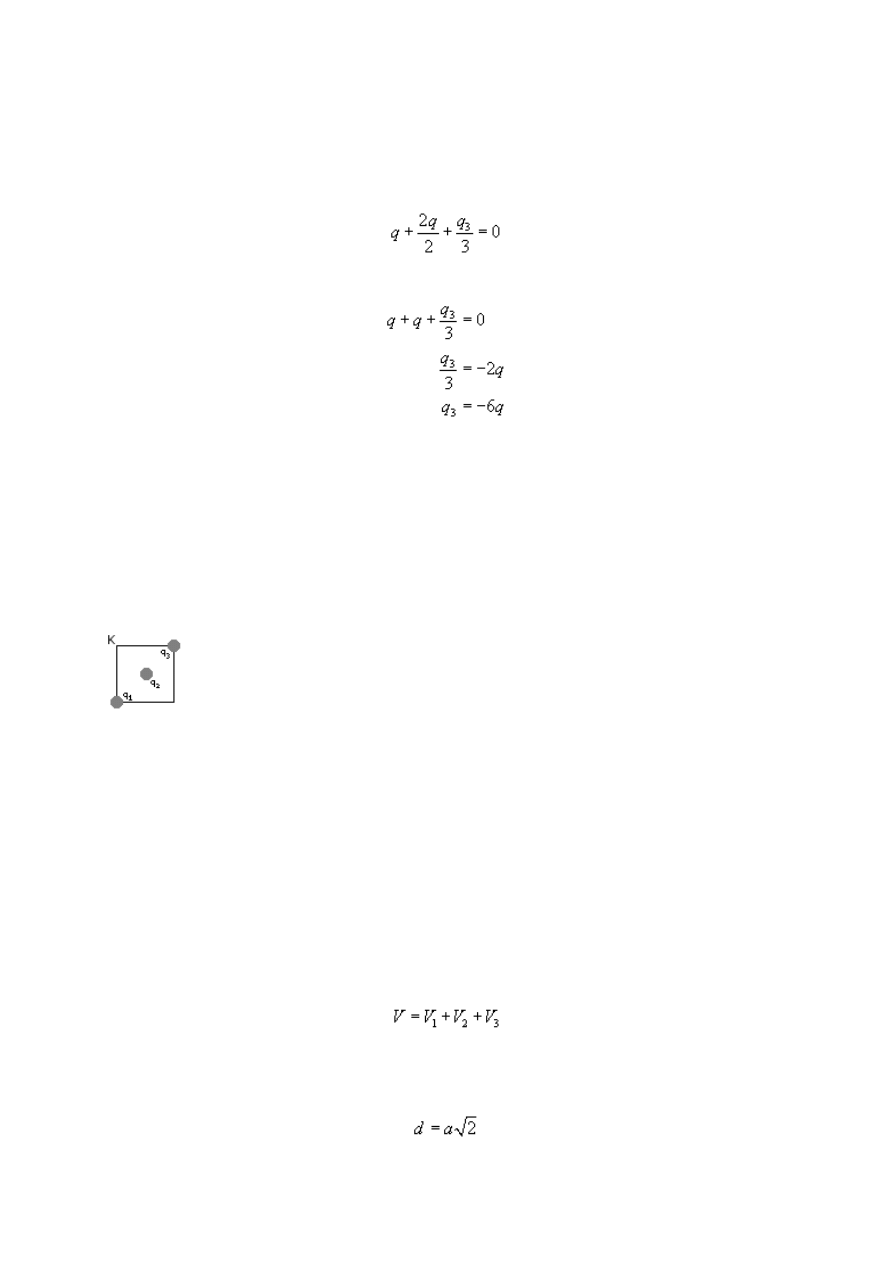
16
Uprościliśmy wzór ze stałej k i odległości d.
Podstawiamy dane wartości ładunków q
1
i q
2
Teraz możemy wyliczyć szukaną wartość ładunku q
3
Zatem szukany ładunek ma wartość -6 q.
Pole elektrostatyczne - Zadanie 13
Treść:
Ładunki punktowe q
1
=q, q
2
=-sqrt(2)q i q
3
=2q umieszczono na
przekątnej kwadratu o boku a. Ile wynosi potencjał w punkcie K
(wierzchołek kwadratu)? Narysuj wektor natężenia pola
elektrostatycznego w tym punkcie oraz określ jego wartość (sqrt(2) oznacza
pierwiastek z 2).
Dane:
q
1
= q
q
2
= - sqrt(2)q
q
3
= 2q
a
Szukane:
V = ?
E = ?
Wzory:
Rozwiązanie:
Podobnie jak w zadaniu poprzednim, musimy skorzystać z zasady obliczania potencjału w
danym punkcie pola, jeżeli w polu jest kilka ładunków. Zasada ta mówi, że potencjał V w
punkcie K jest równy sumie algebraicznej potencjałów związanych z poszczególnymi
ładunkami
Podstawiamy wartości potencjałów zgodnie ze wzorem. Zauważ, że ładunek q
2
oddalony jest
od punktu K o odległość równą połowie przekątnej kwadratu o boku a. Ponieważ przekątna
kwadratu jest równa (można ją wyliczyć z tw. Pitagorasa)
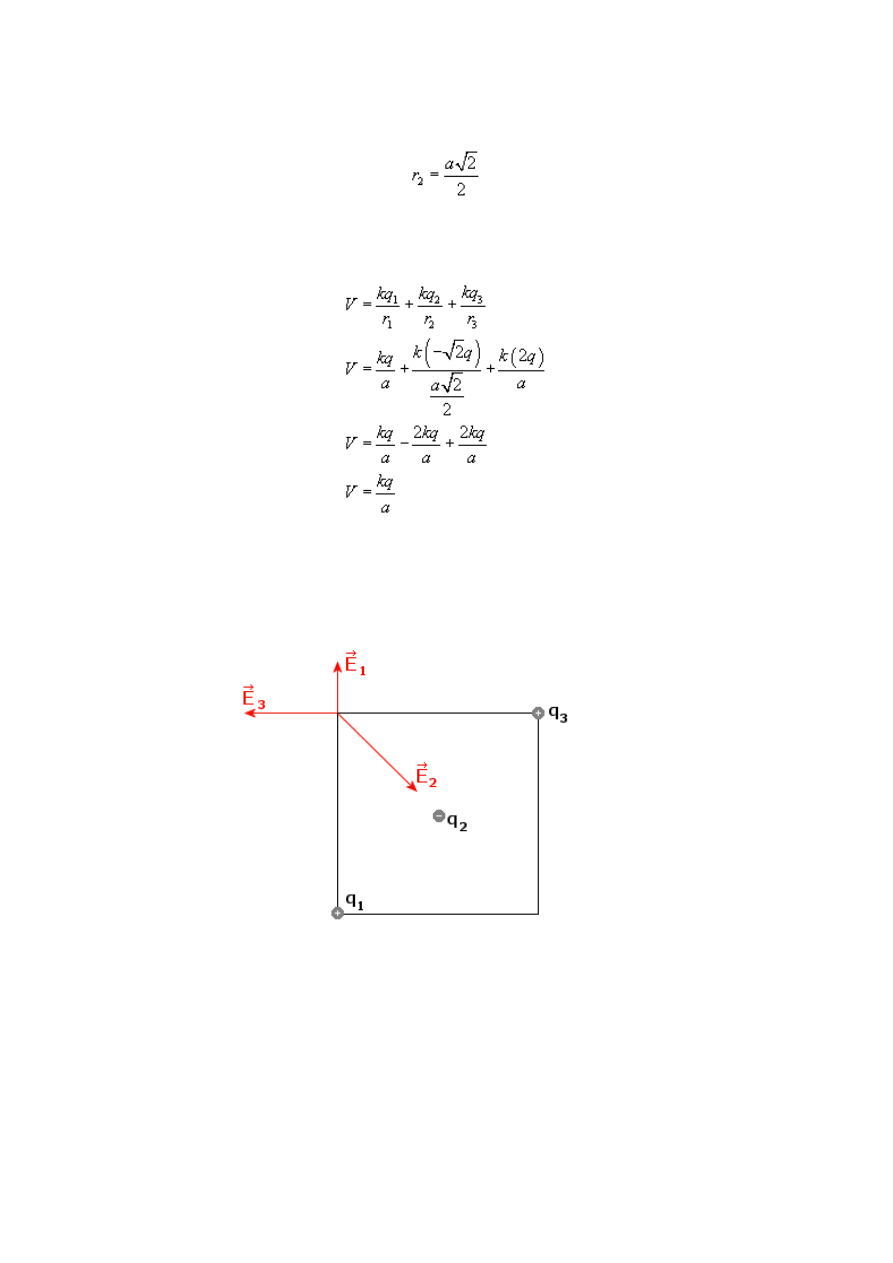
17
to odległość ładunku q
2
od punktu K wynosi
Zatem potencjał V:
Mamy jeszcze narysować wektor natężenia pola E w punkcie K. Wektor natężenia pola ma
zwrot zawsze od ładunku dodatniego (czyli inaczej mówiąc w kierunku ładunku ujemnego).
Rysujemy składowe natężenia pola pochodzącego od każdego z ładunków.
Składowe te zostały narysowane orientacyjnie.
Zasada superpozycji mówi, że aby obliczyć wektor natężenia pola, należy zastosować sumę
wektorową poszczególnych składowych.
Obliczmy wartości poszczególnych składowych wektora natężenia pola:
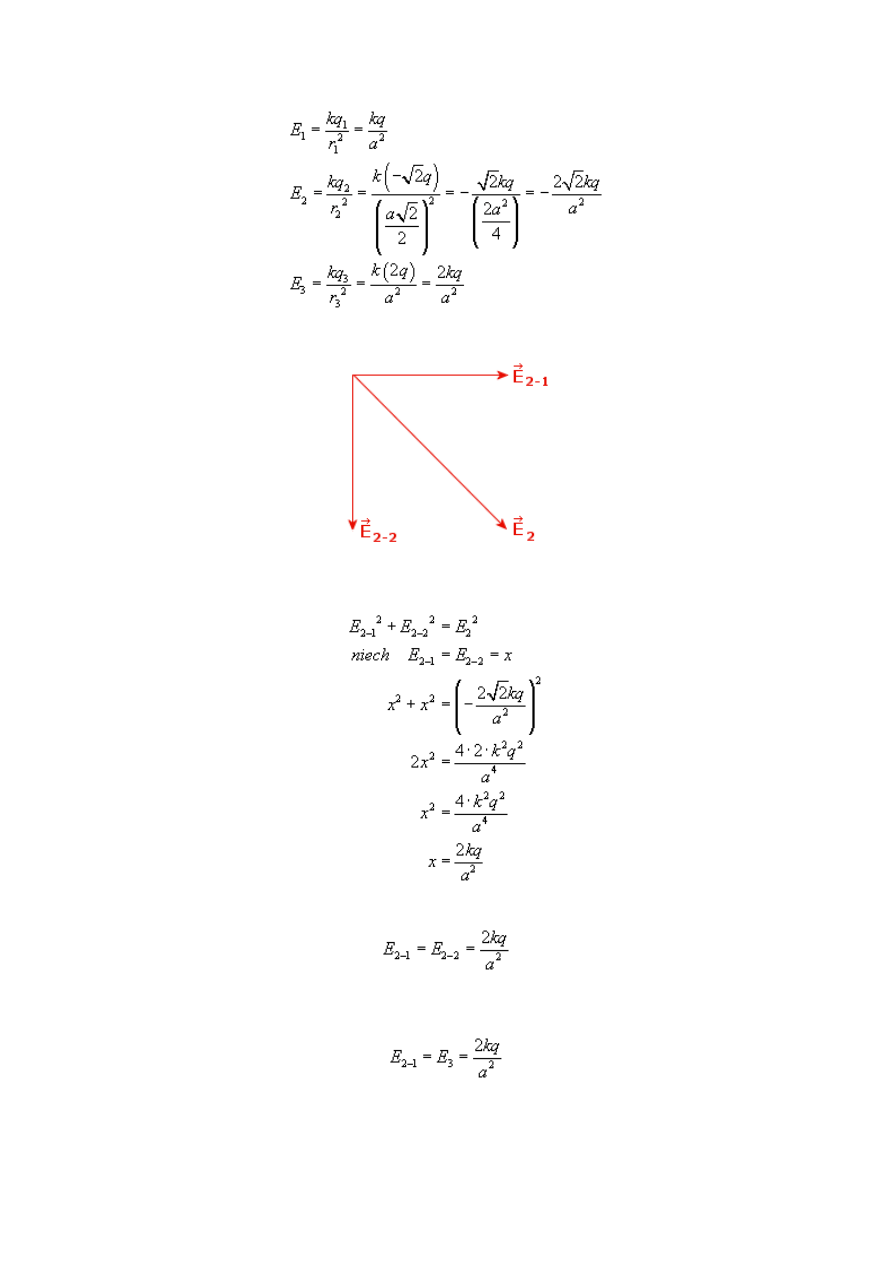
18
Składową E
2
możemy rozłożyć na dwie składowe E
2-1
i E
2-2
E
2-1
i E
2-2
mają tę samą wartość, ponieważ wektor E
2
leży na przekątnej kwadratu, więc
wektory E
2-1
i E
2-2
są również bokami (mniejszego) kwadratu
stąd
Teraz popatrzmy na oba rysunki.
Zauważymy, że w kierunku poziomym
Wektory te równoważą się i nie odgrywają roli w ustalaniu cech wektora natężenia pola E.
Patrzymy teraz na kierunek poziomy. Wektor E
2-2
ma większą wartość niż wektor E
1
.
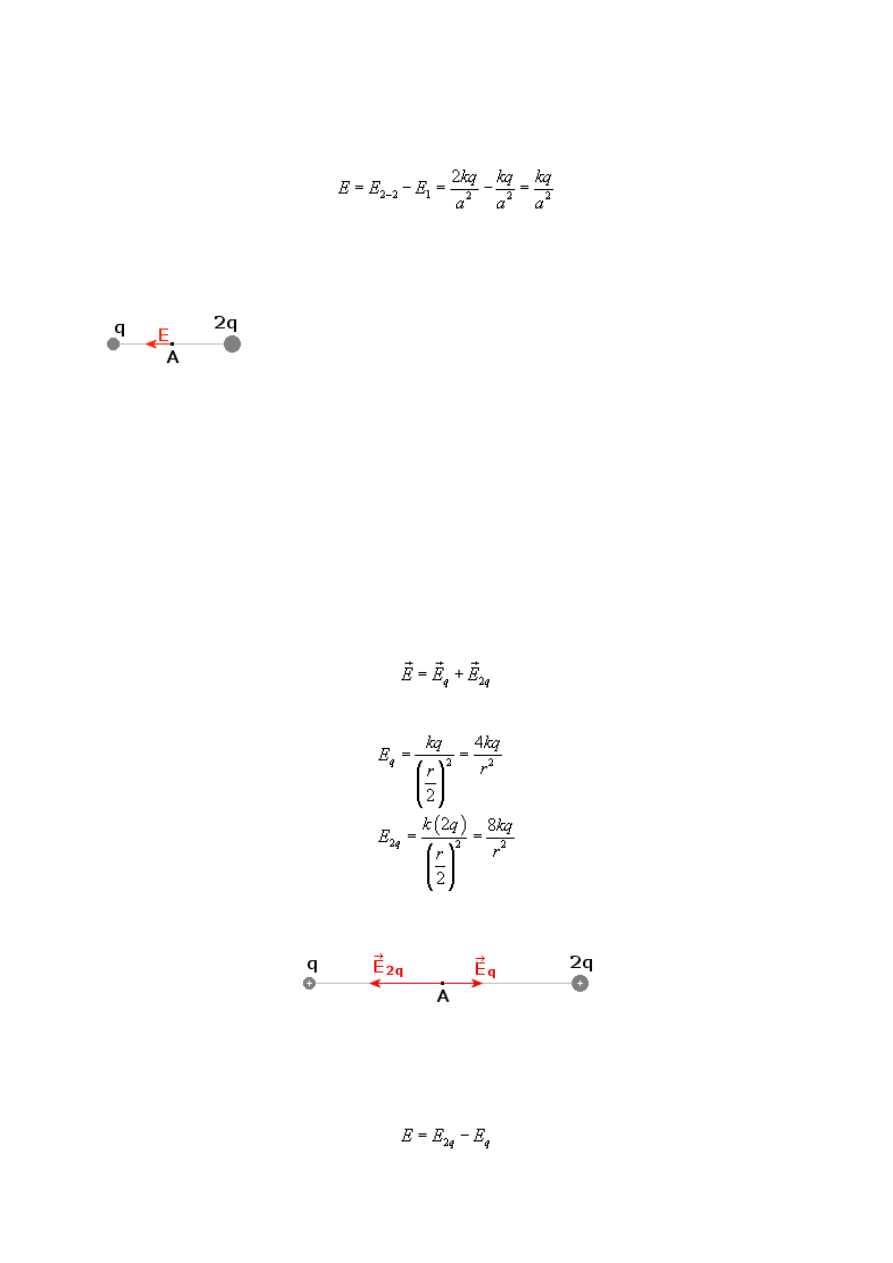
19
Oznacza to, że wektor E skierowany jest w kierunku poziomym ze zwrotem ku dołu o
wartości (wyliczanej zgodnie z zasadami odejmowania wektorów)
Pole elektrostatyczne - Zadanie 14
Treść:
W punkcie A, leżącym w połowie odległości między
ładunkami dodatnimi o nieznanej wartości, natężenie pola
elektrostatycznego jest równe E. Jaką wartość ma ładunek q,
jeżeli odległość między ładunkami wynosi r?
Dane:
r
E
Szukane:
q = ?
Wzory:
Rozwiązanie:
Ładunki q i 2q wytwarzają pewne pole elektrostatyczne. Na rysunku zaznaczano wektor
natężenia pola elektrostatycznego w punkcie A. Zasada superpozycji mówi, że jeżeli chcemy
policzyć natężenie pola elektrostatycznego w jakimś punkcie pola, w którym jest kilka
ładunków, to natężenie tego pola przedstawiamy jako sumę wektorową natężeń pól
pochodzących od każdego z ładunków.
Zatem nasze natężenie E
Obliczmy natężenia pola pochodzące od każdego z ładunków:
Wektor natężenia pola skierowany jest zawsze od ładunku dodatniego
Tak więc zgodnie z zasadą odejmowania wektorów, aby otrzymać wartość wektora E należy
od wektora E
2q
odjąć wektor E
q
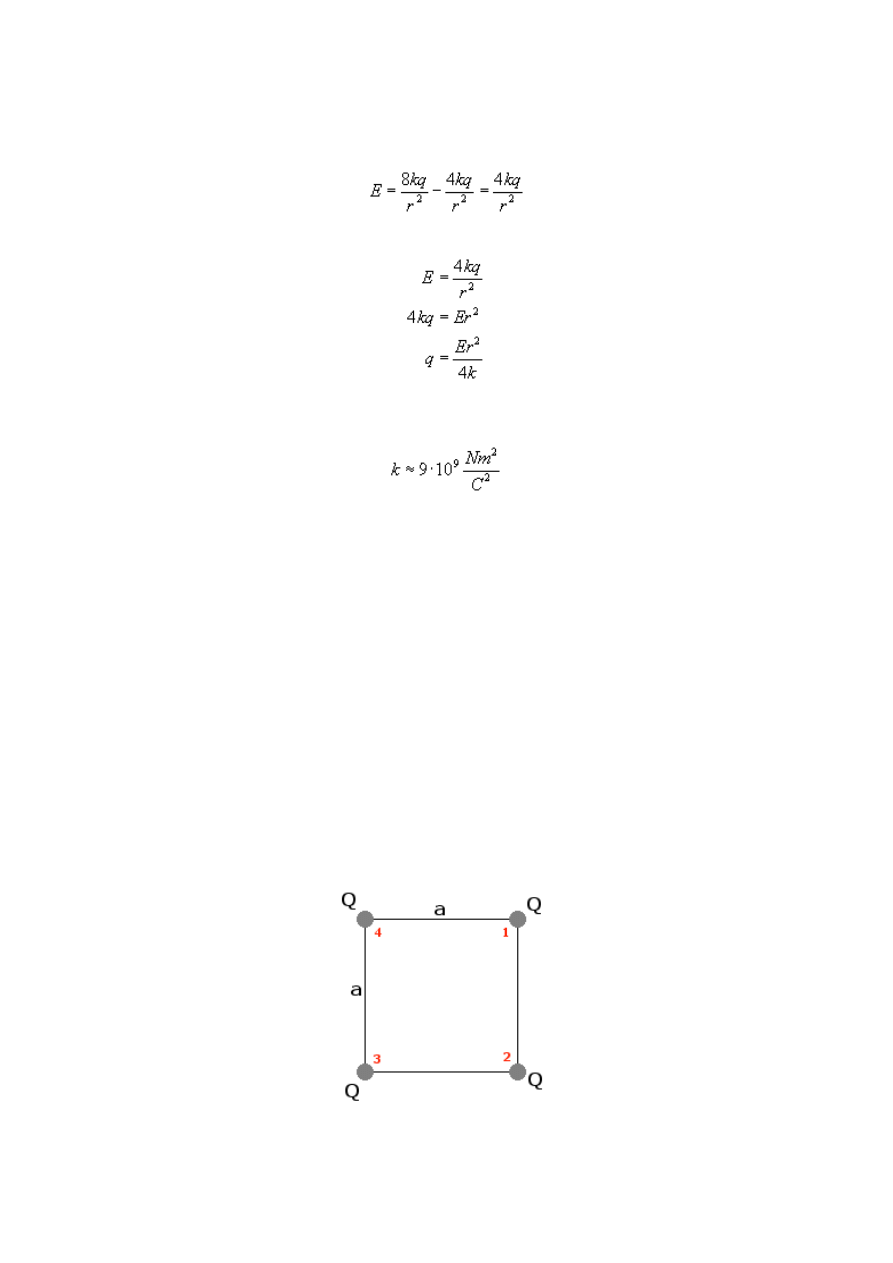
20
Zauważcie, że pierwszy wzór przedstawiał zapis wektorowy sytuacji, ten powyższy natomiast
przedstawia zapis niewektorowy; pozwala on nam wyliczyć wartość wektorów. Zatem
Z otrzymanej zależności możemy wyliczyć ładunek q.
Pamiętajmy, że k to stała, która zależy między innymi od środowiska, w którym znajduje się
pole. Zakładamy, że ładunki znajdują się w próżni.
Jamnik
Pole elektrostatyczne - Zadanie 15
Treść:
Takie same ładunki Q znajdują się w każdym rogu kwadratu o boku a.
Poszczególne ładunki zostają uwalniane pojedynczo zgodnie z ruchem
wskazówek zegara. Uwalniany ładunek osiąga swoją końcową prędkość zanim
kolejny ładunek zostanie uwolniony. Jakie są końcowe energie kinetyczne
wszystkich czterech ładunków?
Dane:
Q
a - bok kwadratu
k - stała
Szukane:
E
K
= ?
Wzory:
Rysunek:
21
Rozwiązanie:
Na rysunku czerwonymi cyframi zaznaczono kolejność "wypadania" ładunków.
Przy rozwiązywaniu zadania korzystamy z zasady zachowania energii. Gdy na początku
ładunek znajduje się w wierzchołku kwadratu posiada on energię potencjalną pola
elektrostatycznego, ale nie posiada energii kinetycznej, ponieważ prędkość ładunku równa
jest zeru. Gdy ładunek zacznie się oddalać, dotrze on do takiego punktu, w którym energia
potencjalna jest równa zeru (punkt taki, zgodnie z teorią, znajduje się nieskończenie daleko).
Wtedy całkowita początkowa energia potencjalna zostanie zamieniona na energię kinetyczną.
Tak więc za każdym razem:
Musimy zastanowić się, jak wyznaczyć energię potencjalną w polu elektrostatycznym. Nie
jest to trudne, należy skorzystać ze wzoru pierwszego, który przekształcamy do postaci:
gdzie V jest potencjałem elektrostatycznym, który wyznaczamy ze wzoru:
Najpierw zajmujemy się ładunkiem pierwszym. Potencjałem całkowitym jest tutaj suma
potencjałów pochodzących od każdego ładunku (zgodnie z zasadą superpozycji):
Zauważmy, że przy ładunku trzecim odległością jest długość przekątnej kwadratu, a w
pozostałych przypadkach - długość boku kwadratu.
Wyliczamy energię potencjalną
A ponieważ E
K
= E
P
Teraz gdy ładunek pierwszy jest daleko w nieskończoności, to nie wpływa on na pozostałe
ładunki, tak więc pozostały nam trzy ładunki.
W podobny sposób liczymy energie kinetyczne dla pozostałych ładunków:
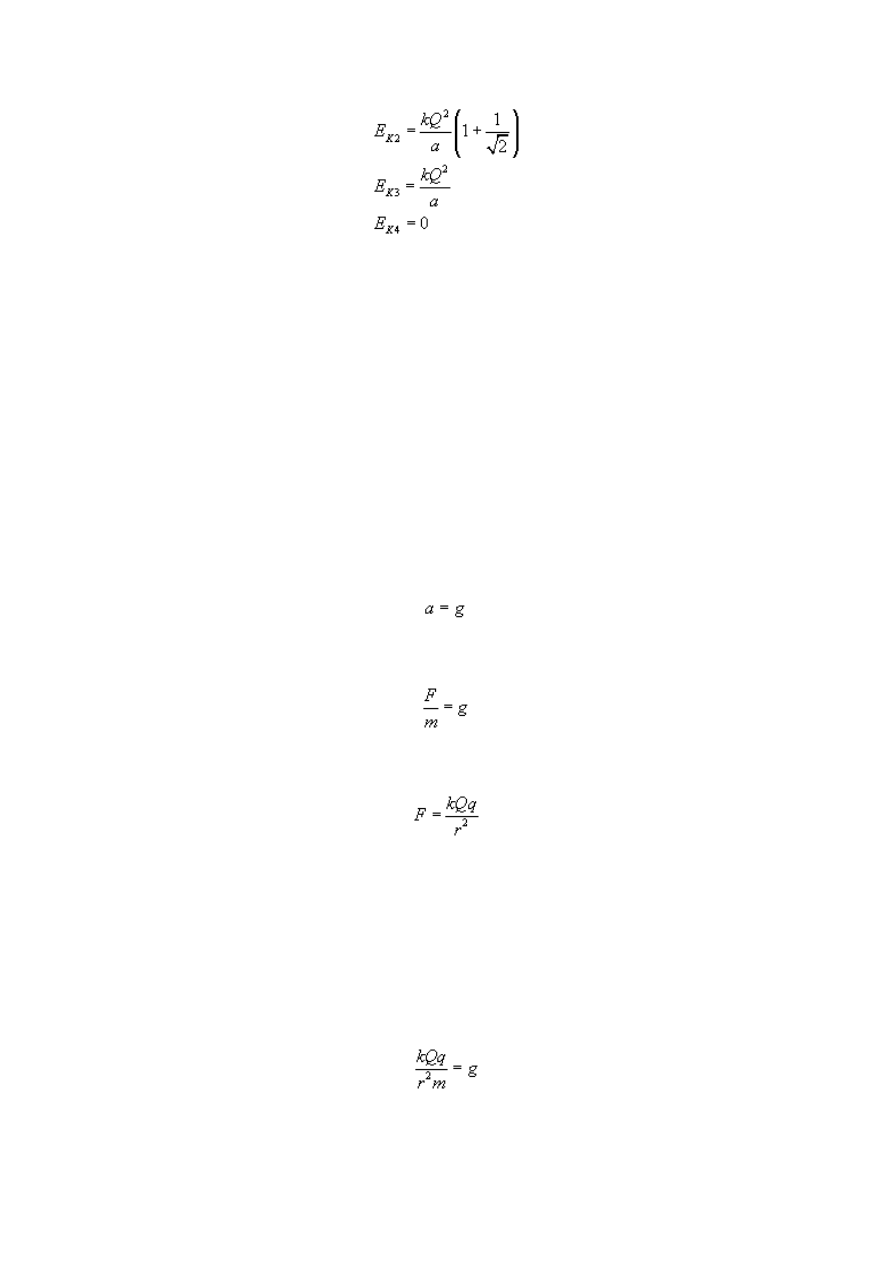
22
Słowo wyjaśnienia należy się w przypadku ostatnim. Otóż wtedy zostaje nam tylko jeden
ładunek, bo pozostałe są w nieskończoności. W takim wypadku ładunek ten nie ma z czym
oddziaływać, a więc pozostaje w spoczynku. Wtedy energia kinetyczna równa jest zeru.
Pole elektrostatyczne - Zadanie 16
Treść:
Jaką wartość powinno mieć natężenie pola, aby pole elektrostatyczne nadało
cząstce o masie m i ładunku q przyspieszenie równe przyspieszeniu ziemskiemu?
Dane:
m
q
g
Szukane:
E = ?
Wzory:
Rozwiązanie:
Pole elektrostatyczne nadaje cząstce przyspieszenie a równe przyspieszeniu ziemskiemu g:
Zgodnie z II zasadą dynamiki przyspieszenie możemy zapisać jako iloraz siły powodującej
przyspieszenie przez masę cząstki:
Działającą siłą jest tu oczywiście siła wynikająca z prawa Coulomba, które zapisujemy
wzorem
gdzie:
q - to ładunek cząstki,
Q - ładunek źródła pola elektrostatycznego,
r - odległość pomiędzy q a Q,
k - stała zależna od środowiska, w którym znajdują się ładunki.
Nasze równanie przyjmuje więc postać
Mamy znaleźć natężenie pola elektrostatycznego, które wyrażamy wzorem
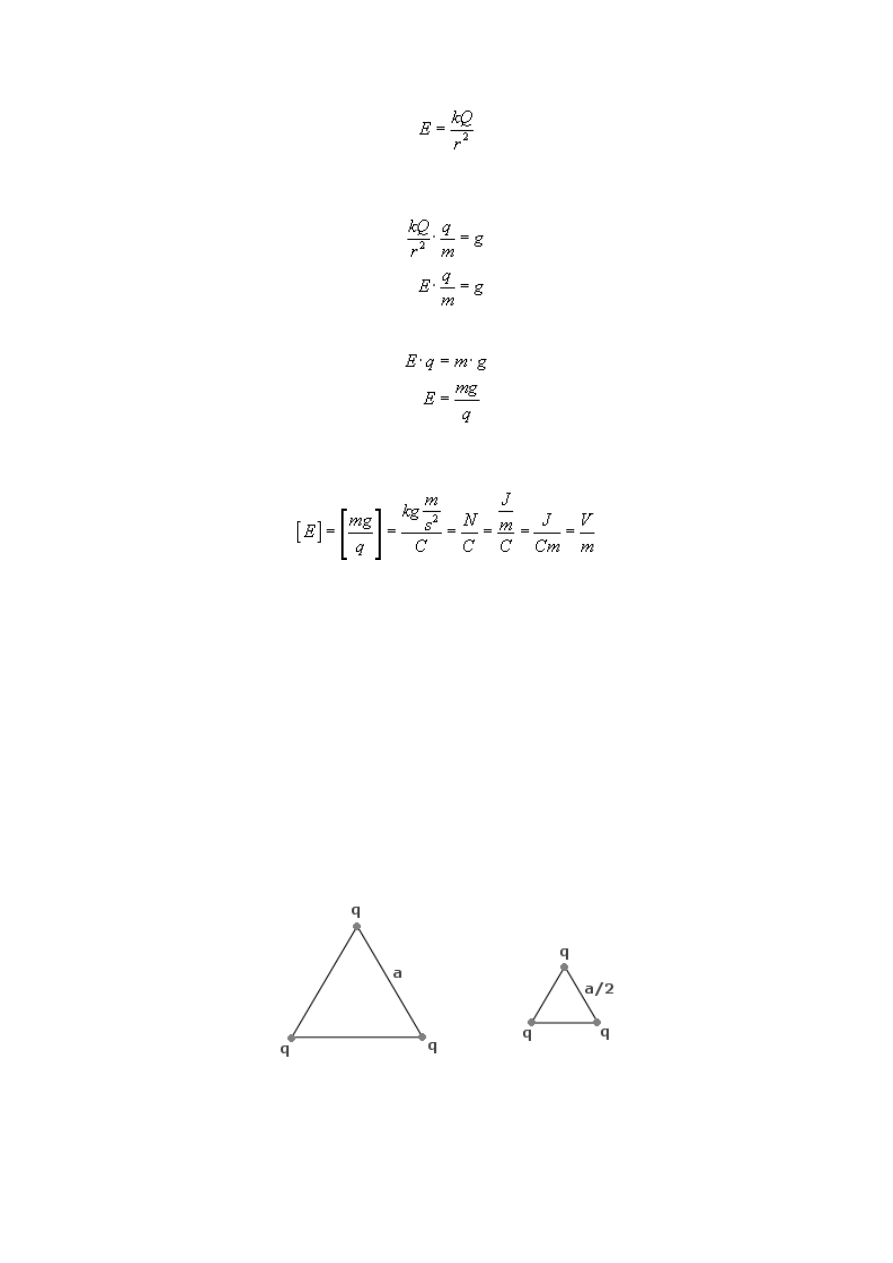
23
Zauważ, że we wzorze tym jest wartość ładunku Q, czyli wartość ładunku źródłowego.
Przekształcając dalej nasze równanie otrzymujemy:
Teraz bez problemu możemy wyprowadzić wzór na natężenie pola
Sprawdzimy jeszcze, czy otrzymamy poprawną jednostkę (pamiętaj, że jednostką natężenia
pola jest wolt na metr).
skorzystaliśmy z tego, że siła to iloraz pracy (energii) przez przesunięcie, a iloraz energii
przez ładunek to napięcie.
Pole elektrostatyczne - Zadanie 17
Treść:
W każdym wierzchołku trójkąta równobocznego o boku a umieszczono ładunek q
i w ten sposób wykonano łącznie pracę W. Jakiej pracy wymaga zbudowanie
takiego samego trójkąta o boku a/2?
Dane:
a - bok trójkąta
q
W
Szukane:
W' = ?
Wzory:
Rysunek:
Rozwiązanie:
24
Aby obliczyć pracę, korzystamy z jednego ze wzorów na pracę w polu elektrostatyczną. My
wybraliśmy wzór
Za ΔV przyjmiemy całkowity potencjał pola, który wyliczymy z zasady superpozycji
potencjałów, która mówi, że potencjał całkowity równy jest sumie algebraicznej potencjałów
składowych.
Spójrzmy najpierw na trójkąt o boku a.
Na każdy ładunek q działają dwa inne ładunki oddalone w każdym przypadku o a. Potencjał
wyliczony dla jednego z ładunków q wynosi:
A ponieważ takich ładunków mamy trzy sztuki, to całkowity potencjał wynosi
Pamiętajmy, że k to stała zależna od środowiska, w którym znajdują się ładunki - jednak, jak
zobaczycie później, ona wcale nie będzie nam potrzebna.
Wykonana praca przy budowie trójkąta pierwszego
Teraz zajmiemy się trójkątem o boku a/2.
Rzecz z potencjałami ma się identycznie jak poprzednio.
Potencjał w punkcie pola, w którym znajduje się jeden z ładunków wyrażamy...
a ponieważ mamy trzy ładunki, to:
25
Czyli wykonana praca wynosi:
Tak więc aby zbudować trójkąt o boku a/2 należy wykonać dwa razy większą pracę, niż przy
budowie trójkąta o boku a.
Pole elektrostatyczne - Zadanie 18
Treść:
Natężenie pola elektrostatycznego w pewnym punkcie ma wartość 10
2
N/C i zwrot
pionowo w dół. Jaki będzie kierunek, zwrot i wartość wektora siły działającej na
ładunek ujemny o wartości 10
-6
C, który umieścimy w tym punkcie?
Dane:
E = 10
2
N/C
q = 10
-6
C
Szukane:
F = ?
Wzory:
Rysunek:
Rozwiązanie:
Wektor natężenia pola elektrostatycznego E ma zawsze zwrot "od plusa do minusa". A
ponieważ ładunek ujemny Q będzie przyciągać się tylko z dodatnim ładunkiem, oznacza to,
że zwrot siły F będzie skierowany ku górze, a kierunek oczywiście będzie pionowy.
Pozostało nam wyliczenie wartości siły F. Korzystamy ze wzoru na natężenie pola
elektrostatycznego
26
Aby wyliczyć z niego siłę, należy go przekształcić i wyliczyć szukaną wartość:
Na ładunek działa siła o wartości 10
-4
N skierowana pionowo w górę.
Pole elektrostatyczne - Zadanie 19
Treść:
Proton i cząstka α (alfa) zostały przyspieszone tą samą różnicą potencjałów. Jaka
jest zależność pomiędzy prędkością protonu oraz prędkością cząstki alfa?
Dane:
U
p
= U
α
Szukane:
v
p
/ v
α
= ?
Wzory:
Rozwiązanie:
Nim zaczniemy rozwiązywać, trzeba znać podstawowe informacje o cząstkach alfa. Cząstka
alfa składa się z dwóch protonów i dwóch neutronów; ma ładunek dodatni.
Teraz spróbujemy wyrazić prędkość ładunku wskutek przyspieszenia go różnicą potencjałów.
Aby przenieść dodatni ładunek przez różnicę potencjałów ΔV (zwaną dalej napięciem U)
należy wykonać pracę
Praca ta w polu elektrostatycznym równa jest oczywiście energii potencjalnej.
Po przebyciu całej różnicy potencjałów, energia potencjalna zostanie całkowicie zamieniona
na energię kinetyczną
I właśnie z tego ostatniego równania spróbujemy wyprowadzić stosowny wzór:
27
Wracamy do treści zadania. Liczymy kolejno prędkość protonu i prędkość cząstki alfa,
uwzględniając to, że przebywają one takie samo napięcie (różnicę potencjałów):
Oznacza to, że:
Pole elektrostatyczne - Zadanie 20
Treść:
Kulę przewodzącą o promieniu r, naładowaną do potencjału V, zetknięto z
nienaelektryzowaną kulą o trzykrotnie większym promieniu. Ile wynosi potencjał
kul po zetknięciu?
Dane:
r
R = 3r
V
Szukane:
V' = ?
Wzory:
Rozwiązanie:
Skorzystamy tutaj z zasady zachowania ładunku. Otóż ładunek który znajdował się w kuli o
promieniu r będzie równy ładunkowi, jaki będzie umieszczony w dwóch kulach po
zetknięciu.
Przed zetknięciem mamy daną kulę o promieniu r. Jej potencjał wynosi
Ze wzoru na potencjał wyprowadzono obok wzór na ładunek.
Stykamy teraz naszą kulę z nienaładowaną kulą (czyli o potencjale równym zeru) o promieniu
3r.
Powstała różnica potencjałów, zatem układ nie jest w równowadze elektrostatycznej.
Następuje przemieszczanie się elektronów swobodnych w stronę potencjału wyższego, aż do
memontu wyrównania się potencjałów obu kul, który oznaczymy przez V'.
Ale oczywiście pozostał ten sam ładunek, który znajduje się teraz w dwóch kulach:
28
Porównujemy dwa powyższe wzory na ładunek
Równanie to możemy uprościć przez stałą k, promień r oraz wyliczyć szukany potencjał kul
po zetknięciu
Potencjał kul po zetknięciu jest równy 0.25 potencjału naładowanej kuli przed zetknięciem.
Pole elektrostatyczne - Zadanie 21
Treść:
Kropla wody została naładowana ładunkiem q>0. Jak zmienił się jej potencjał,
jeżeli wskutek parowania, nie zmieniając ładunku, kropla zmienia swoją objętość
27 razy?
Dane:
q > 0
27 O' = O (O - objętość)
Szukane:
V' = ?
Wzory:
Rozwiązanie:
Kropla wody zmienia 27 razy swoją objętość. Objętość kuli zależy od jej promienia, a od tego
promienia zależy również potencjał (przyjrzyj się wzorom).
Obliczymy na początku zmianę promienia wskutek zmiany objętości kropli. Kula (kropla)
miała na początku objętość O, a potem jej objętość miała wartość O'. Z treści zadania wiemy,
że
Na początku duża kropla miała potencjał V
29
A teraz część kropli wyparowała; liczymy potencjał
Wskutek parowania potencjał kuli zwiększył się 3 razy.
r />