9. Zastosowania całki oznaczonej
9.1. Całka oznaczona jako pole obszaru płaskiego
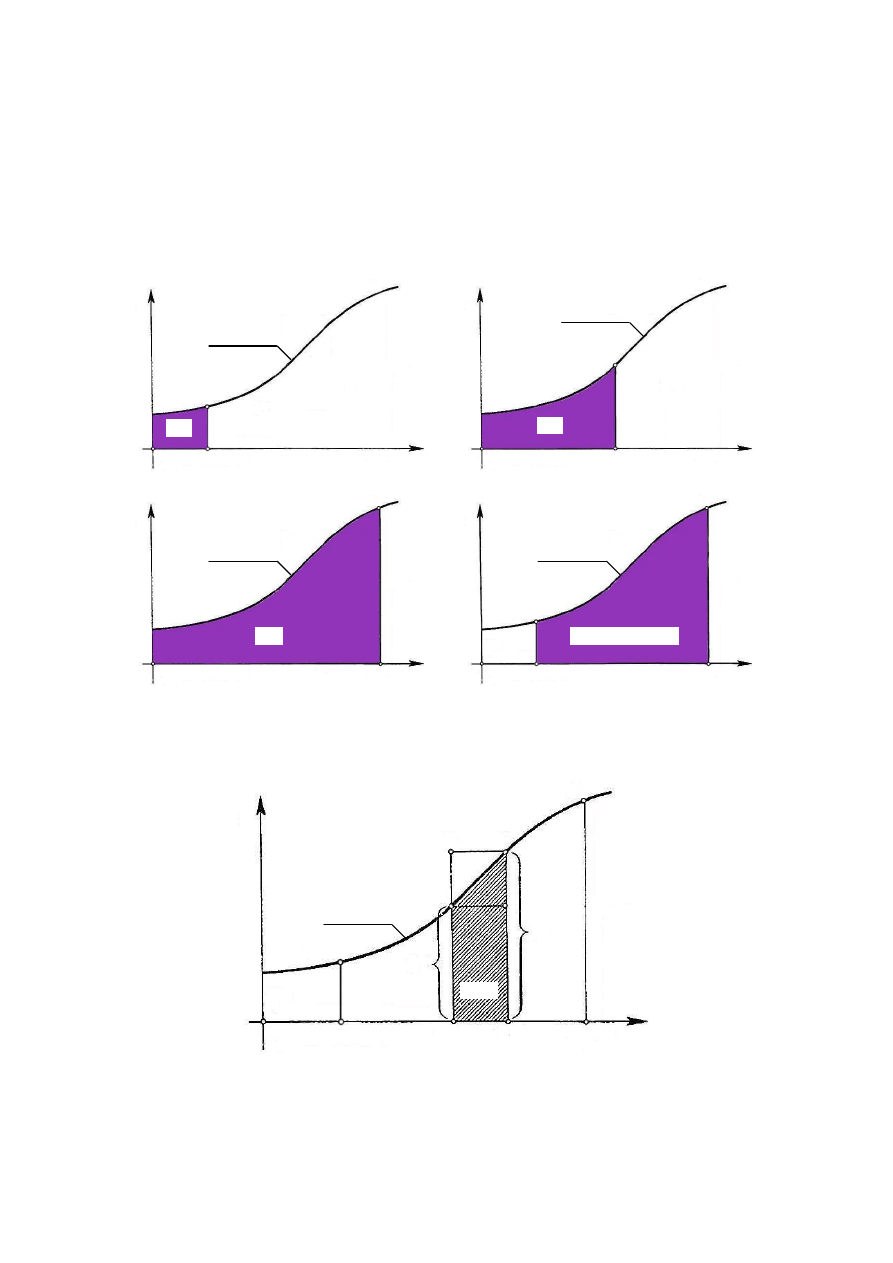
Niech f będzie funkcją ciągłą, rosnącą i dodatnią zmiennej x określoną na pewnym odcinku
osi R. Przez F oznaczamy funkcję, której wartości F(x) oznaczają pole obszaru zawartego
między krzywą
)
(x
f
y
=
oraz osią x na odcinku
R
x
∈
〉
〈 ,
0
, zgodnie z rys. 1b.
Rys. 1
Nadając zmiennej x przyrost ∆x otrzymujemy przyrost pola
)
(
)
∆
(
)
(
∆
x
F
x
x
F
x
F
−
+
=
, rys.2.
Rys. 2
Z rysunku 2 wynika nierówność
f(x)·∆x < F(x + ∆x) – F(x) < f(x +∆x)·∆x, (1)
skąd
x
y
a
b
x
+
∆
x
0
x
F(x)
F(a)
F(b)
a
b
x
a
b
x
x
x
x
y
y
y
y
0
0
0
0
F
ab
= F(b) – F(a)
)
(x
f
y
=
)
(x
f
y
=
)
(x
f
y
=
)
(x
f
y
=
)
(x
f
y
=
)
(x
f
f
(x+∆x)
a)
b)
c)
d
)
F(x)
∆
F(x)

2
f(x) <
x
x
F
x
x
F
∆
)
(
)
∆
(
−
+
< f(x +∆x). (2)
Przechodząc do granicy ∆x → 0 mamy
f(x) ≤
x
x
F
x
x
F
x
∆
)
(
)
∆
(
lim
0
∆
−
+
→
≤ f(x),
zatem
)
(
∆
)
(
)
∆
(
lim
0
∆
x
f
x
x
F
x
x
F
x
=
−
+
→
. (3)
Gdy funkcja f jest malejąca, to zamiast (1) mamy
f(x +∆x)·∆x < F(x + ∆x) – F(x) < f(x)·∆x
skąd po przejściu do granicy ∆x → 0 również otrzymamy (3).
Równość (3) oznacza, że F jest funkcją pierwotną funkcji f. Na podstawie rys. 1d pole F
ab
obszaru zawartego między krzywą
)
(x
f
y
=
oraz osią x na odcinku
〉
〈 b
a,
jest równe
F
ab
= F(b) – F(a). (4)
Ponieważ F jest funkcją pierwotną funkcji f , zatem z definicji całki oznaczonej mamy
∫
=
−
b
a
dx
x
f
a
F
b
F
)
(
)
(
)
(
.
Stąd i z (4) wynika, że pole F
ab
obszaru zawartego między krzywą
)
(x
f
y
=
oraz osią x na
odcinku
〉
〈 b
a,
jest równe
F
ab
=
∫
b
a
dx
x
f
)
(
. (5)
Jeżeli funkcja f jest ujemna, to pole F
ab
obszaru zawartego między krzywą
)
(x
f
y
=
oraz osią
x na odcinku
〉
〈 b
a,
jest równe
F
ab
= –
∫
b
a
dx
x
f
)
(
.
Gdy funkcja f zmienia znak, to całka
∫
b
a
dx
x
f
)
(
przedstawia sumę algebraiczną odpowiednich
pól. Pola nad osią x są liczone ze znakiem +, a pola pod osią x ze znakiem – (rys. 3).
Rys. 3
3
9.2. Całka oznaczona jako granica sum
Jeżeli f jest funkcją ciągłą w przedziale
〉
〈 b
a,
, to istnieje taki punkt
)
,
( b
a
∈
ξ
, że całkę ozna-
czoną
∫
b
a
dx
x
f
)
(
można przedstawić w postaci
)
(
)
(
)
(
ξ
f
a
b
dx
x
f
b
a
⋅
−
=
∫
. (6)
Wartość
)
(
ξ
f
nazywamy
wartością średnią funkcji w przedziale
〉
〈 b
a,
. Oznacza to, że do-
wolny obszar między wykresem funkcji f oraz osią x na odcinku od a do b można zamienić na
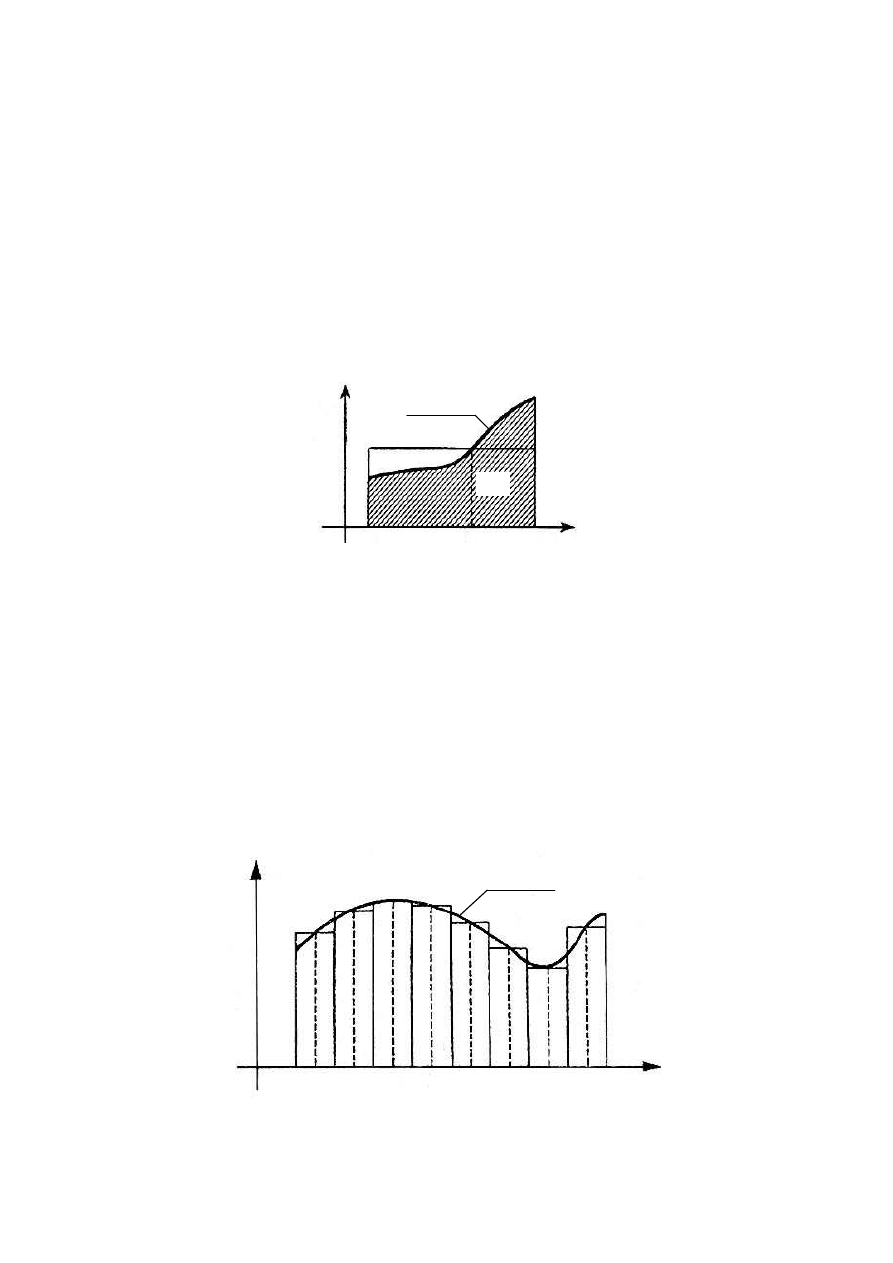
prostokąt o tym samym polu, co ilustruje rys. 4.
Rys. 4.
Ciąg punktów (x
0
, x
1
, x
2
, ... , x
n
) takich, że a = x
0
< x
1
< x
2
< ... < x
i-1
< x
i
< ... < x
n-1
< x
n
= b
nazywamy
podziałem przedziału
〉
〈 b
a,
. Oznaczamy
1
∆
−
−
=
i
i
i
x
x
. Wtedy przedział
〉
〈 b
a,
jest sumą przedziałów
〉
〈
−
i
i
x
x ,
1
. Podział (x
0
, x
1
, x
2
, ... , x
n
) przedziału
〉
〈 b
a,
nazywamy
podziałem normalnym, jeśli n → ∞ oraz
0
∆
max
→
i
przy n → ∞.
Niech f będzie funkcją ciągłą w przedziale
〉
〈 b
a,
oraz niech (x
0
, x
1
, x
2
, ... , x
n
) będzie po-
działem normalnym przedziału
〉
〈 b
a,
. Wtedy dla dowolnego ciągu punktów
)
,
(
1
i
i
i
x
x
−
∈
ξ
,
gdzie i = 1, 2, ... n, zachodzi równość (rys. 5)
∑
∫
=
∞
→
⋅
=
n
i
i
i
n
b
a
f
dx
x
f
1
∆
)
(
lim
)
(
ξ
. (7)
Rys. 5
Wzór (7) można traktować jako definicję całki oznaczonej.
f(ξ)
)
(x
f
y
=
a
b
0
x
1
x
i-1
x
i
ξ
i
x
n-1
y
x
ξ
1
)
(x
f
y
=
y
x
a
b
ξ
0
4
9.3. Obliczanie pola
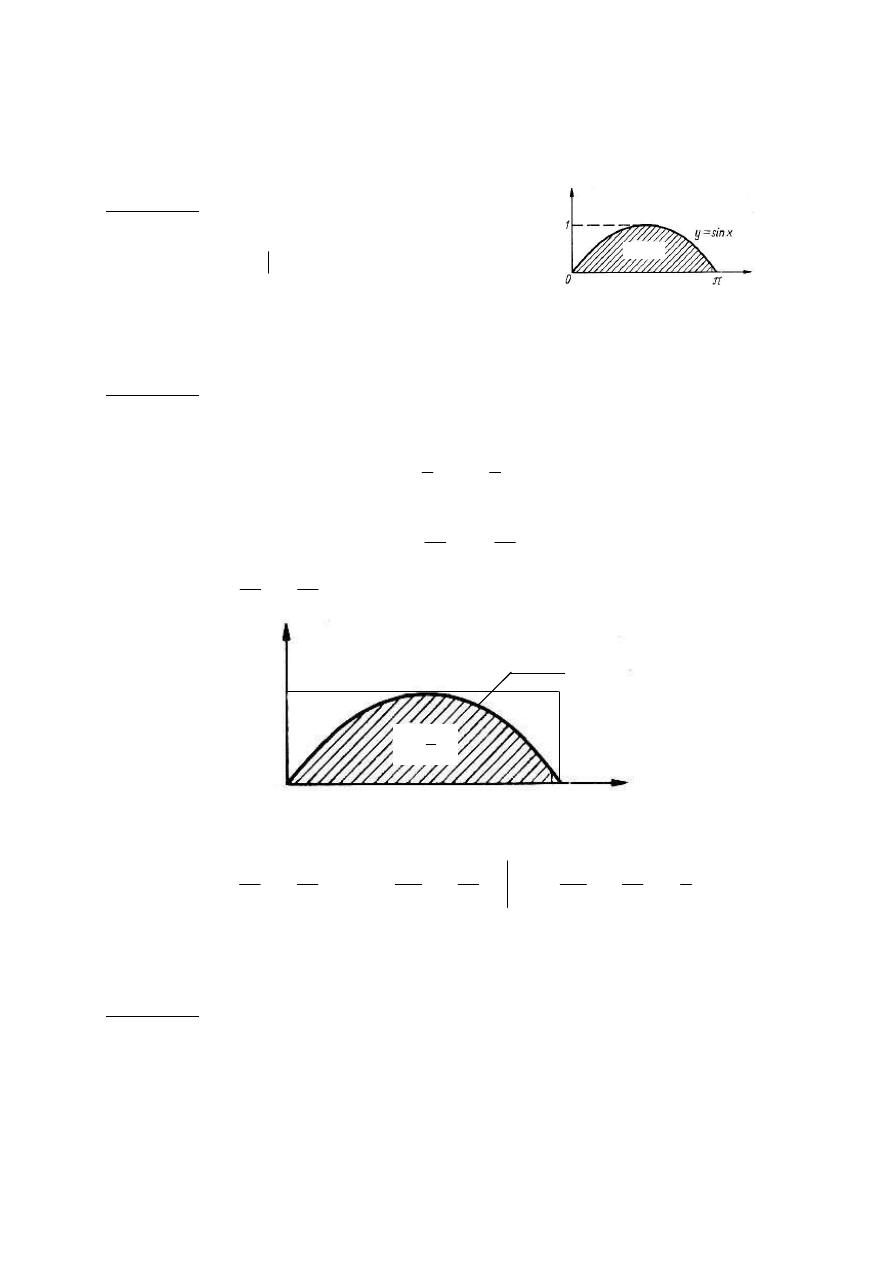
Przykład 1. Obliczyć pole zawarte między łukiem sinusoidy i osią x w przedziale
〉
〈
π
,
0
.
Rozwiązanie. Szukane pole określone jest całką
2
)
1
1
(
)
0
cos
(cos
cos
sin
0
0
=
−
−
−
=
−
−
=
−
=
=
∫
=
=
π
π
π
x
x
x
xdx
F
Przykład 2. Obliczyć pole ograniczone łukiem paraboli w prostokącie a × b.
Rozwiązanie. Równanie paraboli określone jest wzorem
γ
β
α
+
+
=
x
x
y
2
. Współczynniki α,
β , γ wyznaczamy z warunków:
γ
β
α
+
⋅
+
⋅
=
0
0
0
2
,
γ
β
α
+
⋅
+
⋅
=
2
2
2
b
b
a
,
γ
β
α
+
⋅
+
⋅
=
b
b
2
0
.
Po rozwiązaniu tych równań mamy:
2
4
b
a
−
=
α
,
b
a
4
=
β
,
0
=
γ
, zatem parabola jest opisana
równaniem
x
b
a
x
b
a
y
4
4
2
2
+
−
=
.
Pole obszaru ograniczonego parabolą jest równe
ab
b
b
a
b
b
a
x
b
a
x
b
a
dx
x
b
a
x
b
a
F
b
x
x
b
3
2
2
3
4
2
3
4
4
4
2
3
2
0
2
3
2
0
2
2
=
+
−
=
+
−
=
+
−
=
=
=
∫
.
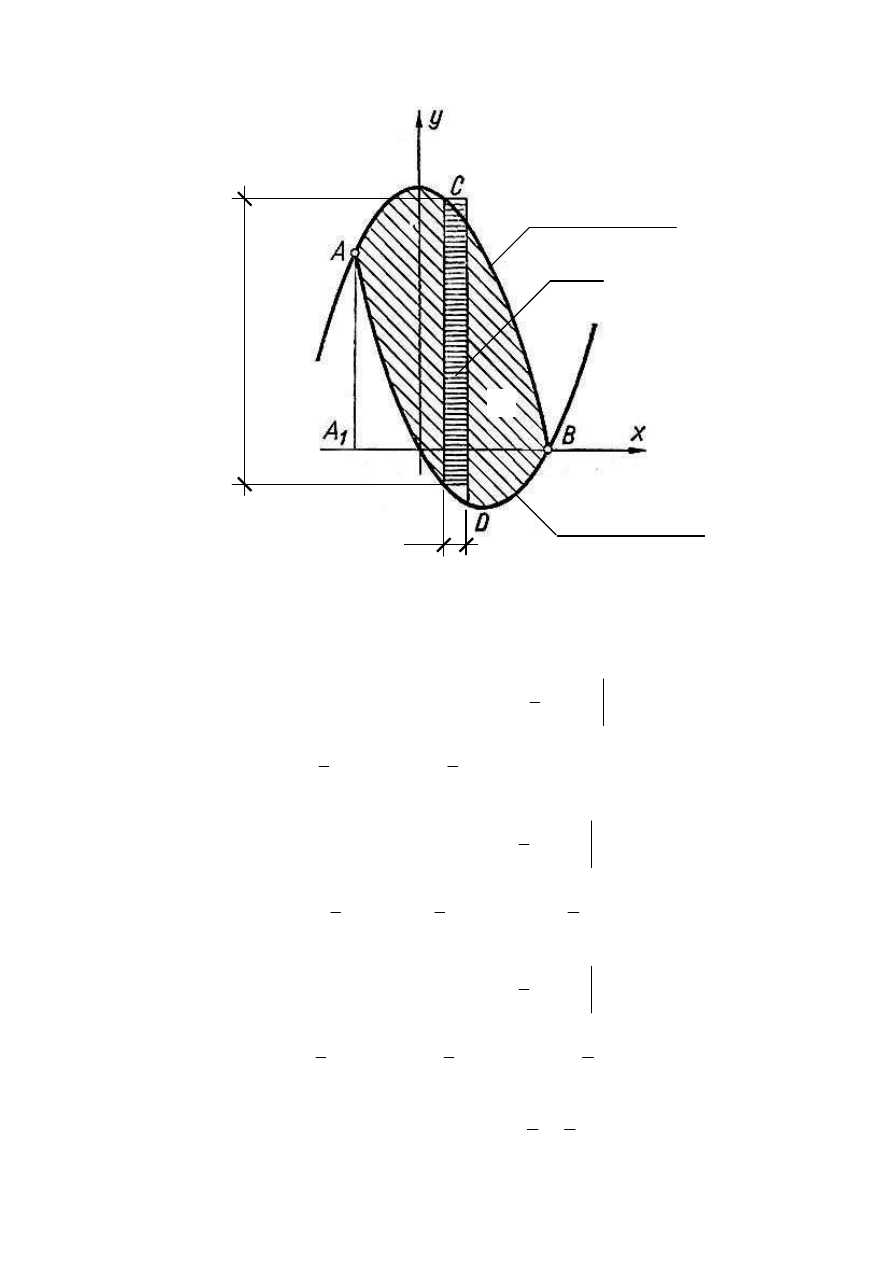
Przykład 3. Obliczyć pole obszaru ograniczonego parabolami
4
2
1
+
−
=
x
y
,
x
x
y
2
2
2
−
=
.
Rozwiązanie. Szukamy punkty A i B przecięcia parabol
4
2
1
+
−
=
x
y
oraz
x
x
y
2
2
2
−
=
. W
tym celu rozwiązujemy równanie
2
1
y
y
=
, czyli równanie
x
x
x
2
4
2
2
−
=
+
−
, które po prze-
kształceniu ma postać
0
2
2
=
−
−
x
x
. Rozwiązaniami tego równania są
1
−
=
A
x
,
2
=
B
x
.
Rzędne wynoszą
3
)
1
(
2
)
1
(
4
)
1
(
2
2
=
−
−
−
=
+
−
−
=
A
y
oraz
0
)
2
(
2
)
2
(
4
)
2
(
2
2
=
−
=
+
−
=
B
y
.
Szukane punkty to
)
3
,
1
(
)
,
(
−
=
=
A
A
y
x
A
oraz
)
0
,
2
(
)
,
(
=
=
B
B
y
x
B
. Obszar ograniczony para-
bolami
1
y
i
2
y
pokazany jest na rysunku
x
y
F = 2
ab
F
3
2
=
y
x
a
b
parabola
5
Szukane pole F jest sumą algebraiczną pól trapezów krzywoliniowych:
0
0
1
1
A
A
DB
ACB
A
F
F
F
F
−
−
=
,
gdzie:
(
)
=
+
−
=
+
−
=
=
=
−
=
−
−
∫
∫
2
1
3
2
1
2
2
1
1
4
3
1
4
)
(
1
x
x
ACB
A
x
x
dx
x
dx
x
y
F
9
)
1
(
4
)
1
(
3
1
2
4
2
3
1
3
3
=
−
⋅
+
−
⋅
−
−
⋅
+
⋅
−
=
,
(
)
=
−
=
−
=
=
=
=
∫
∫
2
0
2
3
2
0
2
2
0
2
0
3
1
2
)
(
x
x
DB
x
x
dx
x
x
dx
x
y
F
3
4
)
0
(
)
0
(
3
1
2
2
3
1
2
3
2
3
−
=
−
⋅
−
−
⋅
=
,
(
)
=
−
=
−
=
=
=
−
=
−
−
∫
∫
0
1
2
3
0
1
2
0
1
2
0
3
1
2
)
(
1
x
x
A
A
x
x
dx
x
x
dx
x
y
F
3
4
)
1
(
)
1
(
3
1
)
0
(
)
0
(
3
1
2
3
2
3
=
−
−
−
⋅
−
−
⋅
=
.
Stąd
9
3
4
3
4
9
0
0
1
1
=
−
−
−
=
−
−
=
A
A
DB
ACB
A
F
F
F
F
.
–1
2
0
F
4
)
(
2
1
+
−
=
x
x
y
x
x
x
y
2
)
(
2
2
−
=
dx
y
1
(x
)
–
y
2
(x
)
dS(x)

6
Pole F można obliczyć inaczej jako sumę elementów pola dS(x) w granicach od –1 do 2:
(
)
9
4
3
2
)
4
2
2
(
)
(
)
(
)
(
2
1
2
3
2
1
2
2
1
2
1
2
1
=
+
+
−
=
+
+
−
=
−
=
=
=
−
=
−
−
−
∫
∫
∫
x
x
x
x
x
dx
x
x
dx
x
y
x
y
dx
x
dS
F
.
Przykład 4. Obliczyć pole elipsy o osiach a i b.
Równanie elipsy ma postać
1
2
2
2
2
=
+
b
y
a
x
. Rozwiązując względem y otrzymamy równanie gór-
nego łuku elipsy
2
2
)
(
x
a
a
b
x
y
−
=
. Ze względu na symetrię wystarczy obliczyć pole pierw-
szej ćwiartki elipsy i wynik pomnożyć przez 4:
∫
∫
−
=
=
a
a
dx
x
a
a
b
dx
x
y
F
0
2
2
0
4
)
(
4
. (*)
Całkę
∫
−
a
dx
x
a
0
2
2
obliczamy przez podstawienie
t
a
x
sin
=
, skąd
tdt
a
dx
cos
=
. Wraz ze
zmiana zmiennej należy również zmienić granice całkowania:
dla x = 0 mamy
t
a sin
0
=
, zatem t = 0,
dla x = a mamy
t
a
a
sin
=
, zatem
1
sin
=
t
, skąd
2
π
=
t
.
∫
∫
∫
=
⋅
−
=
−
2
0
2
2
2
0
2
2
0
2
2
cos
cos
sin
1
π
π
dt
t
a
dt
t
t
a
dx
x
a
a
.
Stosujemy teraz podstawienie
)
2
cos
1
(
2
1
cos
2
t
t
+
=
i otrzymujemy
4
2
sin
2
1
2
)
2
cos
1
(
2
cos
2
2
0
2
2
0
2
2
0
2
2
0
2
2
a
t
t
a
dt
t
a
dt
t
a
dx
x
a
t
t
a
π
π
π
π
=
+
=
+
=
=
−
=
=
∫
∫
∫
.
Wracając do wzoru (*) mamy
ab
a
a
b
dx
x
a
a
b
F
a
π
π
=
⋅
=
−
=
∫
4
4
4
2
0
2
2
.
x
y
a
b
7
9.4. Obliczanie objętości
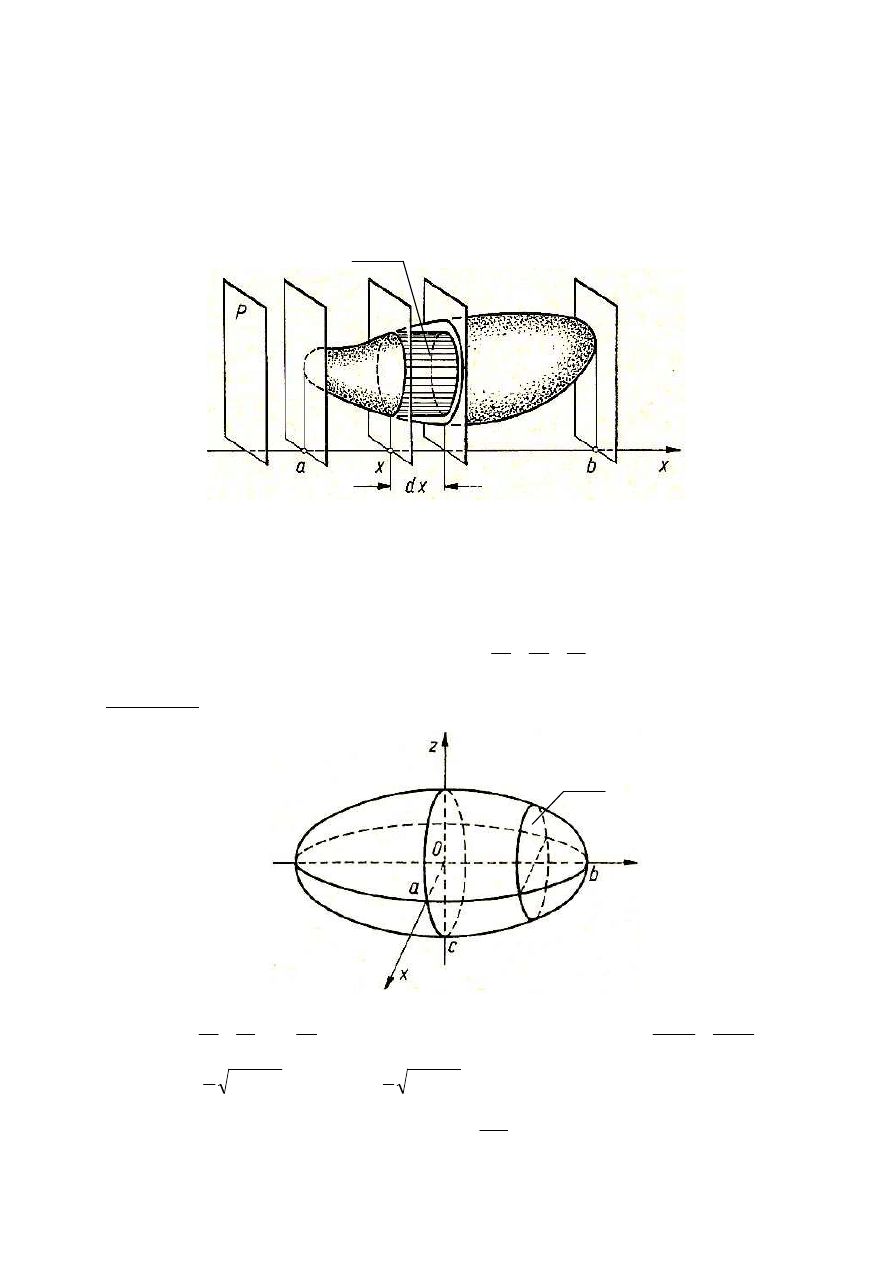
Jeżeli znane jest pole S(x), jako funkcja zmiennej x, dowolnego przekroju bryły płaszczyzną
równoległą do pewnej ustalonej płaszczyzny P (płaszczyzna P nie musi być prostopadła do
osi x), to element objętości bryły jest równy
dx
x
S
x
dV
)
(
)
(
=
.
Wtedy objętość bryły określona jest wzorem
∫
=
b
a
dx
x
S
V
)
(
.
Przykład 5. Obliczyć objętość elipsoidy trójosiowej
1
2
2
2
2
2
2
=
+
+
c
z
b
y
a
x
.
Rozwiązanie. Przekrój S(y) elipsoidy równoległy do płaszczyzny xz w odległości y jest elipsą
o równaniu
2
2
2
2
2
2
1
b
y
c
z
a
x
−
=
+
, które po przekształceniu przyjmuje postać
1
)
(
)
(
2
2
2
2
=
+
y
c
z
y
a
x
,
gdzie
2
2
)
(
y
b
b
a
y
a
−
=
oraz
2
2
)
(
y
b
b
c
y
c
−
=
. Pole elipsy S(y) jest równe
)
(
)
(
)
(
)
(
2
2
2
y
b
b
ac
y
c
y
a
y
S
−
=
⋅
⋅
=
π
π
.
S(x)
)
(x
dV
y
S(y)
y
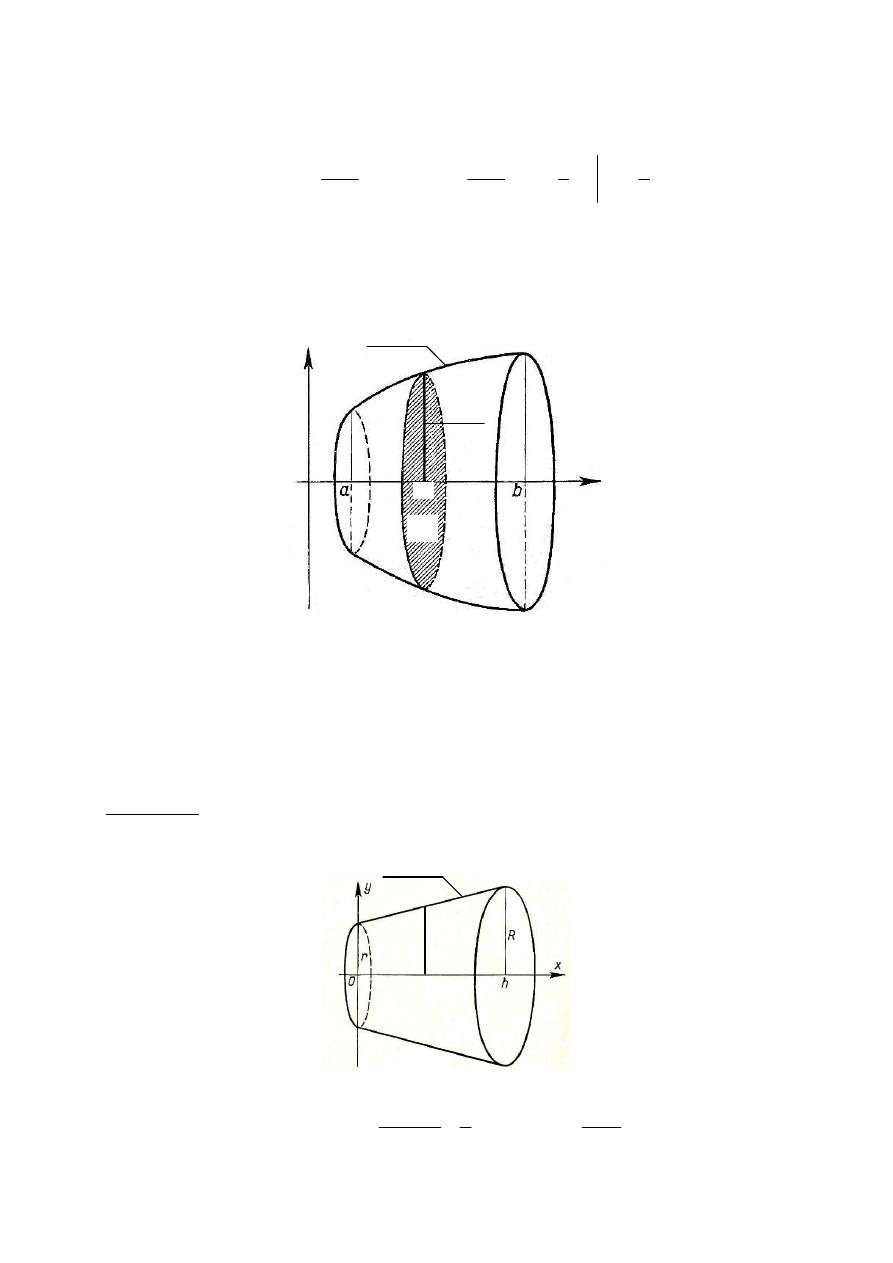
8
Objętość elipsoidy jest równa
abc
y
y
b
b
ac
dy
y
b
b
ac
dy
y
S
V
b
y
y
b
b
π
π
π
3
4
3
1
2
)
(
2
)
(
2
0
3
2
2
0
2
2
0
2
=
−
=
−
=
=
=
=
∫
∫
.
W przypadku bryły obrotowej, która powstaje przez obrót krzywej y = f(x) wokół osi x prze-
krój S(x) jest kołem, którego pole jest równe
2
)
(
)
(
x
f
x
S
π
=
.
Objętość bryły obrotowej jest równa
∫
=
b
a
dx
x
f
V
2
)
(
π
.
Przykład 6. Obliczyć objętość stożka obrotowego ściętego o wysokości h i promieniach pod-
staw r oraz R.
Rozwiązanie. Stożek traktuje się jako bryłę ograniczoną powierzchnią powstałą przez obrót
odcinka AB wokół osi x.
Funkcję f(x) wyznaczmy z proporcji
h
x
r
R
r
x
f
=
−
−
)
(
, skąd
r
x
h
r
R
x
f
+
−
=
)
(
.
x
S(x)
f(x)
y = f(x)
x
y
0
A
B
y = f(x)
x
f(x)
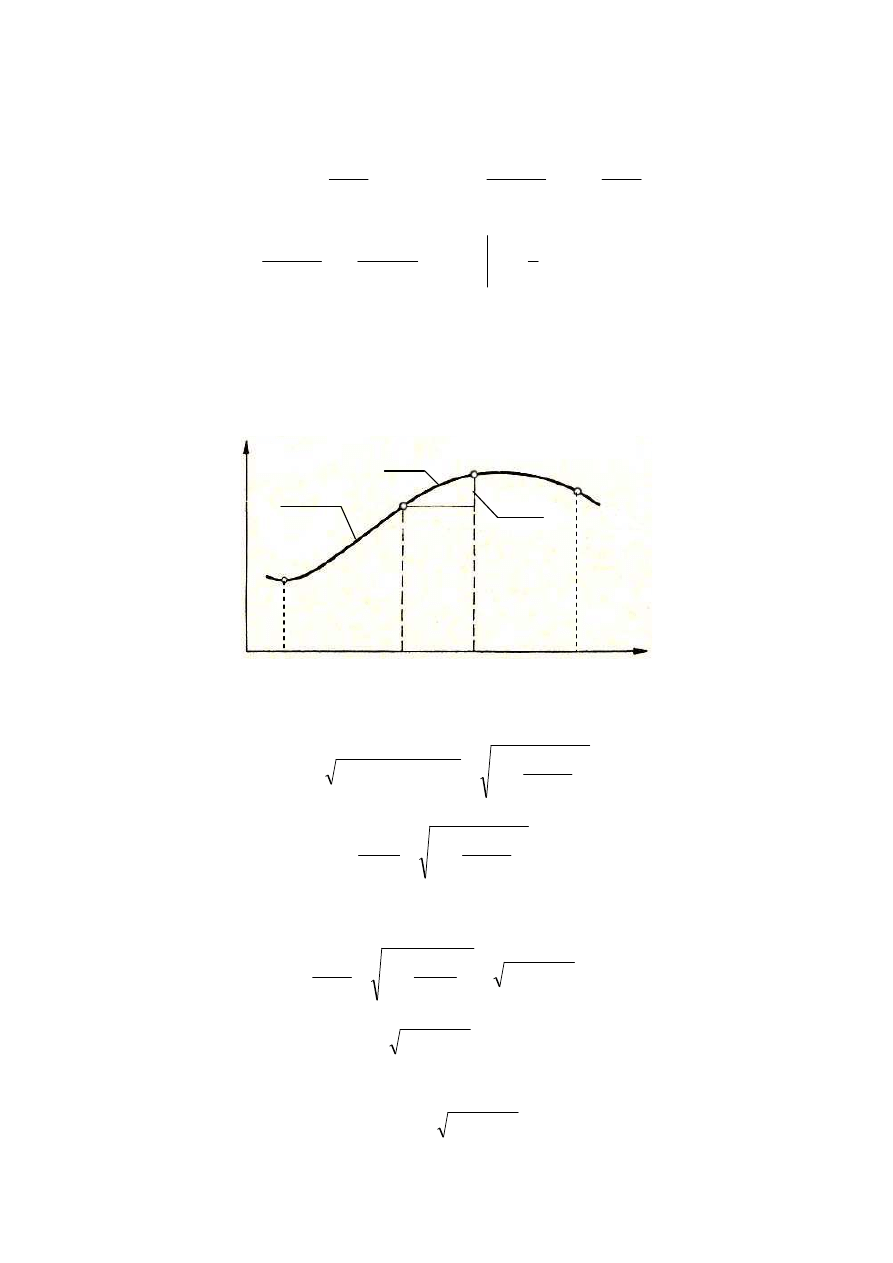
9
Stosując wzór na powierzchnię bryły obrotowej mamy
=
+
−
+
−
=
+
−
=
=
∫
∫
∫
h
h
h
dx
r
x
h
r
R
r
x
h
r
R
dx
r
x
h
r
R
dx
x
f
V
0
2
2
2
2
2
0
0
2
2
)
(
)
(
π
π
π
)
(
3
1
)
(
3
)
(
2
2
0
2
2
3
2
2
r
Rr
R
h
x
r
x
h
r
r
R
x
h
r
R
h
x
x
+
+
=
+
−
+
−
=
=
=
π
π
.
9.5. Długość łuku krzywej płaskiej
Niech dana będzie krzywa płaska
y = f(x), o której zakładamy że jest różniczkowalna.
Długość łuku ∆
l(x) na przyroście ∆x jest w przybliżeniu równa
x
x
x
f
x
f
x
x
l
∆
∆
)
(
∆
1
))
(
∆
(
)
∆
(
)
(
∆
2
2
2
⋅
+
=
+
≈
,
zatem
2
∆
)
(
∆
1
∆
)
(
∆
+
≈
x
x
f
x
x
l
.
Przechodząc obustronnie do granicy ∆
x → 0 mamy
2
2
)
(
1
)
(
1
)
(
x
f
dx
x
df
dx
x
dl
′
+
=
+
=
.
Stąd element łuku jest równy
dx
x
f
x
dl
2
)
(
1
)
(
′
+
=
, zatem długość krzywej od A do B jest
równa
dx
x
f
x
dl
l
b
a
b
a
⋅
′
+
=
=
∫
∫
2
)
(
1
)
(
.
y = f(x)
y
f(x)
∆
f(x)
∆
x
∆
l(x)
x
x
0
A
B
a
b

10
Przykład 7. Obliczyć długość łuku paraboli z przykładu 2.
Rozwiązanie. Obliczenia będą łatwiejsze, jeśli oś y układu współrzędnych będzie osią syme-
trii paraboli. Przy tym przesunięciu długość łuku paraboli oczywiście nie ulegnie zmianie.
W przyjętym układzie współrzędnych parabola dana jest wzorem
2
2
4
)
(
x
b
a
x
f
y
−
=
=
. Stąd
x
b
a
x
f
2
8
)
(
−
=
′
. Korzystając z symetrii, długość łuku paraboli wynosi
dx
x
k
k
dx
x
a
b
b
a
dx
x
b
a
dx
x
f
l
b
b
b
b
∫
∫
∫
∫
⋅
+
=
⋅
+
⋅
=
⋅
−
+
=
⋅
′
+
=
2
0
2
2
2
0
2
2
4
2
2
0
2
2
2
0
2
2
64
8
2
8
1
2
)
(
1
2
, (**)
gdzie
a
b
k
8
2
=
. Obliczamy teraz całkę
∫
+
=
dx
x
k
I
2
2
. Całkujemy przez części stosując wzór
∫
∫
⋅
−
⋅
=
⋅
g
df
g
f
dg
f
.
Przyjmujemy
2
2
)
(
x
k
x
f
+
=
oraz
dx
x
dg
=
)
(
. Stąd
dx
x
k
x
x
df
2
2
)
(
+
=
oraz
x
x
g
=
)
(
.
=
+
−
+
−
+
⋅
=
+
−
+
⋅
=
+
=
∫
∫
∫
dx
x
k
k
x
k
x
k
x
dx
x
k
x
x
k
x
dx
x
k
I
2
2
2
2
2
2
2
2
2
2
2
2
2
2
=
+
+
+
−
+
⋅
=
+
+
+
+
−
+
⋅
=
∫
∫
∫
∫
dx
x
k
k
dx
x
k
x
k
x
dx
x
k
k
dx
x
k
x
k
x
k
x
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
1
dx
x
k
k
I
x
k
x
∫
+
+
−
+
⋅
=
2
2
2
2
2
1
Otrzymaliśmy zatem równanie względem I
dx
x
k
k
I
x
k
x
I
∫
+
+
−
+
⋅
=
2
2
2
2
2
1
,
skąd obliczamy
dx
x
k
k
x
k
x
I
∫
+
+
+
⋅
=
2
2
2
2
2
1
2
2
. (#)
x
y
2
b
−
2
b
a
0
2
2
4
)
(
x
b
a
x
f
y
−
=
=
11
Całkę
dx
x
k
∫
+
2
2
1
obliczamy stosując podstawienie
2
t
t
e
e
k
x
−
−
=
. Stąd
dt
e
e
k
dx
t
t
2
−
+
=
.
Po podstawieniu
x oraz dx do całki i wykonaniu rachunków otrzymuje się
∫
∫
=
=
+
t
dt
dx
x
k
2
2
1
.
Rozwiązując równanie
2
t
t
e
e
k
x
−
−
=
względem
t otrzymamy
k
x
k
x
t
ln
)
ln(
2
2
−
+
+
=
, za-
tem
k
x
k
x
t
dt
dx
x
k
ln
)
ln(
1
2
2
2
2
−
+
+
=
=
=
+
∫
∫
.
Stąd i ze wzoru (#) mamy
k
k
x
k
x
k
x
k
x
dx
x
k
I
ln
2
)
ln(
2
2
2
2
2
2
2
2
2
2
−
+
+
+
+
⋅
=
+
=
∫
.
Powracając do wzoru (**) obliczamy długość łuku paraboli (w całce oznaczonej pomijamy
składnik
k
k
ln
2
2
, gdyż nie zależy on od zmiennej
x)
=
+
+
+
+
⋅
=
⋅
+
=
=
=
∫
2
0
2
2
2
2
2
2
0
2
2
)
ln(
2
2
2
2
b
x
x
b
x
k
x
k
x
k
x
k
dx
x
k
k
l
=
+
+
+
+
⋅
=
=
=
2
0
2
2
2
2
2
)
ln(
b
x
x
x
k
x
x
k
k
x
k
−
+
+
+
+
=
k
b
k
b
b
k
k
b
k
ln
4
2
ln
4
2
2
2
2
2
2
, gdzie
a
b
k
8
2
=
.
9.6. Pole powierzchni bocznej bryły obrotowej
Rozważamy bryłę obrotową, która powstaje przez obrót krzywej
y = f(x) wokół osi x
y = f(x)
x
y
0
f(x)
x
dS(x)
dl(x)
a
b

12
Pole elementarnego paska powierzchni bocznej bryły obrotowej jest równe
dx
x
f
x
f
x
dl
x
f
x
dS
⋅
′
+
⋅
=
⋅
=
2
)
(
1
)
(
2
)
(
)
(
2
)
(
π
π
.
Stąd pole powierzchni bocznej bryły obrotowej jest równe
∫
∫
⋅
′
+
⋅
=
=
b
a
b
a
dx
x
f
x
f
x
dS
S
2
)
(
1
)
(
2
)
(
π
.
Przykład 7. Obliczyć pole powierzchni bocznej stożka obrotowego z przykładu 6.
Rozwiązanie. Funkcja tworząca powierzchnię obrotową określona jest równaniem
r
x
h
r
R
x
f
+
−
=
)
(
. Pochodna jest równa
h
r
R
x
f
−
=
′
)
(
. Powierzchnia boczna stożka wynosi
=
−
+
⋅
+
−
=
⋅
′
+
⋅
=
∫
∫
dx
h
r
R
r
x
h
r
R
dx
x
f
x
f
S
b
a
b
a
2
2
1
2
)
(
1
)
(
2
π
π
=
+
−
−
+
=
+
−
−
+
=
∫
b
a
b
a
rx
x
h
r
R
h
r
R
dx
r
x
h
r
R
h
r
R
2
2
2
2
1
2
1
2
π
π
−
+
−
−
−
+
=
)
(
)
(
2
1
2
2
2
2
a
b
r
a
b
h
r
R
h
r
R
π
.
Całkowita powierzchnia stożka ściętego jest równa sumie powierzchni bocznej i powierzchni
podstaw.
9.7. Droga w ruchu zmiennym
Niech ciało porusza się po linii prostej ze zmienną prędkością
)
(t
υ
. Jeśli prędkość ciała w
chwili
t jest równa
)
(
t
υ
, to w dowolnie krótkim czasie
dt przyrost drogi wynosi
dt
t
x
ds
)
(
)
(
υ
=
. Stąd droga przebyta od chwili
t
1
do chwili
t
2
jest równa
∫
=
2
1
)
(
t
t
dt
t
s
υ
.
Przykład 8. Prędkość ruchu ciała poruszającego się wzdłuż linii prostej dana jest wzorem
1
2
3
)
(
2
−
+
=
t
t
t
υ
m/s. Obliczyć drogę jaką ciało przebywa w czasie od 2 do 10 s.
Rozwiązanie. Droga przebyta przez ciało jest równa
1088
)
1
4
8
(
)
1
100
1000
(
)
1
(
)
1
2
3
(
10
2
10
2
2
3
2
=
−
+
−
−
+
=
−
+
=
−
+
=
=
=
∫
t
t
t
t
dt
t
t
s
m/s.

13
9.8. Praca wykonana przez zmienną siłę
Niech na ciało wzdłuż linii prostej działa zmienna siła F(x). Jeśli w punkcie x siła jest równa
F(x), to praca wykonana przez tę siłę na przyroście przesunięcia dx jest równa dL(x) = F(x)dx.
Wtedy praca wykonana przez siłę F(x) na drodze od punktu x = a do punktu x = b jest równa
∫
=
b
a
dx
x
F
L
)
(
.
Przykład 9. Jaką pracę należy wykonać, aby ciało o masie m w polu grawitacyjnym podnieść
na wysokość h ?
Rozwiązanie. Na wysokości x nad powierzchnią Ziemi na ciało o masie m działa siła grawita-
cji równa
2
)
(
)
(
x
R
GmM
x
F
+
=
, gdzie M oznacza masę Ziemi, R jaj promień, a G jest stałą grawi-
tacji. Praca wykonana przy podnoszeniu ciała o masie m na wysokość h jest równa
+
−
=
+
−
=
+
=
=
=
=
∫
∫
h
R
R
GmM
x
R
GmM
x
R
dx
GmM
dx
x
F
L
h
x
x
h
h
1
1
1
)
(
)
(
0
0
2
0
.
Wyszukiwarka
Podobne podstrony:
ATMiA 29 1 3 id 71755 Nieznany (2)
BBN NR 29 id 81911 Nieznany
5 29 id 39528 Nieznany (2)
29 2 id 32097 Nieznany (2)
29 5 id 32110 Nieznany (2)
29 id 32084 Nieznany
29 8 id 32114 Nieznany (2)
I 29 id 208109 Nieznany
29 4 id 32107 Nieznany (2)
4 29 id 36996 Nieznany (2)
29 9 id 32115 Nieznany (2)
7 29 id 44753 Nieznany (2)
ATMiA 29 1 3 id 71755 Nieznany (2)
lekcja 29 str 2 id 265129 Nieznany
Cw 29 szablon id 97632 Nieznany
lekcja 29 str 5 id 265132 Nieznany
29 PE Events id 32202 Nieznany (2)
DYREKTYWA 2001 29 WE id 145671 Nieznany
Cw 29 zaliczone id 121743 Nieznany
więcej podobnych podstron