POWIERZCHNIE         STOPNIA         DRUGIEGO. 

 

 

/Powierzchnie stopnia pierwszego?/ 

                              

 

                 Z 

                 c 

 

 

 

 

 

 

                                                                                                                                                     Y 

                                                                                                                        b                                                       

 

 

 

 

                                              a 

                                              x 

 

 

 

 

 

 

 

 

 

 

 

Def. 

Powierzchnią stopnia drugiego nazywamy zbiór punktów przestrzeni trójwymiarowej 

 , 

który spełnia równanie:   

, 

gdzie dla stałych rzeczywistych  

 

Można także sformułować 

Twierdzenie: 

Każde równanie powierzchni stopnia drugiego można tak przekształcić 

(przez obrót lub przesunięcie) aby otrzymać równanie w postaci kanonicznej (stałe D…I są równe 0). 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

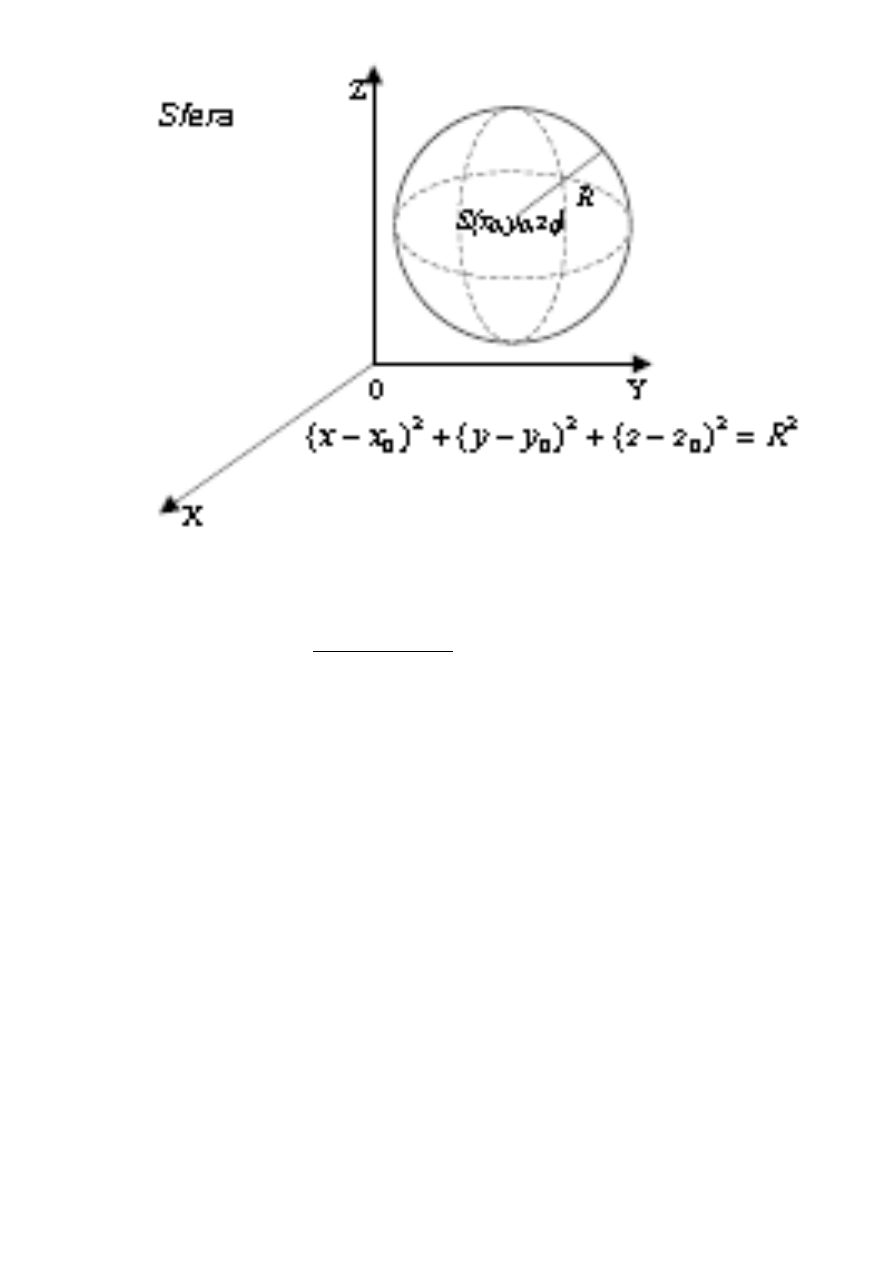
Równanie kanoniczne sfery: 

 

Zauważmy,   

a)…   z = 

 

   b)…   przekroje z powierzchnią stopnia pierwszego… 

c)…   przekroje z powierzchnią stopnia drugiego… 

 

Opiszmy    

obszar domknięty      

  ………………….. 

 

oraz             obszar domknięty      

…………………… 

 

 

 

 

 

 

 

 

 

 

 

 

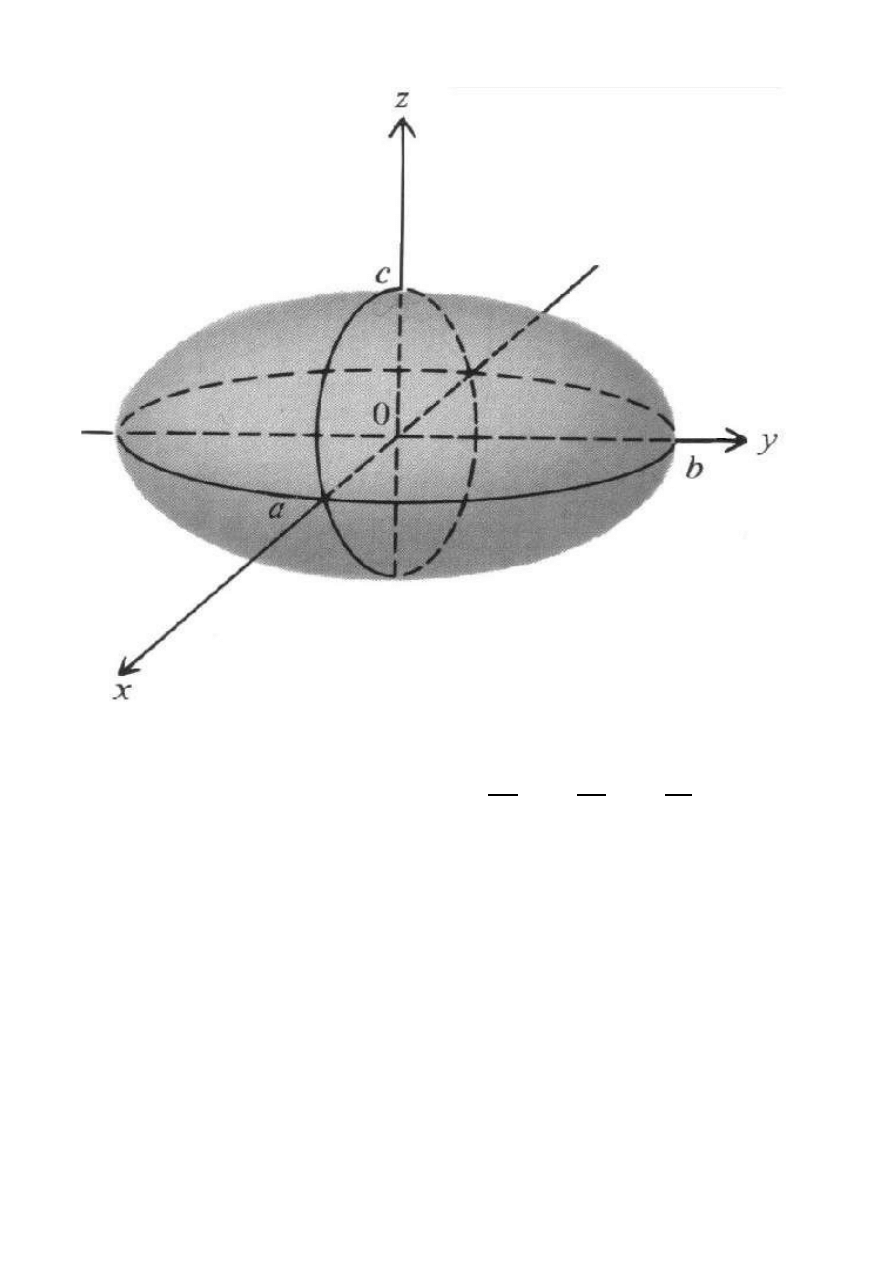
Elipsoida trójosiowa  

 

 

 

 

 

 

 

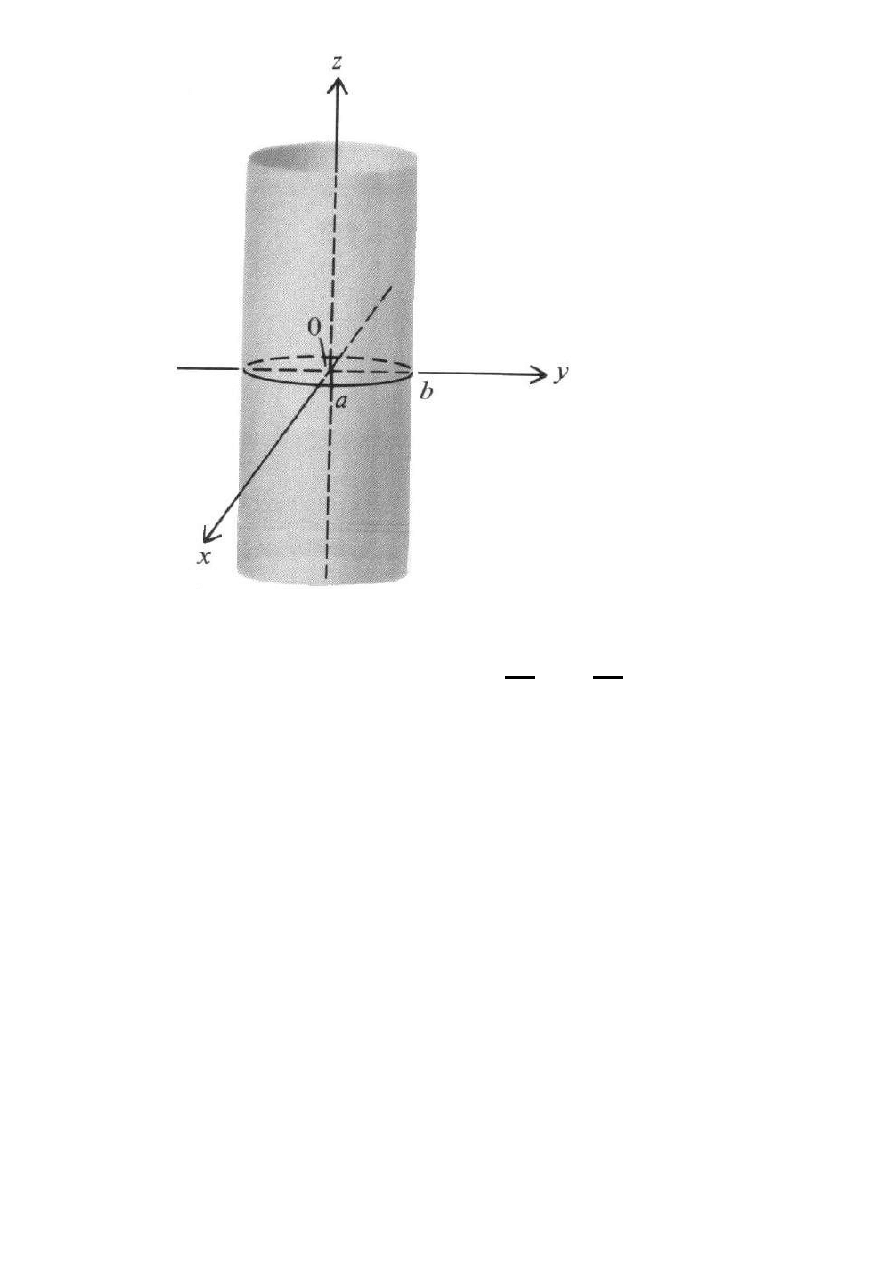
Walec eliptyczny  

 

 

 

 

 

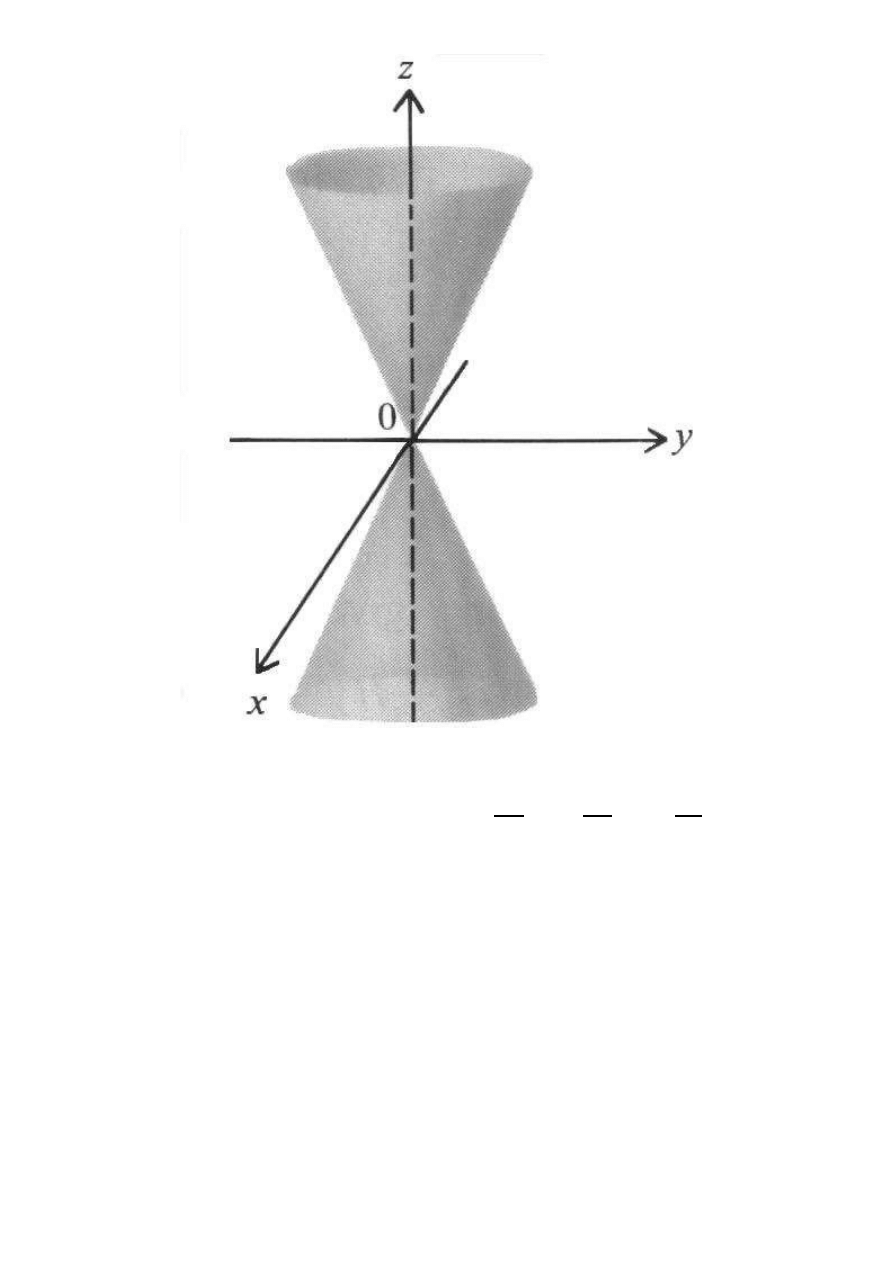
Stożek eliptyczny    

 

 

 

 

 

 

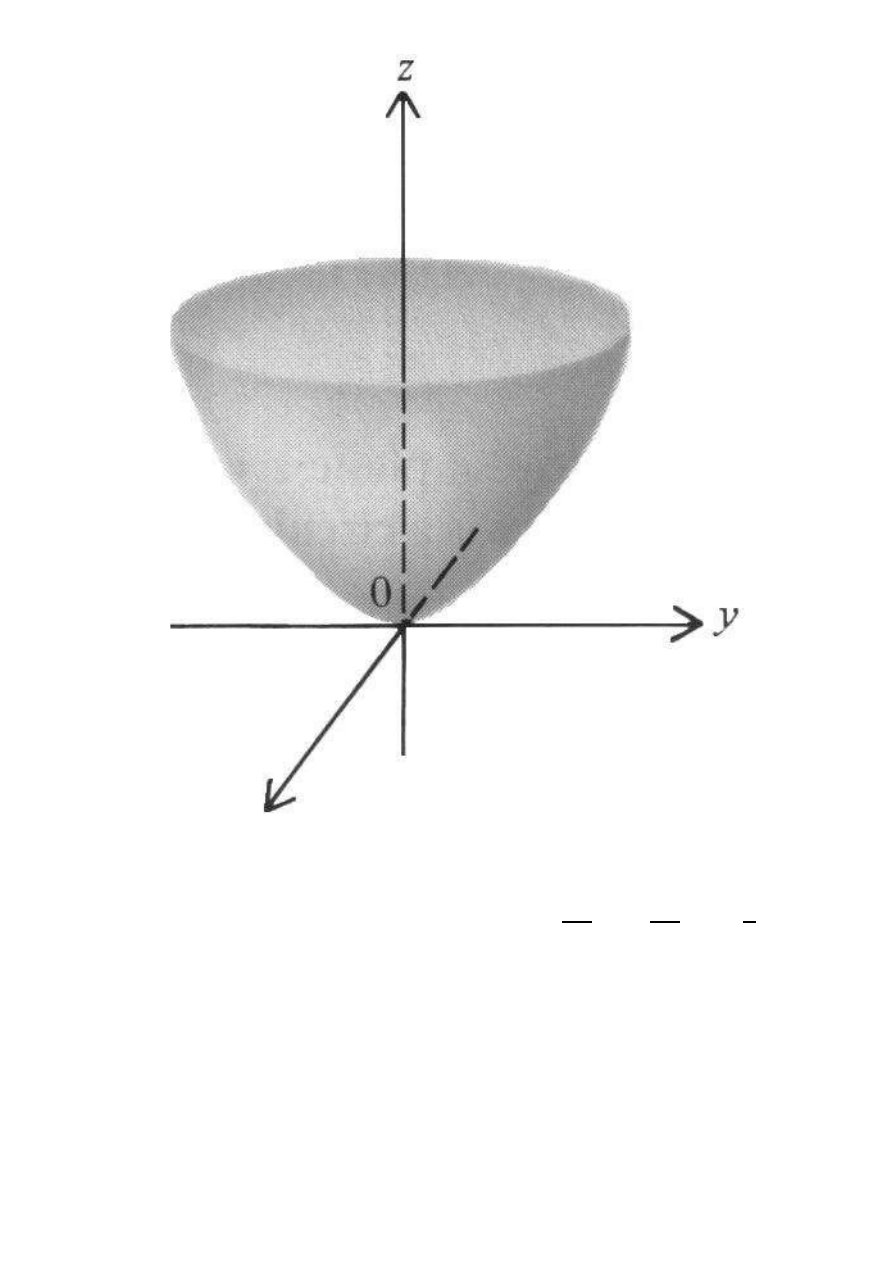
Paraboloida eliptyczna      

 

 

 

 

 

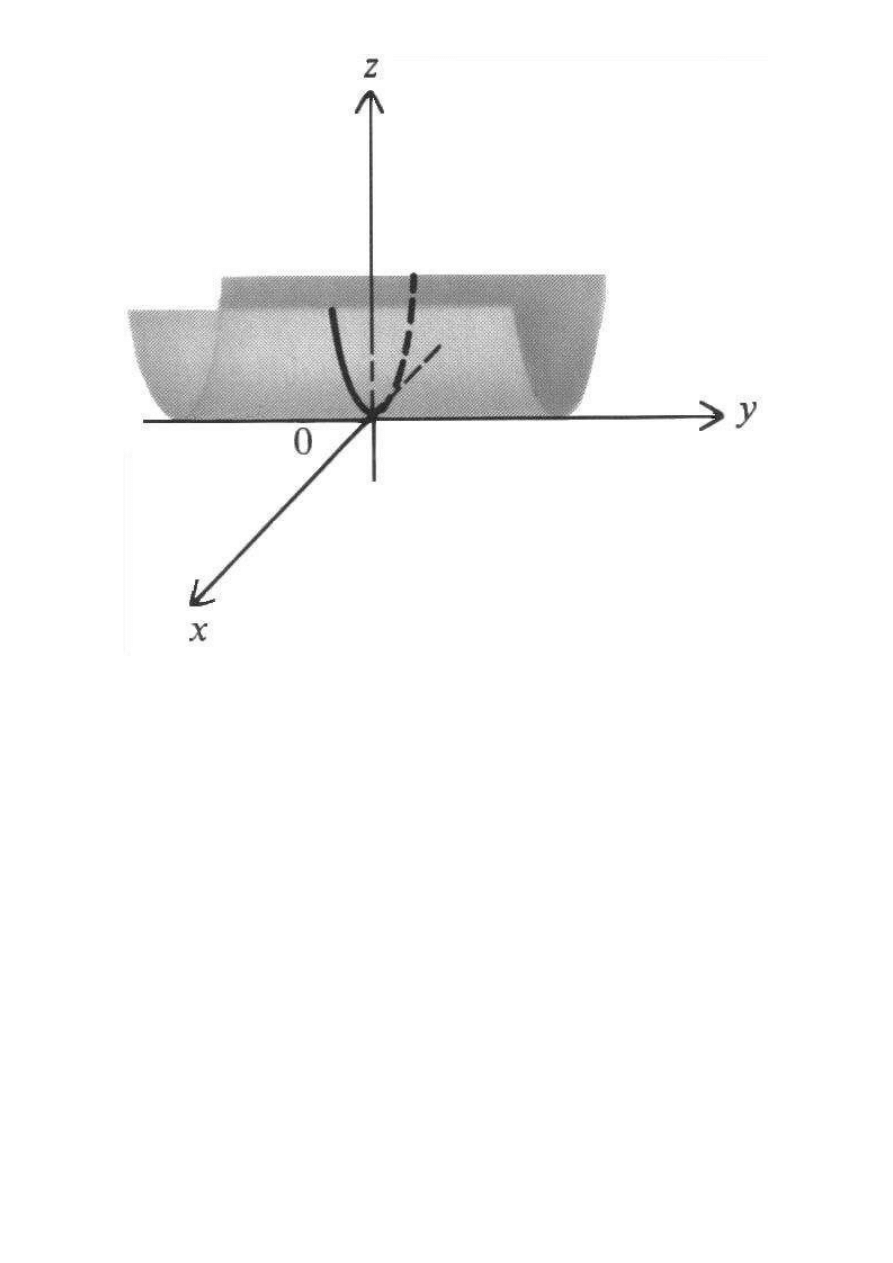
Walec paraboliczny:  

 

 

 

 

 

 

 

 

 

 

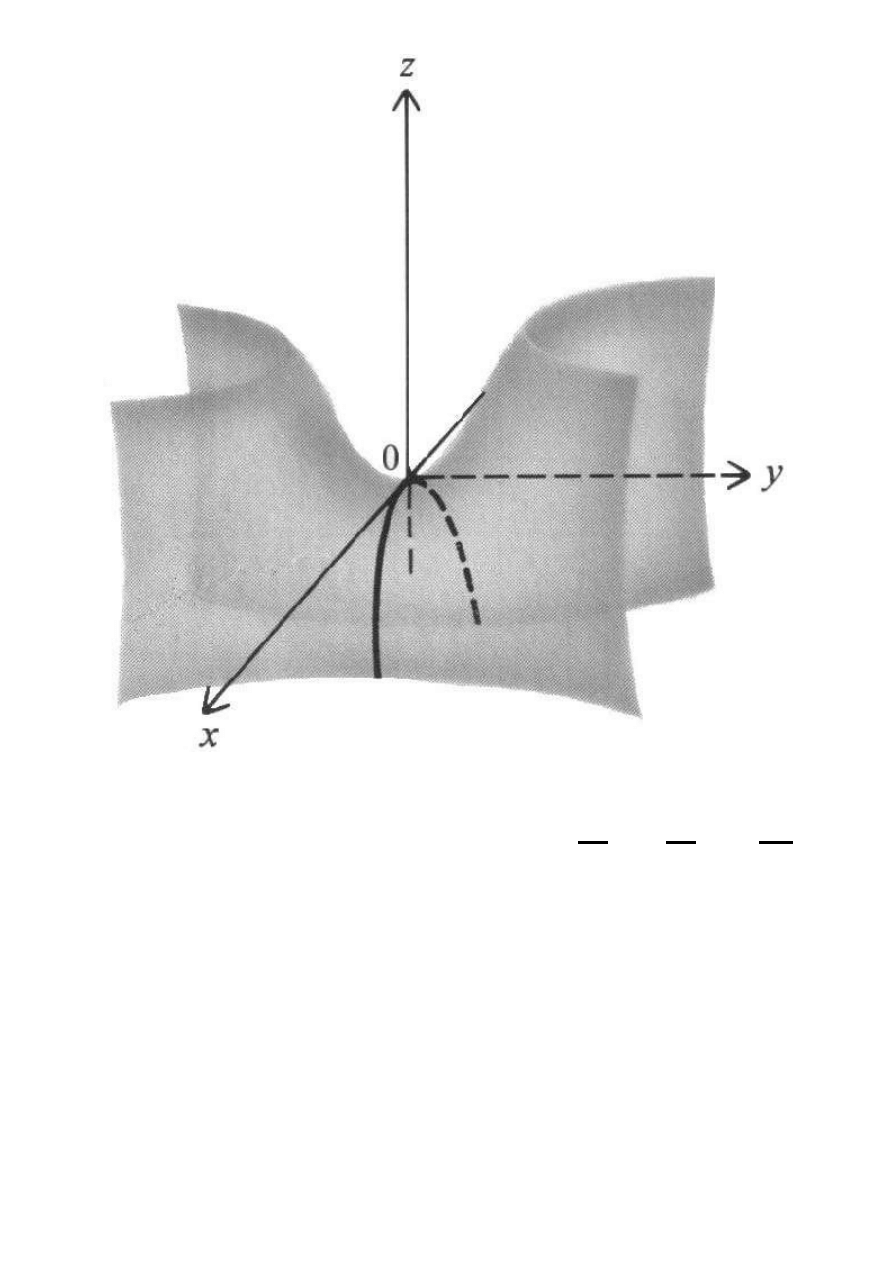
Paraboloida hiperboliczna:  

 

 

 

 

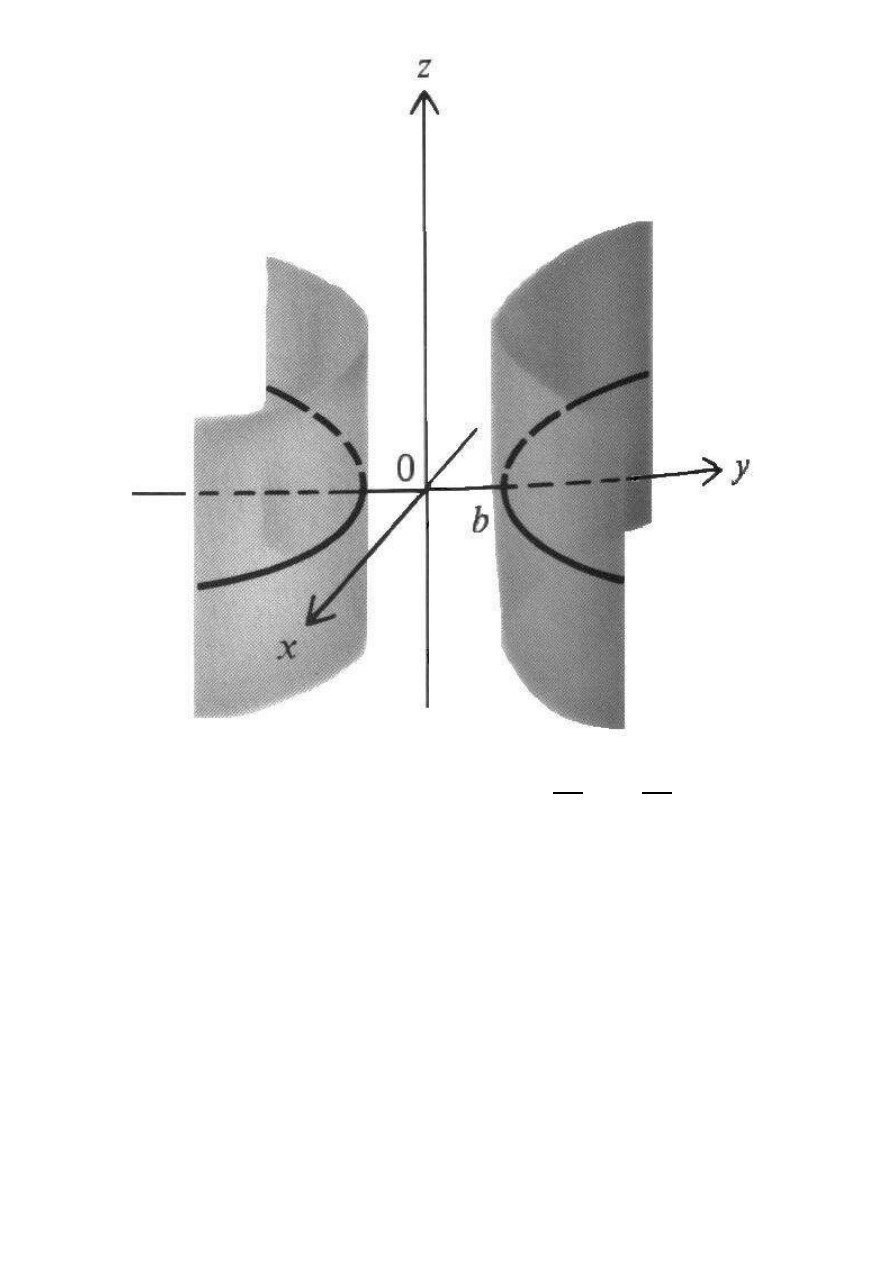
Walec hiperboliczny:   

,  

 

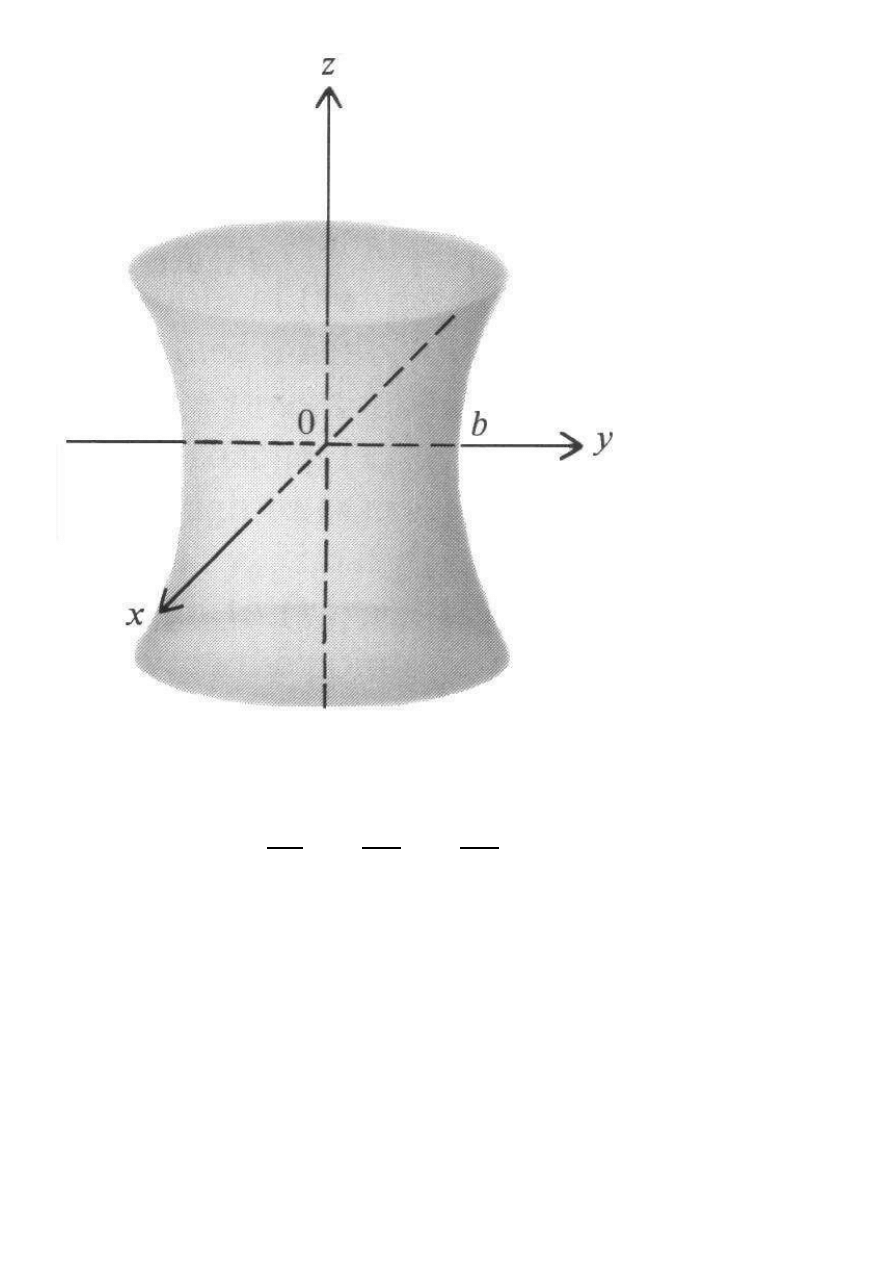
Hiperboloida jednopowłokowa: 

 

 

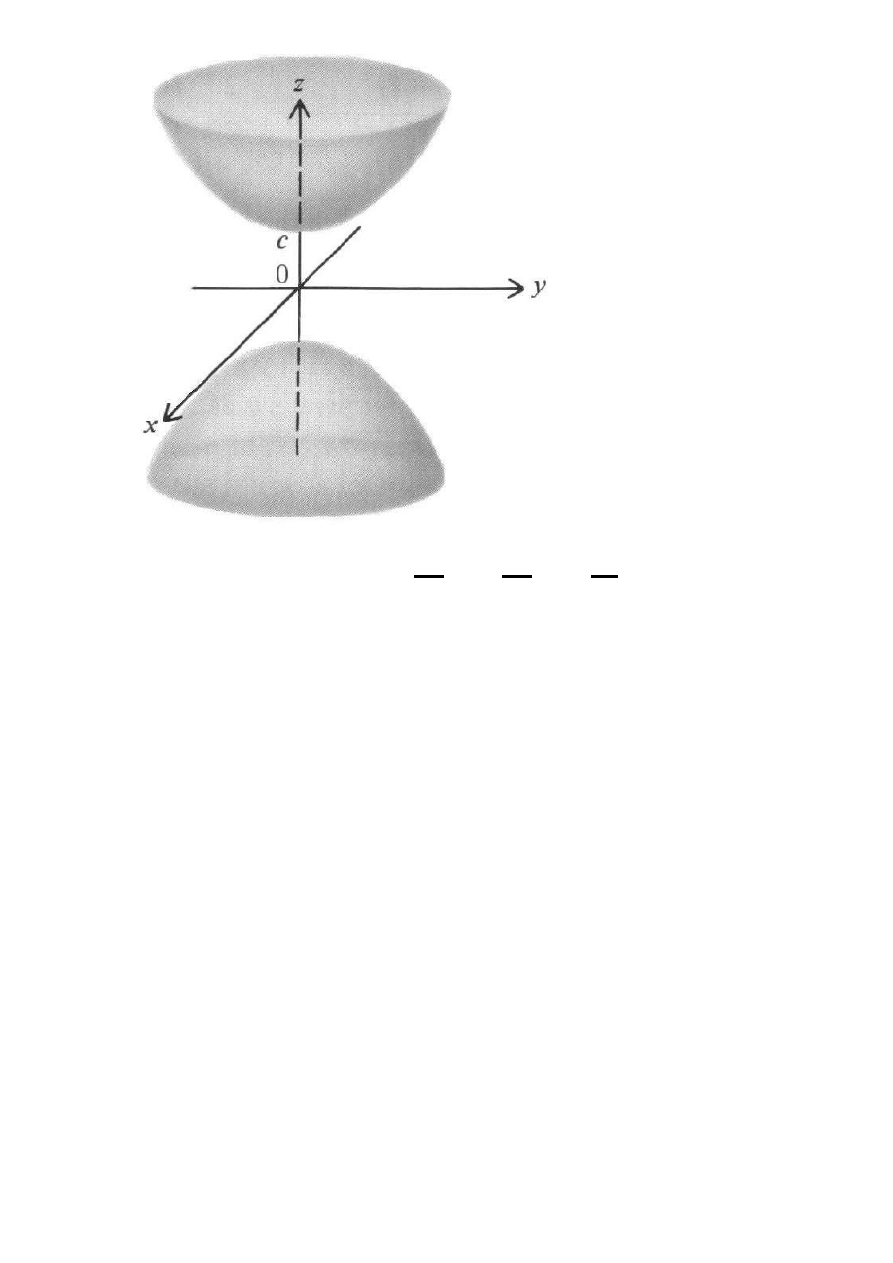
Hiperboloida 

dwupowłokowa: