1
Laboratorium z Hydrauliki i Hydrologii – Kierunek Budownictwo inż – sem. V
Politechnika Gdańska
Katedra Hydrotechniki
WILIŚ
Analiza przepływu wody przez przekrój mostowy (FM)
v.2013
1. Cel ćwiczenia
Celem ćwiczenia jest rozpoznanie hydraulicznych warunków przepływu wody w kanale
laboratoryjnym, w którym może istnieć lokalne utrudnienie przepływu wody, spowodowane
obecnością filarów mostu.
Mosty należą do drogowych obiektów inżynierskich, których projektowanie leży w gestii
inżynierów budownictwa. Niezbędne elementy projektu zawarte są m.in. w Rozporządzeniu
Ministra Transportu i Gospodarki Morskiej z 30 maja 2000 roku. w sprawie warunków
technicznych, jakim powinny odpowiadać drogowe obiekty inżynierskie i ich usytuowanie –
Dz.U. Nr 63 poz. 735. We wspomnianym rozporządzeniu, podane są sposoby uwzględniania
zagadnień hydraulicznych w projektowaniu obiektów inżynierskich, jednakże nie zawsze
odzwierciedlają one w pełni rzeczywisty przebieg zjawisk towarzyszących przepływom przez
tego typu obiekty.
2. Informacje ogólne
Wymienione wcześniej Rozporządzenie Ministra Transportu i Gospodarki Morskiej z dnia 30
maja 2000 r. zwraca uwagę na konieczność zapewnienia bezpieczeństwa obiektów
inżynierskich, z uwagi na możliwość wystąpienia zjawisk ekstremalnych, w tym m.in.
powodzi.
Rozporządzenie przewiduje, że usytuowanie mostu i trasy dojazdowej nie powinno
spowodować istotnych zmian koryta cieku oraz warunków przepływu wód, jeśli nie wynika to
z konieczności regulacji koryta cieku. Tymczasem w rzeczywistości każda inwestycja
drogowa lokalizowana w korycie głównym lub terenach zalewowych cieku istotnie zmienia
warunki hydrauliczne wody płynącej. Omówienie i rozszerzenie rozporządzenia znaleźć
można na przykład w pracy Madaja i Wołowickiego pt. „Podstawy projektowania budowli
mostowych” (2007).
2
W ćwiczeniu laboratoryjnym szczególną uwagę należy zwrócić na porównanie
hydraulicznych warunków przepływu wody w korycie bez filarów oraz opływającej filary
mostu w kanale laboratoryjnym.
Przepływ wody w kanale otwartym opisywany jest układem równań złożonym z równania
ciągłości oraz równania dynamicznego.
Równanie ciągłości w ruchu ustalonym dla strumienia bez dopływu bocznego zapisać można
następująco:
const
A
v
Q
=
⋅
=
(1)
Q oznacza natężenie przepływu wody w kanale (wydatek), który podawany najczęściej jest w
jednostce m
3
/s, A oznacza pole powierzchni przekroju czynnego kanału w m
2
lub cm
2
zaś v
oznacza prędkość średnią w przekroju poprzecznym kanału (wyrażoną w m/s lub cm/s).
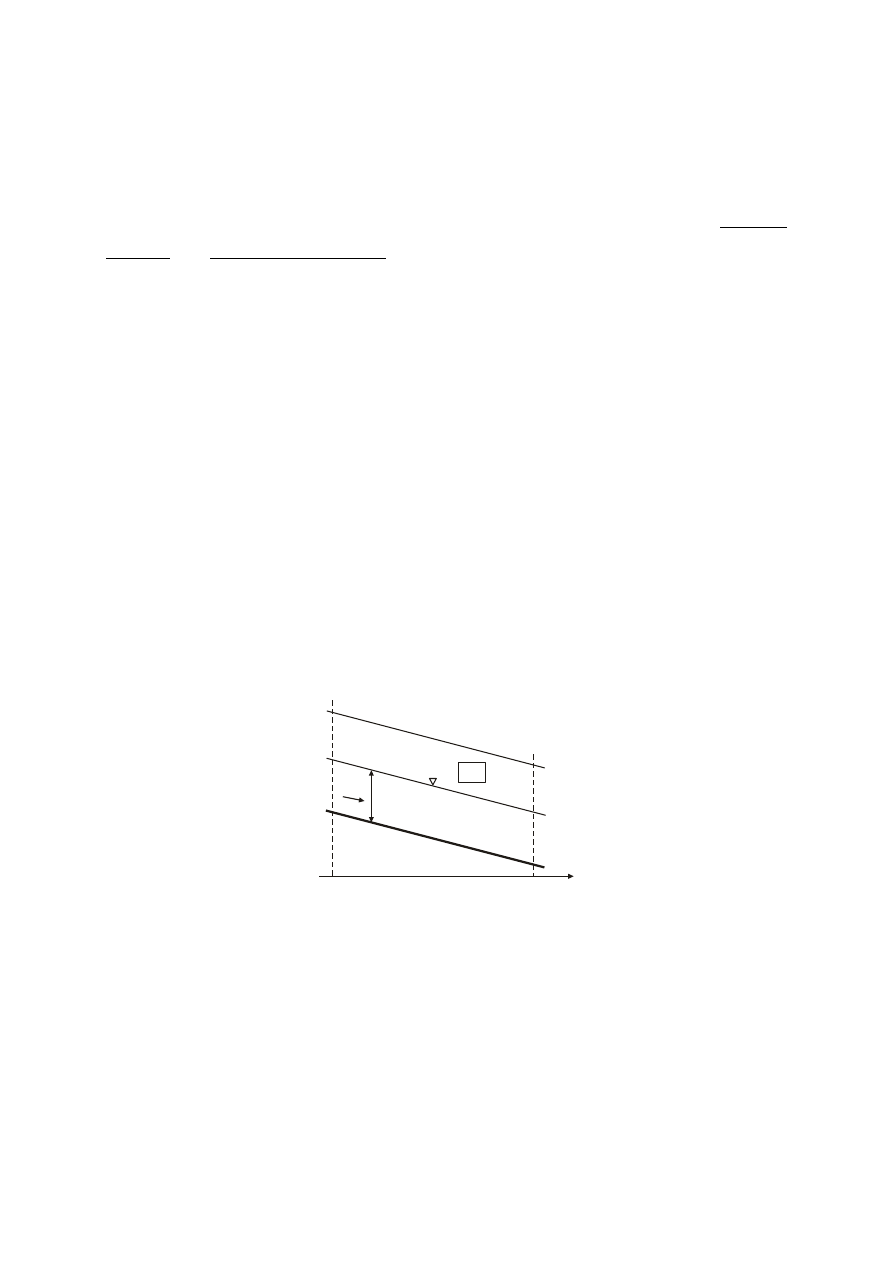
W obliczeniach prędkości średniej w kanałach otwartych przyjmuje się często założenie, że
przepływ jest ustalony i jednostajny. Przepływ ustalony oznacza niezmienność parametrów
opisujących ruch wody w czasie. Przepływ jednostajny oznacza, że w każdym przekroju
poprzecznym kanału otwartego stałe są wartości napełnienia kanału h, natężenia przepływu Q
oraz prędkości średniej v (rys.1).
i - spad
ek dna
LE
LC
I - spad
ek hydra
uliczny
v
h
i=I
x
1
2
rys. 1. Linia energii i linia ciśnienia w warunkach ruchu ustalonego jednostajnego, LE-linia energii, LC-linia
ciśnienia
W rzeczywistości ruch ustalony jednostajny występuje niezmiernie rzadko. Prawie zawsze w
przypadku ruchu ustalonego w kanałach naturalnych występuje ruch niejednostajny, tzn.
parametry przepływu są zmienne w kolejnych przekrojach poprzecznych wzdłuż kanału.
Równanie dynamiczne wynika z podstawowego równania zachowania pędu i jego
ostateczna postać zależy od przyjętych uproszczeń. W ruchu ustalonym i jednostajnym można
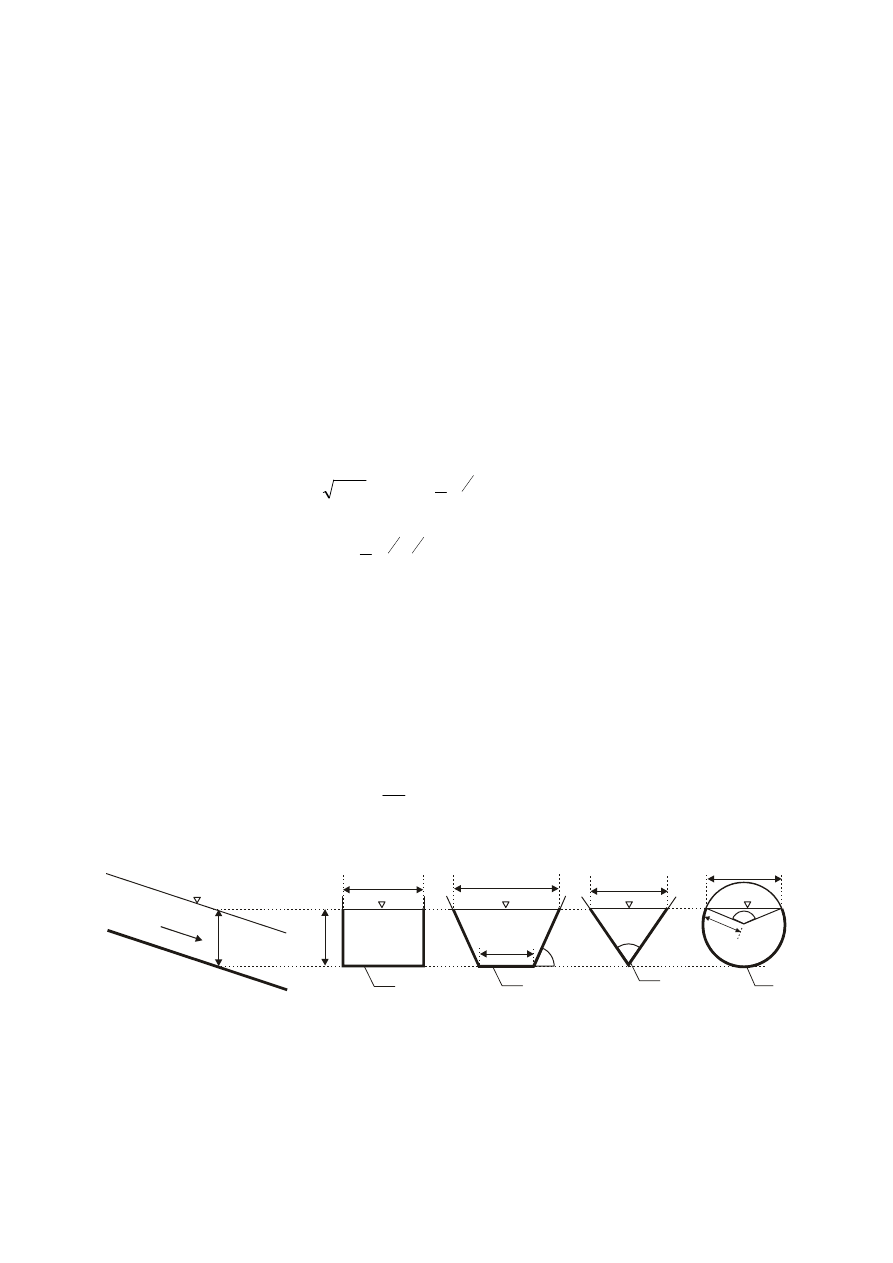
3
je zapisać w postaci zależności Chezy (2) - jednej z podstawowych formuł występujących w
hydraulice koryt otwartych.
2.1 Wyznaczenie prędkości średniej
Do najczęstszych metod oszacowania prędkości średniej w kanałach otwartych służy formuła
Manninga. Dokładniejsze wartości prędkości średniej można oszacować na podstawie
pomiarów prędkości lokalnych (miejscowych) w różnych punktach przekroju poprzecznego.
2.1.1 Wyznaczenie prędkości średniej z formuły Manninga
Przy założeniu ruchu ustalonego jednostajnego w kanale otwartym, prędkość średnią wody
wyznaczyć można z formuły Manninga: (zależności Chezy w której współczynnik
empiryczny C został wyznaczony według Manninga).
I
R
C
v
⋅
=
6
1
1
R
n
C
=
2
1
3
2
1
I
R
n
v
=
(2)
W równaniu powyższym n oznacza współczynnik szorstkości, którego wartości zestawione są
w tabeli (patrz: przydatne informacje). I jest spadkiem hydraulicznym, który w warunkach
ruchu ustalonego jednostajnego jest równy spadkowi zwierciadła wody oraz spadkowi dna i.
Występujący w równaniu Manninga promień hydrauliczny R wyznaczamy na podstawie
znajomości powierzchni pola przekroju czynnego A oraz obwodu zwilżonego Oz (rys.2),
zgodnie z relacją:
Oz
A
R
=
(3)
h
v
A
A
A
O
z
O
z
O
z
B
B
A
O
z
B
h
b
α
α
1
:m
B
ϕ
r
Rys. 2. Parametry kanału otwartego A – pole powierzchni przekroju czynnego, B – szerokość kanału na
wysokości zwierciadła wody, b – szerokość dna, Oz – obwód zwilżony, h – głębokość wody
4
2.1.2 Wyznaczenie prędkości średniej i natężenia przepływu metodami
pośrednimi
Natężenie przepływu Q wody można określić wykorzystując metody pośrednie (np.
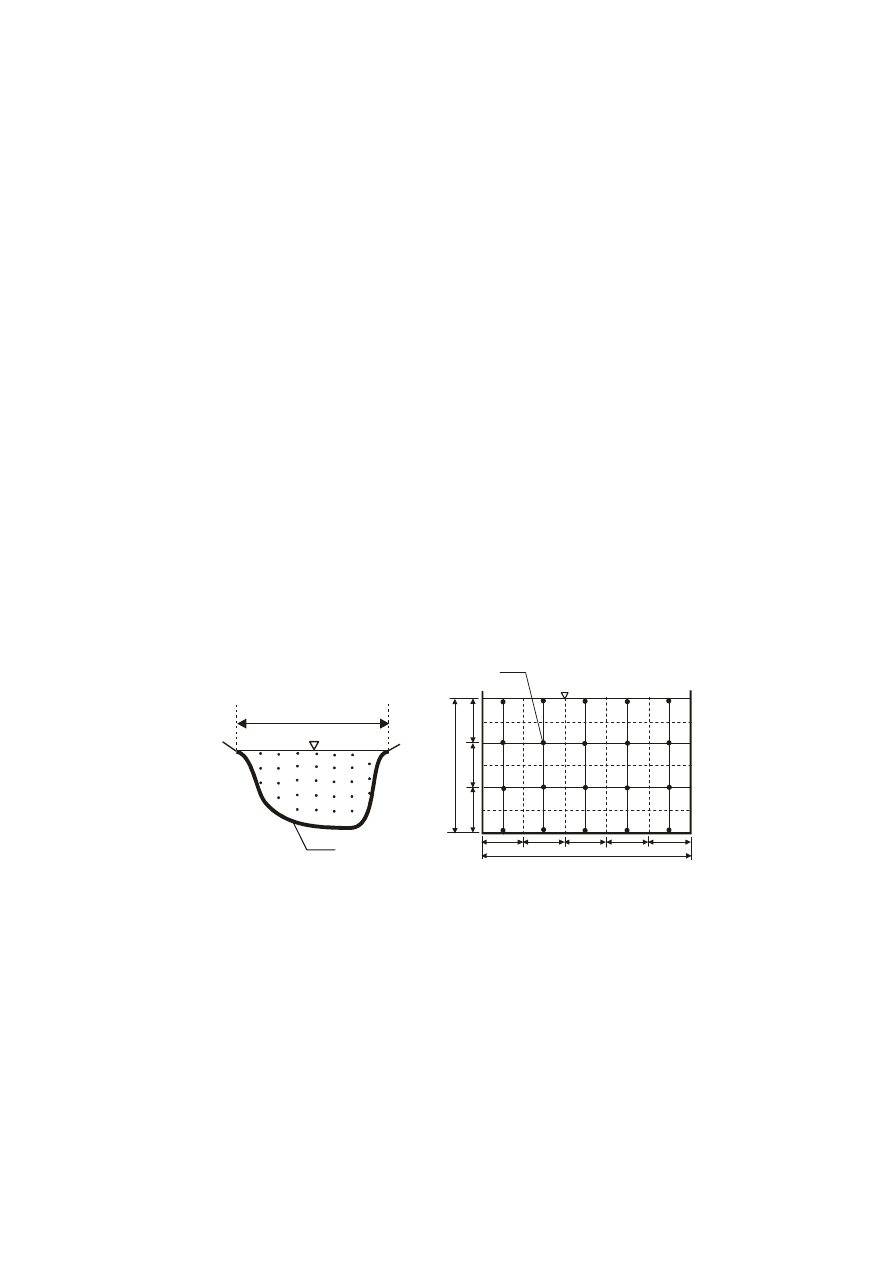
arytmetyczna, Harlachera, Culmanna). Podstawą obliczeń jest pomiar prędkości lokalnych w
wybranych punktach przekroju poprzecznego rozmieszczonych w tzw. pionach pomiarowych
(rys. 3). Prędkość lokalną pomierzyć można wykorzystując młynek hydrometryczny lub rurkę
pomiarową (rurkę Pitota, rurkę Prandla).
Piony pomiarowe w naturalnym cieku oddalone są od siebie o stałą wartość uzależnioną od
szerokości przekroju poprzecznego cieku. W prostokątnym kanale laboratoryjnym, w
zależności od przyjętej liczby pionów pomiarowych X, dwa sąsiednie piony oddalone są od
siebie o odległość równą x = B/X, zaś piony skrajne oddalone są o odległość równą x/2 od
ścianek kanału (rys. 3b).
W każdym pionie pomiarowym liczba punktów pomiarowych zależy od głębokości wody w
tym pionie (rys. 3a), bowiem odległość pomiędzy kolejnymi punktami powinna być stała
(określana na podstawie wyników sondowania). W prostokątnym kanale laboratoryjnym
skrajne punkty pomiarowe w danym pionie umieszczone są przy dnie i przy zwierciadle
swobodnym wody (rys. 3b).
A
O
z
B
I
y
v
i
III
II
V
IV
y
y
h
x
x
x
x
B
x
a)
b)
Rys. 3. Rozkład punktów pomiaru prędkości lokalnych w przekroju poprzecznym : a) naturalnego cieku
b) kanału prostokątnego.
2.1.2.1 Pomiar prędkości lokalnej za pomocą młynka hydrometrycznego
W pomiarach za pomocą młynków hydrometrycznych wykorzystuje się wpływ energii
kinetycznej wody na prędkość obrotową śmigła młynka (rys.4). Obroty młynka są zliczane w
określonym czasie (najczęściej 50 lub 100 sekund). Prędkość wody w punkcie przyłożenia osi
5
młynka v
L
określa się wykorzystując równanie młynka zwane również charakterystyką
młynka:
m
L
n
v
⋅
+
=
β
α
(4)
W powyższym wzorze n
m
oznacza najczęściej prędkość obrotową wirnika, czyli stosunek
ilości obrotów wirnika młynka do czasu rejestracji.
α, β
są stałymi charakterystycznymi dla
każdego młynka hydrometrycznego. Stałe młynka są każdorazowo określane na podstawie
cechowania (tarowania) przyrządu pomiarowego w atestowanym laboratorium Głównego
Urzędu Miar i można je znaleźć w świadectwie tarowania młynka.
Rys. 4. Młynek hydrometryczny na zdjęciach IMGW a) młynek opuszczany na lince, b) młynek pracujący w
wodzie, c) wygląd młynka zamontowanego na żerdzi pomiarowej. (źródło:
www.imgw.pl/internet/zz/wiedza/ogolna/_pom_prog/mlynek.html
09/2009)
2.1.2.2 Pomiar prędkości lokalnej za pomocą rurki Prandla
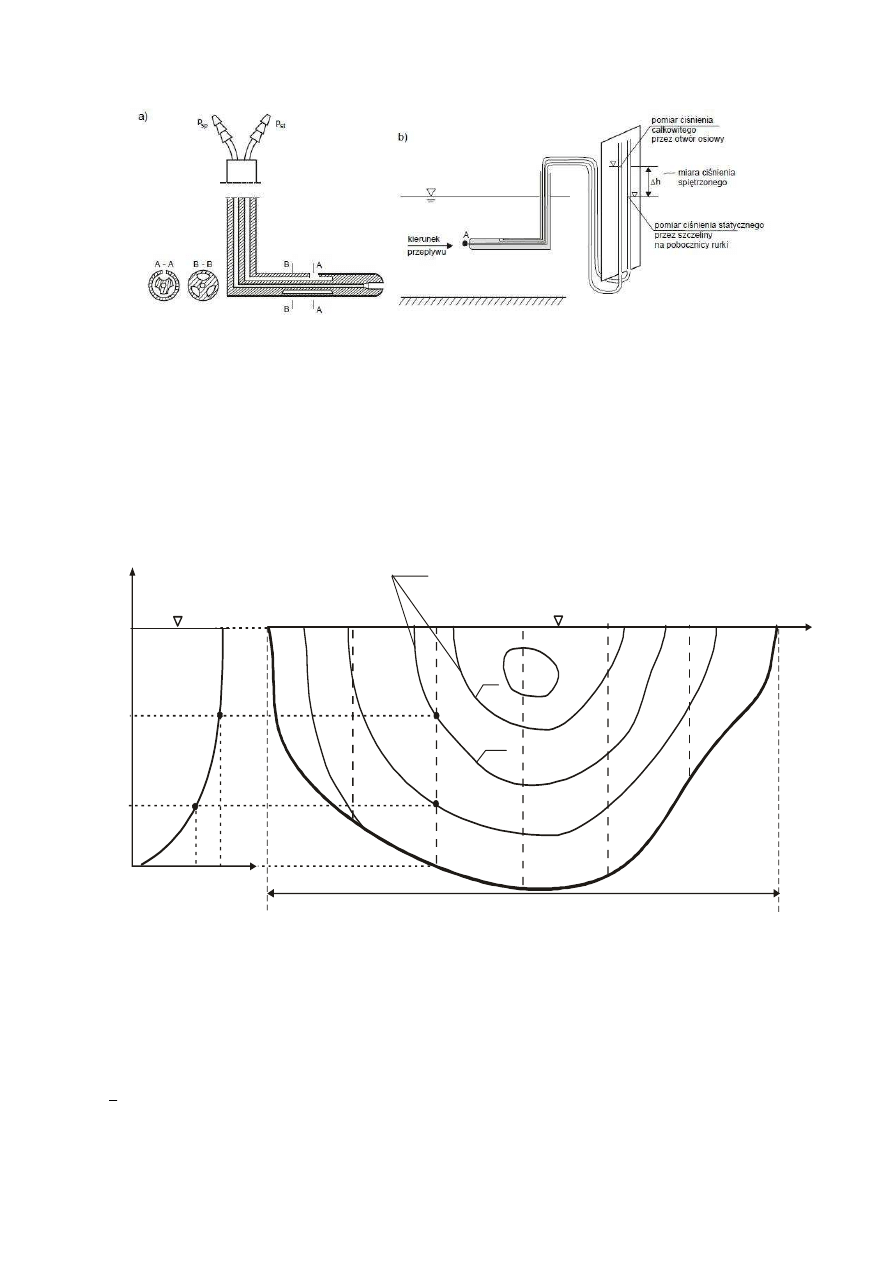
Rurka Prandla (rys. 5) jest wykorzystywana do pomiaru prędkości lokalnej w kanałach
laboratoryjnych, w których woda jest pozbawiona zawiesin. Wewnątrz rurki umieszczone są
dwa kanaliki. Pierwszy z nich połączony jest z boczną ścianką (pobocznicą) rurki i mierzy
ciśnienie statyczne wody w rurce, którego wysokość jest równa wysokości warstwy wody
płynącej ponad korpusem rurki. Drugi kanalik umieszczony jest wzdłuż osi rurki i mierzy
całkowite ciśnienie (sumę ciśnienia statycznego i dynamicznego wody płynącej). Podczas
pomiaru wykorzystywane jest więc zjawisko zamiany energii kinetycznej płynącej cieczy na
energię potencjalną w postaci dodatkowego spiętrzenia wody w rurce.
Pomiar należy wykonywać w ten sposób, aby oś przyrządu była skierowana równolegle do
kierunku napływającej wody (rys. 5). Prędkość lokalną wody w punkcie umieszczenia rurki
Prandla wyznacza się ze wzoru:
h
g
v
L
∆
=
2
(5)
gdzie
∆
h jest różnicą wysokości ciśnień w kanalikach rurki Prandla.
6
Rys. 5. Schemat rurki Prandla a) schemat budowy, b) ustawienie w trakcie pomiaru (źródło: Laboratorium z
mechaniki płynów i hydrauliki pod red. K. Weinerowskiej)
2.1.2.3 Wyznaczenie natężenia przepływu metodą Culmanna
Natężenie przepływu wody Q w przekroju poprzecznym kanału można wyznaczyć
wykorzystując metodę Culmanna. Na podstawie lokalnych wartości prędkości należy
wyznaczyć linie jednakowych prędkości zwane izotachami (rys. 6).
izotachy
H
[m]
∆Α
i
v
i
v
i+1
I
0.8
B
x
III
II
IV
V
0.9
1.0
0.7
1.1
0.8
0.9
0.9
0.8
0.8
0.8
1.0
V
V
[m/s]
0.8 0.9
1.0
0
1.3
0.5
Rys. 6. Tachoida prędkości dla pionu II oraz izotachy prędkości w przekroju poprzecznym
Pomiędzy sąsiednimi izotachami prędkość przepływu wody zawiera się w przedziale
pomiędzy prędkościami odpowiadającymi wartościom izotach. W celu wyznaczenia natężenia
przepływu dla obszaru pomiędzy izotachami wprowadza się średnią prędkość obliczeniową
o
v
równą średniej arytmetycznej z wartości izotach ograniczających rozpatrywany obszar.
7
)
(
5
,
0
1
1
,
+
+
+
=
=
i
i
i
i
oi
v
v
v
v
(6)
W elemencie, w którym występują największe lokalne prędkości przepływu v
max
prędkość
obliczeniowa wyznaczana jest następująco:
)
(
5
,
0
max
,
mav
i
i
oi
v
v
v
v
+
=
=
(7)
natomiast w elemencie, w którym występują najmniejsze lokalne prędkości przepływu v
min
według wzoru:
i
i
oi
v
v
v
⋅
=
=
5
,
0
min
,
(8)
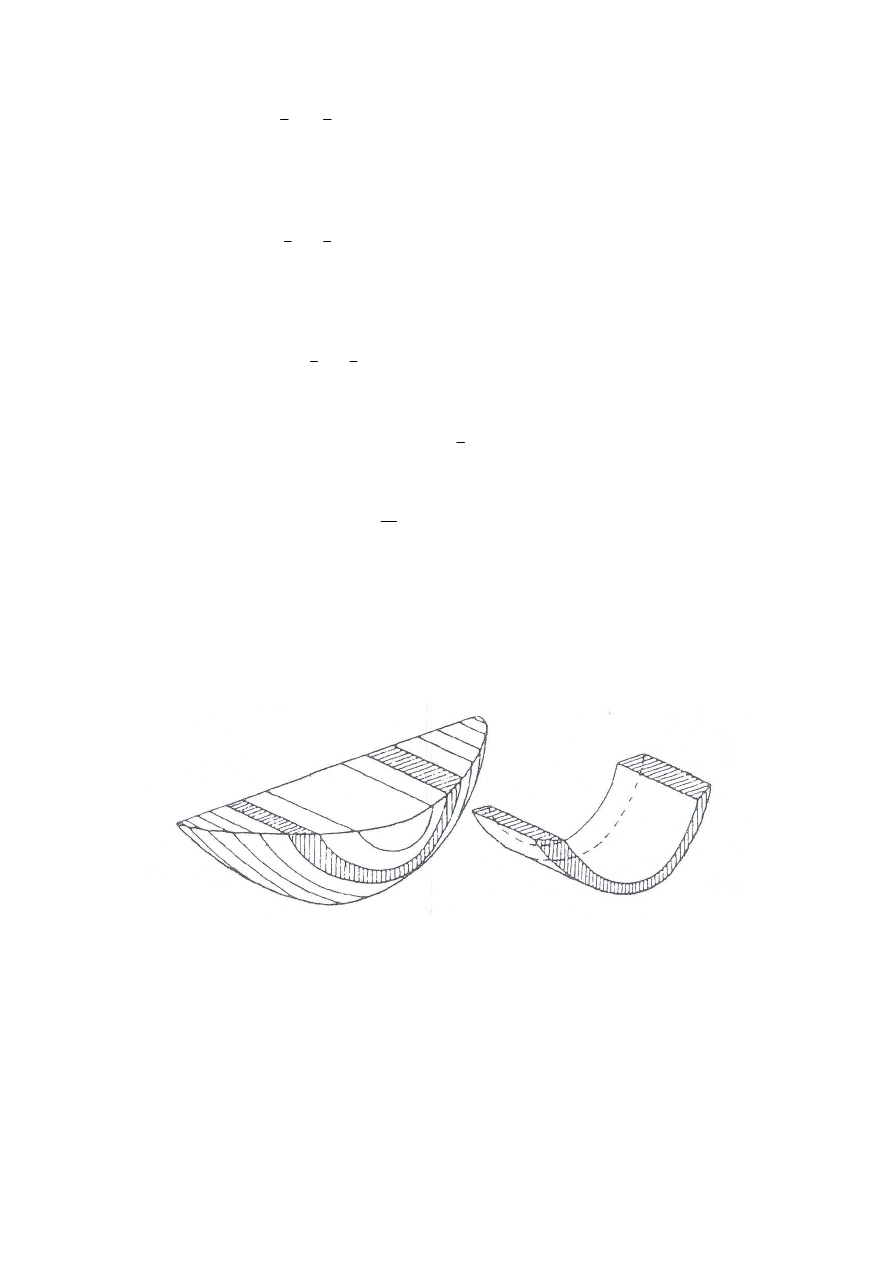
Natężenie przepływu z elementarnego obszaru przekroju poprzecznego A
i
, któremu
przypisuje się średnią prędkość obliczeniową
oi
v
graficznie stanowi elementarną objętość
natężenia przepływu (rys.7), którą można oznaczyć jako
∆
Q
i
.
i
oi
i
A
v
Q
⋅
=
∆
(9)
Całkowite natężenie przepływu stanowi suma natężeń przepływu z elementarnych obszarów
przekroju poprzecznego:
∑
=
∆
=
N
i
i
Q
Q
1
(10)
Rys. 7. Podział bryły przepływu w schemacie Culmanna na elementarne objętości natężenia przepływu
(Byczkowski A. Hydrologia)
Prędkość średnią w przekroju poprzecznym kanału otwartego wyznaczyć można z równania
ciągłości (1). Sposób wyznaczenia przedstawiono poniżej.
8
2.1.3 Wyznaczenie prędkości średniej z równania ciągłości
Znając natężenie przepływu Q oraz pole przekroju poprzecznego kanału otwartego A
prędkość średnią v w przekroju poprzecznym obliczyć można bezpośrednio z równania
ciągłości:
A
Q
v
=
(11)
W kanale laboratoryjnym o przekroju prostokątnym, pole przekroju poprzecznego wyznacza
się na podstawie znajomości jego szerokości B (zmierzonej w trakcie wykonywania
ćwiczenia) oraz głębokości wody w przekroju poprzecznym h (A = B h). Średnia głębokość
wody mierzona jest w osi kanału na podstawie pomiaru rzędnych zwierciadła wody i dna.
W pomiarach hydrometrycznych przekrojów naturalnych prędkość średnią v wyznaczyć
można na podstawie natężenia przepływu obliczonego metodami pośrednimi Q oraz
znajomości pola przekroju poprzecznego A (równanie 11). Pole przekroju poprzecznego A
otrzymuje się na podstawie sondowania dna przekroju poprzecznego. Sondowanie wykonuje
się cechowanymi żerdziami w określonych odstępach (najczęściej co 0,5 metra, 1 metr lub 2
metry w zależności od szerokości cieku) mierzy się względną różnicę rzędnych dna i
zwierciadła wody.
Do wyznaczania parametrów przekroju poprzecznego używane są również echosondy
pomiarowe wykorzystujące sygnał ultradźwiękowy.
2.1.4 Określenie rzeczywistego natężenia przepływu za pomocą urządzeń
kontrolnych
W laboratorium możliwe jest dokonanie dodatkowego pomiaru rzeczywistego natężenia
przepływu za pomocą urządzeń kontrolnych zamontowanych na stanowiskach pomiarowych.
Woda doprowadzona do kanału przepływa uprzednio przez specjalnie wytarowane przelewy
o ostrej krawędzi. Każdy przelew ma swoją indywidualną charakterystykę natężenia
przepływu Q w zależności od poziomu jego wypełnienia. Sposób obliczania natężenia
przepływu w przelewie o ostrej krawędzi znaleźć można w części: przydatne informacje.
Znajomość wartości rzeczywistego natężenia przepływu z urządzenia kontrolnego umożliwia
ocenę dokładności stosowanych metod obliczeniowych. W warunkach rzeczywistych w
większości przypadków brak jest możliwości pomiarów kontrolnych i tym samym weryfikacji
przeprowadzonych obliczeń.
9
2.2 Równanie energii
Bilans energii mechanicznej na długości strumienia kanału otwartego opisuje równanie
Bernoulliego. Przy bilansowaniu energii rozpatruje się dwa przekroje oddalone od siebie o
odległość L. W każdym z przekrojów określa się wysokość energii mechanicznej będącej
sumą: wysokości energii potencjalnej (składającą się z wysokości położenia i wysokości
ciśnienia), oraz wysokości energii kinetycznej (wysokości prędkości) (rys.8). Dla przekroju 1
określa się zatem odpowiednio wysokość położenia z
1
, wysokość ciśnienia p
1
/
γ
, oraz
wysokość prędkości
α
v
1
/2g. Analogicznie wysokości te wyznaczyć można dla przekroju 2.
Równanie Bernoulliego można zapisać w postaci:
2
1
2
2
2
2
2
2
1
1
1
1
2
2
−
+
+
+
=
+
+
str
h
g
v
p
z
g
v
p
z
α
γ
α
γ
(12)
Występujący w równaniu współczynnik
α
zwanym jest współczynnikiem de Saint-Venanta.
Zakres jego wartości w kanale laboratoryjnym rzadko przekracza wartość 1,15. W
obliczeniach można przyjmować wartość
α
= 1,1. Podczas przepływu pomiędzy przekrojami
1-2 występują straty energii mechanicznej h
str1-2
.
poziom porównawczy
dno kanału
linia ci
ś
nienia (zw. w
ody)
linia energii
rzeczywiste
j
z
2
z
1
p
1
2g
h
str 1-2
γ
p
2
γ
v
1
2
α
1
2g
v
2
2
α
2
E=const
L
1
= h
1
= h
2
Rys. 8. Graficzna interpretacja równania Bernoulliego
W przypadku kanału o poziomym dnie, gdzie poziom porównawczy można przyjąć na linii
dna, wysokości położenia z
1
i z
2
będą równe 0, zaś wysokości ciśnienia, określone zgodnie z
10
hydrostatycznym rozkładem ciśnień, będą równe głębokości wody h
1
i h
2
. Wobec
powyższego równanie Bernoulliego można zapisać w postaci:
2
1
2
2
2
2
2
1
1
1
2
2
−
+
+
=
+
str
h
g
v
h
g
v
h
α
α
(13)
2.3 Równanie ruchu krytycznego w korytach otwartych
Podczas ustalonego przepływu wody w dowolnym przekroju poprzecznym można wyznaczyć
całkowitą energię mechaniczną właściwą (liczoną w przekroju poprzecznym koryta
względem poziomu dna). Jest ona równa sumie głębokości (reprezentującej wysokość energii
potencjalnej) oraz wysokości prędkości wody (wysokości energii kinetycznej):
g
v
h
E
2
2
α
+
=
(14)
Po uwzględnieniu równania ciągłości (1) wzór (14) przyjmie postać:
2
2
2gA
Q
h
E
α
+
=
(15)
W ruchu ustalonym jednostajnym głębokość wody jak i energia kinetyczna są stałe na
długości przepływu. Natomiast w ruchu ustalonym, niejednostajnym, w każdym przekroju
kanału zmieniają się składowe energii całkowitej.
W kanale o przekroju prostokątnym szerokość zwierciadła wody B jest stała i nie zależy od
głębokości wody. Dlatego pole przekroju czynnego stanowi iloczyn stałej szerokości kanału
oraz głębokości wody h. Dla takiego koryta całkowita energia mechaniczna właściwa w
warunkach ruchu ustalonego jest tylko funkcją napełnienia kanału.
( )
2
2
2
2
B
gh
Q
h
h
E
E
c
α
+
=
=
(16)
Pierwszy człon (E
p
=h) oznacza udział wysokości energii potencjalnej, zaś drugi
(
2
2
2
2
B
gh
Q
E
k
α
=
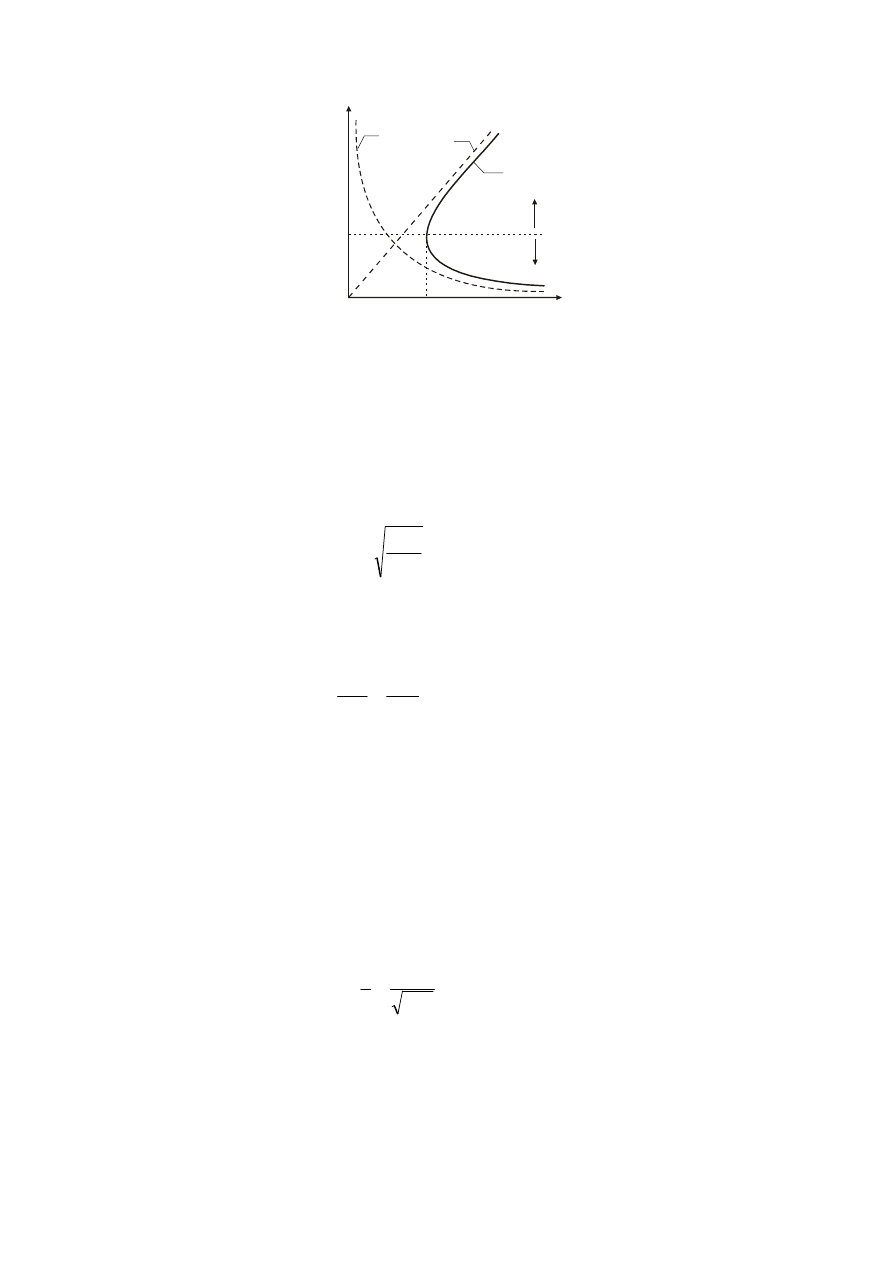
) udział wysokości energii kinetycznej (rys.9).
11
E
h
ruch
nadkrytyczny)
spokojny
(
h
kr
E
min
E
c
E
p
E
k
ruch
krytyczny)
rw
ą
cy
(pod
Rys. 9. Wykres całkowitej energii mechanicznej właściwej E
c
(h) w kanale prostokątnym
Przy ustalonym przepływie istnieje pewna głębokość wody, dla której całkowita energia
mechaniczna właściwa osiąga minimum. Głębokość ta nazywana jest głębokością krytyczną
h
kr
. Głębokość krytyczną wyznaczamy znajdując minimum funkcji E
c
(h). Dla kanału
prostokątnego o stałej szerokości (B=const) głębokość krytyczna jest równa:
3
2
2
gB
Q
h
kr
α
=
(17)
Dla dowolnego przekroju poprzecznego koryta, w warunkach ruchu krytycznego wykorzystać
można ogólne równanie:
g
aQ
B
A
kr
kr
2
3
=
(18)
A
kr
oraz
B
kr
oznaczają odpowiednio pole przekroju czynnego oraz szerokość zwierciadła
wody przy głębokości krytycznej. Jeżeli rzeczywista głębokość wody jest mniejsza od
głębokości krytycznej (
h<h
kr
), w kanale panują warunki ruchu podkrytycznego (rwącego).
Jeżeli rzeczywista głębokość wody jest większa od głębokości krytycznej (
h>h
kr
), w kanale
panują warunki ruchu nadkrytycznego (spokojnego). Kryterium ruchu określa także
bezwymiarowa wartość liczby Froude’a określająca stosunek średniej prędkości przepływu
wody
v do prędkości rozchodzenia się zaburzenia c:
sr
gh
v
c
v
Fr
=
=
(19)
W ruchu nadkrytycznym (spokojnym)
Fr < 1 co oznacza, że prędkość rozchodzenia się
zaburzenia
c jest większa od prędkości przepływu wody v. Wynika z tego, że zaburzenie
przepływu wpływa na warunki przepływu zarówno powyżej jak i poniżej miejsca wystąpienia
samego zaburzenia. W ruchu podkrytycznym (rwącym) Fr > 1, zatem prędkość przepływu
12
wody
v jest większa od prędkości rozchodzenia się zaburzenia c czyli jego wpływ odczuwany
jest tylko poniżej miejsca wystąpienia zaburzenia.
Występująca w równaniu (19) średnia głębokość wody
h
sr
w przekroju poprzecznym koryta
obliczana jest na podstawie ilorazu pola powierzchni przekroju czynnego
A oraz szerokości
zwierciadła wody
B.
B
A
h
sr
=
(20)
O tym, jaki rodzaj ruchu panuje w kanale otwartym, przekonać się również można analizując
równanie ruchu krytycznego (18). W ruchu spokojnym parametry przepływu wskazują na
dominację energii potencjalnej, o czym wskazuje większa wartość lewej strony równania
(18):
P
g
aQ
B
A
L
=
>
=
2
3
(21)
W ruchu rwącym odwrotnie dominującą składową energii jest energia kinetyczna, dlatego też
prawa strona równania przyjmuje wartości większe od lewej:
P
g
aQ
B
A
L
=
<
=
2
3
(22)
Określenie formy ruchu w kanale otwartym przy wykorzystaniu równania ruchu krytycznego
(18) oraz wyznaczenie głębokości krytycznej stanowi podstawę analiz praktycznych w
każdym zagadnieniu inżynierskim ruchu wody w korycie otwartym.
W większości przypadków rzek nizinnych w kanałach otwartych panują warunki ruchu
spokojnego. W rejonie wybudowanego obiektu mostowego warunki przepływu są
uzależnione od wielkości natężenia przepływu wody w kanale oraz geometrii przekroju. Z
reguły woda przepływa przez przekrój mostowy ruchem spokojnym. Jednakże w pewnych
warunkach może wystąpić ruch rwący (
h
kr
>
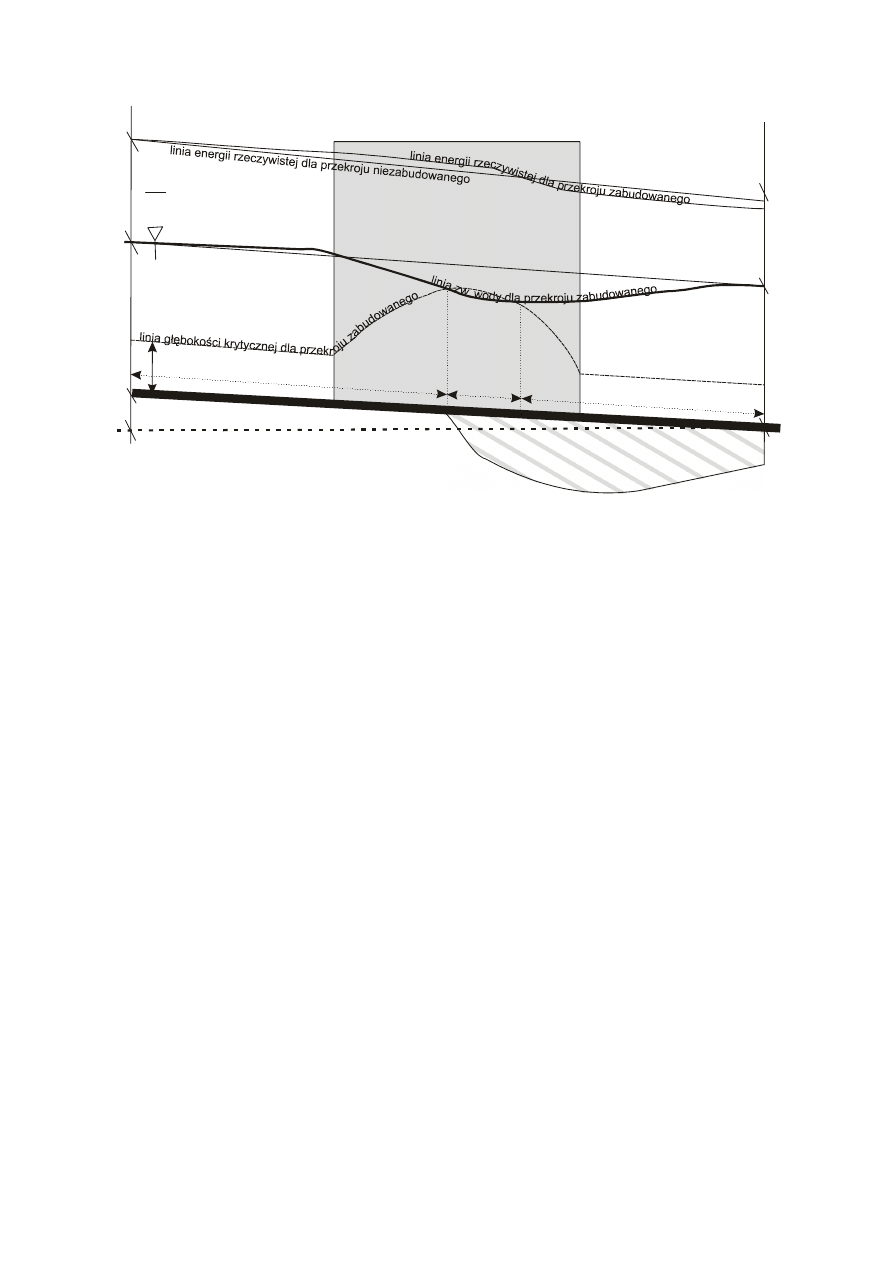
h). Na przykład w przewężeniu przekroju
następuje lokalny wzrost prędkości i rośnie wartość głębokości krytycznej
h
kr
(rys. 10).
W czasie przepływu wody przez profil mostowy, w sąsiedztwie filarów i poniżej samego
przekroju może pojawić się erozja denna powodująca dodatkowy transport materiału dna.
Dlatego też przy obliczeniach hydraulicznych rzeczywistych konstrukcji mostowych należy
każdorazowo przeanalizować i określić możliwe pogłębienie koryta w przekroju mostowym
oraz rozmycia lokalne przy filarach mostu.
13
poziom porównawczy
h
2g
v
2
α
linia zw. wody dla przekroju niez
abudowanego
filar mostu
strefa ruchu spokojnego
dno kanału
L
z=iL
strefa potencjalnego
rozmywania dna
h
kr
strefa ruchu spokojnego
s
tr
e
fa
r
u
c
h
u
r
w
ą
c
e
g
o
Rys. 10. Ogólne warunki przepływu w kanale otwartym zabudowanym przekrojem mostowym dla ruchu
spokojnego
3. Schemat stanowiska pomiarowego
Stanowisko do wykonania ćwiczenia zlokalizowane jest w kanale laboratoryjnym, w którym
woda przepływa w układzie zamkniętym. Zasilanie kanału odbywa się poprzez stanowisko
pomp czerpiących wodę z magazynowego zbiornika wody, zlokalizowanych w części
piwnicznej Laboratorium Hydrauliki i Inżynierii Środowiska. Woda bezpośrednio do kanału
dostaje się poprzez dwie skrzynie pomiarowe zakończone przelewami o ostrej krawędzi i
przekroju kołowym. Po przejściu przez kanał laboratoryjny woda powraca do zbiornika
magazynowego.
Dno kanału jest poziome zbudowane z materiałów nierozmywalnych (wzmacniana masa
betonowa). W kanale mogą być umieszczone dwa filary mostu o przekroju kołowym
(średnica
φ
110) wykonane z tworzywa sztucznego (Polipropylen PP). Możliwa jest regulacja
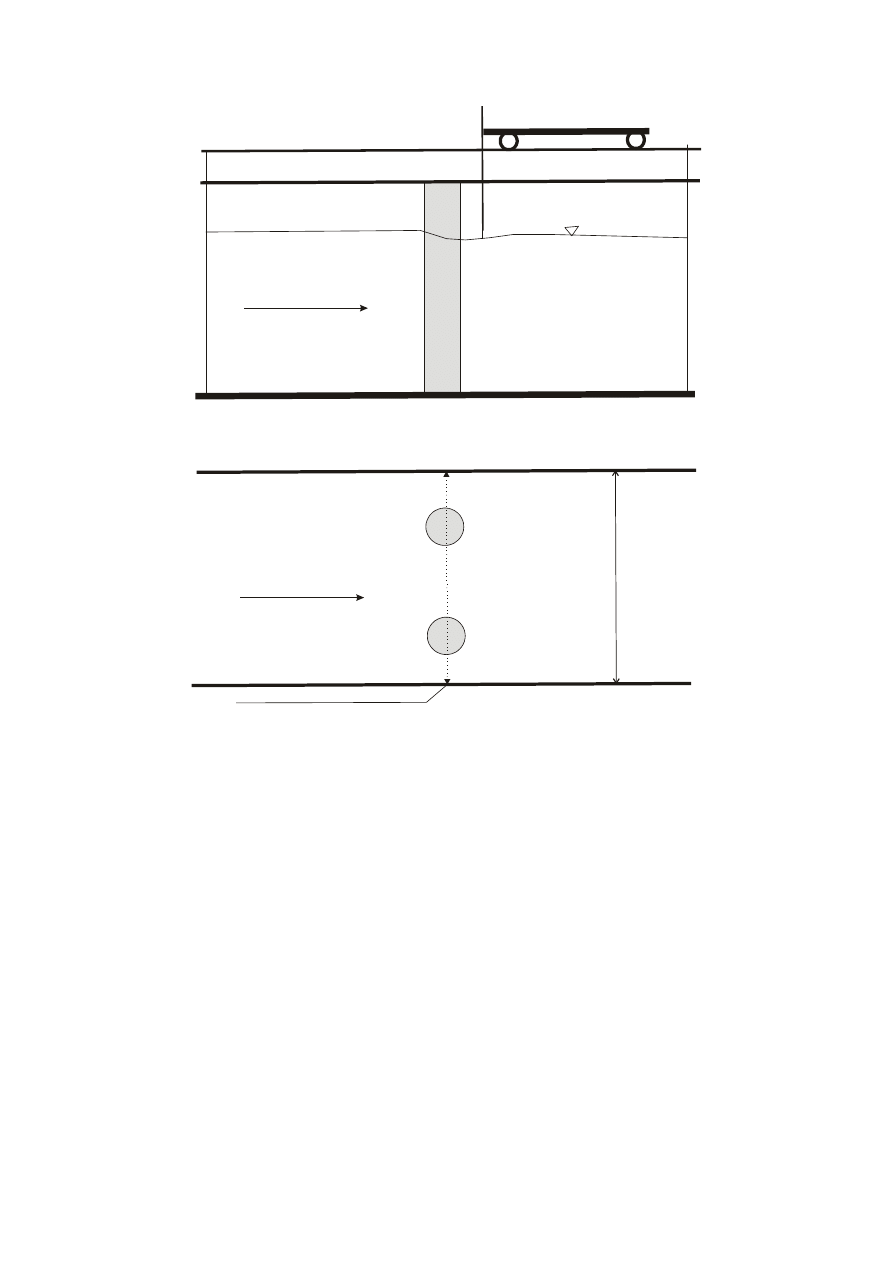
położenia filarów względem osi kanału (rys. 11).
14
dno kanału
przekrój podłu
ż
ny
fi
la
r
m
o
s
tu
1
1
0
Φ
kierunek przep
ływu wody
wózek pomiarowy
rzut z góry
fi
la
r
m
o
s
tu
1
1
0
Φ
kierunek przep
ływu wody
B
-
s
z
e
ro
k
o
ś
ć
k
a
n
a
łu
zwierciad
ło wody
s
z
p
ilk
a
p
o
m
ia
ro
w
a
przekrój mostowy (przekrój centralny)
Rys. 11. Schemat stanowiska pomiarowego
4. Przebieg ćwiczenia
1. Zmierzyć szerokość kanału laboratoryjnego;
2. Przygotować kanał laboratoryjny do przepływu wody bez obecności filarów mostu (wraz z
prowadzącym lub pracownikiem technicznym);
3. Po włączeniu pomp przez pracownika technicznego poczekać do ustalenia się przepływu w
kanale laboratoryjnym;
4. Zmierzyć wartość natężenia przepływu za pomocą kontrolnych przelewów o ostrej
krawędzi;
5. W dwóch przekrojach wskazanych przez prowadzącego zmierzyć rzędne dna i zwierciadła
wody, obliczyć spadek zwierciadła wody w kanale;
6. W przekroju mostowym pomierzyć rurką Prandla prędkości lokalne wody zgodnie z
rysunkiem 3b (Tabela 1), prowadzący może określić inną liczbę pionów pomiarowych;
15
7. Po zatrzymaniu przepływu zamontować filary mostu w przekroju mostowym (wraz z
prowadzącym lub pracownikiem technicznym);
8. Po ponownym włączeniu pomp z niezmienioną charakterystyką ich pracy sprawdzić, czy
rzeczywiste natężenie przepływu pozostało niezmienione (zgodnie z punktem 4);
9. Za pomocą wodowskazu szpilkowego wyznaczyć profil zwierciadła wody w osi kanału na
długości wskazanej przez prowadzącego. (Tabela 5);
10. Poniżej przekroju mostowego rurką Prandla pomierzyć prędkości lokalne wody zgodnie z
rysunkiem 3b (Tabela 1), prowadzący może określić inną liczbę pionów pomiarowych;
11. Korzystając z młynka hydrometrycznego pomierzyć charakterystyczne prędkości lokalne
w przekroju mostowym (Tabela 4);
5. Zawartość sprawozdania
Sprawozdanie powinno zawierać następujące elementy:
1. Krótkie wprowadzenie teoretyczne.
2.
Analiza hydrauliczna przepływu wody w kanale niezabudowanym
a.
Obliczenie natężenia przepływu wody w kanale z formuły Manninga
(równanie 2) i porównanie go z wydatkiem rzeczywistym wyznaczonym
przelewami kontrolnymi (punkt 2.1.4, Tabela 3);
b.
Określenie rozkładu prędkości w przekroju mostowym przy wykorzystaniu
rurki Prandla (punkt 2.1.2.2, Tabela 1) wraz z rysunkiem izotach (rysunek 6);
c.
Obliczenie wydatku kanału w przekroju mostowym przy wykorzystaniu
metody Culmanna (punkt 2.1.2.3, Tabela 2) i porównanie z wydatkiem
rzeczywistym (Tabela 3);
d.
Obliczenie składowych energii całkowitej mechanicznej (równanie 16) i
określenie formy ruchu burzliwego na długości kanału (punkt 2.3);
e.
Narysowanie przekroju podłużnego z zaznaczeniem linii zwierciadła wody i
energii całkowitej płynącej wody (rys. 8).
3.
Analiza hydrauliczna przepływu wody w kanale zabudowanym filarami mostu
a.
Określenie
rozkładu
prędkości
poniżej
przekroju
mostowego
przy
wykorzystaniu rurki Prandla (punkt 2.1.2.2, Tabela 1) wraz z rysunkiem
izotach (rysunek 6);
16
b.
Obliczenie wydatku kanału poniżej przekroju mostowego przy wykorzystaniu
metody Culmanna (punkt 2.1.2.3, Tabela 2) i porównanie z wydatkiem
rzeczywistym (Tabela 3);
c.
Obliczenie składowych energii całkowitej mechanicznej (równanie 16) i
określenie formy ruchu burzliwego na długości kanału (punkt 2.3);
d.
Na rysunku wykonanym w punkcie 2e: narysowanie przekroju podłużnego
zwierciadła wody, linii głębokości krytycznej oraz linii energii całkowitej
(rys.10). W miejscach, gdzie nie policzono prędkości średniej, punkty
odpowiadające energii całkowitej łączyć linią przerywaną (patrz: uwaga do
tabeli 5);
e.
Rozpoznanie i opisanie prędkości lokalnych w przekroju mostowym przy
wykorzystaniu młynka hydrometrycznego (Punkt 2.1.2.1, Tabela 4).
4.
Przykładowe obliczenia obliczanych wartości wraz z jednostkami.
5.
Podsumowanie i wnioski.
6. Literatura:
[1]
Laboratorium z mechaniki płynów i hydrauliki – praca zbiorowa pod kierunkiem K.
Weinerowskiej, Politechnika Gdańska, Gdańsk 2004 (skrypt wydany w formie
elektronicznej).
[2]
Laboratorium z mechaniki płynów i hydrauliki – praca zbiorowa, Politechnika Gdańska,
Gdańsk 1995.
[3]
Hydraulika techniczna – przykłady obliczeń, Kubrak E. i Kubrak J., Wydawnictwo
SGGW, Warszawa 2004.
[4] Rozp. Min. Transportu i Gospodarki Morskiej z dnia 30 maja 2000 r. w sprawie
warunków technicznych, jakim powinny odpowiadać drogowe obiekty inżynierskie i ich
usytuowanie – Dz.U. Nr 63 poz. 735.
[5] Byczkowski A., Hydrologia, Wyd. SGGW 1996.
[6] Madaj A., Wołowicki W., Podstawy projektowania budowli mostowych, WKŁ Warszawa
2007.
7. Przydatne informacje do wykonania ćwiczenia:
Zasada pomiaru natężenia przepływu za pomocą przelewu o ostrej krawędzi
Należy zapoznać się z rozdziałem II/4 (str. 32) skryptu
Laboratorium z mechaniki płynów i
hydrauliki [1].
17
Współczynniki oporów liniowych przy przepływie cieczy w kanałach otwartych
Należy zapoznać się z rozdziałem II/3 (str. 29) skryptu
Laboratorium z mechaniki płynów i
hydrauliki [1].
Podstawy teoretyczne przepływu wody w kanałach otwartych
Należy zapoznać się z rozdziałem III/4.1 (str. 111) skryptu
Laboratorium z mechaniki płynów
i hydrauliki [1].
Określenie szerokości zwierciadła wody w przekroju poprzecznym w którym znajduje
się filar mostu.
W ćwiczeniu filary mostu imitują rury o przekroju kołowym. Aby uzyskać szerokość
zwierciadła wody
B, należy od szerokości kanału laboratoryjnego odjąć szerokości filarów w
odpowiednim przekroju. W przekroju centralnym (rys. 11) szerokość zwierciadła wody
pomniejszona będzie o średnice filarów 220 mm (22cm) względem szerokości kanału. W
każdym innym przekroju, szerokości filarów są zmienne i można je zmierzyć na podstawie
wykonanego w skali rzutu z góry kanału laboratoryjnego.
18
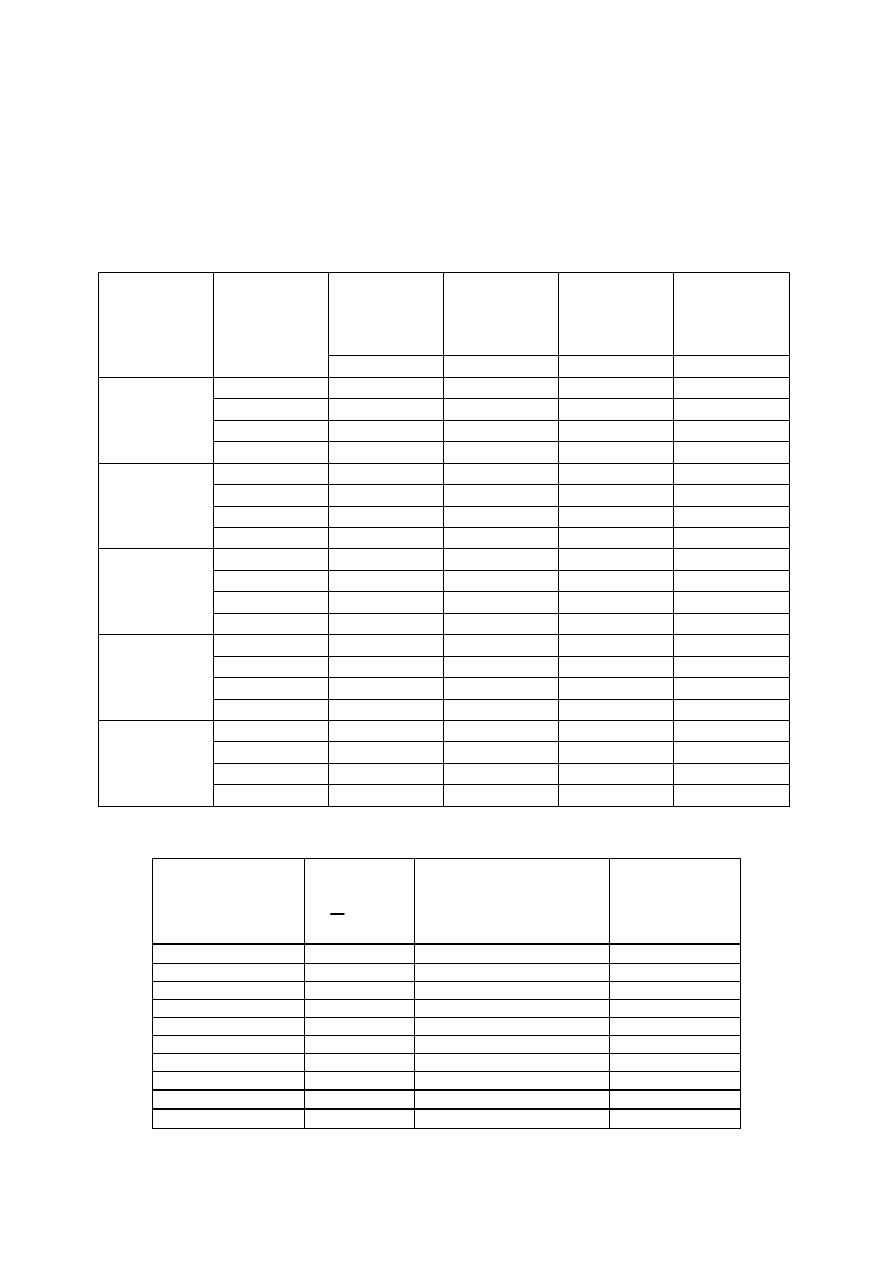
Tabela 1. Obliczenie prędkości lokalnych rurką Prandla
Przekrój …………………………………………
Nr przekroju ……………………………………
Data i godzina pomiaru …………………………
Wydatek kontrolny ………………..m
3
/s …………………dm
3
/s ……………..cm
3
/s
Pion
(odległość
od brzegu
lewego)
Punkt
Wysokość
punktu od
dna
z
i
∆∆∆∆
h
i
v
Li
V
Li
cm
cm
cm/s
m/s
1
I
2
3
……………
4
1
II
2
3
……………
4
1
III
2
3
……………. 4
1
IV
2
3
……………
4
1
V
2
3
……………
4
Tabela 2. Obliczenie natężenia przepływu metodą Culmanna
Izotachy
odpowiadające
prędkościom
[m/s]
Prędkość
średnia
v
[m/s]
Powierzchnia
zawarta pomiędzy
izotachami
∆∆∆∆
A [m
2
]
Natężenie
przepływu
∆∆∆∆
Q [m
3
/s]
Q=
m
3
/s
Q=
dm
3
/s
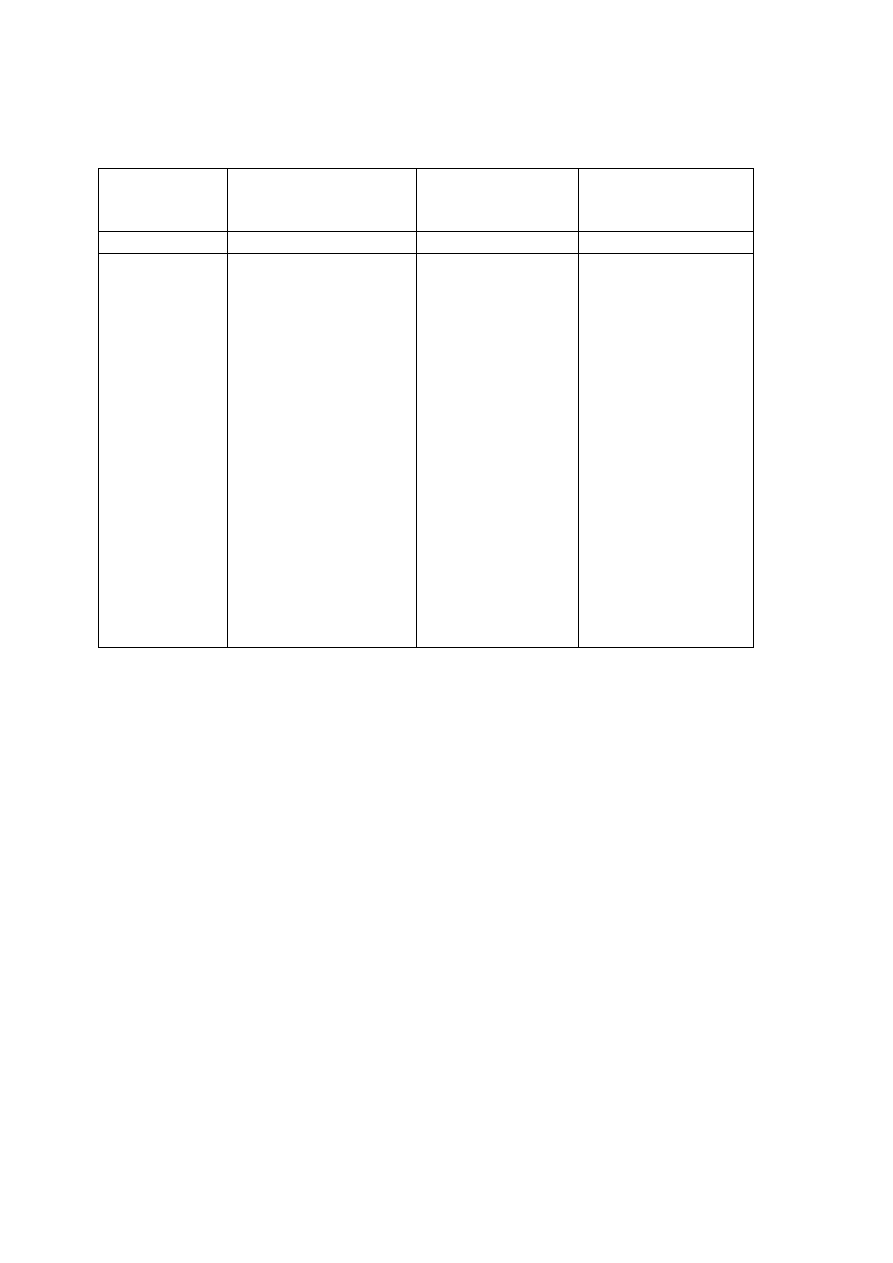
19
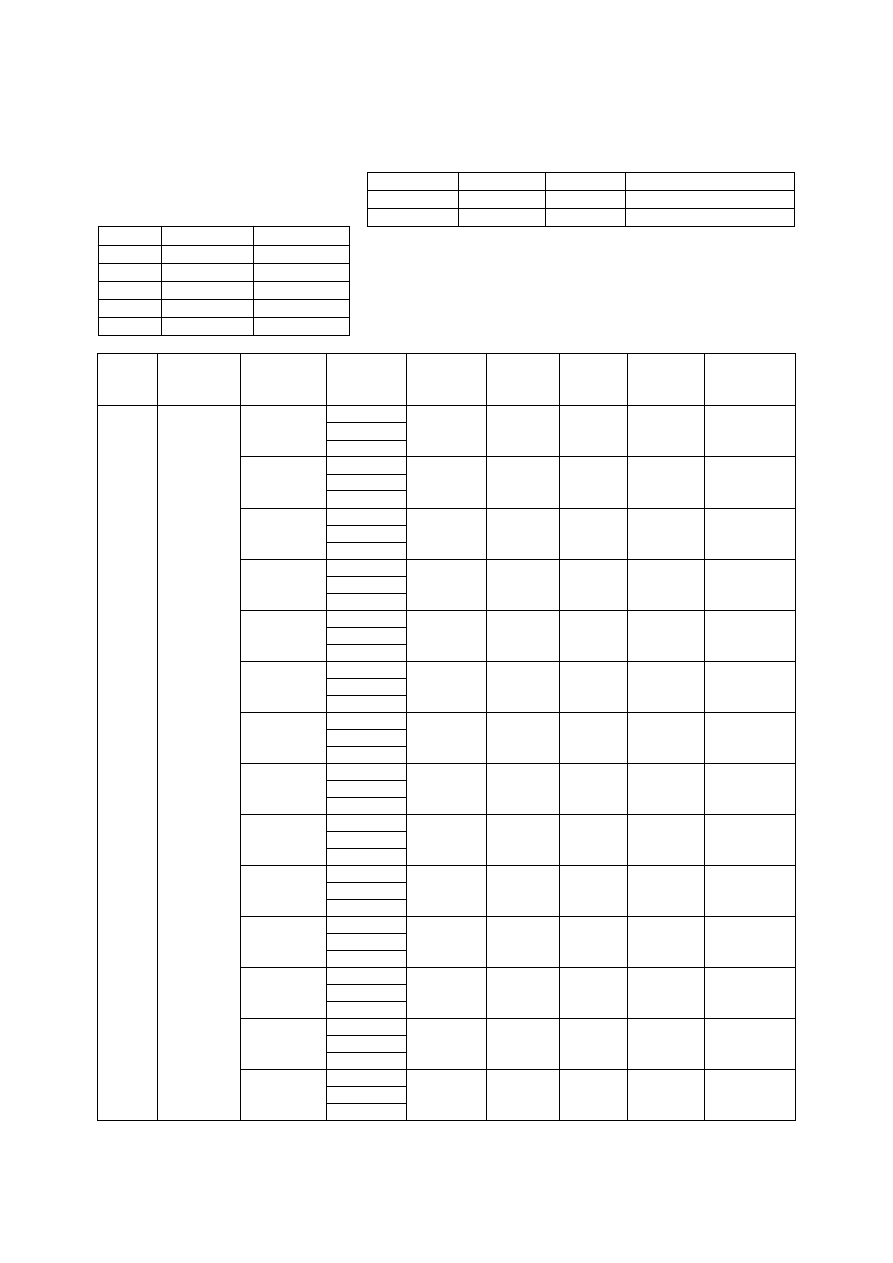
Tabela 3. Zestawienie wyników pomiarów i obliczeń natężenia przepływu w kanale
Wydatek
rzeczywisty
Wydatek w korycie
niezabudowanym z
równania Manninga
Wydatek w korycie
niezabudowanym z
metody Culmanna
Wydatek w korycie
zabudowanym z
metody Culmanna
dm
3
/s
dm
3
/s
dm
3
/s
dm
3
/s
Natężenie
przepływu z
przelewu
kołowego 1
…………dm
3
/s
Natężenie
przepływu z
przelewu
kołowego 2
…………dm
3
/s
SUMA
…………dm
3
/s
20
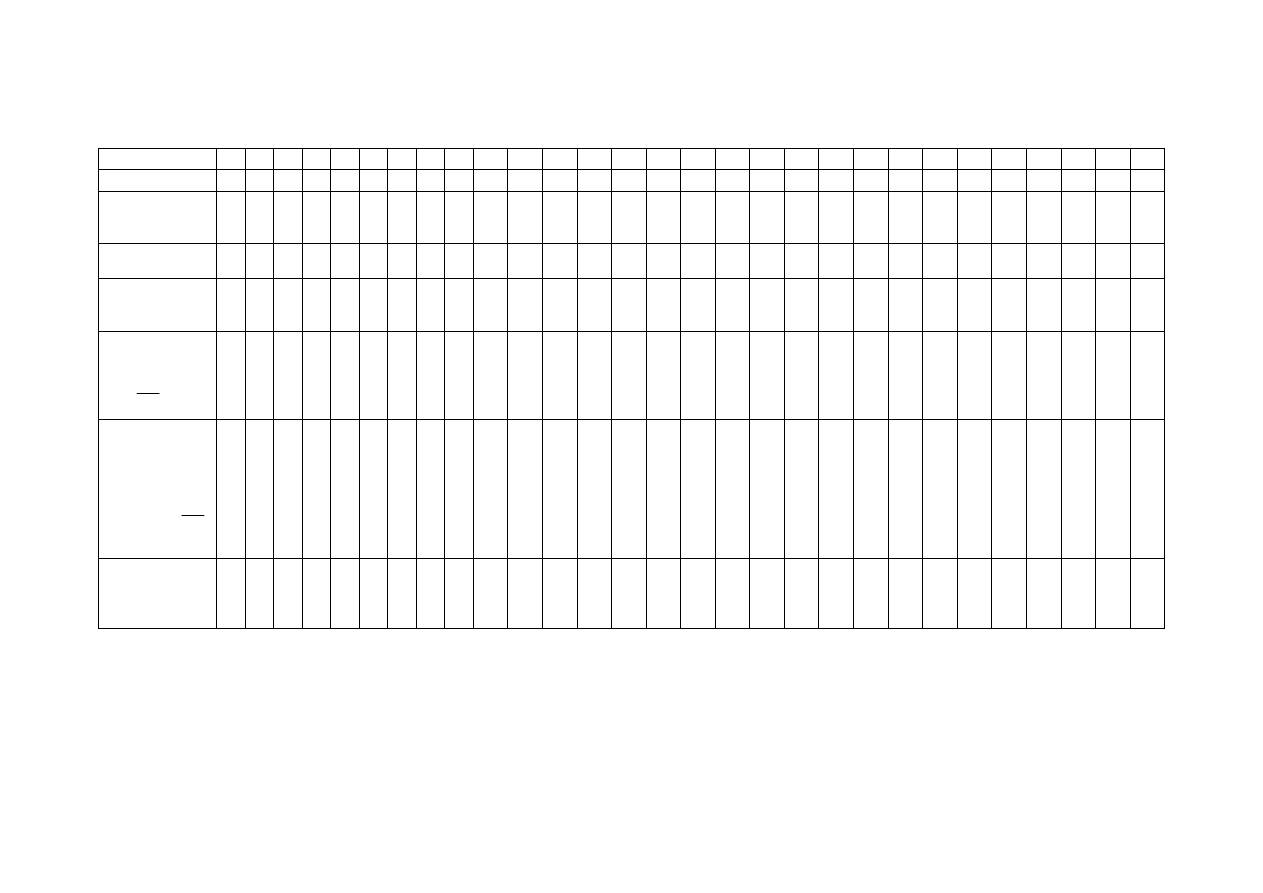
Tabela 4.
KARTA POMIARÓW HYDROMETRYCZNYCH
Rzeka: ………….. Data: ………………………………………
Przekrój: ……………
godzina
stan [cm]
warunki atmosferyczne
początek
koniec
Młynki
α
αα
α
ββββ
A
B
C
D
E
Nr
pionu
Odległość
[m]
Głębokość
pomiaru
[m]
Liczba
impulsów
Średnia
liczba
impulsów
Liczba
obrotów
[1/s]
Młynek
v
[m/s]
Uwagi
21
Tabela 5. Analiza całkowitej energii mechanicznej na długości kanału otwartego dla koryta zabudowanego
Przekrój nr
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
Odległość [cm]
Rzędna zw.
wody w osi
kanału R
zw
[cm]
Głębokość
h=R
zw
-RD [cm]
Prędkość
ś
rednia v
[cm/s]
Wysokość
prędkości
g
v
2
2
α
[cm]
Wysokość
energii
rzeczywistej
(równanie 16)
g
v
h
E
2
2
α
+
=
[cm]
głębokość
krytyczna
(równanie 17)
h
kr
[cm]
Rzędna dna kanału pomiarowego RD: …………… cm
UWAGA: W przekrojach, gdzie rzędna zwierciadła wody zależy od warunków lokalnych (spiętrzenie przed filarem mostowym, obniżenie za
filarem mostowym, istotna zmiana głębokości wody w przekroju poprzecznym) NIE LICZYĆ prędkości średniej, wysokości prędkości oraz
wysokości energii całkowitej. W odpowiednie kratki wstawić X.