1
Laboratorium z Hydrauliki i Hydrologii – Kierunek Budownictwo inż – sem. V
Politechnika Gdańska
Katedra Hydrotechniki
WILIŚ
Analiza przepływu przez przepust o przekroju kołowym (P)
1. Cel ćwiczenia
Celem ćwiczenia jest analiza zjawisk hydraulicznych występujących podczas
przepływu w przepuście oraz zapoznanie się ze sposobami wyznaczania wydatku przepustu
kołowego pracującego w warunkach przepływu ze swobodnym zwierciadłem oraz przepływu
pod ciśnieniem.
2. Wprowadzenie
Przepust jest przewodem służącym do przeprowadzenia wody przez konstrukcje takie
jak np. drogi, nasypy czy groble. Przepusty wykonywane są z różnych materiałów (stal,
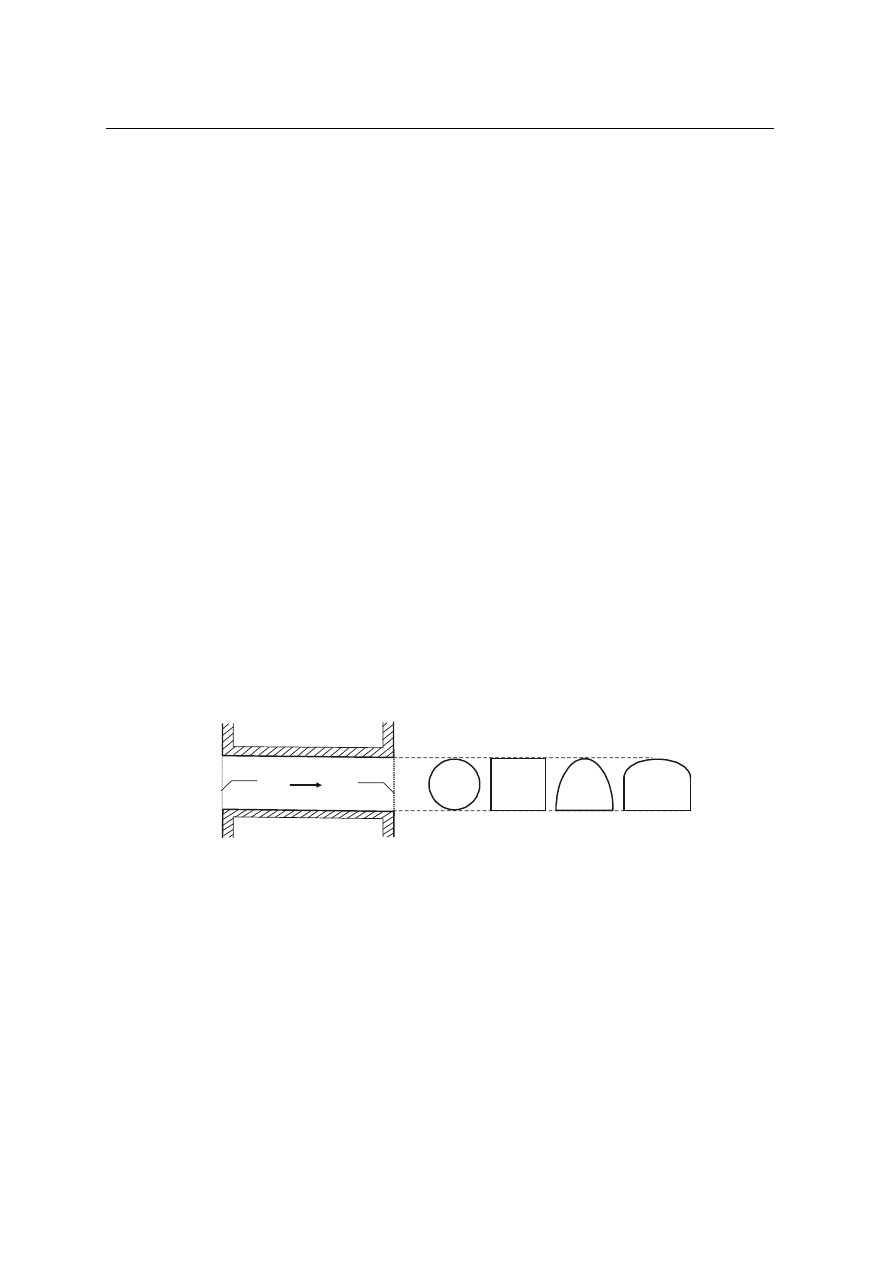
beton, tworzywa sztuczne), mają zróżnicowane kształty przekroju poprzecznego (rys. 1) oraz
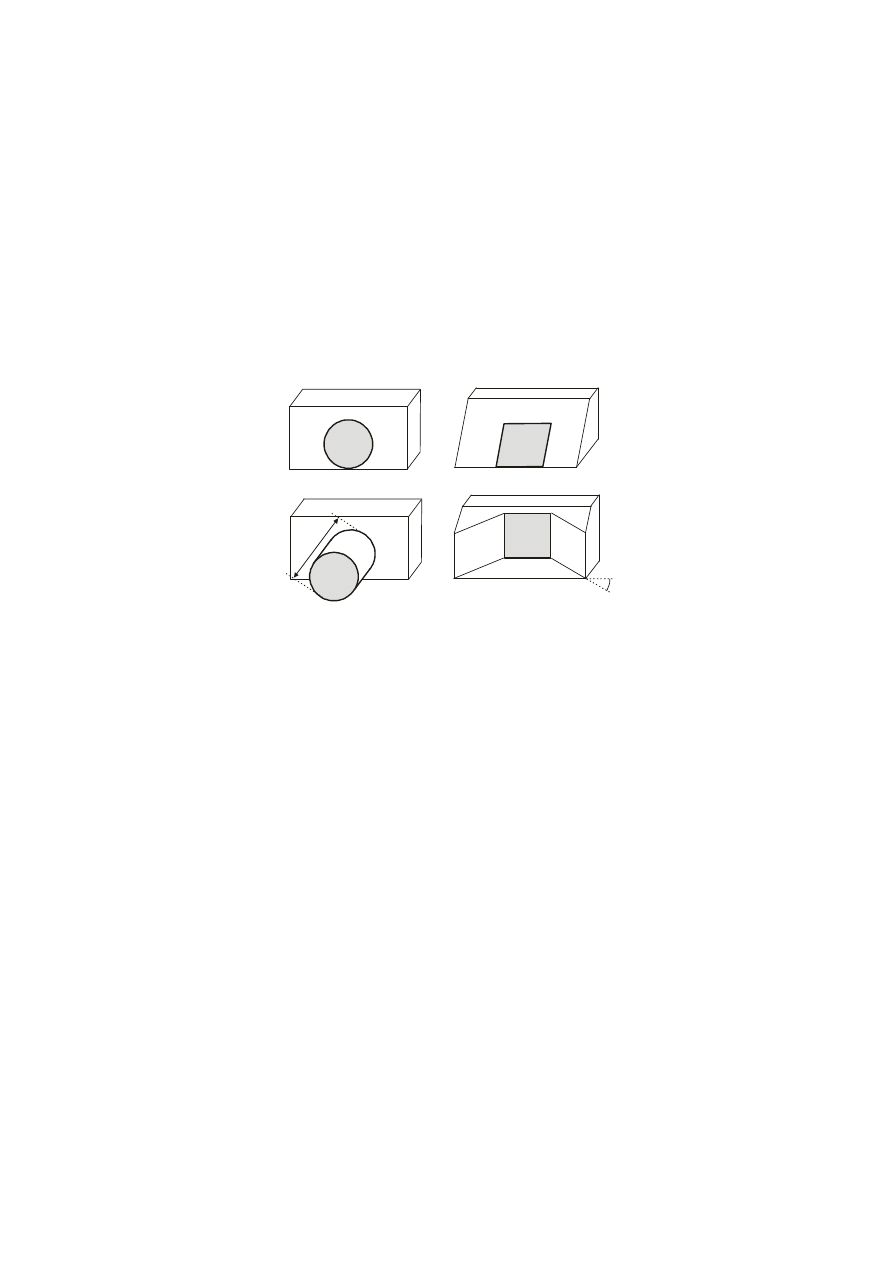
zróżnicowane konstrukcje wlotowe (rys. 2).
a)
b)
wylot
wlot
Rys.1. Przekrój podłużny przepustu (a); podstawowe kształty przekrojów poprzecznych przepustu (b)
W przepuście może wystąpić przepływ ze swobodnym zwierciadłem wody lub
przepływ pod ciśnieniem na całej długości przepustu, bądź tylko jego części. Jednakże należy
pamiętać, że przepływ pełnym przekrojem przepustu, czyli przepływ pod ciśnieniem wstępuje
rzadko lub dopuszcza się chwilowe jego występowanie np. podczas wezbrań. Charakter
przepływu uzależniony jest od warunków hydraulicznych panujących przed i za wylotem
przepustu oraz charakterystyki przepustu, czyli jego geometrii i materiału z jakiego jest
wykonany. W związku z występującą różnorodnością form przepływu, do obliczania
2
przepustów wykorzystuje się elementy teorii przepływów w kanałach otwartych, przepływu
przez przelewy oraz przepływów pod ciśnieniem. Równania służące do obliczenia wydatku
lub świateł przepustów wyprowadza się z równania ciągłości oraz z równania Bernoulliego
zapisanego dla odpowiednich przekrojów obliczeniowych. Jeden z przekrojów znajduje się
zawsze przed wlotem do przepustu w takiej odległości, aby przekrój ten był poza zasięgiem
lokalnego ugięcia zwierciadła wody. Natomiast lokalizacja drugiego, tzw. dolnego przekroju
kontrolnego (DPK) zależy od warunków przepływu i może znajdować się w pobliżu wlotu
(rys. 3) lub wylotu przepustu (rys. 6).
a)
b)
c)
d)
Θ
L
P
Rys.2. Podstawowe konstrukcje wlotów: prostopadły (a); rurowy nieobudowany (b); kołnierzowy (c);
ze skrzydłami (d)
W obliczeniach przepustów można wyróżnić następujące podstawowe układy
hydrauliczne:
- przepływ ze swobodną powierzchnią, niezatopiony wlot i wylot (ruch spokojny oraz rwący),
- przepływ ze swobodną powierzchnią, zatopiony wlot i niezatopiony wylot,
- przepływ pod ciśnieniem, zatopiony wlot (zatopiony lub niezatopiony wylot).
2.1. Przepływ ze swobodną powierzcnhią wody, niezatopiony wlot i wylot
2.1.1 Przypadek ruchu rwącego
Przepływ ze swobodną powierzchnią może wystąpić, gdy spełnione są następujące
warunki niezatopienia wlotu oraz wylotu (Bodhaine, 1976):
H /D < 1.5, h
d
< h
kr
(1a,b)
gdzie: H – głębokość wody przed wlotem do przepustu (nad dnem wlotu),
3
D – wysokość przepustu,
h
d
– głębokość wody dolnej (nad dnem wylotu),
h
kr
– głębokość krytyczna.
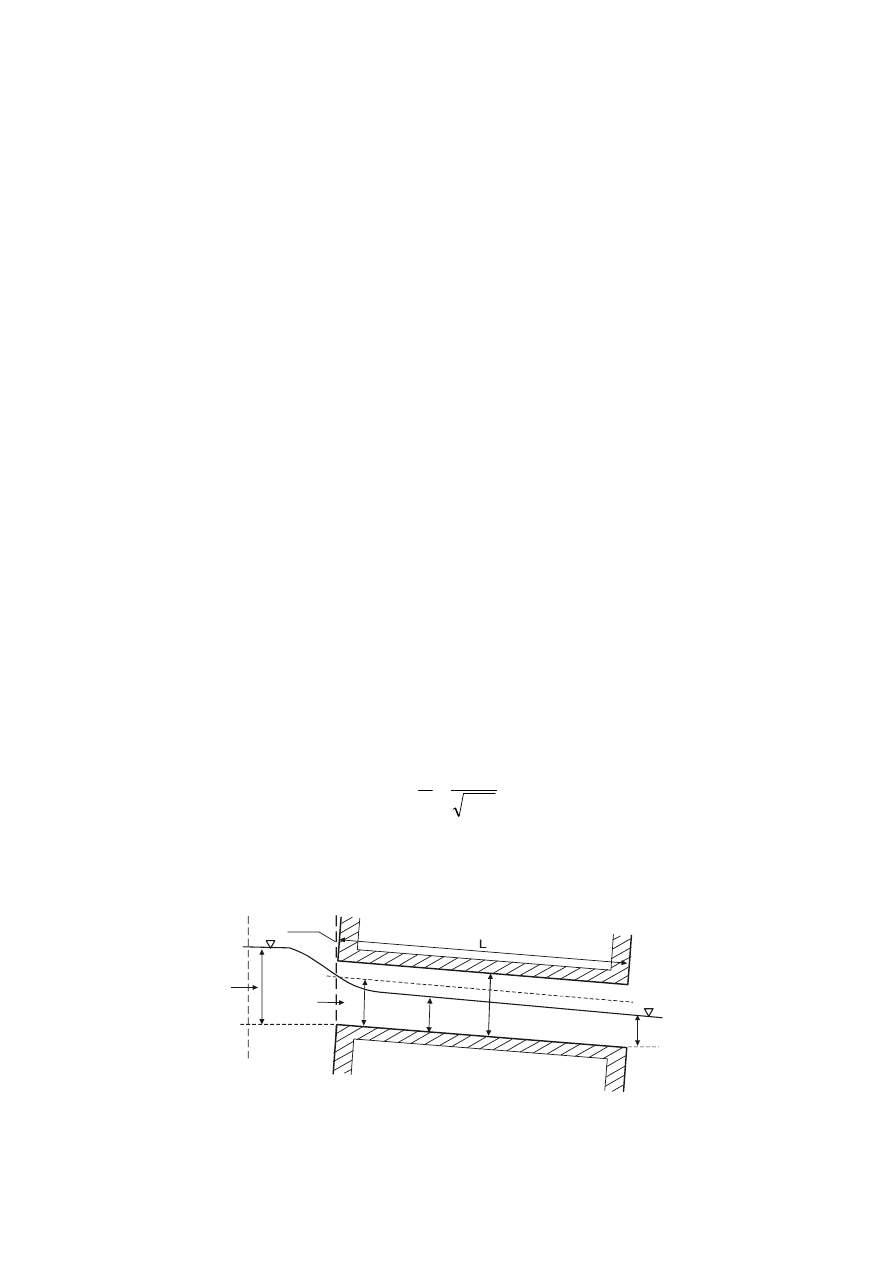
W przypadku przepływu ze swobodną powierzchnią przed przepustem występuje przeważnie
ruch spokojny (liczba Froude’a Fr < 1, h > h
kr
). W wyniku przewężenia strumienia na wlocie
przepustu następuje wzrost prędkości oraz wartości liczby Froude’a przy jednoczesnym
zmniejszeniu głębokości wody h (rys. 3). W efekcie następuje stopniowe przejście od ruchu
spokojnego do ruchu rwącego. Takie przejście jest możliwe jeśli spadek przepustu i
0
jest
większy od spadku krytycznego i
kr
:
i
0
> i
kr
(2)
Wówczas zakłada się, że głębokość krytyczna h
kr
występuje w pobliżu przekroju wlotowego,
który staje się jednocześnie dolnym przekrojem kontrolnym (DPK), a w samym przepuście
występuje przepływ rwący (Fr > 1, h < h
kr
). W takim układzie warunki hydrauliczne panujące
na wylocie przepustu nie mają wpływu na zjawiska zachodzące w samym przepuście,
ponieważ żadne zaburzenie (np. zmiana głębokości na wylocie h
d
w odpowiednim zakresie)
nie może przenosić się w kierunku wlotu. Wynika to z faktu, że średnia prędkość przepływu
wody w przepuście V jest większa od prędkości rozchodzenia się zburzenia c, co potwierdza
także wartość liczby Froude’a dla ruchu rwącego:
sr
gh
V
c
V
Fr
=
=
(3)
gdzie: g – przyspieszenie ziemskie.
h
kr
H
h
hd
1
pp
V
2
i
i
0
kr
>
V
1
2
DPK
D
Rys. 3. Hydrauliczne warunki pracy przepustu ze swobodnym zwierciadłem o niezatopionym wlocie i wylocie w
przypadku ruchu rwącego (DPK – dolny przekrój kontrolny, pp – poziom porównawczy)
4
Dla takiego schematu natężenie przepływu Q oblicza się jak w przypadku
niezatopionego przelewu o szerokiej koronie z założeniem warunków ruchu krytycznego
(Fr=1). Równanie Bernoulliego zapisane dla dwóch przekrojów poprzecznych strumienia -
przekróju 1 przed wlotem oraz przekroju 2 na wlocie (z pominięciem strat energii) przyjmuje
następującą postać:
2
2
1
2
2
2
kr
V
V
H
h
g
g
+
=
+
(4)
gdzie: V
1
- średnia prędkość w przekroju przed wlotem,
V
2
– średnia prędkość w przekroju w pobliżu wlotu równa prędkości krytycznej V
kr
.
Po przekształceniu równania (4), wykorzystaniu równania ciągłości (Q = V
kr
⋅
A
kr
) oraz
uwzględnieniu strat energii mechanicznej na wlocie ostatecznie otrzymujemy formułę na
obliczenie wydatku:
2
1
2
2
N
kr
kr
V
Q
A
g H
h
g
µ
=
⋅
+
−
(5)
gdzie:
µ
N
– współczynnik wydatku przepustu,
A
kr
– pole przekroju poprzecznego przy napełnieniu odpowiadającym głębokości
krytycznej.
Współczynnik wydatku
µ
N
uwzględnia straty energii mechanicznej w obrębie wlotu
spowodowane zawirowaniami oraz kontrakcją (dławieniem) strumienia. Wartość
współczynnika
µ
N
zależy przede wszystkim od geometrii przepustu, konstrukcji wlotu oraz od
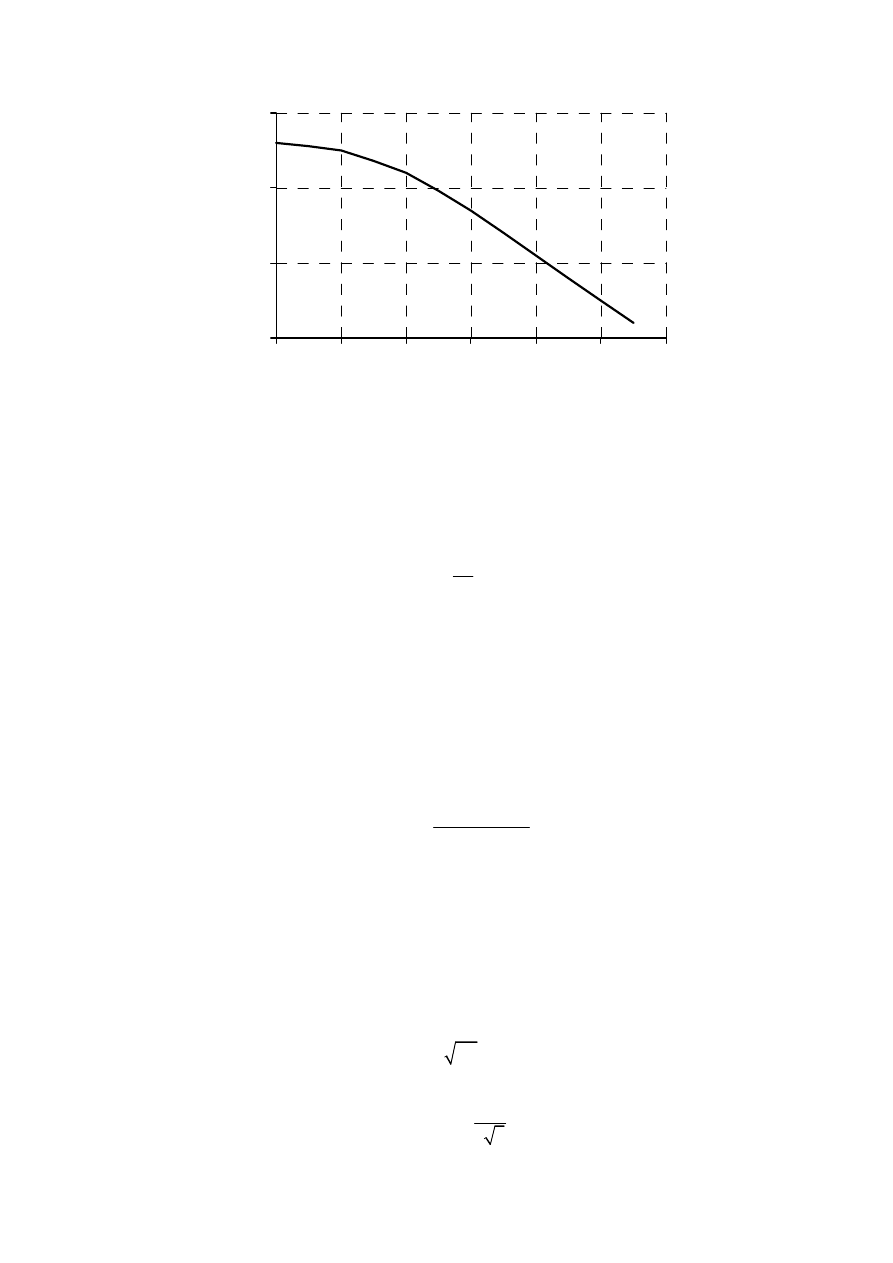
napełnienia kanału H przed wlotem odniesionego do wysokości przepustu D. Na rysunku 4
przedstawiono wartości współczynnika wydatku dla przekroju kołowego w zależności od
parametru H/D. Dla przekroju prostokątnego współczynnik ten uzależnia się od liczby
Froude’a. W przyjętym schemacie obliczeniowym przepustu zakłada się warunki ruchu
krytycznego (Fr = 1), w związku z tym można przyjąć stałą wartość współczynnika wydatku
µ
N
=
0.95 dla przekroju prostokątnego (Bodhaine, 1976).
5
0.4
0.6
0.8
1
1.2
1.4
1.6
H/D
0.8
0.85
0.9
0.95
µ
N
Rys. 4. Współczynnik wydatku przepustu o przekroju kołowym - przepływ ze swobodnym zwierciadłem,
niezatopiony wlot i wylot, k = 0.80 (Bodhaine, 1976)
Wartości współczynnika wydatku
µ
N
przedstawione na rysunku 4 odpowiadają przypadkowi,
gdy współczynnik przekroju kanału k zdefiniowany następująco:
0
1
A
k
A
= −
(6)
gdzie: A – pole przekroju czynnego w przepuście,
A
0
– pole przekroju czynnego w kanale,
przyjmuje wartość k = 0.80. Dla innych wartości parametru k należy skorygować
współczynnik wydatku według formuły:
(
)
0.98
0.98
0.80
N
k
N
k
µ
µ
−
=
−
(7)
W praktyce prędkość dopływającej wody V
1
jest nieduża, tak więc wysokość
prędkości przed wlotem V
1
2
/2g można pominąć. Jeśli dodatkowo przyjmiemy przekrój
prostokątny przepustu (A
kr
= h
kr
⋅
B
kr
) oraz założymy warunki ruchu krytycznego (h
kr
= 2/3H),
to wówczas równanie (5) możemy sprowadzić do następującej postaci:
3/ 2
2
kr
Q
m B
g H
= ⋅
(8)
gdzie: m – współczynnik wydatku przepustu,
2
3 3
N
m
µ
=
,
6
B
kr
– szerokość zwierciadła w przepuście odpowiadająca głębokości krytycznej.
Szerokość zwierciadła B
kr
w przepustach o kształcie prostokątnym równa jest oczywiście
szerokości przepustu, natomiast dla innych kształtów przekroju szerokość ta jest funkcją
napełnienia przepustu. Należy także pamiętać, że wzór (8) został wyprowadzony przede
wszystkim dla przepustów o prostokątnym kształcie przekroju. W przypadku innych
kształtów należy stosować formułę (5), w której natężenie przepływu powiązane jest z
geometrią przepustu poprzez pole przekroju czynnego A
kr
wyznaczone dla głębokości
krytycznej.
Parametry A
kr
oraz h
k
dla danego natężenia przepływu można wyznaczyć posługując
się równaniem ruchu krytycznego w postaci:
3
2
kr
kr
A
Q
B
g
α
⋅
=
(9)
gdzie:
α
- współczynnik de Sain-Venanta (dla koryt otwartych
α
= 1.0 – 1.15).
W przypadku przekroju kołowego o średnicy D parametry takie jak pole przekroju
czynnego, obwodu zwilżonego, szerokości oraz głębokości zależą zarówno od średnicy jak i
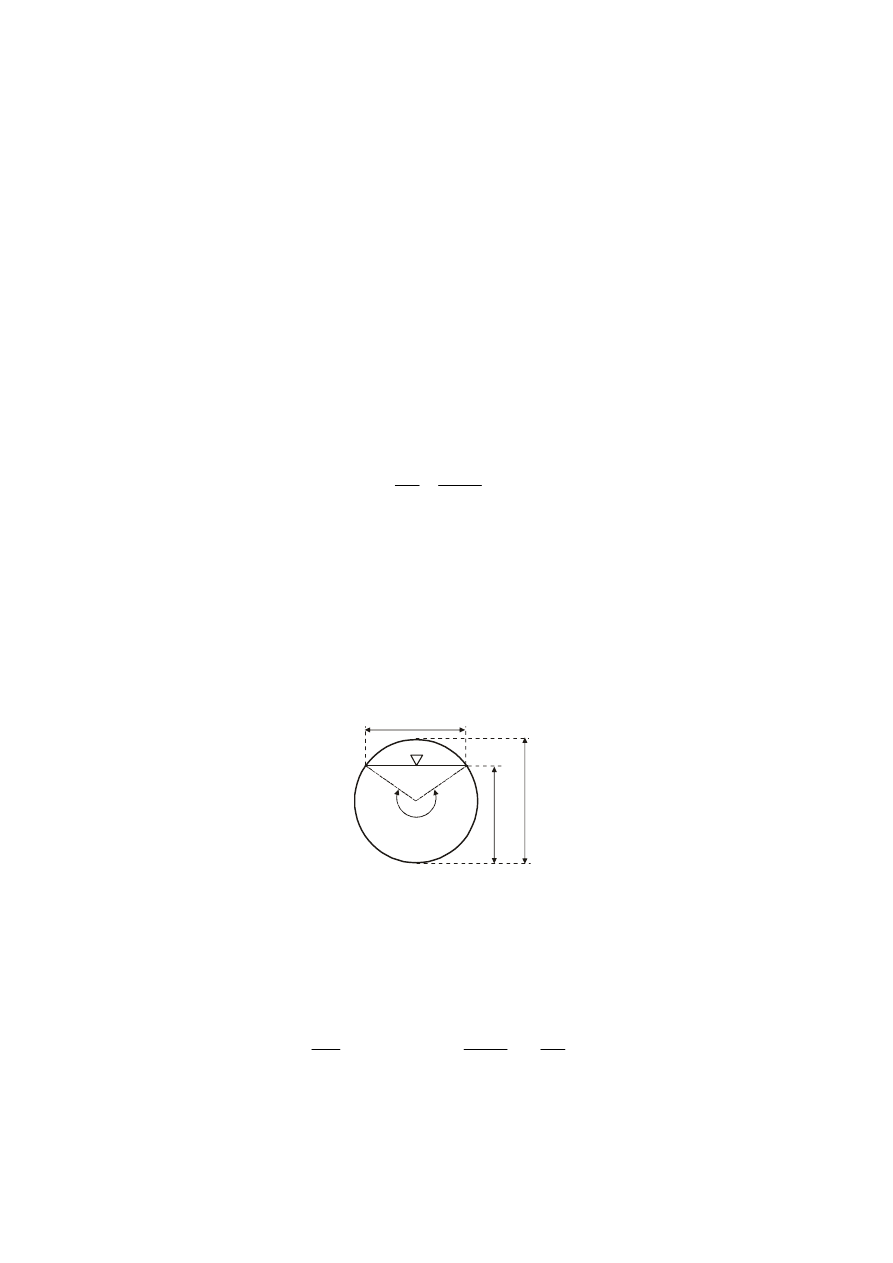
od kąta środkowego β wyznaczonego poprzez położenie zwierciadła wody (rys. 5).
B
kr
h
kr
D
β
kr
Rys. 5. Głębokość krytyczna oraz szerokość zwierciadła wody w przepuście o przekroju kołowym
W związku z tym, aby wyznaczyć parametry ruchu krytycznego w pierwszej kolejności
należy rozwiązać następujące równanie:
(
)
5
2
3
512
2
kr
kr
kr
D
Q
sin
sin
g
β
α
β
β
⋅
−
=
⋅
(10)
7
w którym niewiadomą jest kąt środkowy β
kr
(wyrażony w mierze łukowej) przy przepływie z
głębokością krytyczną. Równanie powyższe jest równaniem ruchu krytycznego dla przekroju
kołowego. Ze względu na nieliniowość równania (10) wyznaczenie kąta β
kr
w sposób
bezpośredni nie jest możliwe. Wartość tego kąta można określić tylko w sposób przybliżony
wykorzystując odpowiednią metodę numeryczną służącą do rozwiązania równań
nieliniowych (np. metodę Newtona) lub posługując się metodą kolejnych przybliżeń.
Obliczona wartość kąta środkowego β
kr
pozwala na wyznaczenie pozostałych parametrów
ruchu krytycznego:
- głębokości krytycznej h
kr
:
1 cos
2
2
kr
kr
D
h
β
=
−
(11)
- szerokości zwierciadła wody B
kr
:
2
kr
kr
B
D sin
β
= ⋅
(12)
- pola przekroju czynnego A
kr
:
(
)
2
8
kr
kr
kr
D
A
sin
β
β
=
−
(13)
- obwodu zwilżonego:
2
z kr
kr
D
O
β
=
(14)
2.1.2 Przypadek ruchu spokojnego
Przepływ w przepuście ze swobodnym zwierciadłem dla ruchu spokojnego (Fr < 1,
h>h
kr
) występuje wtedy, gdy spełnione są warunki niezatopienia wlotu (1a) i wylotu (1b) oraz
gdy dodatkowo spadek przepustu i
0
jest mniejszy od spadku krytycznego i
kr
:
i
0
< i
kr
(15)
Jeśli powyższe warunki są spełnione, to zakłada się że głębokość krytyczna h
kr
występuje w
pobliżu przekroju wylotowego (rys. 6a). Podczas analizy przepływu spokojnego przez
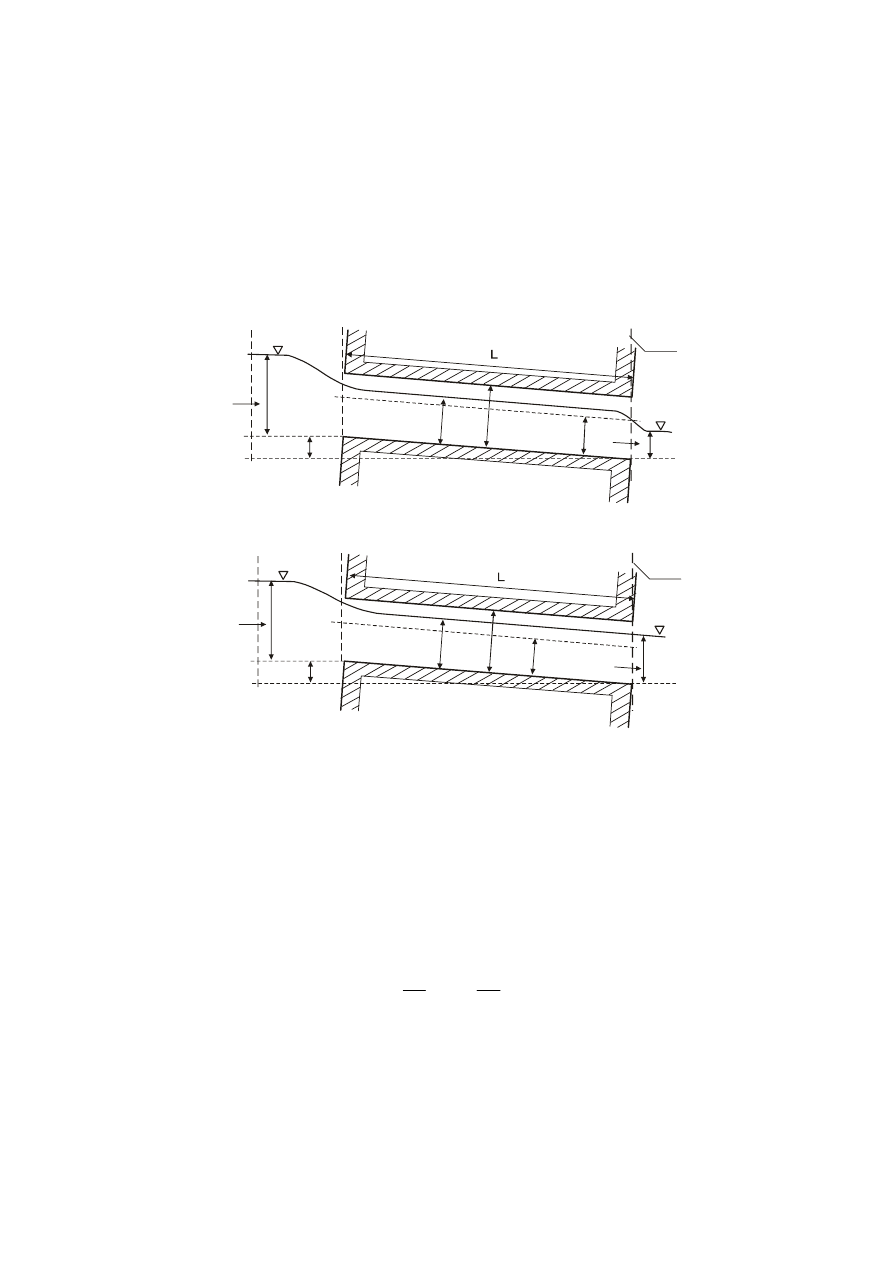
8
przepust należy jeszcze wyróżnić sytuację gdy wylot jest niezatopiony, ale głębokość wody
jest większa od głębokości krytycznej, tzn:
D > h
d
> h
kr
(16)
Profil zwierciadła wody wytworzony dla takich warunków przedstawia rysunek 6b.
h
kr
H
h
hd
z
1
3
pp
i
i
0
kr
<
V
3
2
DPK
V
1
h
kr
H
h
hd
z
1
3
pp
V
3
V
1
2
DPK
a)
b)
D
D
i
i
0
kr
<
i
i
0
kr
>
Rys. 6. Hydrauliczne warunki pracy przepustu ze swobodnym zwierciadłem o niezatopionym wlocie i wylocie w
przypadku ruchu spokojnego: a) h
d
< h
kr
; b) h
d
> h
kr
W przepływie spokojnym na zdolność przepustową mają wpływ warunki panujące zarówno
przed wlotem jak i za wylotem przepustu. W związku z tym dolny przekrój kontrolny (DPK)
znajduje się w pobliżu wylotu przepustu (rys. 6), co należy odpowiednio uwzględnić podczas
zapisu równania Bernoulliego:
2
2
3
1
2
2
d
L
V
V
z
H
h
h
g
g
+ +
= +
+
(17)
gdzie: z – wysokość położenia dna przepustu na wlocie ponad poziom dna przepustu na
wylocie,
0
z
i L
= ⋅
,
L – długość przepustu,
9
i
0
– spadek przepustu,
V
3
– średnia prędkość w przekroju na wylocie,
h
d
– głębokość wody w przekroju na wylocie,
h
L
– wysokość strat energii na długości.
Wysokość strat energii na długości h
L
można wyznaczyć wykorzystując przekształcone
równanie Manninga:
2
2
4/3
2
L
n
L Q
h
R
A
⋅ ⋅
=
⋅
(18)
gdzie: n – współczynnik szorstkości według Manninga charakteryzujący rodzaj powierzchni,
R – promień hydrauliczny określony według relacji:
z
A
R
O
=
(19)
w którym A jest przekrojem czynnym, a O
z
jest obwodem zwilżonym. Dla przepustu
hydraulicznie krótkiego, tzn. gdy spełniony jest warunek L < 20D (Kubrak i Kubrak, 2004),
straty energii na długości h
L
można pominąć. W innym przypadku straty te powinno się
uwzględnić.
Wykorzystanie przekształconego równania Bernoulliego (17) i uwzględnienie strat na
wlocie oraz kontrakcji strumienia poprzez współczynnik wydatku
µ
N
ostatecznie prowadzi do
następującej formuły na natężenie przepływu:
2
1
2
2
N
d
d
L
V
Q
A
g H
z
h
h
g
µ
=
⋅ ⋅
+ +
− −
(20)
gdzie: A
d
- pole przekroju poprzecznego przy napełnieniu odpowiadającym głębokości h
d
.
Jeśli spełnione są warunki (1b) oraz (15), tzn. głębokość krytyczna wystąpi w pobliżu wylotu
przepustu, to wówczas możemy przyjąć, że głębokość wody na wylocie h
d
równa jest
głębokości krytycznej h
kr
, co prowadzi także do relacji A
d
= A
kr
.
10
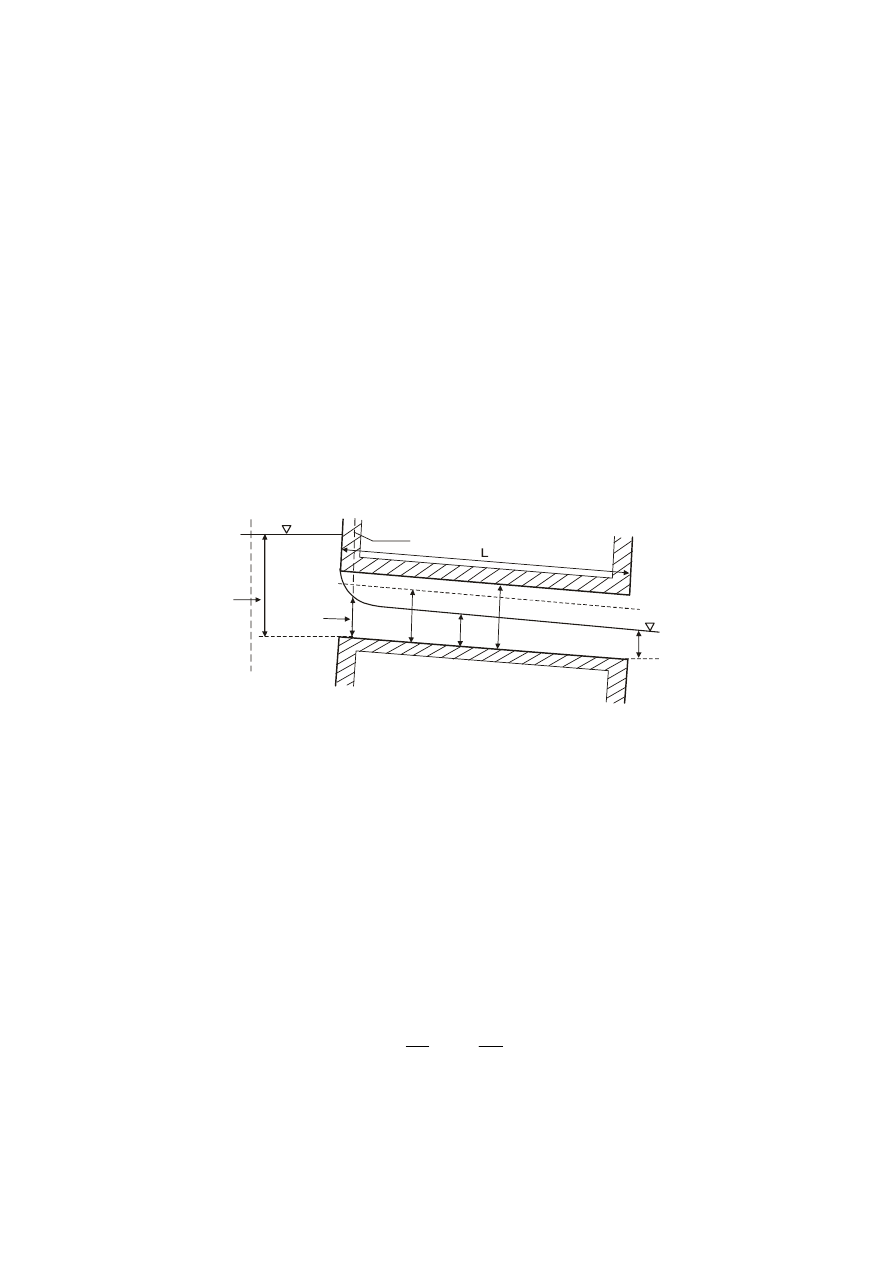
2.2 Przepływ ze swobodnym zwierciadłem wody, zatopiony wlot i niezatopiony wylot
Wlot przepustu uważa się zatopiony, gdy spełniony jest następujący warunek
(Bodhaine, 1976):
H/D > 1.5
(21)
Zatopienie wlotu nie musi oznaczać, że przepust na całej długości będzie całkowicie
wypełniony wodą. Jeśli wlot jest zatopiony oraz dodatkowo spełniony jest następujący
warunek niezatopienia wylotu:
h
d
< D
(22)
to w przepuście również wystąpi przepływ ze swobodną powierzchnią (rys. 7).
h
kr
H
D
h
d
1
pp
V
2
V
1
2
DPK
h
2
h
Rys. 7. Hydrauliczne warunki pracy przepustu ze swobodnym zwierciadłem o zatopionym wlocie i
niezatopionym wylocie.
Analogicznie jak w przypadku niezatopionego wlotu, tak i tutaj na skutek kontrakcji
strumienia na wlocie do przepustu następuje gwałtowny wzrost prędkości przepływu przy
jednoczesnym zmniejszeniu głębokości wody do wartości poniżej głębokości krytycznej w
przepuście. W związku z tym dolny przekrój obliczeniowy (DPK) znajduje się w pobliżu
wlotu do przepustu. W takim układzie natężenie przepływu Q można określać jak dla tzw.
wypływu niezatopionego spod zasuwy, a równanie Bernoulliego (zapisane z pominięciem
strat energii) przyjmuje następującą postać:
2
2
1
2
2
2
2
V
V
H
h
g
g
+
= +
(23)
Wartość głębokości h
2
zależy od dławienia (kontrakcji) strumienia na wlocie, co można
zapisać za pomocą relacji:
11
2
h
D
ε
= ⋅
(24)
w której
ε
jest współczynnikiem kontrakcji zależnym od stosunku głębokości wody przed
wlotem H do wysokości przepustu D (Tabela 1). Pomijając wysokość prędkości wody przed
wlotem i uwzględniając straty energii możemy zapisać następującą formułę na wydatek
przepustu:
(
)
0
2
Q
A
g H
D
µ
ε
= ⋅
− ⋅
(25)
gdzie:
µ
- współczynnik wydatku przepustu zależny od typu konstrukcji wlotowej, przyjmuje
wartości
µ
=0.58 - 0.70 (Kubrak i Kubrak, 2004),
A
0
– pole przekroju porzecznego przepustu (przy pełnym napełnieniu).
W obliczeniach dla takiego układu zamiast formuły (25) często stosuje się wzory z jednym
parametrem, uwzględniającym globalnie kontrakcję oraz straty lokalne na wlocie. Wzór tego
typu można zapisać następująco:
0
2
z
Q
A
g H
µ
=
⋅ ⋅
⋅
(26)
gdzie: µ
Z
– współczynnik wydatku przepustu, którego wartość zależy od stosunku głębokości
H do wysokości przepustu D (Tabela 2).
Tabela 1
Wartości współczynnika dławienia
ε
w zależności od parametru H/D (Sobota, 1994)
H/D
10.0
5.0
3.3
2.5
2.0
1.8
1.7
1.4
1.3
εεεε
0.615
0.620
0.625
0.630
0.645
0.650
0.660
0.690
0.705
Tabela 2
Wartości współczynnika wydatku µ
Z
dla przekroju kołowego i prostokątnego w zależności od parametru H/D
(Bodhaine, 1976)
H/D
1.5
1.6
1.7
1.8
1.9
2.0
2.5
3.0
3.5
5.0
µ
Z
0.46
0.47
0.48
0.49
0.50
0.51
0.54
0.55
0.57
0.59
12
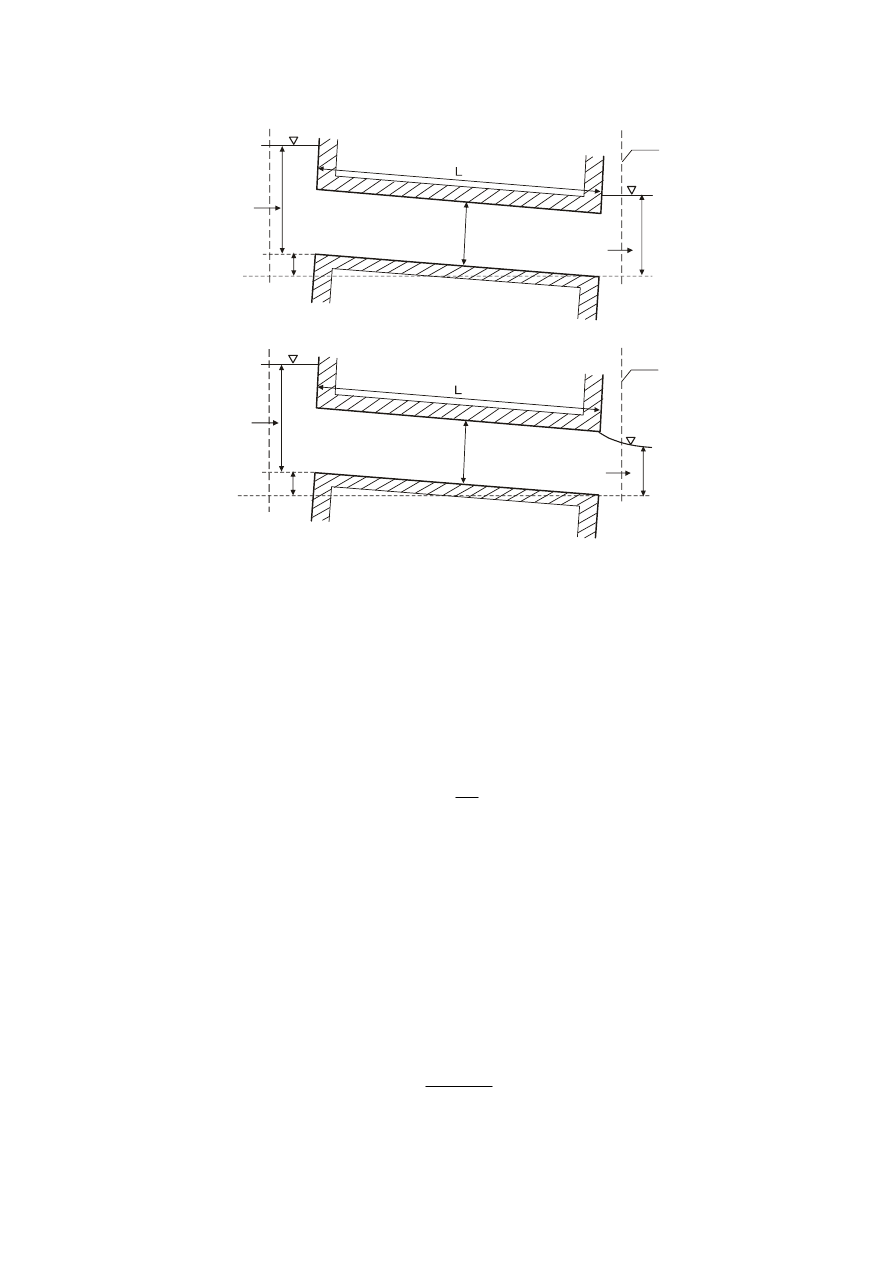
2.3. Przepływ pod ciśnieniem
Przepływ pod ciśnieniem występuje wtedy, gdy przekrój poprzeczny całkowicie
wypełniony jest wodą. W takim przypadku wlot przepustu jest zawsze zatopiony. Przyjmując
odpowiednie kryterium na zatopienie wlotu należy tutaj dodatkowo uwzględnić zatopienie
bądź niezatopienie wylotu przepustu. Zakłada się, że wlot do przepustu jest zatopiony jeśli
spełniony jest następujący warunek (Bodhaine, 1976):
H/D > 1.0
(27)
dla przypadku wylotu zatopionego (rys. 8a)
h
d
> D
(28)
Natomiast gdy wylot jest niezatopiony (rys. 8b)
h
d
< D
(29)
to należy stosować kryterium na zatopienie wlotu w postaci relacji (21), czyli:
H/D > 1.5
(30)
Natężenie przepływu w takim układzie hydraulicznym wyznaczamy jak dla przewodu
zamkniętego, tzn. pracującego pod ciśnieniem. Równanie Bernoulliego dla strumienia
przechodzącego przez przekrój 1 przed wlotem oraz przekrój 3 za wylotem (rys. 8) ma
następującą postać:
L
d
h
h
g
V
h
g
V
H
z
+
+
+
=
+
+
ζ
2
2
2
3
2
1
(31)
gdzie: V
1
– średnia prędkość w przekroju przed wlotem,
V
3
– średnia prędkość w przekroju za wylotem,
h
d
– głębokość wody za wylotem,
h
L
– wysokość strat energii na długości przepustu,
h
ζ
– całkowita wysokość strat lokalnych (miejscowych).
13
a)
b)
V
3
H
D
h
d
z
1
pp
V
1
3
DPK
V
3
H
D
h
d
z
1
pp
V
1
3
DPK
Rys. 8. Hydrauliczne warunki pracy przepustu działającego pod ciśnieniem o zatopionym wlocie oraz a)
zatopionym wylocie; b) niezatopionym wylocie.
Wysokość strat na długości h
L
można wyznaczyć na podstawie równania (18). Straty lokalne
uwzględnia się w obrębie wlotu oraz wylotu przepustu. Wysokość strat na wlocie, gdzie
występują zawirowania i miejscowy znaczny wzrost prędkości, wyznacza się na podstawie
następującej formuły:
2
1
1
2
V
h
g
ζ
ζ
=
(32)
gdzie:
ζ
1
- współczynnik strat lokalnych zależny od rodzaju wlotu (wloty opływowe
ζ
1
= 0.2;
wloty kołnierzowe
ζ
1
= 0.33; bez konstrukcji wlotowej
ζ
1
= 0.55 (Kubrak i Kubrak,
2004).
Natomiast straty na wylocie wynikające m.in. z nagłego rozszerzenia przekroju można
oszacować na podstawie następującej relacji:
(
)
2
3
3
2
V
V
h
g
ζ
−
=
(33)
14
gdzie: V – prędkość wody w przepuście.
Ponieważ zwykle prędkość w przepuście V jest znacznie większa od prędkości V
1
i V
3
(V >> V
1
i V
3
), w związku z tym można pominąć wysokość prędkości przed wlotem i za
wylotem. Wykorzystanie tego założenia oraz relacji (32) i (33) umożliwia ostatecznie
wyznaczenie natężenia przepływu dla przewodu będącego pod ciśnieniem:
(
)
0
1
1
2
1
d
L
Q
A
g H
z
h
h
ζ
=
+ − −
+
(34)
Wysokość strat lokalnych na wlocie i wylocie uwzględnia się zazwyczaj poprzez
współczynnik wydatku i wówczas odpowiednia formuła przyjmuje postać:
(
)
0
2
P
d
L
Q
A
g H
z
h
h
µ
=
⋅ ⋅
+ − −
(35)
gdzie: A
0
– pole przekroju porzecznego przepustu,
µ
P
– współczynnik wydatku przepustu.
Wartość współczynnika wydatku µ
P
zmienia się w granicach od 0.84 do 0.98 i można
go uzależnić od stopnia zaokrąglenia krawędzi wlotowej r przepustu (rys. 9) odniesionego do
jego wysokości D (Tabela 3). W przypadku wylotu niezatopionego (rys. 8b) jeśli nie znamy
głębokości h
d
, to za wartość tą można przyjąć wysokość przepustu D (h
d
= D).
D
r
Rys. 9. Zaokrąglona krawędź wlotowa przepustu
Tabela 3
Wartości współczynnika wydatku µ
p
dla przekroju kołowego i prostokątnego w zależności od parametru r/D
(Bodhaine, 1976)
r/D
0.0
0.02
0.04
0.06
0.08
0.10
0.12
µµµµ
p
0.84
0.88
0.91
0.94
0.96
0.97
0.98
15
W przypadku przepustów (dotyczy wszystkich schematów hydraulicznych), których
wloty wychodzą poza obrys ściany lub skarpy (wlot rurowy nieobudowany (rys. 2b)) należy
dokonać korekty współczynnika wydatku
.
w następujący sposób:
k
L
k
µ
µ
= ⋅
(36)
gdzie:
µ
k
– skorygowany współczynnik wydatku,
µ
– współczynnik wydatku (
µ
N
,
µ
Z
lub
µ
p
),
k
L
– parametr zależny od stosunku długości wystającej części przepustu L
p
do jego
wysokości D
(tabela 4).
Tabela 4
Wartości parametru k
L
w zależności od wartości L
P
/D dla przepustu z wlotem rurowym nieobudowanym
(Bodhaine, 1976).
L
P
/D 0.00
0.01
0.02
0.04
0.06
0.08
0.1
0.2
0.4
0.8
1.0
k
L
1.00
0.99
0.98
0.97
0.95
0.94
0.92
0.92
0.91
0.90
0.90
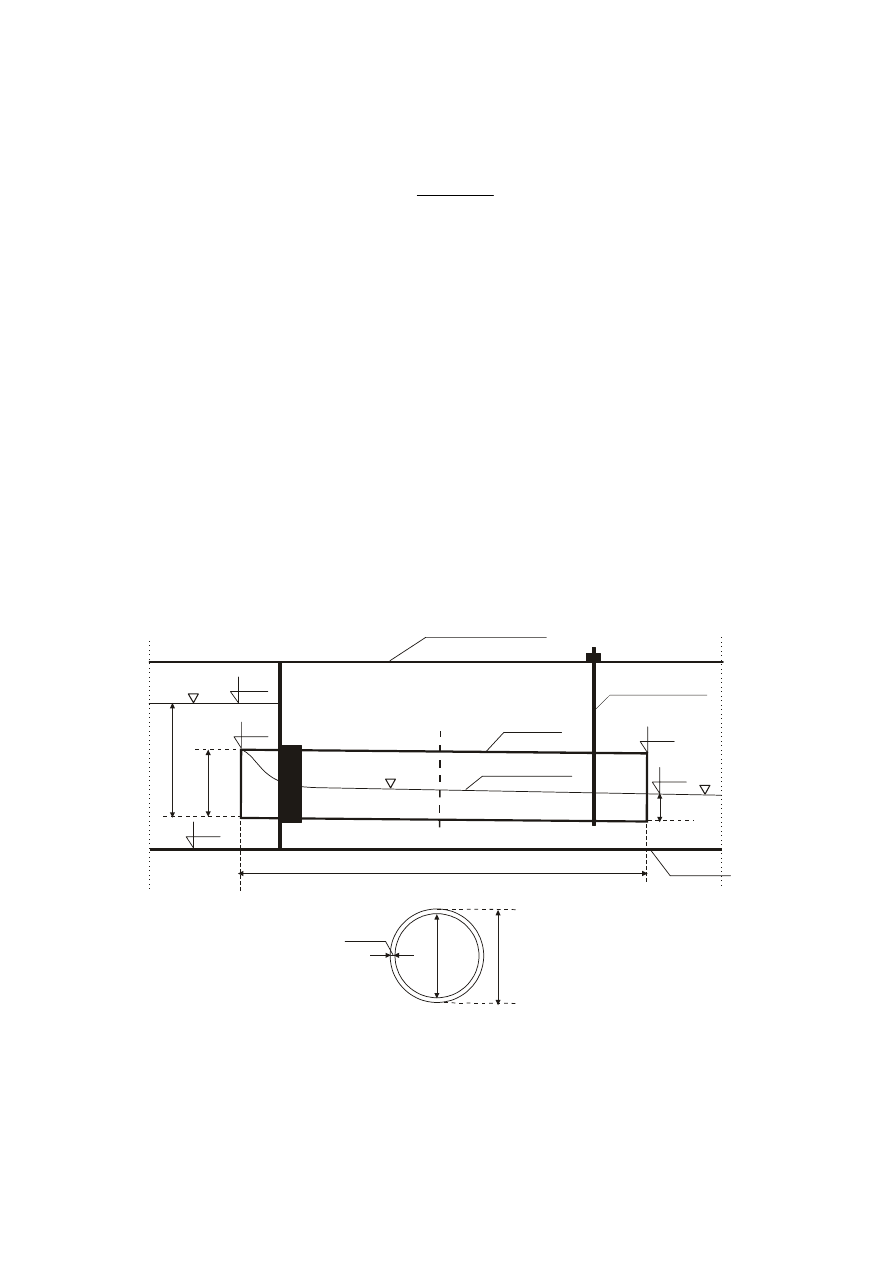
W tabeli 5 zestawiono podstawowe schematy hydrauliczne wraz z kryteriami jakie
muszą być spełnione, aby dany schemat można było przyjąć do obliczeń.
Tabela 5
Zestawienie schematów hydraulicznych wraz z kryteriami oraz formułami na wyznaczenie wydatku przepustu
Schemat hydrauliczny
Kryterium
DPK
Formuła
H/D < 1.5
h
d
< h
kr
i
0
> i
kr
wlot
2
1
2
2
N
kr
kr
V
Q
A
g H
h
g
µ
=
⋅
+
−
H/D < 1.5
h
d
< h
kr
i
0
< i
kr
wylot
2
1
2
2
N
kr
kr
L
V
Q
A
g H
z
h
h
g
µ
=
⋅
+ +
−
−
Niezatopiony
wlot i wylot
H/D < 1.5
D > h
d
> h
kr
wylot
2
1
2
2
N
d
d
L
V
Q
A
g H
z
h
h
g
µ
=
⋅
+ +
− −
P
rz
ep
ły
w
z
e
sw
o
b
o
d
n
ą
p
o
w
ie
rz
ch
n
ią
Zatopiony
wlot
H/D > 1.5
h
d
< h
wlot
0
2
Z
Q
A
g H
µ
= ⋅
⋅
Zatopiony
wlot i wylot
H/D > 1.0
h
d
> D
wylot
(
)
0
2
P
d
L
Q
A
g H
z
h
h
µ
=
⋅
+ − −
P
rz
ep
ły
w
p
o
d
ci
śn
ie
n
ie
m
Zatopiony
wlot oraz
niezatopiony
wylot
H/D > 1.5
h
d
< D
wylot
(
)
0
2
P
L
Q
A
g H
z
D
h
µ
=
⋅
+ − −
DPK – dolny przekrój kontrolny
16
W celu wyznaczenia spadku krytycznego i
kr
można posłużyć się przekształconym
równaniem Manninga zapisanym w następującej formie:
2
2
4/3
2
kr
kr
kr
n Q
i
R
A
⋅
=
⋅
(37)
3. Opis stanowiska badawczego
Stanowisko badawcze składa się z przepustu o przekroju kołowym, który umieszczony
jest w kanale o przekroju prostokątnym. Schemat stanowiska przedstawiono na rysunku 10.
Przepust ma możliwość regulowania nachylenia (spadku) za pomocą odpowiedniego uchwytu
zainstalowanego w pobliżu wylotu przepustu.
Woda do kanału doprowadzana jest
rurociągiem, który wyposażony jest w zasuwę pozwalającą na regulowanie natężenie
przepływu (wydatku). Kanał zakończony jest ruchomą klapą, która umożliwia podpiętrzenie
wody w celu zatopienia wylotu z przepustu. Woda z kanału odprowadzana jest poprzez
skrzynię przelewową wyposażoną w przelew pomiarowy typu Thomsona, który służy do
pomiaru natężenia przepływu wody przepływającej przez kanał oraz przepust. Pomiar układu
zwierciadła wody jest wykonywany za pomocą szpilek wodowskazowych znajdujących się na
ruchomym wózku.
L = 205 cm
dno kanału
D
R
D
poziom maksymalnego
napełnienia kanału
R
WG
R
z1
R
z2
R
WD
H
h
d
przepust
profil zw. wody
A
A
D
A-A
e
regulacja spadku
D
zew
Rys.10. Schemat stanowiska pomiarowego.
17
4. Wykonanie ćwiczenia
W ćwiczeniu należy kolejno zbadać trzy podstawowe układy hydrauliczne:
I. Przepływ ze swobodnym zwierciadłem, niezatopiony wlot i wylot przepustu
1) Zmierzyć średnicę zewnętrzną D
zew
i wewnętrzną D przepustu oraz ustawić odpowiedni
spadek przepustu i (wartość zadana przez prowadzącego). Pomierzyć rzędną dna kanału R
D
oraz rzędne przepustu R
z1
oraz R
z2
w dwóch skrajnych przekrojach w celu precyzyjnego
określenia spadku przepustu i;
2) Za pomocą zasuwy ustawić natężenie przepływu tak, aby wlot i wylot przepustu były
niezatopione (odpowiednio warunek H/D
≤
1.5 oraz h
d
< D). Po ustaleniu się przepływu
zmierzyć rzeczywiste natężenie przepływu Q
rzecz
za pomocą przelewu Thomsona (patrz
rozdział II/4 w pracy [1]);
3) Za pomocą szpilki wodowskazowej pomierzyć rzędną zwierciadła wody przed wlotem R
WG
i za wylotem przepustu R
WD
. Pomiar przed wlotem wykonać w odległości co najmniej 3D od
wlotu;
4) Czynności z punktów od 2) do 3) powtórzyć trzykrotnie dla coraz większych natężeń
przepływu z zachowaniem warunku niezatopionego wlotu H/D
≤
1.5. Wyniki pomiarów wraz
z ewentualnymi uwagami zanotować w tabeli 6;
5) Dla jednego z wydatków pomierzyć profil podłużny zwierciadła wody w przepuście.
Wyniki pomiarów oraz obserwacji dotyczące np. powstania odskoku hydraulicznego lub
innych struktur hydraulicznych zanotować w tabeli 7.
II. Zatopiony wlot i niezatopiony wylot przepustu
1) Za pomocą zasuwy ustawić natężenie przepływu tak aby wlot przepustu był zatopiony, tzn.
głębokość spiętrzonej wody przed wlotem H (w odniesieniu do dna przepustu) spełniała
warunek H/D
≥
1.5. Po ustaleniu się przepływu zmierzyć rzeczywiste natężenie przepływu
Q
rzecz
za pomocą przelewu Thomsona;
2) za pomocą szpilki wodowskazowej pomierzyć rzędną zwierciadła wody przed wlotem R
WG
i za wylotem przepustu R
WD
;
3) Czynności z punktów od 1) do 2) powtórzyć trzykrotnie dla coraz większych natężeń
przepływu z zachowaniem warunku zatopionego wlotu H/D
≥
1.5. Wyniki pomiarów wraz z
ewentualnymi uwagami zanotować w tabeli 6;
4) Dla jednego z wydatków pomierzyć profil zwierciadła wody w przepuście. Wyniki
pomiarów oraz obserwacji dotyczące np. powstania odskoku hydraulicznego lub innych
struktur hydraulicznych zanotować w tabeli 8;
18
III. Przepływ pod ciśnieniem, zatopiony wlot i wylot
1) Za pomocą zasuwy regulującej natężenie przepływu oraz klapy znajdującej się na końcu
kanału ustawić takie warunki przepływu, aby wlot i wylot przepustu były zatopione. Po
ustaleniu się przepływu zmierzyć rzeczywiste natężenie przepływu Q
rzecz
za pomocą przelewu
Thomsona;
2) Za pomocą szpilki wodowskazowej pomierzyć rzędną zwierciadła wody przed wlotem R
WG
i za wylotem przepustu R
WD
;
3) Czynności z punktów od 1) do 2) powtórzyć trzykrotnie dla coraz większych natężeń
przepływu. Wyniki pomiarów zanotować w tabeli 6;
5. Opracowanie wyników pomiarów
Na podstawie wyników doświadczenia należy:
1) Obliczyć spadek przepustu i wykorzystując równanie:
1
2
100%
z
z
R
R
i
L
−
=
⋅
(38)
gdzie: R
z1
– rzędna przepustu w przekroju wlotowym (rys. 10),
R
z2
– rzędna przepustu w przekroju wylotowym,
L
– długość przepustu.
2) Obliczyć głębokość wody przed wlotem H oraz głębokość wody za wylotem h
d
według
relacji:
1
WG
z
H
R
R
D
e
=
−
+ +
,
2
d
WD
z
h
R
R
D
e
=
−
+ +
(39a,b)
gdzie: R
WG
– rzędna wody górnej przed wlotem,
R
WD
- rzędna wody dolnej za wylotem,
R
z1
– rzędna przepustu w przekroju wlotowym,
R
z2
- rzędna przepustu w przekroju wylotowym,
D
– średnica wewnętrzna przepustu (rys. 10),
e
– grubość ścianki przepustu.
3) Określić schemat hydrauliczny w jakim pracuje przepust poprzez sprawdzenie
odpowiednich kryteriów (tabela 5) oraz zapisać wyniki w tabeli 6;
19
4) Dla każdego wydatku rzeczywistego Q
rzecz
obliczyć wydatek przepustu Q według formuły
odpowiadającej danemu schematowi hydraulicznemu (równania (5), (20), (26) lub (35));
5) Obliczyć błąd względny wyznaczenia wydatku według formuły:
100%
rzecz
rzecz
Q
Q
Q
Q
−
∆ =
⋅
(40)
gdzie: Q
rzecz
- wydatek rzeczywisty pomierzony za pomocą przelewu Thomsona,
Q
– wydatek obliczony.
6) Na podstawie wyników zawartych w tabelach 6 i 7 narysować profil zwierciadła oraz linię
głębokości krytycznych. Głębokość krytyczną obliczyć na podstawie równania (11). Rysunki
wykonać w odpowiedniej skali;
6. Zawartość sprawozdania
Sprawozdanie powinno zawierać:
1) krótkie wprowadzenie teoretyczne;
2) szkic stanowiska doświadczalnego;
3) przykłady obliczeniowe;
4) tabele pomiarów i obliczeń;
5) rysunki profilu zwierciadła wody dla przepływu ze swobodnym zwierciadłem wody dla
schematu z niezatopionym wlotem i wylotem oraz dla schematu z zatopionym wlotem i
niezatopionym wylotem, na rysunkach zaznaczyć głębokość krytyczną;
6) wnioski zawierające komentarz dotyczący uzyskanych wyników.
7. Przydatne informacje do wykonania ćwiczenia
Współczynniki oporów lokalnych oraz oporów liniowych przy przepływie cieczy w
rurociągach i kanałach otwartych
- należy zapoznać się z rozdziałem II/3 w pracy [1].
Zasada pomiaru natężenia przepływu za pomocą przelewu Thomsona
- należy
zapoznać się z rozdziałem II/4 w pracy [1].
Podstawy teoretyczne przepływu wody w kanałach otwartych
- należy zapoznać się z
rozdziałem III/4.1 w pracy [1].
20
Literatura
[1] Weinerowska K.: Laboratorium z mechaniki płynów i hydrauliki, Politechnika Gdańska,
Gdańsk 2004 (skrypt wydany w formie elektronicznej).
[2] Bodhaine G. L.: Measurement of Peak Discharge At Culverts by Indirect Methods.
Techniques of Water Resources Investigation of the United States Geological Survey.
U.S.
Geological Survey, Washington 1976.
[3] Kubrak E. i Kubrak J.: Hydraulika techniczna – przykłady obliczeń, Wydawnictwo
SGGW, Warszawa 2004.
[4] Sobota J.: Hydraulika. Wydawnictwo Akademii Rolniczej we Wrocławiu, Wrocław 1994.
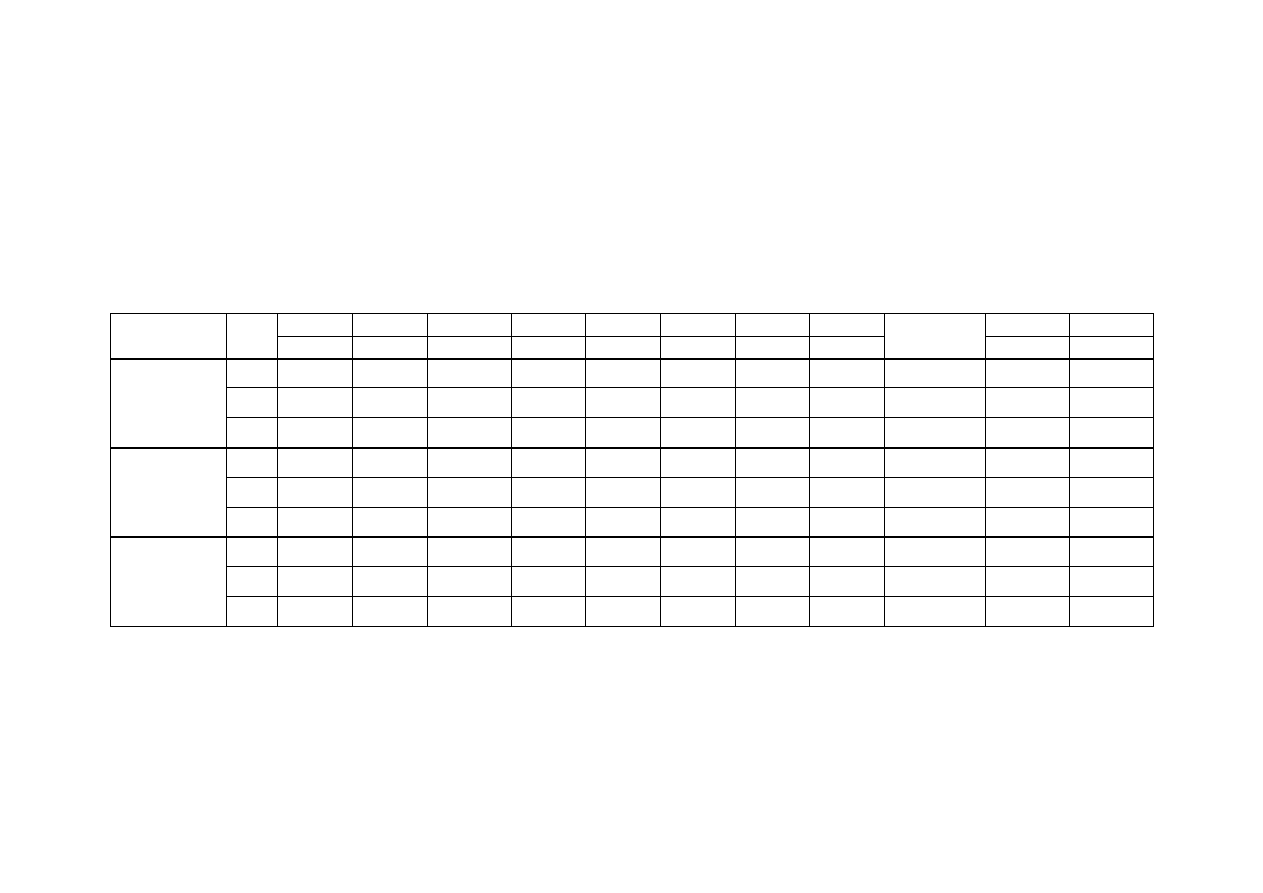
21
Tabela 6
Wyniki pomiarów i obliczeń dla poszczególnych schematów hydraulicznych przepływu przez przepust
Rzędna zera przelewu Thomsona: O
T
= …..... cm Średnica wewnętrzna przepustu: d = …….. cm
Średnica zewnętrzna przepustu: D = …….. cm
Rzędna dna kanału: R
D
= …….. cm
Rzędna przepustu w przekroju wlotowym: R
z1
= …….. cm
Rzędna przepustu w przekroju wylotowym: R
z2
= …….. cm
Spadek przepustu: i = ……… %
R
T
h
T
Q
rzecz
R
WG
H
R
WD
h
d
h
kr
Q
∆∆∆∆
Q
Schemat
hydrauliczny
Lp
[cm]
[cm]
[dm
3
/s]
[cm]
[cm]
[cm]
[cm]
[cm]
kryterium
[dm
3
/s]
[%]
1
2
3
4
5
6
7
8
9
R
T
- rzędna zwierciadła wody na przelewie Thomsona
h
T
- obciążenie przelewu Thomsona, h
T
= R
T
- O
T
R
WG
- rzędna wody górnej przed wlotem
R
WD
- rzędna wody dolnej za wylotem
H - głębokość wody przed wlotem (w odniesieniu do dna przepustu)
h
d
- głębokość wody za wylotem (w odniesieniu do dna przepustu)
h
kr
- głębokość krytyczna
22
Tabela 7
Pomiar profilu podłużnego zwierciadła wody dla przepływu ze swobodnym zwierciadłem (niezatopiony wlot i wylot)
Określenie wydatku przelewem Thomsona
Obciążenie przelewu Thomsona: h
T
= …….. cm
Rzeczywiste natężenie przepływu: Q
rzecz
= …….. dm
3
/s
Nr punktu
1
2
3
4
5
6
7
8
9
10
Odległość [cm]
Rzędna zw. wody Rw [cm]
Głębokość wody h [cm]
Uwagi
Tabela 8
Pomiar profilu podłużnego zwierciadła wody dla przepływu ze swobodnym zwierciadłem (zatopiony wlot, niezatopiony wylot)
Określenie wydatku przelewem Thomsona
Obciążenie przelewu Thomsona: h
T
= …….. cm
Rzeczywiste natężenie przepływu: Q
rzecz
= …….. dm
3
/s
Nr punktu
1
2
3
4
5
6
7
8
9
10
Odległość [cm]
Rzędna zw. wody Rw [cm]
Głębokość wody h [cm]
Uwagi