Fizyka Ciała Stałego

Ć

wiczenie Nr 5

CHARAKTERYSTYKA FOTOOPORNIKA

,

ZJAWISKO FOTOELEKTRYCZNE WEWNĘTRZNE

2

3

1

.

Cel ćwiczenia

1.

Zapoznanie się ze zjawiskiem fotoelektrycznym wewnętrznym.

2.

Wykonanie charakterystyk prądowo-napięciowych.

3.

Wykonanie charakterystyki świetlnej.

2. Wprowadzenie

Fotoopornik to półprzewodnik, którego działanie jest oparte na zjawisku fotoelektrycznym

wewnętrznym tj. na właściwości zmiany oporu elektrycznego półprzewodnika pod wpływem
promieniowania elektromagnetycznego jak schematycznie przedstawiono na rys. 1.

Rys. 1. Schemat budowy i działania
fotoopornika.

Zmianę oporu elektrycznego półprzewodnika pod wpływem promieniowania można wyjaśnić tym,

ż

e fotony przenikające do półprzewodnika, wytwarzają w nim swobodne nośniki ładunku: elektrony i

dziury. Zwiększenie koncentracji swobodnych nośników ładunku pociąga za sobą zwiększenie
przewodnictwa półprzewodnika. Istnieją jednak granice fotoczułości półprzewodnika. Gdy foton o
energii E = hν pada na warstwę półprzewodnika, to w wyniku oddziaływania z materiałem i jego
strukturą elektronową przekazuje materii całą swoją energię. Wzbudzenie elektronu - swobodnego
nośnika jest możliwe tylko wtedy, gdy energia fotonu hν jest co najmniej równa energii aktywacji ∆E
swobodnych nośników ładunku w danym półprzewodniku. Dla półprzewodników samoistnych powinien
być spełniony warunek hν ≥ ∆E, dla domieszkowanych zaś hν ≤ ∆E

d

. Istnieje zatem pewna graniczna

częstotliwość światła ν

gr

, dla której fotoprzewodnictwo danego półprzewodnika występuje. Przy

częstotliwości padającego światła mniejszej od ν

gr

, fotoprzewodnictwo nie istnieje.

Istnieje duża różnorodność fotooporników, szczególnie gdy klasyfikujemy je pod względem zakresu

fotoczułości, ponieważ energia niezbędna do wytworzenia swobodnych nośników w półprzewodniku
zawiera się w przedziale energii od kilku elektronowoltów (eV) do dziesiątych części eV.
Podczas oświetlania półprzewodnika światłem o częstotliwości ν > ν

gr

, część energii fotonu jest

zużywana na pokonanie bariery energetycznej ∆E i przejście elektronu do pasma przewodnictwa,
natomiast pozostała część jest przekazywana elektronowi w postaci energii kinetycznej E

k

zgodnie z

podstawowym równaniem:

hν = ∆E + E

k

.

(1)

Nadmiar energii kinetycznej fotoelektronu w stosunku do średniej energii drgań cieplnych w krysztale
jest przekazywany sieci na zwiększenie energii jej drgań (kryształ się ogrzewa). Fotoaktywność
półprzewodnika dla światła o częstotliwości w zakresie ν >> ν

gr

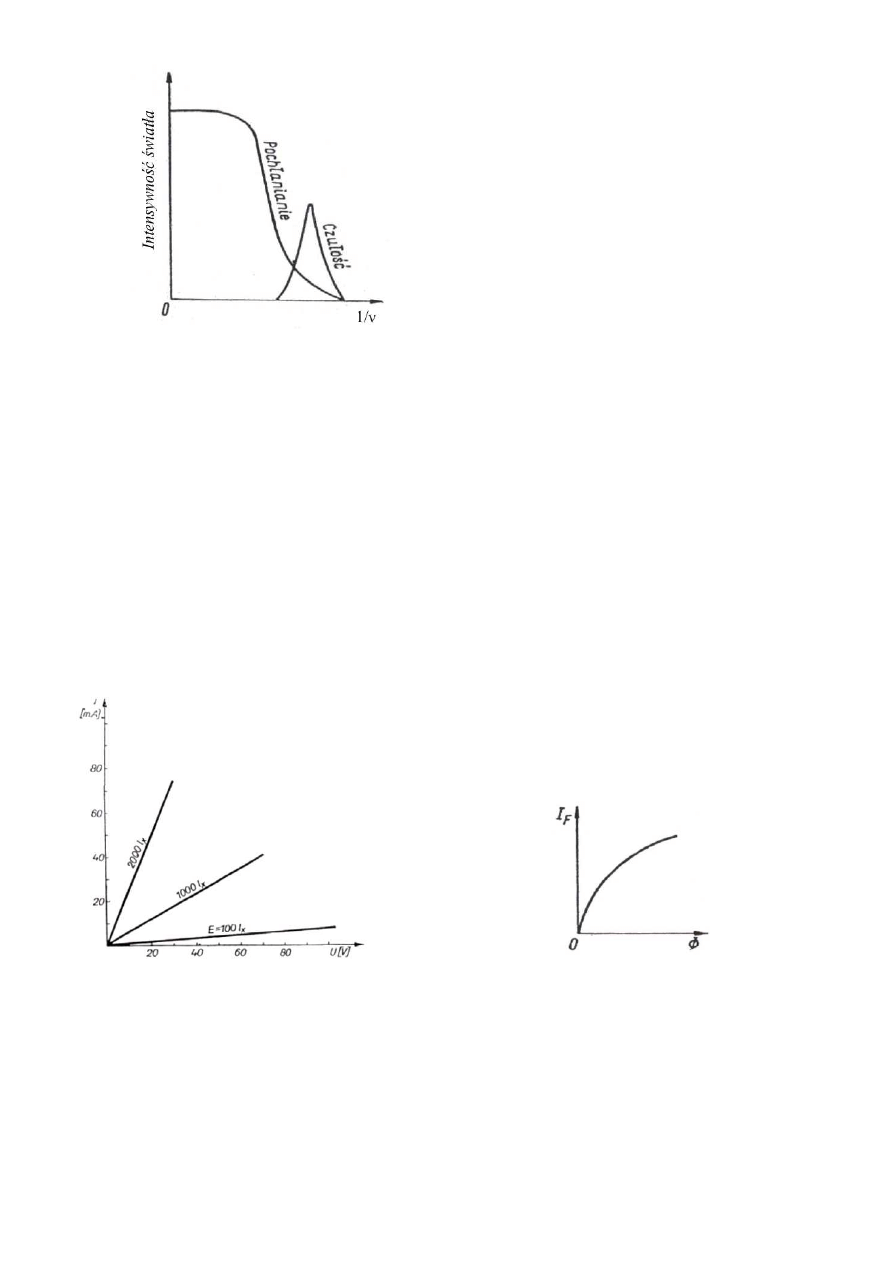
maleje. Jedna z krzywych na rys. 2

przedstawia wykres absorpcji światła w krysztale zależności od 1/ν, natomiast druga przedstawia czułość
tj. zależność fotoprzewodnictwa od 1/ν.

4

Rys. 2. Schematyczne przedstawienie fotoaktywności
półprzewodnika.

Wzrost współczynnika absorpcji światła o wysokiej ν powoduje, że światło jest pochłaniane w

bardzo cienkiej warstwie, wówczas zmiana oporu tej warstwy powierzchniowej nie może w istotny
sposób wpływać na objętościowy opór półprzewodnika. Powoduje to powstanie granicy czułości
fotoprzewodnika od strony małej wartości 1/ν. Ponieważ energia niezbędna do wytworzenia swobodnych
nośników w półprzewodniku samoistnym zawiera się w przedziale energii od kilku elektronowoltów do
dziesiątych części elektronowolta, długofalowa (małe wartości ν) granica fotoprzewodnictwa dla
półprzewodników samoistnych leży w widzialnym lub podczerwonym obszarze widma. Na przykład dla

półprzewodnika o ∆E = 2 eV, częstotliwość graniczna wynosi ν

gr

= 5

—10

14

s

-1

, co odpowiada fali o

długości 6000 Å. Granica czułości od strony małych ν odpowiada małej energii.

Dla scharakteryzowania fotoopornika półprzewodnikowego wykonamy charakterystyki prądowo-

napięciowe oraz charakterystyki świetlne. Charakterystyka prądowo-napięciowa przy stałym natężeniu
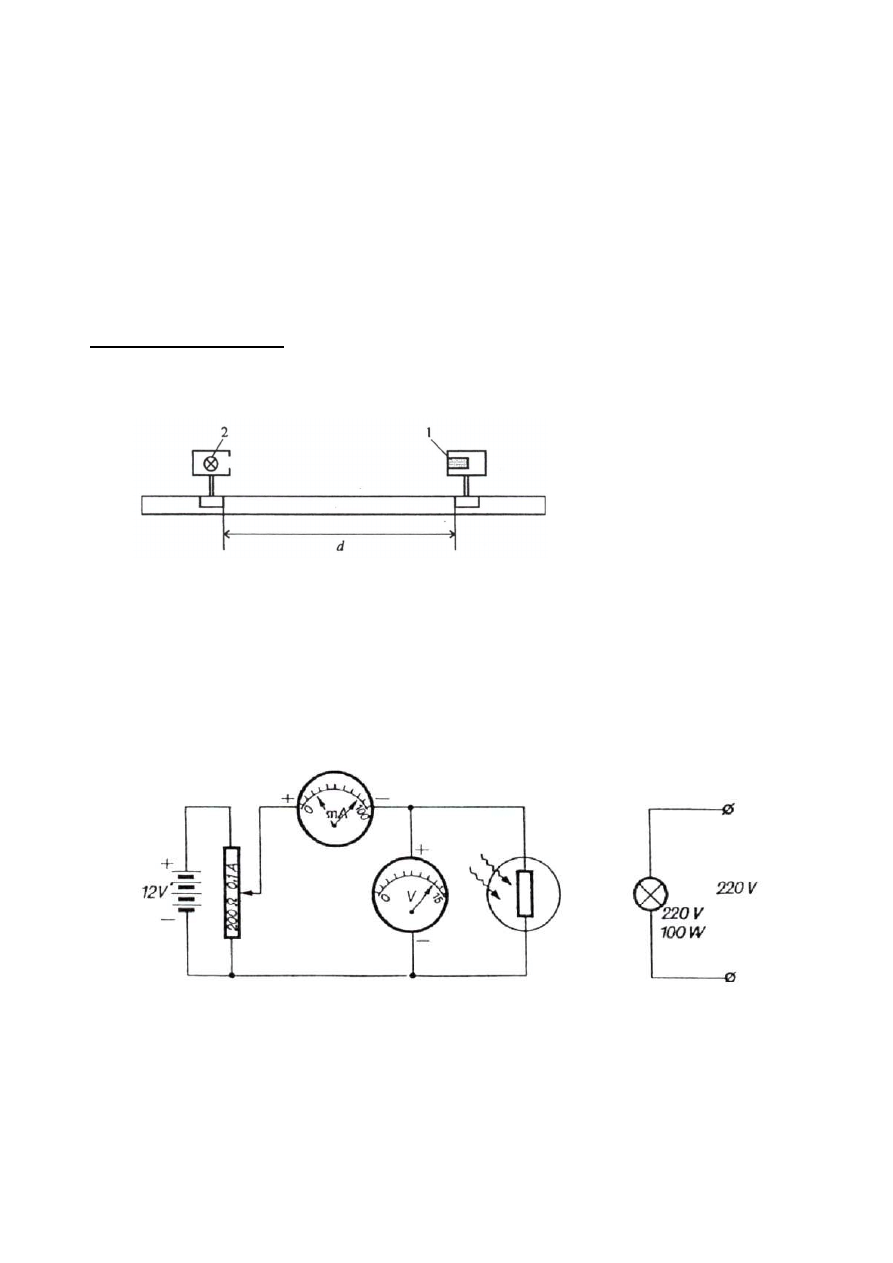
oświetlenia przedstawiona na rys. 3 ma charakter funkcji liniowej. Pochodzenie zależności liniowej
natężenia prądu od napięcia przyłożonego jest oczywiste, gdyż przy stałej wartości natężenia oświetlenia
fotorezystor zachowuje się jak zwykły rezystor.

Rys. 3. Przykładowe charakterystyki prądowo-

napięciowe fotoopornika.

Rys. 4. Charakterystyka świetlna fotoopornika.

Charakterystyka świetlna fotoopornika, czyli zależność natężenia prądu przepływającego przez fotoopór
od natężenia oświetlenia (przy stałym napięciu), przedstawiona na rys. 4, ma charakter funkcji
nieliniowej. Wynika, to ze złożoności wewnętrznego zjawiska fotoelektrycznego. Praktycznie
obserwowana na rys. 4 krzywa może być przedstawiona następującą funkcją:

5

a

F

D

I

Φ

=

,

(2)

gdzie: I

F

– natężenie fotoprądu

Φ

– natężenie oświetlenia

D i a – stałe zależne od fizycznych właściwości fotoopornika, przy czym 0 < a < 1.

Po zlogarytmowaniu wyrażenia (2) otrzymujemy wyrażenie (3):

logI

F

= D + a

—logΦ

(3)

Zależność ta pozwoli nam na określenie stałej a, charakterystycznej dla badanego fotoopornika.

3. Wykonanie ćwiczenia

3.1 Zestawiamy układ pomiarowy wg schematu przedstawionego na rys. 5.

Rys. 5. Schemat układu
pomiarowego.

Zestaw pomiarowy składa się z ławy optycznej, na której umieszczony jest fotoopornik 1 w
odpowiedniej oprawie oraz źródło światła 2 o znanej luminancji świetlnej. W skład zestawu
pomiarowego wchodzi zasilacz oraz mierniki: natężenia prądu i napięcia. Źródłem światła jest
ż

arówka umieszczona w oprawie. Bezpośredni pomiar odległości d fotoopornika od źródła światła

jest dość kłopotliwy i może powodować duże błędy. Ominęliśmy te kłopoty skalując położenia na
ławie optycznej w luksach (lx).

3.2

Wykonanie charakterystyk prądowo-napięciowych.

Rys. 6. Schemat obwodu elektrycznego do badania charakterystyk prądowo-napięciowych

fotoopornika.

3.3

Zestawiamy układ pomiarowy wg przedstawionego na rys. 6 schematu obwodu elektrycznego.

3.4

Wykonujemy pomiary natężenia prądu dla fotoopornika 1 zmieniając napięcie o 1V w zakresie od

1V do 8V. Pomiary dla charakterystyki prądowo-napięciowej wykonujemy przy stałym natężeniu
oświetlenia. Powtarzamy dla wartości natężenia oświetlenia wskazanych przez prowadzącego.
Wyniki zapisujemy w Tabeli 1.

6

Tabela 1

Natężenie oświetlenia

Napięcie [mV]

Natężenie prądu [mA]

3.5

Wykonujemy analogiczne pomiary dla fotoopornika 2.

3.6

Wykonujemy wykres I

A

= f(U) jak przedstawiono na rys. 3.

3.7

Wykonanie charakterystyk świetlnych.

3.8

Wykonujemy pomiary natężenia prądu fotoelektrycznego dla fotooporu 1 dla różnych natężeń

oświetlenia. Natężenie oświetlenia zmieniamy przez zmianę położenia fotooporu względem
ż

arówki (na ławie optycznej).

3.9

Uzyskane wyniki pomiarów zapisujemy w Tabeli 2.

Tabela 2

Natężenie oświetlenia

Φ

[lx]

Natężenie prądu

I

F

[mA]

Log I

F

Log Φ

3.10

Wykonujemy analogiczne pomiary dla fotooporu 2.

3.11

Wykonujemy wykresy zależności I

F

= f(Φ) oraz logI

F

= f(logΦ).

3.12

Z nachylenia wykresu logI

F

= f(logΦ) określamy stałą materiałową a dla dwu badanych

fotooporów.

4.

Sprawozdanie powinno zawierać:

1.

Wyniki pomiarów charakterystyk prądowo-napięciowych zestawione w Tabeli 1.

2.

Wykresy I

F

= f(U).

3.

Wyniki pomiarów charakterystyk świetlnych zestawione w Tabeli 2.

4.

Wykresy I

F

= f(Φ) oraz logI

F

= f(logΦ).

5.

Wyniki obliczeń stałych materiałowych dla dwu fotooporów z uwzględnieniem błędu pomiarów.

6.

Dyskusję wyników i wnioski.

Literatura

Instrukcje do ćwiczeń z Pracowni Fizycznej