Fizyka Ciała Stałego

Ć

wiczenie Nr 4

POMIAR TEMPERATURY TOPNIENIA CIAŁ

KRYSTALICZNYCH

PRZY UŻYCIU TERMOPARY

2

3

1.

Cel ćwiczenia

1. Zapoznanie się ze zjawiskiem termoelektrycznym (zjawisko Seebecka).
2. Cechowanie termoogniwa i użycie go do pomiarów temperatury topnienia ciał krystalicznych.
3. Wykonanie pomiarów zdolności termoelektrycznej termoogniwa.
4. Wyznaczenie względnej koncentracji elektronów swobodnych badanego termoogniwa.

2.

Wprowadzenie

Termoogniwo. Zjawisko Seebecka

Ogniwo termoelektryczne stanowi układ różnych przewodników lub półprzewodników,

przekształcających energię procesów cieplnych w energię elektryczną. Jego działanie jest praktycznym
wykorzystaniem zjawiska Seebecka, polegającym na powstaniu siły elektromotorycznej w zamkniętym
obwodzie złożonym z różnych przewodników, jeśli miejsca ich połączeń mają różne temperatury.
Powstającą w takim obwodzie siłę elektromotoryczną nazywa się SEM termoelektryczną.

Mechanizm powstania SEM termoelektrycznej można wyjaśnić na podstawie klasycznej teorii

przewodnictwa elektronowego metali. Zgodnie z tą teorią, w węzłach sieci krystalicznej metalu znajdują
się jony dodatnie, pomiędzy którymi poruszają się elektrony uwolnione z powłok walencyjnych atomów.
Swobodne elektrony znajdują się w stanie bezładnego ruchu cieplnego, tworząc w metalach gaz
elektronowy podlegający prawom gazowym. Koncentracja swobodnych elektronów (tj. liczba elektronów
przewodnictwa zawartych w jednostce objętości metalu) zależy od struktury fizyko-chemicznej
przewodnika (dla metali jest rzędu 10

24

– 10

28

m

–3

).

W najprostszym przypadku ogniwo termoelektryczne składa się z dwóch różnych, spojonych ze

sobą metali, tworzących obwód zamknięty. Spajając ze sobą dwa różne metale, umożliwia się migrację
gazu elektronowego przez powierzchnię styku. Przy nieuporządkowanym ruchu cieplnym, najszybsze
elektrony będą przechodziły z jednego metalu do drugiego. Migracja ta zachodzi w obu kierunkach przy
czym z uwagi na różne prawdopodobieństwa przejść elektronów przez powierzchnię styku, jeden z metali
uzyskuje ładunek dodatni a drugi ujemny. Miedzy metalami powstaje różnica potencjałów zwana
napięciem kontaktowym. Napięcie kontaktowe warunkowane jest różnymi pracami wyjścia „A” elektronu
z metali i różną koncentracja „n” swobodnych elektronów. Pracę wyjścia z metalu nazywamy pracą jaką
musi wykonać elektron znajdujący się na powierzchni metalu aby wydostać się na zewnątrz pokonując
działanie sił wywieranych przez jony sieci krystalicznej, których wypadkowa jest skierowana do wnętrza
metalu.

Załóżmy, że praca wyjścia A

1

elektronów z metalu M

1

jest mniejsza od pracy wyjścia A

2

z metalu

M

2

. Po spojeniu tych metali, elektrony o odpowiednio dużej energii ruchu cieplnego mogą przechodzić

przez powierzchnię styku, jednakże w jednostce czasu więcej elektronów z metalu M

1

przejdzie do

metalu M

2

niż z metalu M

2

do M

1

. W skutek tego metal M

1

uzyskuje ładunek dodatni, a metal M

2

–

ujemny. Pomiędzy metalami powstaje różnica potencjałów

e

A

A

V

1

2

'

−

=

∆

,

(1)

gdzie e jest ładunkiem elektronu.

W przypadku, gdy połączone ze sobą metale mają różne koncentracje swobodnych elektronów np.:

n

1

> n

2

, zachodzi ukierunkowana migracja elektronów przez powierzchnię styku. W jednostce czasu

4

więcej elektronów przechodzi z metalu M

1

do metalu M

2

niż w kierunku przeciwnym. W wyniku tego

dyfuzyjnego przejścia, metale ładują się różnoimiennie a na ich granicy wytwarza się różnica potencjałów

2

1

ln

'

'

n

n

e

kT

V

=

∆

,

(2)

której wartość zależy tylko od temperatury T, ponieważ stosunek koncentracji n

1

/n

2

jest stały dla danej

pary spojonych metali (k - stała Boltzmana).

Napięcie kontaktowe U

k

jest sumą ∆V’ i ∆V” :

2

1

1

2

ln

)

(

n

n

e

kT

e

A

A

T

U

k

+

−

=

.

(3)

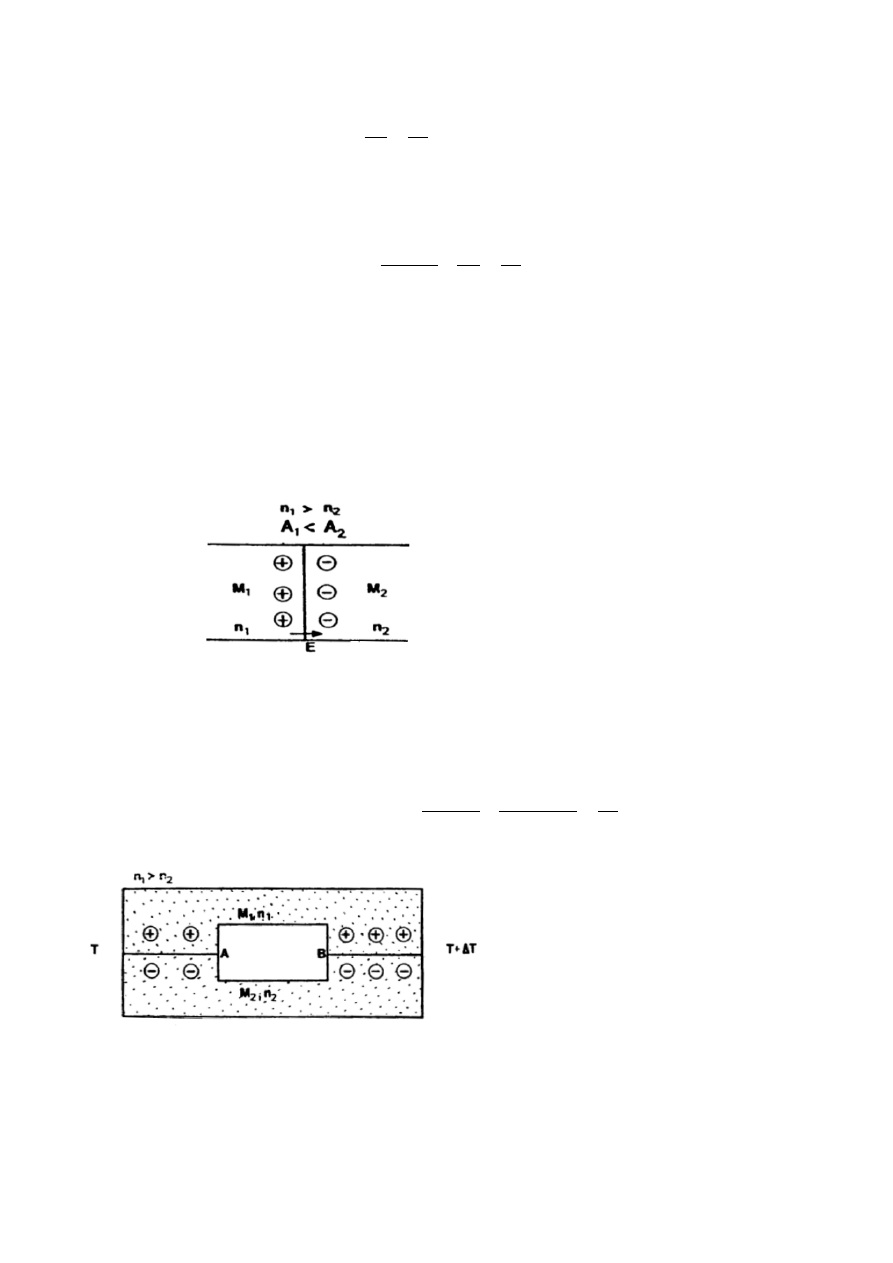
Z przedstawionych wyżej faktów wynika, że po spojeniu ze sobą dwóch różnych metali następuje

chwilowy, ukierunkowany przepływ elektronów przez powierzchnię styku, przy czym jego kierunek
zależy od wartości prac wyjścia i koncentracji swobodnych elektronów. W kierunku tego przepływu
powstaje napięcie kontaktowe U

k

wytwarzające pole elektryczne na styku metali (rys. 1). Pole elektryczne

utrudnia migrację elektronów z metalu M

1

do metalu M

2

a ułatwia w kierunku przeciwnym. W spojeniu

osiągnięty zostaje po pewnym czasie stan równowagi dynamicznej, w którym liczba elektronów
migrujących w obu kierunkach jest taka sama, pomimo wyższej koncentracji swobodnych elektronów w
metalu M

1

.

Rys. 1. Spojenie dwóch metali.

Stan równowagi dynamicznej może być naruszony tylko w przypadku zmiany temperatury spojenia.
Podwyższenie temperatury o ∆T prowadzi do lokalnego wzrostu energii ruchu cieplnego elektronów,
umożliwiając elektronom metalu M

1

pokonanie hamującego działania pola elektrycznego. W spojeniu

zachodzi ukierunkowany przepływ elektronów z metalu M

1

do M

2

aż do momentu, w którym napięcie

kontaktowe osiągnie następującą wartość:

2

1

1

2

ln

)

(

)

(

n

n

e

T

T

k

e

A

A

T

T

U

k

∆

+

+

−

=

∆

+

.

(4)

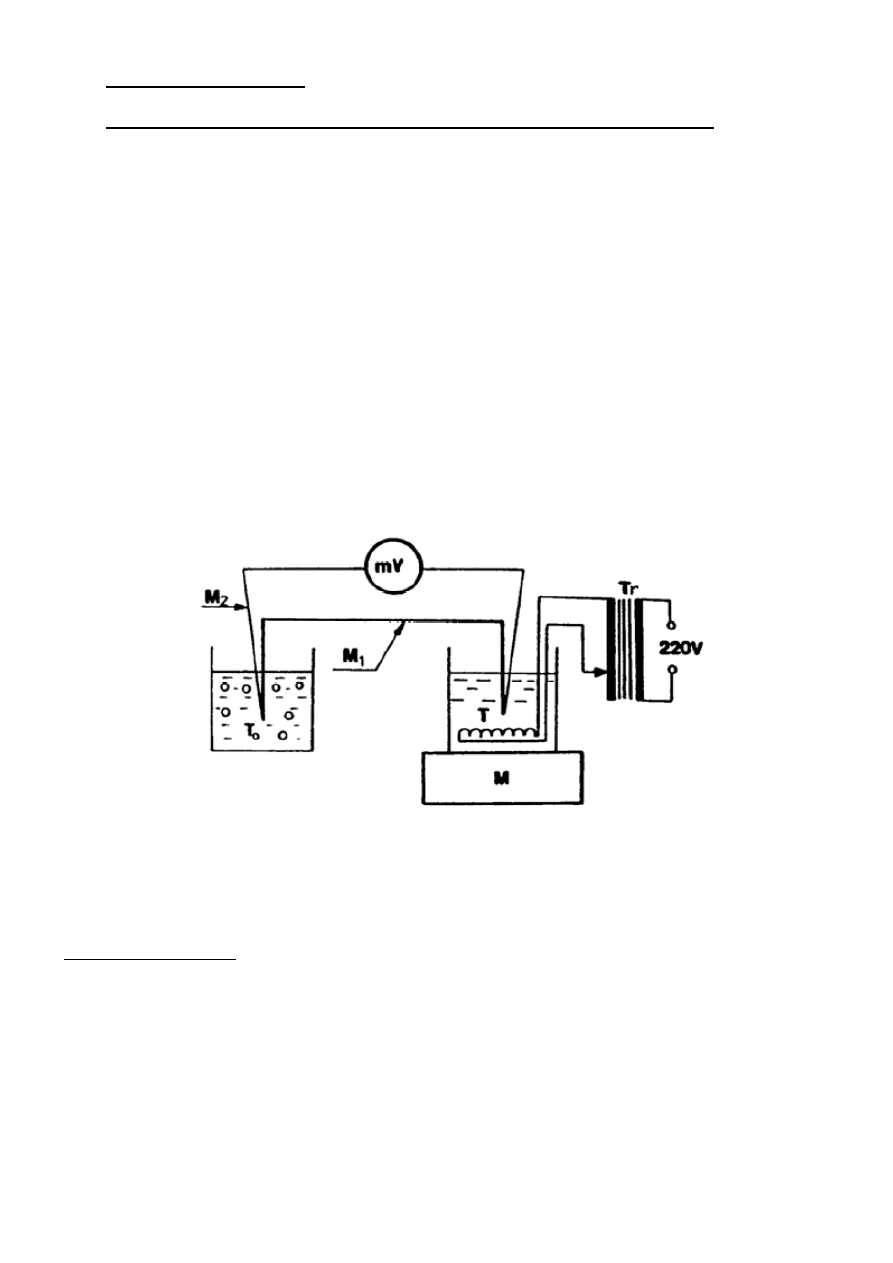
Rys. 2. Schemat ideowy termoogniwa.

Na rysunku 2 przedstawiono schemat ogniwa termoelektrycznego, złożonego z dwóch metali M

1

i M

2

.

Spojenia A i B tych metali utrzymane są odpowiednio w temperaturze T i T+∆T. SEM termoelektryczna
działająca w tym ogniwie jest algebraiczną sumą napięć kontaktowych:

5

)

(

)

(

T

U

T

T

U

k

k

−

∆

+

=

ε

.

(5)

Po podstawieniu do powyższego równania zależności (3) i (4), SEM termoelektryczną można określić
następującym wzorem:

T

n

n

e

k

∆

=

2

1

ln

ε

.

(6)

Z powyższej zależności wynika, że wartość SEM zależy od różnicy temperatur spojeń oraz od
koncentracji swobodnych elektronów w obu metalach.

Dla określonej pary metali SEM termoelektryczną można zapisać następującym wyrażeniem:

T

∆

=

α

ε

(7)

gdzie:

2

1

ln

n

n

e

k

=

α

.

(8)

Wielkość α nazywa się współczynnikiem SEM termoelektrycznej lub zdolnością termoelektryczną. Jak
wynika ze wzoru (7) zdolność termoelektryczna jest równa liczbowo SEM termoelektrycznej przy
różnicy temperatur spojeń termoogniwa równej jeden stopień. Wzór (7), wskazuje na to, że generowana
w obwodzie siła elektromotoryczna, zwana siłą termoelektryczną, jest liniową funkcją temperatury. W
rzeczywistości gęstość elektronów w metalu wprawdzie słabo, lecz jednak zależy od temperatury. Jeśli
zatem temperatury T

A

i T

B

różnią się na tyle, że nie można przyjąć iż gęstość elektronów n

1

i n

2

są stałe w

całych obszarach metali 1 i 2, to zależność siły elektromotorycznej ε od różnicy temperatur T

B

– T

A

wykazują odchylenie od liniowości. Wówczas zależność (7) zwykle zastępuje się wielomianem drugiego
stopnia o następującej postaci:

2

)

(

)

(

A

B

A

B

T

T

T

T

−

+

−

=

γ

β

ε

,

(9)

gdzie β i γ są stałymi niezależnymi od temperatury , przy czym β >> γ. Jednak przy niezbyt dużych
różnicach temperatur spojeń równania (7) i (8) wykazują dość dobrą zgodność z wynikami
eksperymentalnymi. Można więc przyjąć, że w tym zakresie temperatur wartość siły termoelektrycznej
jest wprost proporcjonalna do różnicy temperatur spojeń.

Połączenie termoogniwa innymi przewodnikami nie powoduje zmiany wartości siły

termoelektrycznej; w takim obwodzie popłynie prąd elektryczny o natężeniu:

Z

W

R

R

i

+

=

ε

,

(10)

gdzie R

w

jest oporem przewodników tworzących termoogniwo, a R

z

– sumą oporów przewodników

połączonych szeregowo z termoogniwem.

W celu otrzymania prądu o stałym natężeniu należy utrzymywać stałą różnicę temperatur spojeń

termoogniwa tj. do spojenia o wyższej temperaturze należy nieustannie doprowadzać energię cieplną, a
od chłodniejszego spojenia – odprowadzać. Najogólniej mówiąc, zjawisko Seebecka polega więc na
przekształceniu energii cieplnej w energię elektryczną.

Obecnie termoogniwa mają szerokie zastosowanie techniczne, w szczególności przy pomiarach i

kontroli temperatury.

6

3.

Wykonanie pomiarów

A.

Cechowanie termoogniwa i pomiary temperatury topnienia ciał krystalicznych.

Do pomiarów temperatur służą termopary tj. ogniwa termoelektryczne składające się dwóch drutów

wykonanych z różnych metali, których końce są spojone. Jedno spojenie umieszcza się w środowisku o
znanej temperaturze a drugie w środowisku którego temperaturę należą zmierzyć.

Termopary wykazują szereg zalet w porównaniu z termometrami cieczowymi, umożliwiają bowiem

pomiar temperatur w szerokim zakresie (20-2000 K). Charakteryzują się one bardzo dużą czułością i małą
pojemnością cieplną, mogą być stosowane do pomiarów niewielkich różnic temperatur (od 10

–6

stopnia)

oraz do pomiarów temperatur mikroelementów. W celu zwiększenia czułości termopar, łączy się je
szeregowo w tzw. termostosy. Spojenie drutów mogą się znajdować w dużych odległościach, w związku
z tym termoogniwa nadają się do zdalnego pomiaru temperatury. Obecnie znalazły one powszechne
zastosowanie w urządzeniach kontrolujących temperaturę.

Termoogniwo może być użyte do pomiaru temperatury po uprzednim wycechowaniu. W tym celu

zestawia się przyrządy wg schematu pokazanego na rys.3. Jedno ze spojeń termoogniwa umieszcza się w
mieszaninie wody z lodem gwarantującej stałą temperaturę. Drugie spojenie zanurza się w wodzie, którą
podgrzewa się powoli, grzałką elektryczną zasilaną z autotransformatora.

Rys. 3. Schemat układu pomiarowego: M - mieszadło magnetyczne, Tr – autotransformator.

Kolejność wykonywanych czynności.

Cechowanie termopary:

1.

Przed włączeniem grzałki odczytać temperaturę pokojową wody T.

2.

Ustawić napięcie autotransformatora na podziałkę 30.

3.

Włączyć grzałkę i mieszadło magnetyczne.

4.

Wskazania mikrowoltomierza odczytywać ze wzrostem temperatury co 5°C.

5.

Po osiągnięciu temperatury wody 70°C podwyższyć napięcie na autotransformatorze (podziałka
ustawiona na ok. 65) i odczytywać wskazania miliwoltomierza jak poprzednio co 5°C aż do
osiągnięcia stanu wrzenia wody.

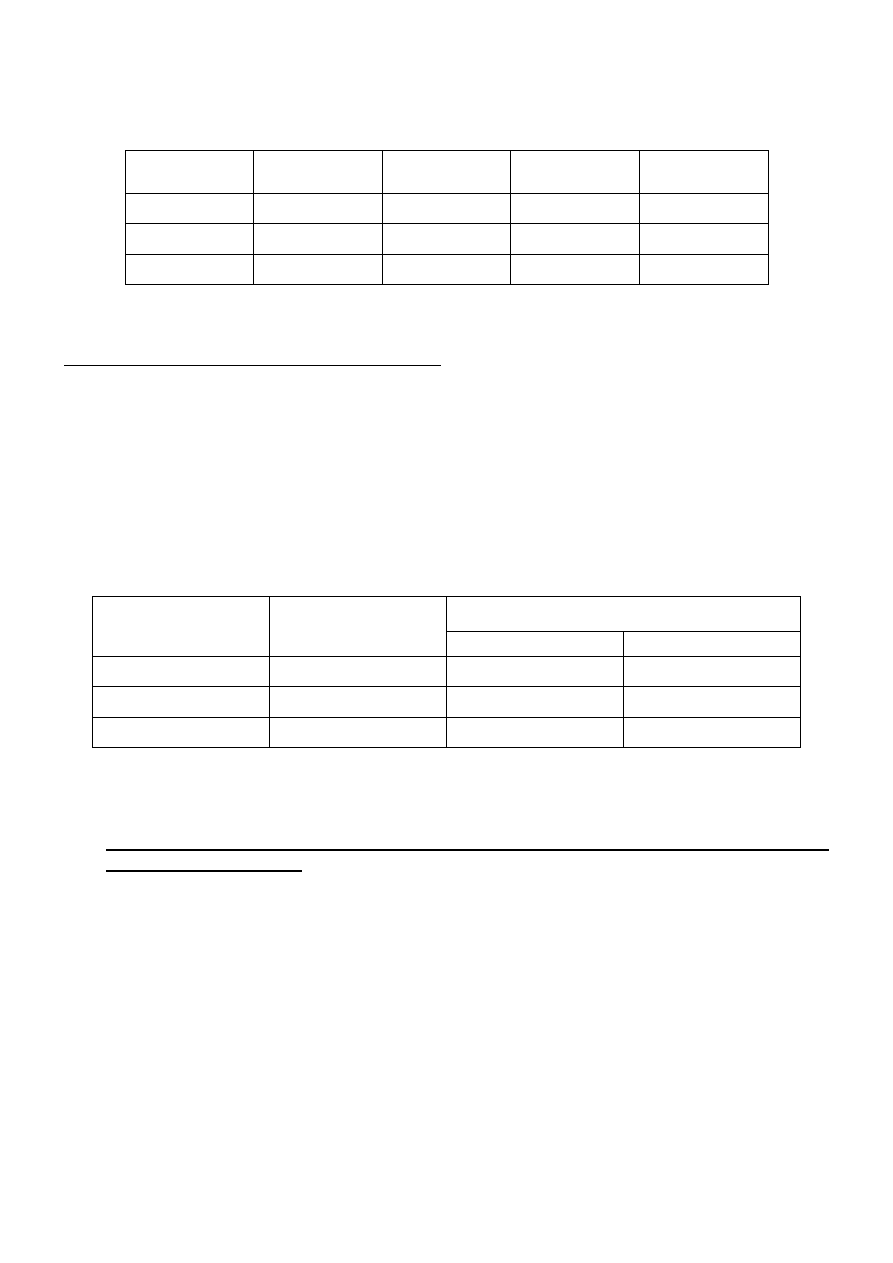
7

6.

Wyniki pomiarów zapisać w Tabeli 1.

Tabela nr 1

Lp.

T

o

[K]

T [K]

∆

T [K]

U [V]

Pomiary temperatury topnienia ciała krystalicznego:

1.

Umieścić kryształki ciała w probówce.

2.

Probówkę z kryształkami wstawić do wrzącej wody.

3.

Po stopieniu kryształów probówkę wyjąć z gorącej kąpieli i umieścić w niej spojenie termoogniwa
(drugie spojenie pozostaje nadal w temperaturze T

0

).

4.

W czasie schładzania notować wskazania woltomierza co 10 sek.

5.

Wyniki pomiarów zapisywać w Tabeli 2.

6.

Podobne pomiary przeprowadzać przy topnieniu ciała.

Tabela nr 2

Lp.

t [s]

U [V]

chłodzenie

ogrzewanie

B.

Wyznaczanie zdolności termoelektrycznej termoogniwa i względnej koncentracji elektronów
swobodnych w metalach.

W obwodzie elektrycznym przedstawionym na rys. 4 termoogniwo połączone jest szeregowo z

opornikiem R

o

i opornikiem dekadowym R

d

. W obwodzie tym popłynie stały prąd elektryczny, jeśli

różnica temperatur spojeń będzie niezmienna w czasie.

8

Rys. 4. Schemat obwodu pomiarowego do
wyznaczania zdolności termoelektrycznej
termoogniwa.

Natężenie tego prądu spełnia równanie:

)

(

0

d

W

R

R

R

i

+

+

=

ε

(11)

w którym R

W

jest oporem elektrycznym metali tworzących termoogniwo. Jeśli na oporniku dekadowym

ustawimy wartość R

d

= 0 to w obwodzie popłynie prąd o natężeniu i

0

, wobec tego można napisać:

)

(

0

0

R

R

i

W

+

=

ε

(12)

stąd

0

0

i

R

R

W

ε

=

+

(13)

Po podstawieniu powyższej zależności do równania (11) otrzymuje się:

)

(

0

d

R

i

i

+

=

ε

ε

(14)

a po przekształceniu:

d

R

i

i

i

i

−

=

0

0

ε

(15)

Należy zauważyć (patrz rys. 4), że opór R

o

połączony jest równolegle z woltomierzem. Opór wewnętrzny

woltomierza R

v

>>R

o

. Woltomierz ten wskazuje napięcie U

o

jeśli w obwodzie płynie prąd o natężeniu i

o

.

0

0

iR

U

=

(16)

Można zatem napisać:

0

0

0

R

U

i

=

oraz

0

R

U

i

=

(17)

Podstawiając powyższe wzory do równania (15), siła elektromotoryczna termoogniwa będzie określona
następująco:

0

0

0

R

R

U

U

U

U

d

−

=

ε

(18)

Jeśli uwzględnimy, że siła elektromotoryczna termoogniwa związana jest różnicą temperatur spojeń
zależności: ε = α (T

1

- T

2

), to zdolność termoelektryczną termoogniwa przedstawia wzór:

)

(

2

1

0

0

0

T

T

R

R

U

U

U

U

d

−

−

=

α

(19)

W celu wyznaczenia zdolności termoelektrycznej termoogniwa korzystamy z obwodu

pomiarowego przedstawionego na rys. 4. Jedno ze spojeń tego ogniwa umieszcza się w mieszaninie wody
z lodem (o temp. T

2

) a drugie we wrzącej wodzie (temp. T

1

) w ten sposób zapewniona jest stała

temperatura podczas wykonywania pomiarów.

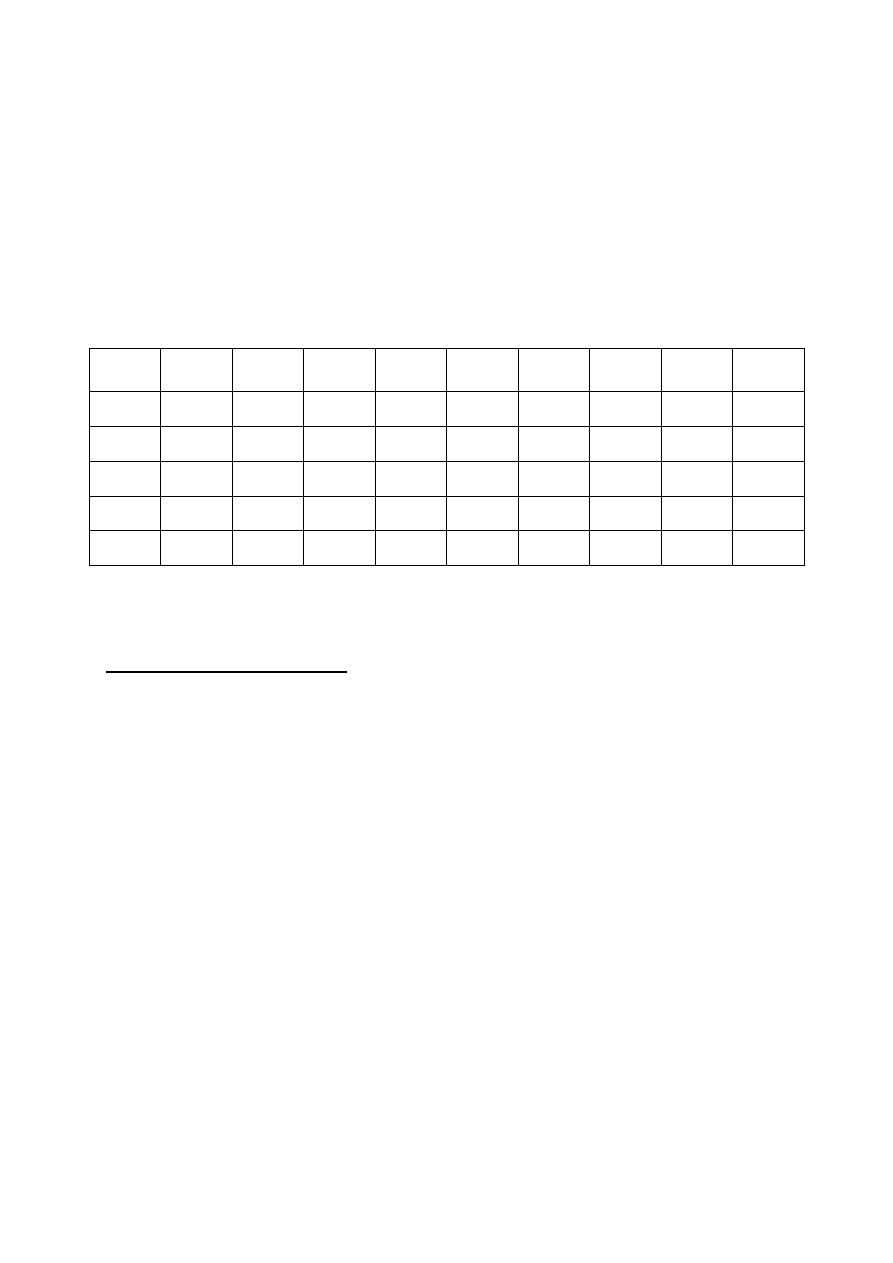
9

Kolejność wykonywanych czynności.

1.

W obwodzie pomiarowym rys. 4 włączyć tylko opornik R

0

(R

d

= 0) i odczytać napięcie U

0

.

2.

Następnie do obwodu pomiarowego włączyć dodatkowo opornicę dekadową i ustawić
R

d

= 1000Ω. Odczytać napięcie U.

3.

Pomiar w punkcie 2 powtórzyć dla oporu R

d

= 2000, 3000, 4000, 5000 Ω. Wyniki pomiarów

zapisać w tabeli 3.

Tabela nr 3

Lp.

T

1

[K]

T

2

[K]

R

0

[Ω]

U

0

[V]

R

d

[Ω]

U

[V]

α

[V/K]

α

śr

[V/K]

n

1

/n

2

1000

2000

3000

4000

5000

4.

Opracowanie wyników (A)

1.

Na podstawie tabeli 1 sporządzić wykres cechowania termoogniwa i metodą najmniejszych
kwadratów określić parametry prostej.

2.

Na podstawie tabeli 2 sporządzić wykres zależności U od czasu chłodzenia (i grzania) ciała
krystalicznego. W pewnym przedziale czasu ∆t , napięcie U nie ulega zmianie. Wartość tego
napięcia U

T

odpowiada zmianie stanu skupienia ciała.

3.

Obliczyć wartość średnią U

T

z pomiarów chłodzenia i ogrzewania.

4.

Z wykresu cechowania termoogniwa odczytać różnicę temperatur ∆T

T

odpowiadającą napięciu

U

T

. Kalkulacje należy zrobić w oparciu o metodę najmniejszych kwadratów dla opisu wykresu

cechowania termoogniwa.

5.

Obliczyć temperaturę topnienia T

T

ze wzoru:

0

T

T

T

T

T

+

∆

=

(20)

6.

Podać oszacowanie błędu obciążającego wyznaczoną temperaturę topnienia.

10

5.

Opracowanie wyników (B)

1.

Na podstawie wzoru (19) obliczyć zdolność termoelektryczną α dla każdej wartości oporu R

d

.

2.

Obliczyć wartość średnią zdolności termoelektrycznej termoogniwa.

3.

Mając obliczoną wartość średnią α

śr

termoogniwa obliczyć ze wzoru (8) względną koncentrację

n

1

/n

2

elektronów swobodnych w metalach tworzących badane termoogniwa.

4.

Na podstawie równania (19) wyprowadzono błąd względny metodą różniczkową:













−

∆

+













−

∆

+













∆

+













∆

+

∆













−

+

∆













−

=









∆

1

2

1

1

2

2

0

0

0

2

0

0

0

0

2

)

(

)

(

T

T

T

T

T

T

R

R

R

R

U

U

U

U

U

U

U

U

U

U

d

d

α

α

(21)

5.

Korzystając z tego wzoru obliczyć błąd względny zdolności termoelektrycznej, a następnie błąd
względny ∆α

max

.

6.

Podać oszacowanie granic wyniku zdolności termoelektrycznej termoogniwa w postaci α = α

obl

.

Wymagania

1.

Jakościowy opis zjawiska termoelektronowego w metalach wg teorii klasycznej.

2.

Znajomość pojęć: praca wyjścia elektronu z metalu, kontaktowa różnica potencjałów, poziom
Fermiego.

3.

Termopara.

4.

Wyprowadzenie wzorów (6) i (19).

Literatura:

1.

Jaworski B., Dietłof H. : Kurs fizyki t.2, PWN W-wa, 1993.

2.

Orear J. : Fizyka WN-T W-wa, 1998.