Kierunek: informatyka, studia dzienne magisterskie

Algorytmy i struktury danych, sem.I

- 1 -

A

Algorytmy i struktury

danych

Imi i nazwisko

1. Dane jest jednorodne, liniowe równanie rekurencyjne:

a

n

= -a

n-1

+12a

n-2

, a

1

= 10, a

0

= 1

Znajd rozwi zanie tego równania.

2.

Skorzystaj z metody rekurencji uniwersalnej i podaj dokładne asymptotyczne oszacowania dla nast puj cych rekurencji:

(a) T(n) = 9T(n/3) + n

(b) T(n) = T(2n/3) + 1

(c) T(n) = 3T(n/4) + n lg n

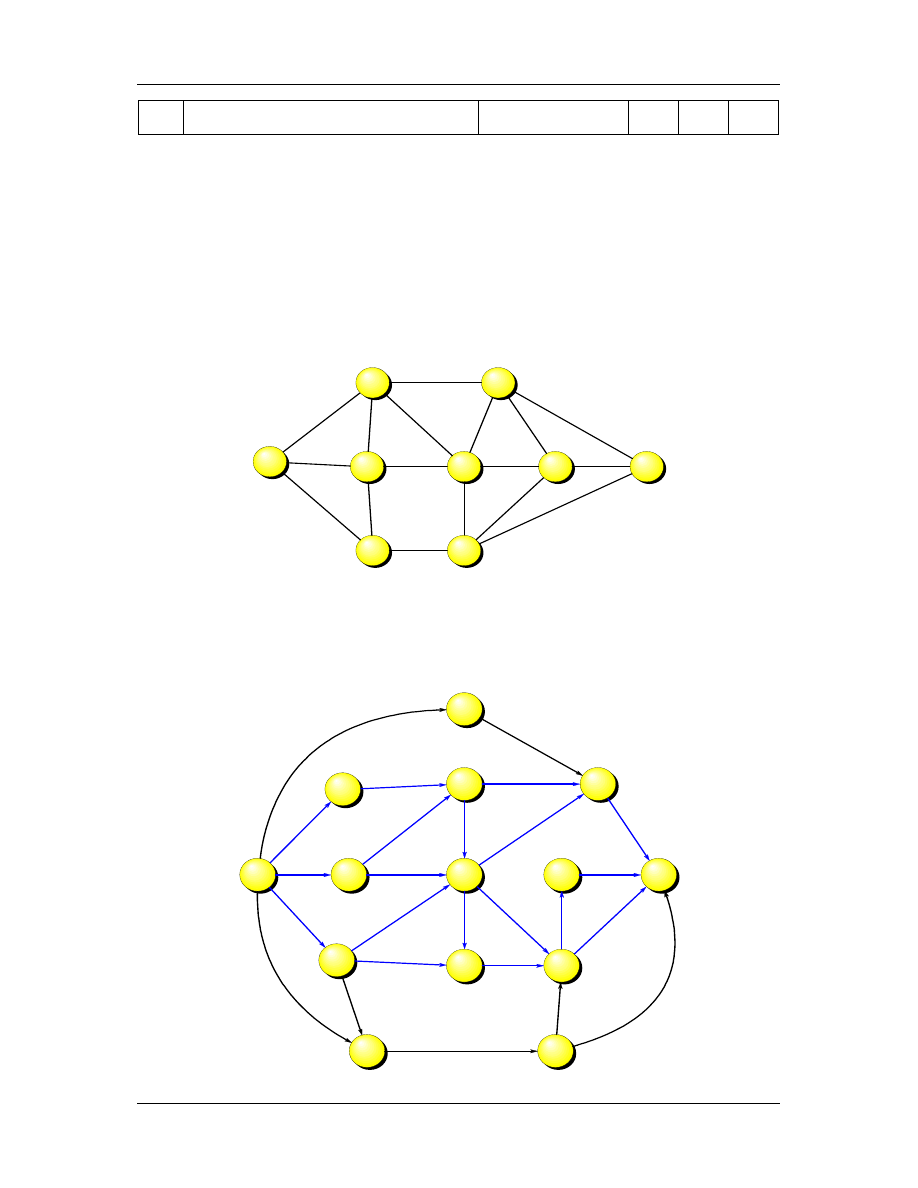
3. Dla poni szego wa onego grafu nieskierowanego wyznaczy

minimalne drzewo rozpinaj ce (MST),

posługuj c si

algorytmem Kruskala.

c

h

d

a

f

g

b

e

i

1

3

2

1

4

2

1

2

4

1

3

2

2

2

4

5

3

4. Przypu my, e w dyskretnym problemie plecakowym kolejno przedmiotów uporz dkowanych rosn co według

ci aru jest taka sama, jak przy uporz dkowaniu malej cym według warto ci. Podaj efektywny algorytm znajduj cy

optymalne rozwi zanie dla tej wersji problemu plecakowego i uzasadnij jego poprawno .

5. Dla poni szej sieci poł cze mi dzy miastami wyznaczy minimaln cie k z miasta a do k, posługuj c strategi

programowania dynamicznego. Podaj wszystkie optymalne rozwi zania.

a

b

c

d

g

g

f

h

e

g

i

g

j

k

2

4

2

1

2

2

1

2

2

2

5

6

3

5

3

3

8

2

3

4

2

5

6

3

2

Kierunek: informatyka, studia dzienne magisterskie

Algorytmy i struktury danych, sem.I

- 2 -

6. Udowodnij, e

{(x > 0)

∧∧∧∧ (y > 0)}

spec

z

←

←

←

←0;

u

←

←

←

←x;

repeat

z

←

←

←

←z + y;

u

←

←

←

←u - 1;

until u = 0

endspec

{z

←

←

←

←x*y}