1

Egzamin ze statystyki

Studia Licencjackie Stacjonarne i Popołudniowe

Termin III – pa

ź

dziernik 2012

Uwaga. W rozwiązaniach – tam gdzie to konieczne – należy przyjąć poziom istotności 0,05 i
współczynnik ufności 0,95.

Zadanie 1

W zbadanej próbie 1000 samochodów firmy A w pierwszym roku użytkowania zgłoszono usterki
w 3% samochodów, natomiast w konkurencyjnej firmie B na 500 zbadanych samochodów 20
okazało się wadliwych w takim samym okresie.

a) Proszę oszacować punktowo (wraz ze standardowym błędem szacunku) oraz przedziałowo

odsetek samochodów marki A, które w pierwszym roku użytkowania okazują się wadliwe. (2,5
pkt.)

b) Czy można stwierdzić, iż samochody firm A i B równie często okazują się wadliwe? (2,5 pkt.)

c) Przy jakim poziomie istotności podjęta zostałaby inna decyzja weryfikacyjna niż w
poprzednim punkcie? (1,5 pkt.)

Zadanie 2

Wartość łącznej sprzedaży jabłek trzech gatunków z pewnego sadu pod Grójcem spadła w 2011

roku w porównaniu z rokiem 2010 o 10%. Natomiast w porównaniu z rokiem 2009 wartość
sprzedaży w 2011 roku była niższa o 15%. Wartość sprzedaż jabłek I, II i III gatunku stanowiła w
2011 roku odpowiednio 50%, 30% i 20% ogólnej wartości sprzedaży. W roku 2011 w
porównaniu z rokiem 2010 ceny jabłek I gatunku wzrosły o 10%, II gatunku wzrosły o 5%, a III
gatunku pozostały bez zmian.

a) Ile wynosiło przeciętne roczne tempo zmian wartości sprzedaży jabłek (wszystkich gatunków

łącznie) w latach 2009-2011? (1,5 pkt.)

b) Wiedząc, że w 2011 roku wartość sprzedaży jabłek wynosiła 200 tys. zł oraz przy założeniu,

ż

e tempo zmian wartości sprzedaży w latach 2009-2011 utrzyma się przez kolejne dwa lata,

jakiej wielkości sprzedaży można spodziewać się w 2013 roku? (1 pkt.)

c) Jak zmiany cen a jak ilości sprzedaży jabłek w latach 2010-2011 wpłynęły na zmianę wartości

sprzedaży? (2,5 pkt.)

2

Zadanie 3

Sześć osób zapytano o poziom ich wykształcenia, a także poproszono o ocenę własnych

dochodów w postaci przypisania im jednej z możliwości: od bardzo złego do bardzo dobrego.
Wyniki ankiety przedstawia poniższa tabela:

Nr osoby Wykształcenie

Ocena dochodu

1

niepełne podstawowe zły

2

podstawowe

bardzo zły

3

zasadnicze zawodowe nieco powyżej przeciętnego

4

ś

rednie

przeciętny

5

wyższe licencjackie

nieco poniżej przeciętnego

6

wyższe magisterskie

bardzo dobry

Należy obliczyć i zinterpretować właściwy współczynnik pozwalający ocenić siłę i kierunek

zależności pomiędzy wykształceniem i oceną dochodu wśród zbadanych osób. (2 pkt.)

Zadanie 4

W próbie 26 osób przeprowadzono badanie zależności pomiędzy miesięcznym dochodem netto

na głowę w gospodarstwie domowym (zmienna Y) i poziomem wykształcenia głowy
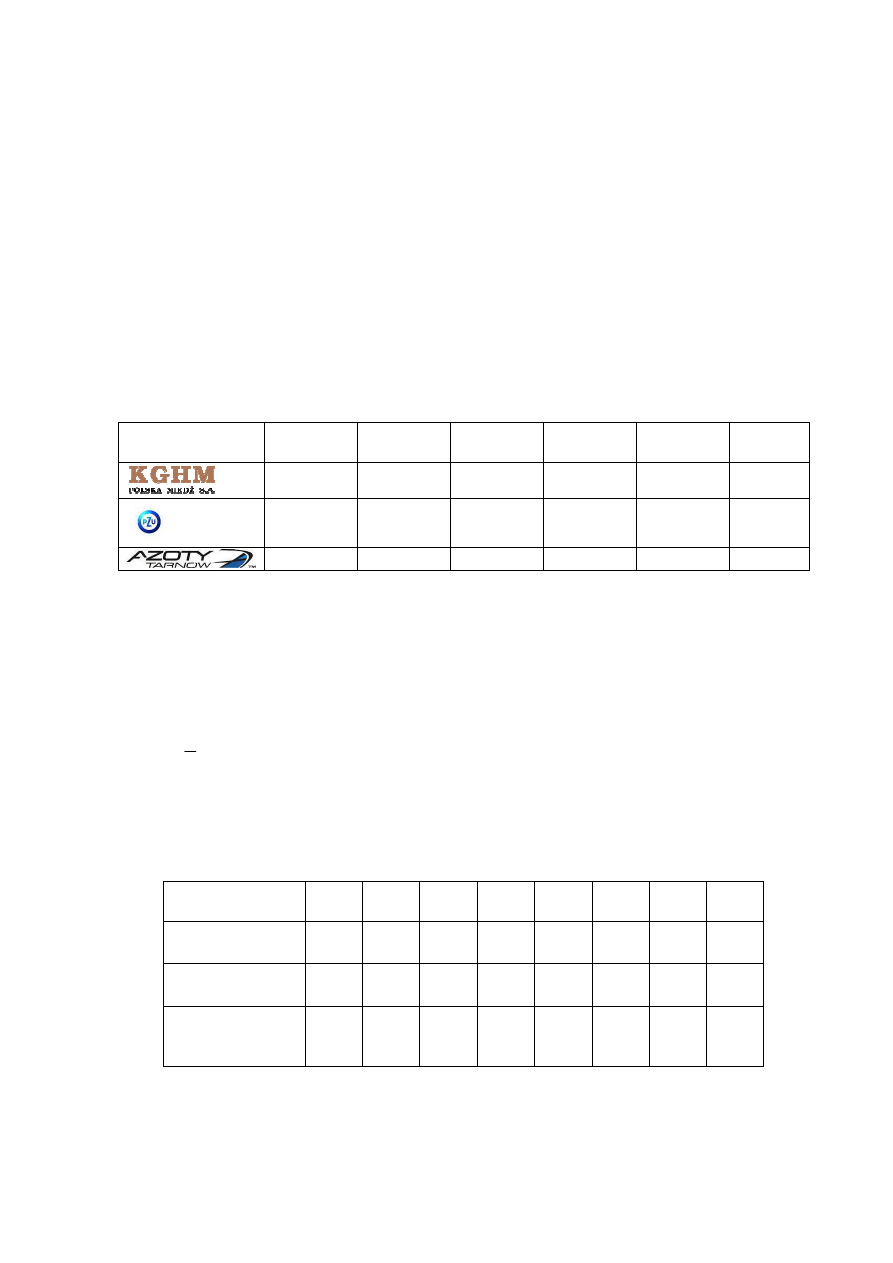
gospodarstwa (w latach edukacji, zmienna X). Dwuwymiarowy rozkład próby przedstawia
poniższy wykres

Dochód w zale

ż

no

ś

ci od edukacji

0

200

400

600

800

1000

1200

6

8

10

12

14

16

edukacja (w latach)

d

o

c

h

ó

d

(

P

L

N

/m

ie

s

)

Ponadto uzyskano m. in. następujące charakterystyki opisowe próby (w wersji nieobciążonej):

S

Y

= 166,01

S

X

= 3,178

C

XY

= 434,38 (kowariancja)

a) Proszę ocenić na podstawie wykresu czy w zbadanej próbie wzrost edukacji powoduje wzrost

ś

redniej wartości dochodu

(1 pkt)

b) Czy byłby to wynik statystycznie istotny? (wskazówka: należy ocenić stosowny parametr).

Wiadomo dodatkowo, że suma kwadratów reszt w modelu regresji wynosi 221883 (2,5 pkt)

3

c) Proszę wykreślić przybliżoną linię regresji (ze zmienną Y jako zmienną objaśnianą) oraz

ocenić na podstawie odpowiedniego miernika dopasowanie tego modelu do danych (2,5 pkt.)

d) Ile wynosi w zbadanej próbie współczynnik korelacji liniowej pomiędzy dochodem i

edukacją? Czy jest on statystycznie większy od zera? (2 pkt.)

Zadanie 5

Poniższa tabela przedstawia notowania na koniec dnia akcji trzech spółek obserwowanych przez

tydzień (w złotych za akcję). Na podstawie dostępnej informacji, za pomocą odpowiedniej miary
wybierz spółkę, w którą inwestowanie wiąże się z największym zróżnicowaniem ceny
zainwestowanego kapitału. (4 pkt)

Zadanie 6

Jedną z obserwacji z testów zderzeniowych samochodów pewnej marki jest ocena obrażeń głowy

wyrażona skalą od 0 do 1000. Tabela poniżej prezentuje wyniki 100 testów.

a) Czy można powiedzieć, że wyniki te mają rozkład normalny o parametrach zaobserwowanych

w próbie

604

=

X

, S

X

= 185? Odpowiedz, uzupełniając miejsca oznaczone gwiazdkami i

testując odpowiednią hipotezę

(4 pkt.)

b) Ile wynosi pierwszy kwartyl badanej zmiennej?

(3 pkt.)

24.09.2012

25.09.2012

26.09.2012

27.09.2012

28.09.2012

ś

rednia w

tygodniu:

151,5

148,9

147

149,9

152,5

149,96

363,4

362,9

359

363,5

360

361,76

49,99

49,77

49,8

49,99

50,15

49,94

Ocena punktowa
obrażeń (przedział)

<300

300-
400

400-
500

500-
600

600-
700

700-
800

800-
900

>900

liczebność
obserwowana

3

*

22

18

20

17

4

8

liczebność
hipotetyczna

5,1

*

15,2

20,4

20,6

15,7

9,0

5,5

Składniki do
statystyki Chi-
kwadrat

0,84

*

3,04

0,28

0,02

0,11

2,77

1,14

4

TEST

Proszę zaznaczyć w każdym przypadku odpowiedź T-tak lub N-nie

Punktacja: odpowiedź poprawna= 1 pkt; brak odpowiedzi= 0 pkt; odpowiedź błędna = –1
pkt; Jeżeli całkowita suma punktów z części testowej będzie ujemna, jako wynik tej części
zostanie przyjęte 0 pkt.

TAK

NIE

1. Czy analiza wariancji:

a/ wykorzystuje statystykę testową o rozkładzie χ

2

?

b/ może być stosowana jeżeli jedna zmienna nie jest ilościowa?

c/ może być stosowana zarówno przy małej (n<30) jak i przy dużej

próbie?

2. Znane są dwa histogramy opisujące rozkłady dwóch zmiennych. Czy

na tej podstawie można, dokładnie lub w przybliżeniu, podać:

a/ kierunek asymetrii dla obu zmiennych?

b/ wszystkie kwartyle dla obu zmiennych?

c/ współczynnik korelacji liniowej pomiędzy tymi zmiennymi?

3. Czy estymator parametru:

a/ który jest zgodny jest zawsze nieobciążony?

b/ który jest zgodny jest estymatorem, w przypadku którego zwiększanie

próby przekłada się przeciętnie na zmniejszenie błędu estymacji?

c/ który jest najefektywniejszy ma najwyższą wariancję ze wszystkich

nieobciążonych estymatorów tego samego parametru?