
1
ELEKTRONIKA CYFROWA

2
SPIS TREŚCI
1.
WPROWADZENIE
3
1.1.
Systemy liczbowe
3
1.1.1.
Dziesi
ętny system liczbowy
4
1.1.2.
Dwójkowy system liczbowy
4
1.1.3.
Szesnastkowy system liczbowy
5
1.2.
Kody
6
2.
PODSTAWOWE FUNKCJE LOGICZNE I FUNKTORY UK
ŁADÓW LOGICZNYCH
8
2.1.
Wst
ęp
8
2.2.
Podstawowe funkcje logiczne
9
2.3.
Sposoby przedstawiania funkcji logicznych
12
2.4.
Funktory uk
ładów logicznych
14
2.5.
Uk
łady TTL
19
3.
UK
ŁADY KOMBINACYJNE I SEKWENCYJNE
22
3.1.
Wst
ęp
22
3.2.
Metoda Karnaugha
23
4.
PRZERZUTNIKI
31
4.1.
Wst
ęp
31
4.2.
Przerzutniki asynchroniczne
33
4.3.
Przerzutniki synchroniczne
34
4.3.1.
Wst
ęp
34
4.3.2.
Przerzutnik synchroniczny D
34
4.3.3.
Przerzutnik synchroniczny T
36
4.3.4.
Przerzutnik synchroniczny RS
36
4.3.5.
Przerzutnik synchroniczny JK
37
5.
REJESTRY
41
5.1.
Wst
ęp
41
5.2.
Rejestry równoleg
łe
42
5.3.
5.3 Rejestry szeregowe
43
6.
PAMI
ĘCI
45
6.1.
6.1 Wst
ęp
45
6.2.
6.2 Pami
ęci o dostępie swobodnym RAM
45
6.3.
Pami
ęci stałe ROM
48
6.3.1.
Zastosowania pami
ęci ROM (PROM)
49
7.
LICZNIKI CYFROWE
51
7.1.
Wiadomo
ści ogólne
51
7.2.
Liczniki asynchroniczne
51
7.3.
Liczniki synchroniczne
55
8.
UK
ŁADY ARYTMETYCZNE
58
8.1.
Wst
ęp
58
8.2.
Sumatory
58
8.2.1.
Sumatory równoleg
łe
61
8.2.2.
Sumatory szeregowe
63
8.3.
Komparatory
64
8.3.1.
Komparatory jednobitowych liczb dwójkowych
64
8.3.2.
Komparatory równoleg
łe
65
8.3.3.
Komparatory szeregowe
67
9.
UK
ŁADY KOMUTACYJNE
69
9.1.
Wst
ęp
69
9.2.
Enkodery
69
9.3.
Dekodery
70
9.4.
Transkodery
74
9.4.1.
Przyk
łady syntezy i rozwiązań transkoderów
74
9.5.
Multipleksery i demultipleksery
80
9.5.1.
Wst
ęp
80
9.5.2.
Multipleksery
80
9.5.3.
Demultipleksery
82
10.
GENERATORY
85
10.1.
Przerzutniki monostabilne
85
10.2.
Generatory fali prostok
ątnej
86
10.2.1.
Generowanie pojedynczego impulsu
87
10.2.2.
Opó
źnienie sygnału o zadany czas
88
10.2.3.
Generowanie ci
ągu impulsów
90
11.
BIBLIOGRAFIA:
91

3
1.
WPROWADZENIE
1.1.
SYSTEMY LICZBOWE
Cyframi arabskimi są znaki: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Cyfry te służą do zapisywania liczb.
Do podstawowych systemów zapisywania liczb należą systemy pozycyjno - wagowe, w których wartość cyfry zależy od miejsca, czyli
pozycji, jaką ta cyfra zajmuje w napisanej liczbie. Każda pozycja ma określoną stałą wagę liczbową (znaczenie).
Oznaczając podstawę dowolnego pozycyjnego systemu liczbowego przez p, można każdą n - cyfrową liczbę całkowitą przedstawić w
postaci szeregu:
∑
−
=
−
−
−
−
=
+
+
+
+
1
0
0
0
1
1
2
2
1
1
...
n
i
i
i
n
n
n
n
p
a
p
a
p
a
p
a
p
a
lub w skróconej postaci:
[
]
p
n
n
a
a
a
a
0
1
2
1
...
−
−
gdzie:
p – podstawa systemu, którą jest liczba całkowita dodatnia,
n – numer pozycji
a
i
– cyfry z zakresu od 0 do p – 1.
Pierwszej cyfrze w lewo od przecinka przypisuje się wagę p
0
, drugiej
−
p
1
, a trzeciej
−
p
2
. Natomiast cyfrom zapisywanym w prawo od
przecinka przypisuje się kolejno następujące wagi: pierwszej
−
p
-1
, drugiej
−
p
-2
, trzeciej p
-3
itd. (patrz przykład 1.1 i 1.2).
W systemach cyfrowych bardzo ważną rolę odgrywają zbiory znaków złożone z 2, 8, 10 i 16 elementów. Zbiory takie nazywamy
odpowiednio:
§
zbiorem dwójkowym (binarnym) o podstawie p = 2,
§
zbiorem ósemkowym (oktalnym) o podstawie p = 8,
§
zbiorem dziesiątkowym o podstawie p = 10,
§
zbiorem szesnastkowym (heksadecymalnym) o podstawie p = 16.
Najważniejszą rolę w systemach cyfrowych odgrywa zbiór dwójkowy, ponieważ układy podstawowe, z których zbudowane są te systemy,
mają naturę dwójkową.
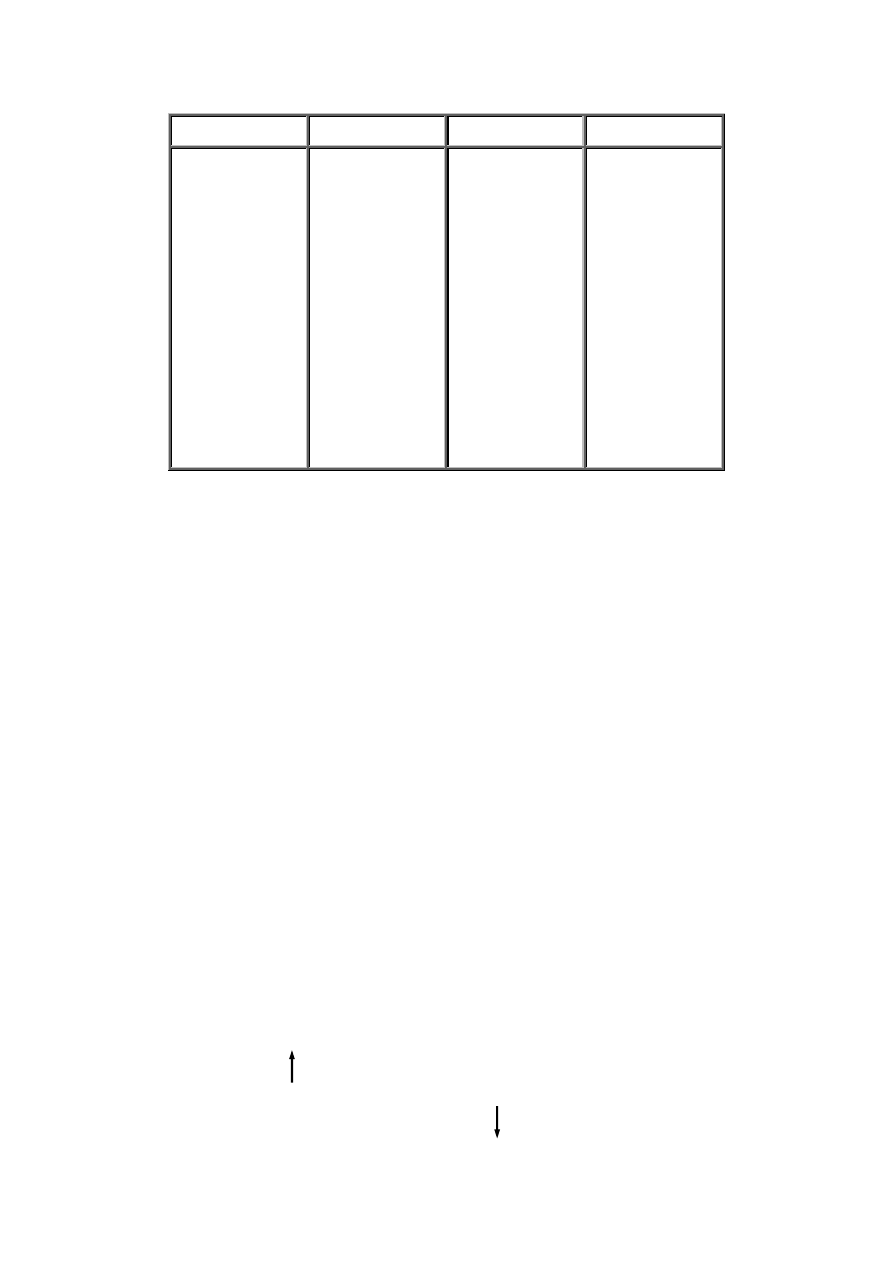
W tablicy 1.1 przedstawiono cyfry używane w systemach o p = 2, 3, 8, 10 i l6. Zauważmy, że dla p > 10 należy wprowadzić dodatkowe
znaki.
Tablica 1.1
Podstawa p
System liczbowy
Cyfry używane w systemie liczbowym
2
Dwójkowy
0, 1
3
Trójkowy
0, 1, 2
8
Ósemkowy
0, 1, 2, 3, 4, 5, 6, 7
10
Dziesiętny
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
16
Szesnastkowy
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
4
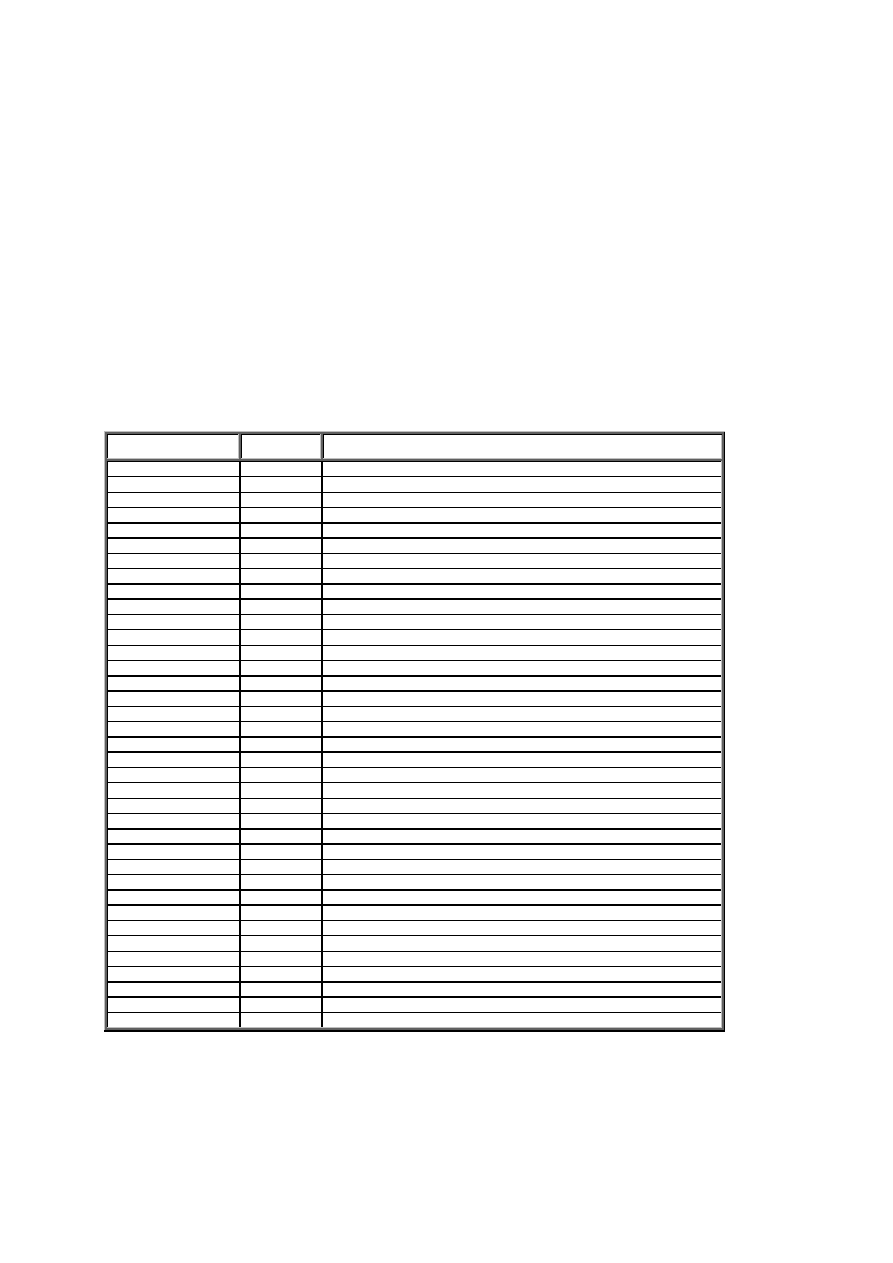
Tablica 1.2 Przykłady liczb wyrażonych w różnych systemach
System dziesiętny
System dwójkowy
System
ósemkowy
System
szesnastkowy
0
0
0
0
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
16
10000
20
10
17
10001
21
11
18
10010
22
12
19
10011
23
13
20
10100
24
14
100
1100100
144
64
1000
1111101000
1750
3E8
1.1.1.
Dziesi
ętny system liczbowy
Do zapisania dowolnej liczby w powszechnie stosowanym dziesiętnym systemie liczbowym wykorzystuje się dziesięć (wszystkie) cyfr
arabskich. W dziesiętnym systemie liczbowym podstawa systemu p = 10. Kilka wybranych liczb dziesiętnych przedstawiono w pierwszej kolumnie
tablicy 1.2.
Przykład 1.1:
Liczbę 15, zapisana w systemie dziesiętnym można zapisać:
15 = (1 x 10
1
)+(5 x 10
0
)
Liczba ta składa się z elementów o wadze 10
0
= 1 i jednego elementu o wadze 10
1
= 10
Przykład 1.2:
Zapis:
574, 28
10
jest skróconym zapisem wyrażenia :
(5 x 10
2
)+(7 x 10
1
)+(4 x 10
0
)+(2 x 10
-1
)+(8 x 10
-2
)
W tym przykładzie 5 jest na pozycji setek (10
2
), 7 na pozycji dziesiątek (10
1
), 4 na pozycji jedności (10
0
), 2 na pozycji dziesiętnych (10
-1
) i 8 na
pozycji setnych (10
-2
).
1.1.2.
Dwójkowy system liczbowy
Najprostszym systemem liczbowym wykorzystującym zapis pozycyjny jest system dwójkowy. Elementami zbioru znaków systemu
dwójkowego jest para cyfr: 0 i 1. Znak dwójkowy (ang. Binary Digit) często jest nazywany w skrócie bit. W dwójkowym systemie liczbowym
podstawa systemu p = 2. Kilka wybranych liczb dwójkowych przedstawiono w drugiej kolumnie tablicy 1.2.
Przykład 1.3:
Zapis:
1101
2
oznacza liczbę powstałą z sumowania
(1 x 2
3
)+(1 x 2
2
)+(0 x 2
1
)+(1 x 2
0
) = 13
10
Przykład 1.4:
Zapis:
1001, 1 101
2
jest zapisem skróconym wyrażenia:
(1 x 2
3
)+(0 x 2
2
)+(0 x 2
1
)+(1 x 2
0
)+(1 x 2
-1
)+(1 x 2
-2
)+(0 x 2
-3
)+(1 x 2
-4
) = 9,8125
10
Przykład ten może posłużyć również jako ilustracja konwersji liczby dwójkowej na równoważną jej liczbę dziesiętną.
Konwersji dziesiętno – dwójkowej można dokonać na drodze wielokrotnego dzielenia na 2 całkowitej części oraz mnożenia przez 2
ułamkowej części przetwarzanej liczby dziesiętnej.
Przykład 1.5:
Niech N
10
= 9,8125
9 : 2 = 4 reszta
1 (LSB)
4 : 2 = 2
0
2 : 2 = 1
0
1 : 2 = 0
1 (MSB)
0,8125 x 2 = 1,6250 = 0,6250 nadmiar
1 (MSB)
0,6250 x 2 = 1,2500 = 0,2500
1
0,2500 x 2 = 0,5000 = 0,5000
0
0,5000 x 2 = 1,0000 = 0,0000
1 (LSB)
Ostatecznie otrzymujemy:
9,8125
10
= 1001,1101
2
5
1.1.3.
Szesnastkowy system liczbowy
Szesnastkowy system liczbowy jest to taki system pozycyjny, którego podstawa p = 2
4
. Do przedstawienia liczb w tym systemie
potrzebnych jest 16 znaków. Dziesięć znaków stanowią cyfry arabskie, a pozostałe 6 znaków pierwsze litery alfabetu: A reprezentuje 10, B
reprezentuje 11, ..., F reprezentuje l5. Kilka wybranych liczb szesnastkowych przedstawiono w czwartej kolumnie tablicy 1.2.
Przykład 1.6:
Niech liczba wyrażona w systemie szesnastkowym ma postać:
F3A, C8
16
Równoważną jej liczbą dziesiętną jest liczba o postaci:.
(15 x 16
2
) + (3 x 16
1
) + (10 x 16
0
) + (12 x 16
-1
) + (8 x 16
-2
) = 3898,78125
10
Przykład 1.7:
Liczba zapisana w systemie heksadecymalnym ma postać: 3F
16
. Liczba ta oznacza liczbę powstałą przez sumowanie:
(3 x 16
1
) + (15 x 16
0
) = 63.
Konwersji dziesiętno - szesnastkowej można dokonać na drodze wielokrotnego dzielenia na 16 części całkowitej oraz mnożenia przez 16
części ułamkowej przetwarzanej liczby dziesiętnej.
Przykład 1.8:
Niech N
10
= 2527,78125
10
2527
10
= 9DF
16
0,78125
10
= C8
16
Wynik konwersji: 2527,78125
10
= 9DF, C8
16
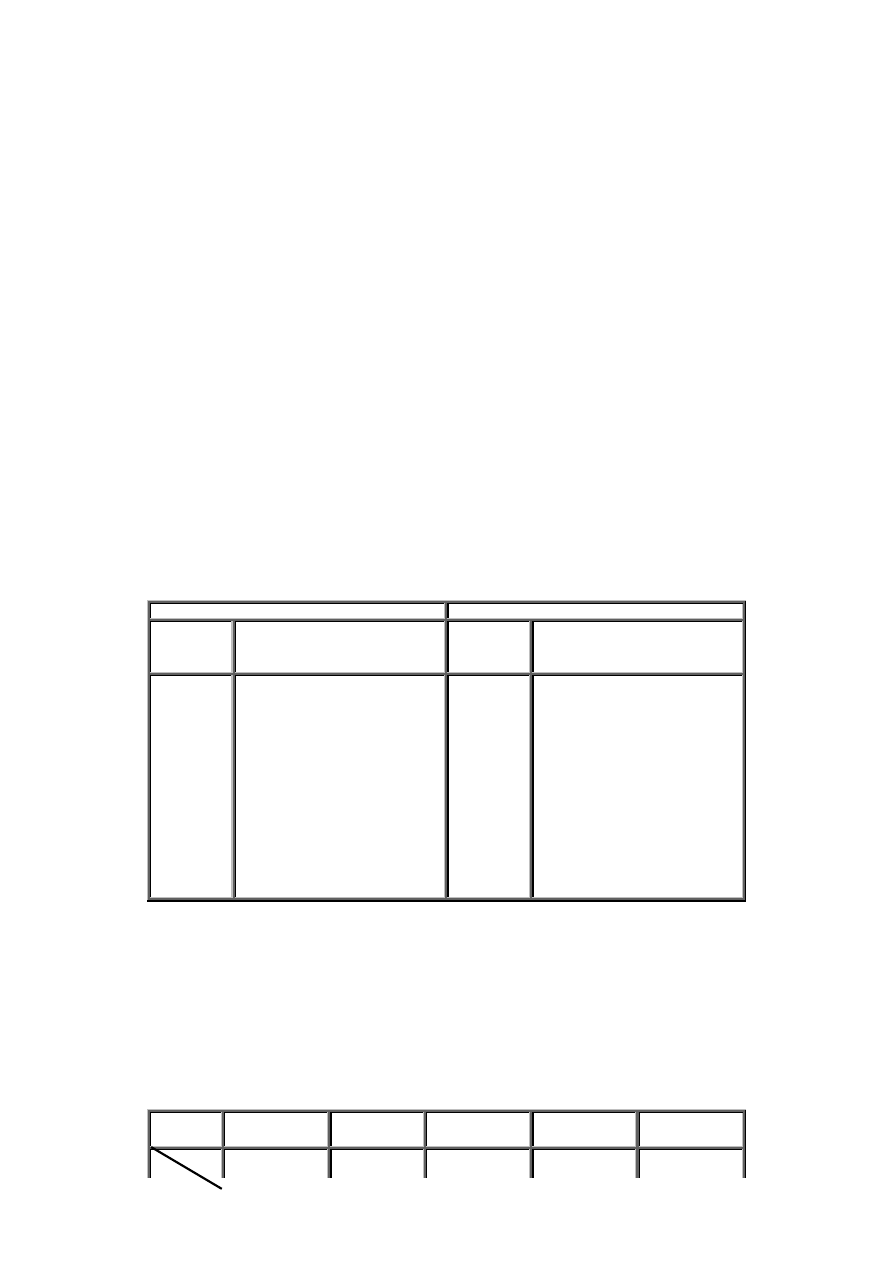
Tablica 1.3 Tablica potęg liczby 2
2
n
n
2
-n
1
0
1.0
2
1
0.5
4
2
0.25
8
3
0.125
16
4
0.062 5
32
5
0.031 25
64
6
0.015 625
128
7
0.007 812 5
256
8
0.003 906 25
512
9
0.001 953125
1 024
10
0.000 976 562 5
2 048
11
0.000 488 281 25
4 096
12
0.000 244 140 625
8 192
13
0.000 122 070 312 5
16 384
14
0.000 061 035 156 25
32 768
15
0.000 030 517 578 125
65 536
16
0.000 015 258 789 062 5
131 072
17
0.000 007 629 394 531 25
262 144
18
0.000 003 814 697 265 625
524 288
19
0.000 001 907 348 632 812 5
1 048 576
20
0.000 000 953 674 316 406 25
2 097 152
21
0.000 000 476 837 158 203 125
4 194 304
22
0.000 000 238 418 579 101 562 5
8 388 608
23
0.000 000 019 209 289 550 781 25
16 777 216
24
0.000 000 059 604 644 775 390 625
33 554 432
25
0.000 000 029 802 322 387 695 312 5
67 108 864
26
0.000 000 014 901 161 193 847 656 25
134 217 728
27
0.000 000 007 450 580 596 923 828 125
268 435 456
28
0.000 000 003 725 290 298 461 914 062 5
536 870 912
29
0.000 000 001 862 645 149 230 957 031 25
1 073 741 824
30
0.000 000 000 931 322 574 615 478 515 625
2 147 483 648
31
0.000 000 000 465 661 287 307 739 257 812 5
4 294 967 296
32
0.000 000 000 232 830 643 653 869 628 906 25
8 589 934 592
33
0.000 000 000 116 415 321 826 934 814 453 125
17 179 869 184
34
0.000 000 000 058 207 660 913 467 407 226 562 5
34 359 738 368
35
0.000 000 000 029 103 830 456 733 703 613 281 25
68 719 476 736
36
0.000 000 000 014 551 915 228 366 851 806 640 625
Liczba przedstawiona w systemie dwójkowym może być bezpośrednio przetworzona na liczbę przedstawioną w systemie szesnastkowym.
W tym celu należy liczbę dwójkową podzielić na grupy czterobitowe (tetrady) poczynając od przecinka w lewo i w prawo i zastąpić otrzymane
tetrady ekwiwalentnymi cyframi szesnastkowymi.
Przykład 1.9
Niech N
2
= 11010101000,1111010111
0110
1010
1000,
1111
0101
1100
6
A
8,
F
5
C
zatem 1101010100,1111010111
2
= 6A8,F5C
H
6
1.2.
Kody
Kodem nazywamy reguły uporządkowujące poszczególne kombinacje zmiennych. Parametry określające kod to:
§
długość m – jest to liczba bitów informacji albo liczba zmiennych,
§
pojemność P – jest to liczba kombinacji wartości zmiennych występujących w kodzie.
W celu zautomatyzowania procesów przetwarzania i transmisji informacji dyskretnej, zamiast znaków graficznych, którymi posługujemy
się na co dzień, są wykorzystywane specjalne kody zbudowane z bardzo prostych symboli w systemach cyfrowych. Za pomocą kodów najczęściej
opisuje się liczby. W układach cyfrowych najczęściej stosuje się dwójkowy system kodowy, zwany kodem binarnym, i jego szczególny przypadek
system dwójkowo – dziesiętny.
Kody zbudowane z symboli dwuwartościowych noszą nazwę kodów dwójkowych. Symbole dwuwartościowe (lub dwójkowe), które
przyjmują wartości cyfrowe 0 lub 1, nazywają się bitami. Znaki przedstawia się w postaci ciągów symboli dwójkowych, a ciągi te nazywane są
słowami kodowymi. Inaczej mówiąc, m (czyt. liczba) bitów, które odpowiadają wartościom M zmiennych tworzy tzw. słowo dwójkowe (kodowe).
Jedno słowo dwójkowe składające się z m bitów informacji może reprezentować 2
m
różnych elementów informacji, np. kod dwójkowy złożony z
siedmiu bitów umożliwia zakodowanie 2
7
= 128 znaków. Kodowanie za pomocą kodu dwójkowego oznacza zapisanie liczb w systemie dwójkowym.
Najlepiej jest, gdy wszystkie znaki są przedstawione za pomocą słów kodowych o jednakowej długości. Z uwagi na szybkość i wydajność
procesów przetwarzania informacji, należy posługiwać się słowami o jak najmniejszej długości.
Kodowanie informacji pozwala na zmniejszenie liczby torów transmisji potrzebnych do przesłania tej informacji. Natomiast dekodowanie
pozwala nam przywrócić do pierwotnego systemu.
Kody możemy podzielić na:
1.
W zależności od parametru P kody zupełne i niezupełne:
§
kody zupełne, które zawierają wszystkie możliwe kombinacje wartości zmiennych,
§
kody niezupełne, które nie wykorzystują wszystkich kombinacji.
2.
Kody systematyczne i niesystematyczne:
§
kody systematyczne tworzy się na podstawie reguły formalnej, w której każda kombinacja wartości zmiennych jest zdefiniowana w sposób
jednoznaczny, do kodów systematycznych zaliczamy m.in. wszystkie kody wagowe,
§
kody niesystematyczne wymagają podania tabeli, która określa kolejność poszczególnych kombinacji występujących w dowolnym porządku, do
kodów niesystematycznych zaliczamy kod Watha, dalekopisowy i inne.
3.
Kody dwójkowe wagowe i niewagowe.
Jeśli każdy bit (pozycja) kodu dwójkowego ma określoną i niezmienną wagę (znaczenie) liczbową to taki kod nazywamy kodem
wagowym; pozostałe kody są kodami niewagowymi. Wagi są przeważnie liczbami całkowitymi i mogą przyjmować wartości ujemne. Wartości
liczbowe słowa kodowego będą sumą wag tych pozycji, które zawierają jedynki. Najprostszym wagowym kodem dwójkowym jest tzw. naturalny kod
dwójkowy (kod binarny, kod BIN) (tablica 1.4).
Wagi naturalnego kodu dwójkowego n - bitowego (n - pozycyjnego) wynoszą 2
i
, (gdzie i = 0, 1, 2, ..., 2
n-1
), tzn. są kolejnymi potęgami
liczby 2.
Powszechnie stosowanym kodem dwójkowym niewagowym jest kod Graya, w którym sąsiednie słowa różnią się wartością tylko jednego
bitu.
Tablica 1.4 Kody 4 – bitowe: naturalny i Graya
Kod Dwójkowy
Kod Graya
A B C D
8 4 2 1
X Y W Z
Niewagowy
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 0 0 0
0 0 0 1
0 0 1 1
0 0 1 0
0 1 1 0
0 1 1 1
0 1 0 1
0 1 0 0
1 1 0 0
1 1 0 1
1 1 1 1
1 1 1 0
1 0 1 0
1 0 1 1
1 0 0 1
1 0 0 0
4.
Kody dwójkowo – dziesiętne.
Ważną odmianę kodów dwójkowych stanowią kody dwójkowo - dziesiętne BCD (ang. Binary Coded Decimal). W kodach tych
poszczególne cyfry dziesiętne są przedstawione w kodzie dwójkowym, każdej cyfrze kodu dziesiętnego są przyporządkowane cztery bity kodu
binarnego. Do zakodowania dziesięciu cyfr potrzebne są co najmniej cztery bity, bo: 2
3
< 10 < 2
4
. Sześć spośród szesnastu kombinacji kodu 4 -
bitowego nie będzie wykorzystanych.
Kody BCD mogą być wagowe i niewagowe (przedstawione w tablicy 1.5 i 1.6). W kodach wagowych każda pozycja ma określoną wagę.
Ciąg wag kodu jest zwykle używana jako nazwa kodu.
Podstawowym wagowym kodem BCD jest kod 8421 BCD lub po prostu kod BCG (tablica 1.5), w którym wykorzystuje się pierwsze
dziesięć tetrad 4 – bitowego naturalnego kodu dwójkowego.
Przykładem kodu niewagowego BCD jest kod z nadmiarem 3 (tablica 1.6). Kod ten otrzymuje się dodając trzy do cyfry dziesiętnej i
zapisując ją następnie w kodzie 8421. W kodzie nie ma możliwości przypisania wagi każdej pozycji.
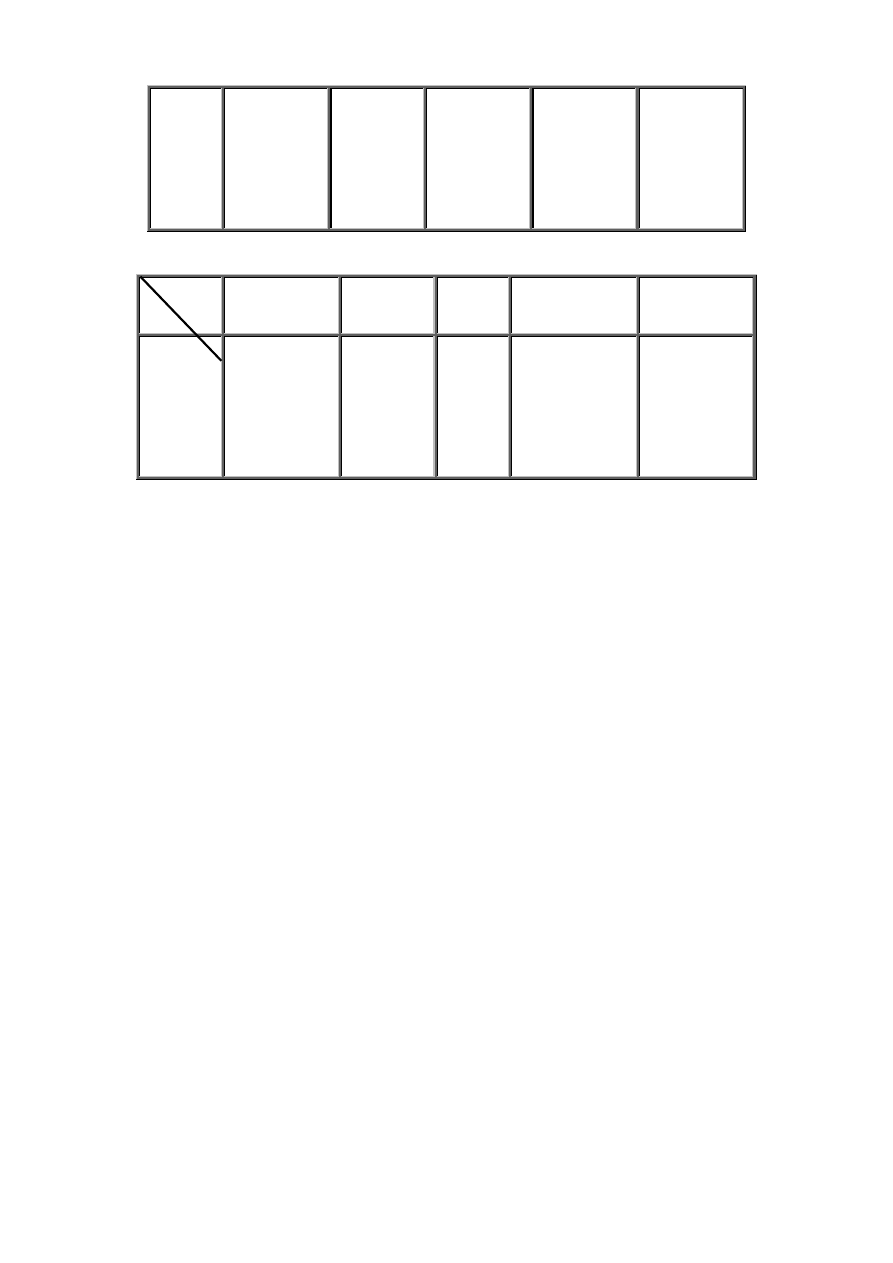
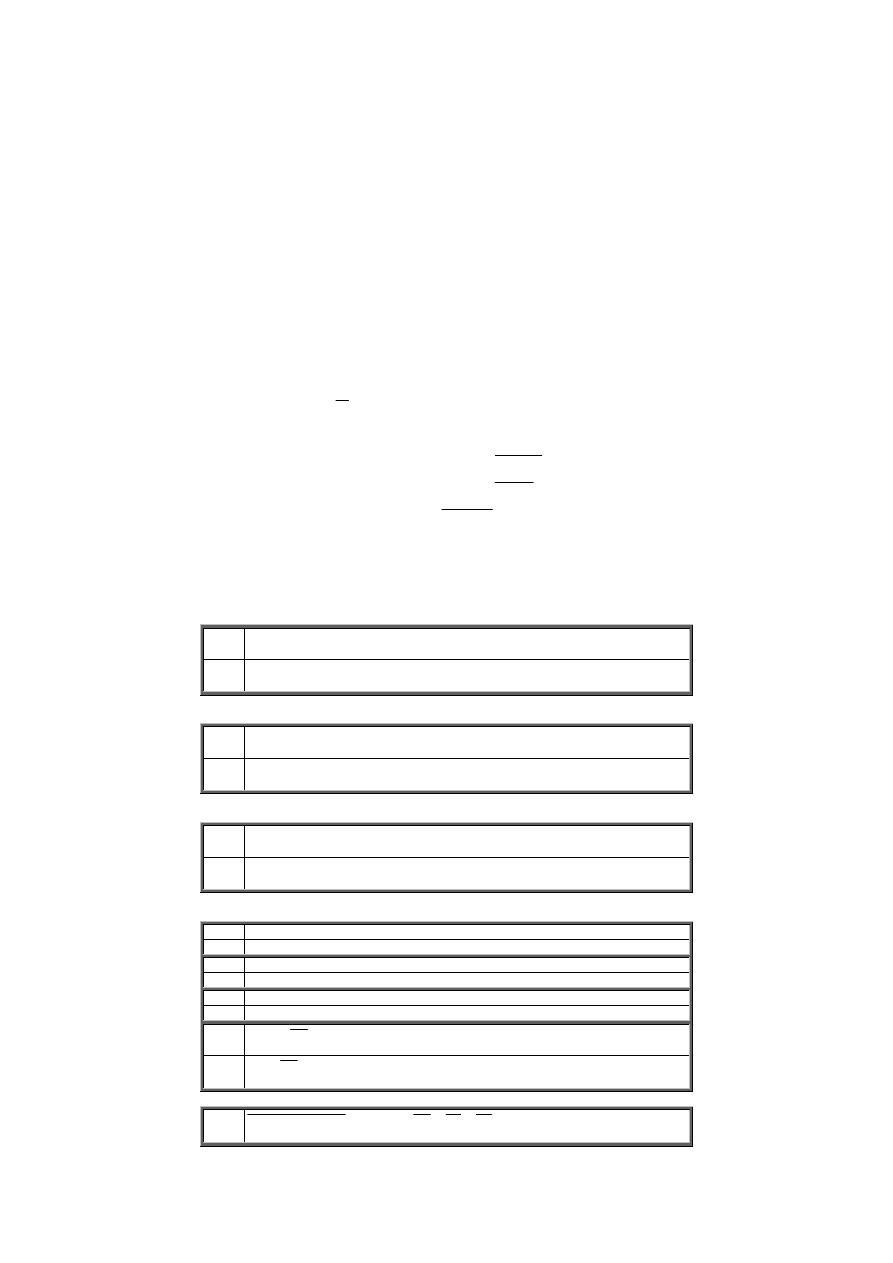
Tablica 1.5 Kody dwójkowo – dziesiętne wagowe
Kod:
Naturalny
Aikena
Wagi
Cyfra
8 4 2 1
2* 4 2 1
2 4 2 1
7 4 2 1
8 4-2-1
7
0
1
2
3
4
5
6
7
8
9
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 1 1 0
1 1 1 1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
0 0 0 1
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
1 0 0 0
1 0 0 1
1 0 1 0
0 0 0 0
0 1 1 1
0 1 1 0
0 1 0 1
0 1 0 0
1 0 1 1
1 0 1 0
1 0 0 1
1 0 0 0
1 1 1 1
Tablica 1.6 Kody dwójkowo – dziesiętne niewagowe
Kod:
Cyfra
Z nadmiarem 3 ( + 3,
plus 3,
excess 3. XS3)
Graya z
nadmiarem 3
Wattsa
Johnsona
pseudopierście
niowy
Wskaźników
cyfrowych
siedmiosegmentowyc
h
0
1
2
3
4
5
6
7
8
9
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
0 0 1 0
0 1 1 0
0 1 1 1
0 1 0 1
0 1 0 0
1 1 0 0
1 1 0 1
1 1 1 1
1 1 1 0
1 0 1 0
0 0 0 0
0 0 0 1
0 0 1 1
0 0 1 0
0 1 1 0
1 1 1 0
1 0 1 0
1 0 1 1
1 0 0 1
1 0 0 0
0 0 0 0 0
0 0 0 0 1
0 0 0 1 1
0 0 1 1 1
0 1 1 1 1
1 1 1 1 1
1 1 1 1 0
1 1 1 0 0
1 1 0 0 0
1 0 0 0 0
0 1 1 1 1 1 1
0 0 0 0 1 1 0
1 0 1 1 0 1 1
1 0 0 1 1 1 1
1 1 0 0 1 1 0
1 1 0 1 1 0 1
1 1 1 1 1 0 0
0 0 0 0 1 1 1
1 1 1 1 1 1 1
1 1 0 0 1 1 1
8
2.
PODSTAWOWE FUNKCJE LOGICZNE I FUNKTORY UK
ŁADÓW LOGICZNYCH
2.1.
Wst
ęp
Istotą techniki cyfrowej jest wytwarzanie cyfrowych sygnałów wyjściowych jako odpowiedzi na cyfrowe sygnały wejściowe. Na przykład
sumator przetwarza doprowadzone do wejść dwie liczby 16 – bitowe na sumę 16 - bitową tych liczb oraz bit przeniesienia. Można także zbudować
układ do mnożenia dwóch liczb. Są to operacje w rodzaju tych, jakie powinna wykonywać jednostka arytmetyczna komputera. Innym zadaniem może
być porównanie dwóch liczb w celu sprawdzenia, która z nich jest większa.
Typowymi zadaniami układów cyfrowych jest pobranie pewnych liczb binarnych, ich wyświetlenie, wydrukowanie lub wydziurkowanie
jako znaków dziesiętnych. We wszystkich tych zadaniach sygnały (stany) wyjściowe są zdeterminowanymi funkcjami sygnałów (stanów)
wejściowych. Wszystkie zadania mogą być wykonane za pomocą urządzeń zwanych bramkami, które realizują działania algebry Boole’a w
dziedzinie układów dwustanowych (binarnych) i sieci złożonych z takich elementów, którymi są bramki. Każda ze zmiennych boolowskich może być
równa tylko zeru lub równa tylko jedynce. To założenie można zapisać w postaci:
X = 0, jeśli X
≠ 1
X
≠ 1, jeśli X = 0
Funkcję, której zmienne lub ona sama przyjmuje wartości ze zbioru {0, 1} nazywamy funkcją boolowską (logiczną, przełączającą).
Natomiast układ przetwarzający logiczne sygnały wejściowe na logiczne sygnały wyjściowe nazywa się układem logicznym.
Przy projektowaniu dwustanowych (0 – stan niski, 1 – stan wysoki) układów cyfrowych posługujemy się algebrą Boole’a.
Algebra Boole’a, którą stosujemy w układach, opiera się na trzech zasadniczych funkcjach, którymi są:
§
Iloczyn logiczny I (ang. AND),
Y = A · B
§
Suma logiczna LUB (ang. OR),
Y = A + B
§
Negacja (inwersja) NIE (ang. NOT),
A
Y
=
Stosowane są również operatory złożone (pochodne), jak:
§
Suma zanegowana:
B
A
Y
+
=
NOR
§
Iloczyn zanegowany:
B
A
Y
⋅
=
NAND
§
Równoważność:
B
A
Y
⊕
=
EX-NOR
§
Nierównoważność, zwana sumą modulo 2:
B
A
Y
⊕
=
EOR, XOR
Jedną z postaci algebry Boole’a jest znany rachunek zdań, gdzie zamiast znaków sumy + stosuje się łącznik lub, zamiast znaku iloczynu –
łącznik i, a do negacji używamy słowa nie. Algebra Boole’a posługuje się szeregiem praw i tożsamości.
W algebrze Boole’a obowiązują następujące podstawowe prawa:
1.
Prawo przemienności mnożenia i dodawania:
a
A+B = B+A
b
A · B = B · A
2.
Prawo łączności:
a
mnożenia
A+B+C = A+(B+C) = (A+B)+C
b
dodawania
A · B · C = A · (B · C) = (A · B) ·C
3.
Prawo rozdzielczości:
a
mnożenia względem dodawania
A ·(B + C) = A · B + A ·C
b
dodawania względem mnożenia
A + B · C = (A + B) · (A + C)
4.
Prawa podstawowe:
a
A + 1 = 1
b
A · 1 = A
a
A + 0=A
b
A · 0 = 0
a
A + A = A
b
A · A = A
a
A
A
A
=
+
b
0
A
A
=
⋅
5.
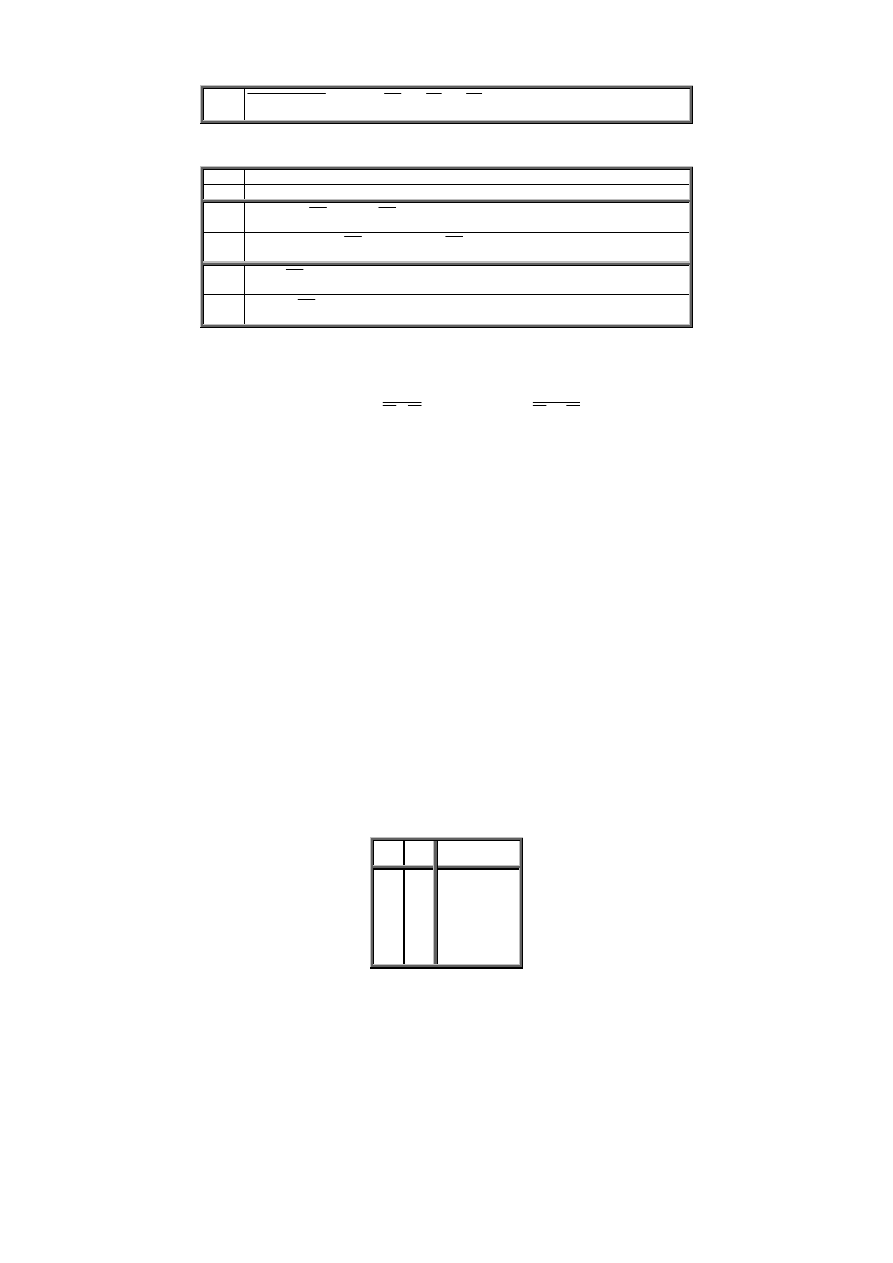
Prawa de Morgana:
a
...
C
B
A
...
C
B
A
⋅
⋅
⋅
=
+
+
+
9
b
...
C
B
A
...
C
B
A
+
+
+
=
⋅
⋅
⋅
6.
Podstawowe tożsamości algebry Boole’a:
a
A · B + A · C = A · (B + C)
b
(A + B) · (A + C) = A + B · C
a
A · B +B·C+
A
·C=A·B+
A
-C
b
(A + B) · (B + C) · (
A
+C) = (A+B) · (
A
+ C)
a
A · B +
A
· B = B
b
(A + B) · (
A
+ B) = B
Funkcje: sumy, iloczynu i negacji tworzą tzw. podstawowy system funkcjonalnie pełny. System funkcji logicznych nazywamy
funkcjonalnie pełnym, jeśli za pomocą zasad superpozycji i podstawiania argumentów można uzyskać dowolną funkcję logiczną. Podstawowy system
funkcjonalnie pełny nie jest minimalny, ponieważ sumę lub iloczyn można zrealizować za pomocą dwóch pozostałych operatorów, korzystając z
praw de Morgana:
B
A
B
A
⋅
=
+
B
A
B
A
+
=
⋅
Operacja sumy logicznej jest zdefiniowana następująco:
§
jeżeli co najmniej jeden z argumentów jest równy 1, to wynik jest równy 1. Zatem suma logiczna jest równa 0 tylko dla przypadku, gdy
wszystkie argumenty są równe 0.
Operacja iloczynu logicznego jest zdefiniowana następująco:
§
wynik iloczynu jest równy 1, wtedy i tylko wtedy, gdy wszystkie argumenty przyjmują wartość 1.
Operacja negacji jest operacją jednoargumentową i jest zdefiniowana jako zmiana wartości argumentu, tj. jeśli argument ma wartość 1, to
operacja ta daje w wyniku wartość 0, a jeśli argument ma wartość 0, to operacja ta daje w wyniku wartość 1.
Łatwo można wykazać, że:
§
dowolna n - argumentowa funkcja logiczna jest określona dla 2
n
różnych kombinacji argumentów,
§
liczba różnych n - argumentowych funkcji logicznych jest skończona i równa 2
n
.
Dowolną funkcję logiczną można wyrazić przez funkcje logiczne dwóch zmiennych (tablica 2.1). Kilka funkcji przedstawionych w tablicy
2.1 jest szczególnie interesujących, ponieważ są one realizowane za pomocą układów w postaci bramek scalonych TTL.
Do funkcji takich należą funkcje:
§
I (AND),
§
LUB (OR),
§
I - NIE (NAND),
§
LUB - NIE (NOR),
§
ALBO (Ex - OR),
§
NIE (NOT) oraz wzmacniacz logiczny (IDENTITY), które są omówione w podrozdziale 2.4.
2.2.
Podstawowe funkcje logiczne
Funkcja I (AND)
Do przedstawienia iloczynu logicznego X np. dwu zmiennych A i B są stosowane wyrażenia:
B
A
B
A
AB
A·B
X
∧
=
∩
=
=
=
Najczęściej używane jest pierwsze i drugie wyrażenie. Funkcję I (AND) dwóch zmiennych boolowskich przedstawiono na rys. 2.1.
Funkcja iloczynu logicznego przyjmuje wartość 1 wtedy i tylko wtedy, gdy wszystkie zmienne, A i B przyjmują wartość 1. W każdym
innym przypadku iloczyn logiczny tych sygnałów wynosi 0.
A
B
X = AB
0
0
0
0
1
0
1
0
0
1
1
1
Rys. 2.1 Tablica dwuargumentowej funkcji I (AND).
10
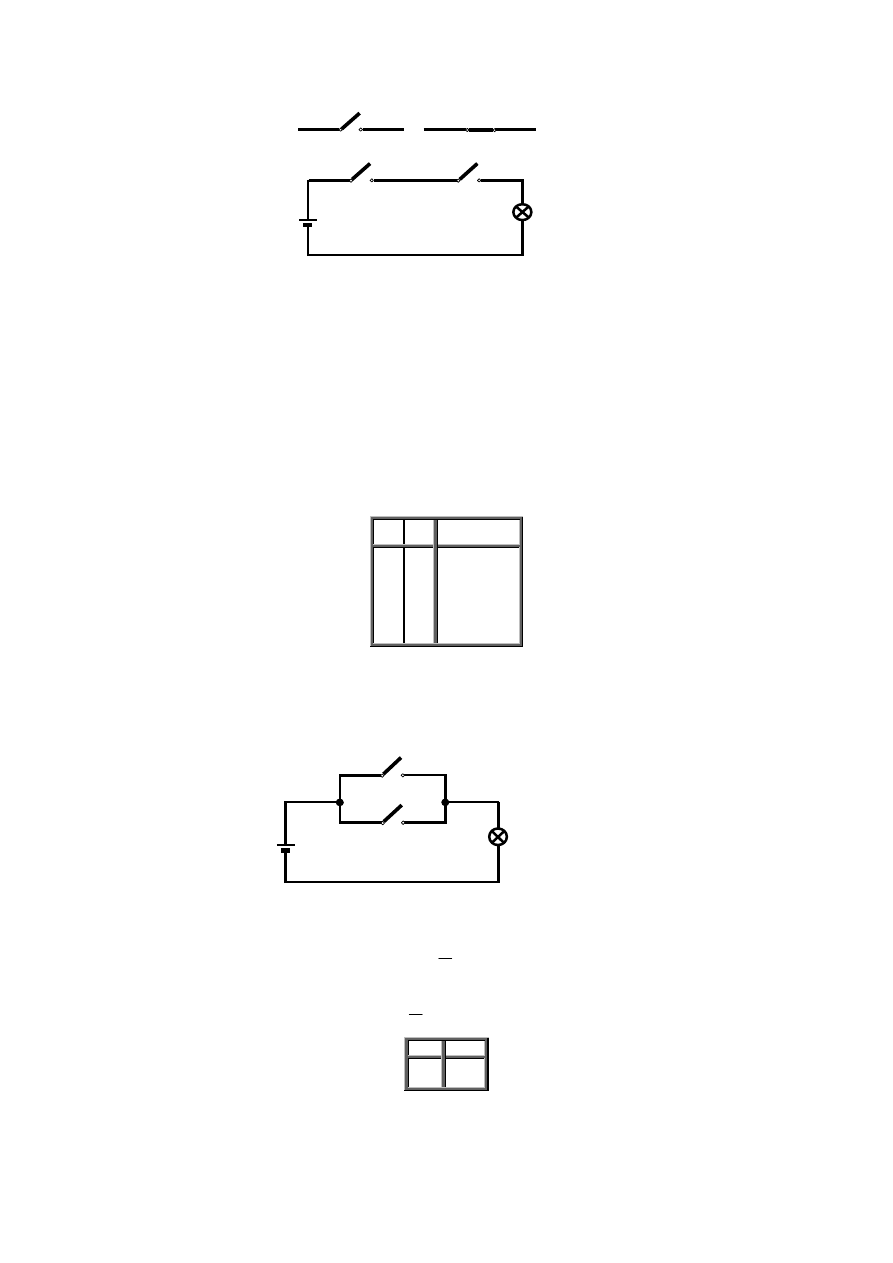
Rys. 2.2 Realizacja fizyczna dwuargumentowej funkcji I (AND)
Operację iloczynu logicznego X, realizują szeregowo połączone klucze A i B w obwodzie elektrycznym. Napięcie baterii będzie
wykorzystane do rozświecenia żarówki, tzn. X = 1 tylko wtedy, jeśli zarówno klucz A, jak i klucz B będą zamknięte, tzn. A = 1 i B = 1 (patrz rys.
2.1).
Funkcja LUB (OR)
Do przedstawienia sumy logicznej Y np. dwu zmiennych A i B są stosowane wyrażenia:
B
A
B
A
B
A
Y
∨
=
∪
=
+
=
Najczęściej używane jest pierwsze wyrażenie.
Jeżeli na wejścia układu podamy sygnał A i sygnał B, to na jego wyjściu otrzymamy sygnał będący ich sumą A + B. Przyjmuje ona poziom
1, gdy A lub B ma poziom 1. Funkcja sumy logicznej przyjmuje wartość 0 wtedy, gdy wszystkie zmienne przyjmują wartość 0.
Funkcję LUB (OR) dwóch zmiennych boolowskich przedstawiono na rys. 2.3, który ilustruje różnicę między sumą logiczną a sumą
arytmetyczną. W ostatnim wierszu tablicy widzimy, że 1 + 1 = 1 dla sumy logicznej. Liczba zmiennych sumowanych logicznie może być dowolna.
A
B
Y=A+B
0
0
0
0
1
1
1
0
1
1
1
1
Rys. 2.3 Tablica dwuargumentowej funkcji LUB (OR).
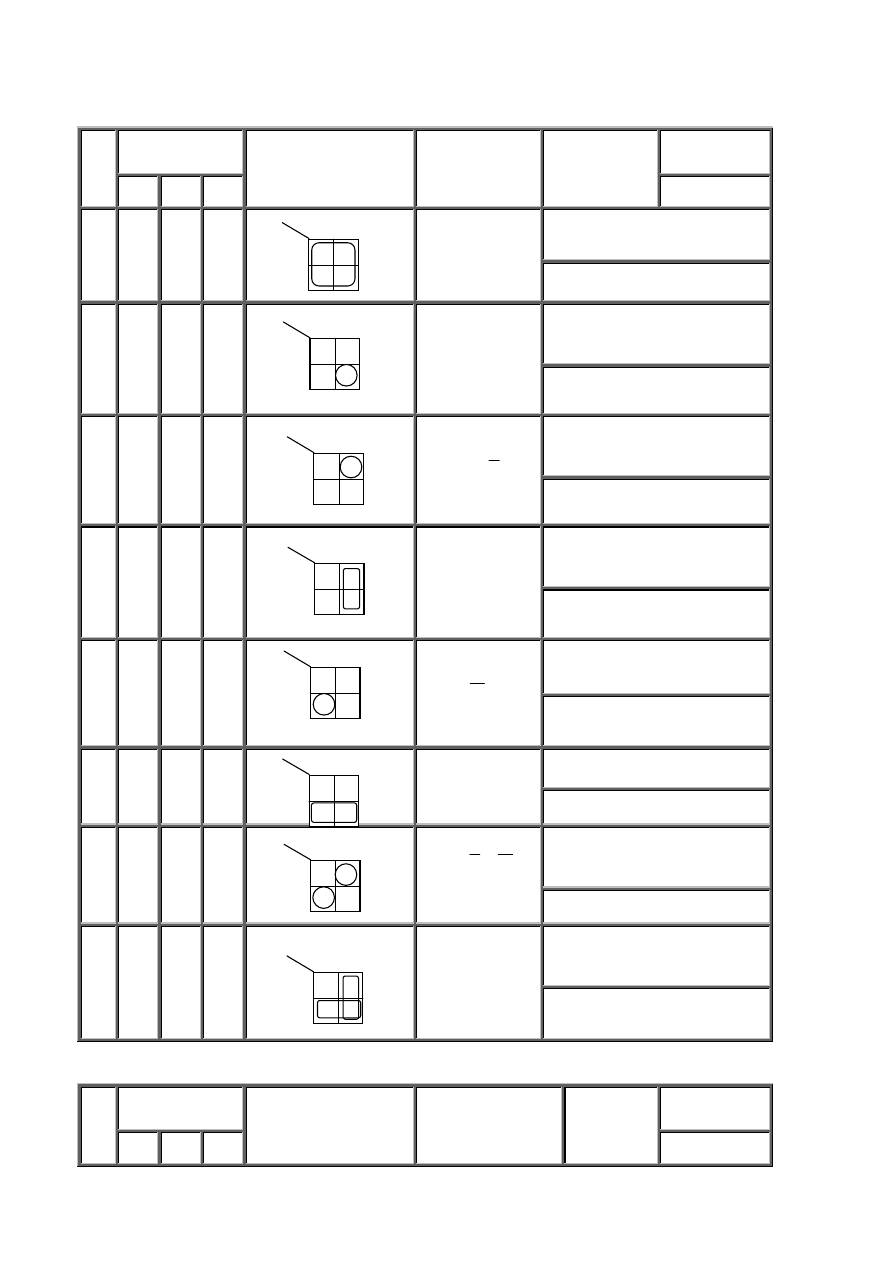
Obwód elektryczny z równolegle połączonymi kluczami A i B, które realizują operację sumy logicznej Y, jest przedstawiony na rys. 2.4.
Napięcie baterii rozświeci żarówkę, tzn. Y = l, wówczas, gdy klucz A lub klucz B, lub obydwa są zamknięte (patrz rys. 2.3).
Rys. 2.4 Realizacja fizyczna dwuargumentowej funkcji LUB (OR).
Funkcja NIE (NOT)
Do przedstawienia negacji N np. zmiennej A są stosowane wyrażenia:
'
A
A
N
=
=
Najczęściej używane jest pierwsze wyrażenie. Symbol A odczytuje się jako „nie A” lub „A zanegowane”, lub „dopełnienie A".
Funkcja NIE (NOT) polega na inwersji (negacji) zmiennej, zamienia stan wysoki (1) na stan niski (0) lub odwrotnie. Jeżeli na wejście
podamy sygnał logiczny A, to na wyjściu otrzymamy jego negację
A
(„nie A”). Funkcję NIE (NOT) przedstawiono na rys. 2.5.
A
N
0
1
1
0
Rys. 2.5 Tablica funkcji NIE (NOT).
1.
2.
3.
4.
U
1
A
B
X = AB
Y = A+B
A
B
11
Tablica 2.1 Funkcje dwóch zmiennych
Tablica wartości
polskim
i
X
Y
f
i
Tablica Karnaugha
Zapis algebraiczny
Nazwa funkcji w
języku
angielskim
stała 0
0
0
0
1
1
0
1
0
1
0
0
0
0
f
0
= 0
ZERO
NULL FUNCTION
I
Koniunkcja
1
0
0
1
1
0
1
0
1
0
0
0
1
f
1
= X
⋅
Y
AND
CONJUNCTION
Zakaz przez Y
2
0
0
1
1
0
1
0
1
0
0
1
0
f
2
= X
⋅
Y
INHIBIT
Zmienna X
3
0
0
1
1
0
1
0
1
0
0
1
1
f
3
= X
INDENTITY X
Zakaz przez X
4
0
0
1
1
0
1
0
1
0
1
0
0
f
4
=
Y
X
⋅
INHIBIT
Zmienna Y
5
0
0
1
1
0
1
0
1
0
1
0
1
f
5
= Y
IDENTITY Y
ALBO
Suma modulo 2
Wyłącznie LUB
6
0
0
1
1
0
1
0
1
0
1
1
0
f
6
=
Y
X
Y
X
+
Y
X
⊕
=
EXCLUSIVE - OR
LUB
Dysjunkcja
Alternatywa
7
0
0
1
1
0
1
0
1
0
1
1
1
f
7
= X +Y
OR
DISJUNCTION
Tablica 2.1 Funkcje dwóch zmiennych – ciąg dalszy
Tablica wartości
polskim
i
X
Y
f
i
Tablica Karnaugha
Zapis algebraiczny
Nazwa funkcji w
języku
angielskim
X
0 1
Y
0
1
0
0 1
0 1
X
0 1
Y
0
1
0
0 1
0 0
X
0 1
Y
0
1
0
0 0
0 1
X
0 1
Y
0
1
0
0 0
0 0
X
0 1
Y
0
1
0
0 0
1 0
X
0 1
Y
0
1
0
0 0
1 1
X
0 1
Y
0
1
0
0 1
1 0
X
0 1
Y
0
1
0
0 1
1 1
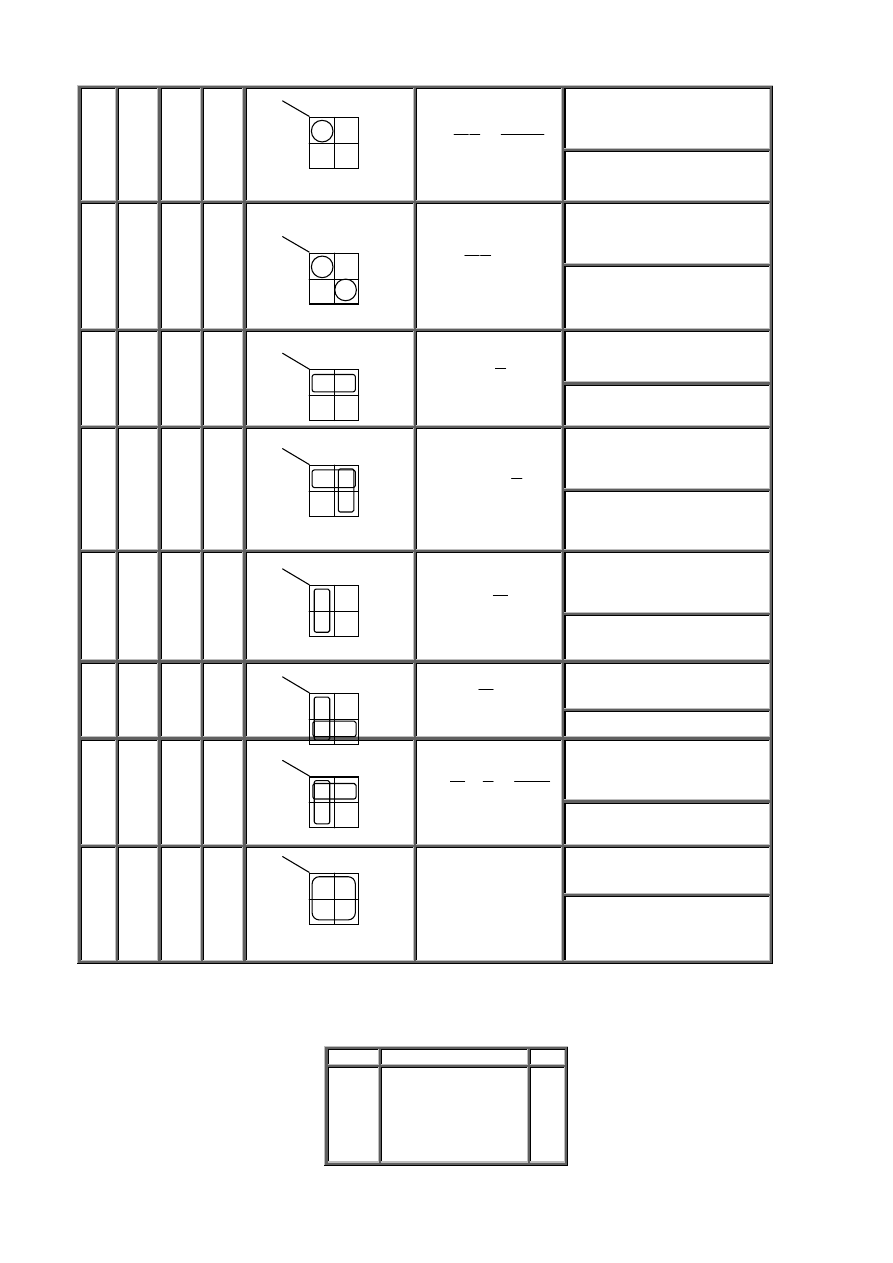
12
LUB – NIE
Strzałka Peirce’a
8
0
0
1
1
0
1
0
1
1
0
0
0
f
8
=
Y
X
Y
X
+
=
NOR
PEIRCE FUNCTION
ALBO – NIE
Równoważność
9
0
0
1
1
0
1
0
1
1
0
0
1
f
9
=
Y
X
Y
X
XY
⊗
=
+
EXCLUSIVE – NOR
EQUALITY
COINCIDENCE
Negacja Y
10
0
0
1
1
0
1
0
1
1
0
1
0
f
10
=
Y
NOT Y
Implikacja X przez Y
11
0
0
1
1
0
1
0
1
1
0
1
1
f
11
=
Y
X
+
IMPLICATION
Negacja X
12
0
0
1
1
0
1
0
1
1
1
0
0
f
12
=
X
NOT X
Implikacja Y przez X
13
0
0
1
1
0
1
0
1
1
1
0
1
f
13
=
Y
X
+
IMPLICATION
I – NIE
Kreska Sheffera
14
0
0
1
1
0
1
0
1
1
1
1
0
f
14
=
Y
X
Y
X
⋅
=
+
NAND
SHEFFER STROKE
Stała1
15
0
0
1
1
0
1
0
1
1
1
1
1
f
15
= 1
ONE
2.3.
SPOSOBY PRZEDSTAWIANIA FUNKCJI LOGICZNYCH
Do przedstawiania funkcji logicznych służy nam opis słowny. Na podstawie opisu można sporządzić tablicę wartości (rys. 2.6), zwaną
tablicą wierności lub tablicą prawdy (ang. Truth Table).
j
X
0
X
1
X
2
. . X
n-1
f
0
1
2
3
M
2
n
– 1
0 0 0 . . . 0
0 0 0 . . . 1
1 1 1 . . . 1
X
0 1
Y
0
1
0
1 0
0 0
X
0 1
Y
0
1
0
1 0
0 1
X
0 1
Y
0
1
0
1 1
0 1
X
0 1
Y
0
1
0
1 1
0 0
X
0 1
Y
0
1
0
1 0
1 0
X
0 1
Y
0
1
0
1 0
1 1
X
0 1
Y
0
1
0
1 1
1 0
X
0 1
Y
0
1
0
1 1
1 1
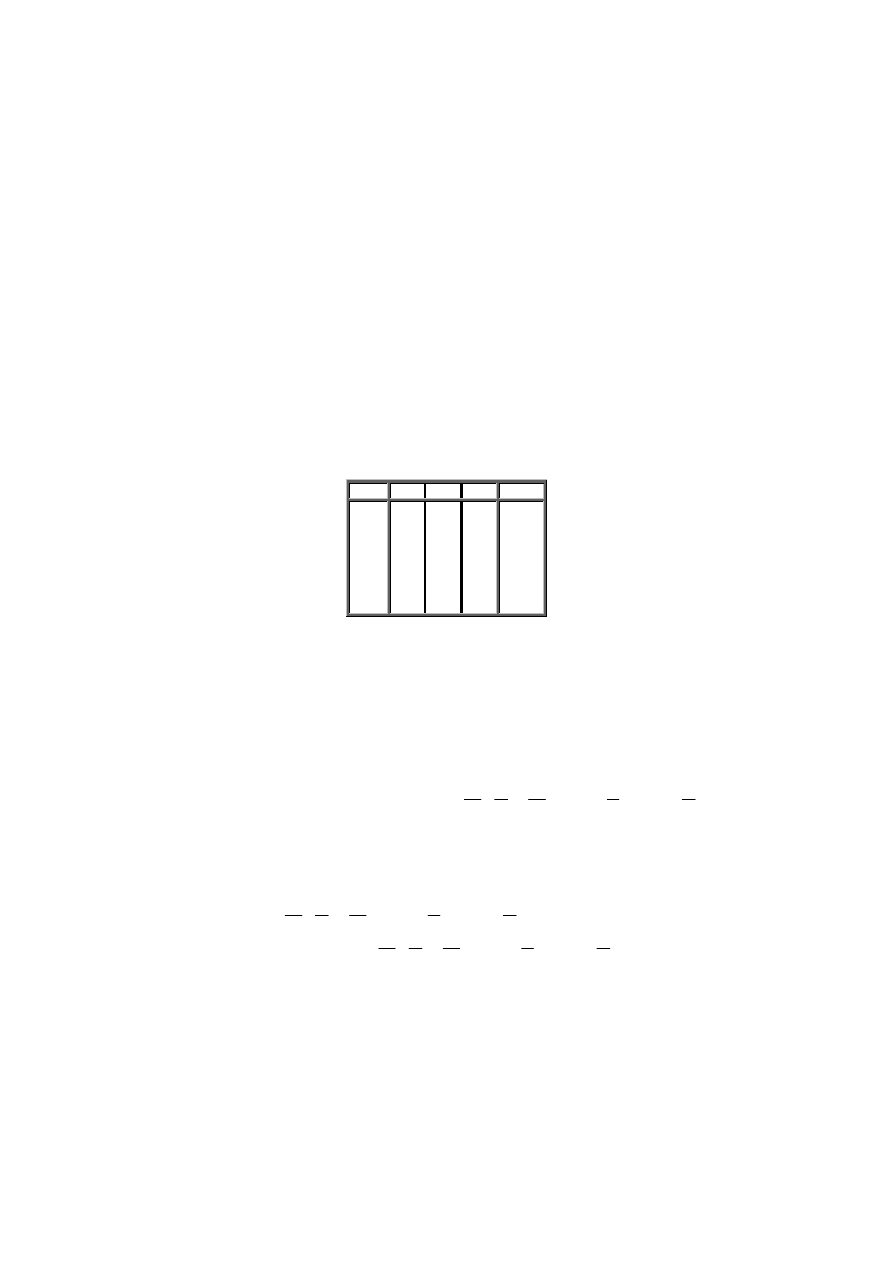
13
Rys. 2.6 Tablica wartości n – argumentowej funkcji logicznej.
Tablice prawdy bramek rzeczywistych operują bądź abstrakcyjnymi stanami logicznymi 0 i 1, bądź dwoma poziomami wielkości
fizycznych określanych umownie jako niski (L) i wysoki (H). Tablica ta składa się z wierszy, w których wpisuje się wszystkie kombinacje zero –
jedynkowe zmiennych niezależnych. Wszystkie kombinacje zmiennych zapisujemy tak, aby tworzyły kolejne liczby dziesiętne zapisane w systemie
dwójkowym. Ostatnia kolumna jest przeznaczona do zapisania wartości funkcji dla poszczególnych kombinacji zero – jedynkowych.
Inną metodą bezpośredniego zapisu funkcji n zmiennych są tablice Karnaugha. Tablice te są prostokątne i zwierają 2
n
pól. Jest to zapis
bardzie zwarty i prostszy w użyciu niż tablica wartości. Tablice Karnaugha są dokładniej opisane w podrozdziale 3.2.
Funkcję logiczną o dowolnej liczbie argumentów można również przedstawić w postaci algebraicznej, za pomocą algebry Boole’a. Postać
ta nie jest zazwyczaj tworzone bezpośrednio z opisu, lecz pośrednio bądź z tablicy wartości, bądź z tablic Karnaugha.
Dowolną funkcję logiczną n zmiennych można przedstawić jako:
U
1
2
0
j
j
j
1
n
1
0
n
I
a
)
X
,...,
X
,
X
(
f
Y
−
=
−
=
=
(2.1)
gdzie:
0
a
j
=
lub 1, a znak
U
oznacza sumę logiczną.
Współczynnik a
j
przyjmuje wartość 1, gdy dla danego j jest
1
I
Y
j
j
=
=
, natomiast wartość 0, gdy
0
I
Y
j
j
=
=
.
Ta postać algebraiczna zapisu funkcji nosi nazwę dysjunkcyjnej postaci kanonicznej i jest nazywana krótko postacią
U
I
.
Przykład 2.1:
Wyrazić funkcję f(X, Y, Z), zadaną tablicą wartości z rys. 2.7 w postaci
U
I
.
j
X
Y
Z
f
0
1
2
3
4
5
6
7
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
0
1
1
0
1
1
0
Rys. 2.7 Tablica wartości funkcji f(X, Y, Z).
Jak wynika z tablicy wartości, funkcja ta przyjmuje wartość 1 w wierszach 2, 3, 5 i 6, a wartość 0 w pozostałych wierszach. Zatem funkcja
f(X, Y, Z) wyrażona jako
U
I
przyjmuje postać:
7
6
5
4
3
2
1
0
1
2
0
j
j
j
I
0
I
1
I
1
I
0
I
1
I
1
I
0
I
0
I
a
)
Z
,
Y
,
X
(
f
3
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
=
−
=
U
Każdy składnik typu
0
I
0
j
=
⋅
nie zmienia wartości funkcji, może więc być wyeliminowany. Wtedy funkcja ta przyjmuje postać:
Z
XY
Z
Y
X
YZ
X
Z
Y
X
I
I
I
I
)
Z
,
Y
,
X
(
f
6
5
3
2
+
+
+
=
+
+
+
=
Jako składniki sumy wchodzą te iloczyny I
j
, które odpowiadają kombinacjom zero – jedynkowym zmiennych niezależnych i, dla których
funkcja przyjmuje wartość 1.
Jeśli funkcja zależy od wielu argumentów, to tworzenie postaci kanonicznej jest pracochłonne i dlatego często jest stosowany zapis
skrócony (liczbowy), polegający na wpisywaniu odpowiednich liczb dziesiętnych, symbolizujących składniki jedności.
Przykład 2.2:
Wyrazić funkcję
Z
XY
Z
Y
X
YZ
X
Z
Y
X
)
Z
,
Y
,
X
(
f
+
+
+
=
w postaci zapisu liczbowego
U
I
.
=
+
+
+
=
Z
XY
Z
Y
X
YZ
X
Z
Y
X
)
Z
,
Y
,
X
(
f
{
{
{
{
U
)
6
,
5
,
3
,
2
(
110
101
011
010
6
5
3
2
=
=
+
+
+
=
Drugą postacią algebraiczną funkcji n – zmiennych jest koniunkcyjna postać kanoniczna, nazywana
I
S
.
I
1
2
0
j
j
j
1
n
1
0
n
)
S
a
(
)
X
,...,
X
,
X
(
f
Y
−
=
−
+
=
=
(2.2)
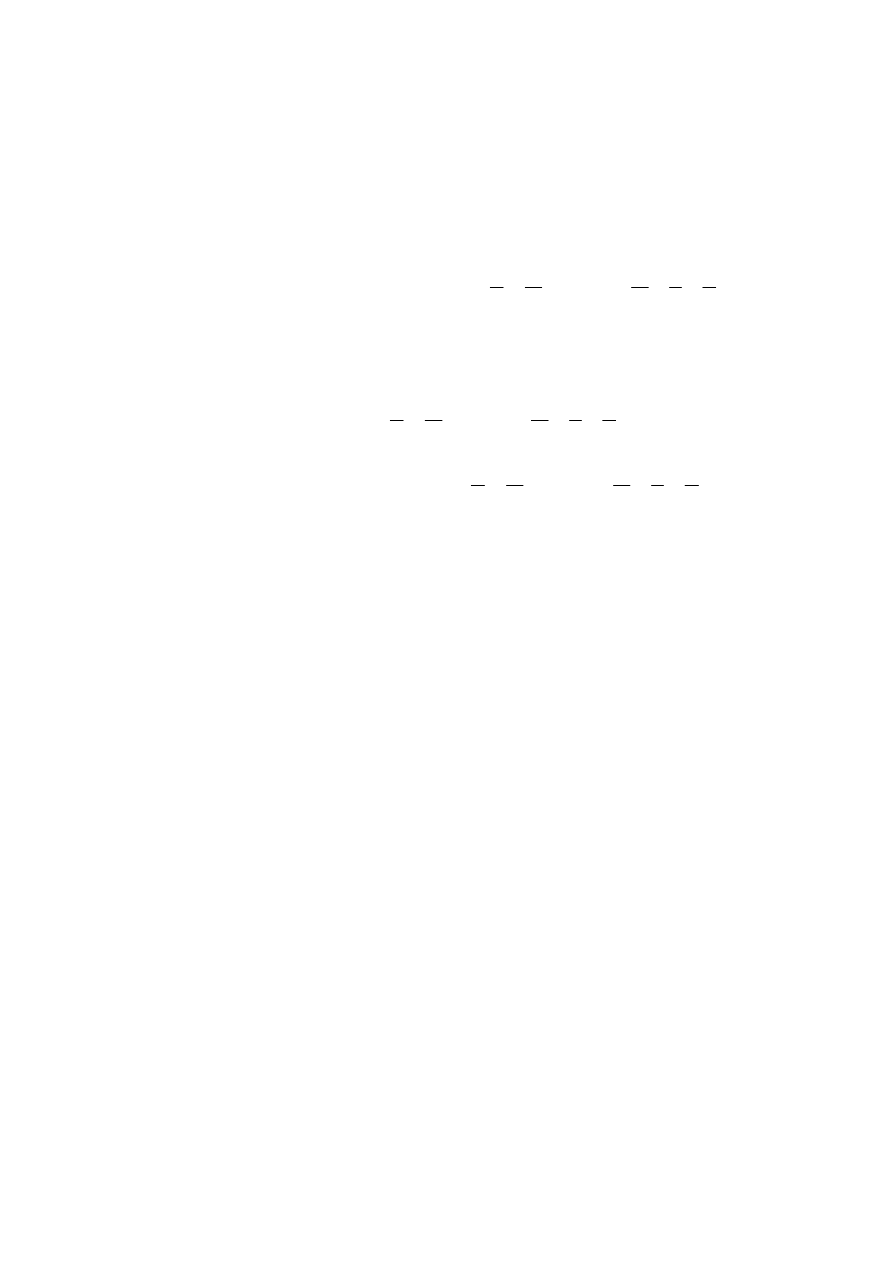
14
gdzie:
0
a
j
=
lub 1, a znak
I
oznacza iloczyn logiczny.
Przykład 2.3:
Wyrazić funkcję f(X, Y, Z) zadaną tablicą wartości z rys. 2.7 w postaci
I
S
.
Jak wynika z tablicy wartości, funkcja ta przyjmuje wartość 0 w wierszach 0, 1, 4 i 7, a wartość 1 w pozostałych wierszach. Zatem funkcja
wyrażona jako
I
S
przyjmuje postać:
)
S
0
)(
S
1
)(
S
1
)(
S
0
)(
S
1
)(
S
1
)(
S
0
)(
S
0
(
)
Z
,
Y
,
X
(
f
7
6
5
4
3
2
1
0
+
+
+
+
+
+
+
+
=
Każdy
czynnik typu
1
S
1
j
=
+
nie zmienia wartości funkcji, może więc być wyeliminowany. Zatem:
)
Z
Y
X
)(
Z
Y
X
)(
Z
Y
X
)(
Z
Y
X
(
S
S
S
S
)
Z
,
Y
,
X
(
f
7
4
1
0
+
+
+
+
+
+
+
+
=
=
Jako
czynniki do iloczynu wchodzą te sumy S
j
, które odpowiadają kombinacjom zero – jedynkowym zmiennych niezależnych, dla których funkcja
przyjmuje wartość 0.
Jeśli funkcja zależy od wielu argumentów, podobnie jak w przypadku zapisu
U
I
, jest stosowany liczbowy zapis
I
S
.
Przykład 2.4:
Wyrazić funkcję
)
Z
Y
X
)(
Z
Y
X
)(
Z
Y
X
)(
Z
Y
X
(
)
Z
,
Y
,
X
(
f
+
+
+
+
+
+
+
+
=
w postaci zapisu liczbowego
I
S
.
{ { { {
I
)
7
,
4
,
1
,
0
(
111
100
001
000
)
Z
Y
X
)(
Z
Y
X
)(
Z
Y
X
)(
Z
Y
X
(
)
Z
,
Y
,
X
(
f
7
4
1
0
=
⋅
⋅
⋅
=
=
+
+
+
+
+
+
+
+
=
2.4.
FUNKTORY UK
ŁADÓW LOGICZNYCH
Bramkami nazywane są kombinacyjne układy cyfrowe, realizujące proste funkcje logiczne jednej lub wielu zmiennych logicznych.
Zmienną logiczną jest sygnał elektryczny występujący na wejściach i wyjściach tych układów.
Poniżej zostanie przedstawione działanie logiczne podstawowych typów bramek logicznych.
BRAMKA I (AND)
Bramka ta jest układem o dwu lub większej liczbie wejść, realizującym funkcję iloczynu logicznego zmiennych wejściowych.
W przypadku ogólnym bramki mogą mieć dowolną liczbę wejść, ale typowy układ scalony zawiera zwykle cztery bramki 2 – wejściowe,
trzy bramki 3 – wejściowe lub dwie bramki 4 – wejściowe. Wyjście bramki AND jest w stanie wysokim tylko wtedy, gdy oba wejścia są w stanie
wysokim (rys. 2.8).
W algebrze Boole’a symbolowi AND odpowiada kropka (·). „A I B” jest zapisywane jako A · B lub po prostu AB.
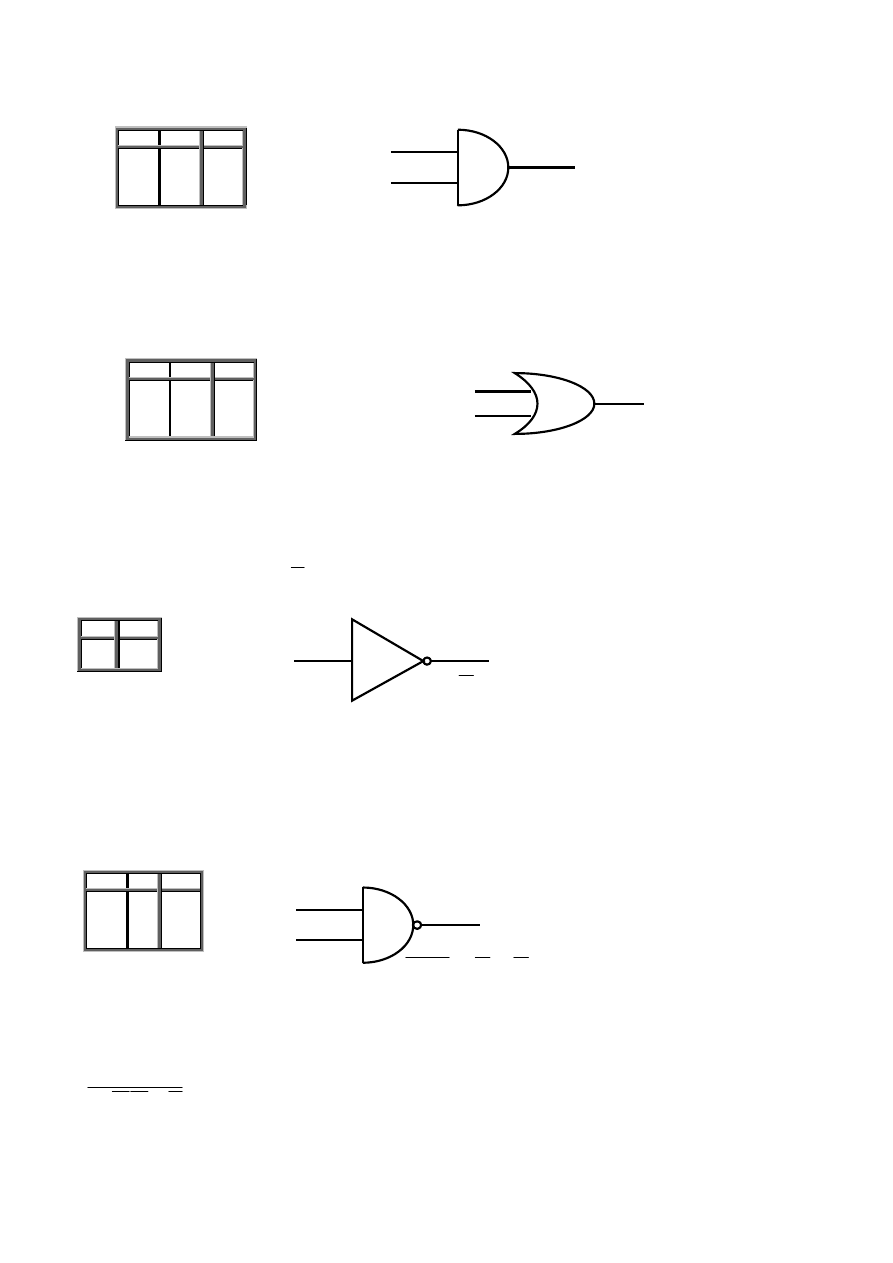
15
a)
b)
A
B
F
0
0
0
0
1
0
1
0
0
1
1
1
B
A
F
⋅
=
Rys. 2.8 Dwuwejściowa bramka I (AND): a) tablica prawdy, b) symbol graficzny.
BRAMKA LUB (OR)
Bramka ta jest układem o dwu lub większej liczbie wejść, realizującym funkcję sumy logicznej zmiennych wejściowych (rys. 2.9).
Wyjście bramki OR (LUB) jest w stanie wysokim, jeżeli któreś z wejść (lub oba) jest w stanie wysokim. Można to wyrazić za pomocą „tablicy
prawdy”.
a)
b)
A
B
F
0
0
0
0
1
1
1
0
1
1
1
1
B
A
F
+
=
Rys. 2.9 Dwuwejściowa bramka LUB (OR): a) tablica prawdy, b) symbol graficzny.
W algebrze Boole’a symbolowi OR odpowiada symbol „+”. „A LUB B” jest zapisywane jako A + B.
BRAMKA NIE (NOT)
Często potrzebujemy zmienić stan logiczny na przeciwny, nazywa się to również negowaniem stanu logicznego. Jest to funkcja inwertora,
„bramki” o jednym wejściu (rys. 2.10).
Boole’owskim odpowiednikiem symbolu NOT (negacji Nie) jest kreska pozioma stawiana nad negowanym elementem, a czasem
apostrof(‘). „NIE A” jest zapisywane jako
A
lub jako A’.
a)
b)
A
F
0
1
1
0
A
F
=
Rys. 2.10 Bramka NIE (NOT): a) tablica prawdy, b) symbol graficzny.
Do podstawowych bramek negacyjnych należy bramka I-NIE (Not AND lub krócej NAND) oraz bramka LUB-NIE (Not OR lub krócej
NOR).
BRAMKA I – NIE (NAND)
Bramka ta jest układem realizującym funkcję negacji iloczynu, a więc zgodnie z prawem de Morgana również funkcje sumy negacji
zmiennych wejściowych (rys. 2.11).
Funkcja NOT może być połączona z innymi funkcjami, tworząc NAND. Bramka I-NIE (NAND) jest bramką podstawową w kilku klasach
scalonych układów cyfrowych.
a)
b)
A
B
F
0
0
1
0
1
1
1
0
1
1
1
0
B
A
B
A
F
+
=
⋅
=
Rys. 2.11 Bramka I - NIE (NAND): a) tablica prawdy, b) symbol graficzny.
BRAMKA LUB – NIE (NOR)
Bramka ta jest układem realizującym funkcję negacji sumy, a więc zgodnie z prawem de Morgana również funkcję iloczynu negacji
zmiennych wejściowych. Podobnie jak bramka I-NIE (NAND), również i ta bramka jest podstawową bramką w kilku klasach scalonych układów
cyfrowych (rys. 2.12). Ponieważ funkcje I-NIE (NAND) i LUB-NIE (NOR) są wzajemnie dualne, zatem układ bramek LUB-NIE (NOR) realizujący
funkcję f(A, B, ..., Z) po zamianie bramek LUB-NIE (NOR) na bramki I-NIE (NAND), bez zmiany jego struktury, realizować będzie funkcję dualną
)
Z
....
,
B
,
A
(
f
.
a)
b)
A
F
B
F
A
A
B
F
A
F
B

16
A
B
F
0
0
1
0
1
0
1
0
0
1
1
0
B
A
B
A
F
⋅
=
+
=
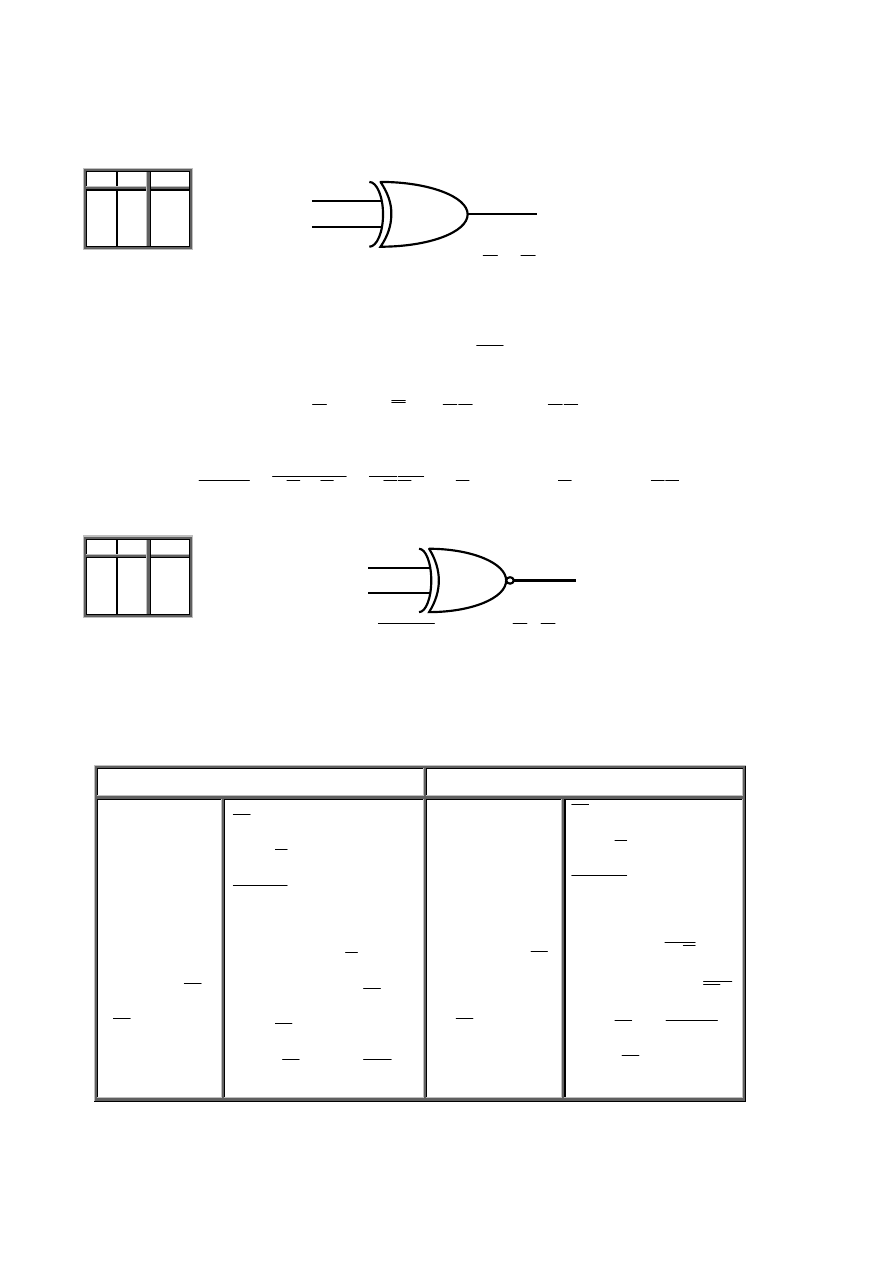
Rys. 2.12 Bramka LUB - NIE (NOR): a) tablica prawdy, b) symbol graficzny.
A
F
B

17
18
BRAMKA ALBO (EX – OR)
Exclusive – OR (czyli WYŁĄCZNIE LUB) – wyjście bramki XOR jest w stanie wysokim, jeżeli jedno albo drugie wejście jest w stanie
wysokim – jest to zawsze funkcja dwóch zmiennych (rys. 2.13). Mówiąc inaczej, wyjście jest w stanie wysokim, jeżeli stany wejść są różne. Bramka
XOR realizuje dodawanie bitów modulo – 2.
a)
b)
A
B
F
0
0
0
0
1
1
1
0
1
1
1
0
B
A
B
A
B
A
F
+
=
⊕
=
Rys. 2.13 Bramka ALBO (EX – OR): a) tablica prawdy, b) symbol graficzny.
BRAMKA ALBO – NIE (EX – NOR)
Bramka ALBO (Ex-OR) umożliwia bardzo prostą realizację funkcji ALBO - NIE (rys. 2.14), która ma postać:
F(A, B) = AB+
AB
= A
⊗B
Funkcja ALBO-NIE (Exclusive-NOR lub krócej funkcja Ex-NOR), może być zrealizowana bądź za pomocą bramki ALBO (Ex-OR), jeśli
na jedno z jej wejść zostanie podany, zamiast sygnału prostego, sygnał zanegowany:
=
+
=
+
=
⊕
=
B
A
AB
B
A
B
A
B
A
F
A
⊗B
bądź przez zanegowanie sygnału wyjściowego tej bramki:
A
B
A
AB
)
B
A
)(
B
A
(
B
A
B
A
B
A
B
A
B
A
F
=
+
=
+
+
=
=
+
=
⊕
=
⊗B
a)
b)
A
B
F
0
0
1
0
1
0
1
0
0
1
1
1
B
A
AB
B
A
F
⋅
+
=
⊕
=
Rys. 2.14 Bramka ALBO – NIE (EX –NOR): a) tablica prawdy, b) symbol graficzny.
Podstawowe tożsamości dla funkcji ALBO (Ex - OR) i funkcji ALBO - NIE (Ex - NOR) przedstawiono poniżej w tablicy 2.2.
Tablica 2.2 Podstawowe tożsamości dla funkcji ALBO (Ex - OR) i ALBO-NIE (Ex - NOR)
Y
X
⊕
Y
X
⊗
0
1
1
0
0
1
1
1
0
1
1
1
0
0
0
0
=
⊕
=
⊕
=
⊕
=
⊕
=
⊕
=
⊕
=
⊕
=
⊕
X
X
X
X
X
X
X
X
XY
Y
X
X
Y
X
Y
X
X
Y
X
Y
X
X
Y
X
XY
X
Y
X
XY
Y
X
Y
X
Y
X
Y
X
Y
X
Y
X
Y
X
=
+
⊕
+
=
⊕
=
+
⊕
=
⊕
+
=
⊕
⊕
⊗
=
⊕
⊗
=
⊕
⊗
=
⊕
)
(
)
(
1
0
1
0
1
1
1
0
0
1
0
1
0
1
0
0
=
⊗
=
⊗
=
⊗
=
⊗
=
⊗
=
⊗
=
⊗
=
⊗
X
X
X
X
X
X
X
X
XY
Y
X
X
Y
X
Y
X
X
Y
X
Y
X
X
Y
X
XY
X
Y
X
XY
Y
X
Y
X
Y
X
Y
X
Y
X
Y
X
Y
X
=
+
⊗
+
=
⊗
=
+
⊗
=
⊗
+
=
⊗
⊗
⊕
=
⊗
⊕
=
⊗
⊕
=
⊗
)
(
)
(
Przy projektowaniu układów cyfrowych należy mieć na uwadze, że za pomocą pewnych rodzajów bramek można utworzyć inne. Na
przykład, jeżeli potrzebna jest bramka AND, a mamy do dyspozycji dwie dwuwejściowe bramki NAND, możemy zastosować chwyt jaki przedstawia
rys. 2.15a.
A
F
B
A
F
B
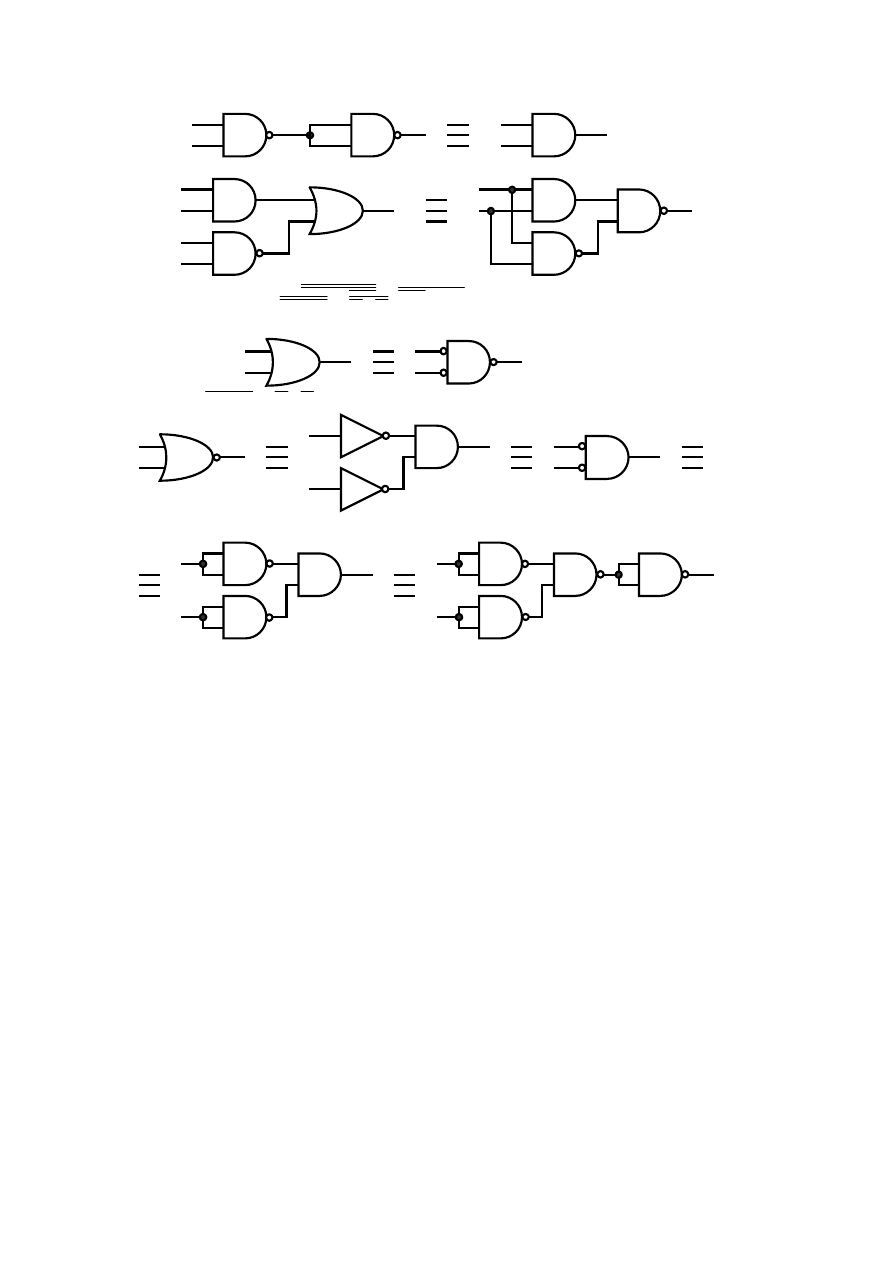
19
a)
b)
c)
d)
Rys. 2.15 Przykłady realizacji podstawowych funkcji logicznych.
2.5.
Uk
łady TTL
Funktory (bramki logiczne) są produkowane w postaci scalonej.
Wyróżnia się dwie główne technologie wytwarzania cyfrowych układów scalonych:
1.
TTL (ang. Transistor – Transistor Logic – logika tranzystorowo – tranzystorowa) – technologia bipolarna,
2.
CMOS (ang. Complementary Metal – Oxide – Semiconductor) – technologia unipolarna.
Z daną technologią wiąże się określony standard. Standard TTL określa charakterystyczne właściwości scalonych układów logicznych
zbudowanych z tranzystorów bipolarnych.
Określony standard jest to ogólnie przyjęta norma definiująca poziomy napięć zasilających, sygnałów wejściowych i wyjściowych, które
gwarantują wymienność układów wykonywanych przez różnych producentów oraz poprawne działanie cyfrowych układów scalonych.
W układach TTL najważniejszą częścią standardu są wymagania dotyczące zakresów wartości napięć wejściowych, które układ wykonany
w tym standardzie będzie traktował jako określony stan logiczny (0 lub 1) na wejściu oraz zakresów wartości napięć wyjściowych, które układ będzie
gwarantował przy określonym poziomie logicznym (0 lub 1) na wyjściu.
Na rys. 2.16 przedstawiono zakres napięć wejść i wyjść scalonych układów logicznych.
AB
AB
AB
AB
⋅
=
+
B
A
B
A
⋅
=
+
B
A
B
A
⋅
=
+
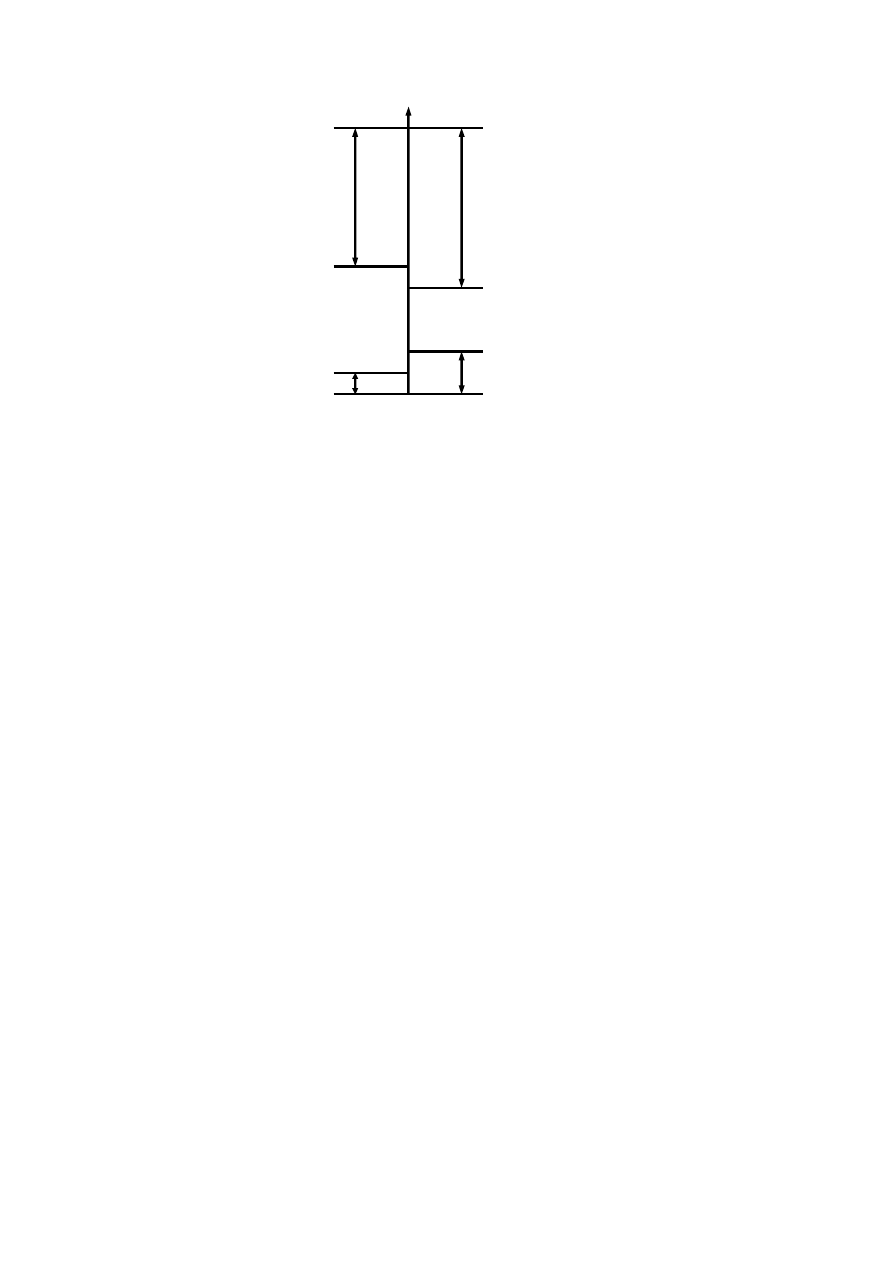
20
Rys. 2.16 Zakresy napięć wejściowych i wyjściowych scalonych układów logicznych wykonanych w technice TTL.
Po prawej stronie osi zaznaczono dozwolone zakresy wartości napięć wejściowych układu TTL:
0,5
÷ 0,8 V – poziom niski (stan 0);
2
÷ 5 V – poziom wysoki (stan 1).
Po lewej stronie osi zaznaczono gwarantowane zakresy wartości napięć na wyjściu:
0
÷ 0,4 V – poziom niski (stan 0);
2,5
÷ 5 V – poziom wysoki (stan 1).
Do głównych zalet układów TTL należy:
§
duża szybkość przełączania,
§
mały pobór mocy,
§
duża odporność na zakłócenia,
§
duża obciążalność,
§
duży współczynnik powielania logicznego,
§
małe impedancje wyjściowe w stanie 0 i 1,
§
pojedyncze źródło napięcia zasilania,
§
praca w szerokim zakresie temperatur,
§
duża pewność działania,
§
duży asortyment, który obejmuje ponad 500 różnych układów logicznych od pojedynczych bramek po wielkie pamięci i mikroprocesory.
Przykładem układu wykonanego w technice TTL jest układ 7400, zawierający cztery bramki NAND. Schemat jednej bramki NAND
pokazano na rys. 2.17.
Dozwolony zakres napięć
na wejściu bramki dla
stanu 1
Dozwolony zakres napięć
na wejściu bramki dla
stanu 0
Gwarantowany zakres
napięć na wyjściu bramki
w stanie 0
Gwarantowany zakres
napięć na wyjściu bramki
w stanie 1
U
U
CC
=5
2,4
2
0,4
0,8
0
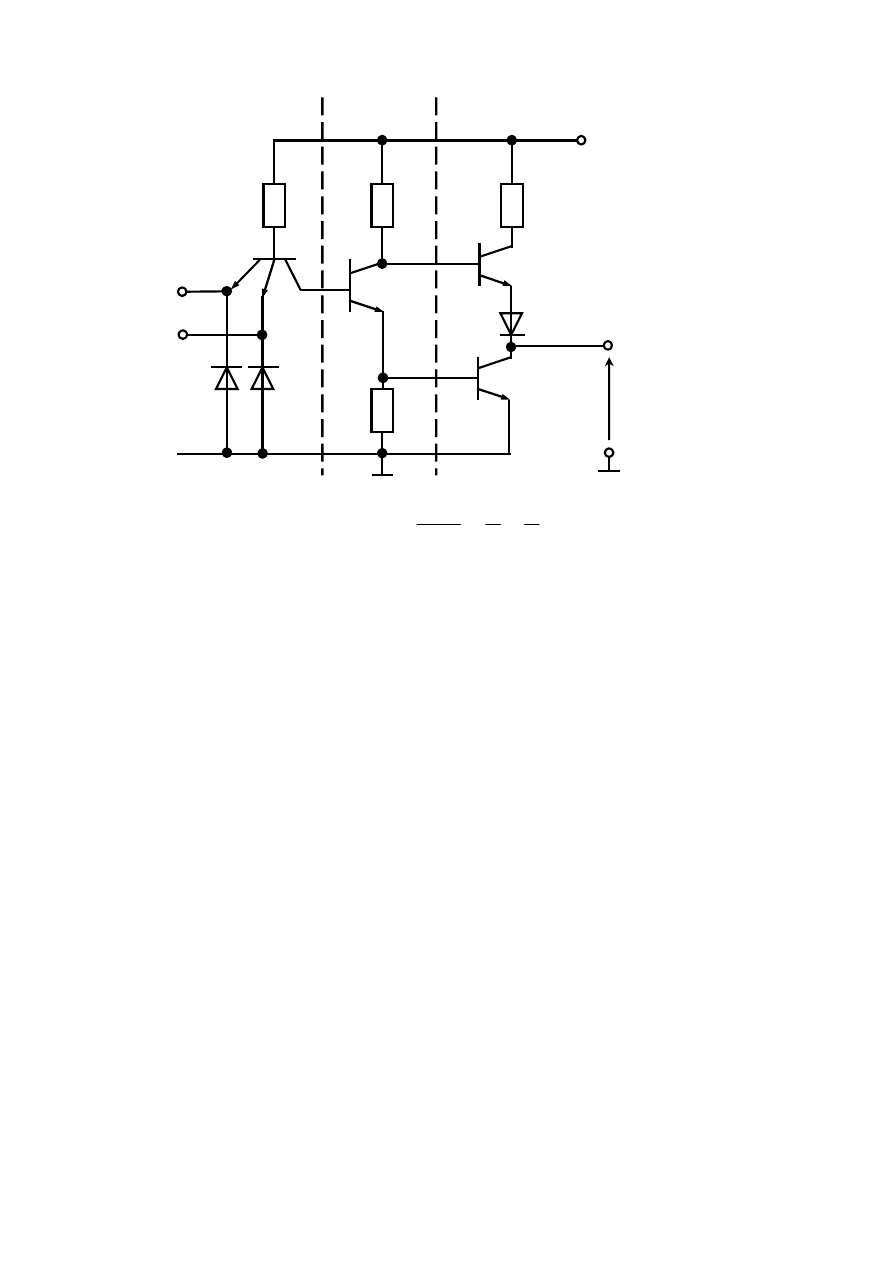
21
Rys. 2.17 Schemat ideowy bramki podstawowej NAND (I – NIE).
Bramka spełnia funkcję iloczynu, czyli:
B
A
B
A
F
+
=
⋅
=
. Stopień wejściowy bramki stanowi tranzystor
wieloemiterowy T
1
. Tranzystor T
2
pracuje w układzie jako wzmacniacz sterujący (rozdzielacz faz), który dostarcza sygnał o odpowiedniej
amplitudzie i wydajności prądowej do stopnia wyjściowego zrealizowanego na tranzystorach T
3
i T
4
.
Do wejść bramki są dołączone diody, które tłumią oscylacje powstałe w liniach łączących bramki w czasie ich przełączania i zapobiegają
powstawaniu ujemnych napięć o wartości większej niż około 0,5 V.
Jeśli na oba wejścia bramki zostaną podane jedynki, to złącza Baza – Emiter tranzystora T
1
będą w stanie nieprzewodzenia (czyli zostaną
spolaryzowane zaporowo), prąd Bazy popłynie przez złącze Baza – Kolektor T
1
do Bazy tranzystora T
2
, powodując jego nasycenie (tranzystor T
2
przewodzi) oraz zatkanie tranzystora T
3
.
Typowa wartość napięcia wyjściowego bramki będącej w stanie 0 (na wyjściu jest stan 0) przy prądzie 16 mA – wynosi 220 mV. Dla
bramki NAND w stanie 0 napięcie wyjściowe powinno wynosić U
OL
≤ 0,4 V, jeżeli prąd wyjściowy I
OL
≤ 16 mA.
Gdy choć na jedno wejście będzie podany sygnał 0, spowoduje to przewodzenie (nasycenie) złącza Baza – Emiter tranzystora T
1
i
spolaryzowanie złącza Baza – Kolektor w kierunku zaporowym. Wynikiem tego jest zatkanie tranzystorów T
2
i T
4
, przewodzenie tranzystora T
3
i
diody D
3
.
Jeśli pobór prądu wyjściowego (w stanie wysokim)wynosi 400
µA, a napięcie wejściowe wynosi 0,8 V, to napięcie wyjściowe jest nie
mniejsze niż 2,4 V. Jeżeli napięcie wejściowe jest mniejsze niż 0,8 V, to typowa wartość napięcia wyjściowego wynosi około 3,3 V.
5.
A
B
+U
CC
U
WY
R
1
R
2
R
4
R
3
D
1
D
2
D
3
T
1
T
2
T
3
T
4
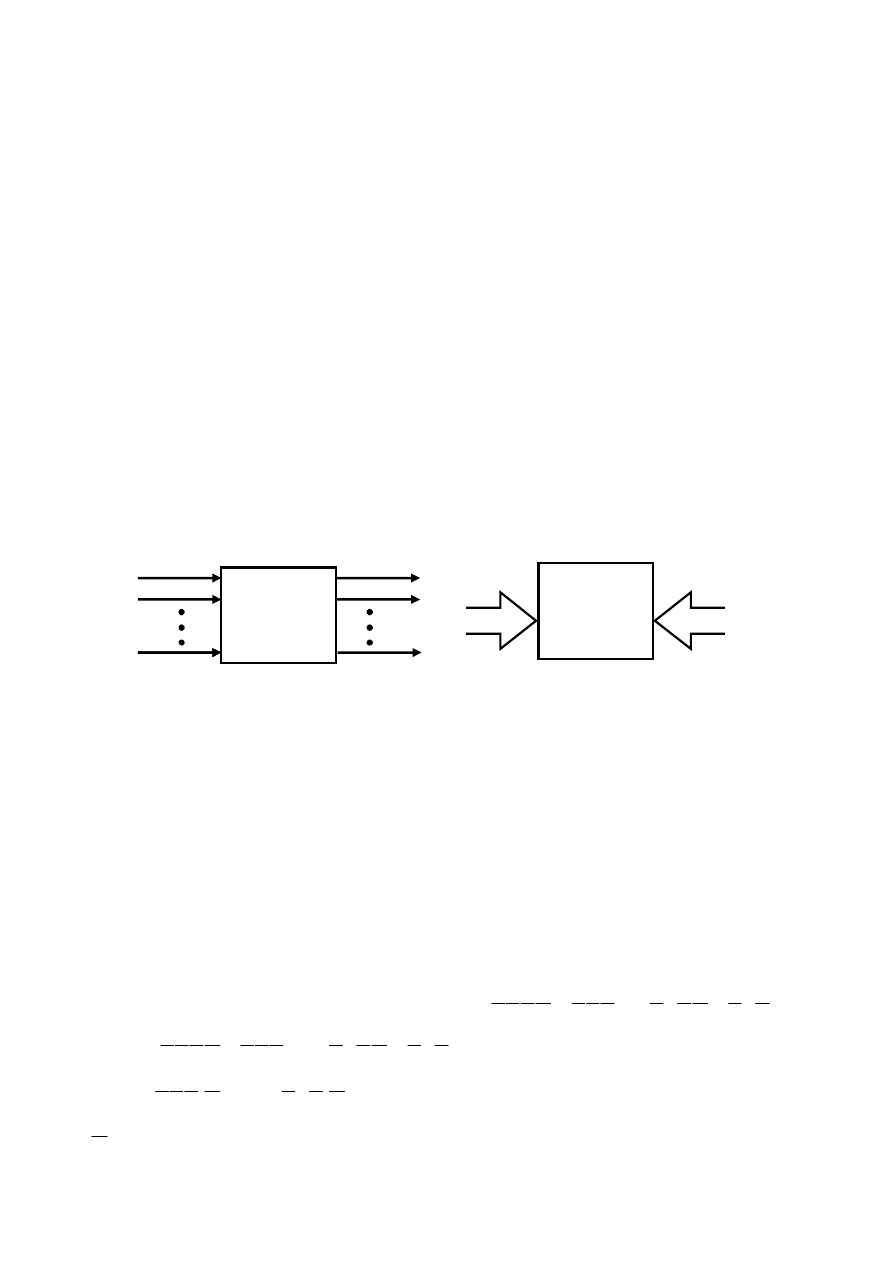
22
3.
UK
ŁADY KOMBINACYJNE I SEKWENCYJNE
3.1.
Wst
ęp
Do układów przełączających logicznych zaliczamy:
§
układy kombinacyjne,
§
układy sekwencyjne.
Cechą odróżniającą układy kombinacyjne i sekwencyjne jest właściwość pamiętania stanów logicznych, które charakteryzują się układy
sekwencyjne, a której są pozbawione układy kombinacyjne.
Układ kombinacyjny służy do przetwarzania informacji dyskretnej dwuwartościowej. Informacja dyskretna składa się ze znaków,
którymi mogą być zarówno litery, cyfry, jak i inne symbole.
W układzie kombinacyjnym każda kombinacja sygnałów wejściowych określa jednoznacznie kombinację sygnałów wyjściowych. Sygnały
wejścia i sygnały wyjścia przyjmują skończoną liczbę kombinacji i skończoną liczbę wartości. Kombinacje sygnałów wejściowych są to stany wejść
układu, a kombinacje sygnałów wyjściowych – stany wyjść układu.
Z układem kombinacyjnym mamy do czynienia, jeżeli wartość zmiennych ze zbioru Y zależy od wartości zmiennych ze zbioru X.
Działanie układu kombinacyjnego możemy opisać wyrażeniem:
Y = f (X)
(3.1)
gdzie: X – zbiór wszystkich możliwych, dla danego układu stanów wejść,
X = {x
1
, x
2
,...,x
n
,},
Y – zbiór wszystkich możliwych, dla danego układu stanów wyjść,
Y = {y
1
, y
2
,,...,y
n
}.
Zależność Y = f (X) jest równoważna zespołowi (rodzinie) funkcji logicznej:
y
1
= f
1
(x
1
...x
n
)
(3.2)
y
2
= f
2
(x
2
...x
n
)
(3.3)
y
m
= f
m
(x
1
...x
n
)
(3.4)
gdzie: n – liczba wejść układu kombinacyjnego,
m – liczba wyjść układu kombinacyjnego.
Układ przełączający (logiczny) o n wejściach i m wyjściach można przedstawić w postaci wielobiegunnika pokazanego na rys. 3.1.
Rys. 3.1 Wielobiegunnik układu przełączającego X = {x
1
, x
2
,...,x
n
}, Y = {y
1
, y
2
,,...,y
n
}: a) wyróżniający poszczególne zmienne, zapis
uproszczony.
Do realizacji fizycznej kombinacyjnych układów cyfrowych są stosowane bramki logiczne, omówione w rozdziale 2, a także generatory
funkcji logicznych, omówione w rozdziale 10.
W układach kombinacyjnych stosuje się metodę Karnaugha.
Synteza układu kombinacyjnego sprowadza się do realizacji zespołu funkcji logicznych określonych na tym samym zbiorze zmiennych. O
złożoności układowej świadczy liczba funktorów w układzie oraz liczba połączeń, czyli sumaryczna liczba wejść wszystkich funktorów. Obie te
liczby stanowią o koszcie układu.
Przy syntezie zespołu funkcji logicznych należy dążyć do minimalizacji funkcji kosztu, biorąc pod uwagę możliwość wykorzystania
wspólnych iloczynów (sum) wchodzących w skład rozpatrywanych funkcji.
W celu dokonania realizacji układu kombinacyjnego należy:
§
określić funkcję logiczną rozpatrywanego problemu, np. za pomocą tablicy wartości,
§
dokonać minimalizacji funkcji logicznej wykorzystując tablice Karnaugha, przedstawione w poniższym rozdziale, lub metody algebraiczne,
§
sporządzić schemat układu logicznego, realizującego zminimalizowaną funkcję logiczną.
Istnieją dwie podstawowe metody minimalizacji funkcji:
1.
Metoda analityczna algebry Boole’a.
2.
Metoda z użyciem tablicy Karnaugha (czyt. karnafa).
Minimalizacja analityczna metodą algebry Boole’a polega na zapisaniu funkcji logicznej, a następnie zminimalizowaniu (skróceniu zapisu
jej z zastosowaniem praw algebry Boole’a (podanych w rozdz. 2).
Przykład 3.1:
Zapisać i zminimalizować funkcję logiczną
Y(A, B, C, D) = (0, 1, 4, 5).
Zapisujemy tę funkcję jako sumę logiczną wszystkich jej elementów: Y(A,B,C,D) =
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
A
+
+
+
.
Grupujemy po dwa iloczyny logiczne:
Y(A,B,C,D) =
(
) (
)
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
A
+
+
+
.
Korzystamy z prawa rozdzielności mnożenia względem dodawania:
Y(A,B,C,D) =
(
)
(
)
D
D
C
B
A
D
D
C
B
A
+
+
+
.
Następnie korzystamy z tożsamości:
(
D
+D = 1)
i z prawa rozdzielności mnożenia względem dodawania:
f(X)
x
1
x
2
x
n
f(X)
X
Y
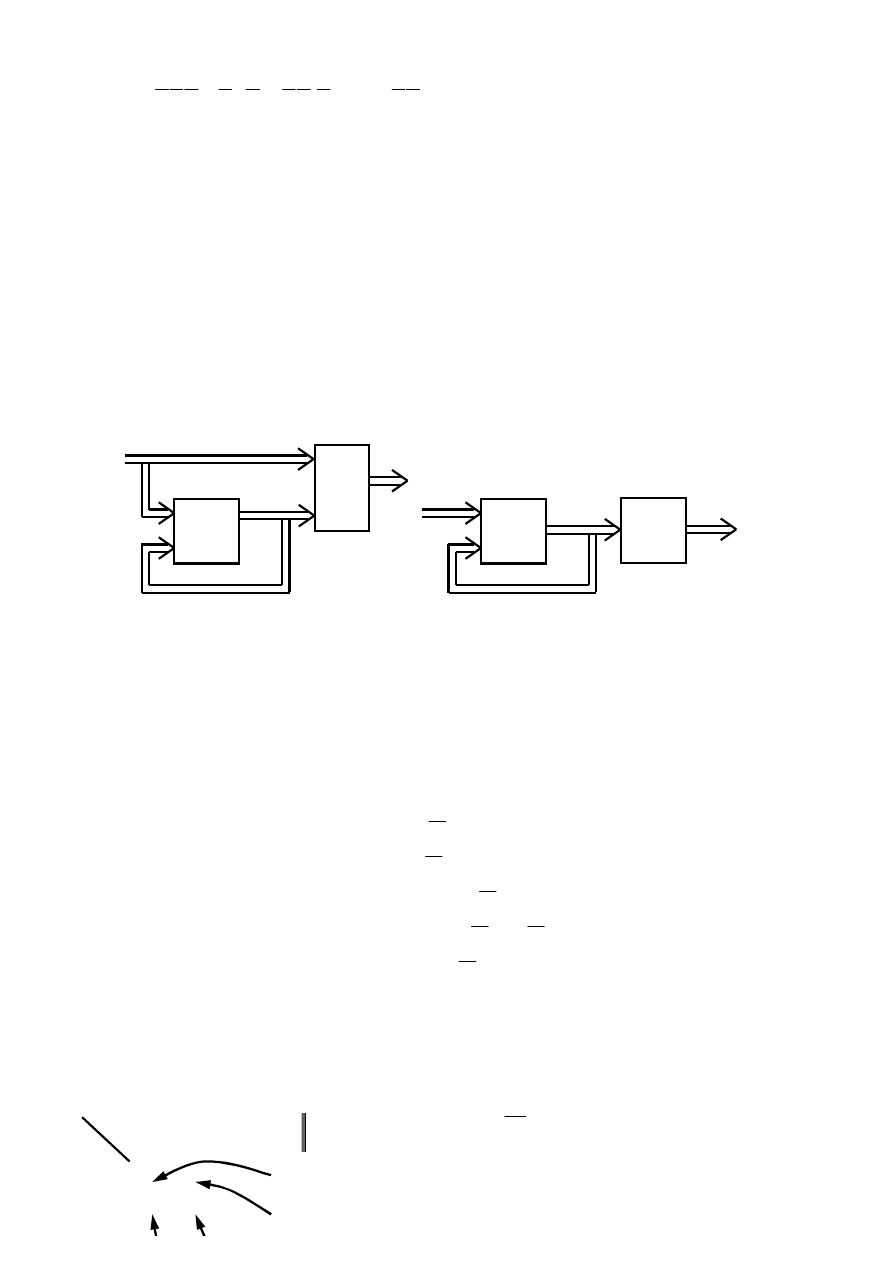
23
Y(A,B,C,D) =
(
)
C
A
B
B
C
A
C
B
A
C
B
A
=
+
=
+
.
Układ sekwencyjny jest to układ dyskretny, którego stan wyjścia nie tylko zależy od stanu wejścia, ale także od wcześniejszego stanu
wyjścia. Inaczej mówiąc stan wyjścia zależy od stanu wejścia i stanu wyjścia w chwili T. Oprócz zmiennych wejściowych i wyjściowych, istnieją
tzw. stany wewnętrzne Q, a zbiór stanów wewnętrznych określa pamięć układu Q
1
, Q
2
,...
Układy sekwencyjne dzielimy na:
§
układy synchroniczne
§
układy asynchroniczne.
Układ synchroniczny to układ, w którym zmiany stanów wewnętrznych i stanów wyjścia odbywa się w ściśle określonych interwałach
czasu, czyli w takt impulsu zegarowego.
Układ asynchroniczny to układ, w którym sygnały na wejściu bezpośrednio oddziałują na stany wewnętrzne układu i stany na wyjściu.
Układ ten pracuje z szybkością wyznaczoną przez opóźnienie elementów wewnętrznych układu. W układach asynchronicznych sekwencyjnych
stosuje się metodę Huffmana.
Układ sekwencyjny może być opisany następującymi równaniami:
( ) ( )
[
]
t
Q
,
t
x
F
)
t
t
(
Q
1
1
=
+
∆
(3.5)
( ) ( )
[
]
t
Q
,
t
x
F
)
t
t
(
Y
2
2
=
+
∆
(3.6)
Równanie (3.5) zwane jest równaniem stanów wewnętrznych. Równanie (3.6) zwane jest równaniem wyjść układu sekwencyjnego.
Czasami przyjmuje ono postać:
( )
[ ]
t
Q
F
)
t
t
(
Y
3
2
=
+
∆
(3.7)
Wyżej wymienione równania można przedstawić za pomocą schematów blokowych.
a)
b)
Rys. 3.2 Schemat blokowy układu sekwencyjnego: a) Mealy’ego,
b) Moore’a: UP – układ pamięci, KBW –Kombinacyjny Blok Wyjściowy.
Równanie (3.5) i (3.6) opisują układ sekwencyjny zwany układem Mealy`ego, a wyrażenia (3.5) i (3.7) układ Moore`a (rys. 3.2).
Podstawowymi funktorami sekwencyjnych układów cyfrowych są funktory, umożliwiające budowę układu kombinacyjnego, czyli bramki
logiczne oraz przerzutniki, które są omówione w rozdziale 4.
3.2.
Metoda Karnaugha
Najczęściej stosowanym i najprostszym rodzajem opisu układu kombinacyjnego jest tablica wartości, która ukazuje zależność sygnałów
wyjściowych Y od sygnałów zmiennych wejściowych X.
Tablice Karnaugha służą do bezpośredniego zapisu n zmiennych. Tablice te są prostokątne i zawierają 2
n
pól. Kolumnom (i wierszom)
siatek zostały przypisane wartości w kodzie, zwanym kodem cyklicznym Graya, gdzie dwie sąsiednie pozycje różnią się jednym znakiem.
Kolejność taka jest charakterystyczną właściwością tablicy Karnaugha, która jest wykorzystana do przeprowadzenia uproszczenia w
oparciu o tzw. regułę sklejania (patrz tabel 2.2):
B
0
1
B
B
B
0
)
X
X
(
B
B
B
X
X
X
B
BX
B
B
)
X
B
)(
X
B
(
A
)
X
X
(
A
A
X
A
AX
2
=
+
⋅
+
=
+
+
+
=
+
+
+
=
+
+
=
+
=
+
gdzie: A, B – zmienne lub funkcje logiczne.
Zmienną, która w dwóch sąsiednich polach przyjmuje różne wartości można pominąć.
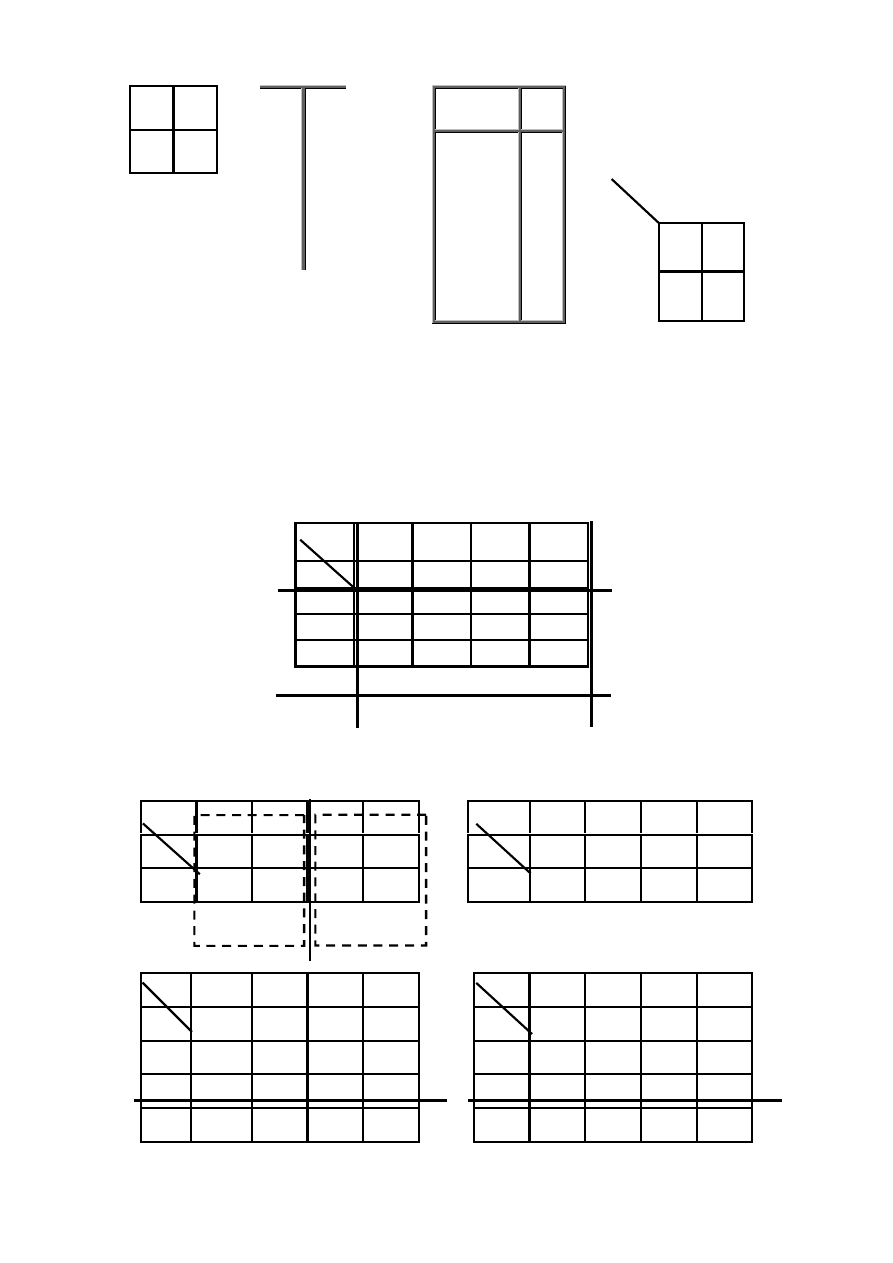
Najprostszą z możliwych tablic Karnaugha dla układu dwuwejściowego przedstawiono na rys. 3.3. Za jej pomocą możemy opisać funkcję
logiczną dwu sygnałów wejściowych (D
0
i D
1
).
a)
b)
D
0
D
1
0
1
D
1
D
0
Y = D
1
0
D
x(t)
x(t)
K B W
K B W
U P
U P
Q(t)
Q(t)
Q(t+
∆t
1
)
Q(t+
∆t
1
)
Y=(t+
∆t
2
)
Y=(t+
∆t
2
)
24
CB
A
B
A
L’
L
T’
T
0
0
0
0
D
1
D
0
Y
1
0
1
1
0
0
0
1
1
3
0
1
0
D
0
D
1
0
1
1
0
2
1
1
0
0
0
0
1
0
1
1
1
0
Rys. 3.3 Tablica Karnaugha dla układu dwuwejściowego: a) niewypełniona,
b) przykładowe jej wypełnienie.
Na rysunku zaznaczono strzałkami, jakim kombinacjom sygnałów wejściowych odpowiada dane pole. Tablica ta jest niewypełniona, tzn.
nie opisuje żadnej funkcji logicznej. Jej wypełnienie polega na wpisaniu w każde pole takiego stanu (0, 1), jaki powinien pojawić się na wyjściu
układu przy danej kombinacji sygnałów wejściowych.
Na rys. 3.3b przedstawiono wypełnioną przykładowo tablicę Karnaugha. Obok niej zapisano występujące możliwe kombinacje stanów
logicznych sygnałów wejściowych D
0
i D
1
oraz odpowiadający im sygnał wyjściowy Y.
Zatem, tablica Karnaugha jest to specjalny rodzaj tablicy, do której w pola opisane jednoznacznie kombinacją sygnałów wejściowych
wpisuje się odpowiadającą im wartość sygnału wyjściowego. Na rys. 3.4 przedstawiono tablicę czterech zmiennych. Każde dwa sąsiadujące ze sobą
pola (stykające się jednym bokiem oraz leżące przy krawędziach A - A’ i B-B’) tej tablicy różnią się w opisach odpowiadających im sygnałów
wejściowych tylko jednym bitem (jedną pozycją).
CD AB
00
01
11
10
00
0
1
3
2
01
4
5
7
6
11
12
13
15
14
10
8
9
11
10
Rys. 3.4 Tablica Karnaugha czterech zmiennych.
Aby zapisać do tablicy Karnaugha funkcję o większej liczbie sygnałów wejściowych, należy stopniowo zwiększać jej rozmiary, stosując w
tym celu tzw. metodę odbiciu lustrzanego. Sposób tworzenia tablicy dla czterech zmiennych z tablicy dwóch zmiennych przedstawiono na rys. 3.5.
a)
b)
c)
d)
00
01
11
10
00
01
11
10
00
00
01
01
11
11
10
10
0
1
1
0
00
01
11
10
0
0
1
1
A
A'
B
B'
DA
CB
AB
CD
L’
L

25
Rys 3.5 Etapy tworzenia tablicy Karnaugha dla czterech sygnałów wejściowych L - L' – oś odbicia lustrzanego.
Polega on na przekształceniu tablicy Karnaugha dla dwóch sygnałów wejściowych A, B (rys. 3.5a) w tablicę dla trzech sygnałów
wejściowych A, B, C (rys. 3.5b) a następnie w tablicę dla czterech sygnałów A, B, C, D (rys. 3.5c,d).
Każde zwiększenie liczby sygnałów wejściowych o jeden powoduje podwojenie rozmiarów tablicy.
Następnym krokiem jest wypełnienie pól tak utworzonej tablicy. Funkcja logiczna może być podana na przykład w postaci: opisu
słownego, zbioru liczb, dla których reprezentacji dwójkowej odpowiada na wyjściu poziom 1 lub innego jednoznacznego opisu.
Przykład 3.2
Utworzyć tablicę Karnaugha dla funkcji Y(A, B, C, D) = (0, 1 , 4, 5, 10, 14).
Sposób wypełniania tablicy:
1.
Każdą liczbę, dla której funkcja wyjściowa przyjmuje wartość 1 przedstawiamy za pomocą kodu dwójkowego (rys. 3.6a).
2.
Każdą liczbę możemy zapisać za pomocą czterech bitów (czterech sygnałów wejściowych). Zatem potrzebna jest czterowejściowa tablica
Karnaugha.
3.
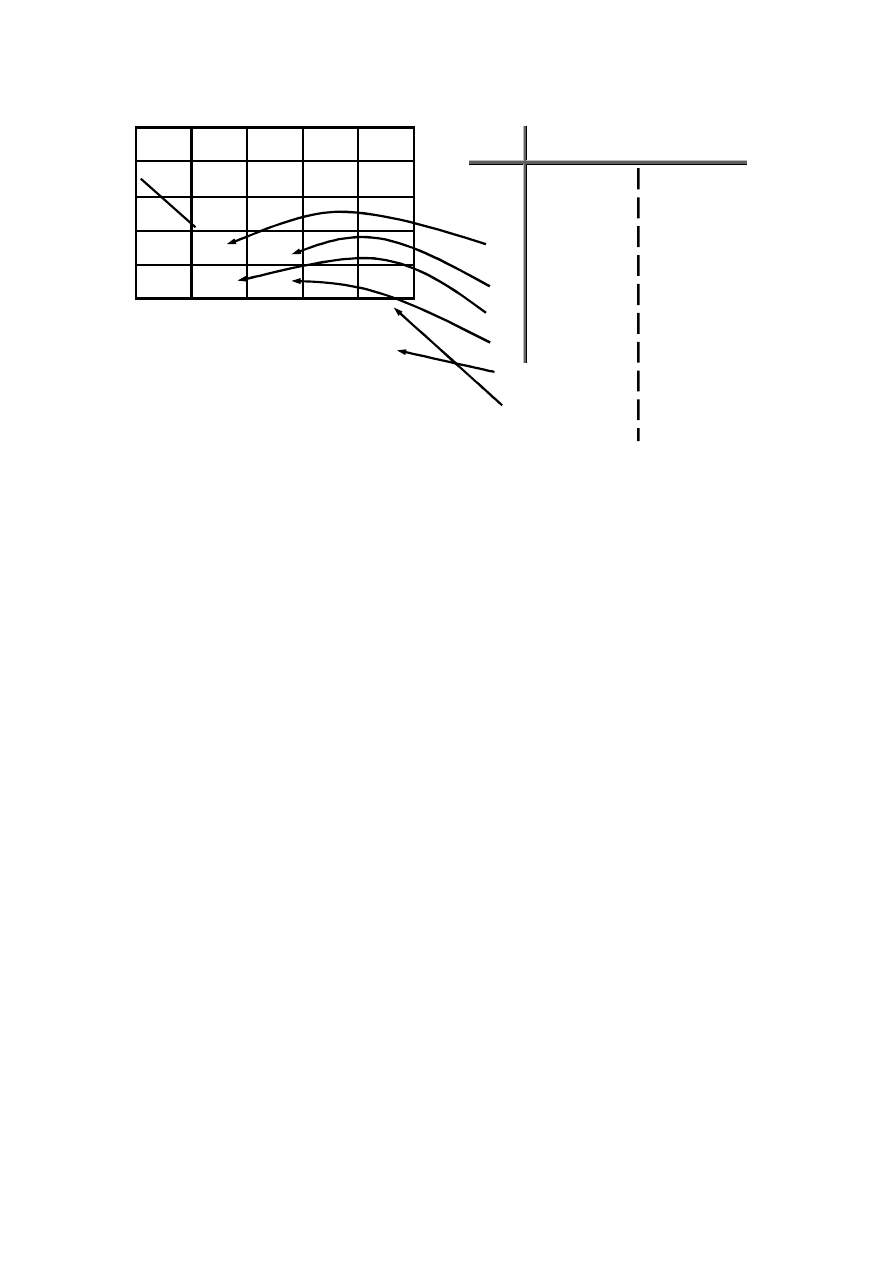
W poszczególne pola tej tablicy należy wpisać wartości funkcji Y dla poszczególnych kombinacji sygnałów wejściowych. W tym miejscu
zwykle wyłania się problem. Jak w stosunkowo krótkim czasie znaleźć pola odpowiadające danej kombinacji wejściowej (problem ten ma
większe znaczenie, gdy tworzymy tablice o większej liczbie sygnałów wyjściowych). Kombinacje sygnałów wejściowych dzielimy przerywaną
linią w taki sposób, aby przebiegała ona między sygnałami opisującymi kolumny a sygnałami opisującymi wiersze tablicy Karnaugha (rys.
3.6a). W naszym przykładzie bity A, B opisują wiersze, a bity C,. D - kolumny. Zatem każde pole jest opisane kolumną i wierszem.
4.
W tablicy Karnaugha odszukujemy wiersz opisany kombinacją AB (sygnałów wejściowych).
5.
Po odnalezieniu odpowiedniego wiersza. poruszamy się wzdłuż niego, szukając kolumny opisanej kombinacja CD.
6.
W pole tablicy leżące na przecięciu odszukanego wiersza i kolumny wpisujemy wartość 1. (Strzałkami zaznaczono pola, które odpowiadają
poszczególnym kombinacjom).
7.
Jeżeli funkcja określała pola, którym odpowiadają poziomy 1, to w pozostałe wolne pola należy wpisać 0.
26
8.
Wypełnioną w ten sposób tablicę funkcji Y(A, B, C, D) przedstawiono na rys. 3.6b.
a)
b)
00
01
11
10
MSB
A B
LSB
C D
00
1
1
0
0
0
0
0
0
0
01
1
1
0
0
1
0
0
0
1
11
0
0
0
1
4
0
1
0
0
10
0
0
0
1
5
0
1
0
1
10
1
0
1
0
14
1
1
1
0
Rys 3.6 Sposób wypełnienia tablicy Karnaugha.
Na podstawie wypełnionej tablicy Karnaugha można przystąpić do realizacji funkcji na bramkach logicznych. Każdemu polu tablicy
odpowiada bramka AND. Powstaje pytanie, czy przy dużej liczbie jedynek w tablicy należy również stosować tak dużo bramek, czy nie można
zmniejszyć ich liczby? Okazuje się, że można. Liczba bramek zależy od tego, w jakim stopniu uda się zminimalizować funkcję Y.
Jeżeli dwie kombinacje sygnałów wejściowych, przy których na wyjściu powinien pojawić się poziom 1 różnią się między sobą na jednym
bicie (jednym sygnałem wyjściowym, np. 0001 i 0011), oznacza to, że sygnał wyjściowy dla tych kombinacji nie zależy od wartości tego bitu. Zatem,
zamiast dwóch bramek AND czterowejściowych można użyć tylko jednej bramki AND trójwejściowej.
W tablicy Karnaugha odpowiada to połączeniu w odpowiedni sposób jedynek w pary. Jedynki można również łączyć w czwórki, ósemki,
szesnastki itp. Taką operację nazywamy sklejaniem jedynek lub sprowadzeniem zapisu funkcji do kanonicznej postaci sumy (suma iloczynów).
Sklejanie dwóch jedynek w tablicy Karnaugha jest możliwe, jeżeli:
§
są one położone obok siebie, tzn. w sąsiednich polach,
§
jedynka ma odbicie lustrzane wzdłuż osi L – L’ lub M – M’.
CD
kolumny
w
ie
rs
ze
AB
kolumny
wiersze
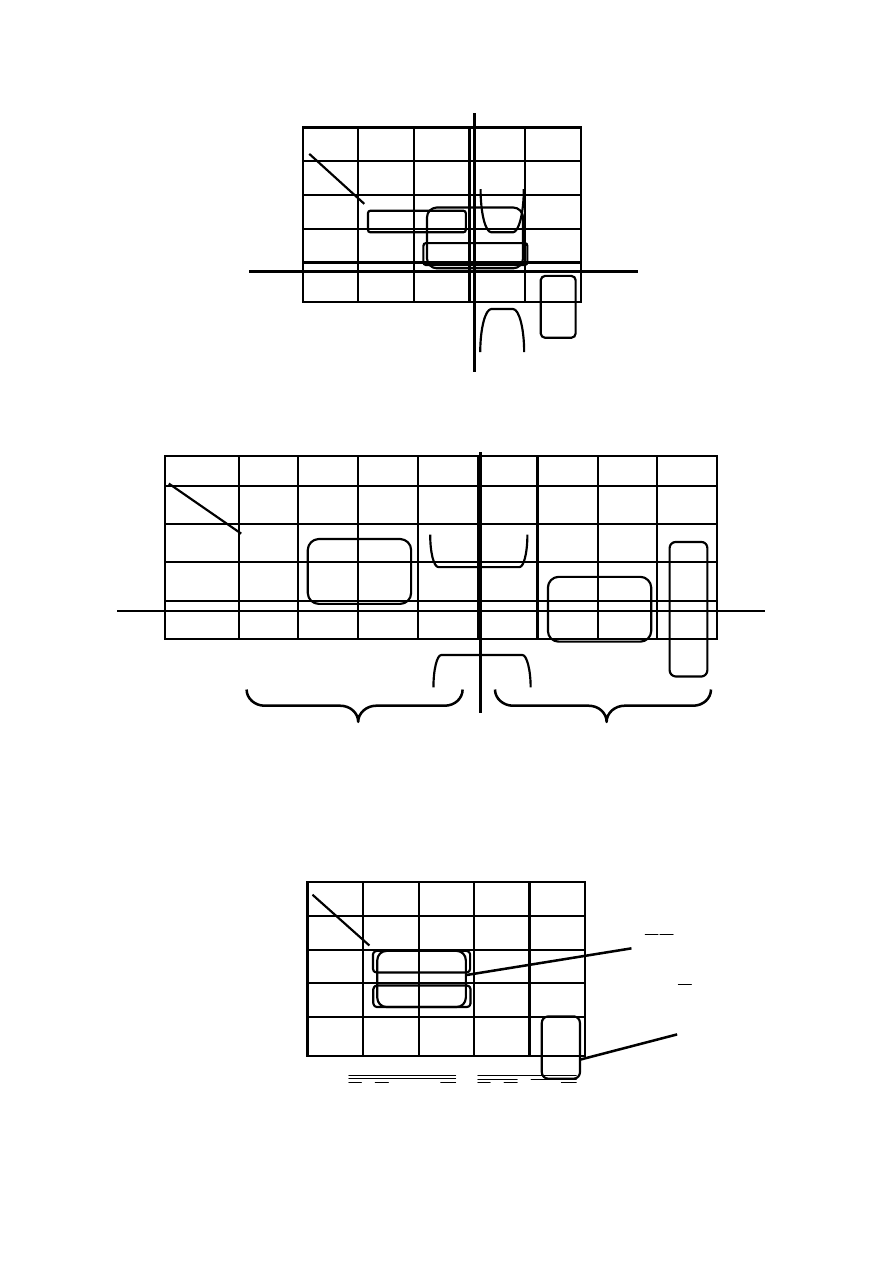
27
Na rys. 3.7 przedstawiono tablicę Karnaugha ze sklejonymi parami jedynek.
00
01
11
10
00
1
1
1
0
01
0
1
1
0
11
0
0
0
1
10
0
0
1
1
Rys 3.7 Przykłady sklejenia dwóch jedynek.
Sklejane dwójki jedynek można połączyć w czwórki (rys. 3.7), jeżeli:
§
jedna para jedynek jest odbiciem lustrzanym drugiej pary wzdłuż osi L - L’ lub M – M’,
§
obie pary stykają się bokiem w obrębie jednego z kwadratów T lub T’. W analogiczny sposób skleja się czwórki w ósemki, a ósemki w
szesnastki.
000
001
011
010
110
111
101
100
00
0
1
1
1
1
0
0
1
01
0
1
1
0
0
1
1
1
11
0
0
0
0
0
1
1
1
10
0
0
0
1
1
0
0
1
Rys 3.8 Przykłady sklejenia dwóch dwójek.
Najogólniej mówiąc minimalizację siatki Karnaugha otrzymamy, gdy zastosujemy następujące zasady:
§
wyszukujemy grupy o największej liczbie konstytuent, zawierające te same wartości (jedynki lub zera),
§
liczba konstytuent musi być liczbą parzystą siatek 2
n
,
§
poszczególne konstytuent muszą być cyklicznie sąsiednie (tzn. pierwsza musi być sąsiednia z drugą, druga z trzecią , ..., a ostatnia z pierwszą.
Przykład 3.3:
Zminimalizować funkcję Y(A, B, C, D) =
U
(0, 1, 4, 5, 10, 14) za pomocą tablicy Karnaugha.
W tablicy na rys. 3.6b znajduje się sześć jedynek, które można połączyć w trzy dwójki (rys. 3.9a). Dwie dwójki można połączyć w
czwórkę (rys. 3.9a). Realizację tej funkcji logicznej na bramkach przedstawiono na rys. 3.9b.
a)
00
01
11
10
00
1
1
0
0
01
1
1
0
0
11
0
0
0
1
10
0
0
0
1
D
AC
C
A
D
AC
C
A
Y
⋅
⋅
=
+
⋅
=
b)
L’
CD
AB
L
M’
M
CDE
AB
L
M’
M
L’
T
T’
D
AC
CD
AB
C
A
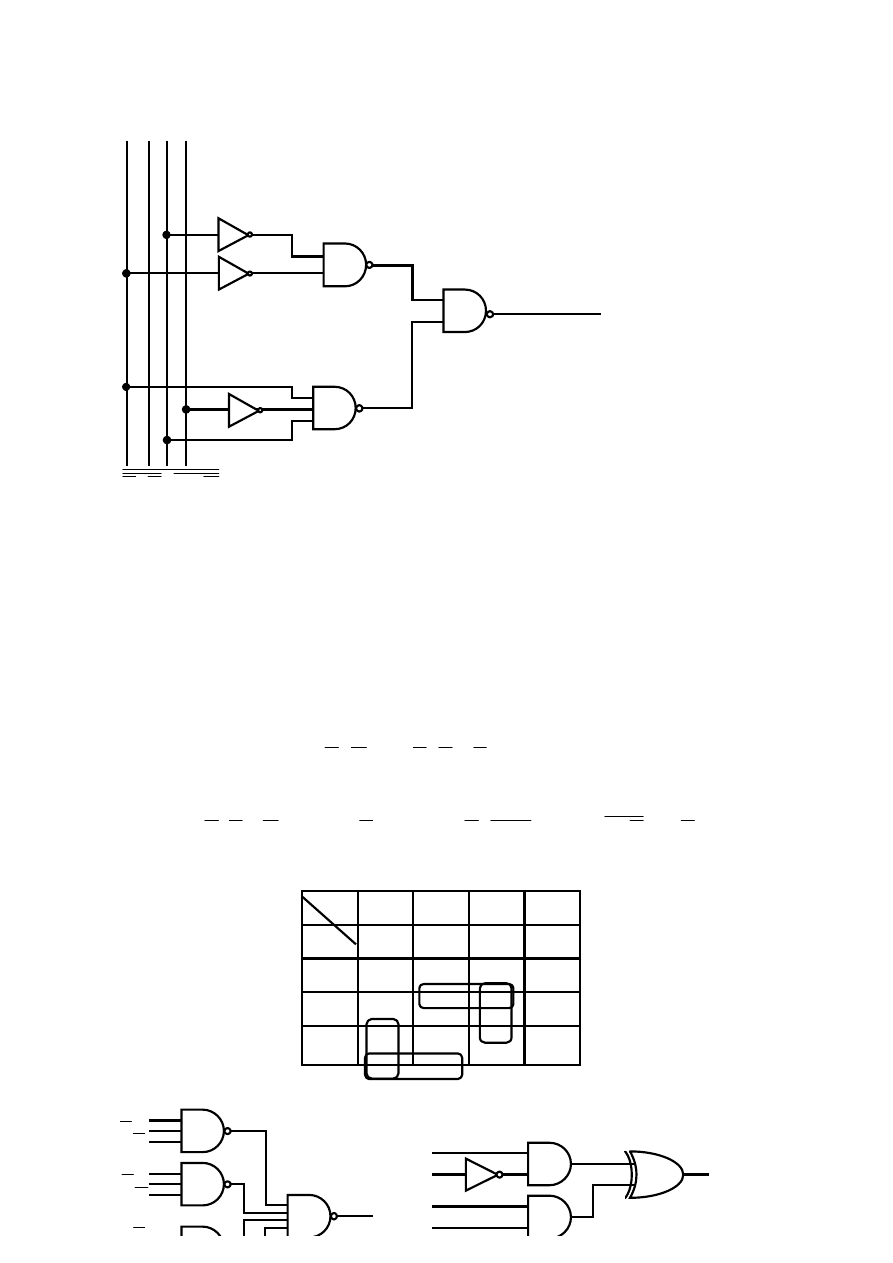
28
D
AC
C
A
Y
⋅
⋅
=
Rys 3.9 Realizacja funkcji Y = (0, 1, 4, 5, 10, 14): a) wypełniona tablica Karnaugha z zakreślonymi parami jedynek (pary jedynek połączone
w czwórki), b) układ zbudowany z bramek
Może się zdarzyć, że fizyczne warunki działania urządzenia nie dopuszczają wystąpienia pewnych kombinacji zmiennych. Jeśli dana
kombinacja zero – jedynkowa nigdy na wejściu układu się nie pojawia lub gdy nie jest istotne, jaki stan logiczny pojawi się na wyjściu przy tej
kombinacji, można przyjąć, że dla takiej kombinacji wartość funkcji może wynosić 0, jak również 1. Taka możliwość przyjęcia dowolnej wartości
funkcji jest bardzo przydatna w procesie minimalizacji.
W tablicach, dla oznaczenia dowolnej wartości funkcji zapisuje się umownie symbol: -,
∼
,
∅
, X.
Niektóre funkcje logiczne , zwłaszcza takie, w których przeważa liczba jedynek nad liczbą zer, można zrealizować w prosty sposób dzięki
sklejaniu zer (tak samo jak jedynek). Jedyną różnicą jest to, że otrzymaną funkcję należy zanegować, czyli podać na wyjście układu przez negator.
Przykład 3.4:
Zrealizować funkcję Y(A, B, C, D) =
U
(5, 7, 8, 9, 12, 15).
W celu zminimalizowania funkcji należy przedstawić ją w tablicy Karnaugha (rys. 3.10a). W tablicy znjduje się sześć jedynek, które
można połączyć w cztery pary. Z tablicy otrzymuje się:
D
C
B
D
B
A
C
B
A
D
C
A
Y
⋅
⋅
+
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
Układ służący do realizacji tej funkcji można zbudować z bramek I (AND), LUB (OR), NIE (NOT). Układem równoważnym jest układ
zbudowany z bramek I – NIE (NAND), który przedstawiono na rys. 3.10b.
Po przekształceniach funkcja przyjmie postać:
BD
C
A
C
A
D
B
D
B
C
A
)
C
A
(
D
B
)
D
B
(
C
A
Y
⊕
=
⋅
⋅
⋅
+
⋅
⋅
⋅
=
+
⋅
+
+
⋅
=
Układ służący do realizacji tej funkcji zbudowany z bramek I (AND), NIE (NOT) i ALBO (Ex – OR) przedstawia rys. 3.10c.
a)
00
01
11
10
00
0
0
0
0
01
0
1
1
0
11
1
0
1
0
10
1
1
0
0
b)
c)
CD
AB
A
C
D
A
B
C
A
Y
Y
6.
C
B
D
A B C D
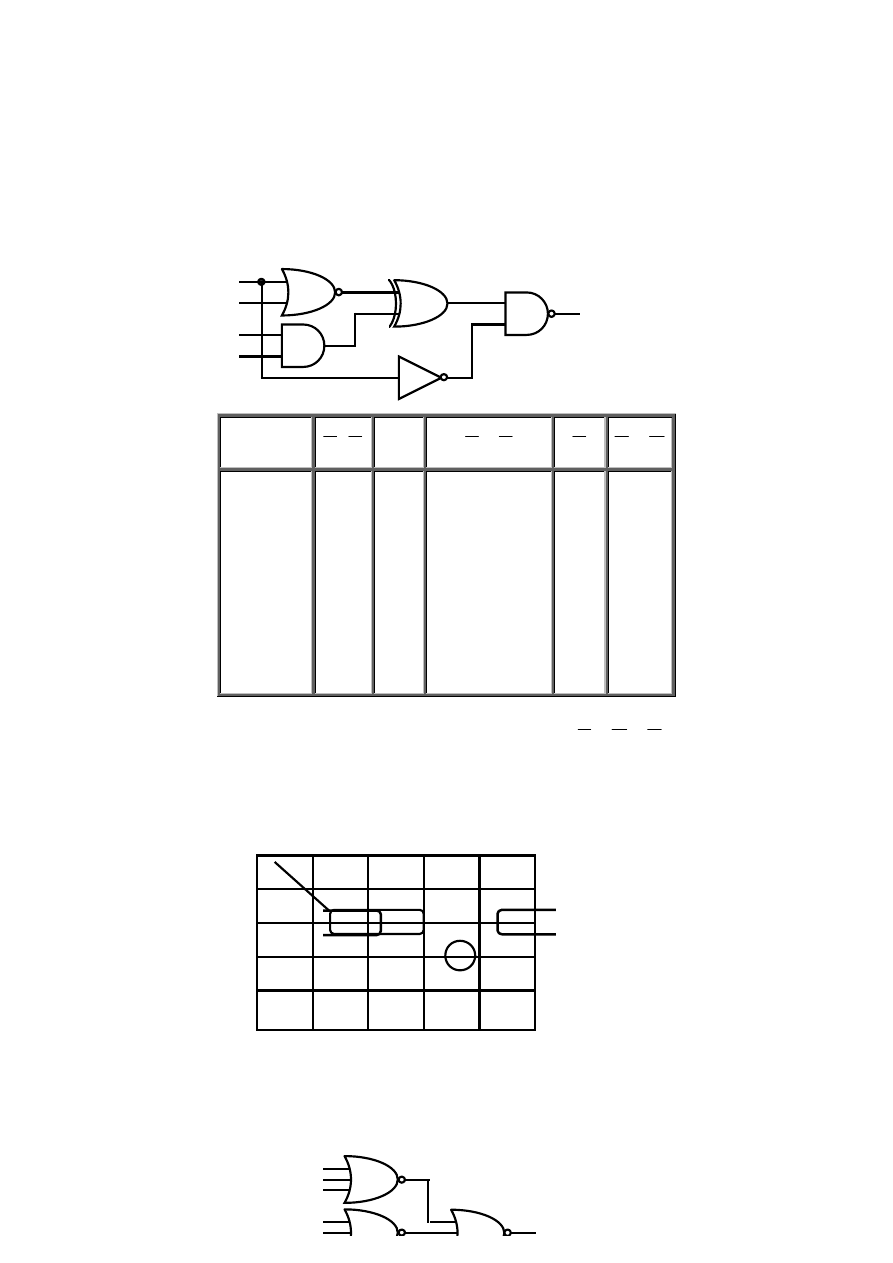
29
CD
AB
Rys. 3.10 Funkcja Y(A, B, C, D) =
U
(5, 7, 8, 9, 12, 15):
a) tablica Karnaugha, b, c)schematy logiczne.
Przykład 3.5:
1.
Wypełnić siatkę Karnaugha dla funkcji, której schemat logiczny pokazano na rys. 3.11.
2.
Zrealizować funkcję na bramkach NOR.
Rys. 3.11 Schemat logiczny funkcji.
Aby uzupełnić siatkę Karnaugha należy najpierw określić stany w punktach a, b, c, d, e, co pokazano w tabeli 3.1.
Tablica 3.1
A B C D
a
B
A
⋅
b
D
C
⋅
c
B
A
B
A
⋅
+
⋅
d
A
e
D
C
+
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
1
1
1
1
0
0
0
0
1
0
0
0
1
0
0
0
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
0
1
1
1
1
1
1
1
1
Następnie wpisujemy wynik z punktu e w tablicę Karnaugha (rys. 3.12). Z tablicy otrzymujemy:
)
C
D
B
A
(
)
C
B
A
(
)
D
B
A
(
Y
+
+
+
⋅
+
+
⋅
+
+
=
00
01
11
10
00
0
0
1
0
01
1
1
0
1
11
1
1
1
1
10
1
1
1
1
Rys. 3.12 Siatka Karnaugha dla funkcji.
Układ budujemy z trzech 3 – wejściowych i jednej 4 – wejściowej bramki NOR (rys. 3.13).
a
c
e
Y
d
b
A
B
C
D
Y
A
D
A
C
B
B
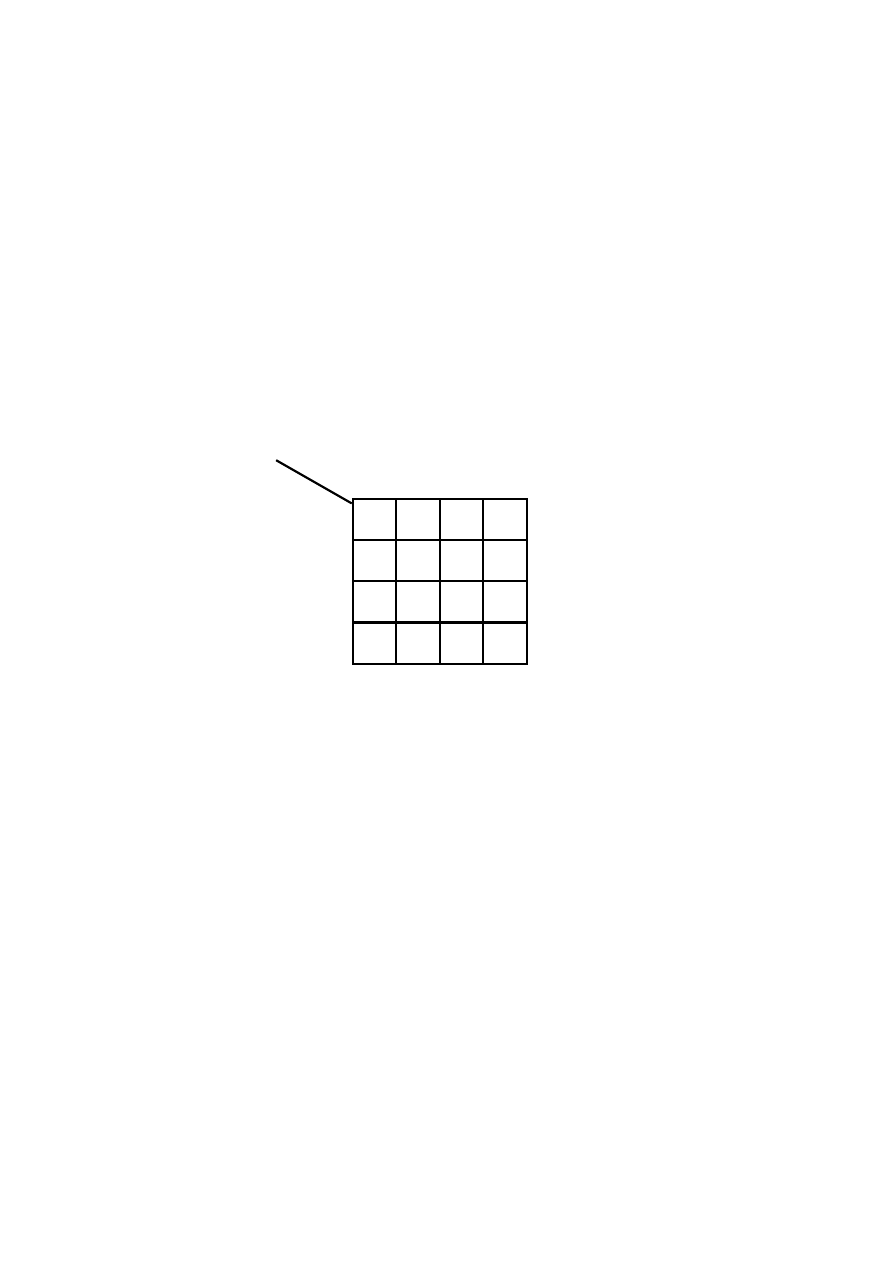
30
Rys. 3.13 Realizacja funkcji na bramkach NOR.
Oprócz przedstawionej wyżej metody, minimalizację funkcji logicznych można przeprowadzić stosując:
-
metodę Quine’a,
-
metodę Quine’a – Mc Cluskeya,
-
metodę Patricka,
-
metodę Blake’a i inne.
Zadanie:
Udowodnić, że dla siatki Karnaugha pokazanej na rys. 3.14 funkcja ma postać:
Y = X
2
X
0
X
1
X
0
X
3
X
2
00
01
11
10
00
0
X
X
0
01
X
X
X
0
11
X
X
X
X
10
0
X
X
0
Rys. 3.14 Siatka Karnaugha do zadania.

31
4.
PRZERZUTNIKI
4.1.
Wst
ęp
Zapamiętywanie wartości zmiennych binarnych, jak również sekwencji tych wartości odbywa się w układach zwanych elementami
pamięci. Podstawowym elementem jest funktor, którego podstawową funkcją jest pamiętanie jednego bitu informacji, zwany przerzutnikiem.
Przerzutniki mogą występować oddzielnie lub w zespołach, połączone w rejestry, liczniki lub bloki pamięci.
W przerzutnikach scalonych TTL wyróżnia się dwa podstawowe rodzaje wejść informacyjnych:
§
wejścia asynchroniczne - oznaczone małymi literami,
§
wejścia synchroniczne - oznaczone dużymi literami.
Wejścia asynchroniczne – to takie, w których zmiana wartości informacji wywołuje bezpośrednio zmianę wartości zmiennych
wyjściowych.
Wejścia synchroniczne – używane są do wywołania zmiany wartości zmiennych wyjściowych, ale zmiana następuje w takt impulsu
synchronizującego, zwanego też impulsem zegarowym (ang. clock) lub taktującym. Brak impulsu taktującego oznacza, że przerzutnik nie będzie
reagował na zmiany wartości zmiennych informacyjnych synchronicznych przerzutnika.
Przerzutnik jest układem posiadającym (rys. 4.1):
1.
Dwa wejścia informacyjne asynchroniczne s i r.
Zmienne s i r oddziałują na wartości zmiennych wyjściowych Q i
Q
. Zmienna s zwana jest zmienną wpisującą (ang. set) lub ustawiającą
(ang. preset). Służy ona do ustawiania przerzutnika w stan wysoki (Q = 1;
Q
= 0). Zmienna r zwana jest zmienną zerującą (ang. reset lub clear).
Służy ona do zerowania przerzutnika w stan niski (Q = 0;
Q
= 1).
2.
Dwa wejścia informacyjne synchroniczne A i B (programujące).
Zmienne A i B w różny sposób oddziałują na zmienne wyjściowe Q i
Q
. Decyduje to o nazwie typu przerzutnika.
3.
Wejście zegarowe C.
Na wejście zegarowe, oznaczone literą C, wprowadza się impuls taktujący. Wejście to zwane jest inaczej synchronizującym albo
wyzwalającym.
4.
Dwa wyjścia komplementarne Q i
Q
(proste i zanegowane).
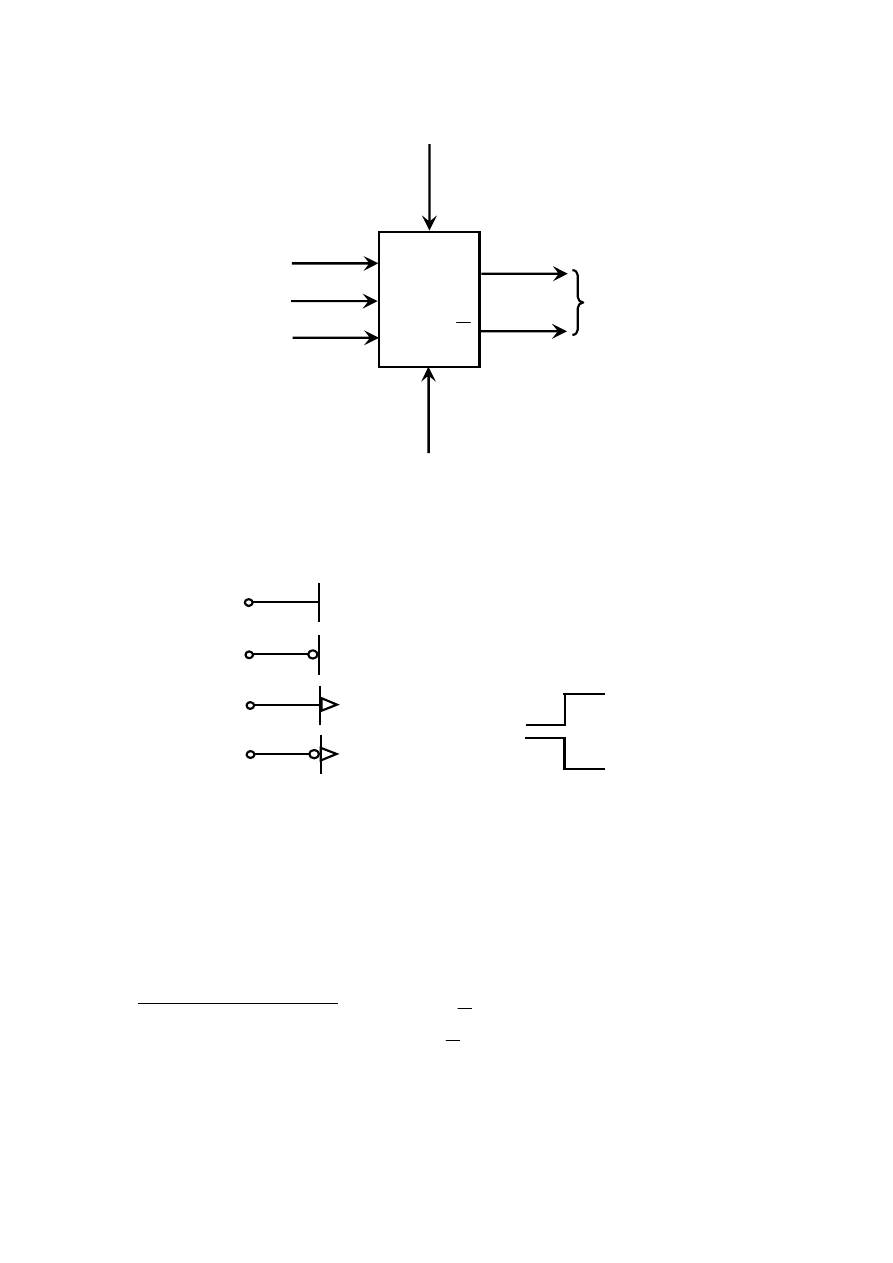
32
Rys. 4.1 Schemat graficzny przerzutnika.
W symbolach graficznych i wielu bardziej złożonych układów logicznych niektóre wejścia są oznaczone literą z zaznaczoną nad nią
poziomą kreską (negacją). Oznacza to, że funkcja przypisana temu wejściu jest uaktywniana pojawieniem się na nim stanu logicznego 0 (poziomem
aktywnym jest stan niski). Do zaznaczenia sposobu oddziaływania wejść na układ stosuje się również oznaczenia graficzne (rys.4.2).
Rys. 4.2 Oznaczenia graficzne wejść przerzutnika.
Jeśli o wartości zmiennej wyjściowej przerzutnika decydują tylko wejścia asynchroniczne to mamy do czynienia z przerzutnikiem
asynchronicznym W przerzutniku tym informacja na wyjściu pojawia się w chwilach uzależnionych tylko od zmiany stanu na jego wejściach. Do tej
grupy zaliczamy głównie przerzutnik s r.
Gdy stan przerzutnika ulega zmianie pod wpływem impulsu zegarowego, mówimy wtedy o przerzutniku synchronicznym.
Podstawowymi typami przerzutników synchronicznych są: RS, D, T i JK.
W układach TTL stosuje się:
§
przerzutniki wyzwalane poziomem,
§
przerzutniki wyzwalane zboczem,
§
przerzutniki dwuzboczowe (dwustopniowe).
Wyzwalanie przerzutnika należy rozumieć jako sposób oddziaływania impulsu zegarowego na wartość zmiennych wyjściowych
przerzutnika.
Wyzwalanie poziomem polega na tym, że sygnał z wejść informacyjnych może oddziaływać na stan przerzutnika tylko wtedy, gdy
przebieg zegarowy ma wysoki poziom (H).
Wyzwalanie zboczem polega na tym, że sygnał z wejść informacyjnych może oddziaływać na stan przerzutnika tylko w czasie narastania
(lub opadania) zbocza przebiegu zegarowego.
W impulsie taktującym wyróżnia się zbocze narastające (pozytywne, dodatnie) oraz zbocze opadające (negatywne, ujemne).
Wyzwalanie dwuzboczowe polega na tym, że sygnał z wejść informacyjnych w czasie trwania pierwszego zbocza (zbocze narastające)
przebiegu zegarowego jest wpisywany do przerzutnika, a w czasie trwania drugiego zbocza (zbocze opadające) jest przekazywany na wyjście.
Podstawowe parametry przerzutników to:
§
czasy propagacji sygnałów od wejścia synchronizującego do wyjść Q i
Q
,
§
czasy propagacji sygnałów od wejść asynchronicznych do wyjść Q i
Q
,
§
czas ustalenia t
s
(t setup),
§
czas przetrzymywania t
h
(t thold),
§
minimalny czas trwania określonych sygnałów,
§
maksymalna częstotliwość przebiegu synchronizującego.
Czas propagacji jest to czas, po którym następuje zmiana poziomu logicznego zmiennej wyjściowej przerzutnika.
Czas ustalania (t
s
) jest to minimalny czas, w którym sygnał wejściowy musi być obecny na wejściach informacyjnych
(synchronizowanych) przerzutnika przed nadejściem wyzwalającego zbocza impulsu synchronizacji.
C
s
r
Q
Q
Wyjścia
Asynchroniczne
wejście zerujące
Asynchroniczne
wejście ustawiające
Wejście
zegarowe
Synchroniczne
wejście informacyjne
Synchroniczne
wejście informacyjne
aktywny stan 1
aktywny stan 0
oddziałuje zbocze
narastające
oddziałuje
zbocze opadające
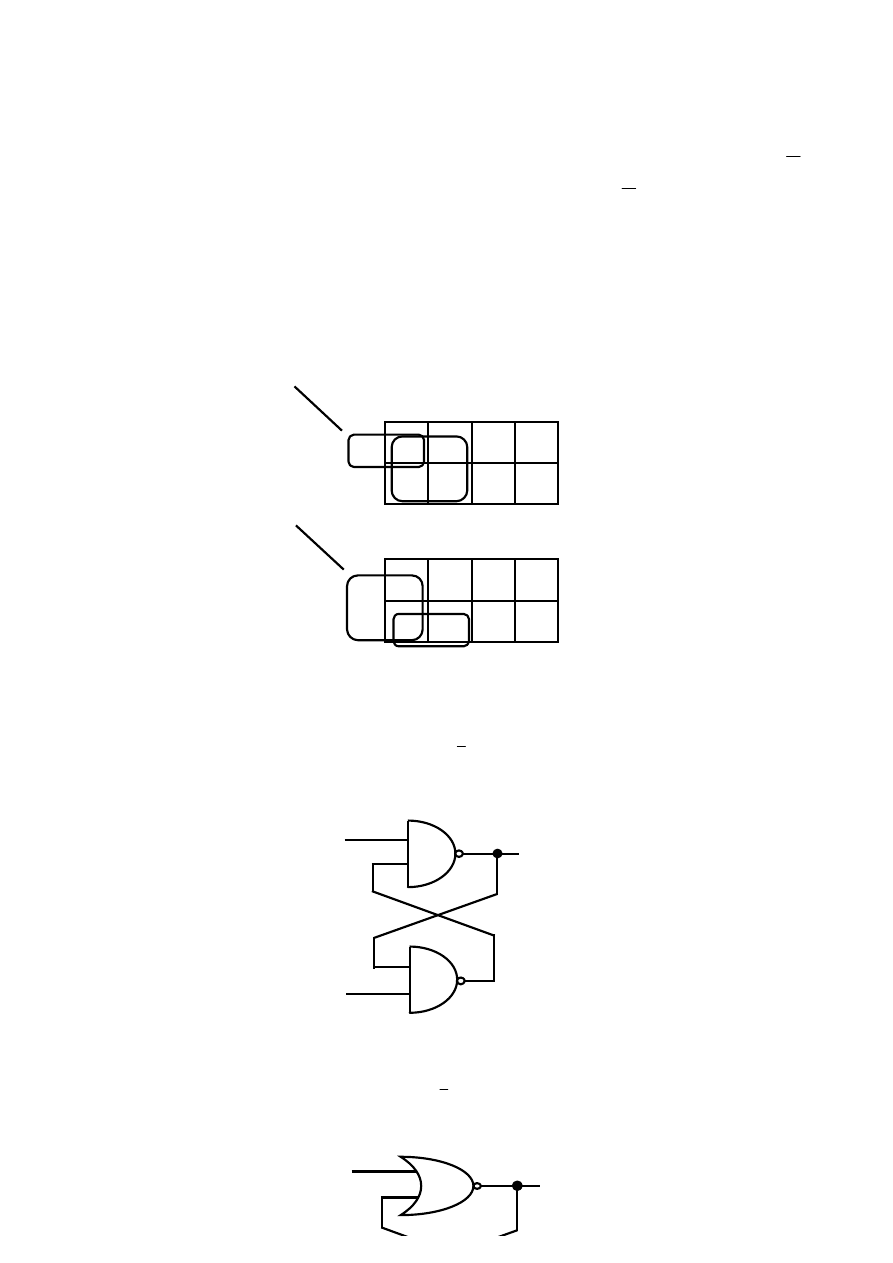
33
Czas przetrzymywania (t
h
) jest to minimalny czas, w którym sygnał wejściowy musi pozostać na wejściu informacyjnym
(synchronizowanym) po wystąpieniu wyzwalającego zbocza sygnału synchronizacji.
4.2.
Przerzutniki asynchroniczne
Najprostszym przerzutnikiem asynchronicznym jest przerzutnik s r. Posiada on dwa wejścia informacyjne s i r oraz dwa wyjścia Q i
Q
.
Wejścia s i r są wejściami asynchronicznymi, tzn. ich stany natychmiast oddziałują na wartości zmiennych Q i
Q
.
W przerzutniku s r wyróżnia się cztery podstawowe cechy:
§
dominujące wejście wpisujące,
§
dominujące wejście zerujące,
§
aktywny poziom (sygnał) wysoki H, (ustawienie wartości Q = 1 odbywa się sygnałem s = 1, jeśli s = 0 wtedy nie zmienia się stan układu),
§
aktywny poziom (sygnał) niski L, (ustawienie wartości Q = 1 odbywa się sygnałem s = 0, jeśli s = 1 wtedy nie zmienia się stan układu),
Na podstawie wyżej wymieniony cech możemy zaprojektować cztery układy:
§
aktywny sygnał wysoki i dominujący sygnał wpisujący,
§
aktywny sygnał niski i dominujący sygnał wpisujący,
§
aktywny sygnał wysoki i dominujący sygnał zerujący,
§
aktywny sygnał niski i dominujący sygnał zerujący.
Na rys. 4.3 przedstawiono siatki Karnaugha dla przerzutników asynchronicznych.
a)
sr q
00
01
11
10
0
0
0
0
1
1
1
0
0
1
b)
sr q
00
01
11
10
0
1
1
0
0
1
1
1
1
0
Rys. 4.3 Siatka Karnaugha dla przerzutników asynchronicznych:
aktywny sygnał wysoki, dominujące wejście zerujące,
aktywny sygnał niski, dominujące wejście wpisujące.
Siatka Karnaugha na rys. 4.3a przedstawia funkcję logiczną dla przerzutnika o wysokim poziomie aktywnym i dominującym wejściu
zerującym (r). Z siatki otrzymujemy funkcję logiczną:
)
q
s
(
r
Q
+
=
Funkcję tę można zrealizować za pomocą dwóch elementów NOR (rys 4.4).
Rys. 4.4 Przerzutnik asynchroniczny o aktywnym poziomie wysokim i dominującym wejściem zerującym
Z siatki Karnaugha (rys. 4.3b) dla przerzutnika o niskim poziomie aktywnym i dominującym wejściu wpisującym (s), otrzymujemy
funkcję:
rq
s
Q
+
=
Na rys. 4.5 przedstawiono najprostszą realizację.
s
r
r
Q
q
Q

34
Rys. 4.5 Przerzutnik asynchroniczny o aktywnym poziomie niskim i dominującym wejściu wpisującym
Opis pracy przerzutnika można przedstawić za pomocą tablicy charakterystycznej (inaczej tablicy przejść, rys. 4.6).
s
n
r
n
Q
n+1
0
0
Q
n
0
1
0
1
0
1
1
1
X
X – stan nieokreślony,
Q
n
– stan poprzedni,
Rys. 4.6 Tablica charakterystyczna przerzutnika s r z wysokim sygnałem aktywnym.
Tablica ta opisuje zależność wyjścia Q przerzutnika w chwili n + 1 od wartości zmiennych s i r w chwili n. Przykład tablicy dotyczy
przerzutnika zmieniającego wartości na wyjściach Q pod wpływem wysokiego poziomu logicznego sygnału wejściowego. Stan „nieokreślony” w
tablicy oznacza, że wartości zmiennych Q
n+1
będą zależne od dominacji wybranego wejścia przerzutnika (dominuje s lub r).
4.3.
Przerzutniki synchroniczne
4.3.1.
Wst
ęp
Przerzutniki synchroniczne posiadają oprócz wejść informacyjnych synchronicznych i asynchronicznych także wejście synchronizujące,
czyli wejście zegarowe.
Oddziaływanie stanu wejść informacyjnych na stan przerzutnika możliwe jest tylko w obecności impulsu zegarowego na wejściu C.
Działanie przerzutnika synchronicznego można ogólnie scharakteryzować w sposób następujący:
§
na wejścia informacyjne synchroniczne podaje się odpowiednie stany, stosownie do tablicy stanów przerzutnika,
§
impuls zegarowy umożliwia oddziaływanie tych stanów na stan przerzutnika,
§
stany na wyjściach przerzutnika można ustalić przez chwilową lub dowolnie długo trwającą zmianę stanu wejść informacyjnych
asynchronicznych niezależnie od impulsu zegarowego i stanu na wejściach informacyjnych synchronicznych; wejścia asynchroniczne zawsze
mają priorytet w stosunku do innych wejść przerzutnika.
Działanie logiczne przerzutnika synchronicznego najczęściej ilustruje się za pomocą tablicy stanów oraz tablicy charakterystycznej,
inaczej zwaną tablicą przejść (częściej używane).
W tablicy stanów są przedstawione stany na wejściach informacyjnych synchronicznych układu przed nadejściem impulsu zegarowego w
chwili t
n
(Q
n
) oraz stany na wyjściach po wystąpieniu impulsu zegarowego w chwili t
n+1
(Q
n+1
).
W tablicy charakterystycznej w kolumnie odpowiadającej stanowi Q
n+1
wpisuje się stan, jaki następuje po obecnym stanie Q
n
, czyli przy
danej kombinacji sygnałów wejściowych. W kolumnie Q
n+1
mogą wystąpić różne symbole, które mają następujące znaczenie:
§
0 – zerowanie przerzutnika,
§
1 – ustawianie przerzutnika,
§
Q
n
– niezmieniony stan wyjścia,
§
n
Q
- zmieniony stan wyjścia, (na przeciwny),
§
X – niedozwolony stan na wejściu, tzn. że nie jest określony stan jaki pojawi się na wyjściach Q i
Q
. Na obu wyjściach mogą się pojawić zera
lub jedynki.
Działanie logiczne przerzutnika synchronicznego można również zilustrować za pomocą tablicy Karnaugha oraz tablicy wzbudzeń.
4.3.2.
Przerzutnik synchroniczny D
Przerzutnik D (przepisujący) stanowi układ pamiętający, opóźniający i synchronizujący. Na rys. 4.7 przedstawiono symbol graficzny
przerzutnika D i tablice ilustrujące działanie.
q
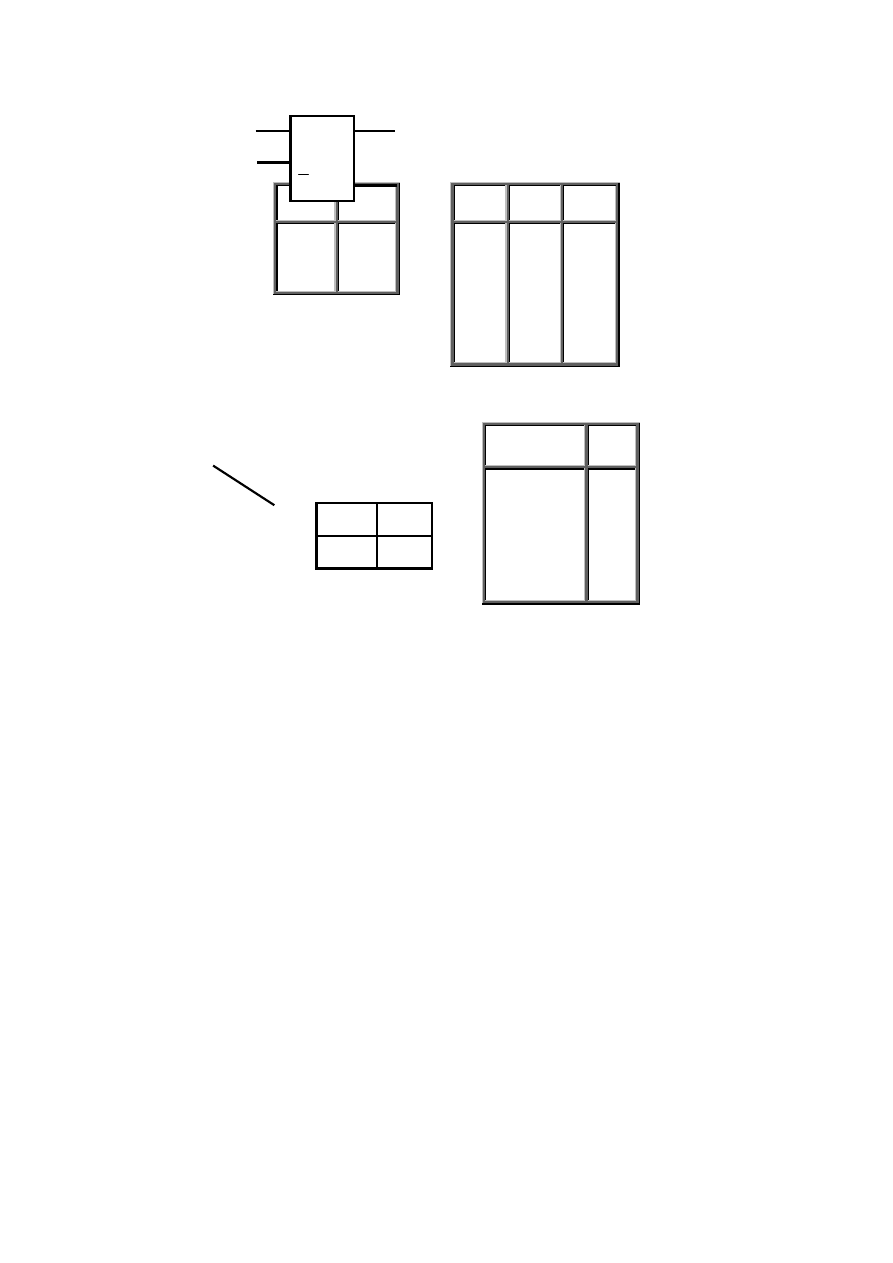
35
a)
b)
c)
D
n
Q
n+1
Q
n
D
n
Q
n+1
0
0
0
0
0
1
1
0
1
1
1
0
0
1
1
1
d)
e)
Q
n+1
Q
n
Q
n+1
D
n
D
n
Q
n
0
1
0
0
0
0
0
1
0
1
1
1
0
1
1
0
0
1
1
1
Rys. 4.7 Przerzutnik D: a) symbol graficzny, b) tablica charakterystyczna,
c) tablica stanów, d) tablica Karnaugha dla Q
n+1
, e) tablica wzbudzeń.
Na jego wyjściu Q pojawi się w następnym takcie zegarowym (Q
n+1
) taki stan, jaki panował na wejściu informacyjnym D w bieżącym
takcie zegarowym (Q
n
).
Równanie logiczne przerzutnika D otrzymane na podstawie tablicy Karnaugha (rys 4.7d) ma postać:
Q
n+1
= D
n
Przerzutnik typu D jest typowym przedstawicielem przerzutników, których wartość zmiennej ustalana jest w chwili osiągnięcia wysokiego
poziomu (minimum 2,4 V) impulsu zegarowego, czyli w trakcie narastania sygnału taktującego.
Wartość zmiennej wejściowej D zostaje przesunięta na wyjście Q przednim (dodatnim) zboczem impulsu zegarowego i zapamiętana tak
długo, dopóki nie pojawi się następny impuls taktujący. Na rys. 4.8 przedstawiono przebiegi czasowe dla przerzutnika typu D.
D Q
C
Q
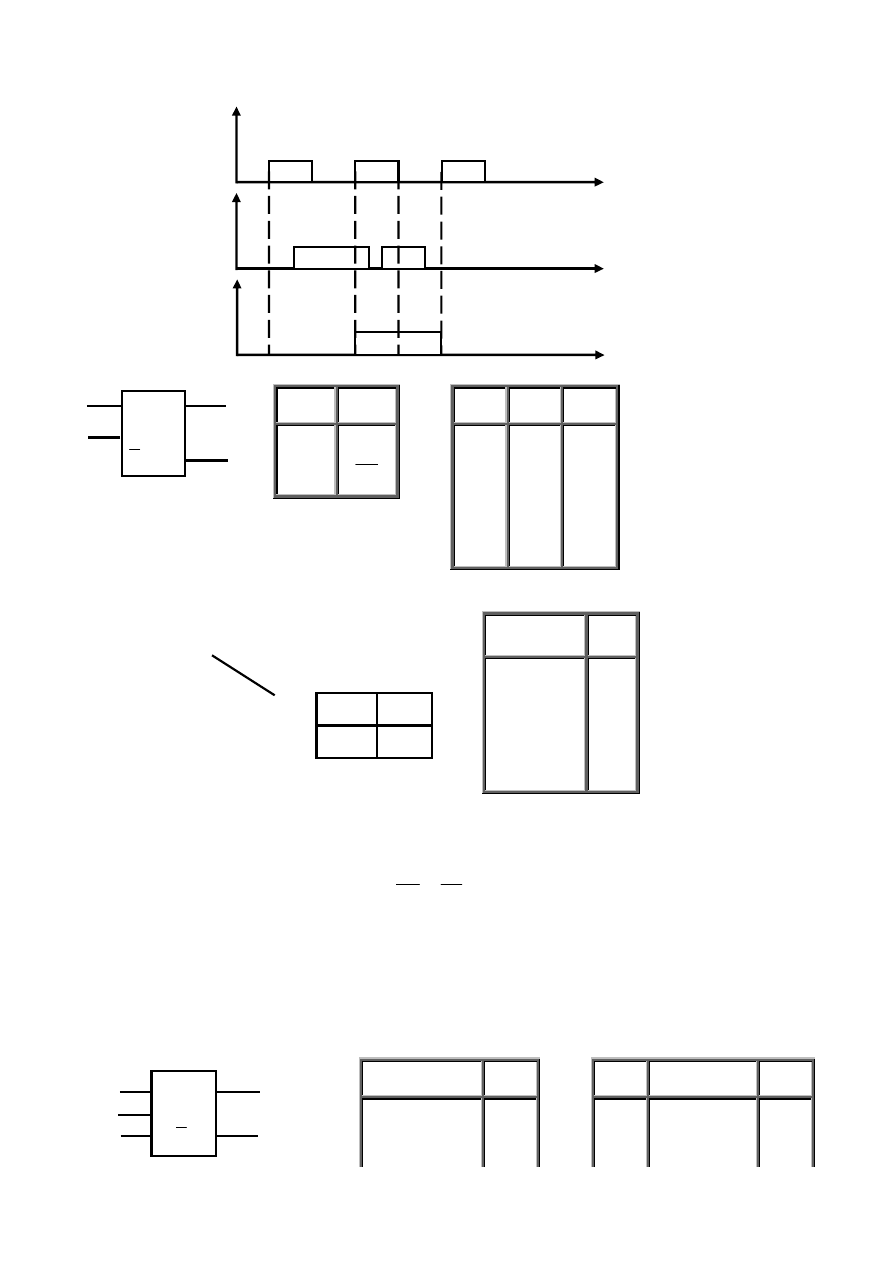
36
Rys. 4.8 Przebiegi czasowe dla przerzutnika typu D
4.3.3.
Przerzutnik synchroniczny T
Symbol graficzny przerzutnika T i jego działanie zilustrowano na rys. 4.9.
a)
b)
c)
T
n
Q
n+1
Q
n
T
n
Q
n+1
0
n
Q
0
0
0
1
n
Q
0
1
1
1
0
1
1
1
0
d)
e)
Q
n+1
Q
n
Q
n+1
T
n
T
n
Q
n
0
1
0
0
0
0
0
1
0
1
1
1
1
0
1
0
1
1
1
0
Rys. 4.9 Przerzutnik T: a) symbol graficzny, b) tablica charakterystyczna,
c) tablica stanów, d) tablica Karnaugha dla Q
n+1
, e) tablica wzbudzeń.
Równanie logiczne przerzutnika T otrzymane na podstawie tablicy Karnaugha (rys. 4.9d) ma postać:
n
n
n
n
n
n
1
n
Q
T
Q
T
Q
T
Q
⊕
=
+
=
+
Zmiana stanu przerzutnika T występuje zawsze podczas opadającego zbocza. Jeżeli Q
n
jest w stanie wysokim przerzutnik T zmienia swój
stan na przeciwny.
4.3.4.
Przerzutnik synchroniczny RS
Na rys. 4.10 przedstawiono symbol graficzny przerzutnika RS i jego działanie.
a)
b)
c)
S
n
R
n
Q
n+1
Q
n
S
n
R
n
Q
n+1
0
0
n
Q
0
0
0
0
0
1
0
0
0
1
0
T Q
C
Q
S Q
C
R
Q
t
t
t
C
D
Q
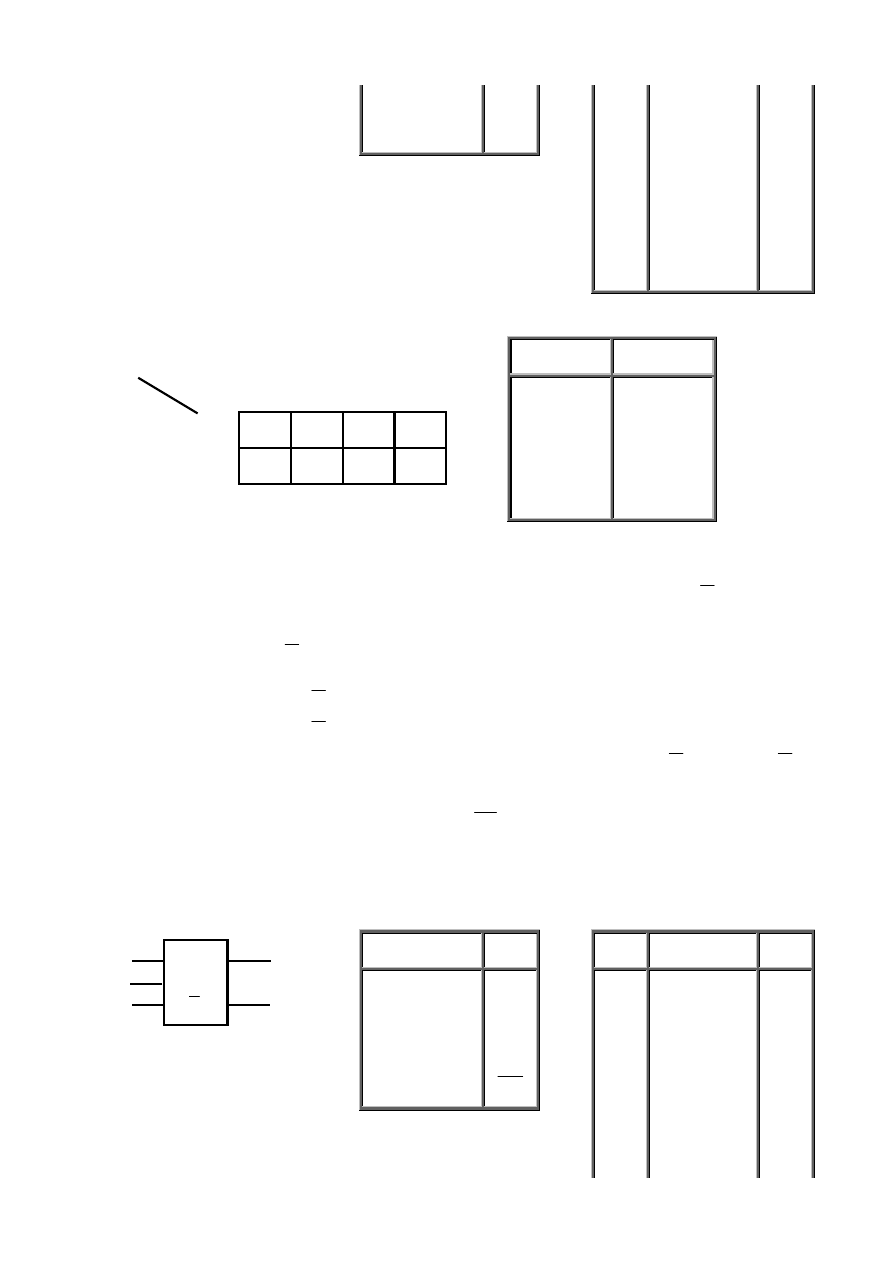
37
1
0
1
0
1
0
1
1
1
X
0
1
1
X
1
0
0
1
1
0
1
0
1
1
0
1
1
1
1
X
d)
e)
Q
n+1
Q
n
Q
n+1
S
n
R
n
S
n
R
n
Q
n
00
01
11
10
0
0
0
X
0
0
0
X
1
0
1
1
0
1
1
0
X
1
1
0
0
1
1
1
X
0
Rys. 4.10 Przerzutnik RS: a) symbol graficzny, b) tablica charakterystyczna,
c) tablica stanów, d) tablica Karnaugha dla Q
n+1
,e) tablica wzbudzeń.
Przerzutnik RS posiada dwa synchroniczne wejścia informacyjne (R i S), wejście zegarowe C oraz dwa wyjścia (Q i
Q
).
Zależnie od trzech dozwolonych kombinacji stanów na dwóch wejściach informacyjnych RS, przerzutnik może spełniać 3 funkcje podczas
wyzwalania go impulsem zegarowym:
1.
nie zmienić stanu na wyjściach Q i
Q
, jeśli R = S = 0,
Q
n
= Q
n+1
2.
przyjąć na wyjściu Q stan 0 i na wyjściu
Q
stan 1 (stan na wyjściu Q
n
= 0), jeśli R = 1 i S = 0,
3.
przyjąć na wyjściu Q stan 1 i na wyjściu
Q
stan 0 (stan na wyjściu Q
n
= 1), jeśli R = 0 i S = 1.
Przy stanie R = S = 1 stan wyjściowy przerzutnika jest nieokreślony, tzn. że może zaistnieć albo stan Q = 0 i
Q
= 1, albo Q = 1 i
Q
=
0.
Równanie logiczne przerzutnika RS otrzymane na podstawie tablicy Karnaugha ma postać:
n
n
n
1
n
Q
R
S
Q
+
=
+
4.3.5.
Przerzutnik synchroniczny JK
Na rys. 4.11 przedstawiono symbol graficzny oraz tablice ilustrujące jego działanie.
a)
b)
c)
J
n
K
n
Q
n+1
Q
n
J
n
K
n
Q
n+1
0
0
n
Q
0
0
0
0
0
1
0
0
0
1
0
1
0
1
0
1
0
1
1
1
n
Q
0
1
1
1
1
0
0
1
1
0
1
0
J Q
C
K
Q
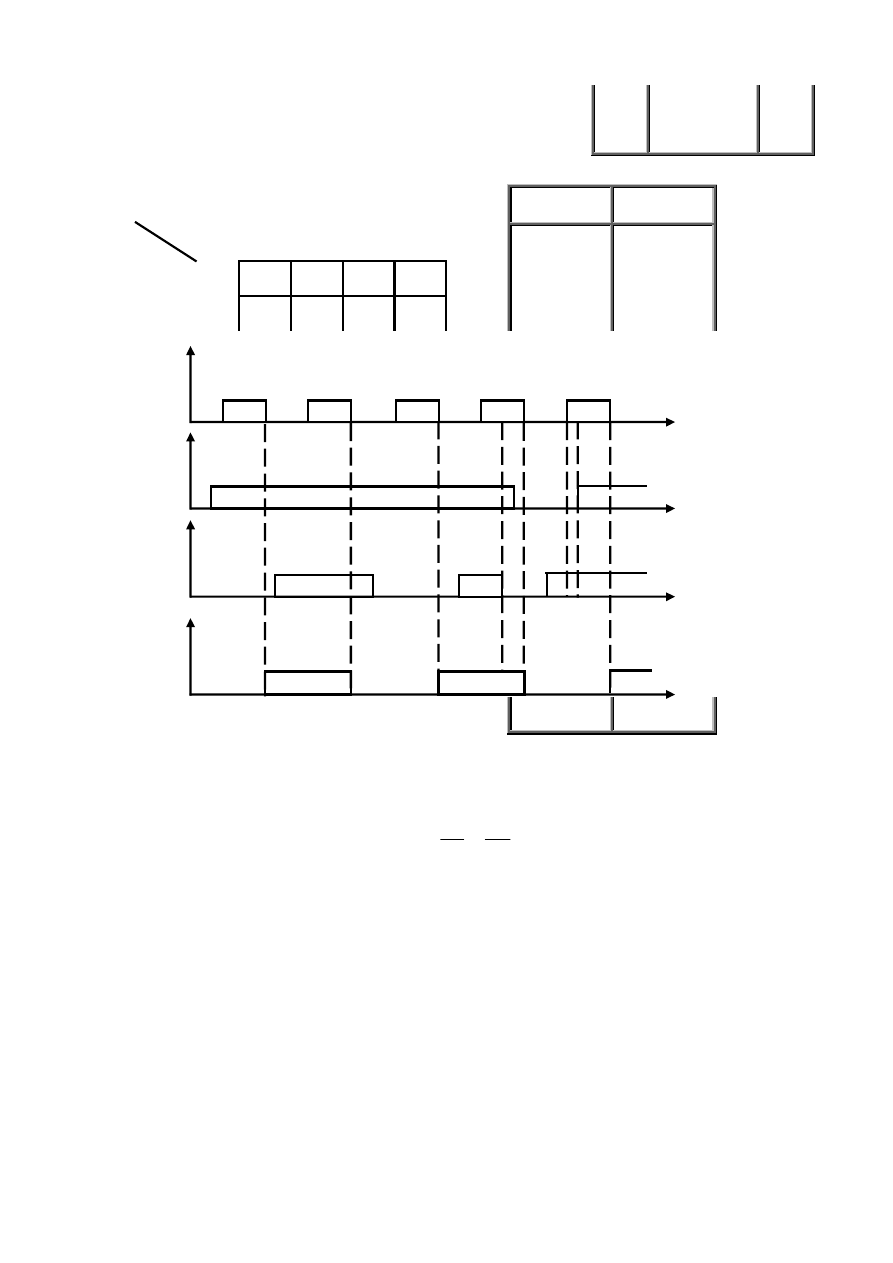
38
1
1
0
1
1
1
1
0
d)
e)
Q
n+1
Q
n
Q
n+1
J
n
K
n
J
n
K
n
Q
n
00
01
11
10
0
0
0
X
0
0
0
1
1
0
1
1
X
1
1
0
0
1
1
0
X
1
1
1
X
0
Rys. 4.11 Przerzutnik JK: a) symbol graficzny, b) tablica charakterystyczna,
c) tablica stanów, d) tablica Karnaugha dla Q
n+1
,e) tablica wzbudzeń.
Dla przerzutnika JK dozwolona jest kombinacja sygnałów wejściowych J = K = 1, zmieniająca stany na wyjściach przerzutnika na
przeciwne.
Równanie logiczne JK otrzymane na podstawie tablicy Karnaugha ma postać:
n
n
n
n
1
n
Q
K
Q
J
Q
+
=
+
Przerzutnik JK jest przerzutnikiem wyzwalanym dwustopniowo, zwanym również przerzutnikiem Master – Slave. Przerzutnik ten składa
się z dwóch przerzutników połączonych kaskadowo (szeregowo) (rys. 4.12). Pierwszy z nich nosi nazwę Master (M) – ang. pan, drugi - Slave (S) –
ang. niewolnik.
a)
t
t
t
C
J
Q
K
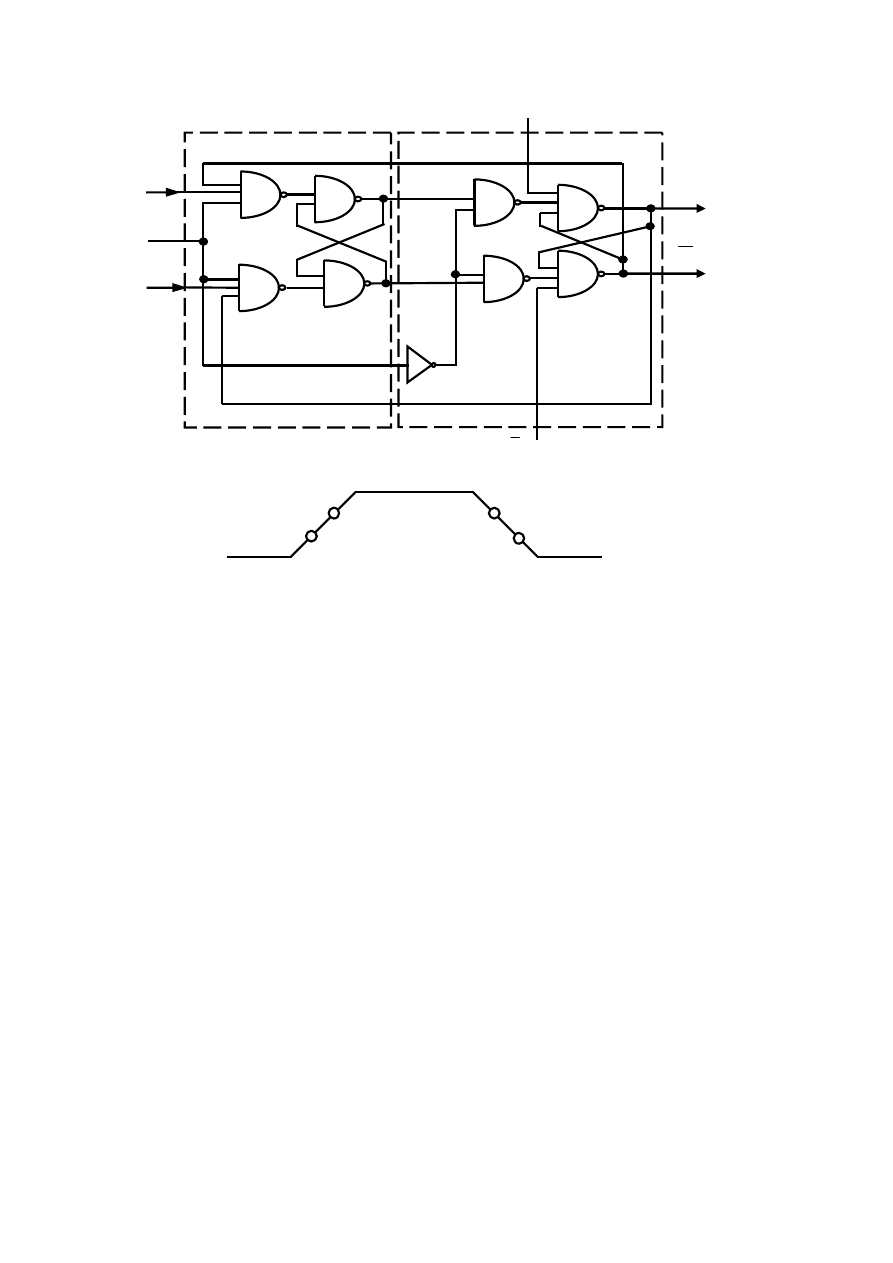
39
b)
c)
Rys. 4.12 Przerzutnik synchroniczny JK wyzwalany dwustopniowo:
a)
schemat logiczny: M – część Master, S – część Slave,
b)
fazy przełączania przerzutnika
c)
przebiegi czasowe.
W celu zilustrowania działania przerzutnika przedstawiono na rys. 4.12b impuls synchronizujący z wyróżnionymi czterema chwilami:
1.
przerwanie połączenia między częścią Master i częścią Slave (odseparowanie wejść przerzutnika Slave od wyjść Master), zablokowanie bramek
3 i 4;
2.
zmiana stanu przerzutnika Master stosownie do stanu wejść informacyjnych, otwarcie wejść bramek (1 i 2) dla sygnałów J i K oraz
zapamiętanie pobudzeń w części Master;
3.
zablokowanie wejść części Master (zablokowanie bramek 1 i 2);
4.
przepisanie wartości zmiennych wyjściowych przerzutnika Master do przerzutnika Slave, tzn. na wyjście układu.
W rozpatrywanym przerzutniku JK – MS zmiana stanu przerzutnika Master odbywa się podczas zmiany poziomu z 0 na 1 na wejściu
zegarowym, natomiast przepisanie informacji z przerzutnika Master do Slave podczas zmiany poziomu na tym wejściu z 1 na 0.
Przepisanie informacji do Slave odbywa się podczas zmiany poziomu z 1 na 0 jest przedstawione na symbolu graficznym za pomocą kółka
przy wejściu zegarowym.
Przerzutnik JK jest najczęściej stosowanym przerzutnikiem synchronicznym.
Przerzutnik JK często bywa stosowany jako dzielnik częstotliwości. Wejścia J i K są wtedy łączone równolegle i dołączane do punktu o
potencjale wysokim (H). Przełączanie przerzutnika następuje zawsze przy opadającym zboczu sygnału taktującego. Jeżeli obydwa wejścia J i K mają
potencjał niski (L), to mimo zmian sygnału taktującego wyjście przerzutnika pozostaje niezmienione.
1
2
3
4
J
C
K
M
S
s
r
Q
Q
1
2
3
4
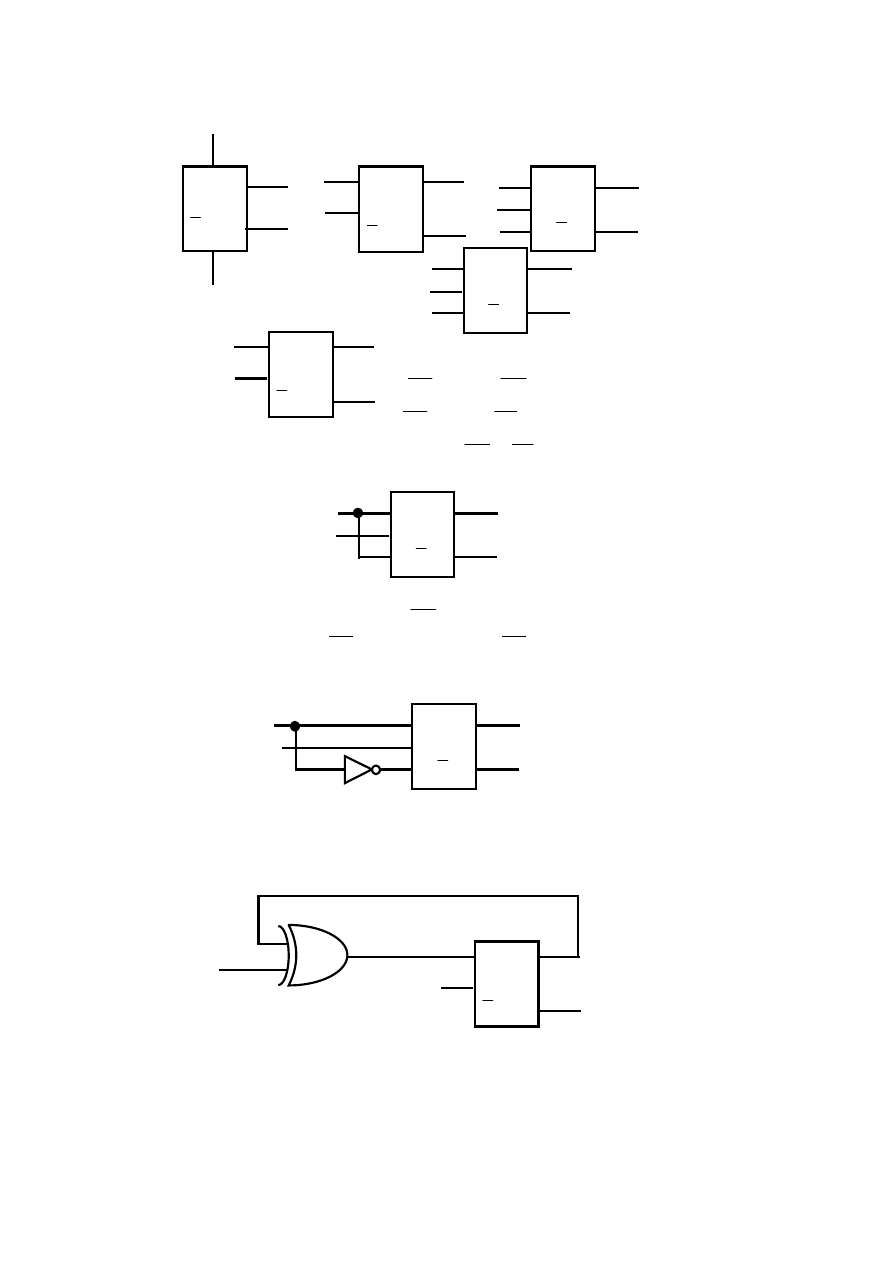
40
Na rys. 4.13 podano symbole ważniejszych przerzutników scalonych.
Rys. 4.13 Symbole ważniejszych przerzutników scalonych.
Jeśli nie dysponujemy odpowiednim przerzutnikiem, można go zbudować na podstawie innego rodzaju przerzutnika.
Zamiana przerzutnika JK na T:
n
n
n
n
K
Q
J
Q
:
JK
+
n
n
n
n
T
Q
T
Q
:
T
+
n
n
T
J
=
n
n
T
K
=
Zamiana przerzutnika JK na D:
n
n
D
J
=
n
n
D
K
=
(
)
n
n
n
n
n
n
n
n
1
n
D
Q
Q
D
D
Q
D
Q
Q
=
+
=
+
=
+
Zamiana przerzutnika D na T:
n
1
n
D
Q
:
D
=
+
n
n
1
n
Q
T
Q
:
T
⊕
=
+
S Q
C
R
Q
J Q
C
K
Q
T
J Q
C
K
Q
D
D Q
C
Q
T
J Q
C
K
Q
T Q
C
Q
D Q
C
Q
Q
Q
s
r
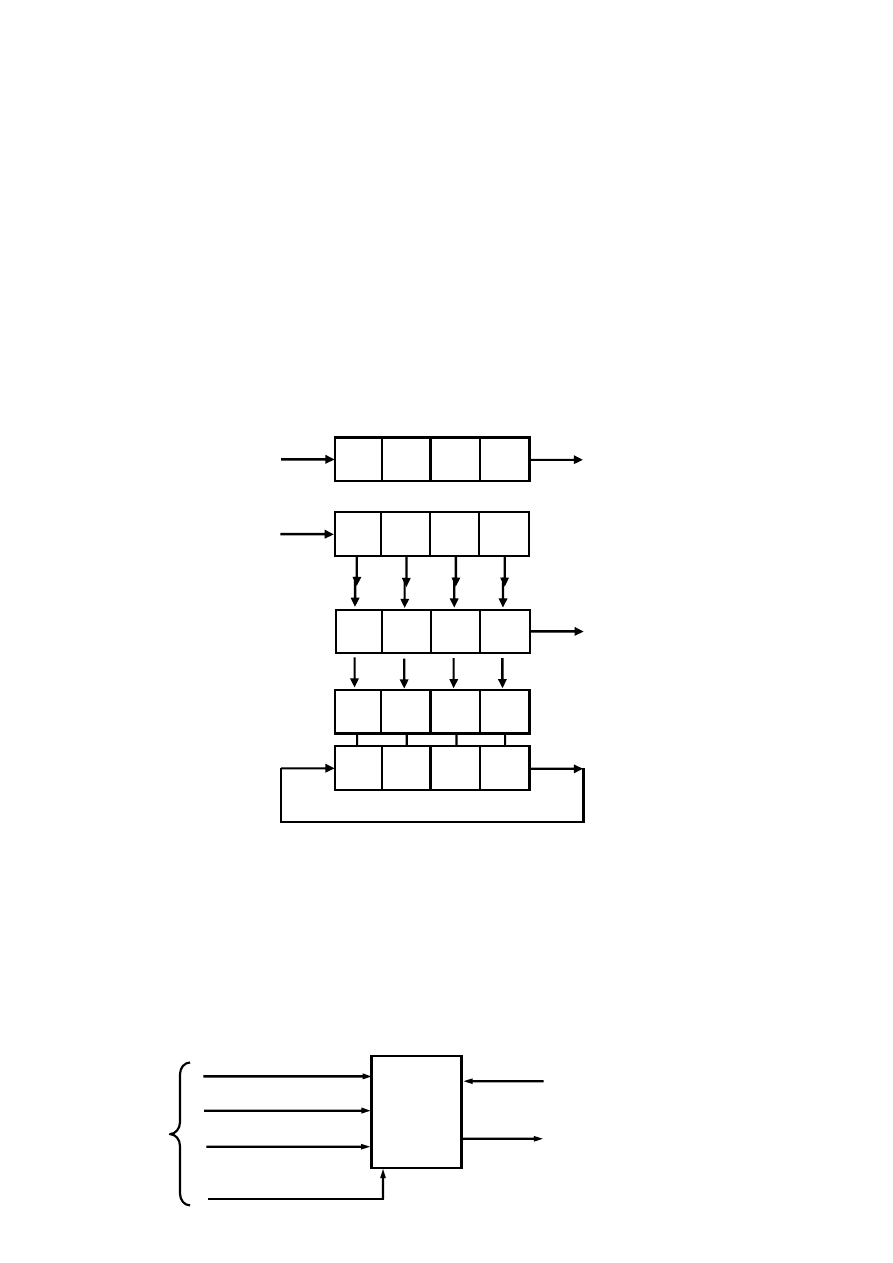
41
5.
REJESTRY
5.1.
WST
ĘP
Rejestrem nazywamy układ składający się z zespołu przerzutników, służący do przechowywania informacji w postaci słów (cztero -,
ośmio - lub więcej bitowych ) w systemie cyfrowym. O długości słowa zapamiętywanego w rejestrze decyduje liczba użytych przerzutników.
Ze względu na sposób wprowadzania i wyprowadzania informacji rejestry dzielą się na:
§
równoległe – umożliwiające równoległe wprowadzanie i wyprowadzanie informacji (całymi słowami) jednocześnie do wszystkich i ze
wszystkich pozycji,
§
szeregowe – umożliwiające szeregowe wprowadzanie i wyprowadzanie informacji, tzn. bit po bicie , w takt sygnału zegarowego,
§
szeregowo – równoległe – umożliwiające szeregowe wprowadzanie i równoległe wyprowadzanie informacji,
§
równoległo – szeregowe – umożliwiające równoległe wprowadzanie i szeregowe wyprowadzanie informacji.
Pierwszy rodzaj rejestrów zalicza się do grupy równoległych, natomiast trzy pozostałe zalicza się ogólnie do rejestrów szeregowych lub
przesuwających.
Wielkości charakteryzujące rejestr to:
§
długość rejestru równa liczbie n zawartych w nim przerzutników,
§
szybkość pracy rejestru równa czasowi trwania lub wyprowadzania informacji dla rejestru równoległego, a dla rejestru szeregowego jest to
maksymalna częstotliwość impulsów taktujących.
Podstawową funkcją rejestrów jest zapamiętywanie informacji. Do tego celu służą przerzutniki, zdolne do zapamiętania wartości jednej
zmiennej logicznej. W odróżnieniu od przerzutników rejestry są zdolne zapamiętywać całe słowa. Rejestry spełniają w urządzeniach cyfrowych
funkcję pomocniczych pamięci o niewielkich pojemnościach.
Na rys. 5.1 pokazano podstawowe sposoby wpisywania i pobierania informacji w rejestrach.
a)
b)
c)
d)
e)
Rys.5.1 Podstawowe sposoby wpisywania i pobierania informacji w rejestrach:
a)
szeregowo – szeregowy,
b)
szeregowo – równoległy,
c)
równoległo – szeregowy,
d)
równoległo – równoległy,
e)
pierścieniowy.
Rejestr, w zależności od trybu pracy (szeregowy, równoległy), może mieć jedno lub więcej wejść informacyjnych, jedno lub więcej wyjść
oraz grupę wejść sterujących. Na rys. 5.2 przedstawiono symbol rejestru uniwersalnego A - bitowego.
Rys. 5.2 Symbol rejestru uniwersalnego A – bitowego.
We
Wy
⇓
⇓
Wejścia równoległe
Wyjścia równoległe
Rejestr A
Wejście szeregowe
(przesuw wstecz)
Wyjście szeregowe
W
ej
śc
ia
Szeregowe
(przesuw w przód)
Zegarowe
Sterujące
Zerujące
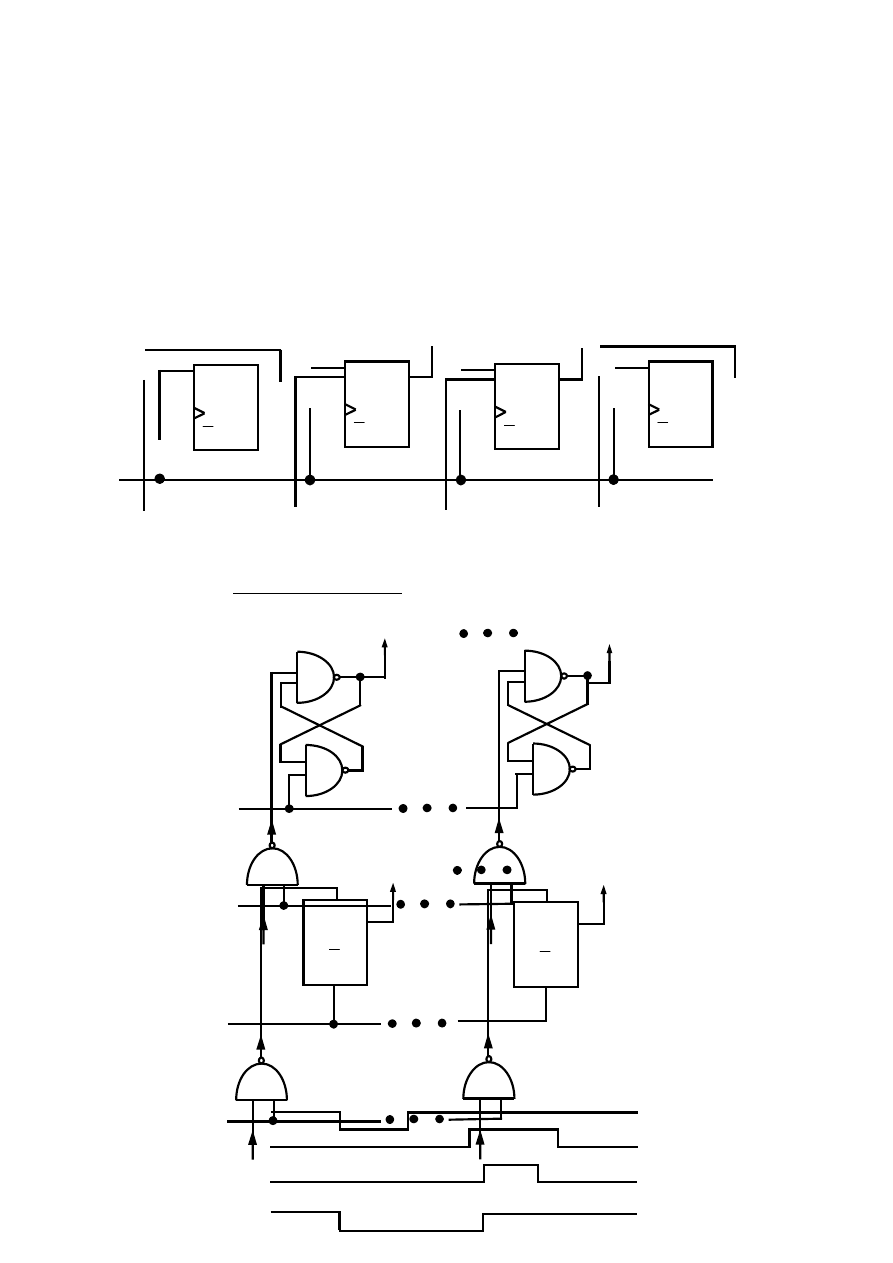
42
Rejestry możemy podzielić na:
§
rejestry asynchroniczne – zbudowane z przerzutników asynchronicznych,
§
rejestry synchroniczne – zbudowane z przerzutników synchronicznych.
5.2.
REJESTRY RÓWNOLEG
ŁE
Najprostszymi rejestrami są rejestry równoległe, ponieważ nie wymagają żadnych połączeń między tworzącymi je przerzutnikami np.
układy UCY 74174 i UCY 74175. Z zespołu rejestrów równoległych budowane są tzw. pamięci buforowe, służące do przechowywania informacji
podawanej w sposób równoległy. Bufory najczęściej pośredniczą między jednostkami cyfrowymi działającymi z różnymi szybkościami.
W rejestrze równoległym zarówno wprowadzanie i wyprowadzanie informacji odbywa się równolegle. Rejestr równoległy można sobie
wyobrazić jako zestaw przerzutników typu D, których ani wejścia informacyjne D, ani wyjścia nie są ze sobą połączone. Połączone są jedynie wejścia
synchronizujące i ewentualnie asynchroniczne wejścia zerujące. Rejestr taki wykonuje mikrooperacje wpisywania do rejestru informacji wejściowej i
zerowanie jego zawartości.
Najogólniej rejestr równoległy można przedstawić jak na rys. 5.3.
Rys. 5.3 Rejestr równoległy.
Rejestry równoległe asynchroniczne są zbudowane z przerzutników asynchronicznych nie połączonych ze sobą bezpośrednio, a
wpisywanie informacji do tych przerzutników odbywa się w tym samym interwale czasu.
Rejestry asynchroniczne możemy podzielić na:
§
rejestry o „wpisywaniu jednoprzewodowym”,
§
rejestry o „wpisywaniu dwuprzewodowym”.
Rejestr równoległy „wpisywaniu jednoprzewodowym” zbudowany z przerzutników s r pokazano na rys. 5.4a.
a)
b)
c)
D
0
Q
0
C
Q
0
D
1
Q
1
C
Q
1
D
2
Q
2
C
Q
2
D
3
Q
3
C
Q
3
Wy
0
Wy
1
Wy
2
Wy
3
We
0
We
1
We
2
We
3
C
Z
A
a
0
We
0
We
n-1
a
n-1
Q
0
Q
n-1
J Q
C
K
Q
s
r
J Q
C
K
Q
s
r
Z
We
i
A
Q
i
Z
A
a
0
We
0
We
n-1
a
n-1
Q
0
Q
n-1
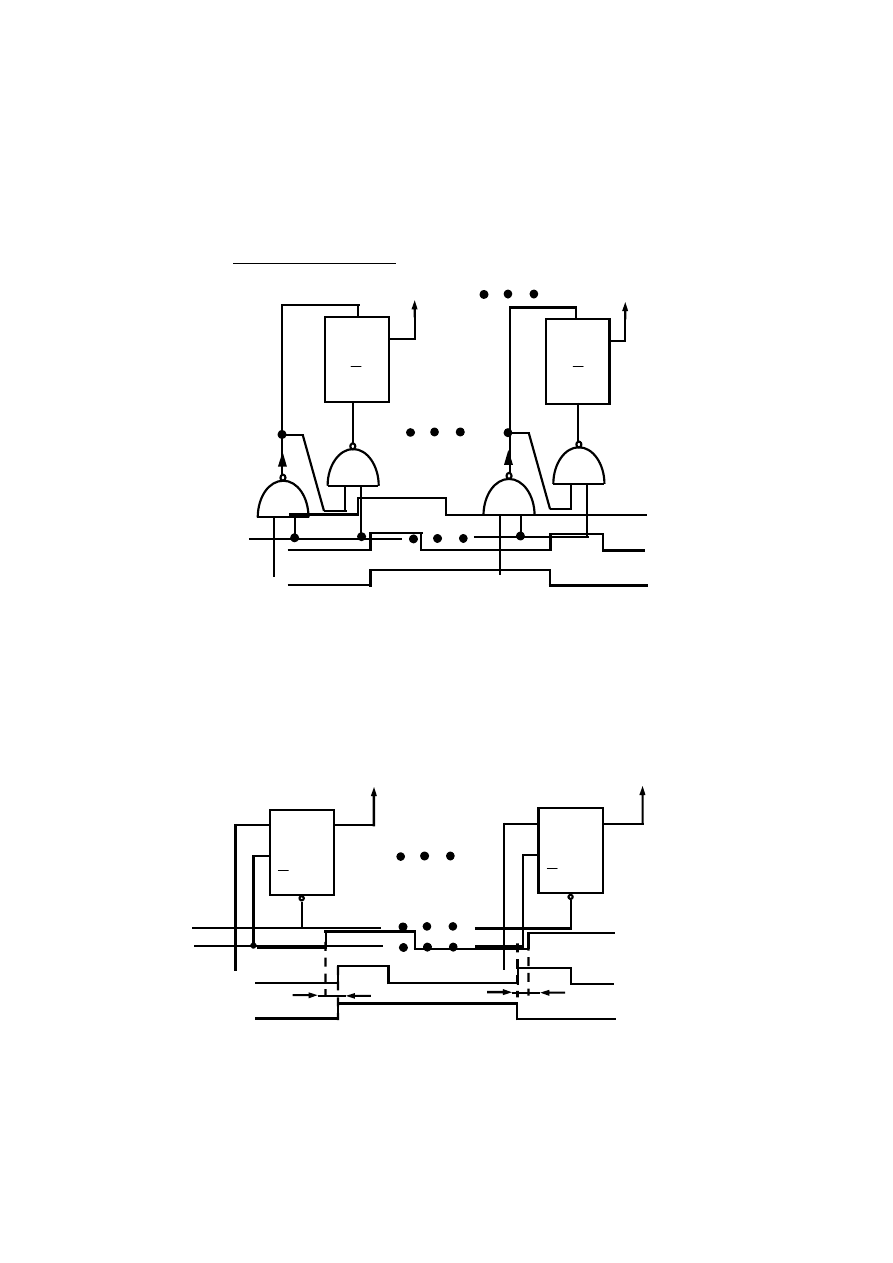
43
Rys. 5.4 Rejestr równoległy asynchroniczny z wpisywaniem jednoprzewodowym:
a), b) przykłady rozwiązań,
c)przebiegi czasowe.
W przypadku asynchronicznego wprowadzenia informacji do rejestru, jeżeli dostępne są tylko pozycje We
0
,...We
n
każdego bitu informacji,
należy przed podaniem sygnału przepisującego A = 1 wyzerować rejestr.
Zerowanie wyjść Q odbywa się przewodem Z, natomiast wpisywanie wartości zmiennych We jest bramkowane sygnałem A.
Na rys. 5.4b przedstawiono rozwiązanie o identycznym działaniu wykorzystujące zmienne s r przerzutników scalonych JK.
Zasady działania rejestrów ilustrują przebiegi czasowe pokazane na rys. 5.4c. Wpisywanie informacji We
i
na wyjście Q
i
odbywa się
jednym przewodem a
i
po uprzednim wyzerowaniu rejestru, a sygnał wpisujący jest równy A = 1.
Rejestr równoległy „wpisywaniu dwuprzewodowym” przedstawiono na rys. 5.5.
a)
b)
Rys. 5.5 Rejestr równoległy asynchroniczny z wpisywaniem dwuprzewodowym: a)schemat ideowy, b)przebiegi czasowe.
W tym układzie zerowanie przerzutników przed wprowadzeniem informacji jest niepotrzebne.
Informacja We
i
zostaje przepisana na wyjście Q
i
, którego wartość jest określona dwoma sygnałami (dwuprzewodowo) na wejściach s i r
przerzutnika.
Zasada działania rejestru jest pokazana na rys. 5.5b. Dla A = 1, wartość a
i
jest określona przez wartość zmiennej We
i
. Gdy a
i
= 1 oraz A =
1, następuje wyzerowanie Q
i
, gdy a
i
= 0, następuje ustawienie Q
i
= 1.
Poprawne ustawienie informacji do rejestru w czasie trwania sygnału wpisującego A = 1 ma miejsce wtedy, gdy informacja We
i
w czasie
trwania wpisywania nie ulega zmianie.
Rejestry równoległe synchroniczne są zbudowane z przerzutników synchronicznych, do których informacja We
i
jest wpisywana w takt
impulsu zegarowego.
Przykład rejestru synchronicznego przedstawiono na rys. 5.6a.
a)
b)
Rys. 5.6 Rejestr równoległy z wpisywaniem synchronicznym:
a)schemat ideowy, b)przebiegi czasowe.
W układzie tym wpisywanie We
i
odbywa się na przednim zboczu impulsu taktującego. Pracę rejestru pokazano na rys. 5.6b. Wartości
zmiennych We
i
muszą być ustalone, zanim pojawi się impuls taktujący T. Wyprzedzenie wartości We
i
względem T oznaczono przez t
s
– czas
ustalania. Wyzerowanie Q
i
nastąpi przednim zboczem sygnału T, gdy czas trwania We
i
= 0 i T = 1 jest większy lub równy wartości t
h
, zwanej czasem
utrzymania.
5.3.
5.3 REJESTRY SZEREGOWE
W rejestrach szeregowych wejścia i wyjścia informacyjne kolejnych przerzutników wchodzących w skład rejestrów są połączone ze sobą
tak, że możliwe jest „przepisywanie” zapamiętanych wartości logicznych do sąsiednich przerzutników i w rezultacie „przesuwanie”
zapamiętywanego słowa w kolejnych taktach sygnału zegarowego.
A
a
0
We
0
We
n-1
a
n-1
Q
0
Q
n-1
J Q
C
K
Q
s
r
J Q
C
K
Q
s
r
We
i
A
Q
i
D Q
C
Q
r
We
0
T
Z
D Q
C
Q
r
We
n-1
Q
0
Q
n-1
We
i
T
Q
i
t
s
t
h
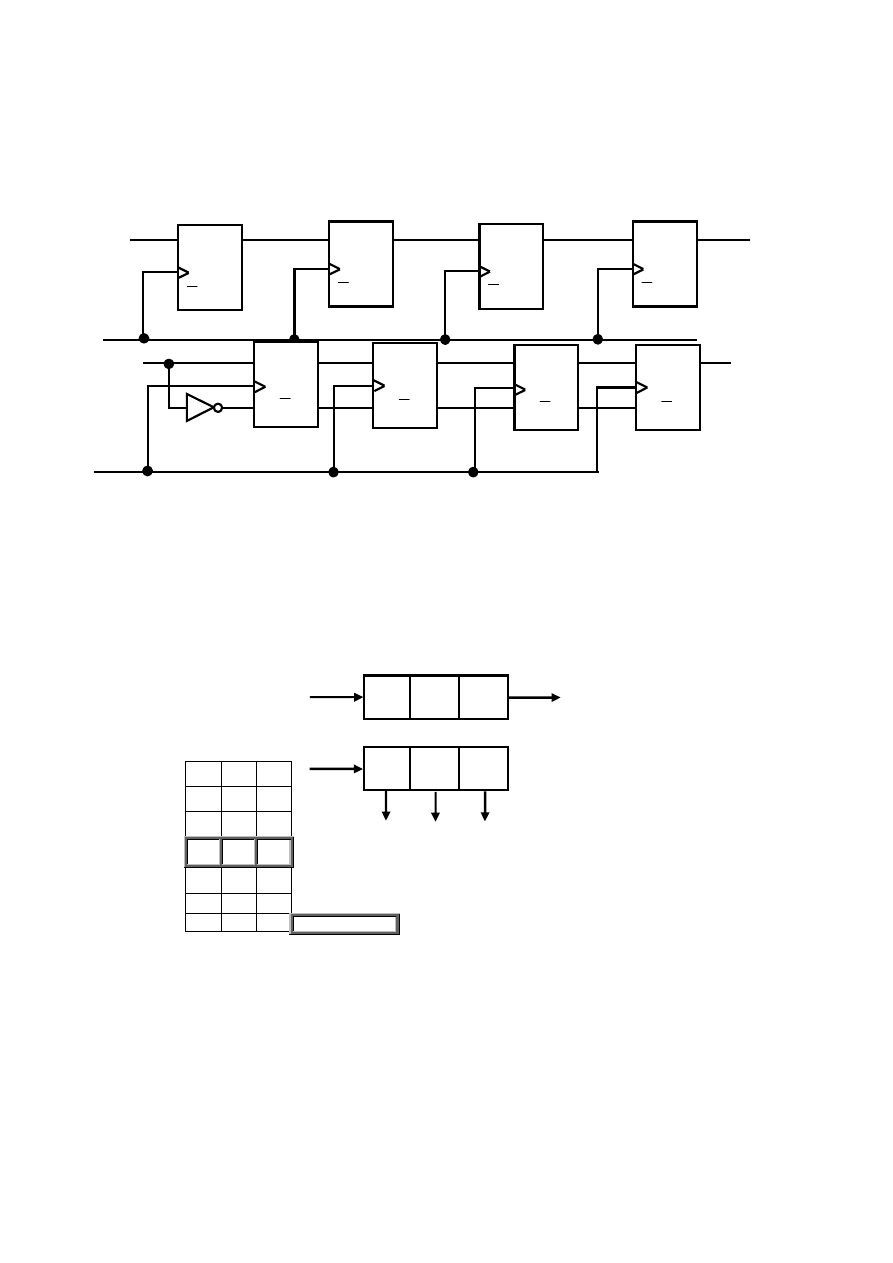
44
Rejestry szeregowe charakteryzują się możliwością przesuwania wprowadzonej informacji bądź w prawo lub w lewo - rejestry
jednokierunkowe, bądź też zarówno w prawo jak i w lewo - rejestry dwukierunkowe, inaczej zwane rewersyjnymi. Rejestry te stosuje się najczęściej
jako układy pośredniczące między urządzeniami o różnym sposobie przetwarzania informacji, o różnych szybkościach pracy.
Rejestry szeregowe zwane przesuwającymi, przyjmują lub przekazują informację szeregowo.
Na rys. 5.7 i 5.8 przedstawiono przykłady rejestrów, w których informacja jest wprowadzana szeregowo, natomiast jej wyprowadzenie
odbywa się szeregowo (rejestr szeregowy) lub równolegle (rejestr przesuwający). Układy te różnią się sposobem taktowania. W pierwszym
przypadku układ jest taktowany przednim zboczem impulsu T (rys. 5.7), natomiast w drugim przypadku (rys. 5.8), układ jest taktowany
dwustopniowo.
Rys. 5.7 Rejestr szeregowy.
Rys. 5.7 Rejestr przesuwający.
Szeregowe taktowanie przednim zboczem pociąga za sobą problemy związane z właściwym doborem czasów propagacji. W układzie z
szeregowo połączonymi przerzutnikami czas propagacji następnego przerzutnika jest większy od czasu propagacji przerzutnika poprzedniego.
Wówczas proces przepisywania wartości z wejścia informacyjnego na stopniu następnym nie jest jeszcze zakończony, podczas gdy zakończony
został ten proces na stopniu poprzednim. Może się więc zdarzyć, że następny przerzutnik będzie miał zmienioną wartość zmiennej informacyjnej w
trakcie procesu przepisywania, przejmując w ten sposób nową wartość tej zmiennej. Nastąpi jak gdyby dwukrotne przepisanie wartości zmiennej
informacyjnej w jednym takcie impulsu zegarowego. W układzie taktowanym dwustopniowo nie ma problemów z czasami propagacji.
Na rys. 5.9 przedstawiono pracę trzybitowego rejestru przesuwającego. Odczyt równoległy słowa wpisanego (zapamiętanego) szeregowo
do rejestru następuje równolegle po trzech taktach, natomiast wyprowadzenie szeregowe informacji odbywa się po sześciu taktach impulsu
zegarowego, licząc od momentu rozpoczęcia wprowadzania informacji.
1
0
1
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
0
1
0
1
Rys. 5.9 Przesuwanie liczb w rejestrze przesuwającym.
Rejestry szeregowe służą przede wszystkim do realizacji dwóch mikrooperacji – mnożenia i dzielenia przez dwa (przesuwanie zawartości
w prawo i w lewo) oraz do zmiany postaci informacji z szeregowej na równoległą i odwrotnie. Para rejestrów, równoległo – szeregowy i szeregowo –
równoległy, może służyć np. do przesyłania długich słów za pomocą niewielkiej liczby przewodów. Słowo wprowadza się równolegle do rejestru
równoległo – szeregowego i wyprowadza (nadaje) szeregowo; odbierane kolejne bity słowa wprowadza się do rejestru szeregowo – równoległego i
po zakończeniu operacji wyprowadza się równolegle.
D Q
C
Q
0
D Q
C
Q
D Q
C
Q
D Q
C
Q
We
Wy
C
J Q
C
K
Q
We
J Q
C
K
Q
C
J Q
C
K
Q
J Q
C
K
Q
Wy
Kierunek przesuwu
słowo zapamiętane
Słowo przesunięte w
lewo
Takt
0
I
II
III a) odczyt równoległy
IV
V
VI b) odczyt szeregowy

45
6.
PAMI
ĘCI
6.1.
6.1 WST
ĘP
Pamięci są to układy logiczne służące do przyjmowania, przechowywania i wydawania zakodowanych informacji (danych). Jednym z
rodzajów pamięci są pamięci półprzewodnikowe. Informacja jest zapisywana i pamiętana w postaci ciągów zer – jedynkowych. Jeden element takiej
informacji nazywa się bitem (1b), 8 – bitowy element – bajtem (1B), a 16 – bitowy element – słowem 32 – bitowym.
Najważniejszymi parametrami specyfikowanymi dla pamięci są:
1) pojemność,
2) szybkość,
3) koszt,
4) pobór mocy.
Pojemność pamięci (wielkość) oznacza ilość informacji jaką można w niej przechowywać. Mierzy się ją w jednostkach informacji takich
jak: bity, bajty lub słowa. Może być ona wyrażona w kilobitach (Kb), megabitach (Mb), gigabitach (Gb), lub kilobajtach (KB), megabajtach (MB),
gigabajtach (GB). Pojemność pamięci operacyjnych określa się podając liczbę słów i długość słowa. Liczbę słów podaje się używając przedrostków
odpowiadających odpowiednim mnożnikom.
1 KB odpowiada 2
10
= 1024 bajtom;
1 MB odpowiada 2
20
= 1024 · 1024bajtom;
1 GB odpowiada 2
30
= 1024 · 1024 · 1024bajtom.
Przykładowo pojemność pamięci może wynosić 512Kx64, co oznacza, że jest to 2
19
słów 64-bitowych. W przypadku gdy słowo ma
długość 8 bitów pojemność pamięci jest podawana w bajtach. Wówczas np. 128 KB oznacza 2
17
bajtów.
Szybkość pracy pamięci jest parametrem wskazującym na to, jak często procesor lub inne urządzenie może korzystać z niej. Jest ona określana
kilkoma parametrami. Są to:
-
czas dostępu (ang. access time),
-
czas cyklu (ang. cycle time),
-
szybkość transmisji (ang. transfer speed).
Czas dostępu jest to czas jaki upływa od momentu zażądania informacji z pamięci do momentu, w którym ta informacja ukaże się na
wyjściu pamięci. Dla pamięci operacyjnych czas ten wynosi od 20 ns do 200 ns.
Czas cyklu jest to najkrótszy czas jaki musi upłynąć pomiędzy dwoma żądaniami dostępu do pamięci. Zwykle czas ten jest nieco dłuższy
od czasu dostępu, a wynika to z fizycznej realizacji pamięci, tj. opóźnień wnoszonych przez układy elektroniczne.
Szybkość transmisji mierzy się liczbą bitów (bajtów) jaką można przesłać w jednostce czasu pomiędzy pamięcią a innym urządzeniem.
Parametr ten jest szczególnie ważny w pamięciach, w których adresowane są fragmenty większe niż słowo (np. pamięci dyskowe). Ponieważ w takich
pamięciach odczytuje się lub zapisuje bloki słów, to mniej istotny jest czas dostępu do pamięci, a bardziej istotny jest czas w jakim taka porcja
informacji może zostać przesłana. Najczęściej szybkość transmisji mierzy się w bitach lub bajtach na sekundę.
Nowe technologie pozwalają na ciągłe zmniejszanie kosztu produkcji pamięci i ulepszanie ich parametrów. Dlatego pamięci dość szybko
starzeją się, a często po paru latach są wycofywane z użytku. Taki los spotkał rdzeniowe pamięci ferrytowe, które w latach sześćdziesiątych
dominowały jako pamięci operacyjne komputerów, a teraz nie są już spotykane. Najniższym kosztem, wśród pamięci operacyjnych komputerów,
charakteryzują się pamięci półprzewodnikowe. Jednak one także różnią się między sobą pojemnością i szybkością działania, a co za tym idzie i ceną.
Produkowane są tanie układy scalone pamięci półprzewodnikowych, ale charakteryzują się one niezbyt dużą szybkością działania. Natomiast szybkie
układy pamięciowe mają niewielkie pojemności a cena ich jest stosunkowo duża. Dlatego poszukuje się nowych rozwiązań w architekturze
komputerów, które pozwolą na optymalizację pracy komputerów, a w szczególności parametrów pamięci. Jednym ze stosowanych rozwiązań dla
pamięci operacyjnych jest zastosowanie dwóch rodzajów pamięci półprzewodnikowych: pamięci szybkich, ale o mniejszej pojemności i pamięci
wolniejszych, ale o dużych pojemnościach. Pamięci wolniejsze umożliwiają budowanie pamięci operacyjnych o dużych pojemnościach, a pamięci
szybkie, o mniejszych pojemnościach, umożliwiają przyspieszenie pracy. Szybka pamięć o niewielkiej pojemności współpracująca z pamięcią
operacyjną jest nazywana pamięcią kieszeniową (ang. Cache memory).
Pobór mocy jest też ważnym parametrem, którego znaczenie uwypukla się przy budowaniu pamięci operacyjnych o bardzo dużych
pojemnościach, gdzie istnieje problem połączenia dużej liczby układów scalonych i odprowadzenie wydzielanego ciepła. Innym przykładem
konieczności dążenia do zmniejszania pobieranej mocy komputerów, a co za tym idzie i pamięci, są komputery kieszonkowe.
Pamięć jest zbudowana z rejestrów (komórek), w których zapamiętywane jest słowo 1 -, 4 -, 8 – bitowe. W każdej komórce przypisany jest
adres, czyli numer zapisany w kodzie dwójkowym oznaczający położenie informacji.
Jeśli chcemy odczytać (lub zapisać) daną informację, trzeba na wejścia adresowe pamięci podać numer komórki, w której się ona znajduje,
a także na wejścia sterujące, odpowiednie sygnały.
Do zaadresowania N = 2
n
komórek pamięci potrzebnych jest n wejść adresowych. Dla przykładu: 1 KB = 2
10
bajtów informacji, trzeba 10
wejść adresowych, a 16 KB = 2
16
bajtów informacji – 14 wejść adresowych.
Jak już wspomniano, informacja jest zapisywana i odczytywana w postaci ciągów zero – jedynkowych, dlatego też numery komórek
zapisuje się w kodzie szesnastkowym.
Pamięci posiadają:
§
wejścia adresowe (A
0
,...,A
n
);
§
wejścia / wyjścia danych (D
0
,...,D
n
);
§
wejścia sterujące (WE, CS, OE), służące do wyboru funkcji wykonywanej przez układ,
§
niekiedy wejścia strobujące adresów (ALE, RAS, OE).
Ze względu na budowę oraz właściwości pamięci półprzewodnikowe dzieli się na:
§
pamięci o dostępie swobodnym, typu zapis / odczyt
§
pamięci stałe , tylko do odczyt
6.2.
6.2 PAMI
ĘCI O DOSTĘPIE SWOBODNYM RAM
Pamięci RAM są wykorzystywane do ciągłego zapisu w postaci słowa lub bitu, zapamiętania i odczytu informacji. Zapewniają one
jednakowo szybki dostęp do każdej komórki pamięci. Czynność zapamiętania (odczytu) oznacza konieczność stosowania układów sekwencyjnych, w
których informacje są zapisywane (odczytywane) w określonej kolejności. Dlatego dostęp do danej informacji zależy od miejsca (adresu) jej
przechowywania i czasu oczekiwania na rozpoczęcie operacji zapisu (odczytu).
Rozróżnia się pamięci:
§
statyczne SRAM - komórką pamiętającą jest przerzutnik bistabilny (najczęściej asynchroniczny typu RS) w technologii MOS lub technologii
bipolarnej. Zapisana informacja utrzymuje się w nich dopóki nie zostanie zastąpiona inną albo nie zaniknie napięcie zasilające.
§
dynamiczne DRAM – funkcje elementów pamiętających pełnią pojemności wejściowe tranzystorów MOS gromadzące ładunek lub
odprowadzające go. Zawartość tych elementów musi być odświeżana, musi być uzupełniany ubytek ładunku.
Blokowy schemat pamięci jest przedstawiony na rys. 6.1 niżej.
46
Rys. 6.1 Schemat blokowy pamięci RAM.
Pamięci RAM komórki pamięciowe ułożone są w słowa, wybierane wejściem adresowym – całość można przedstawić jako
dwuwymiarową matrycę składającą się z n słów m - bitowych, czasami podzieloną na robocze obszary zwane np. strefami (ang. zone).
Dekoder wejściowy oraz wyjścia współpracują z rejestrami równoległymi, gdyż operacja odczytywania i zapisywania w pamięci trwa z
reguły kilka cykli zegarowych, podczas których zawartość informacji na szynach adresowej i danych może się zmieniać.
W zależności od stanu logicznego na wejściu R/W układ komórek pamięciowych przyjmuje informację z rejestru danych (zapisywanie) lub
wprowadza na rejestr danych (odczytywanie). Poprzez 2-kierunkowy bufor rejestr przekazuje lub odbiera informację z szyny danych.
Na rys. 6.2 przedstawiono uproszczony schemat funkcjonalny pamięci o dostępie swobodnym.
Rys. 6.2 Uproszczony schemat funkcjonalny pamięci o dostępie swobodnym.
PAMIĘĆ DRAM
Na rys. 6.3 przedstawiono najekonomiczniejsze rozwiązanie komórki pamięci dynamicznej, stosującej tylko jeden tranzystor MOS
oznaczony T
1
.
Informacja w niej przechowywana w postaci ładunku zgromadzonego na kondensatorze C
1
. W wyniku rozładowania kondensatora (Q =
0)powstaje na nim napięcie równe zeru logicznemu, natomiast w wyniku ładowania – napięcie o wartości odpowiadającej logicznej jedynce.
Przy organizacji adresu jak wyżej, komórka ta ma wejście adresowe ak dla wierszy i jedną linie danych wspólną dla komórek w kolumnie
adresowej bj. Tranzystor T
2
jest wspólny dla kolumny adresowej bj. Gdy komórka jest wybrana, tzn. na wejściach adresowych ak i bj jest stan
wysoki, pojemność C
1
jest dołączona do linii danych.
⇓
⇓
Układy kontroli
(sterowania)
wejścia/wyjścia
Adresy Y
Matryca
pamięciowa
⇓
⇓
⇓
A
d
re
sy
X
Dekoder Y
D
ek
o
d
er
X
⇔
WE/WY
47
Rys. 6.3 Schemat elementarnej komórki pamięci dynamicznej.
Przy zapisie jest doprowadzone do niej ze wzmacniacza zapisu napięcie odpowiadające jedynce lub zeru logicznemu. Przy odczycie
ładunek z pojemności C
1
przemieszcza się do pojemności C
2
przez co napięcie odczytu
2
1
1
1
C
ODCZ
C
C
C
U
U
+
=
Pojemność C
2
>> C
1
, gdyż składa się z pojemności dren, stąd U
odcz
<< U
c1
. Właściwość ta wymaga dobrych wzmacniaczy odczytu
uzupełnionych układem odświeżania pamięci (odświeżanie dokonywane po każdym odczycie i cyklicznie bez względu na odczyt).
Inne możliwe rozwiązanie polega na zastosowaniu komórek pamięciowych wielotranzystorowych lecz z prostym układem wzmacniacza
odczytu i zapisu oraz układem odświeżania.
Typową strukturę pamięci dynamicznej o pojemności 64 kbitów pokazano na rys. 6.4. Matryca pamięciowa jest zbudowana 256 kolumn i
256 wierszy. W celu zmniejszenia liczby końcowej pamięci dynamicznej i ułatwienia jej odświeżania, wejścia adresowe są multipleksowane.
Adresowanie polega na podaniu najpierw ośmiu bardziej znaczących bitów adresu (adres wiersza), a następnie ośmiu mniej znaczących
bitów (adres kolumny).
Adres wiersza jest wpisywany z wejść adresowych do rejestru wiersza RR przy narastającym zboczu sygnału RAS (ang. Row Addres
Select). Stąd poprzez demultiplekser (dekoder adresu) wybierany jest odpowiadający mu wiersz.
Adres kolumny jest wpisywany z wejść do rejestru kolumny CR przy narastającym zboczu sygnału CAS (ang. Column Addres Select). Stąd
poprzez demultiplekser wybierana jest odpowiadająca mu kolumna. Jednoczesne wybranie wiersza i kolumny w matrycy odpowiada wskazaniu ściśle
określonej komórki pamięci.
Rys. 6.4 Struktura pamięci dynamicznej RAM.
Gdy wejście WE = 0 wówczas zawartość wybranej komórki jest przesyłana na wyjście układu (operacja czytania danych z komórki
pamięci). Gdy natomiast WE = 1 następuje zapisanie informacji wejściowej do komórki wybranej według odpowiedniego adresu.
PAMIĘĆ SRAM
Na rys. 6.5 przedstawiono schemat podstawowej komórki pamięci statycznej.
Zasadniczą częścią komórki jest przerzutnik bistabilny zbudowany z tranzystorów T
1
i T
2
. Tranzystory T
3
i T
4
pełnią funkcję kluczy
przyłączających i odłączających przerzutnik od linii bitów. Podczas odczytywania (zapisywania) informacji z komórki pamięci stanowią one zwarcie,
przyłączając przerzutnik do wejścia (wyjścia) – linia bitu.
Poszczególne pamięci tworzą matrycę zbudowaną z wierszy i kolumn. Położenie komórki w takiej matrycy określa adres składający się z
numeru wiersza i numeru kolumny.
Rejestr
wiersza
RR
Adres
we
RAS
CAS
WE
8
Matryca
pamięciowa
256 x 256
0
255
Wzmocnienie
kolumn i układy
we-wy
0 255
Linie
wierszy
Układy
stero-
wania
Rejestr
kolumn
CR
wy
48
Rys. 6.5 Schemat elementarnej komórki pamięci statycznej RAM.
Na rys. 6.6 przedstawiono strukturę pamięci statycznej RAM o pojemności wynoszącej 16 KB. Pamięć ta ma trzy wejścia sterujące:
CS
- uaktywnienie pamięci,
OE
- zezwolenie na odczyt
WE
- zezwolenie na zapis.
Rys. 6.6 Struktura pamięci statycznej RAM: a) symbol ogólny,
b) przykładowa organizacja.
Gdy wejście CS = 1, wówczas pamięć jest „wyłączona” i wejścia / wyjścia danych są w stanie wielkiej impedancji (odłączone). Gdy CS =
0, pamięć jest aktywna. Jeżeli wówczas OE = 0, to układ wykonuje operację odczytu danych z komórek o numerze określonym za pomocą wejść
adresowych. Jeżeli natomiast WE = 0, to układ wykonuje operację zapisu danych do pamięci.
Pamięć ta jest zbudowana z ośmiu matryc po 128 wierszy i 128 kolumn. Do jej zaadresowania potrzeba 14 wejść adresowych. Bardziej
znaczące bity adresu (A
0
- A
6
) są podawane na wejścia adresowe demultipleksera, w celu wybrania jednego ze 128 wierszy. Z kolei mniej znaczące
bity adresu (A
7
– A
13
) są podawane na wejścia adresowe innego demultipleksera, w celu wybrania jednej ze 128 kolumn. W ten sposób zostało
wybranych 8 komórek (o takim samym adresie) po jednej z każdej matrycy, co umożliwia odczyt lub zapis jednego słowa 8-bitowego (bajta).
Spotyka się różne rozwiązania adresowania, zapisywania i odczytywania pamięci RAM. W stosowanych aktualnie pamięciach o dużych
pojemnościach adresowanie jest dwuwymiarowe, podzielone na wiersze i kolumny.
Pamięci DRAM są wolniejsze od pamięci SRAM. Stosuje się je jednak znacznie częściej, ponieważ są tańsze. Na jedną komórkę pamięci
dynamicznej potrzeba czterokrotnie mniej tranzystorów, co powoduje czterokrotne zmniejszenie pobieranej mocy i zwiększenie gęstości upakowania
(na takiej samej powierzchni mieści się cztery razy więcej komórek pamięci dynamicznej niż statycznej).
Pamięci RAM o dużych rozmiarach (rzędu Mbitów) są również realizowane jako dynamiczne. Tylko technologia MOS jest przydatna do
tego celu gdyż tylko tranzystory MOS mogą zapewnić wielkie rezystancje wejściowe i wyjściowe oraz długotrwałe utrzymanie ładunku na
pojemności. Ładunek ten utrzymuje się przez czas rzędu ms, pamięci DRAM wymagają więc cyklicznego odświeżania z f = kilkaset Hz.
6.3.
PAMI
ĘCI STAŁE ROM
Pamięć stała zawiera informację, która nie może być zmieniona w czasie pracy systemu cyfrowego, realizuje tylko operację odczytu. Zapis
informacji jest dokonywany jednokrotnie u producenta.
Pamięć ROM dla każdego adresu doprowadzonego do jej wejścia wyprowadza na wyjście (zazwyczaj równolegle, 4- lub 8- bitowe)
pewien zestaw bitów np. pamięć o organizacji 1Kx8 wydaje 1024 zestawy ośmiobitowe w odpowiedzi na 1024 stany wejściowe określone przez
stany 10 linii adresowych (rys.6.7).
T
1
T
2
T
3
T
4
R
C
R
C
+U
CC
Q
Q
Linia bitu
Linia wyboru
wiersza
Wejście - wyjście
Wejście - wyjście
Linia bitu
A
6
A
0
0
127
Matryca
pamięciowa
128 x 128
0 127
Układ
zapisu / odczytu
7.
Stero
wanie
0 127
D
7
D
0
Dane
WE
CS
OE
Adres
A
13
A
7
Wejścia
adresowe
9.
W
ej
śc
ia
49
Rys. 6.7 Struktura pamięci ROM.
Pamięci stałe nie tracą zapisanej w nich informacji po wyłączeniu (przy zaniku) napięcia zasilającego.
Ze względu na sposób programowania pamięci ROM wyróżnia się:
•
Pamięć programowana maską MROM – bitową strukturę jej wnętrza ustala się w czasie produkcji (macierz tranzystorów MOS).
•
Programowalna pamięć stała PROM – programowana przez użytkownika przez przepalanie cienkich połączeń po odpowiednim ich
zaadresowaniu i po odprowadzeniu właściwych sygnałów sterujących. Pamięci PROM są dość szybkie (25
÷ 50 ns), które pobierają dużo mocy
(bipolarne 0,5
÷ 1 W), o małych i średnich pojemnościach (od 32x8 do 8Kx8). Są to pamięci bipolarne i są wykonywane w technice MOS.
•
Reprogramowalna pamięć stała EPROM– bity informacji są zapisywane jako ładunki elektryczne na pływających bramkach tranzystorów
MOS. Kasowanie tych ładunków z bramek następuje przez naświetlenie matrycy pamięciowej promieniami UV – ultrafioletowymi o dużej
intensywności przez kilkadziesiąt minut (gdy w obudowie tych pamięci znajdują się okienka kwarcowe przepuszczające ultrafiolet), lub
promieniami X (gdy obudowa układu jest nieprzezroczysta). Pamięci EPROM są niezbyt szybkie (200 ns), pobierają niewiele mocy i mają duże
pojemności (od 8Kx8 do 12Kx8). Pamięci tego typu produkuje się techniką NMOS i CMOS.
•
Elektrycznie kasowalne PROM – EEPROM – zachowuje się jak pamięć EPROM, ale jest programowana i kasowana elektrycznie, napięciem
+5 V, bez wyjmowania z układu aplikacyjnego. Polega to na podaniu impulsów prądowych o określonych parametrach (wartość, kształt, czas
trwania), które powodują przepalenie połączeń matrycy pamięciowej. Czas programowania pamięci EEPROM jest długi i wynosi ok. 100
µs.
6.3.1.
Zastosowania pami
ęci ROM (PROM)
Pamięci ROM (PROM) wykorzystywane są głównie do:
•
konwersji kodów, '
•
realizacji funkcji logicznych,
•
realizacji funkcji arytmetycznych,
•
realizacji generatorów funkcji,
•
tablicowania funkcji,
•
mikroprogramowania.
Zastosowanie pamięci stałych do realizacji transkoderów jest oczywiste. Kod wejściowy jest podawany na wejścia adresowe pamięci, w
której wierszach każdemu adresowi jest przyporządkowane odpowiednie słowo kodu wyjściowego, pojawiające się na wyjściach pamięci (rys. 6.8).
Rys. 6.8 Pamięć ROM (PROM) w układzie transkodera.
Pamięci stałe mogą być wykorzystywane do realizacji funkcji logicznych. Przykładowo, pamięć o pojemności 256 słów 4-bitowych może
być zastosowana do realizacji czterech funkcji ośmiu zmiennych (8 bitów adresowych). Przez łączenie równoległe pamięci można zwiększyć liczbę
wejść. Cztery pamięci o pojemności 256x4 bity umożliwiają realizację 16 funkcji 8 zmiennych. W wielu publikacjach spotyka się informację, że 8
÷
16 bitów pamięci stałej zastępuje jedną bramkę logiczną.
Pamięci stałe mogą być wykorzystane do realizacji podstawowych operacji arytmetycznych dodawania, odejmowania, mnożenia i
dzielenia. W przypadku mnożenia liczb dwójkowych część wejść adresowych pamięci zostaje przyporządkowana mnożnej, a część mnożnikowi.
Kombinacja zer i jedynek słowa adresowego, utworzona przez bity mnożnej i mnożnika, wskazuje słowo w pamięci określające wartość iloczynu.
Bezpośrednie generowanie wyniku iloczynu wymaga zastosowania pamięci o dużych pojemnościach. Przykładowo, pomnożenie dwu czterobitowych
liczb dwójkowych wymaga pamięci o pojemności 256x8 bitów. Można jednak postępować nieco odmiennie.
Wyjście
A
d
re
s
Pamięć ROM
(PROM)
Kod wejściowy
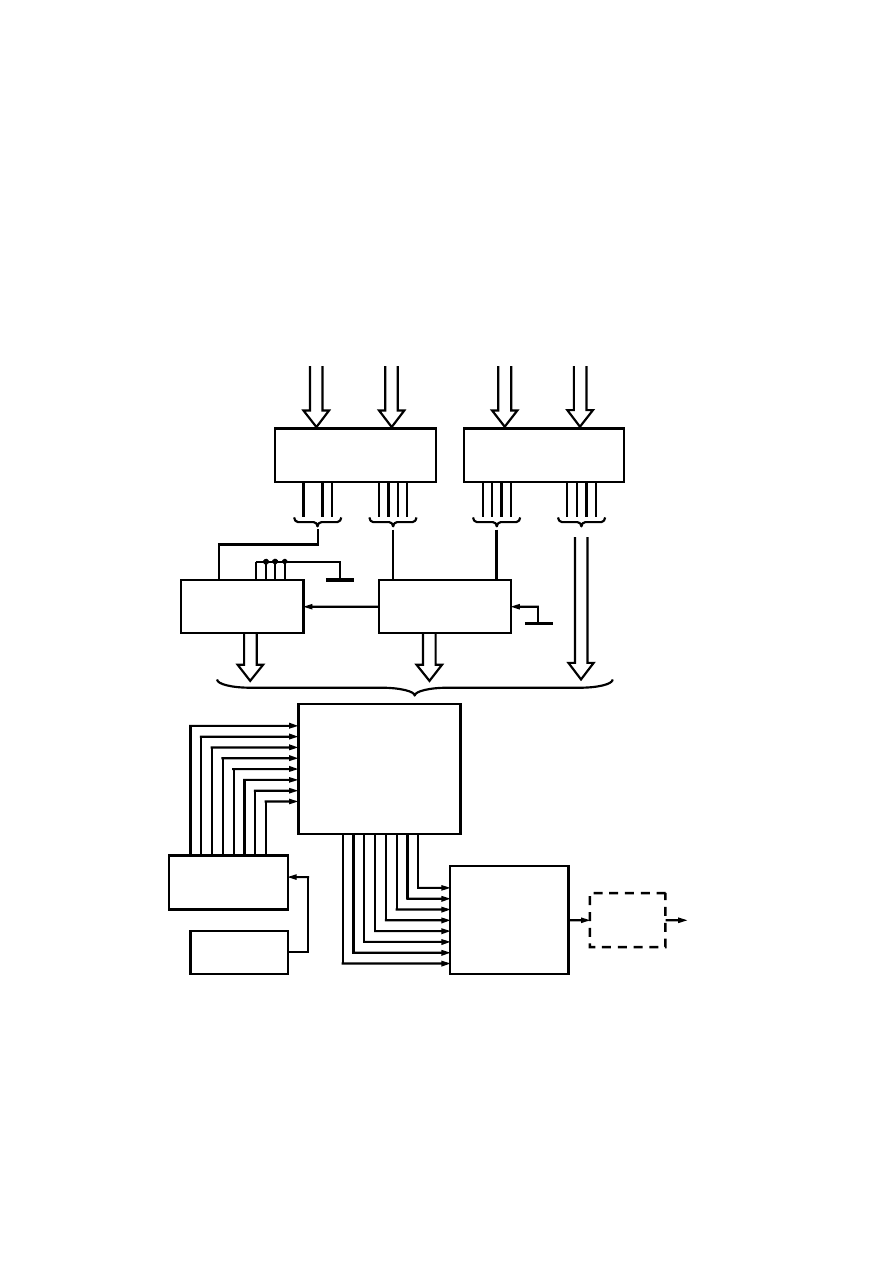
50
Przykład:
Pomnożyć 4-bitową liczbę A przez 8-bitową liczbę B.
0
0
1
1
2
2
3
3
2
A
2
A
2
A
2
A
A
⋅
+
⋅
+
⋅
+
⋅
=
0
0
6
6
7
7
2
B
2
B
2
B
B
⋅
+
+
⋅
+
⋅
=
K
Jeśli czynnik B zostanie przedstawiony w postaci:
7
4
3
0
B
B
B
÷
÷
+
=
wówczas iloczyn AB może być zapisany jako:
7
4
3
0
3
0
3
0
7
4
3
0
3
0
B
A
B
A
)
B
B
(
A
AB
÷
÷
÷
÷
÷
÷
÷
+
=
+
=
Dwa powyższe iloczyny można zrealizować z dwu pamięci o pojemności 256x8 bitów, a następnie zsumować wyniki częściowe (rys. 6.9).
Podobnie można postępować w przypadku dla większych, niż rozpatrywane, zakresów liczbowych. Należy podkreślić dużą szybkość realizacji
operacji mnożenia w porównaniu z układami klasycznymi. Mnożenie jest bowiem realizowane w czasie trwania jednego taktu.
Rys. 6.9 Schemat ideowy układu mnożącego w oparciu o pamięć stałą.
Pamięci stałe są często wykorzystywane do realizacji generatorów funkcji. Przykład implementacji generatora funkcji wykorzystującego
pamięć stałą jest przedstawiony na rys. 6.10. Sygnały z wyjść licznika 8-bitowego są podawane na wejścia adresowe pamięci stałej. natomiast
sygnały z wyjść pamięci na wejścia przetwornika C/A. Zapisując w pamięci 256 słów, odpowiadających kolejnym wartościom funkcji, można w
prosty sposób generować funkcje o różnych kształtach. W opisywanym przykładzie przyrost zawartości licznika o 1 odpowiada przesunięciu fazy o
256 stopni. Na wyjściu przetwornika C/A pojawi się przebieg schodkowy. W celu uzyskania przebiegu monotonicznego należy do wyjścia
przetwornika dołączyć filtr.
Rys. 6.10 Schemat ideowy generatora funkcji.
W oparciu o pamięci stałe są budowane mikroprogramowane urządzenia sterujące, umożliwiające realizację dowolnie skomplikowanych
sieci działań.
Typowe mikroprogramowane urządzenie sterujące składa się z:
•
pamięci stałej,
•
układu zmiany adresu (adres zmieniany jest w zależności od postaci ostatniej instrukcji oraz od stanu warunków wymuszających skoki
warunkowe i bezwarunkowe),
•
rejestru mikroinstrukcji.
Urządzenie działa w sposób sekwencyjny, w takt impulsów taktujących. Informacja wyjściowa (mikrooperacja) zmienia się raz na jeden
cykl (takt). Słowo wyjściowe matrycy pamięci składa się z dwóch podstawowych części. Pierwsza określa adres następnej mikroinstrukcji z
uzależnieniem warunkowym, druga natomiast określa mikroinstrukcje sterujące. Długość części pierwszej słowa wyjściowego z pamięci ogranicza
liczbę możliwych adresów następnych mikroinstrukcji, natomiast długość drugiej części słowa wyjściowego z pamięci określa liczbę i rodzaj
rozkazów wykonawczych. Jest ona zwykle podzielona na grupy, w których umieszczone są wzajemnie wykluczające się mikrooperacje sterujące.
Mikroprogramowane urządzenie sterujące działa w sposób cykliczny. W ramach każdego cyklu następuje:
§
wygenerowanie słowa wyjściowego z pamięci z dokonaniem ewentualnej modyfikacji adresu słowa pamięci,
§
przekazanie do układów wykonawczych danych określających następną mikrooperację sterującą.
ROM (PROM)
(256 x 8)
ROM (PROM)
(256 x 8)
83
83
C
A
4
÷
7
B
4
÷
7
A
0
÷
3
B
0
÷
3
ROM (PROM)
(256 x 8)
A
7
A
0
Licznik
dwójkowy
Generator
Przetwornik
C/A
Filtr
Wy
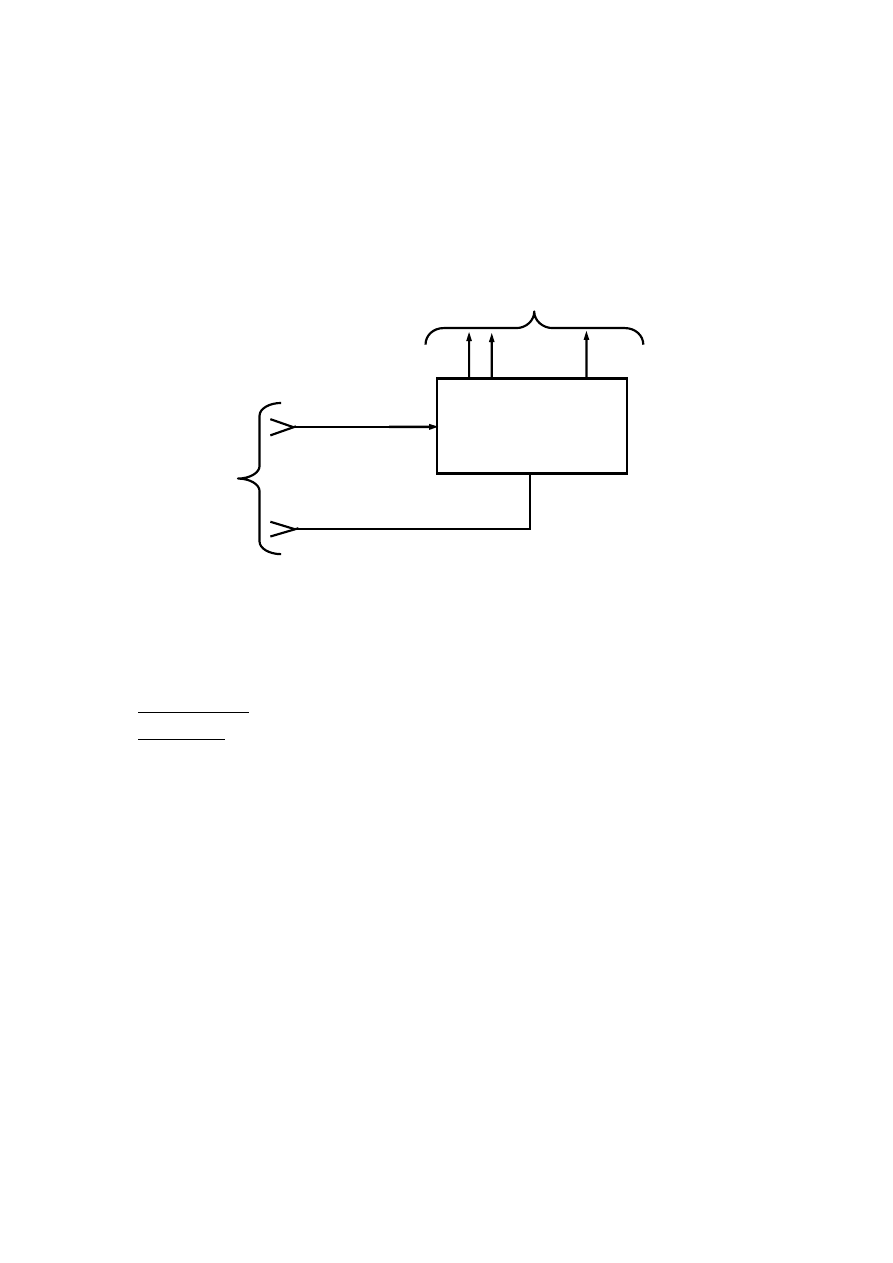
51
7.
LICZNIKI CYFROWE
7.1.
WIADOMO
ŚCI OGÓLNE
Licznikiem nazywamy sekwencyjny układ cyfrowy służący do zliczania i zapamiętywania liczby impulsów zero – jedynkowych,
podawanych w określonym przedziale czasu na jego wejście zliczające. Licznik cyfrowy jest zbudowany z odpowiednio ze sobą połączonych
przerzutników TTL.
Ogólnie biorąc, licznik posiada wejścia dla impulsów zliczających, wejście ustawiające (zerujące) jego stan początkowy asynchronicznie
względem impulsów zliczanych lub synchronicznie z nimi.
Ustawienie wszystkich przerzutników, wchodzących w skład licznika, w stan 0 nazywa się zerowaniem. Symbol graficzny licznika
pokazano na rys. 7.1, na którym zaznaczono wejście impulsów zliczanych, wejście ustawiające stan początkowy oraz wyjścia.
Rys. 7.1 Symbol graficzny licznika.
Na podstawie stanu wyjść można określić ile impulsów pojawiło się na wejściu układu od chwili, kiedy licznik był ostatnio w stanie
początkowym.
Każdy licznik posiada określoną pojemność (zwana długością cyklu), tzn. może zliczyć określoną liczbę impulsów, co odpowiada liczbie
stanów układu przyjmowanych przez licznik w jednym pełnym cyklu.
Licznik jest układem sekwencyjnym, zbudowany z przerzutników i układu kombinacyjnego zapewniającego takie ich sterowanie, aby pod
wpływem impulsu wejściowego przeszły do kolejnego stanu działania. Licznik posiada s – stanów, a kolejne stany licznika są ponumerowane
liczbami: 0, 1, 2,... s – 2, s – 1. Każdemu określonemu stanowi licznika odpowiada jedna, ściśle określona kombinacja stanów przerzutników, z
których jest on zbudowany. Jeden przerzutnik może być w dwu stanach, dwa przerzutniki mogą dać kombinację 2
⋅
2 = 2
2
= 4 stanów, a n
przerzutników może opisać 2
n
stanów. Dlatego do utworzenia licznika o s stanach potrzeba n przerzutników:
(2
n-1
≤ s ≤ 2
n
)
Pojemność zależy od liczby przerzutników wchodzących w skład licznika.
Ze względu na długość cyklu liczniki można podzielić na:
1.
Liczniki o stałej długości cyklu,
2.
Liczniki o nastawionej długości cyklu.
Ze względu na sposób powtarzania cyklu liczniki można podzielić na:
§
Liczniki modulo s (dzielnik liczby lub częstotliwości impulsów przez s),
§
Liczniki do s.
Licznikiem modulo s nazywamy licznik posiadający s wyróżnialnych stanów, przez które przechodzi cyklicznie (powtarza cykl) pod
wpływem impulsów wejściowych.
Licznikiem do s nazywamy licznik posiadający s wyróżnialnych stanów, przez które przechodzi jednokrotnie. Jeśli licznik do s, po
osiągnięciu ostatniego stanu cyklu, ma mieć ponownie s wyróżnialnych stanów, to należy sprowadzić go do stanu początkowego.
Ze względu na kierunek zliczania liczniki dzielimy na:
1.
Liczniki jednokierunkowe:
- zliczające w przód, jeśli liczby reprezentujące zawartość informacyjną licznika wzrastają w trakcie liczenia kolejnych impulsów,
- zliczające wstecz, jeśli liczby reprezentujące zawartość informacyjną licznika maleją w trakcie liczenia kolejnych impulsów,
2.
Liczniki dwukierunkowe
Liczniki dwukierunkowe (rewersyjne) są to liczniki zliczające impulsy zarówno w przód jak i wstecz.
Ze względu na sposób oddziaływania impulsów zliczanych na stan przerzutników licznika, liczniki można sklasyfikować następująco:
1.
Liczniki asynchroniczne (szeregowe),
2.
Liczniki synchroniczne (równoległe).
W liczniku asynchronicznym impulsy zliczane są podawane tylko na jedno z wejść zegarowych przerzutników licznika.
W liczniku synchronicznym impulsy zliczane są podawane na wejścia zegarowe wszystkich przerzutników jednocześnie wchodzących w
skład licznika.
Układ asynchronicznego licznika jest układem szeregowym (połączenie szeregowe). Natomiast układ synchronicznego licznika jest
układem równoległym. Dlatego liczniki asynchroniczne są nazywane licznikami szeregowymi, a liczniki synchroniczne – licznikami równoległymi.
Układ równoległy zapewnia jednoczesność zmian stanów przerzutnika, a więc najkrótszy czas propagacji i największą częstotliwość
impulsów wejściowych.
7.2.
LICZNIKI ASYNCHRONICZNE
W licznikach asynchronicznych (szeregowych) zmiana stanu kolejnego przerzutnika odbywa się pod wpływem zmiany stanu przerzutnika
poprzedniego. Najprostszym przykładem licznika szeregowego jest kaskada n szeregowo połączonych przerzutników.
Liczniki szeregowe realizujemy najczęściej na przerzutnikach typu T lub JK o zwartych wejściach informacyjnych.
Algorytm projektowania liczników szeregowych:
1.
Ustalić liczbę przerzutników niezbędnych do realizacji licznika (w zależności od pojemności licznika 2
n
).
2.
Na wejścia informacyjne T lub JK (zwarte) – podać „1”.
Wyjścia
…
…
W
ej
śc
ia
Układ
sekwencyjny
s - stanowy
Impulsy zliczane
Impuls zerujący
(ustawiający)
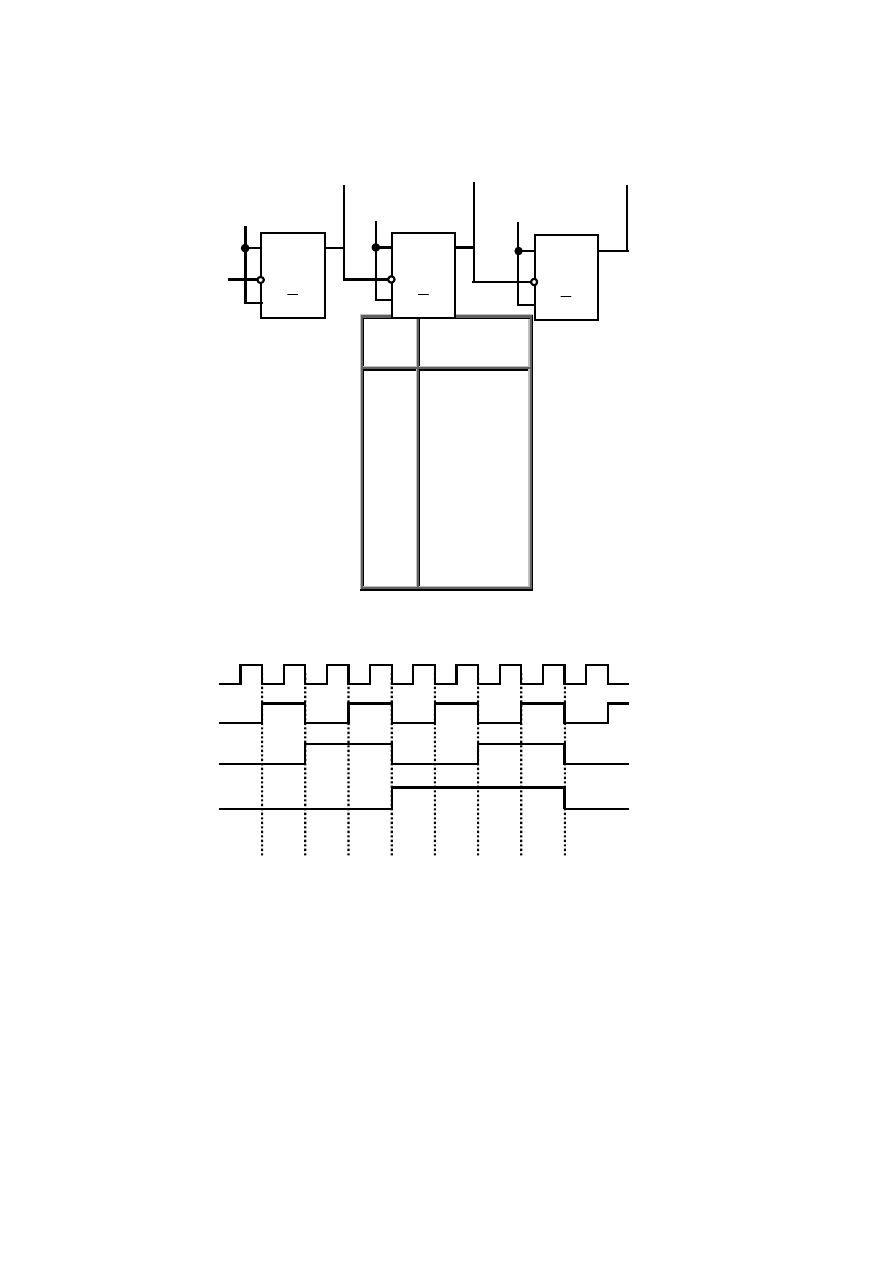
52
3.
Jeżeli licznik liczy w przód – połączyć wejścia zegarowe następnego przerzutnika z wyjściem „Q” poprzedniego.
Przykład 7.1:
Na rys. 7.2 przedstawiono schemat logiczny licznika szeregowego zbudowanego z trzech przerzutników JK, zliczającego w przód.
a)
b)
We
Q
0
Q
1
Q
2
0
1
2
3
4
5
6
7
8
0
1
0
1
0
1
0
1
0
0
0
1
1
0
0
1
1
0
0
0
0
0
1
1
1
1
0
c)
Rys. 7.2 Licznik szeregowy zliczający w przód o pojemności 8:
a) schemat logiczny, b) tablica stanów, c) przebiegi czasowe.
Wejścia synchroniczne przerzutników JK są przyłączone do jedynki logicznej. Czasami mogą być one nie użyte, co jest równoznaczne z
przyłączeniem ich do jedynki logicznej.
Impuls zliczany We jest wprowadzony na wejście zegarowe pierwszego przerzutnika. Wejścia zegarowe kolejnych przerzutników są
połączone z wyjściem Q poprzednich przerzutników. Zmienna Q
0
reprezentuje wagę 2
0
– czyli 1, waga zmiennej Q
1
wynosi 2
1
– czyli 2, a zmiennej
Q
2
– 2
2
, czyli 4.
W chwili początkowej wszystkie przerzutniki są w stanie 0 (Q
0
= Q
1
= Q
2
= 0). Jeśli na wejście zegarowe pierwszego przerzutnika zostanie
podany impuls, to powoduje on zmianę stanu jego wyjścia Q
0
z 0 na 1. Stan drugiego przerzutnika nie ulegnie zmianie, ponieważ na wejściu
zegarowym przerzutnika Q
1
nie wystąpiła zmiana sygnału z 1 na 0.
Pod wpływem drugiego impulsu pierwszy przerzutnik zmieni stan z 1 na 0. Ta zmiana stanu powoduje zmianę stanu drugiego przerzutnika
z 0 na 1.
Pod wpływem trzeciego impulsu pierwszy przerzutnik zmieni stan z Q
2
na 1. Ta zmiana nie powoduje zmiany stanu przerzutnika drugiego.
Czwarty impuls zmieni stan przerzutnika pierwszego z 1 na 0. Zmiana ta powoduje zmianę stanu z 1 na 0 przerzutnika drugiego, a ta z
kolei zmianę stanu z 0 na 1 przerzutnika trzeciego.
Przed pojawieniem się ósmego impulsu wszystkie przerzutniki licznika są w stanie 1. Po ósmym impulsie pierwszy przerzutnik zmieni
stan z 1 na 0. Ta zmiana powoduje zmianę stanu z 1 na 0 drugiego przerzutnika, a ta z kolei zmianę stanu z 1 na 0 przerzutnika trzeciego.
Przedstawiony licznik charakteryzuje się więc ośmioma stanami. Przerzutnik pierwszy tego licznika zmienia swój stan za każdym razem
pojawienia się zmiany impulsu wejściowego z 1 na 0, a więc dzieli częstotliwość impulsów wejściowych przez 2. Drugi przerzutnik zmienia swój
stan za każdym pojawieniem się zmiany stanu z 1 na 0 przerzutnika pierwszego, a więc na wyjściu Q
1
otrzymuje się impulsy o częstotliwości cztery
razy mniejszej, niż częstotliwość impulsów wejściowych. Natomiast trzeci przerzutnik zmieni swój stan, jeśli poprzednie przerzutniki zmieniają swój
stan z 1 na 0, otrzymując impulsy o częstotliwości osiem razy mniejszej (pojawia się jeden impuls na osiem impulsów wejściowych).
Uzyskano w ten sposób kaskadę trzech przerzutników asynchronicznych pracująca zgodnie z przebiegami czasowymi z rys. 7.2c.
Jeśli licznik ma liczyć w tył (odejmować) – wejścia zegarowe łączymy z wyjściem poprzedniego.
Przykład 7.2:
Na rys. 7.3 przedstawiono przykład licznika szeregowego odejmującego, który pomniejsza swój stan w takt impulsu zliczanego oraz przebiegi
czasowe.
We
Q
0
Q
1
Q
2
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
0
J
0
Q
0
C
K
0
Q
0
„1”
J
1
Q
1
C
K
1
Q
1
Q
0
Q
1
Q
2
J
2
Q
2
C
K
2
Q
2
„1”
„1”
We
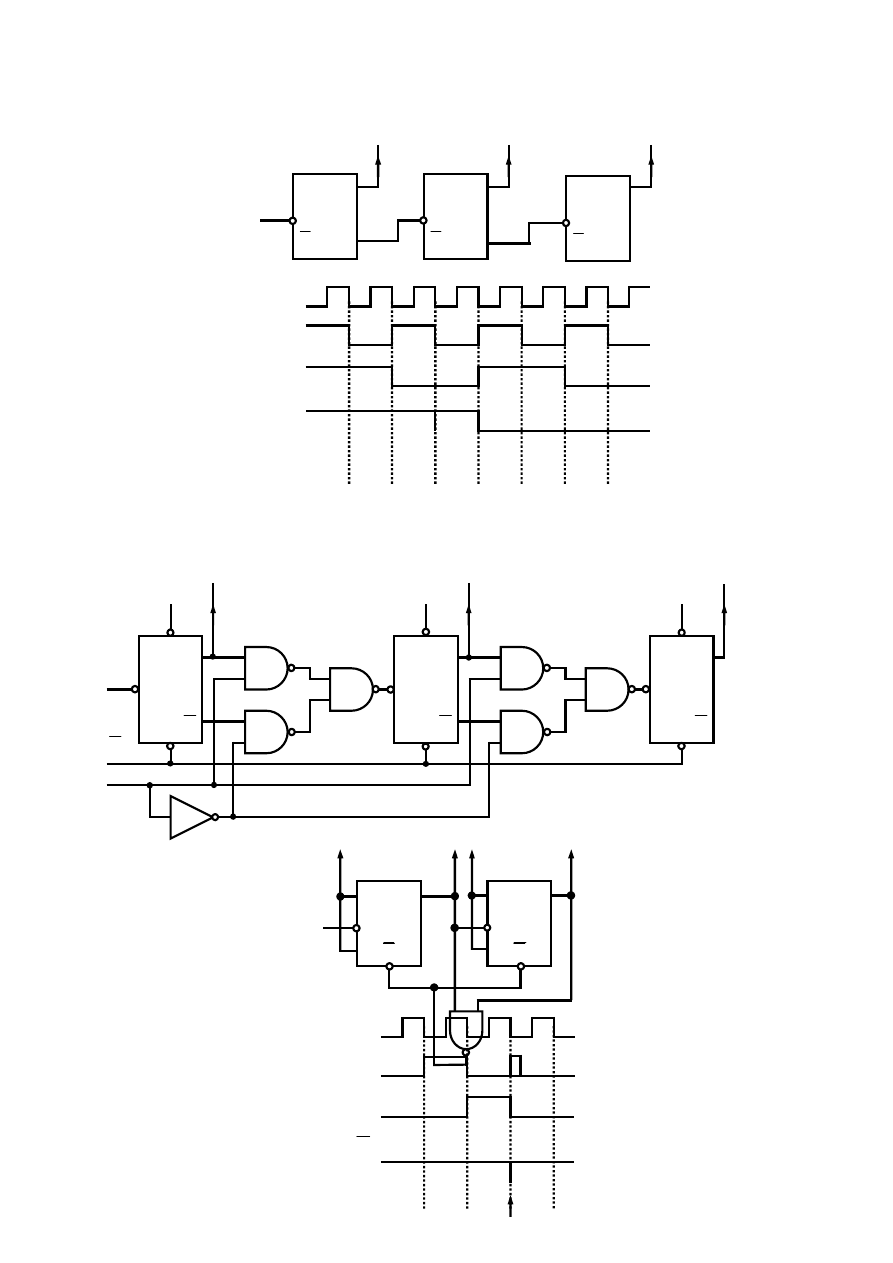
53
a)
b)
Rys. 7.3 Szeregowy licznik odejmujący: a) schemat połączeń,
b) przebiegi czasowe.
Jeżeli chcemy zaprojektować licznik a s nie jest równe s = 2
n
.
Tworzymy licznik o większej liczbie stanów takiej, że s = 2
n
, ale jednocześnie s > 2
n-1
. Do takiego licznika dołącza się bramki NAND lub
AND w zależności od tego, na co reagują wejścia asynchroniczne przerzutników (NAND – gdy na „0”). Bramki te służą do ograniczania impulsów
zliczanych przez licznik.
Na bramkę podajemy z wyjść przerzutników impuls przy którym nastąpi zerowanie licznika. Natomiast wyjście bramki łączymy z
wejściami ustawiającymi.
Przykład 7.3:
Na rys. 7.4 przedstawiono licznik pracujący w dwóch kierunkach. Jest on połączeniem liczników z rys. 7.2 i 7.3. Zmiany kierunku zliczania dokonuje
się za pomocą sygnału K. Zmiana wartości K może spowodować wyzwolenie przerzutnika. Z tego powodu po zmianie kierunku zliczania należy
ustawić warunek początkowy, od którego licznik zaczyna swoją pracę.
Rys. 7.5 Licznik szeregowy rewersyjny.
K – zmienna programująca kierunek zliczania.
Przykład 7.4:
Na rys. 7.5a przedstawiono licznik modulo 3. Do określenia liczby przerzutników zastosujemy zależność (2
n-1
≤ s ≤ 2
n
). Liczba n spełniająca ten
warunek wynosi 2.Tworzymy więc licznik binarny złożony z dwóch przerzutników.
a)
b)
Rys. 7.5 Licznik modulo 3: a) schemat połączeń,
b) przebiegi czasowe.
Q
0
C
Q
0
Q
1
C
Q
1
Q
0
Q
1
Q
2
Q
2
C
Q
2
We
J
0
Q
0
C
K
0
Q
0
1
J
1
Q
1
C
K
1
Q
1
Q
0
Q
1
We
1
R
R
3
We
Q
0
Q
1
Q
2
1
2
3
4
5
6
7
7
6
5
4
3
2
1
8
0
We
Q
0
Q
1
R
1
2
3
1
1
2
0
0
K
X
C
C
C
Q
1
Q
2
Q
0
Q
Q
Q
s
s
s
r
r
r
Q
Q
Q
Z
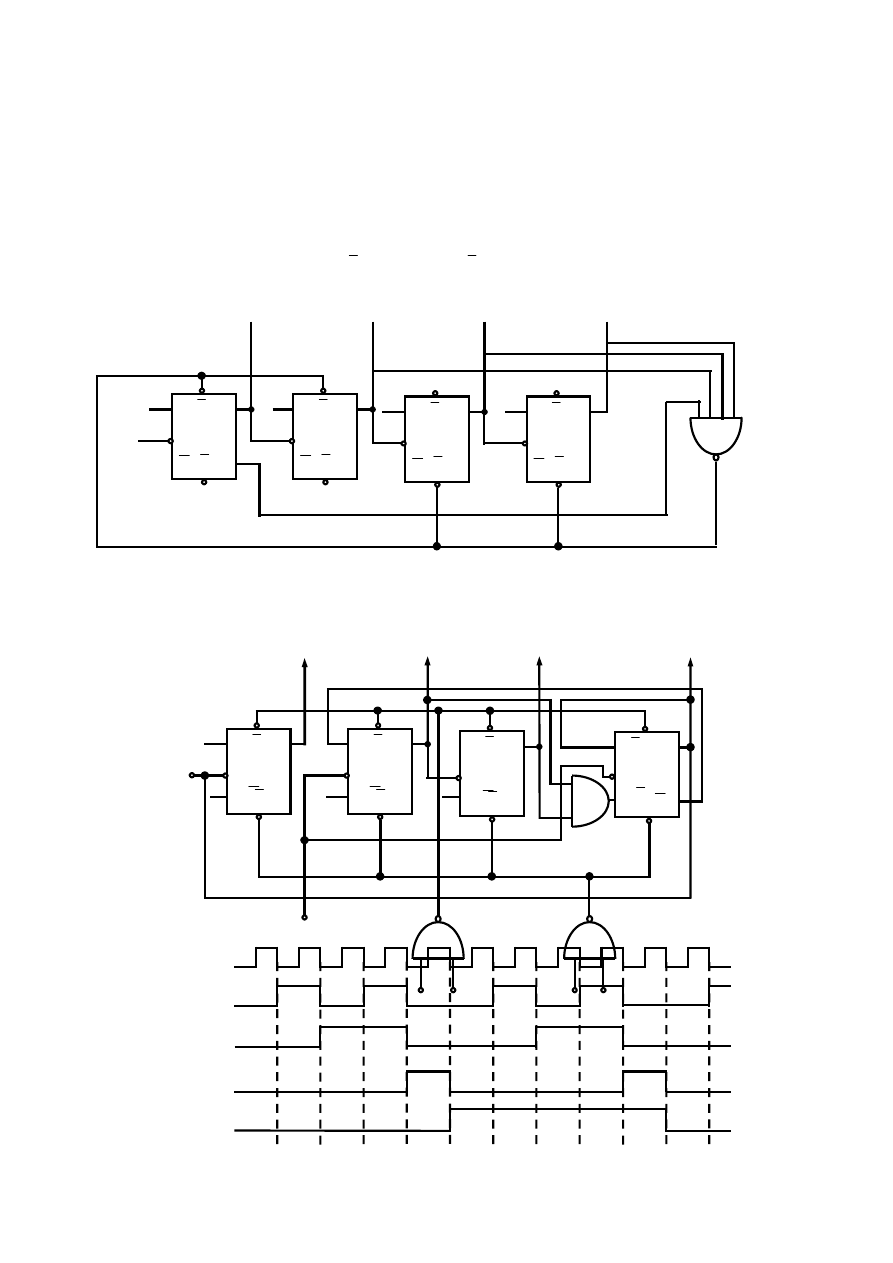
54
Zerowanie licznika nastąpi, gdy pojawi się impuls odpowiadający liczbie 3, czyli 11
2
. Na wejścia bramki podajemy B = A = 1, a na
wyjściu bramki pojawi się stan niski („0”) zerujący wszystkie przerzutniki licznika.
Jeśli stanem początkowym jest stan 0 (stan wyjść BA = 0), pod wpływem impulsu wejściowego wyjście A przechodzi do stanu 1. Na
wejściu bramki NAND są wówczas sygnały: 1, 0, a na jej wyjściu stan 1 (rys. 7.4b). Pod wpływem drugiego impulsu wejściowego licznik przechodzi
do stanu 2. Na wejściu bramki NAND są wówczas sygnały: 1, 0, a na jej wyjściu stan 1. Pod wpływem następnego impulsu wejściowego na wyjściu
licznika pojawi się stan 3. Wówczas na wyjściu bramki NAND, a więc i na wejściu R pojawi się sygnał 0, który spowoduje wyzerowanie licznika,
czyli powrót do stanu 0. Licznik ten ma trzy stany, przez które przechodzi cyklicznie. Jest to więc licznik modulo 3.
Przykład 7.5:
Na rys. 7.6 pokazano licznik zliczający od 3 do 13 włącznie. Do zapisania liczb w zakresie od 3 do 13 w kodzie dwójkowym potrzebne są cztery bity,
czyli cztery przerzutniki. Na bramkę NAND podajemy z wyjść przerzutników impuls przy którym następuje zerowanie licznika, czyli impuls 14,
Q
3
Q
2
Q
1
Q
0
= 1110.Natomiast wyjście bramki łączymy z wejściami ustawiającymi, czyli początek zliczania zaczyna się od 3, Q
3
Q
2
Q
1
Q
0
= 0011. Jeżeli
jest 0, łączymy wyjście bramki z wejściem zerującym
r
, jeśli 1 – z wejściem
s
.
Rys. 7.6 Licznik zliczający od 3 do 13.
Odmianą liczników są tzw. dzielniki częstotliwości tzn. układy, które po określonej liczbie impulsów zliczanych generują jeden impuls
wyjściowy.
Największy zakres zastosowań spośród wszystkich liczników asynchronicznych mają tzw. dekady liczące, tj. dzielniki przez 10. Zwykle
jest to połączenie dwójki liczącej z dzielnikiem przez 5. Przykładem takiego rozwiązania jest licznik asynchroniczny 7490 przedstawiony na rys.
7.7a. Jest to licznik modulo 2 i licznik modulo5 z oddzielnymi wejściami i wyjściami. Może on pracować jako dzielnik przez 10 zliczający w kodzie
BCD (wyjście Q
0
połączone z wejściem Q
1
Q
3
), lub jako licznik modulo 10 z symetrycznym przebiegiem wyjściowym (wyjście Q
3
połączone z
wejściem Q
0
), o przebiegach czasowych przedstawionych na rys. 7.7b.
a)
b)
Rys. 7.7 Scalony licznik asynchroniczny 7490: a) schemat połączeń,
b) przebiegi czasowe.
Licznik ten posiada dwa wejścia sterujące:
§
R9(1) i R9(2) – ustawia (w dwójkową reprezentację liczby 9),
§
R0(1) i i – zerowania.
Aby wyzerować wyjścia tego licznika, należy na oba wejścia R0(1) i R0(2) podać sygnał 1, natomiast aby ustawić jego wyjścia w
dwójkową reprezentację liczby 9, należy na oba wejścia R9(1) i R9(2) podać sygnał 1.
Zadanie:
T Q
C
Q
s
r
C
„1”
T Q
C
Q
s
r
„1”
0
Q
0
1
Q
1
1
Q
2
1
Q
3
T Q
C
Q
s
r
C
„1”
T Q
C
Q
s
r
„1”
1
1
0
0
J Q
C
K Q
s
r
We
Q
0
1
J Q
C
K Q
s
r
Q
0
Q
1
Q
2
Q
3
J Q
C
K Q
s
r
1
J
s
Q
C
K
r
Q
1
1
We
Q
0
Q
3
R9(1) R9(2) R0(1) R0(2)
We Q
1
Q
3
Q
1
Q
2
Q
3
, We Q
0
1
2
3
4
5
6
7
8
9
10
1
Q
1
R9(1) = 0 R9(2) = 0 R0(1) = 0 R0(2) = 0 WeQ
0
= 0
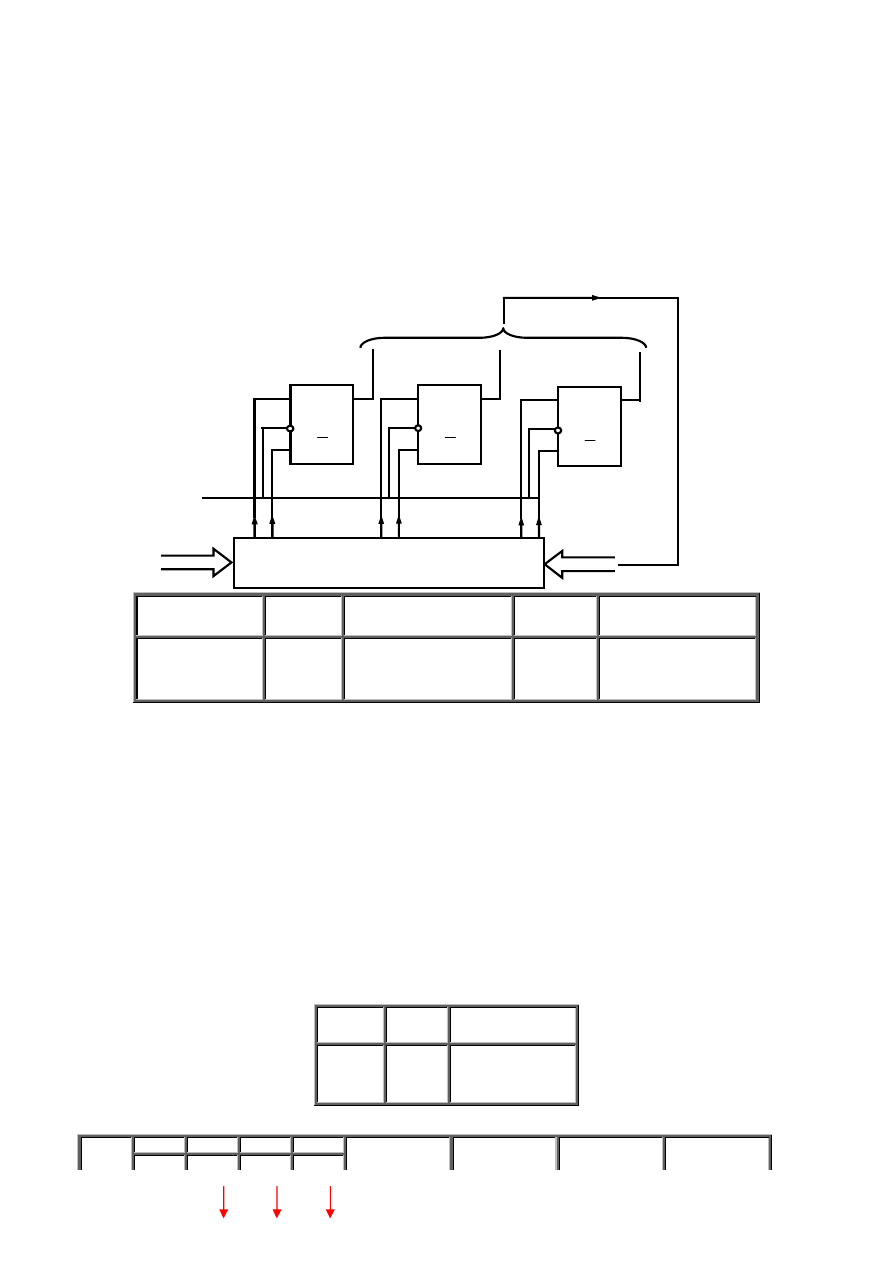
55
1.
Zaprojektować licznik liczący od 3 do 14 w przód (zerowanie przy impulsie 15).
2.
Zaprojektować licznik liczący od 7 do 3 w przód (zerowanie przy impulsie 4).
3.
Zaprojektować licznik liczący od 9 do 4 w tył (zerowanie przy impulsie 3).
7.3.
LICZNIKI SYNCHRONICZNE
Liczniki synchroniczne (równoległe) są budowane z na dowolnym typie przerzutników w oparciu o siatki Karnaugha . Zmiany stanów
poszczególnych przerzutników odbywają się jednocześnie w takt impulsów zegarowych X wprowadzanych równolegle na każdy z przerzutników.
Wartość zmiennej wyjściowej Q
i
określają wartość zmiennych wejściowych synchronicznych, określanych przez kombinacyjny układ
programujący (UP).
Rys. 7.8 Schemat blokowy licznika synchronicznego.
UP – Kombinacyjny Układ Programujący.
Na rys. 7.8 przedstawiono schemat blokowy licznika synchronicznego, w którym układ tworzą niezależne przerzutniki. Przejście licznika z
jednego stanu do drugiego odbywa się na podstawie zadanych wzbudzeń zmiennych informacyjnych. Wektor A reprezentuje dodatkowe zmienne
programujące, pozwalające zmienić sposób pracy licznika.
W rozdziale 4 przedstawiono tablice ilustrujące działanie przerzutników synchronicznych. Przy projektowaniu liczników synchronicznych
należy wziąć pod uwagę tablice wzbudzeń. Zadane są przejścia przerzutników, bo zadany jest program pracy licznika, natomiast należy ustalić
wzbudzenia przerzutników dla zapewnienia tych przejść.
Tablice wzbudzeń wszystkich przerzutników synchronicznych przedstawiono na rys. 7.9.
Q
i
t
→
Q
i
t+1
T
t
J
t
K
t
D
t
S
t
R
t
0
→
0
0
→
1
1
→
0
1
→
1
0
1
1
0
0
1
-
-
-
-
1
0
0
1
0
1
0
1
0
-
-
0
1
0
Rys. 7.9 Tablica wzbudzeń przerzutników synchronicznych.
Układ programujący (UP) zawiera funkcje kombinacyjne określające wartości zmiennych informacyjnych poszczególnych przerzutników
w takcie t, które wymuszą zadaną wartość Q
i
w takcie t + 1, po przejściu impulsu taktującego.
Liczniki równoległe projektujemy następująco:
1.
Ustalić liczbę przerzutników w zależności od pojemności licznika.
2.
Ustalić i wykonać tabele stanów licznika (uwzględniając tabele wzbudzeń przerzutników, na których realizujemy licznik). Polega to na
rozpisaniu kolejności następujących po sobie stanów i odpowiadającym im stanów przerzutnika, czyli wypełnienie tablicy stanów, a następnie
na podstawie tablicy wzbudzeń przerzutnika wypełnia się tablicę Karnaugha, osobno dla poszczególnych wejść informacyjnych każdego
przerzutnika.
3.
Zaprojektować układ kombinacyjny ograniczający zliczanie.
Przykład 7.6:
Zaprojektować licznik równoległy zliczający od 5 do 14 na przerzutnikach JK.
Do zapisania liczb od 5 do 14 w kodzie dwójkowym potrzeba czterech bitów, czyli cztery przerzutniki.
5 = 0101 = Q
3
Q
2
Q
1
Q
0
14 = 1110 = Q
3
Q
2
Q
1
Q
0
W tablicy stanów (rys. 7.10b) zapisujemy stany jakie będą występowały od 5 do 14 w kodzie dwójkowym. Stany wyjściowe odpowiadają
stanom przerzutników, które wyznaczamy na podstawie tablicy wzbudzeń (rys. 7.10a).
a)
Q
n
Q
n+1
J
K
0
0
0
-
0
1
1
-
1
0
-
1
1
1
-
0
b)
8
4
2
1
Stany
Q
3
Q
2
Q
1
Q
0
J
3
K
3
J
2
K
2
J
1
K
1
J
0
K
0
J
0
Q
0
C
K
0
Q
0
J
1
Q
1
C
K
1
Q
1
J
2
Q
2
C
K
2
Q
2
A
UP
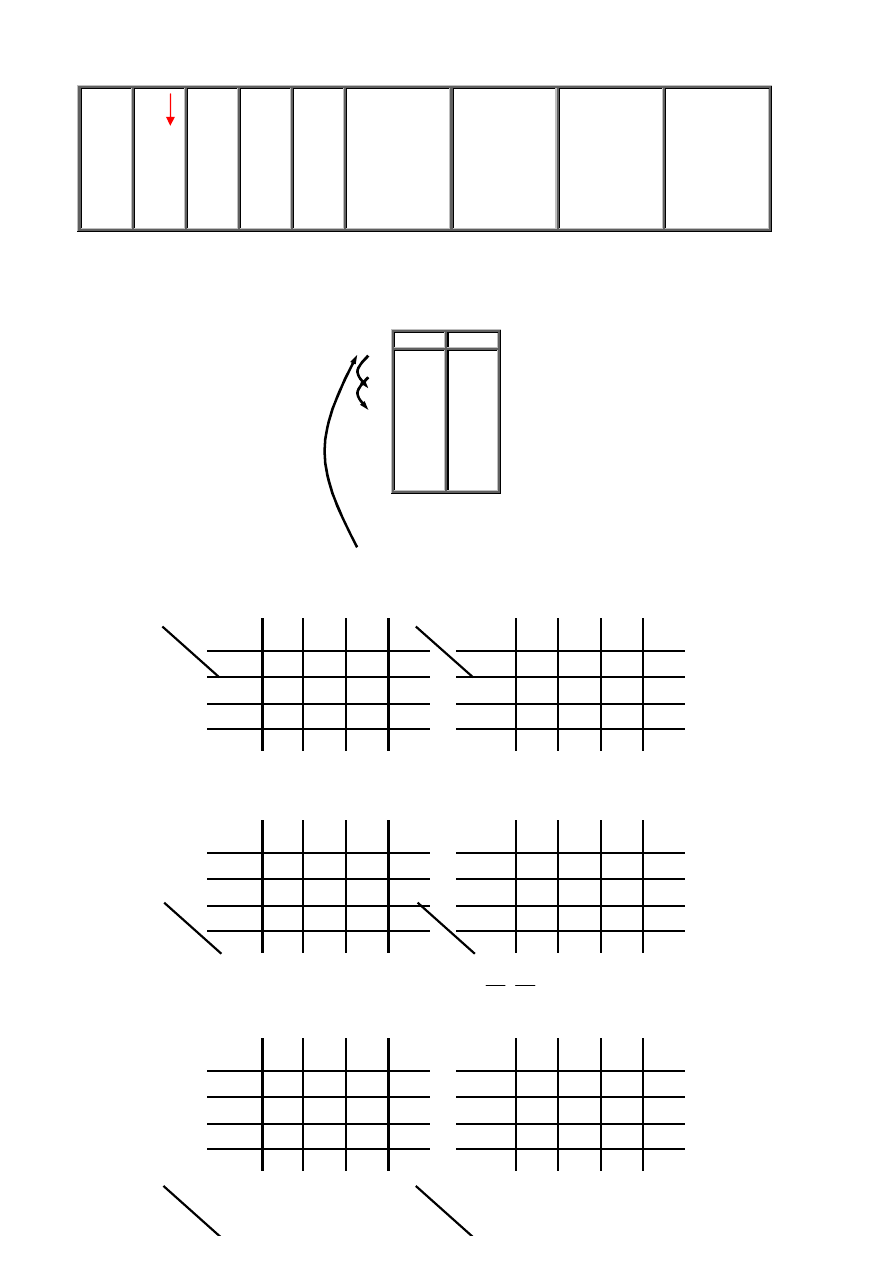
56
Q
1
Q
0
Q
3
Q
2
Q
1
Q
0
Q
3
Q
2
Q
1
Q
0
Q
3
Q
2
Q
1
Q
0
Q
3
Q
2
Q
1
Q
0
Q
3
Q
2
Q
1
Q
0
Q
3
Q
2
5
0
1
0
1
0
-
-
0
1
-
-
1
6
0
1
1
0
0
-
-
0
-
0
1
-
7
0
1
1
1
1
-
-
0
-
1
-
1
8
1
0
0
0
-
0
0
1
0
-
1
-
9
1
0
0
1
-
0
0
-
1
-
-
1
10
1
0
1
0
-
0
0
-
-
0
1
-
11
1
0
1
1
-
0
1
-
-
1
-
1
12
1
1
0
0
-
0
-
0
0
-
1
-
13
1
1
0
1
-
0
-
0
1
-
-
1
14
1
1
1
0
-
1
-
0
-
1
1
-
Rys. 7.10 Licznik równoległy zliczający od 5 do 14:
a) tablica wzbudzeń przerzutnika JK,
b) tablica stanów.
Na przykład dla Q
3
mamy (rys. 7.11):
Q
3
J
3
0
0
0
0
0
1
1
-
1
-
1
-
1
-
1
-
1
-
1
-
Rys. 7.11 Stany wyjściowe J
3
.
Aby otrzymać stan J
3
– 5 łączymy stan 5 i 6 Q
3
sygnału wyjściowego i mamy: 00 – daje nam (z tablicy wzbudzeń dla J) 0, 00 – daje nam
również 0, 01 – otrzymujemy 1. Jako końcowy stan dla J
3
, łączymy ostatni stan 14 z pierwszym 5.
Na podstawie tablicy stanów sporządzamy tablice Karnaugha dla wejść informacyjnych poszczególnych przerzutników (J
n
K
n
) (rys. 7.12a,
b, c), a na podstawie tablic Karnaugha wyznaczamy funkcje sterujące dla wejść informacyjnych.
00
01
11
10
00
01
11
10
00
-
-
-
-
00
-
-
-
-
01
-
0
1
0
01
-
-
-
-
11
-
-
-
-
11
0
0
-
1
10
-
-
-
-
10
0
0
0
0
J
3
= Q
1
Q
0
K
3
= Q
2
Q
1
00
01
11
10
00
01
11
10
00
-
-
-
-
00
-
-
-
-
01
-
-
-
-
01
-
0
0
-
11
-
-
-
1
11
0
0
-
0
10
0
0
-
0
10
1
0
-
-
J
2
= Q
2
K
2
=
2
0
Q
Q
⋅
00
01
11
10
00
01
11
10
00
-
-
0
0
00
-
-
-
-
01
-
1
1
1
01
-
-
1
0
11
-
-
-
-
11
-
-
-
1
10
-
-
-
-
10
-
-
1
0
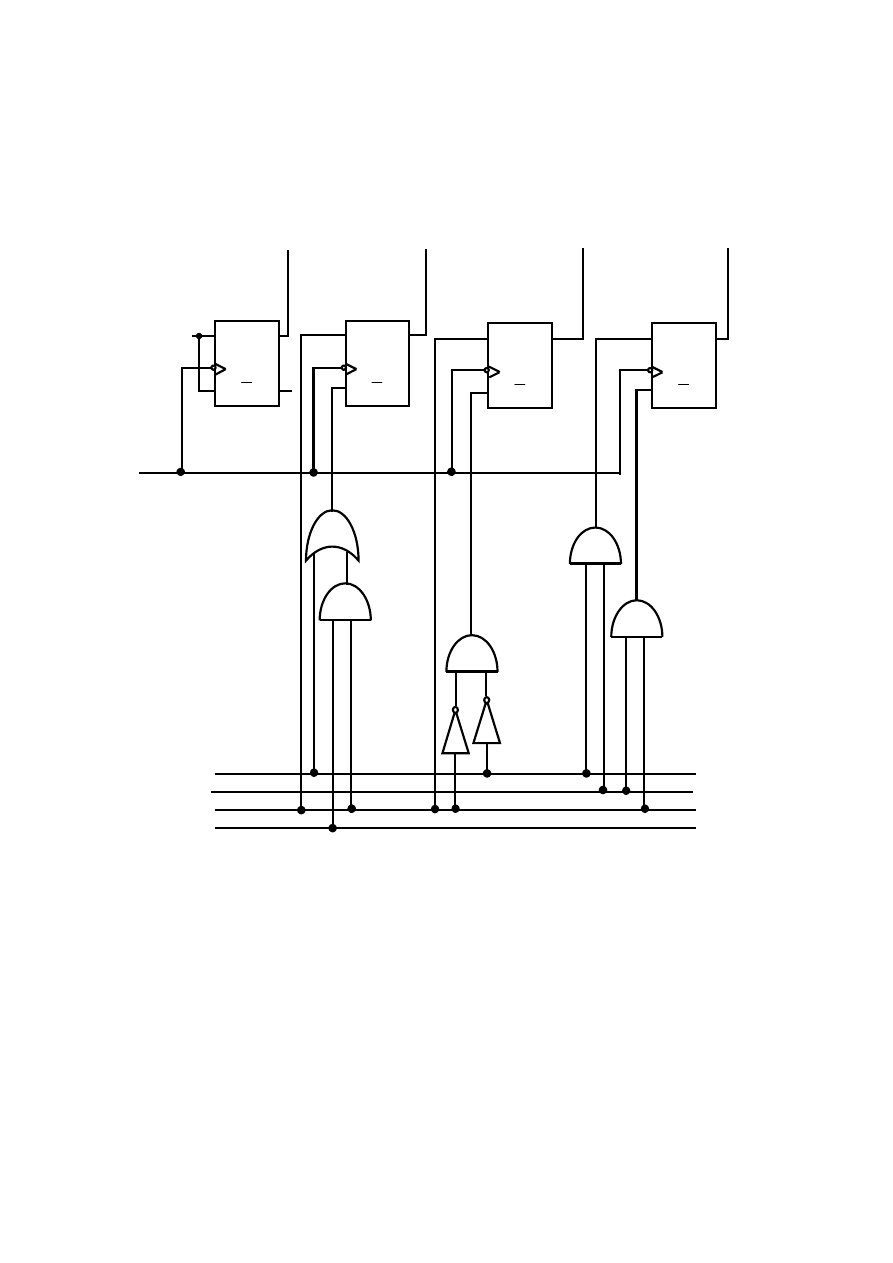
57
J
1
= Q
2
K
1
= Q
3
Q
2
+ Q
0
J
0
= „1”
K
0
= „1”
Rys. 7.12 Synchroniczny licznik zliczający od 5 do 14: a), b), c), tablice Karnaugha dla poszczególnych wejść informacyjnych przerzutników JK,
d) schemat połączeń.
Na podstawie funkcji sterujących projektujemy układ kombinacyjny ograniczający zliczanie (rys. 7.12d).
Przykładowo dla przerzutnika drugiego, w pole 0101 w tablicy J
0
wpisujemy „-”, a w tablicy K
0
wpisujemy 1. Licznik jest w stanie 0101
to następnym jego stanem jest stan 0110, czyli stan na wyjściu Q
0
zmieni się z 1 na 0, co zapewnia kombinacja J
0
K
0
= - 1. Podobnie w pole 1110 w
tablicy J
0
wpisujemy 1, a w tablicy K
0
„-”.Licznik jest w stanie 1110, to następnym stanem jest 0101, czyli na wyjściu Q
0
stan zmieni się z 0 na 1, co
zapewnia kombinacja J
0
K
0
= 1 -.
J
0
Q
0
C
K
0
Q
0
C
„1”
J
1
Q
1
C
K
1
Q
1
Q
0
Q
1
Q
2
Q
3
J
2
Q
2
C
K
2
Q
2
J
3
Q
3
C
K
3
Q
3
Q
0
Q
1
Q
2
Q
3
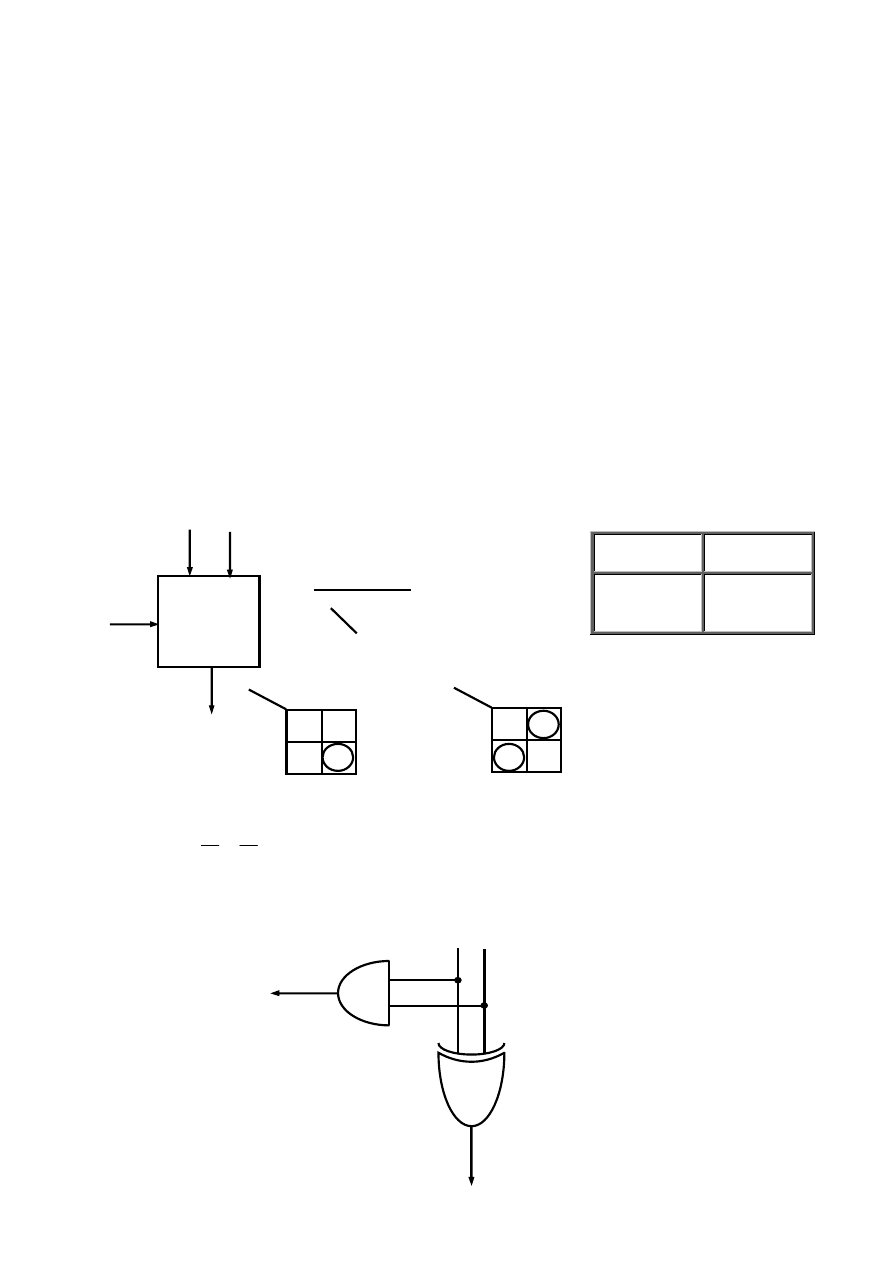
58
8.
UK
ŁADY ARYTMETYCZNE
8.1.
WST
ĘP
Prawie wszystkie praktyczne obliczenia matematyczne dają się sprowadzić do działań arytmetycznych, wszystkie zaś działania
arytmetyczne sprowadzają się do dodawania. Do podstawowych układów arytmetycznych zalicza się więc sumator, którego zasadniczym zadaniem
jest dodawanie (lub odejmowanie) liczb.
Jeżeli sumator uzupełnimy o układ przesuwający dane – to otrzymamy układ umożliwiający realizacje operacji mnożenia i dzielenia,
dzięki wykonaniu ciągu kolejnych dodawań (odejmowań) i przesunięć.
Sumatory dzielimy na :
a)
dwójkowe, gdzie działania dokonuje się na liczbach dwójkowych,
b)
dziesiętne, wykonujące działania na liczbach dziesiętnych kodowanych dwójkowo.
Sumatory można również podzielić ze względu na sposób podawania składników sumy:
a)
równoległe:
§
z przeniesieniem szeregowym,
§
z przeniesieniem równoległym,
b)
szeregowe.
Do układów arytmetycznych zaliczane są również komparatory. Są to układy służące do porównywania wielkości dwu lub więcej liczb
binarnych. Można wyróżnić dwa zasadnicze typy komparatorów:
a)
komparatory równoległe,
b)
komparatory szeregowe.
8.2.
SUMATORY
Sumatory są to układy służące do sumowania arytmetycznego dwu liczb binarnych n – bitowych A i B, z jednobitowym przeniesieniem C
i
,
dając w wyniku n – bitową sumę S
i
i przeniesienie C
i +1
.
Dodawanie liczb dwójkowych odbywa się według tych samych zasad co liczb dziesiętnych. Dodawanie dwu liczb dwójkowych A i B jest
pokazane na rys. 8.1.
a)
b)
A
B
S
C
0
0
1
1
0
1
0
1
0
1
1
0
0
0
0
1
c)
Rys. 8.1 Dodawanie jednobitowych liczb dwójkowych:
a) symbol, b) tablica prawdy, c) tablice Karnaugha.
Zmienna S
i
reprezentuje wynik operacji, jej wartość jest sumą modulo 2 (EX – OR) składników A
i
, B
i
i C
i
.
Zmienna C
i
reprezentuje przeniesienie z pozycji młodszej sumatora wielopozycyjnego, natomiast C
i +1
jest przeniesieniem do pozycji
starszej. C
i
nie występuje w tzw. półsumatorze, a obecność C
i
daje sumator pełny.
Na podstawie siatek Karnaugha przedstawionych na rys. 8.1 otrzymujemy wyrażenia logiczne dla półsumatora:
§
suma
i
i
i
i
i
i
i
B
A
B
A
B
A
S
⊕
=
+
=
§
przeniesienie
i
i
1
i
B
A
C
=
+
Przykładowy schemat logiczny przedstawia rys. 8.2.
Rys. 8.2 Schemat logiczny półsumatora.
W przypadku dodawania wielobitowych liczb dwójkowych należy uwzględnić przeniesienie z pozycji sąsiedniej, mniej znaczącej od
rozpatrywanej. Operację dodawania bitów z i – tej pozycji dodawanych liczb wielobitowych ilustruje rys. 8.3b.
Za pomocą siatek Karnaugha można opisać zasadę działania sumatora pełnego (rys.8.3c, d). Z siatek tych otrzymujemy zależności:
§
suma
Σ
A
B
C
S
A
B
C
S
Dodajna
Dodajnik
Suma
Przeniesienie
A 0 1
0 0
0 1
B
0
1
A 0 1
0 1
1 0
B
0
1
A B
C = AB
S = A
⊕
B
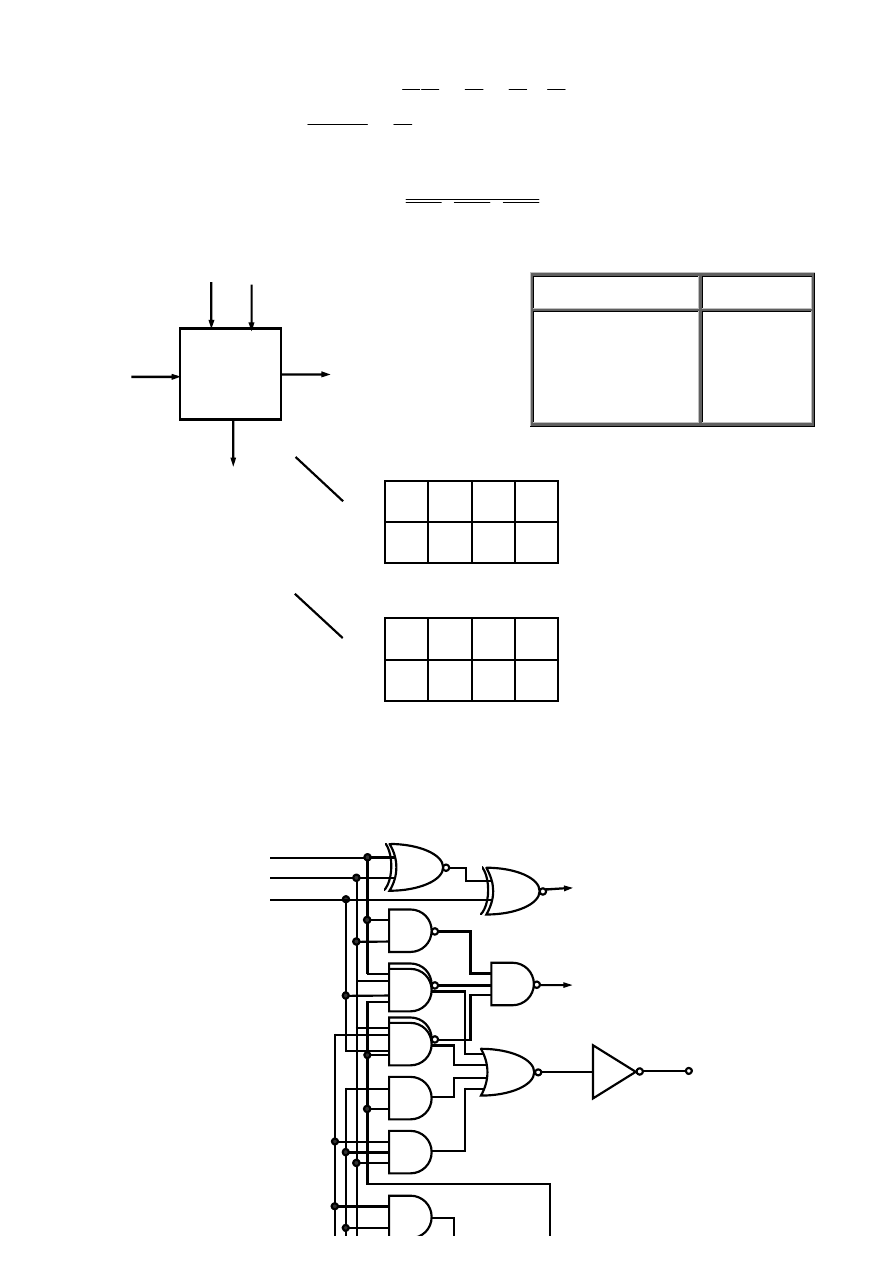
59
(
) (
)
(
)
(
)
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
B
A
C
B
A
C
B
A
C
B
A
B
A
C
B
A
B
A
C
S
⊕
⊕
=
⊕
+
⊕
=
+
+
+
=
§
przeniesienie
i
i
i
i
i
i
1
i
C
B
C
A
B
A
C
+
+
=
+
i
i
i
i
i
i
1
i
C
B
C
A
B
A
C
⋅
⋅
=
+
a)
b)
A
i
B
i
C
i
S
i
C
i+1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
1
0
1
0
0
1
0
0
0
1
0
1
1
1
c)
00
01
11
10
0
0
1
0
1
1
1
0
1
0
d)
00
01
11
10
0
0
0
1
0
1
0
1
1
1
Rys. 8.3 Sumator dwuargumentowy jednobitowy:
a) symbol, b) tabela zależności, c) siatka zależności dla sumy, d) siatka zależności dla przeniesienia.
Ponieważ istnieje wiele równoważnych postaci funkcji S
i
i C
i
zatem istnieje możliwość różnej ich interpretacji. Schemat sumatora pełnego,
dwuargumentowego z przeniesieniem z pozycji poprzedniej C
i
oraz przeniesienie do pozycji wyższej C
i + 1
pokazano na rys. 8.4a. Sumator z rys. 8.4b
jest podstawową komórką występującą w sumatorach średniej skali integracji: 480,482 i 483.
a)
b)
Σ
A
i
B
i
C
i
S
i
C
i+1
A
i
B
i
C
i
A
i
B
i
C
i
S
i
C
i+1
A
i
B
i
C
i
S
i
C
i+1
S
i
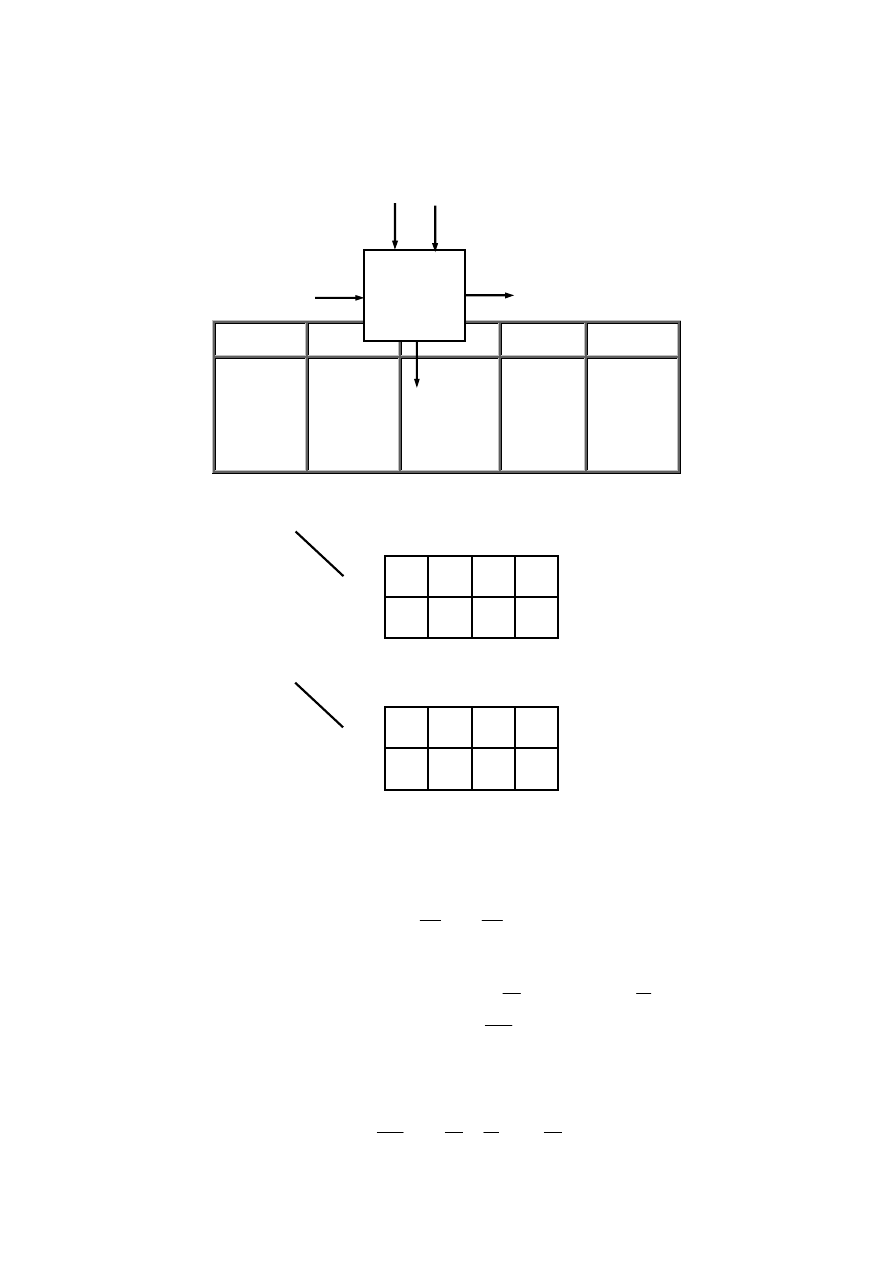
60
Rys. 8.4 Schemat logiczny sumatora pełnego dwuargumentowego (a), jednobitowego (b).
Szczególnym przypadkiem sumatora jest układ realizujący odejmowanie dwu liczb dwójkowych. Układ służący do odejmowania nazywa
się substraktorem. Wartości funkcji dla różnicy D
i
i pożyczki V
i
– tej komórki substraktora ilustruje tabela na rys. 8.5.
a)
b)
Pożyczka
V
i
Odjemna
A
i
Odjemnik
B
i
Różnica
D
i
Pożyczka
V
i+1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
1
0
1
0
0
1
0
1
0
0
1
1
0
1
c)
00
01
11
10
0
0
1
0
1
1
1
0
1
0
00
01
11
10
0
0
1
0
0
1
1
1
1
0
Rys. 8.5 Sumator jednobitowy odejmujący - substraktor:
a) symbol, b) tabela zależności, c) siatka Karnaugha.
Z tablic Karnaugha (rys. 8.5c) otrzymujemy następujące funkcje logiczne:
I
I
I
I
V
B
A
D
⊕
⊕
=
I
I
I
I
I
I
1
I
V
B
V
A
B
A
V
+
+
=
+
Porównując funkcje sumatora i substraktora możemy zauważyć, że różnica D
i
jest identyczna z sumą S
i
, natomiast są różne wyrażenia dla
pożyczki V
i +1
i przeniesienia C
i +1
.
Jeśli w wyrażeniach opisujących działanie substraktora zamiast B
i
wstawić
i
B
, a zamiast C
i
wstawić
i
V
otrzymamy:
1
i
1
i
V
C
+
+
=
i
i
D
S
=
Korzystając z tej własności, znajdujemy:
(
)
i
i
i
i
i
1
i
i
i
i
i
B
A
V
B
A
V
,
B
A
V
D
±
+
=
⊕
⊕
=
+
Sumator może być zatem stosowany jako układ odejmujący po dokonaniu powyższych przełączeń.
Σ
A
i
B
i
V
i
D
i
V
i+1
A
i
B
i
V
i
D
i
V
i+1
A
i
B
i
V
i
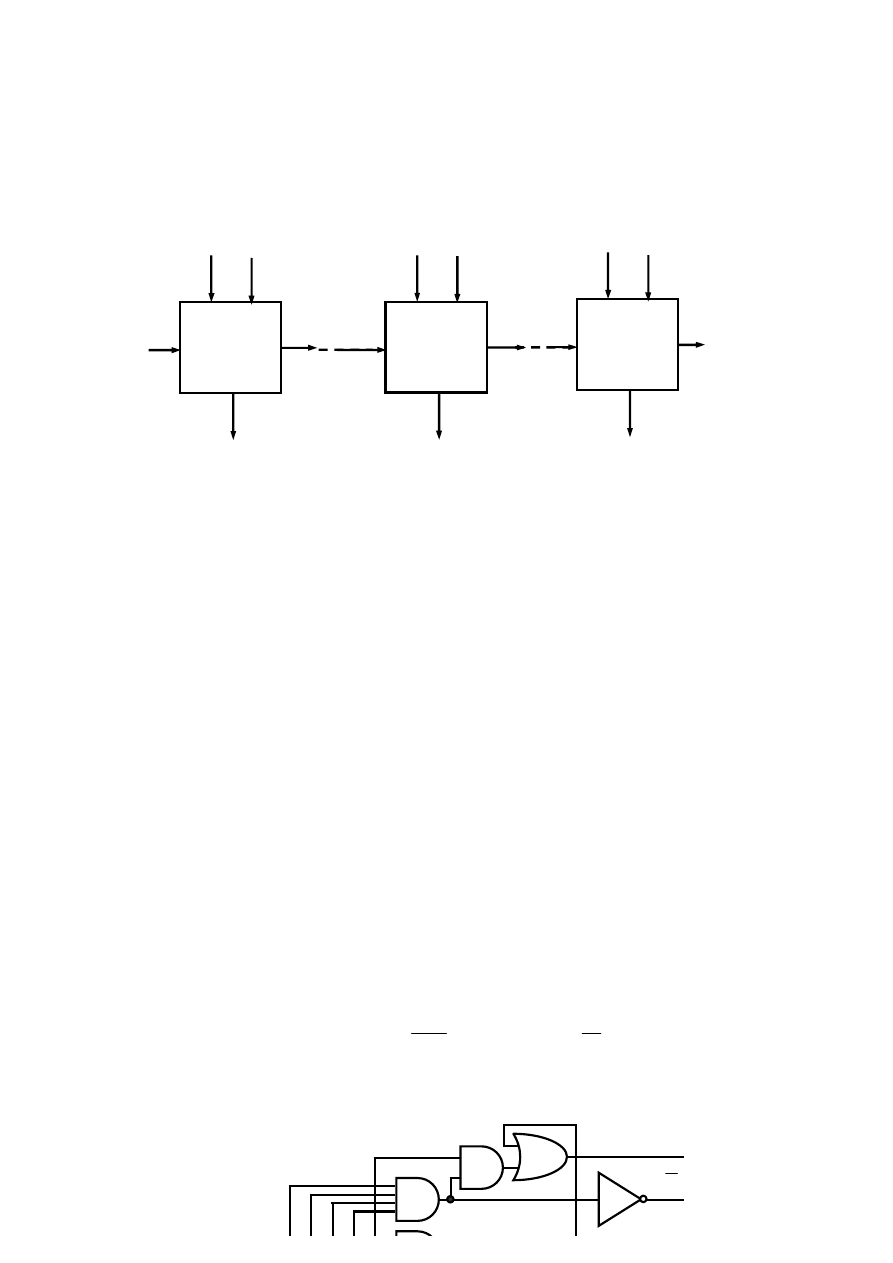
61
8.2.1.
Sumatory równoleg
łe
Sumatory równoległe ze względu na sposób wytwarzania przeniesień dzielimy na:
§
sumatory z przeniesieniem szeregowym, zwane również sumatorami kaskadowymi albo iteracyjnymi,
§
sumatory z przeniesieniem równoległym.
Sumator kaskadowy n – bitowy jest układem powstałym przez połączenie n sumatorów jednobitowych. Schemat blokowy sumatora
kaskadowego przedstawiono na rys. 8.6.
Rys. 8.6 Schemat blokowy sumatora kaskadowego.
Przy sumowaniu liczb dodatnich wejście przeniesienia początkowego C
0
nie jest wykorzystywane (C
0
= 0). Wszystkie cyfry dodawanych
liczb dwójkowych podawane są na sumator jednocześnie. Czas uformowania się wyniku zależy od prędkości propagacji sygnału przeniesienia przez
kolejne komórki sumatora. W najbardziej niekorzystnym przypadku sygnał C musi przejść przez wszystkie komórki sumatora.
Sumator z przeniesieniem równoległym generuje wszystkie wartości przeniesień jednocześnie na podstawie wartości na poszczególnych
bitach obu operandów.
Przeniesienie:
(
)
i
i
i
i
i
i
i
i
i
i
i
1
i
C
B
A
B
A
C
B
C
A
B
A
C
+
+
=
+
+
=
+
można wyrazić w postaci:
,
C
T
G
C
i
i
i
1
i
+
=
+
gdzie:
i
i
i
B
A
G
=
i
i
i
B
A
T
+
=
inaczej:
0
0
2
i
1
i
i
0
1
1
i
i
2
i
1
i
i
1
i
i
i
1
i
0
0
1
2
0
1
2
1
2
2
3
0
0
1
0
1
1
2
0
0
0
1
C
T
T
T
T
G
T
T
T
G
T
T
G
T
G
C
,
C
T
T
T
G
T
T
G
T
G
C
,
C
T
T
G
T
G
C
,
C
T
G
C
K
K
K
K
M
−
−
−
−
−
−
+
+
+
+
+
+
+
=
+
+
+
=
+
+
=
+
=
Dla modułu czterobitowego
}
3
,
2
,
1
,
0
{
i
∈
:
0
1
2
3
0
1
2
3
1
2
3
2
3
3
4
T
T
T
T
G
T
T
T
G
T
T
G
T
G
C
+
+
+
+
=
lub
0
4
TC
G
C
+
=
gdzie:
0
1
2
3
1
2
3
2
2
3
G
T
T
T
G
T
T
G
T
G
G
+
+
+
=
0
1
2
3
T
T
T
T
T
=
gdzie:
G – przeniesienie generowane w bloku,
T – sygnał warunkujący transmisję przeniesienia początkowego C
0
.
Wyrażenie dla sumy:
i
i
i
i
C
B
A
S
⊕
⊕
=
można przekształcić do postaci:
(
)
i
i
i
i
i
i
i
i
i
T
G
C
B
A
B
A
C
S
⊕
=
+
⊕
=
.
Na rys. 8.7 przedstawiono schemat czterobitowego sumatora z przeniesieniami równoległymi.
Σ
A
0
B
0
C
0
S
0
C
1
Σ
A
i
B
i
C
i
S
i
C
i+1
Σ
A
n-1
B
n-1
C
n-1
S
n-1
C
n
C
4
T
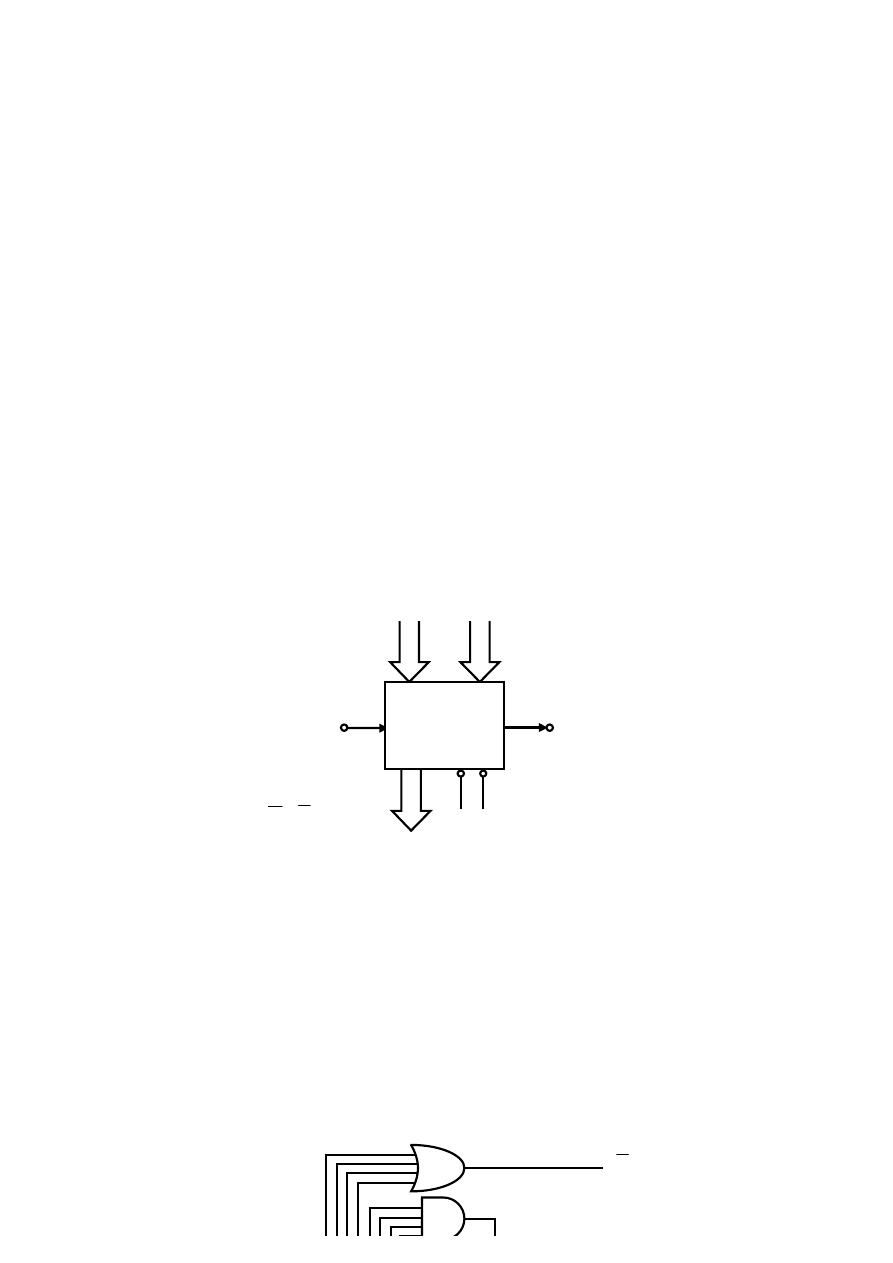
62
Rys. 8.7 Czterobitowy sumator z przeniesieniami równoległymi - schemat logiczny.
Rys. 8.7 Czterobitowy sumator z przeniesieniami równoległymi - oznaczenie.
Układy wielobitowe – n x 4 bity, montuje się wykorzystując sumator czterobitowy z przeniesieniami równoległymi oraz expander, zwany
generatorem przeniesień równoległych (4182). Schemat ideowy expandera pokazano na rys. 8.8. W sumatorze jak i w generatorze zastosowano
zamiast zmiennych G i T ich negacje
G
i
T
, ze względów praktycznych.
Na rys. 8.9 przedstawiono tzw. dwupoziomowy sposób łączenia sumatorów równoległych z generatorem przeniesień.
W szesnastobitowym sumatorze nominalny czas dodawania z rys. 8.9 wynosi około 36 ns. Natomiast w szesnastobitowym sumatorze z
przeniesieniami kaskadowymi czas ten wynosi około 60 ns, prawie dwa razy tyle. Ze wzrostem ilości bitów przewaga sumatora z przeniesieniami
równoległymi nad sumatorem z przeniesieniami kaskadowymi (szeregowymi) staje się jeszcze bardziej widoczna.
Σ
A
B
C
0
S
G T
C
4
T
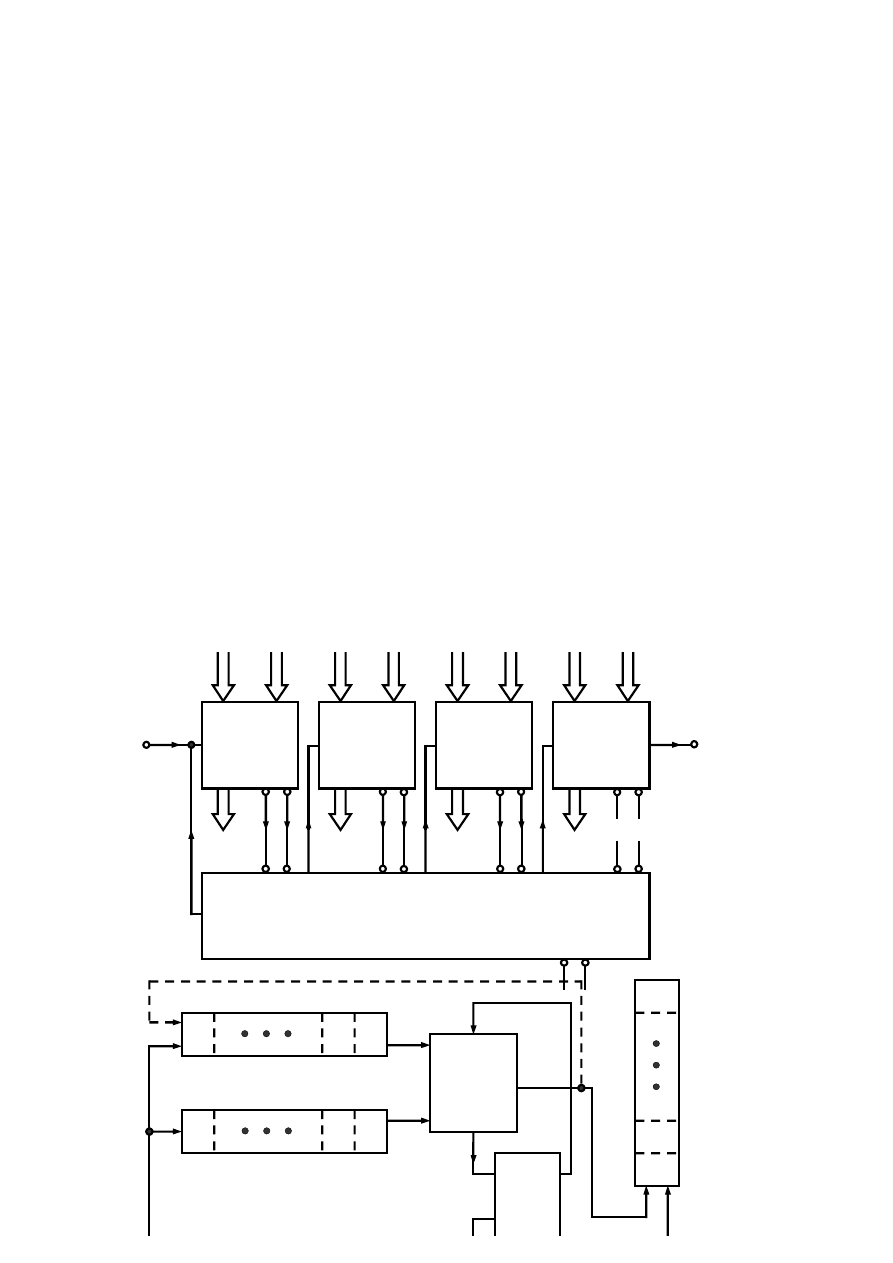
63
Rys. 8.8 Generator przeniesień równoległych.
Rys. 8.9 Dwupoziomowy sposób łączenia sumatorów równoległych z generatorem przeniesień.
8.2.2.
Sumatory szeregowe
W sumatorze szeregowym składniki sumy są podawane kolejno, bit po bicie, zaczynając od bitu o najniższej wadze.
Schemat ideowy sumatora szeregowego przedstawiono na rys. 8.10.
Rys. 8.10 Schemat ideowy sumatora szeregowego.
G
0
T
0
C
1
T
G
A
B
C
0
S
C
4
Σ
T
G
A
B
C
0
S
C
4
Σ
T
G
A
B
C
0
S
C
4
Σ
T
G
A
B
C
0
S
C
4
Σ
G
1
T
1
C
2
G
2
T
2
C
3
G
3
T
3
G T
C
C
0
C
0
74182
n
–
b
it
o
w
y
r
ej
es
tr
p
rz
es
u
w
aj
ąc
y
C
C
n – bitowy rejestr przesuwający
Składnik B
n – bitowy rejestr przesuwający
Składnik B
A
C
C
i-1
C
i
Σ
S
A Q
C
S
u
m
a
Takt
1
2
3
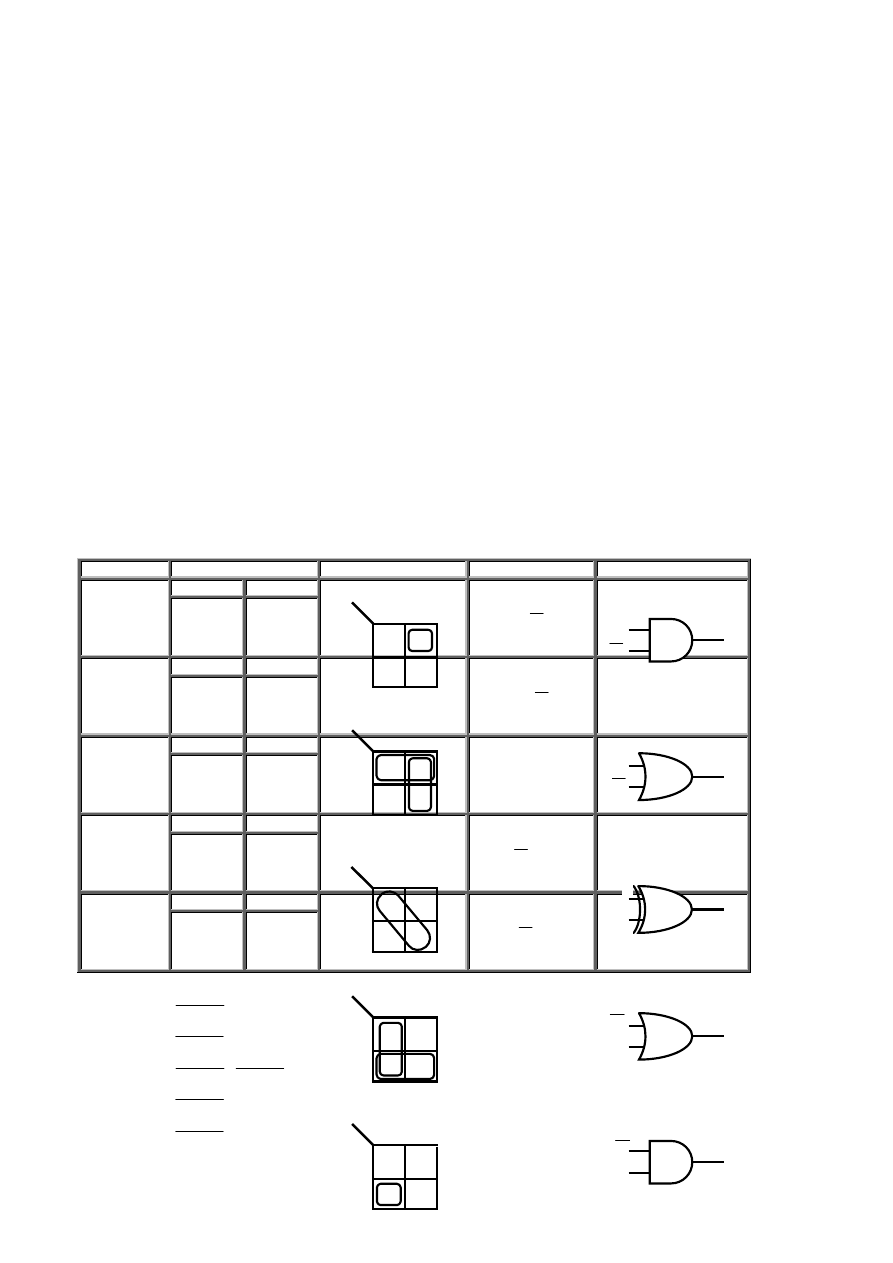
64
Sumator szeregowy składa się z sumatora jednobitowego z dodatkiem trzech rejestrów przesuwających oraz przerzutnika typu D
zapamiętującego przeniesienie. Dodajna (A) i dodajnik (B) są wprowadzane do sumatora z rejestrów przesuwających.
Przed rozpoczęciem dodawania, do rejestrów 1 i 2 muszą zostać wpisane składniki A i B, a przerzutnik D służący do przekazywania
przeniesień z poprzednich pozycji musi zostać wyzerowany. Dodawanie dwóch bitów składników z odpowiadających sobie pozycji i bitu
przeniesienia z poprzedniej pozycji następuje w kolejnych taktach wyznaczanych sygnałem zegarowym. Bity składników pojawiają się kolejno na
wyjściach szeregowych rejestrów przesuwających 1 i 2, zaś bity wyniku są szeregowo wprowadzane do rejestru 3.
Sumator jest układem synchronicznym taktowanym ciągiem impulsów zegarowych. Przeniesienie z przerzutnika D jest wprowadzane do
sumatora pełnego w każdym następnym takcie (cyklu).
W sumatorze akumulacyjnym suma podawana jest na miejsce dodajnej, zamiast rejestru 3 można użyć rejestru 1 lub 2 (linia przerywana
rys. 8.10). W miarę dodawania nowych składników cała suma akumuluje się w tym rejestrze.
Zaletami sumatora szeregowego są:
§
jego prostota,
§
mała liczba elementów logicznych potrzebnych do jego realizacji.
Wadą sumatora jest jego mała szybkość (około 60 ns). Czas sumowania składników n – bitowych wynosi nT.
Sumator szeregowy jest układem sekwencyjnym a równoległy kombinacyjnym, dodawanie równoległe trwa krótko, a szeregowe długo.
Dlatego można stwierdzić, że różne operacje arytmetyczne można wykonać szybko za pomocą układów kombinacyjnych, bardzo rozbudowanych, lub
wolniej za pomocą układów sekwencyjnych, ale o prostszej budowie.
8.3.
KOMPARATORY
Komparatory cyfrowe są to układy służące do porównywania dwóch lub więcej słów (liczb) dwójkowych n – bitowych.
Najprostsze komparatory określają, czy porównywane liczby są sobie równe (A = B?). Bardziej złożone układy mogą określać, która z
porównywanych liczb jest większa (A > B?). Istnieją również komparatory tzw. uniwersalne, które określają trzy możliwe, wzajemnie wykluczające
się relacje: A > B, A = B i A < B.
Komparatory liczb mogą być zrealizowane jako układy równoległe bądź szeregowe.
8.3.1.
Komparatory jednobitowych liczb dwójkowych
Relacje zachodzące pomiędzy jednobitowymi liczbami dwójkowymi A i B są przedstawione w tablicy 8.1.
Tablica 8.1 Relacje zachodzące między jednobitowymi liczbami dwójkowymi
Relacja
Tablica wartości
Tablica Karnaugha
Funkcja przełączająca
Schemat logiczny
A B
A > B
A > B
0 0
0 1
1 0
1 1
0
0
1
0
(A > B) =
A
B
A B
A
≥
B
A
≥
B
0 0
0 1
1 0
1 1
1
0
1
1
(A
≥
B) =
A +
B
A B
A = B
A = B
0 0
0 1
1 0
1 1
1
0
0
1
(A = B ) =
A
⊗
B
A B
A
≤
B
A
≤
B
0 0
0 1
1 0
1 1
1
1
0
1
(A
≤
B ) =
A
+ B
A B
A < B
A < B
0 0
0 1
1 0
1 1
0
1
0
0
(A < B) =
A
B
Nietrudno jest wykazać, że następujące zależności są prawdziwe:
(
)
(
)
B
A
B
A
≤
=
>
(8.1)
(
)
(
)
B
A
B
A
<
=
≥
(8.2)
(
)
(
)(
)
B
A
B
A
B
A
<
>
=
=
(8.3)
(
)
(
)
B
A
B
A
>
=
≤
(8.4)
(
)
(
)
B
A
B
A
≥
=
<
(8.5)
0 1
0 0
A
B
0
1
0 1
1 0
0 1
A
B
0
1
0 1
1 1
0 1
A
B
0
1
0 1
1 0
1 1
A
B
0
1
0 1
0 0
1 0
A
B
0
1
0 1
A
B
A
B
A
B
A
B
B
A
B
B
(A>B)
(A
≥
B)
(A=B)
(A
≤
B)
(A<B)
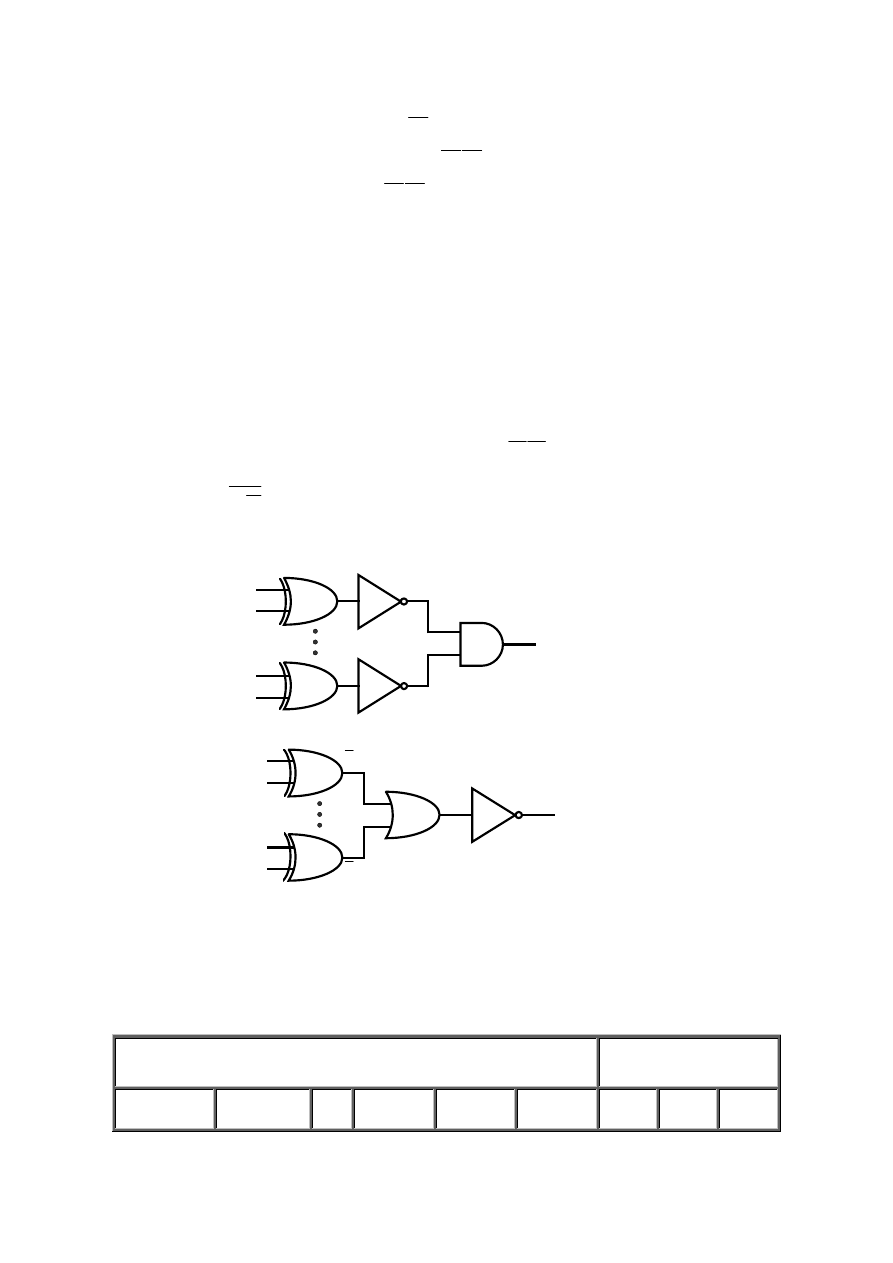
65
Komórkę komparatora opisują następujące funkcje przełączające z tablicy 8.1:
i
i
i
B
A
X
=
dla (A > B)
i
i
i
i
i
B
A
B
A
Y
+
=
dla (A = B)
i
i
i
B
A
Z
=
dla (A < B)
8.3.2.
Komparatory równoleg
łe
Komparator równoległy to taki układ, na wejścia którego są podawane jednocześnie wszystkie bity porównywalnych liczb.
Określenie tożsamości dwóch liczb n – bitowych A i B, gdzie:
A = A
n-1
A
n-2
... A
i
... A
0
B = B
n-1
B
n-2
... B
i
... B
0
polega na sprawdzeniu czy bity na odpowiadających sobie pozycjach tych liczb są tożsame, co zapisujemy:
(A = B) = (A
n-1
= B
n-1
) (A
n-2
= B
n-2
)...(A
i
= B
i
)...(A
0
=B
0
) =
= (A
n-1
⊗
B
n-1
) (A
n-2
⊗
B
n-2
)...(A
i
⊗
B
i
)...(A
0
⊗
B
0
)
(8.6)
lub krócej:
(A = B) = T
n-1
T
n-2
...T
i
...T
0
=
I
1
n
0
i
i
T
−
=
(8.7)
przy czym T
i
= A
i
⊗
B
i
= A
i
B
i
+
i
i
B
A
Wyrażenie (7) może być również przedstawione w postaci:
U
I
1
n
0
i
i
1
n
0
i
i
T
T
)
B
A
(
−
=
−
=
=
=
=
(8.8)
Wyrażenia (8.7) i (8.8) realizują układy pokazane na rys. 8.11.
a)
b)
Rys. 8.11 Schemat logiczny układu realizującego:
a) wyrażenie (8.7), b) wyrażenie (8.8).
W celu określenia tożsamości trzech n – bitowych liczb A, B i C należy określić funkcję:
(
)(
)
i
i
1
n
0
i
i
i
C
A
B
A
)
C
B
A
(
⊗
⊗
=
=
=
−
=
I
(8.9)
Funkcja ta może być odpowiednio rozszerzona na większą grupę liczb.
Aby określić relację A > B, a także relację A < B dla n – bitowych liczb dwójkowych A i B, należy rozpocząć komparację (porównanie) od
bitów z pozycji najwięcej znaczącej (czyli z pozycji n – 1) tych liczb:
§
jeśli bit liczby A z pozycji n – 1 jest równy 1 (albo 0), a bit liczby B z tej pozycji jest równy 0 (albo 1), to A > B (albo A < B) i określenie
nierówności jest dokonane,
§
jeśli bity z pozycji n – 1 liczb A i B są tożsame (równe), to porównujemy, tak jak poprzednie, bity z pozycji n – 2.
Czynności te powtarzamy aż do uzyskania jednoznacznej odpowiedzi.
Z powyższych rozważań można wyznaczyć tablicę wartości (tablica 8.2) opisująca działanie logiczne uniwersalnego komparatora n –
bitowych liczb dwójkowych.
Tablica 8.2 Tablica wartości uniwersalnego komparatora n – bitowych liczb dwójkowych
Wejścia komparacyjne
Wyjścia
A
n-1
, B
n-1
A
n-2
, B
n-2
...
A
2
, B
2
A
1
, B
1
A
0
, B
0
A>B
A<B
A=B
A
0
B
0
A
n-1
B
n-1
0
T
1
−
n
T
A
0
B
0
A
n-1
B
n-1
T
0
T
n-1
(A=B)
(A=B)
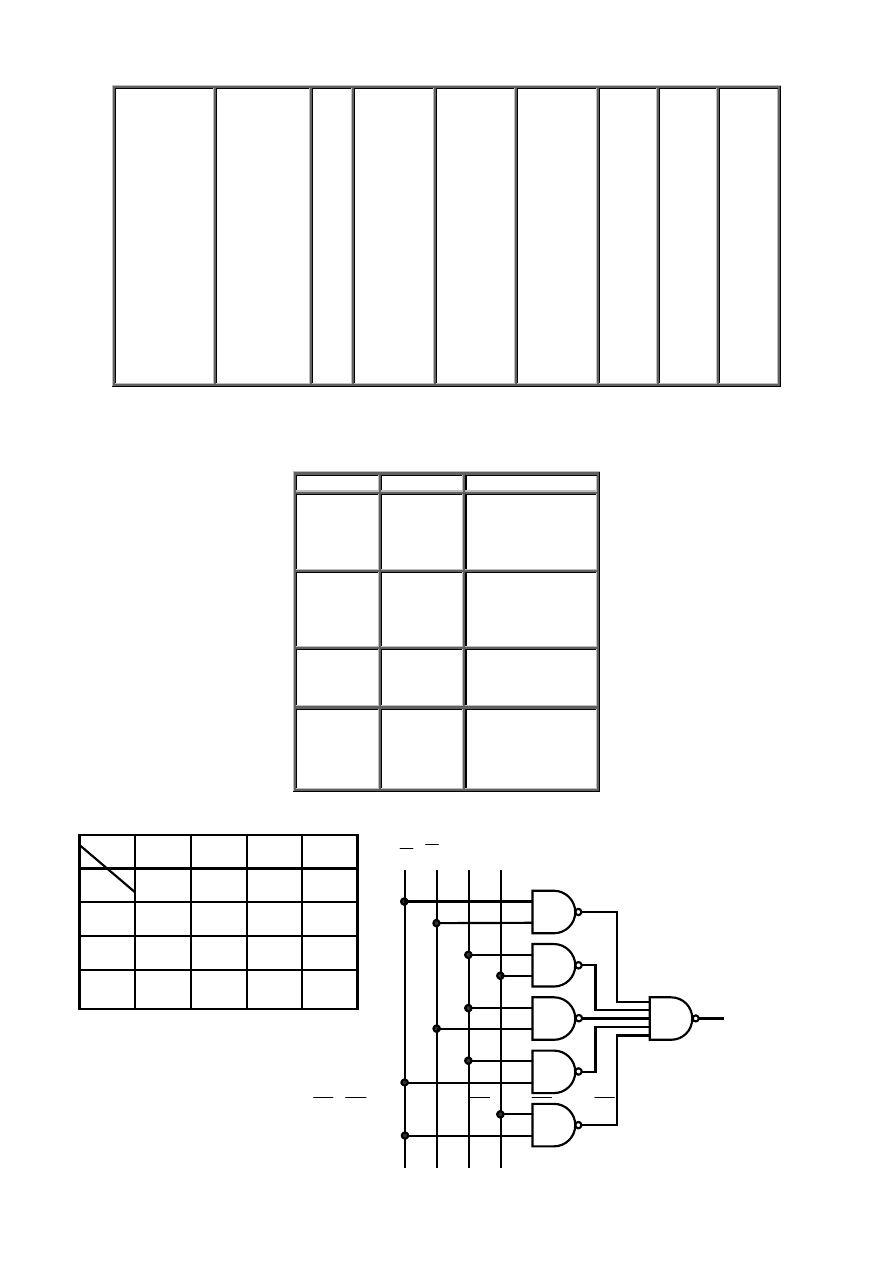
66
A
1
A
0
B
1
B
0
A
n-1
>B
n-1
A
n-1
<B
n-1
A
n-1
=B
n-1
A
n-1
=B
n-1
M
A
n-1
=B
n-1
A
n-1
=B
n-1
A
n-1
=B
n-1
A
n-1
=B
n-1
A
n-1
=B
n-1
A
n-1
=B
n-1
A
n-1
=B
n-1
X
X
A
n-2
>B
n-2
A
n-2
<B
n-2
M
A
n-2
=B
n-2
A
n-2
=B
n-2
A
n-2
=B
n-2
A
n-2
=B
n-2
A
n-2
=B
n-2
A
n-2
=B
n-2
A
n-2
=B
n-2
K
K
K
K
M
K
K
K
K
K
K
K
X
X
X
X
M
A
2
>B
2
A
2
<B
2
A
2
=B
2
A
2
=B
2
A
2
=B
2
A
2
=B
2
A
2
=B
2
X
X
X
X
M
X
X
A
1
>B
1
A
1
<B
1
A
1
=B
1
A
1
=B
1
A
1
=B
1
X
X
X
X
M
X
X
X
X
A
0
>B
0
A
0
<B
0
A
0
=B
0
1
0
1
0
M
1
0
1
0
1
0
0
0
1
0
1
M
0
1
0
1
0
1
0
0
0
0
0
M
0
0
0
0
0
0
1
Przykład 8.1:
Zaprojektować komparator dwubitowy realizujący funkcję A
1
A
0
≥ B
1
B
0
, napisać równanie określające powyższą relację oraz podać przykładowy
układ realizujący to równanie.
a)
A
1
A
0
B
1
B
0
A
1
A
0
≥
B
1
B
0
0 0
0 0
0 0
0 0
0 0
0 1
1 0
1 1
1
0
0
0
0 1
0 1
0 1
0 1
0 0
0 1
1 0
1 1
1
1
0
0
1 0
1 0
1 0
1 0
0 0
0 1
1 0
1 1
1
1
1
0
1 1
1 1
1 1
1 1
0 0
0 1
1 0
1 1
1
1
1
1
b)
c)
00
01
11
10
00
1
1
1
1
01
0
1
1
1
11
0
0
1
0
10
0
0
1
1
1
0
1
1
0
1
0
1
0
1
B
A
B
A
B
A
A
A
B
B
Y
+
+
+
+
⋅
=
Rys. 8.12 Tablica wartości (a), siatka Karnaugha (b),
przykładowa realizacja (c).
A
1
A
0
1
B
0
B
Y
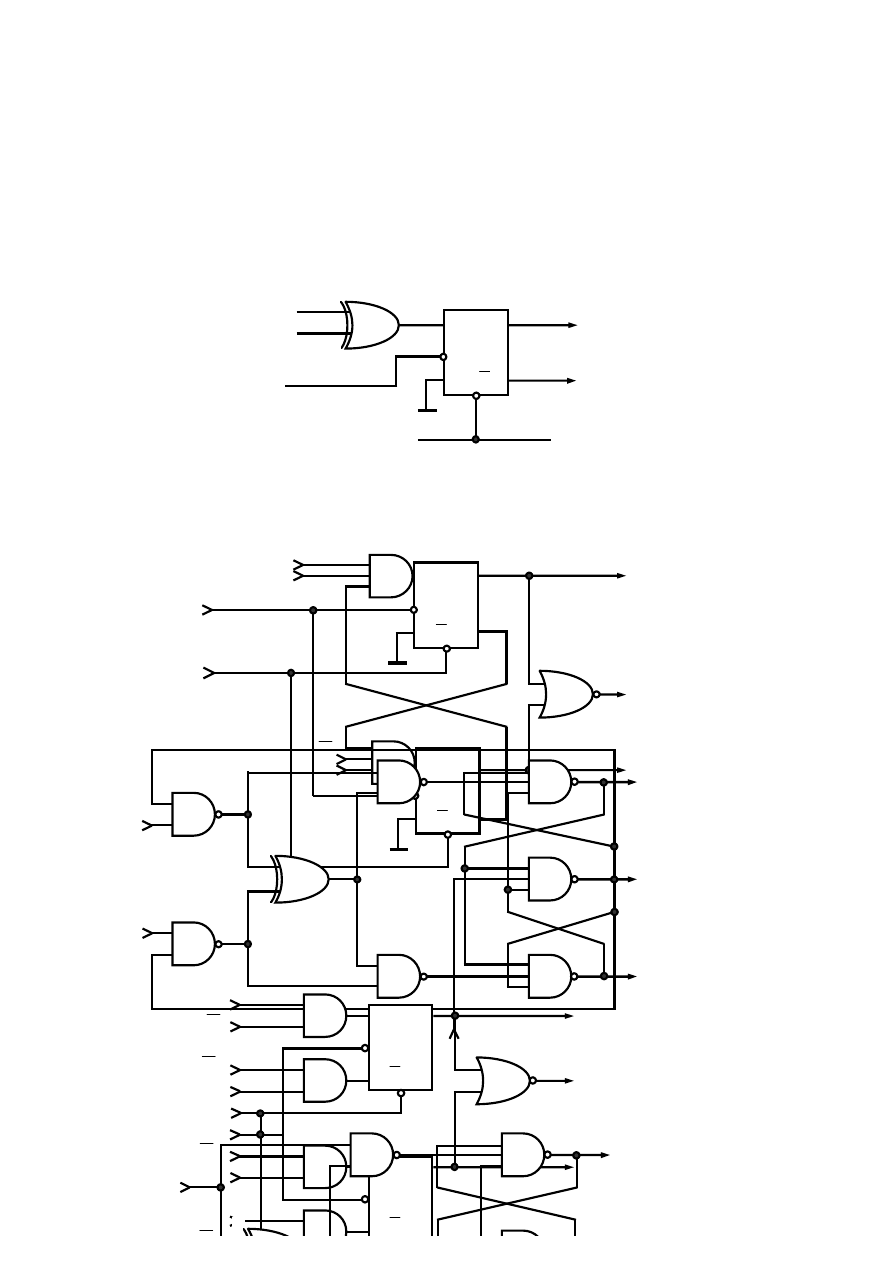
67
8.3.3.
Komparatory szeregowe
Komparator szeregowy to taki układ, w którym porównywane są kolejno bity poszczególnych pozycji porównywanych liczb.
Jeśli dwie liczby dodatnie porównujemy począwszy od najbardziej znaczącego bitu, to liczbą większą jest liczba mająca większy pierwszy
bit. Jeśli porównania dokonujemy począwszy od najmniej znaczącego bitu, to liczbą większą jest liczba mająca większy ostatni bit. Liczby dodatnie
są równe, jeśli bity tych liczb na odpowiadających sobie pozycjach są jednakowe.
Komparatory szeregowe mogą być zrealizowane na wiele sposobów. Wynika to z faktu, że do zaimplementowania układu mogą być użyte
różnego typu elementy logiczne. Na rys. 8.13 jest przedstawiony schemat logiczny komparatora szeregowego służącego do określenia czy zachodzi
relacja A = B, czy A
≠ B.
Układ przed porównaniem powinien być wyzerowany. Po wyzerowaniu stan wyjścia Q przerzutnika jest równy 1. Stan ten zmieni się na 0,
jeśli kolejne bity liczb A i B będą różne. Stan taki utrzymuje się aż do ponownego wyzerowania układu.
Rys.8.13 Schemat logiczny komparatora szeregowego służącego do określania czy między liczbami A i B zachodzi relacja A = B czy A
≠ B ?
Przykłady implementacji komparatorów szeregowych służących do wyznaczania relacji A > B, A = B i A < B między liczbami A i B
przedstawiono na rys. 8.14 i 8.15.
a)
b)
Rys. 8.14 Komparatory szeregowe porównujące liczby poczynając od najbardziej znaczącego bitu: a) zbudowane w oparciu o przerzutnik JK,
b) zbudowane z bramek I – NIE (NAND) oraz bramki ALBO (EX – OR).
a)
b)
J Q
C
K R Q
We
A
B
Zerowanie
A
≠
B
A = B
J Q
C
K Q
We
A
B
Zer
A > B
A = B
J Q
C
K Q
A < B
A
B
A
B
Zer
A = B
A < B
A > B
J Q
C
K Q
J Q
C
K Q
A > B
A = B
A < B
A
B
Zer
We
B
A
A
A
B
B
A
A > B

68
Rys. 8.15 Komparatory szeregowe porównujące liczby poczynając od najmniej znaczącego bitu: a) zbudowane w oparciu o przerzutnik JK,
b) zbudowane z bramek I – NIE (NAND) oraz bramki ALBO (EX – OR).
Porównywanie dokonywane począwszy od najbardziej znaczącego bitu jest pokazane w układach na rys. 8.14. W układach tych wynik
pojawia się na wyjściu natychmiast po stwierdzeniu, że jedna z liczb jest większa, tzn. A
i
≠B
i
.
Na rys. 8.15 są pokazane przykłady implementacji komparatora, w którym porównywanie dokonuje się począwszy od najmniej
znaczącego bitu. W układach tych prawidłowy wynik ustala się na wyjściu komparatora dopiero po podaniu bitów z pozycji najczęściej znaczącej.
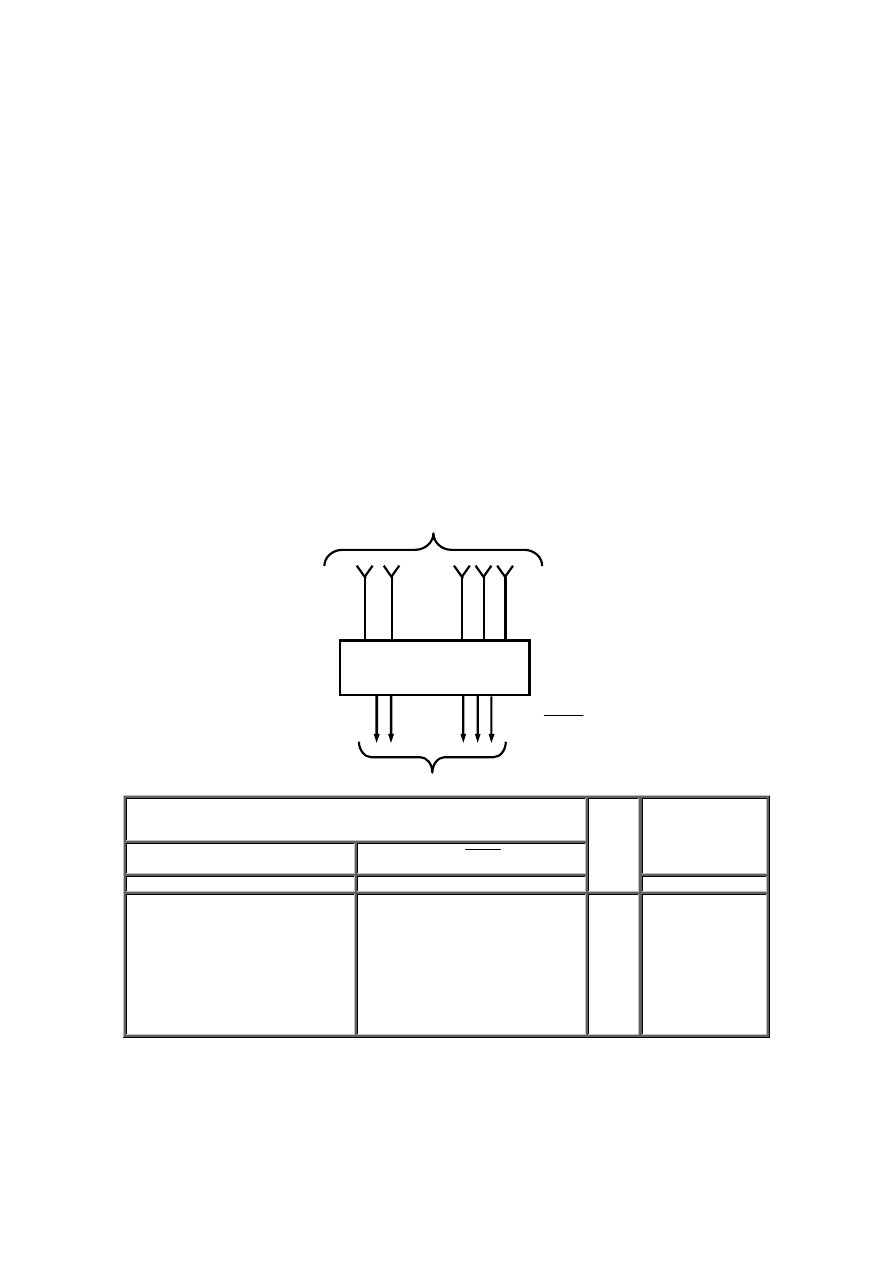
69
9.
UK
ŁADY KOMUTACYJNE
9.1.
WST
ĘP
Układy komutacyjne służą do łączenia ze sobą bloków funkcjonalnych i przełączania sygnałów cyfrowych.
Określony kod stosujemy zależnie od jego zastosowania. Przy wyborze należy brać pod uwagę możliwość osiągnięcia minimum kosztów
układu realizującego daną operację oraz zapewnienie prawidłowości jej realizacji w obecności zakłóceń i uszkodzeń w systemie.
Aby dokonać konwersji danego kodu na inny kod, liczba słów kodowych w obydwu kodach musi być identyczna, natomiast długość słów
obydwu kodów nie musi być jednakowa.
Układy komutacyjne służą do łączenia ze sobą bloków funkcjonalnych i przełączania sygnałów cyfrowych. Do układów komutacyjnych
systemów cyfrowych zaliczamy:
§
konwertery kodów (w tym kodery i dekodery),
§
demultipleksery,
§
multipleksery.
Konwerterem (przetwornikiem) nazywamy układ służący do przekształcenia jednego kodu w inny kod. Przetwornik przekształcający kod
pierścieniowy „1 z n” na żądany kod, nazywa się koderem (zwany też enkoderem), natomiast przetwornik zmieniający dowolny kod w kod „1 z n” –
dekoderem. Pozostałe przetworniki noszą nazwę transkoderów. Szczególnym rodzajem dekoderów są multipleksery i demultipleksery, zwane
wybierakami bezstykowymi.
9.2.
ENKODERY
Enkodery zwykłe są to układy zmieniające kod „1 z n” na określony binarny kod wyjściowy. Układy te posiadają n - wejść, przy czym
tylko jedno z wejść jest w danym czasie aktywne. Jeśli kodem wejściowym jest kod „1 z n” bez negacji, to wejście aktywne znajduje się w stanie 1, a
pozostałe w stanie 0. Natomiast jeśli kodem wejściowym jest kod „1 z n” z negacją, to wejście aktywne znajduje się w stanie 0, a pozostałe w stanie
1.
Sygnał aktywny, pojawiający się na jednym z n wejść, zostaje zakodowany w słowo binarne m – bitowe (m – wyjść enkodera) i na
wyjściach pojawia się numer wyjścia aktywnego, przedstawiony w żądanym kodzie dwójkowym.
Rys. 9.1 Enkoder zwykły.
Przykładem może być zamiana kodu 1 z 10 na kod BCD 8421, oraz zamiana kodu
10
z
1
na kod BCD 8421. Tablica prawdy opisująca
działanie logiczne tych układów jest przedstawiona w tablicy.
Tablica 9.1 Tablica prawdy enkoderów zwykłych
Wejścia
Kod 1 z 10
Kod
10
1z
Wyjścia
9 8 7 6 5 4 3 2 1 0
9 8 7 6 5 4 3 2 1 0
D C B A
0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 0
1 1 1 1 1 1 1 1 0 1
1 1 1 1 1 1 1 0 1 1
1 1 1 1 1 1 0 1 1 1
1 1 1 1 1 0 1 1 1 1
1 1 1 1 0 1 1 1 1 1
1 1 1 0 1 1 1 1 1 1
1 1 0 1 1 1 1 1 1 1
1 0 1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 1 1
0
1
2
3
4
5
6
7
8
9
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
Na podstawie tablicy prawdy możemy wywnioskować, że wyjście A = 1, jeśli wejście 1 jest w stanie 1 lub jeśli wejście 3 jest w stanie 1,
lub jeśli wejście 5 jest w stanie 1, lub jeśli wejście 7 jest w stanie 1, lub wejście 9 jest w stanie 1.
Wobec tego w notacji algebry Boole'a można to za pisać w postaci funkcji:
A = 1+3+5+7+9
Podobnie
B = 2+3+6+7
9.1.
KOD 1
…
…
KOD WYJŚCIOWY
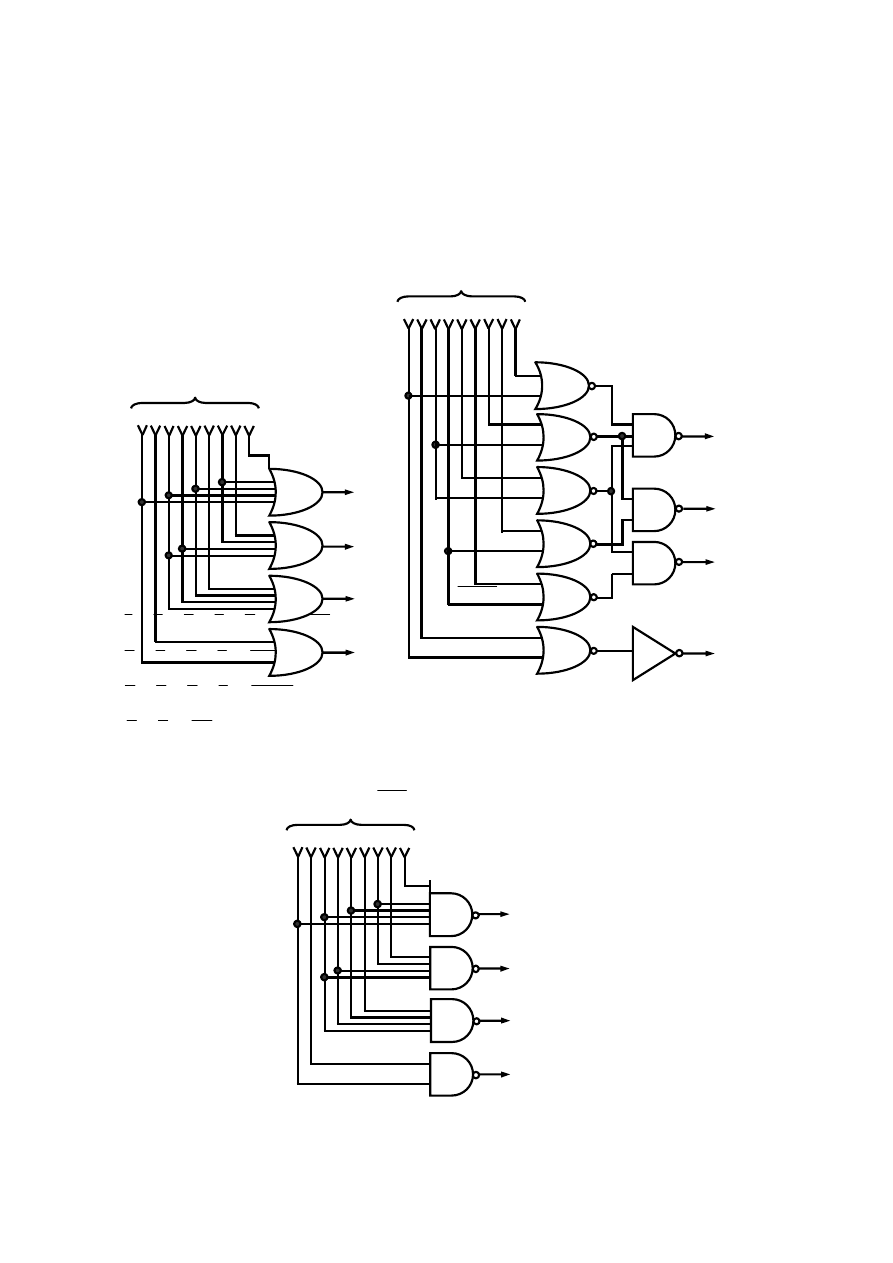
70
C = 4+5+6+7
(1)
D = 8+9
Funkcje (1) mogą być przedstawione w postaci:
A = (1+9)+(3+7)+(5+7)
R = (3+7)+(2+6)
(2)
C = (4+6)+(5+7)
D = 8+9
Implementacje funkcji (1) i (2) przedstawiono na rys. 9.2.
Rys. 9.2 Schematy logiczne enkoderów zwykłych realizujących funkcje:
a) (1), b) (2).
Jeśli żadne z wejść nie będzie aktywne tzn. suwak przełącznika obrotowego znajduje się między kolejnymi pozycjami, to na wyjściach
pojawią się same jedynki, a więc kombinacja nie należąca do rozpatrywanego kodu wejściowego.
Funkcje wyznaczone na podstawie tablicy 9.1 dla układu zmieniającego kod
10
z
1
na kod 8421 mają postać:
89
9
8
D
4567
7
6
5
4
C
2367
7
6
3
2
B
13579
9
7
5
3
1
A
=
+
=
=
+
+
+
=
=
+
+
+
=
=
+
+
+
+
=
(3)
Schemat logiczny układu realizującego funkcje (3) przedstawiono na rys. 9.3.
Rys. 9.3 Schemat logiczny enkodera zwykłego realizującego funkcje (3).
W układzie tym, jeśli żadne wejście nie będzie aktywne (wybrane), to na wyjściach pojawią się same zera, a więc taka sama kombinacja,
jak przy wybranym wejściu o numerze 0, co może być niedozwolone w niektórych zastosowaniach.
Enkodery zwykłe są stosowane głównie do wprowadzania informacji w postaci liczb dziesiętnych, np. z przełączników 10-pozycyjnych
obrotowych lub klawiszowych, do systemów cyfrowych.
9.3.
DEKODERY
Dekodery są to układy kombinacyjne n / m (liczba wejść / liczba wyjść) przekształcające określony kod wejściowy o długości m na kod
wyjściowy „1 z n”.
Dekoder posiada m wyjść, a każdemu ze słów wyjściowych jest przyporządkowany sygnał aktywny (1 lub 0), pojawiający się tylko na
jednym z m wyjść, pozostałe zmienne wyjściowe mają wartość przeciwną.
Rozróżniamy dwa rodzaje dekoderów:
§
pełny, jeśli dla rozpatrywanego dekodera zachodzi równość 2
n
= m,
§
niepełny, jeśli dla rozpatrywanego dekodera zachodzi nierówność 2
n
> m, gdzie nie wszystkie słowa kodowe są wykorzystane.
1
2
3
4
5
6
7
8
9
10.
Kod 1
z 10
A
B
C
D
a)
A
B
C
D
1
2
3
4
5
6
7
8
9
11.
Kod
b)
1
2
3
4
5
6
7
8
9
12.
Kod
10
1z
A
B
C
D
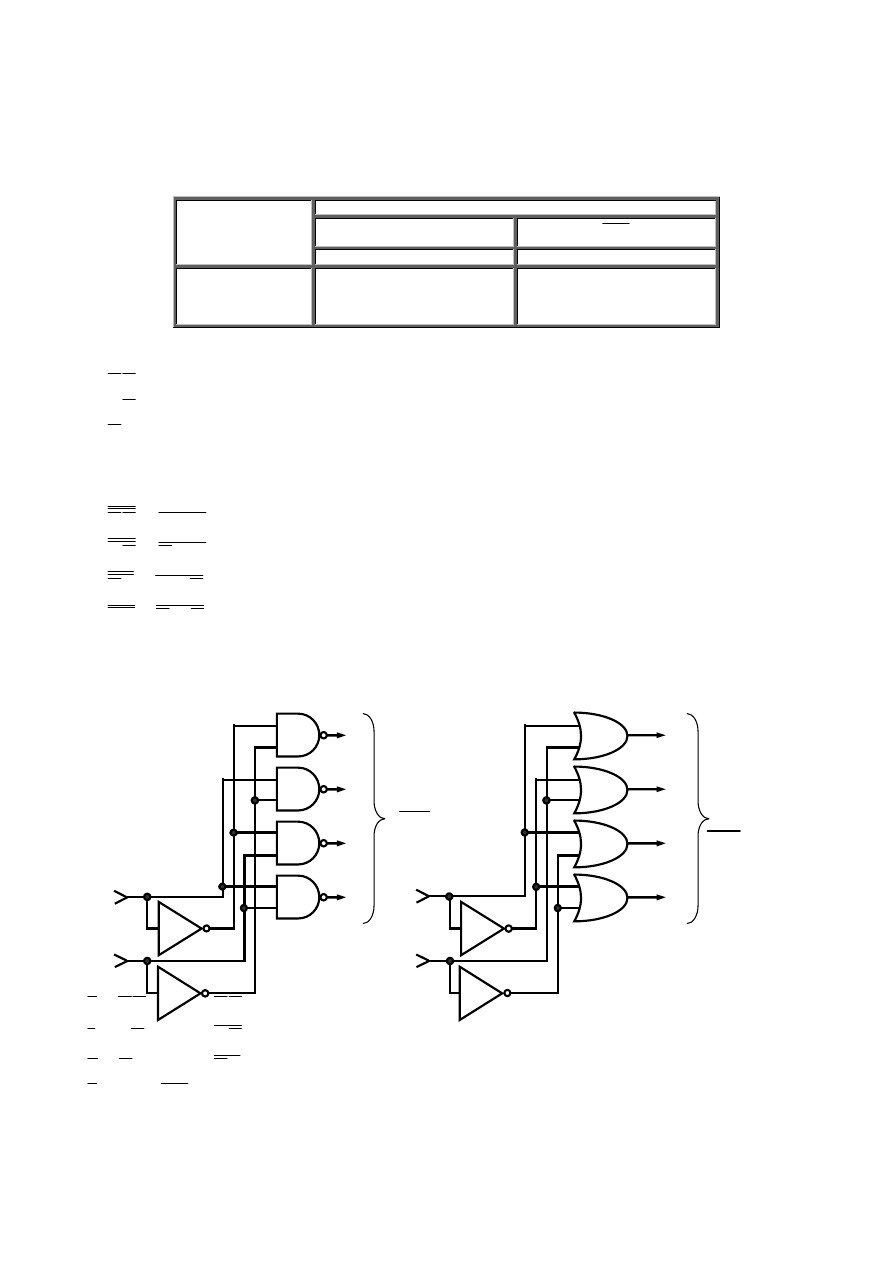
71
Przykładowo rozpatrzmy syntezę dekodera pełnego 2/4, czyli dekodera posiadającego 2 wejścia i 4 wyjścia. Wejścia rozpatrywanego
dekodera oznaczono literami: A, B a wyjścia liczbami: 0, 1, 2, 3.
Kod wejściowy i kod wyjściowy dekodera przedstawiono w tablicy 9.2.
Tablica 9.2 Tablica prawdy dekodera pełnego 2/4
Wyjścia
1 z 4
4
1z
Wejścia
B A
0 1 2 3
0 1 2 3
0 0
0 1
1 0
1 1
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
0 1 1 1
1 0 1 1
1 1 0 1
1 1 1 0
Gdy kodem wyjściowym dekodera jest kod 1 z 4 bez negacji, to dekoder jest układem realizującym następujące funkcje przełączające:
0 =
B
A
1 =
B
A
(1)
2 =
B
A
3 = AB
albo
0 =
B
A
B
A
+
=
1 =
B
A
B
A
+
=
(2)
2 =
B
A
B
A
+
=
3 =
B
A
AB
+
=
Schematy logiczne układów realizujących funkcje (1) oraz funkcje (2) przedstawiono na rys. 9.4.
Rys. 9.4. Schematy logiczne układów realizujących funkcje:
a) (1), b) (2).
Jeśli kodem wyjściowym rozpatrywanego dekodera jest kod
4
z
1
to dekoder jest układem, którego działanie logiczne opisują
następujące funkcje przełączające:
B
A
0
=
;
0 =
B
A
B
A
1
=
;
1 =
B
A
(3)
B
A
2
=
;
2 =
B
A
=
3
AB; 3 =
AB
albo
0
1
2
3
4
1z
0
1
2
3
4
1z
A
A
B
B
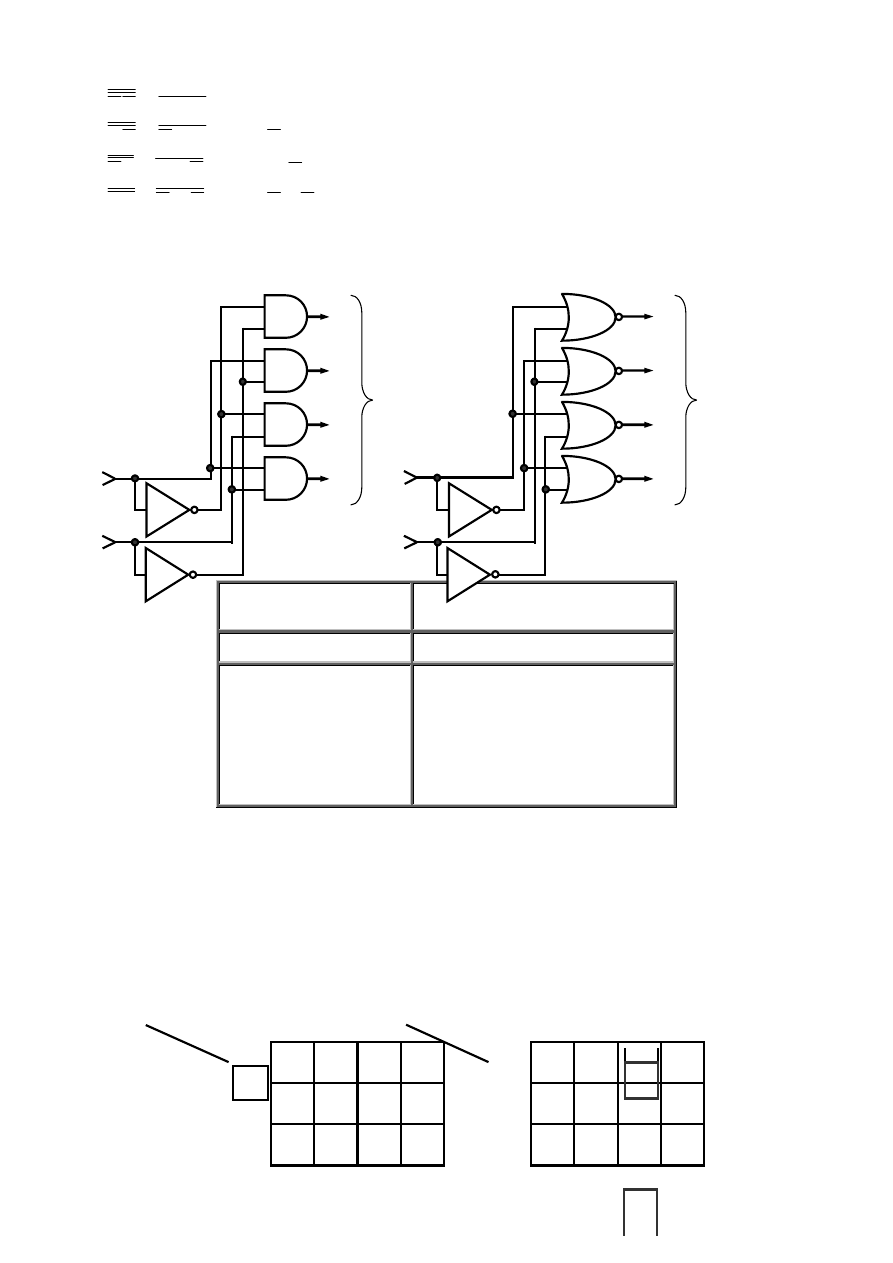
72
0 =
B
A
B
A
+
=
;
0 = A + B
1 =
B
A
B
A
+
=
;
1 =
A
+ B
(4)
2 =
B
A
B
A
+
=
;
2 = A +
B
3 =
B
A
AB
+
=
;
3 =
A
+
B
Implementacje układów realizujących funkcje (3) oraz funkcje (4) przedstawiono na rys. 9.5.
Rys. 9.5 Schematy logiczne układów realizujących funkcje: a) (3), b) (4).
W przypadku dekodera niepełnego (tzn. 2
n
> m) przykładem może służyć dekoder służący do konwersji naturalnego 4-bitowego kodu
dwójkowego na kod 1 z l0 (2
4
> l0) – tablica 9.3.
Tablica 9.3 Tablica prawdy dekodera niepełnego
Wejścia
Wyjścia
8421 BCD
D C B A
1 z 10
0 1 2 3 4 5 6 7 8 9
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0 1
W dekoderze niepełnym nie wszystkie słowa kodowe są wykorzystane. Nasuwa się pytanie: jak układ ma działać jeśli na jego wejścia
zostaną podane kombinacje nie wykorzystane?
Jeśli wiemy, że na wejścia dekodera nie pojawią się kombinacje nie wykorzystywane, to można dopuścić, by stany wyjściowe dekodera
były dla nich dowolne (zależne tylko od stopnia uproszczenia układu). Są to tzw. „stany fałszywe”, które są omówione w rozdziale 3.
Na podstawie tablicy wypiszmy tablicę Karnaugha dla funkcji 0.
W tablicy tej określone jest tylko dziesięć stanów spośród szesnastu możliwych. Na podstawie tablicy możemy stwierdzić, że w przypadku
funkcji 0, nadmiarowe stany (stany nieustalone) nie mogą być wykorzystane do jej uproszczenia. To samo spostrzeżenie dotyczy funkcji 1. Dopiero
dla funkcji 2 „stany fałszywe” mogą wykorzystane, a funkcja 2 może być uproszczona (rys. 9.6):
a)
b)
00
01
11
10
00
01
11
10
00
1
0
0
0
00
0
0
0
1
01
0
0
0
0
01
0
0
0
0
11
X
X
X
X
11
X
X
X
X
0
1
2
3
1z4
0
1
2
3
1z4
A
A
B
B
BA
BA
DC
DC
0
2
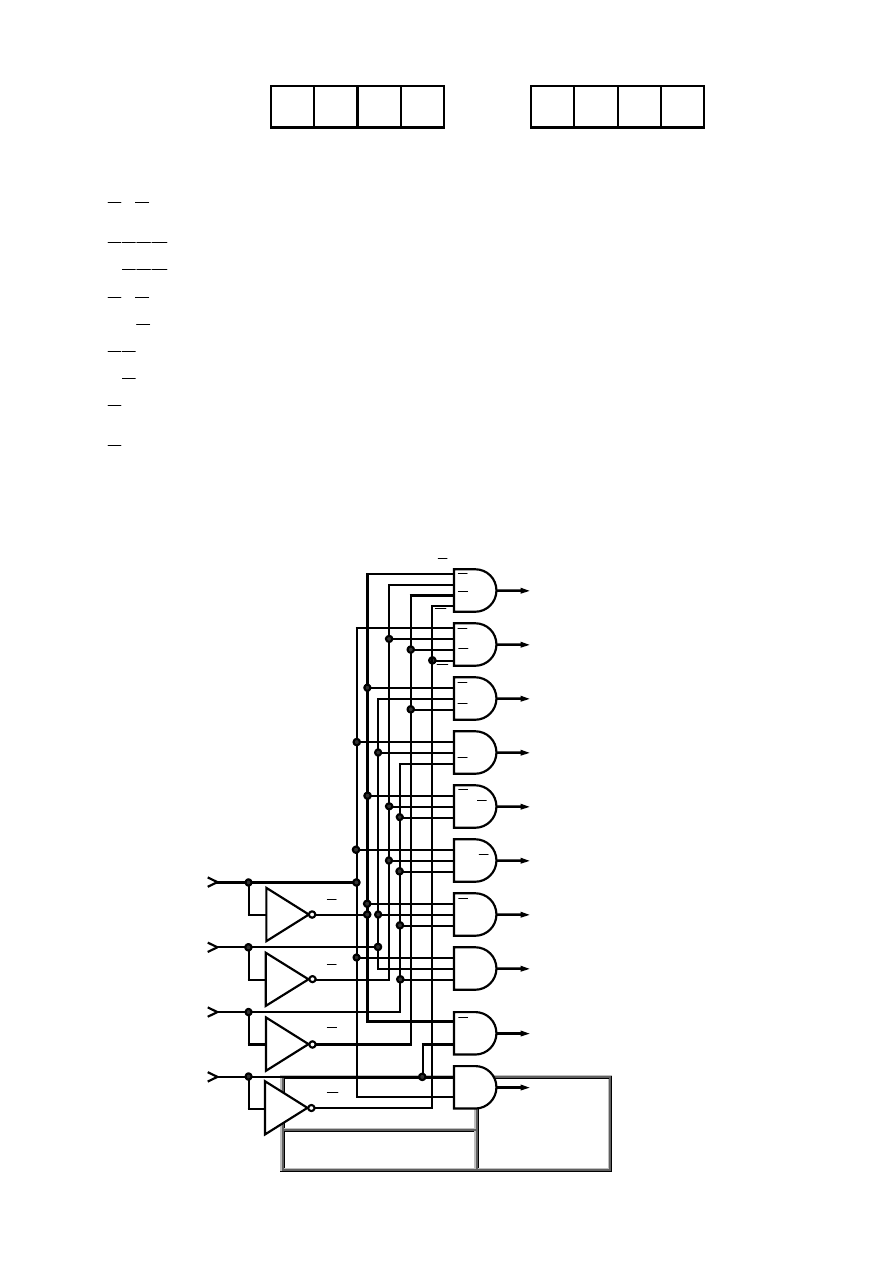
73
10
0
0
X
X
10
0
0
X
X
Rys. 9.6 Tablice Karnaugha dla funkcji zrealizowanych przez dekoder
8421 BCD
→ 1 z 10:a) dla funkcji (4). b) dla funkcji (2).
Funkcja 2;
2 =
C
B
A
Uproszczone funkcje, wyznaczone na podstawie tablic Karnaugha mają postać:
0 =
D
C
B
A
1 =
D
C
B
A
2 =
C
B
A
3 =
C
AB
4 =
C
B
A
5 =
C
B
A
6 =
BC
A
7 = ABC
8 =
D
A
9 = AD
Przedstawione wyrażenia mogą być zaimplementowane jak pokazano to na rys. 9.7. Dekoder taki posiada zamiast dziesięciu 4-
wejściowych funktorów I (AND) tylko dwa takie funktory, pozostałe funktory mają po trzy lub dwa wejścia.
a)
b)
Kod wejściowy
D C B A
8 4 2 1
Nr wyjścia
wyróżnionego
0
1
2
3
4
5
6
7
8
9
B
C
C
A
B
C
C
B
B
A
A
A
A
A
B
C
D
D
D
A
A
A
A
A
A
B
B
B
B
B
B
C
C
C
C
C
D
D
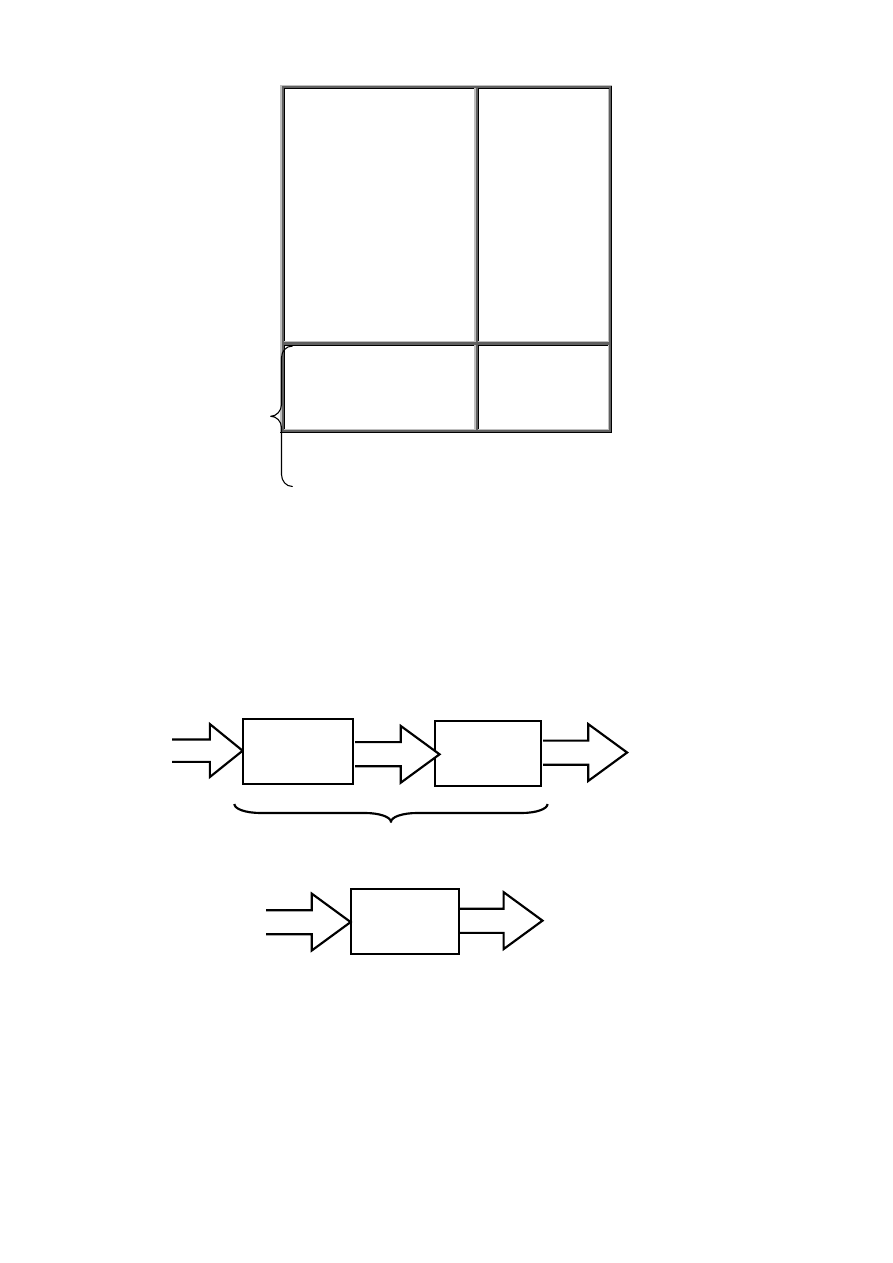
74
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
0
1
2
3
4
5
6
7
8
9
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
2
3
4,8
5,9
6,8
7,9
Rys. 9.7 Schemat logiczny dekodera 8421 BCD
→ 1 z 10 (a) oraz tablica ilustrująca działanie (b).
Gdy zmienna wyjściowa ma przyjmować poziom aktywny (niski lub wysoki) tylko dla zdefiniowanych kombinacji wartości zmiennych
wejściowych, dekoder odrzuca stany nieustalone. Jeśli dekoder ma odrzucać „stany fałszywe”, to uproszczenie układu jest niemożliwe.
9.4.
TRANSKODERY
Transkodery są to układy służące do konwersji kodu dwójkowego, innego niż kod pierścieniowy (1 z n), na inny kod dwójkowy, ale
również nie pierścieniowy. Przykładem transkodera jest konwerter kodu wskaźnika siedmiosegmentowego na kod 8421 BCD. Transkodery są często
zaliczane do grupy dekoderów.
Transkodery można zrealizować w postaci układu (rys. 9.8a), złożonego z dekodera (zmieniającego kod wejściowy X na kod
pierścieniowy) i enkodera (zmieniającego kod pierścieniowy uzyskany na wyjściach dekodera na żądany kod wyjściowy Y).
Takie rozwiązanie jest korzystne wtedy, gdy zarówno wymagany dekoder jak i enkoder, albo przynajmniej jeden z nich, są dostępne w
postaci scalonej.
Rys. 9.8 Schematy ideowe transkoderów:
a)
zbudowanych z enkodera i dekodera,
b)
zbudowanych w postaci kombinacyjnego układu wielowyjściowego.
Jeśli zarówno dekoder jak i enkoder nie są dostępne w postaci układów scalonych, to lepsze rozwiązanie można uzyskać w wyniku syntezy
transkodera jako wielowyjściowego układu kombinacyjnego (rys. 9.8b).
9.4.1.
Przyk
łady syntezy i rozwiązań transkoderów
Przykład 9.1:
Zaprojektować transkoder służący do przetwarzania kodu 8421 BCD na kod 2*421 BCD.
W celu zaprojektowania transkodera: 8421 BCD na kod 2*421 BCD należy przedstawić rozpatrywane kody w tablicy (rys. 9.9a). Tablica
kodów stanowi tablicę wartości rozpatrywanego układu kombinacyjnego. Jest to układ 4 - wyjściowy. Kolumny wejścia A i D (patrz tablica kodów)
są tożsame z kolumnami wyjściowymi A' i D', a zatem:
A' = A
D' = D
W celu wyznaczenia funkcji B' i C' należy zastosować metody minimalizacji, np. za pomocą tablic Karnaugha (rys. 9.9b), lub dostrzec
związki logiczne, jakie otrzymuje się z tych tablic, czyli:
B' = B+D
C' = C+D
Schemat logiczny układu realizującego powyższe funkcje przełączające pokazano na rys. 9.9c.
a)
S
ta
n
y
z
ab
ro
n
io
n
e
Kod
wejściowy X
Enkoder
Dekoder
Kod
pierścieniowy
Kod
wyjściowy X
Transkoder
Kod
wejściowy X
Kod
wyjściowy X
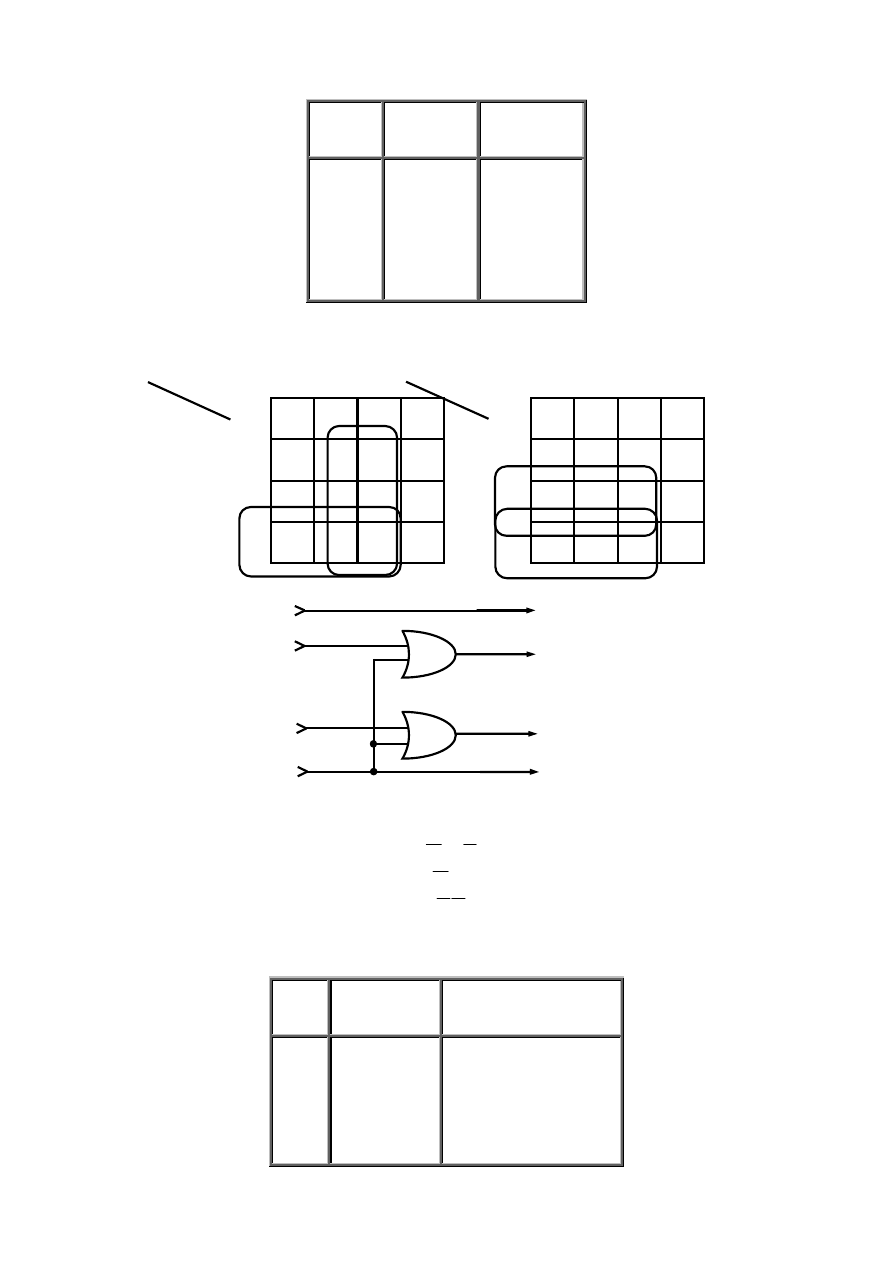
75
D
C
B
A
D’
C'
B'
A'
8
4
2
1
2*
4
2
1
0
1
2
3
4
5
6
7
8
9
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 1 1 0
1 1 1 1
b)
00
01
11
10
00
01
11
10
00
0
0
1
1
00
0
0
0
1
01
0
0
1
1
01
1
1
1
1
11
X
X
X
X
11
X
X
X
X
10
1
1
X
X
10
1
1
X
X
Rys. 9.9 Transkoder służący do konwersji kodu 8421 BCD na kod 2*421 BCD:
a)
tablica rozpatrywanych kodów,
b)
tablice Karnaugha,
c)
schemat logiczny.
Przykład 9.2:
Zaprojektować transkoder przetwarzający 4 - bitowy naturalny kod dwójkowy na kod 8421 BCD.
Transkoder taki jest układem realizującym następujące funkcje przełączające otrzymane na podstawie tablicy kodów (rys. 9.10a) i tablic
Karnaugha (rys. 9.10b):
A' = A
B' =
CD
B
D
B
+
C' =
BC
D
C
+
D' =
D
C
B
A'' = BD + CD
Schemat logiczny układu realizującego powyższe funkcje przełączające przedstawiono na rys. 9.10c.
a)
D C B A
8 4 2 1
A’’
D' C' B' A'
2* 4 2 1
0
1
2
3
4
5
6
7
8
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
0
0
0
0
0
0
0
0
0
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
BA
BA
DC
DC
B’
C’
A
B
C
D
A’
B’
C’
D’
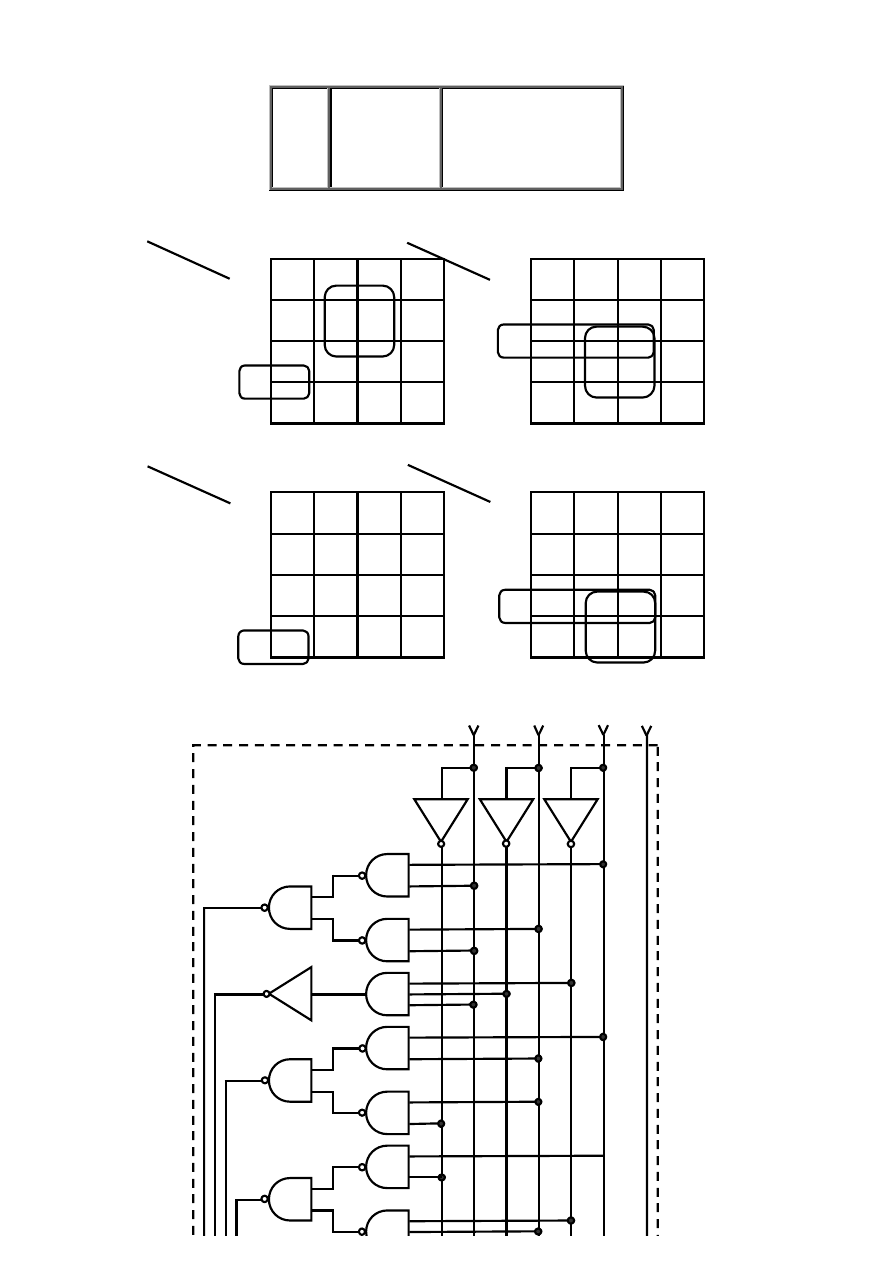
76
9
10
11
12
13
14
15
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
0
1
1
1
1
1
1
1 0 0 1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
b)
00
01
11
10
00
01
11
10
00
0
0
1
1
00
0
0
0
0
01
0
0
1
1
01
1
1
1
1
11
1
1
0
0
11
0
0
1
1
10
0
0
0
0
10
0
0
0
0
00
01
11
10
00
01
11
10
00
0
0
0
0
00
0
0
0
0
01
0
0
0
0
01
0
0
0
0
11
0
0
0
0
11
1
1
1
1
10
1
1
0
0
10
0
0
1
1
c)
Rys. 9.10 Transkoder służący do konwersji 4 - bitowego naturalnego kodu dwójkowego na kod 8421 BCD: a) tablica rozpatrywanych kodów,
b) tablice Karnaugha, c) schemat logiczny.
Przykład 9.3:
Zaprojektować transkoder przetwarzający kod 8421 BCD na kod wskaźnika siedmiosegmentowego.
Taki transkoder posiada siedem wyjść służących do sterowania siedmioma segmentami wskaźnika (rys.9.11a). Użycie siedmiu
segmentów, z których każdy może przyjmować dwa stany: "włączony" albo "wyłączony", umożliwia wyświetlenie 2
7
= 128 znaków. Dziesięć z nich
BA
DC
BA
DC
B’
C’
BA
DC
BA
DC
D’
A’
A
B
C
D
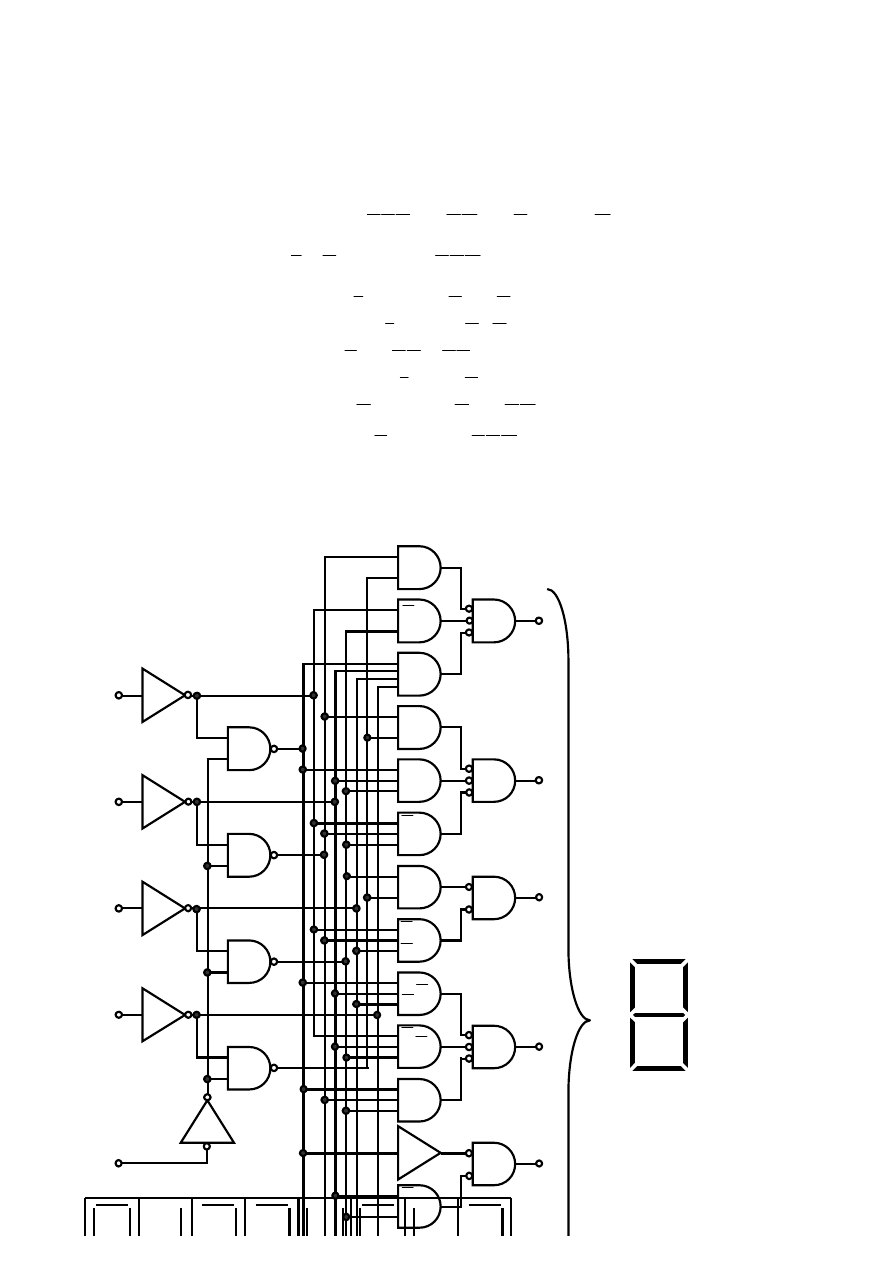
77
a
jest użytych do przedstawienia dziesięciu cyfr (rys. 9.11b). Rozpatrywany transkoder ma 4 wejścia, a więc liczba możliwych stanów wejściowych
wynosi 16. Spośród 118 pozostałych znaków można dodatkowo wybrać 16 - 10 = 6 znaków, np. takich, jakie pokazano na rys. 9.11b. Tablica prawdy
takiego transkodera przedstawia się tak, jak pokazano na rys. 9.11c.
Z tablicy prawdy można wyznaczyć funkcje logiczne dla siedmiu wyjść: a, b, c, d, e, f, g. W tym celu należy wypisać stany wejściowe, dla
których rozpatrywane wyjście przyjmuje stan 1, tzn. rozpatrywany segment jest włączony.
Jako przykład rozważymy funkcję dla segmentu a. Z tablicy prawdy wynika, że jest on włączony, gdy wyświetlany jest: znak o numerze 0,
lub znak o numerze 2, lub znak o numerze 3, lub znak o numerze 5, lub znak o numerze 7, lub znak o numerze 8, lub znak o numerze 9, lub znak o
numerze 13.
Korzystając z tablicy Karnaugha dla funkcji a (rys. 9.11d) trzymamy następujące wyrażenie:
D
AC
D
B
A
D
C
B
C
B
A
a
+
+
+
=
Jeśli zamiast funkcji a zminimalizowanej po jedynkach wykorzystamy funkcję a zminimalizowaną po zerach, to otrzymamy wyrażenie:
D
C
B
A
BD
C
A
a
+
+
=
prostsze do zaimplementowania.
Wykorzystując tablice Karnaugha możemy określić wyrażenia logiczne: b, c, d, e, f, g, które są następujące:
BC
A
C
B
A
BD
b
+
+
=
C
B
A
CD
c
+
=
ABC
C
B
A
C
B
A
d
+
+
=
C
B
A
e
+
=
D
C
A
C
B
AB
f
+
+
=
D
C
B
ABC
g
+
=
Transkoderem działającym zgodnie z tablicą (rys. 9.11c) jest transkoder scalony 49. Schemat logiczny tego układu przedstawiono na rys.
9.11e.
e)
a)
b)
d)
0 1 2 3 4 5 6 7
a
b
c
d
f
e
g
C
12.1.
13.
D
A
14.
15.
16.
17.
18.
19.
20.
D
21.
C
A
C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
B
a
b
c
d
e
A
B
C
D
BI
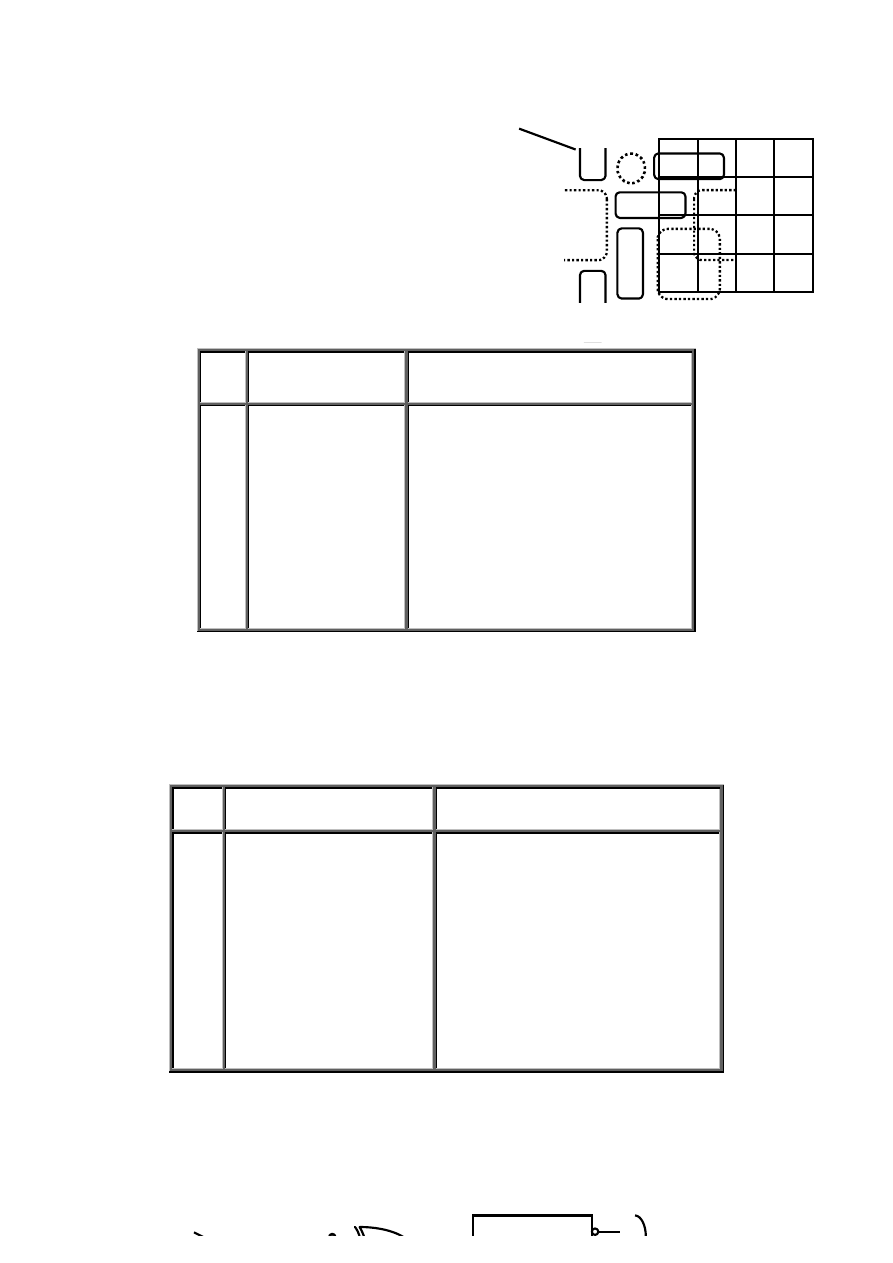
78
00
01
11
10
00
1
0
1
1
01
0
1
1
0
11
0
1
0
0
10
1
1
0
0
c)
D
C
B
A
a
b
c
d
e
f
g
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
1
0
1
1
0
1
0
1
1
1
0
0
0
1
0
0
1
1
1
1
1
0
0
1
1
1
0
0
1
0
0
0
1
1
0
1
1
1
1
1
1
1
0
1
0
0
0
0
1
0
1
1
0
1
1
0
1
0
1
1
0
1
1
0
1
0
1
0
0
0
1
0
1
0
1
0
0
0
1
0
1
0
0
0
1
1
1
0
1
1
0
0
1
1
1
0
0
0
1
1
1
1
1
0
1
1
1
1
1
1
1
0
Rys. 9.11 Transkoder przetwarzający kod 8421 BCD na kod wskaźnika 7 - segmentowego:
a)
oznakowanie segmentów wskaźnika,
b)
przedstawienie cyfr i znaków dodatkowych,
c)
tablica prawdy,
d)
tablice Karnaugha dla funkcji a,
e)
schemat logiczny transkodera scalonego 49.
Działanie logiczne układu 49 przedstawiono w tablicy 9.4.
Tablica 9.4 Tablica prawdy transkodera scalonego 49
D
C
B
A
BI
a
b
c
d
e
f
g
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
BI
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
X
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
X
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
X
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
X
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
0
1
1
0
1
0
1
1
1
0
0
0
1
0
0
0
1
1
1
1
1
0
0
1
1
1
0
0
1
0
0
0
0
1
1
0
1
1
1
1
1
1
1
0
1
0
0
0
0
0
1
0
1
1
0
1
1
0
1
0
1
1
0
1
1
0
0
1
0
1
0
0
0
1
0
1
0
1
0
0
0
1
0
0
1
0
0
0
1
1
1
0
1
1
0
0
1
1
1
0
0
0
0
1
1
1
1
1
0
1
1
1
1
1
1
1
0
0
Przykład 9.4:
Zaprojektować układ służący do przetwarzania kodu wskaźnika 7 - segmentowego na kod 8421 BCD.
Transkoder taki może być zrealizowany m. in. W postaci układu złożonego z układu do przetwarzania kodu wskaźnika 7 - segmentowego
na kod 1 z 10 (rys. 9.12) oraz z układu zmieniającego kod 1 z 10 na kod BCD, dostępnego w postaci układu scalonego 147.
0
0
a
DC
BA
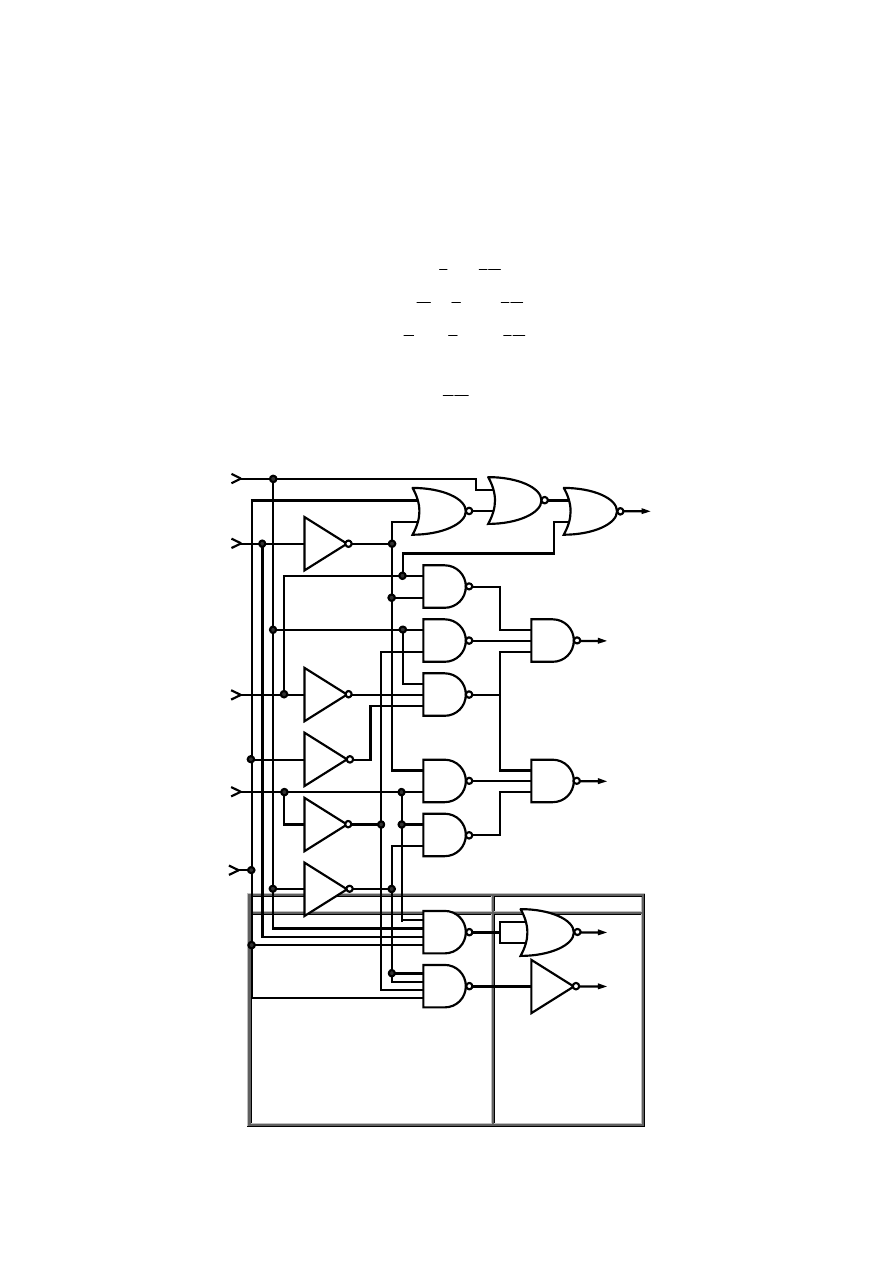
79
Rys. 9.12 Schemat logiczny transkodera przetwarzającego kod wskaźnika 7 - segmentowego na kod 1 z 10.
Znane są również rozwiązania rozpatrywanego układu w postaci układu kombinacyjnego służącego do bezpośredniego przetwarzania
kodu wskaźnika 7-segmentowego (rys. 9.13a) na kod 8421 BCD.
Transkoder taki realizuje następujące funkcje przełączające:
g
e
b
e
a
A
+
=
g
e
a
e
b
f
a
B
+
+
=
g
e
a
f
b
f
a
C
+
+
=
abfg
D
=
„ - „=
g
f
a
Schemat logiczny takiego układu przedstawiono na rys. 9.13a.
a)
b)
a b c d e f g
„-„
D C B A
0
1
2
3
4
5
6
6
7
7
8
9
9
Wygaszenie
„ - „
1 1 1 1 1 1 0
0 1 1 0 0 0 0
1 1 0 1 1 0 1
1 1 1 1 0 0 1
0 1 1 0 0 1 1
1 0 1 1 0 1 1
0 0 1 1 1 1 1
1 0 1 1 1 1 1
1 1 1 0 0 0 0
1 1 1 0 0 1 0
1 1 1 1 1 1 1
1 1 1 0 0 1 1
1 1 1 1 0 1 1
0 0 0 0 0 0 0
0 0 0 0 0 0 1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 0
0 1 1 1
0 1 1 1
1 0 0 0
1 0 0 1
1 0 0 1
0 0 0 0
0 0 0 0
Rys. 9.13 Transkoder przetwarzający kod wskaźnika 7 - segmentowego na kod 8421 BCD: a) schemat logiczny,
b) tablica prawdy.
A
B
C
D
–
a
b
e
f
g
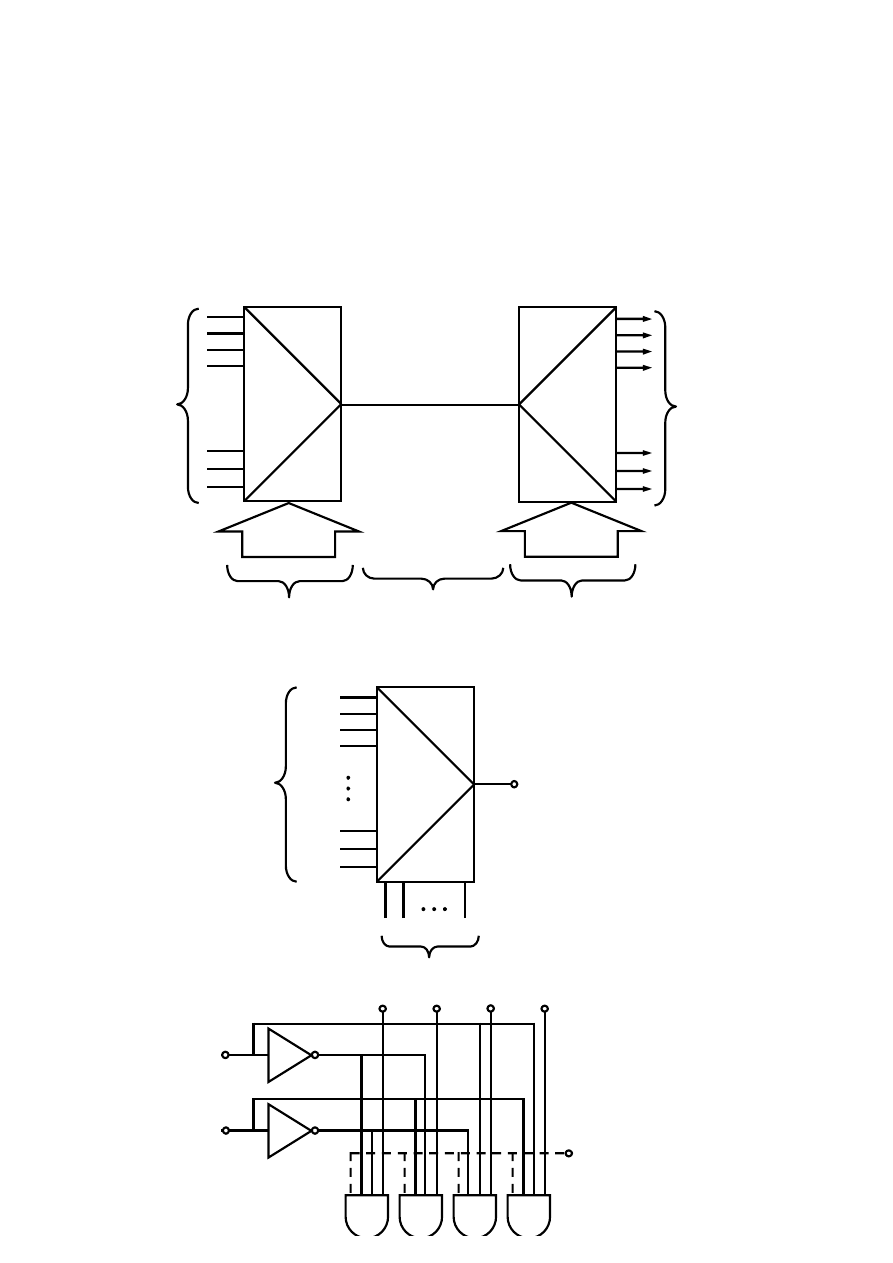
80
9.5.
MULTIPLEKSERY I DEMULTIPLEKSERY
9.5.1.
Wst
ęp
W systemach cyfrowych często istnieje potrzeba przesyłania selektywnie wybranej informacji dwójkowej. Do tego celu służy technika
multipleksowa. Podstawowymi układami są multipleksery i demultipleksery, które umożliwiają zrealizowanie multipleksowego systemu transmisji
informacji (rys. 9.14).
Do zrealizowania takiego systemu jest niezbędny po stronie nadawczej przetwornik formatu słów z równoległego na szeregowy
(multiplekser), a po stronie odbiorczej przetwornik formatu słów z szeregowego na równoległy (demultiplekser). Układy tych przetworników
funkcjonalnie odpowiadają wielopozycyjnym jednobiegunowym przełącznikom z kodowym wyborem pozycji za pomocą dekodera adresu.
Multiplekser przekazuje sygnał cyfrowy z jednego z wejść na pojedyncze wyjście, tzw. linię przesyłową, natomiast demultiplekser
przenosi sygnał cyfrowy z pojedynczego wejścia na jedno z wielu wyjść. Adresy wejść i wyjść multipleksera i demultipleksera muszą być zgodne.
Nazwa obydwu elementów pochodzi od łacińskiego „multiplex” oznaczającego „wiele razy”.
Rys. 9.14 Schemat ideowy multipleksowego systemu transmisji informacji.
W celu zrealizowania transmisji informacji bez zmiany jej postaci, przetworniki powinny być wyposażone w takie same dekodery adresu.
Zazwyczaj jest stosowane adresowanie w naturalnym kodzie dwójkowym.
9.5.2.
Multipleksery
Multiplekser zwany również selektorem, jest układem cyfrowym o M wejściach adresowych i N wejściach informacyjnych oraz o jednym
wyjściu Y tj. linię przesyłową (rys. 9.15). Istnieje zależność N = 2
M
, co oznacza, że zamiast N linii przesyłowych potrzebnych jest tylko M łączy
adresowych i jedno łącze informacyjne.
Rys. 9.15 Multiplekser - symbol ogólny.
Multiplekser umożliwia wybór i przesłanie na wyjście Y sygnału z jednego z N wejść informacyjnych. Numer wejścia (k) jest wyznaczony
przez stan wejść adresowych czyli adres. Realizuje on funkcję wielopołożeniowego przełącznika z cyfrowym wyborem pozycji.
Na jego wejścia adresowe podaje się binarnie zakodowany numer wejścia, z którego informacja (albo jego negacja) ma być przeniesiona
na wyjście układu.
Zasadę działania multipleksera pokazano za pomocą przykładowego schematu multipleksera jednobitowego służącego do komutacji
czterech sygnałów (rys. 9.16a). Zasadę działania ilustruje tablica na rys. 9.16b.
a)
Multiplekser
22.
W
e
23.
A
d
Wy
Demultiplekser
24.
A
d
Linia
przesyłowa
0
1
2
3
2
M
– 1
A B
Wyjście
25.
Y
2
M
w
e
jś
ć
in
fo
r
m
a
c
y
jn
y
c
h
M wejść adresowych
X
0
X
1
X
2
X
3
S
A
1
A
0
Wejście
adresowe
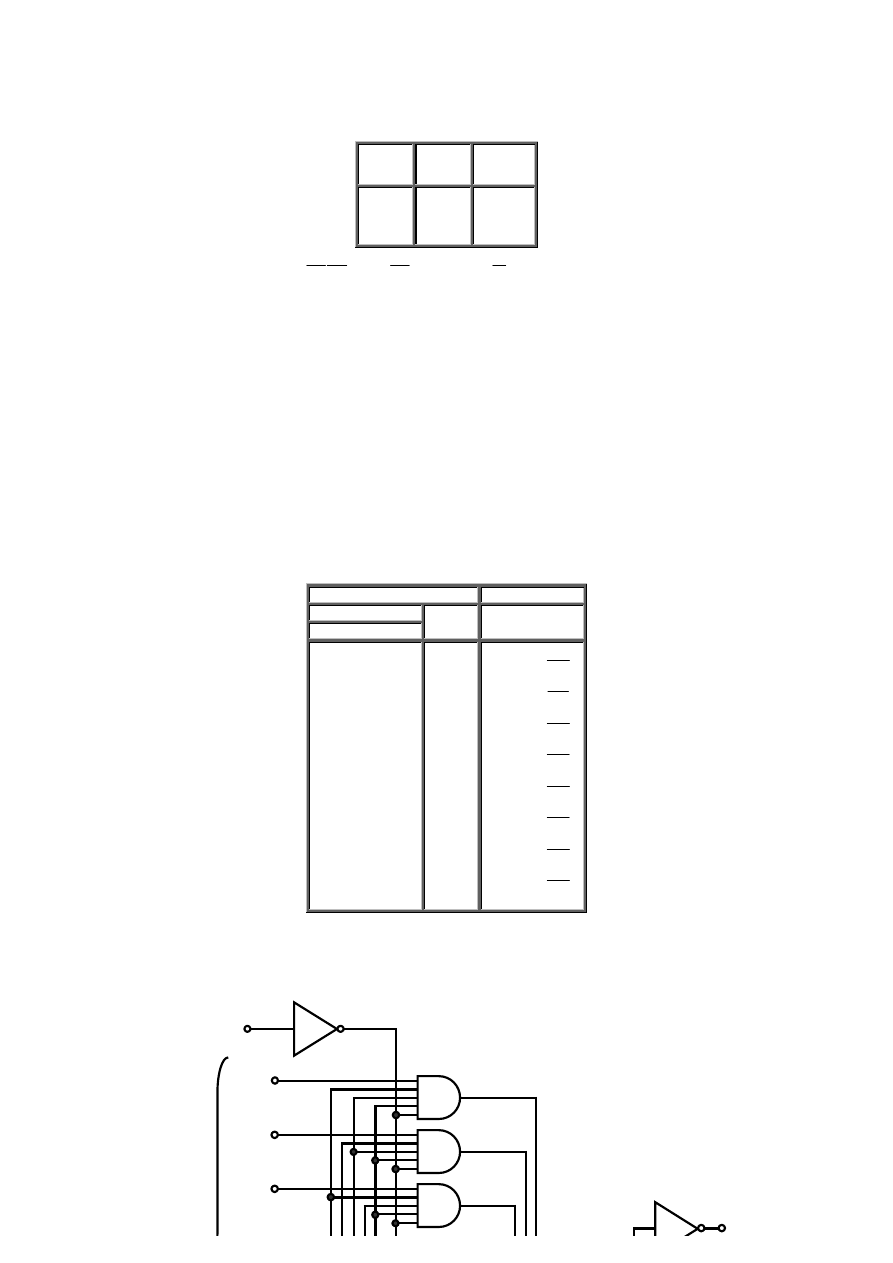
81
b)
A
1
A
0
Y
0
0
1
1
0
1
0
1
X
0
X
1
X
2
X
3
3
0
1
2
0
1
1
0
1
1
0
1
X
A
A
X
A
A
X
A
A
X
A
A
Y
+
+
+
=
Rys. 9.16 Multiplekser: a) schemat logiczny,
b) tablica ilustrująca działanie.
Dwubitowy adres służy do wybrania jednego z czterech sygnałów wejściowych X. Linią kreskową zaznaczono możliwość uwzględnienia
dodatkowego sygnału strobującego, które umożliwia funkcję blokowania lub zezwolenia.
Multipleksery również są wykonane w postaci układów scalonych. Mogą mieć one dodatkowe wejścia lub wyjścia. Wejścia te służą służąc
do łączenia scalonych układów w celu uzyskania większej liczby wyjść. Dodatkowe wyjście natomiast może służyć do podawania zanegowanej
informacji wyjściowej.
Inne multipleksery różnią się od opisanego wyżej głównie liczbą wejść. Układ 151 jest multiplekserem mającym:
§
8 wejść informacyjnych,
§
3 wejścia adresowych,
§
wejście strobujące S (próbkujące)
§
wyjście komplementarne (pozycyjne lub negacyjne).
Układ ten pokazano na rysunku 9.17a, a działanie logiczne przedstawia tablica (rys. 9.17b).
Na wyjściu Y pojawi się poziom wysoki (logicznie 1) wówczas, gdy wejście informacyjne, wybrane odpowiednią kombinacją stanów
wejść adresowych, jest w stanie wysokim (1), a wejście próbkujące w stanie niskim (0), czyli zezwolenia.
b)
Wejścia
Wyjścia
Adresowe
C
B
A
Strob
S
Y
W
X
X
X
1
0
1
0
0
0
0
0
D
0
D
0
0
1
0
1
D
1
D
0
1
0
0
2
D
2
D
0
1
1
0
3
D
3
D
1
0
0
0
4
D
4
D
1
0
1
0
5
D
5
D
1
1
0
0
6
D
6
D
1
1
1
0
7
D
7
D
a)
D
0
D
1
D
2
D
śc
ia
i
n
fo
rm
ac
y
jn
e
Wejście
strobujące
S
Y
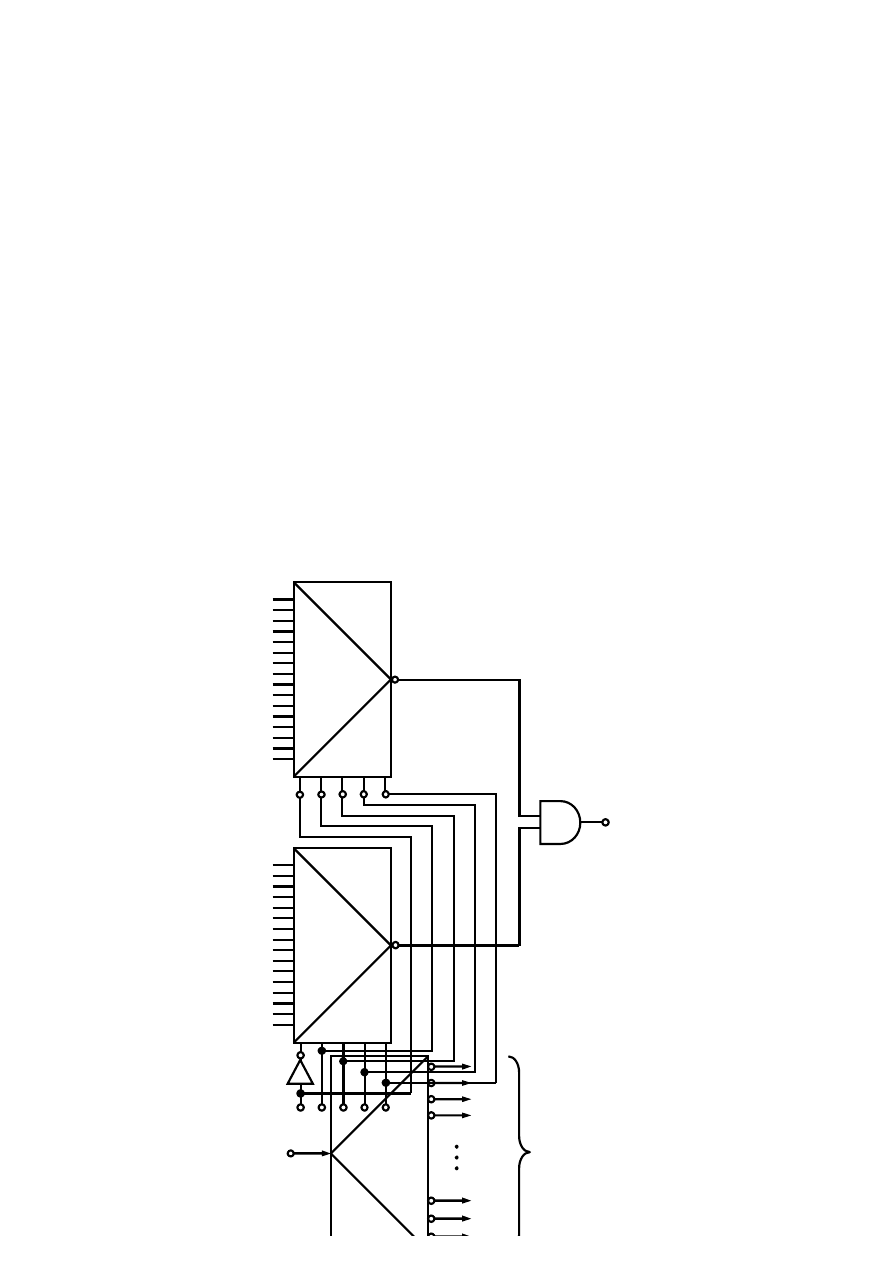
82
Rys. 9.17 Multiplekser scalony 151:
a)
schemat logiczny, b) tablica ilustrująca działanie.
Wejście strobujące można wykorzystać do łączenia dwu multiplekserów. Powstanie wówczas układ o 32 wejściach informacyjnych (rys
9.18). Dodatkowym wejściem adresowym jest wejście strobujące.
W celu otrzymania 32-wejściowego multipleksem należy:
§
połączyć odpowiadające sobie wejścia adresowe;
§
wejście strobujące S multipleksera, mającego odpowiadać za wejścia adresowe o niższych numerach, przyłączyć do dodatkowego wejścia E;
§
wejście strobujące S multipleksera, mającego odpowiadać za wejścia adresowe wyższych numerach, przyłączyć do dodatkowego wejścia E
przez negator;
§
wyjścia połączyć przez bramkę AND, jeżeli dane są zanegowane, lub przez bramkę NAND, jeżeli dane są nienegowane.
Multipleksery stosuje się w układach przetworników informacji z postaci równoległej na szeregową, w generatorach określonych
sekwencji bitów.
Rys. 9.18 Sposób połączenia dwóch multiplekserów.
9.5.3.
Demultipleksery
Demultipleksery należą również do grupy dekoderów. Umożliwiają one przełączanie jednego wejścia na N wyjść. Jest to układ
komutacyjny (wielowyjściowy) o M wejściach adresowych i o jednym wejściu informacyjnym X oraz o N = 2
M
wyjściach. Wejścia adresowe są
opisane zwykle wielkimi literami alfabetu, natomiast wejścia informacyjne - liczbami całkowitymi od 0 do 2
M
– 1 (rys. 9.19).
Układ ten jest sterowany przełącznikiem cyfrowym. Na wejścia adresowe tego układu podaje się binarnie zakodowany numer wyjścia
(określoną kombinację stanów ), na który ma być przeniesiony sygnał wejściowy (lub jego negacja).
5
1
0
2
3
4
6
7
9
8
10
12
11
13
14
15
16
18
19
20
21
17
26
25
24
23
22
29
27
28
30
31
W
S
A B C D
E A B C D
0
1
2
3
2
M
– 1
2
M
wyjść
Wejście
Informacyjne
X
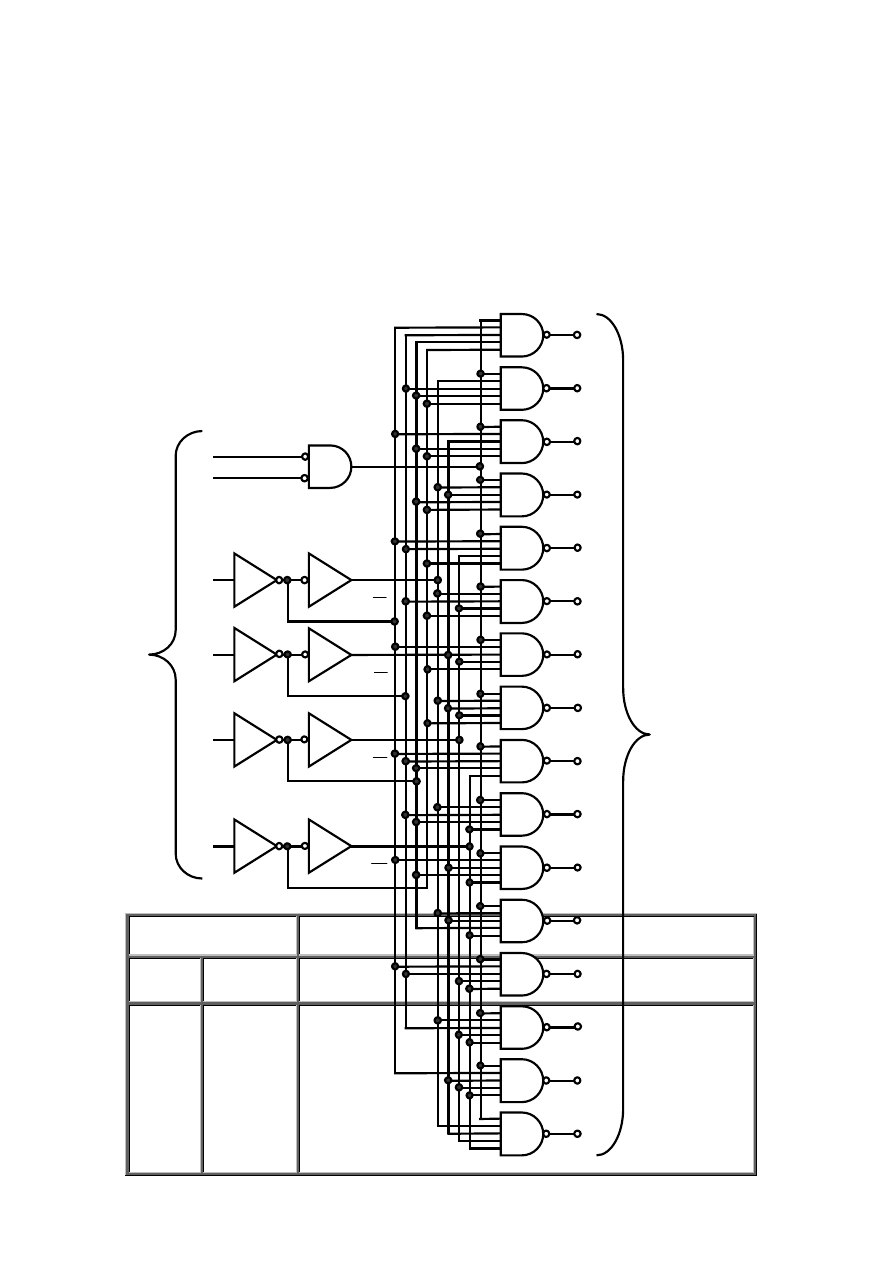
83
Rys. 9.19 Demultiplekser – symbol ogólny.
Demultipleksery również są wykonane w postaci układów scalonych. Mogą mieć one dodatkowe wejścia strobujące S, umożliwiające
zablokowanie wszystkich wyjść.
Typowym demultiplekserem scalonym jest układ 154 o 4 wejściach adresowych, 2 wejściach informacyjnych i 16 wyjściach (rys. 9.20).
Układ ten spełnia funkcję dekodera naturalnego 4 – bitowego kodu dwójkowego na kod 1 z 16. Wejścia informacyjne G
1
i G
2
mają aktywny sygnał
niski L (0). Jedno z tych wejść może służyć jako wejście informacyjne, a drugie jako wejście strobujące.
Słowo adresowe (dekodowane) jest podawane na wejścia A, B, C i D powodując, że jedno z wyjść znajdzie się w stanie niskim, jeśli na
obydwu wejściach informacyjnych jest poziom niski, na innych wyjściach pojawi się stan wysoki. Jeśli na jednym z dowolnych wejść
informacyjnych pojawi się sygnał wysoki, to na wszystkich wyjściach otrzymamy stan wysoki.
Demultipleksery są stosowne do realizacji logicznych funkcji kombinacyjnych np. jako konwertery kodu BCD na kod 1 z 10.
a)
b)
Wejścia
Wyjścia
G
1
G
2
B C B A
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
L L
L L
L L
L L
L L
L L
L L
L L
L L
L L
L L
L L
L L L L
L L L H
L L H L
L L H H
L H L L
L H L H
L H H L
L H H H
H L L L
H L L H
H L H L
H L H H
L
H
H
H
H
H
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
G
1
G
2
A
B
C
D
D
C
B
A
G
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
6
.
W
y
jś
c
2
7
.
W
e
jś
c
B
A
C
D

84
L L
L L
L L
L L
L H
H L
H H
H H L L
H H L H
H H H L
H H H H
X X X X
X X X X
X X X X
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
L
H
H
H
H
H
H
H
L
H
H
H
Rys. 9.20 Demultiplekser 154: a) schemat logiczny,
b) tablica wartości.
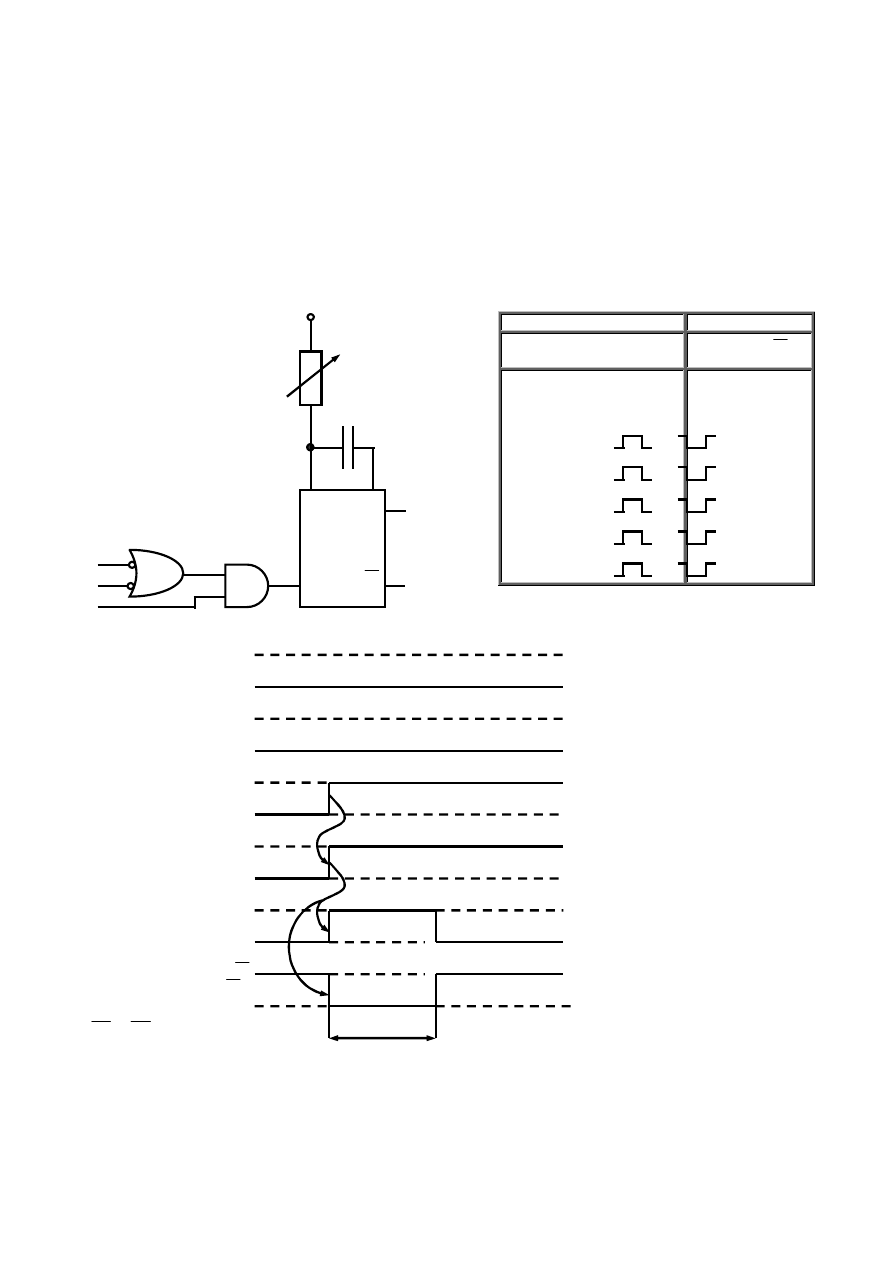
85
10.
GENERATORY
10.1.
PRZERZUTNIKI MONOSTABILNE
Przerzutniki monostabilne w technice cyfrowej służą do generacji impulsu o określonej długości w celu dostarczenia impulsów
bramkujących, kasujących, itp. Są to układy, które w odpowiedzi na sygnały wyzwalające wytwarzają impulsy prostokątne o czasie trwania ściśle
zależnym od wartości dołączonych do niego zewnętrznych elementów R, C.
Układy monostabilne mogą być tworzone z bramek, podobnie jak z tranzystorów w technice analogowej. Parametry tego typu
przerzutników nie są często zadawalające, szczególnie przy dużych częstotliwościach wyzwalania nie następuje zdecydowany podział częstotliwości.
Oprócz tego szerokość impulsu w takich układach zależy dość znacznie od temperatury. Z tych powodów skonstruowano specjalnie bardziej złożone
układy przerzutników, których reprezentantem jest układ typu UCY 74121, którego schemat, zasadę działania i przebiegi czasowe przedstawiono na
rys. 10.1.
a)
b)
Wejście
Wyjście
A
1
A
2
B
Q
Q
–
–
0
0
1
1
1
–
0
1
0
1
0
→
1
1
0
0
→
1
1
→
0
0
1
0
1
→
0
1
0
0
0
→
1
c)
Rys. 10.1 Przerzutnik monostabilny 74121: a) schemat, b) zasada działania,
c) przebiegi czasowe.
Układ ten posiada:
§
wejścia wyzwalające A
1
, A
2
oraz B,
§
wejścia służące do dołączenia zewnętrznych elementów (R, C) ustalających czas trwania impulsów wyjściowych,
§
wyjścia przerzutnika Q i
Q
.
W multiwibratorze 4121 następny impuls wyzwalający może się pojawić dopiero po pewnym czasie od chwili zaniku sygnału
wyjściowego. Na wyjściu Q przerzutnika w stanie stabilnym jest poziom niski (0). Jeżeli tak spolaryzujemy wejścia A
1
, A
2
oraz B, że sygnał W =
(
2
1
A
A
+
)B zmieni wartość z 0 na 1, to przerzutnik ten zostanie wzbudzony. Stan wyjścia Q zmieni się z 0 na 1 na czas określony t
i
= 0,69 RC.
Po upływie tego czasu wyjście Q wraca do stanu 0. Pożądany czas trwania impulsu wyjściowego ustala się, dobierając odpowiednie wartości
elementów R i C.
Innym przykładem scalonego przerzutnika monostabilnego jest układ 74123, którego schemat i zasadę działania przedstawiono na rys.
10.2. Jest to podwójny przerzutnik monostabilny o wspólnym asynchronicznym wejściu zerującym Z.
Multiwibrator 4123 generuje impuls przy zmianie sygnału wejściowego B z 0 na 1, gdy A = 0, lub przy zmianie sygnału A = 1 na 0, gdy B
= 1.Jeżeli przed upływem czasu
τ ponownie pojawi się zmienna wyzwalająca, nastąpi wydłużenie sygnału wyjściowego o czas τ, mierzony od
momentu pojawienia się tej przyczyny.
Podanie niskiego poziomu (0) na wejście Z powoduje natychmiastowe zakończenie generowanego impulsu i przejście wyjścia Q do stanu
0. Przerzutniki mogą być wyzwalane osobno lub współbieżnie. Układ jest wyzwalany narastającym zboczem sygnału W=Ā·B·Z. Do założonego czasu
A
1
A
2
B
W
Q
Q
C
R
+U
CC
1
0
1
0
1
0
1
0
1
0
1
0
T
1
A
1
A
2
B
W
Q
Q
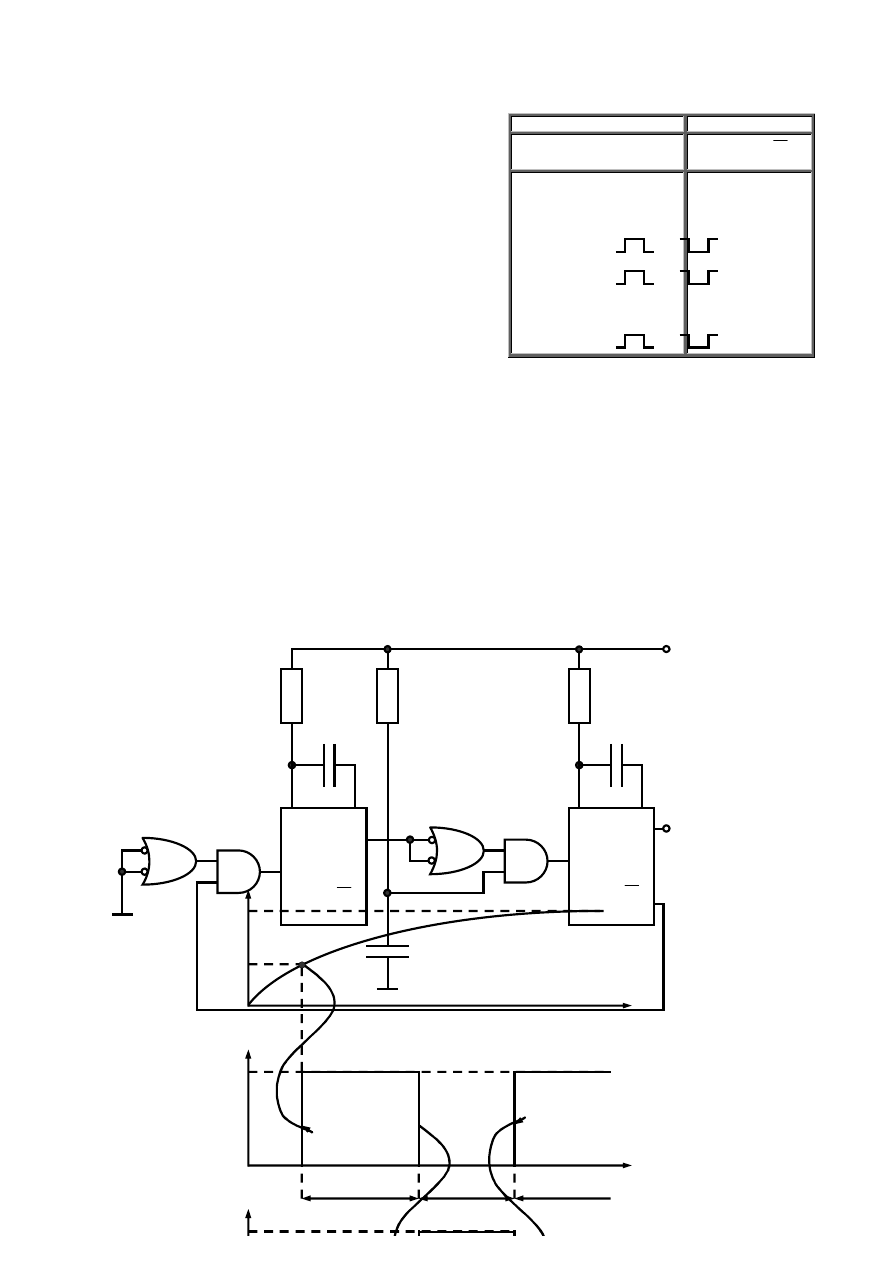
86
trwania impulsu wyjściowego t
i
= 0,32RC dobiera się wartości elementów R i C.
a)
b)
Wejście
Wyjście
A
B
R
Q
Q
1
–
1
0
1
–
0
1
0
1
0
0
→
1
1
1
→
0
1
1
–
–
0
0
1
0
1
0
→
1
Rys.10.2 Przerzutnik monostabilny 74123: a) schemat; b) zasada działania.
10.2.
GENERATORY FALI PROSTOK
ĄTNEJ
W tym rozdziale będą omówione układy generujące impulsy prostokątne o poziomach napięć wyjściowych zgodnych z obowiązującymi
standardami sygnałów cyfrowych (w zależności od stosowanych elementów: TTL, CMOS lub inne). Przebiegi takie są wytwarzane w generatorach
zbudowanych z przerzutników monostabilnych lub bramek logicznych. Projektując układ generatora należy przede wszystkim zwrócić uwagę na
zapewnienie stałości częstotliwości drgań.
Na rys. 10.3a przedstawiono schemat generatora fali prostokątnej zbudowanego z dwóch przerzutników 74121, a na rys. 10.3b
przebiegi powstające w tym układzie. Jest to układ generujący drgania o poziomach TTL. W chwili włączenia napięcia zasilania kondensator C
powoli ładuje się, napięcie U
c
narasta od zera ze stałą czasową τ = RC do wartości +U
cc
. Dopóki napięcie to nie osiągnie poziomu 1,55 V, dopóty
przerzutnik P2 jest zablokowany (w układzie tym powinny ustać wszelkie procesy przejściowe). Gdy U
c
= 1,55 V, wówczas stan na wejściu B zmieni
się z 0 na 1 (B = 0
→
1), co spowoduje (przy A
1
= 0; A
2
= 0) wygenerowanie impulsu o czasie trwania t
2
. Wraz z zakończeniem tego impulsu na
wejściu przerzutnika P1 pojawi się sygnał wyzwalający go (A
1
= 0; A
2
= 0; B = 0
→
1). Spowoduje to wygenerowanie impulsu o czasie trwania t
1
,
wraz z zakończeniem tego impulsu na wejściu przerzutnika P2 pojawi się sygnał wyzwalający go (A
1
, A
2
= 0
→
1; B = 1).
a)
b)
Rys. 10.3 Generator fali prostokątnej zbudowany z monostabilnych przerzutników scalonych 74121: a) schemat połączeń; b) przebiegi czasowe
napięć.
Q
1
Q
1
Q
2
Q
2
C
1
R
1
C
2
R
2
R
C
+U
CC
B
A
1
A
2
A
1
A
2
B
U
C
↑
P
1
P
2
Wy
t
0
0
U
C
U
02
U
01
U
CC
U
CC
U
CC
t
2
t
1
t
2
1,55V
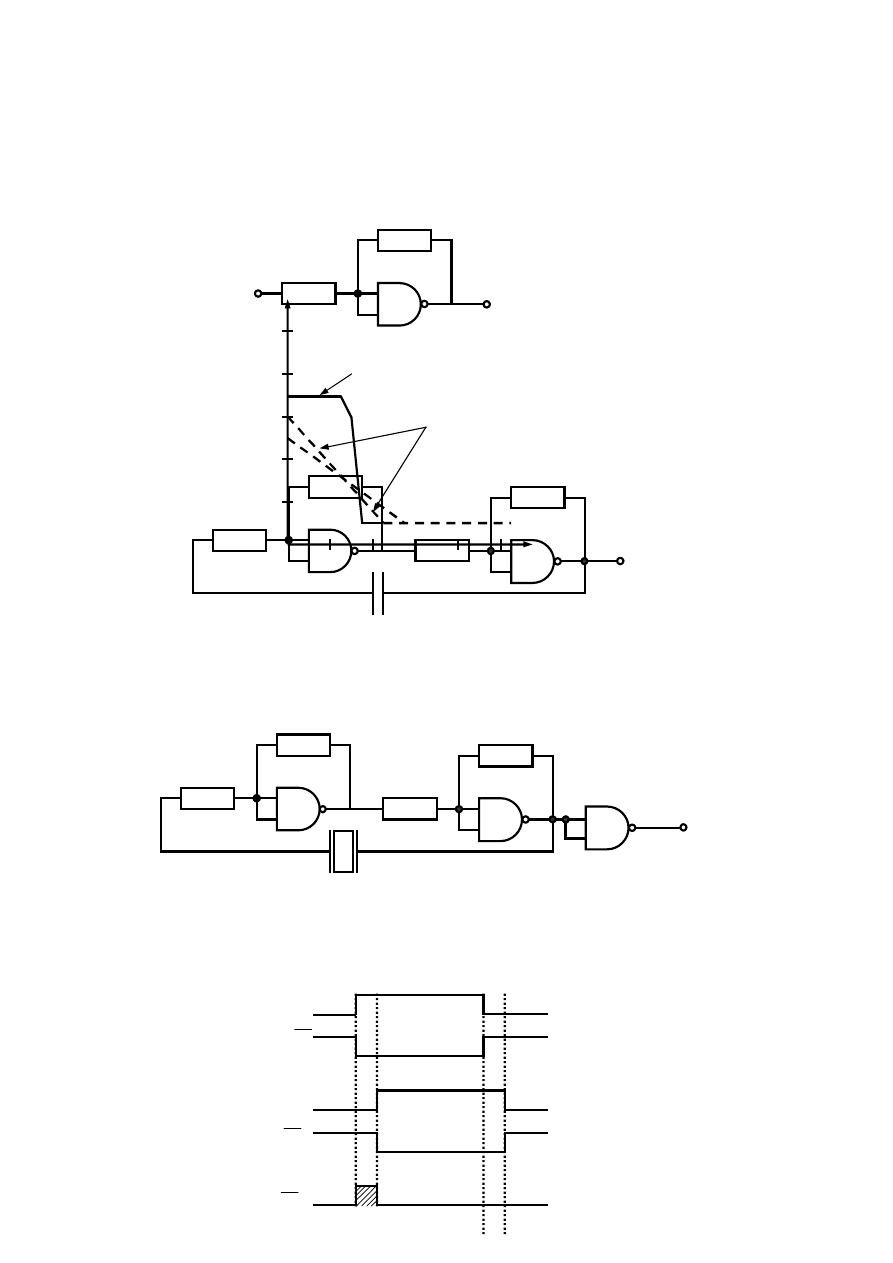
87
Stany układu powtarzają się cyklicznie, w rezultacie otrzymuje się na wyjściu przebieg prostokątny. Jego częstotliwość i wypełnienie
można regulować przez dobór wartości zewnętrznych elementów R
1
, C
1
, R
2
, C
2
. Zakres regulowanych częstotliwości wynosi od 0,01 Hz do kilku
MHz.
Drugą grupę generatorów fali prostokątnej stanowią układy budowlane z linearyzowanych bramek logicznych. Są to bramki objęte
ujemnym sprzężeniem zwrotnym. Schemat zlinearyzowanej bramki NAND oraz jej charakterystykę statyczną przedstawiono na rys. 10.4. Każda
zlinearyzowana bramka jest z układowego punktu widzenia wzmacniaczem odwracającym (przesuwającym fazę sygnału o 180
°
). w wyniku
zastosowania dwóch takich bramek uzyskuje się wzmacniacz o przesunięciu fazowym równym 360
°
. W pętle sprzężenia zwrotnego może być
włączony kondensator lub rezonator kwarcowy.
a)
b)
c)
Rys. 10.4 Generator przebiegu prostokątnego zbudowany z użyciem zlinearyzowanych bramek logicznych, ze sprzężeniem pojemnościowym: a)
schemat zlinearyzowanej bramki NAND; b) charakterystyka przejściowa tej bramki; c) schemat generatora.
Gdy elementem sprzęgającym jest kondensator (rys. 10.4c), wówczas fazowy warunek powstawania drgań jest spełniony w szerokim
zakresie widma sygnałów. Z tego powodu przebieg wyjściowy układu nie jest przebiegiem sinusoidalnym, ale zbliżonym do prostokątnego. Jego
częstotliwość reguluje się przez zmianę wartości rezystorów i kondensatora. Przebieg uzyskany w takim układzie charakteryzuje się małą stałością
częstotliwości.
Gdy elementem sprzęgającym jest rezonator kwarcowy (rys. 10.5), wówczas fazowy warunek powstawania drgań jest spełniony tylko
dla częstotliwości rezonansu szeregowego rezonatora. Z sygnału wyjściowego w obwodzie generacji drgań rezonator kwarcowy (odgrywający tutaj
role filtru wąskopasmowego - przepustowego) wydziela składową harmoniczną o częstotliwości f
s
, która jest podawana na wejście zlinearyzowanej
bramki B1.
Rys. 10.5 Schemat generatora przebiegu prostokątnego zbudowanego z użyciem zlinearyzowanych bramek logicznych, z rezonatorem kwarcowym w
pętli sprzężenia zwrotnego.
Sygnał o przebiegu sinusoidalnym po wzmocnieniu i ograniczeniu w bramkach B1 i B2 przyjmuje kształt prostokątny. Dodatkowa bramka
logiczna (B3) separuje wyjście układu od obwodu wytwarzania drgań. W generatorach fali prostokątnej zbudowanych z bramek logicznych z
rezonatorem kwarcowym uzyskuje się dużą stałość częstotliwości generowanego przebiegu.
10.2.1.
Generowanie pojedynczego impulsu
W tym rozdziale będą omówione wybrane rozwiązania budowane z bramek logicznych lub produkowane jako monolityczne (scalone)
generatory monostabilne w technologii TTL. Poszczególne rozwiązania różnią się od siebie parametrami otrzymanych przebiegów, zakresem zmian
czasu trwania impulsu wyjściowego, stałością czasu trwania tego impulsu, stałością amplitudy impulsu itp.
Impulsy o krótkim czasie trwania można uzyskać przez odpowiednie połączenie ze sobą układów o różnych czasach propagacji impulsu
sterującego X. Zasadę tę ilustrują przebiegi czasowe przedstawione na rys. 10.6.
R
1
R
2
R
1
R
2
R
3
R
4
B1
B2
C
Wy
R
1
R
2
R
3
R
4
B1
B2
Wy
B3
1
2
1
2
3
4
5
1
2
3
4
5
0
V
V
U
Wy
U
We
X
X
0
τ
X
0
τ
X
0
τ
X
X
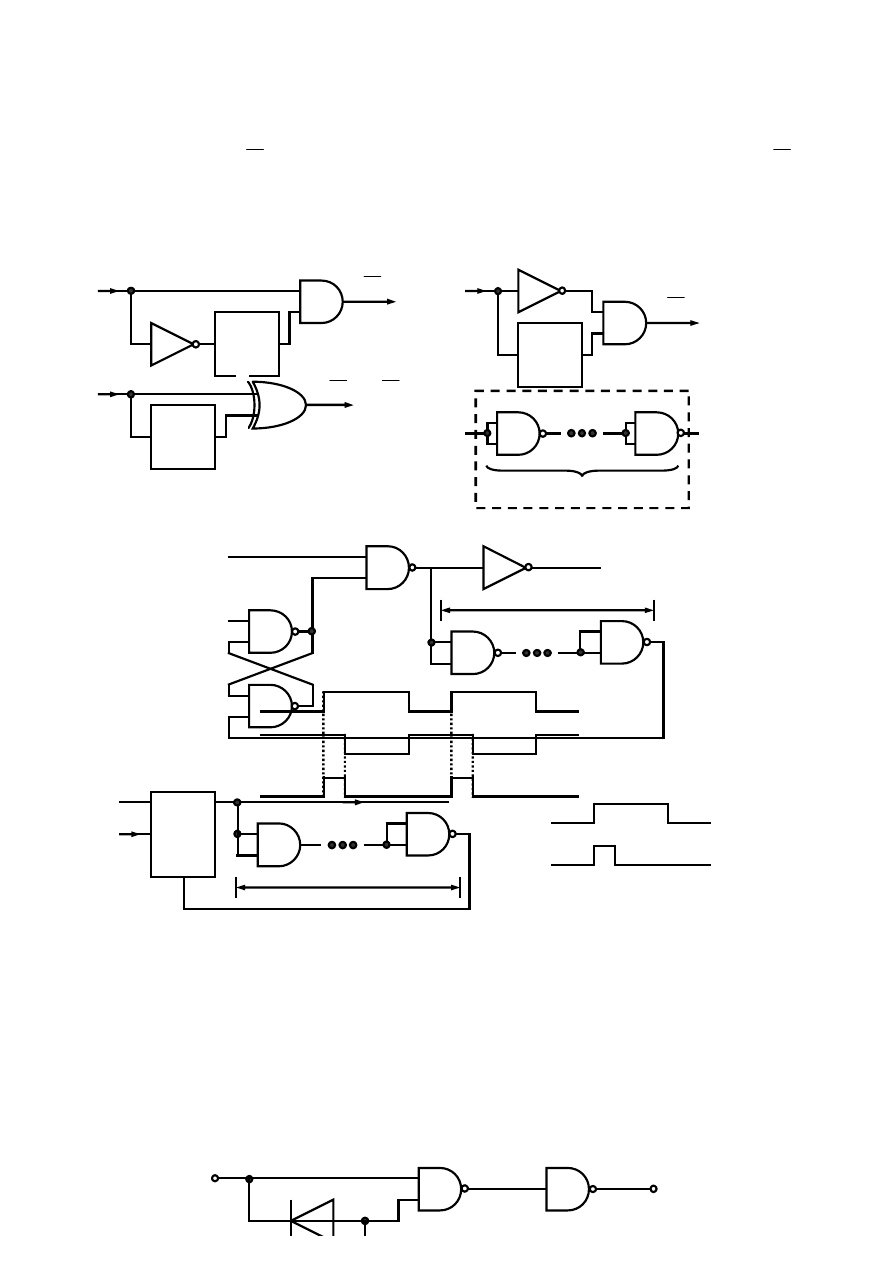
88
Rys. 10.6 Przebiegi czasowe ilustrujące zasadę generacji krótkich impulsów.
Przez zastosowanie opóźnienia
0
τ
i inwersji zmiennej sterującej X można uzyskać impulsy sygnalizujące zmianę sygnału sterującego z
wartości niskiej na wysoką (
0
X
X
τ
), czyli jak gdyby w odpowiedzi na przednie zbocze X. Otrzymać można również krótki impuls
0
X
X
τ
,
sygnalizujący zanik sygnału sterującego. Przykłady realizacji takich generatorów przedstawiono na rys. 10.7a, b i c. Na rys. 10.7d pokazano sposób
uzyskania opóźnienia
0
τ
, wykorzystując czasy propagacji kaskadowo połączonych bramek NAND. Ponieważ impulsy są generowane w wyniku
zmian wartości zmiennej sterującej X z poziomu 0 na 1 lub 1 na 0, mówimy często o tzw. różniczkowaniu zbocza tej zmiennej.
a)
b)
c)
d)
Rys. 10.7 a), b) i c) Przykłady realizacji generatorów pojedynczych impulsów,
d) układ opóźniający o
0
τ
.
Na rys. 10.8a przedstawiono układ różniczkujący przednie zbocze zmiennej A. W układzie tym oprócz bramek zastosowano przerzutnik
sr, stanowiący dodatkowy układ opóźniający. Pracę tego układu zilustrowano przebiegami czasowymi na rys. 10.8b.
a)
b)
c)
d)
Rys. 10.8 Generatory pojedynczych impulsów: a) i c) przykładowe schematy logiczne,
b) i d) przebiegi czasowe ilustrujące pracę generatorów.
Tak samo jak układ z rys. 10.8a, działa układ przedstawiony na rys. 10.8c, w którym wykorzystano przerzutnik synchroniczny typu D
wyzwalany przednim zboczem impulsu różniczkowanego A. W układzie opóźniającym
0
τ
wymagane są dość znaczne czasy opóźnień. Do tych
celów produkuje się specjalne bramki o długich czasach propagacji (SN 49703). Wadą układów impulsowych budowanych na bramkach jest fakt, że
uzyskane czasy trwania impulsu wyjściowego będą różne dla różnych egzemplarzy bramek.
Duża stałość czasu trwania impulsu wyjściowego charakteryzuje układy impulsowe zbudowane za pomocą monolitycznego multiwibratora
monostabilnego.
10.2.2.
Opó
źnienie sygnału o zadany czas
W układach cyfrowych zachodzi czasem potrzeba opóźnienia przedniego lub tylnego zbocza sygnału sterującego lub przesunięcia sygnału
względem wartości wejściowej. Podamy kilka takich rozwiązań o różnych własnościach.
Przedstawiony na rys. 10.9 układ generuje impuls, którego przednie zbocze jest opóźnione względem przedniego zbocza impulsu
wejściowego o czas, którego wartość zależy od wartości pojemności C. Gdy sygnał wejściowy A zmieni wartość z poziomu 0 na 1, na wyjściu trwać
będzie nadal sygnał 0 tak długo, dopóki pojemność C nie naładuje się do poziomu przełączenia bramki. Zależność czasów opóźnień od wartości C
przedstawiono w tabeli na rys. 10.9c.
a)
X
0
τ
0
τ
X
X
X
0
τ
0
τ
X
X
X
0
τ
0
0
τ
τ
X
X
X
X
+
0
τ
k
2
X
Y
28.
2k
X
29.
Y
Y
X
2k + 1
D
C
1
X
Y
A
Y
B
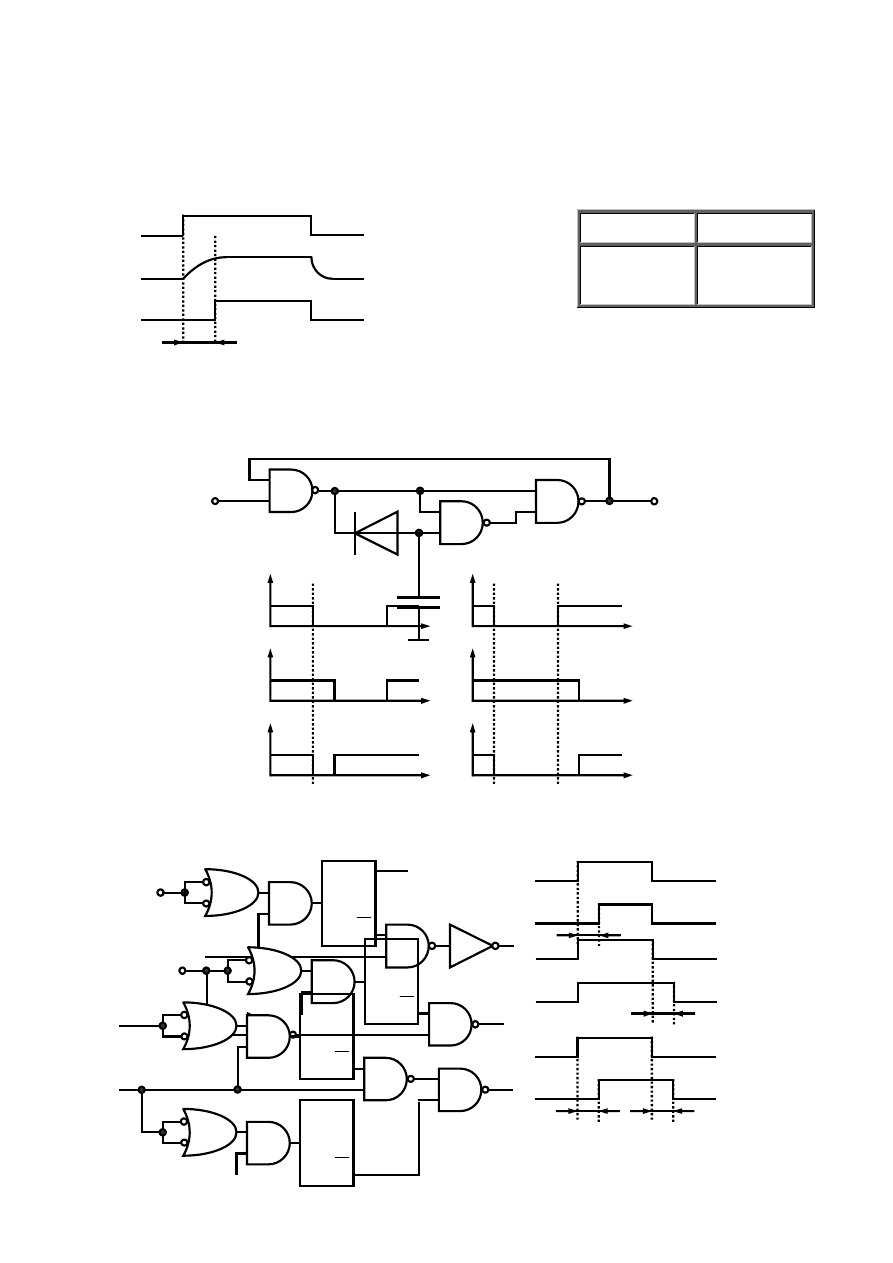
89
b)
c)
C
0
τ
20 pF
100 pF
1 nF
10 nF
37 ns
130 ns
1
µ
s
10
µ
s
Rys. 10.9 Układ opóźniający przednie zbocze impulsu wejściowego: a) schemat ideowy,
b) przebiegi czasowe, c) wartości opóźnień dla różnych pojemności.
W układzie na rys. 10.10a czas trwania impulsu wyjściowego może być dłuższy od czasu trwania impulsu wejściowego. Dzięki sprzężeniu
zwrotnemu czas trwania impulsu wyjściowego nie zależy od czasu trwania niskiego poziomu napięcia na wejściu układu. Przebiegi czasowe z rys.
10.10b pokazują zależność czasu trwania impulsu wyjściowego od wartości pojemności C.
a)
b)
Rys. 10.10 Generator pojedynczego impulsu (aktywny niski poziom logiczny) o czasie trwania niezależnym od czasu trwania zmiennej A: a) układ
połączeń,
b) przebiegi czasowe dla C = 50 pF i C = 250 pF.
Osobną grupę stanowią układy opóźniające zbudowane z multiwibratorów monostabilnych 4121 o dużej stałości czasu trwania impulsu
wyjściowego. Oznaczenia multiwibratora 4121 oraz przebiegi czasowe ilustrujące jego pracę przedstawiono na rys. 10.1.
Przykłady realizacji opóźnień za pomocą omawianego multiwibratora przedstawiono na rys. 10.11. Otrzymane tu opóźnienia nie
przekraczają kilkudziesięciu sekund. W celu uzyskania większych opóźnień stosujemy bardziej złożone układy zawierające liczniki. Generator
pojedynczego impulsu można wykonać z bramek NOR lub NAND.
a)
b)
c)
Rys. 10.11 a), b) i c) Przykłady realizacji opóźnień za pomocą multiwibratora 4121.
Rys. 10.12 jest przykładem rozwiązania generatora monostabilnego zbudowanego z bramek NOR (402) i inwertora z otwartym kolektorem
(405 lub 403). Znaczenie tych rozwiązań jest obecnie niewielkie ze względu na znaczne rozpowszechnienie elementu 4121.
A
30.
Y
0
τ
A
Y
B
C
A
A
B
B
Y
Y
t
t
t
t
t
t
C=50pF
C=250pF
X
0
Y
Q
Q
0
τ
X
Y
X
1
Q
Q
Y
0
τ
X
Y
X
0
1
Y
Q
Q
Q
Q
1
τ
2
τ
X
Y
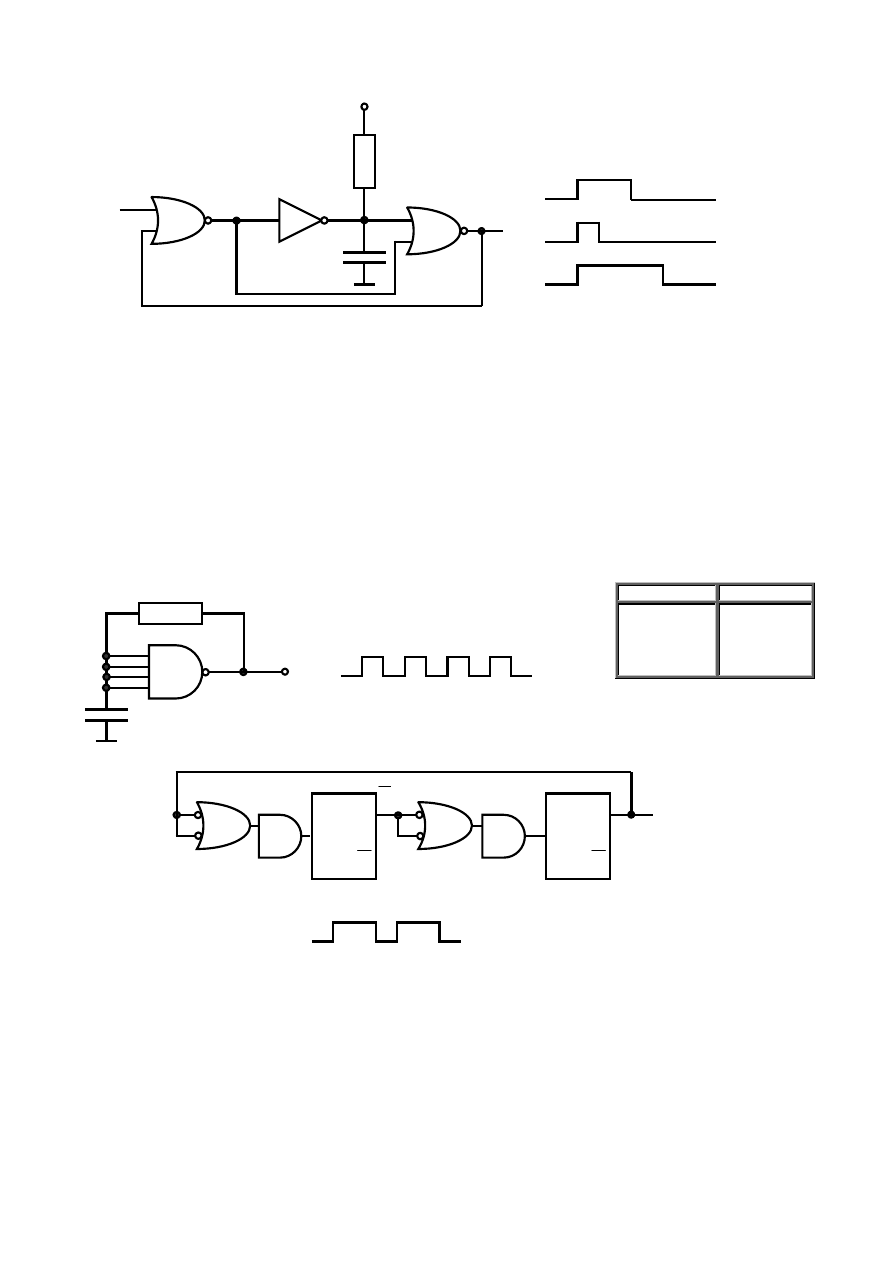
90
Rys. 10.12 Przykładowa realizacja generatora pojedynczego impulsu na bramkach NOR.
10.2.3.
Generowanie ci
ągu impulsów
W serii elementów scalonych nie produkuje się generatorów ciągów impulsów, zwanych multiwibratorami astabilnymi. Wykonuje się je
zatem z innych elementów scalonych. Najprostszym rozwiązaniem jest układ przedstawiony na rys. 10.13a.
Multiwibrator astabilny zbudowano na podstawie bramki Schmitta 4132, charakteryzującej się histerezą zmian
)
U
(
f
U
we
wy
=
.
W przedstawionym układzie jest sprzężenie zwrotne poprzez rezystor R. Pojemność C opóźnia zadziałanie sygnału zwrotnego, który po załadowaniu
pojemności C do wartości przełączania wejścia, spowoduje zmianę stanu wyjścia bramki. Następuje rozładowanie kondensatora i przełączenie
wyjścia bramki do wartości przeciwnej. Stan ten powtarza się cyklicznie. Współczynnik wypełnienia przebiegu wyjściowego zależy od wartości R i
C.
Częstotliwość pracy multiwibratora zilustrowano przykładami zawartymi w tabeli przedstawionej na rys. 10.13b. Rezystor R można
zmieniać w zakresie 100
÷ 1200 Ω. Układ charakteryzuje niewielka obciążalność i wrażliwość na zmiany napięcia zasilającego.
a)
b)
C
f
20 pF
100 pF
1 nF
10 nF
0,1
µ
F
21,7 MHz
10,6 MHz
1,8 MHz
195 kHz
21,6 kHz
Rys. 10.13 Generator ciągu impulsów prostokątnych: a) przykładowy schemat, b) tablica przykładowych wartości C i f.
Największą stałością generacji impulsów charakteryzują się układy przedstawione na rys. 10.14.
a)
b)
Rys. 10.14 Generator ciągu impulsów prostokątnych: a) schemat układu zbudowanego na podstawie elementów 4121, b)przebieg czasowy
zmiennej wyjściowej.
31.
Y
Y
R
1
,C
1
R
2
,C
2
X
+U
cc
1/4 402
1/6 505
1/4 402
Y
C
R
R
C
Y
Y
Y
Q
4121
4121
Q
Q
Q
Y

91
11.
BIBLIOGRAFIA:
1.
Chwaleba Augustyn, Moeschke Bogdan, Płoszajski Grzegorz: Elektronika, Wydawnictwo Szkolne i Pedagogiczne, Warszawa 1996.
2.
Piecha Jan: Elementy cyfrowe TTL, Katowice 1985.
3.
Piecha Jan: Elementy i układy cyfrowe, PWN, Warszawa 1990.
4.
Pieńkoś Jan, Turczyński Janusz: Układy scalone TTL w systemach cyfrowych, Wydawnictwo Komunikacji i Łączności, Warszawa 1980.
5.
Pióro Barbara, Pióro Marek: Podstawy elektroniki cz.1, cz.2, Wydawnictwo Szkolne i Pedagogiczne, Warszawa 1996.
6.
Rusek Andrzej: Podstawy elektroniki, Wydawnictwo Szkolne i Pedagogiczne, Warszawa 1986.
7.
Skorupski Andrzej: Podstawy budowy i działania komputerów, Wydawnictwo Komunikacji i Łączności, Warszawa 1997.
…:::PDF made by nobody the fallen one:::...
Document Outline
- 1.
- 2.
- 1. 2.3. 4.
- 5.
- 3.
- 6.
- 4.
- 5.
- 6.
- 9.
- 7.
- 7.
- 8.
- 9.
- KOD 1
- 11.
- 10.
- 12.
- 13.
- 14.15.16.17.
- 19.20.
- 21.
- 18.
- 22.
- 24.
- 23.
- 25.
- .
- 7
- 2
- .
- 6
- 2
- 10.
- 28.
- 29.
- 30.
- 31.
- 11.
Wyszukiwarka
Podobne podstrony:
Modul 3 Podstawy elektroniki cyfrowej
Elektronika Cyfrowa, Wstęp
elektronika cyfrowa -pytania dla ib
Elektronika cyfrowa 2
Elektronika Cyfrowa, S
Elektronika cyfrowa-2, WSTĘP
elektronika cyfrowe układy kombinacyjne 3F2Z7LBV3UQWMPV3OADNTCQLCZHPW2DOT4WVVJQ
Badanie parametrów elektrycznych cyfrowych układów TTL i MOS, Klasa
Modul 3 Podstawy elektroniki cyfrowej
prof dr hab inż Handkiewicz Andrzej, Elektronika Cyfrowa, Automat synchroniczny 2
prof dr hab inż Handkiewicz Andrzej, Elektronika Cyfrowa, Rejestr cykliczny 2
Cyfrowy pomiar podstawowych wielkości elektrycznych
Przekazniki i styczniki, Nauki Ścisłe Politechnika, Elektronika Teoria, Technika Cyfrowa, Technika C
więcej podobnych podstron