Politechnika Warszawska
Wydział Fizyki
Laboratorium Fizyki I „Płd.”
Grażyna Chendor
Jerzy Filipowicz
ZJAWISKO SKRĘCENIA PŁASZCZYZNY POLARYZACJI ŚWIATŁA
1. Podstawy fizyczne
W zjawisku dyfrakcji, interferencji i polaryzacji światło zachowuje się jak fala
elektromagnetyczna czyli rozchodzący się w przestrzeni ciąg zmiennych pól elektrycznych
i magnetycznych wzajemnie się wytwarzających. Fala elektromagnetyczna opisana jest przez wektor
natężenia pola elektrycznego (
E
r
), wektor indukcji pola magnetycznego
)
(B
r
oraz wektor falowy
)
(k
r
określający kierunek rozchodzenia się fali,
λ
π
2
=
k
r
gdzie λ jest długością fali. Wektory
B
E
r
r
,
i
k
r
są do siebie wzajemnie prostopadłe a zatem fala elektromagnetyczna jest falą poprzeczną.
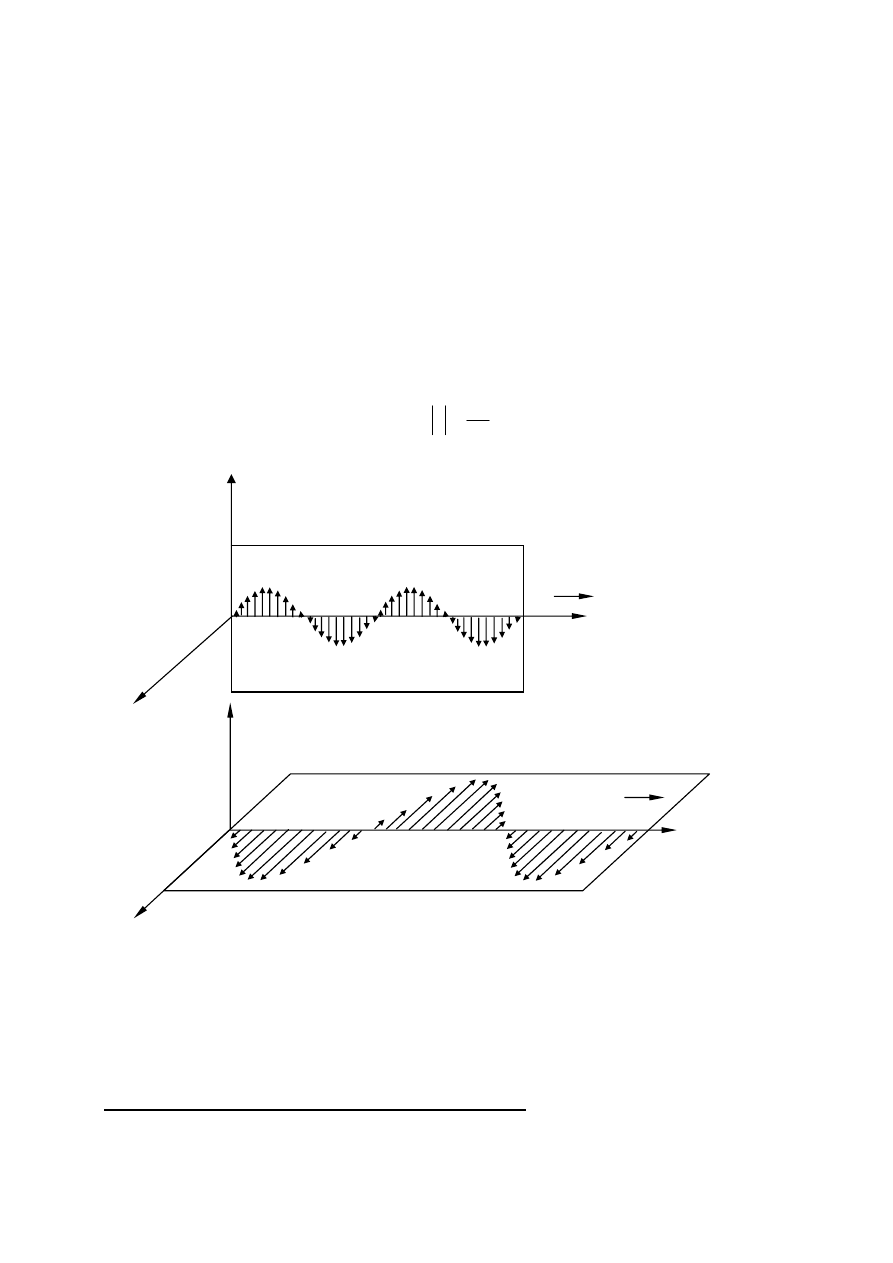
Rys. 1 Fala spolaryzowana liniowo, wektor
E
r
drga w płaszczyźnie: a) yz , b) xy.
Światło może być spolaryzowane liniowo, kołowo lub eliptycznie. Polaryzacja liniowa ma
miejsce gdy drgania wektora natężenia pola elektrycznego zachodzą tylko w jednej płaszczyźnie, która
nie zmienia w czasie swej orientacji w przestrzeni (rys.1). Inaczej mówiąc płaszczyzna drgań wektora
E
r
jest ta sama wzdłuż całego promienia. Gdy koniec wektora natężenia pola elektrycznego fali
opisuje linię śrubową kołową lub eliptyczną mówimy o świetle spolaryzowanym kołowo lub eliptycznie.
1.1. Metody wytwarzania światła liniowo spolaryzowanego.
Światło spolaryzowane liniowo można otrzymać za pomocą polaryzatorów dwójłomnych,
polaryzatorów odbiciowych oraz polaroidów czyli błon polaryzujących.
Najczęściej stosowany polaroid H można otrzymać ogrzewając a następnie szybko rozciągając
przezroczystą błonę z alkoholu poliwinylowego. Podczas procesu wydłużania większość długich
cząsteczek polimeru jakim jest alkohol poliwinylowy, rozmieszczonych początkowo zupełnie
k
r
E
r
y
x
z
a)
k
r
E
r
x
y
z
b)
28
Badanie zjawiska skręcenia płaszczyzny polaryzacji światła
2
chaotycznie, obraca się i układa niemal wzdłuż tego samego kierunku a mianowicie w kierunku siły
wydłużającej. Następnie błonę zanurza się w roztworze bogatym w jod. Atomy jodu przenikają do
warstwy ułożonej z alkoholu poliwinylowego. Dzięki temu atomy jodu układają się również w łańcuchy
podobne do łańcuchowych cząstek polimeru. Prawie równoległe do siebie łańcuchy nasycone jodem,
dzięki dobremu przewodnictwu jodu silnie pochłaniają drgania elektryczne zachodzące w kierunku do
nich równoległym. Drgania w kierunku prostopadłym do łańcuchów cząsteczek zostają przepuszczone
praktycznie bez strat energii.
Światło spolaryzowane można uzyskać również przez odbicie od dielektryka. Jednak wiązka
odbita na ogół nie jest spolaryzowana całkowicie. Polaryzację całkowitą wiązki odbitej można uzyskać
jedynie dla jednej wartości kąta padania. Kąt ten nosi nazwę kąta Brewstera [czytaj brjustera].
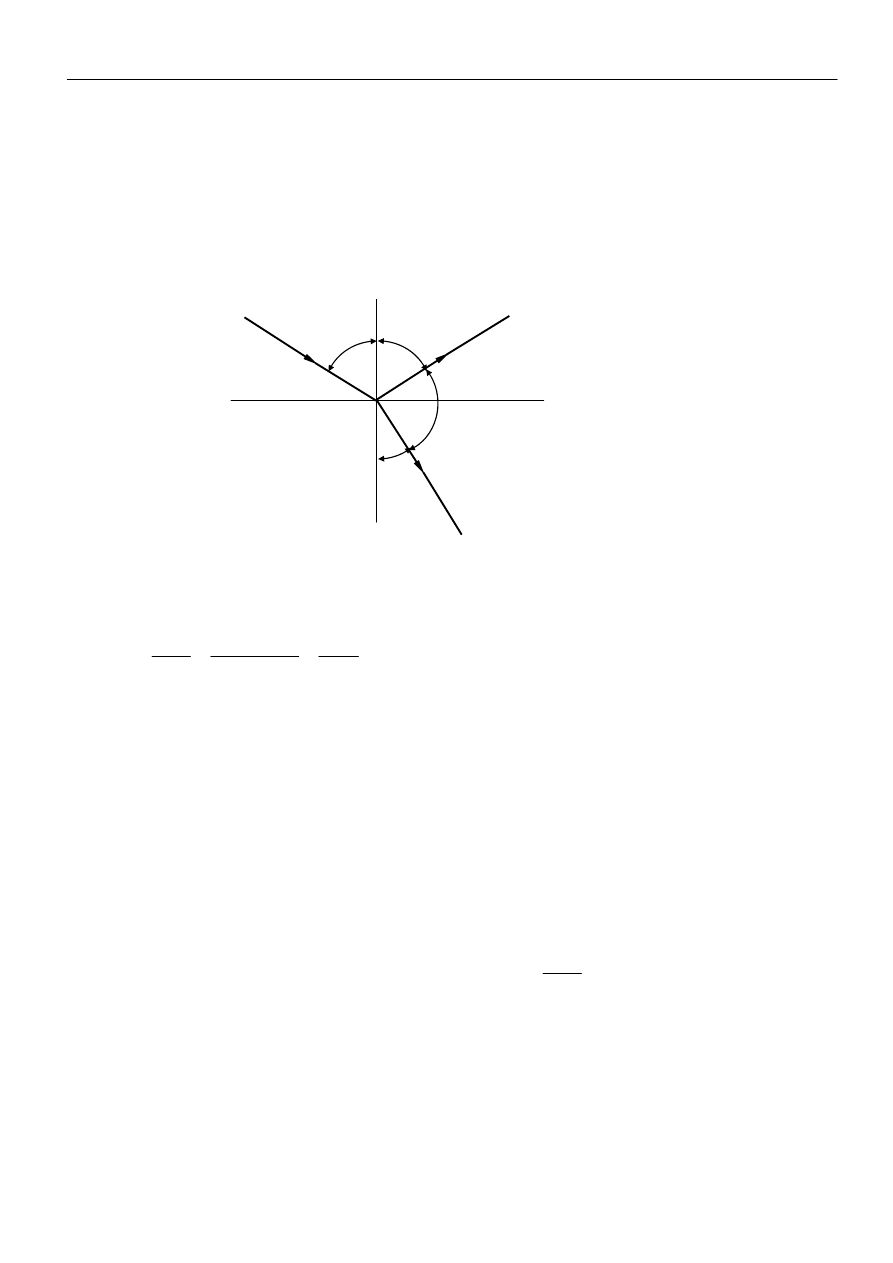
Rys. 2 Całkowita polaryzacja światła podczas odbicia.
α
- kąt padania,
β
- kąt załamania.
Wiązka odbita zostaje spolaryzowana całkowicie gdy jest prostopadła do wiązki załamanej. Kąt
padania odpowiadający całkowitej polaryzacji określony jest wiec równaniem:
α
α
α
α
α
β
α
tg
n
=
=
−
°
=
=
cos
sin
)
90
sin(
sin
sin
sin
(1)
Wiązka załamana spolaryzowana jest jedynie częściowo. Światło spolaryzowane można również
uzyskać wykorzystując zjawisko podwójnego załamania, które ma miejsce w pewnej grupie
kryształów zwanych kryształami dwójłomnymi. Kryształy dwójłomne mają własność rozdzielania
padającej wiązki na dwie wiązki załamane jak pokazuje rysunek 3. Własności wiązek załamanych są
następujące:
1. Obie wiązki mogą rozchodzić się w różnych kierunkach.
2. Prędkość rozchodzenia obu wiązek są różne.
3. Każda wiązka jest całkowicie spolaryzowana liniowo.
4. Kierunki drgań wektora natężenia pola elektrycznego w obu wiązkach są do siebie wzajemnie
prostopadłe.
Jedna z fal ma zawsze stałą prędkość niezależną od tego w jakim kierunku rozchodzi się
w krysztale. Wiązka ta ma zatem stały współczynnik załamania i spełnia prawo Snelliusa. Jest to tak
zwana wiązka zwyczajna. Dla drugiej wiązki zwanej nadzwyczajną, prędkość fali jest różna i zależy od
kierunku w którym ta fala rozchodzi się w krysztale. Stosunek
β
α
sin
sin
dla różnych kątów padania α nie
ma dla fali nadzwyczajnej stałej wartości i traci on dla tej wiązki sens fizyczny. Świadczy o tym
przykład przedstawiony na rys. 3b, gdy światło pada prostopadle na powierzchnię kryształu. Dla wiązki
nadzwyczajnej stosunek sinusów byłby w tym przypadku równy zero (α = 0, β ≠ 0). Wobec tego
współczynnikiem załamania fali nadzwyczajnej nazywamy stosunek prędkości fali w próżni do
prędkości fali nadzwyczajnej w krysztale. Prędkość wiązki nadzwyczajnej zależy od kąta jaki tworzy
wiązka światła z pewnym wyróżnionym kierunkiem zwanym osią optyczną kryształu. Jeśli w krysztale
jest tylko jeden taki kierunek mówimy, że kryształ jest jednoosiowy. Gdy wiązka biegnie wzdłuż osi
optycznej kryształu, podwójne załamanie nie zachodzi; obie wiązki zwyczajna i nadzwyczajna
rozchodzą się z jednakową prędkością. W miarę wzrostu kąta pomiędzy kierunkiem wiązki
nadzwyczajnej i kierunkiem osi optycznej rośnie różnica między prędkością wiązki nadzwyczajnej
β
α
α
o
90
Badanie zjawiska skręcenia płaszczyzny polaryzacji światła
3
i
prędkością wiązki zwyczajnej, przybierając wartość ekstremalną dla kierunku prostopadłego do osi
optycznej.
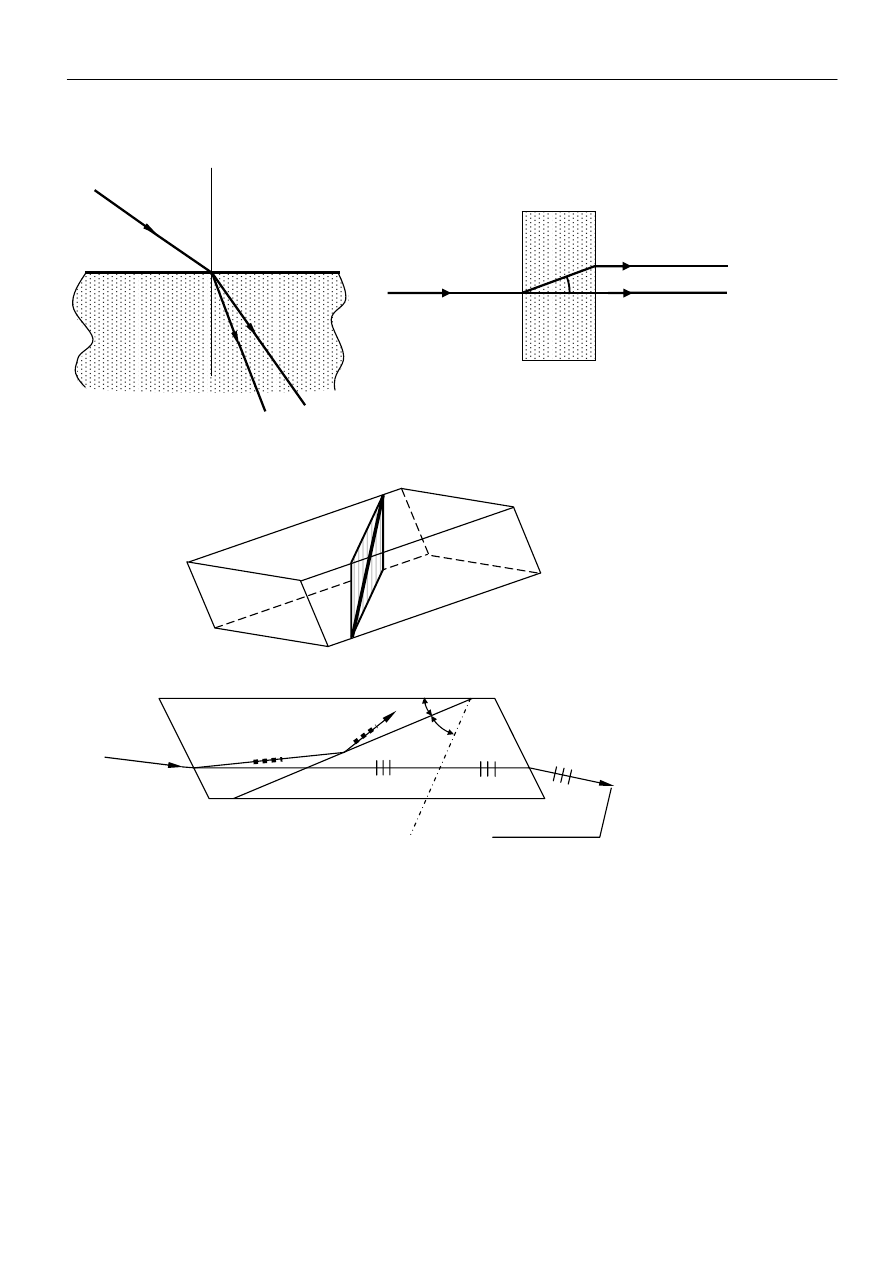
Rys.3 Podwójne załamanie wiązki w krysztale dwójłomnym.
Rys.4 Bieg wiązki światła w pryzmacie Nicola.
Problem otrzymania światła liniowo spolaryzowanego przy wykorzystaniu ciał dwójłomnych
polega na znalezieniu metody usunięcia jednego z promieni załamanych. Zasłonięcie którejś z wiązek
nie jest metodą skuteczną ze względu na to, że rozsunięcie promieni powstających przy dwójłomnym
załamaniu jest nieduże. Dla rozdzielenia ich tą metodą należałoby stosować bardzo grube kryształy.
Jednym z najbardziej znanych polaryzatorów dwójłomnych jest polaryzator skonstruowany
przez szkockiego fizyka Nicola. Naturalny kryształ kalcytu należy rozciąć wzdłuż płaszczyzny
przekątnej w sposób przedstawiony na rys.4, a następnie skleić obie części za pomocą materiału
wykazującego współczynnik załamania o wartości pośredniej między współczynnikami załamania dla
wiązki zwyczajnej i nadzwyczajnej w kalcycie. Najlepszym materiałem do sklejania pryzmatów jest
balsam kanadyjski. Otrzymany układ dzieli wiązkę padającą na dwie wiązki załamane i powoduje
całkowite wewnętrzne odbicie wiązki zwyczajnej. Wiązka zwyczajna po całkowitym wewnętrznym
odbiciu pada na wyczernione boczne ścianki pryzmatu Nicola (nazywanego nikolem) i zostaje w nich
pochłonięta.
Wiązka nadzwyczajna ulega tylko nieznacznemu osłabieniu przez odbicie, przechodzi przez
warstewkę balsamu kanadyjskiego i wychodzi z nikola równolegle do kierunku, w którym padła na
nikol. W ten sposób z nikola wychodzi tyko wiązka nadzwyczajna, która jest liniowo spolaryzowana.
α = 0
β
nadzwyczajna
zwyczajna
b)
ndzw.
zw.
a)
A
B
F
G
C
E
H
D
P
1
q
2
q
1
P
2
wiązka zwyczajna (zw.)
wiązka
nadzwyczajna (ndzw.)
oś optyczna
B
C
A
D
P
1
P
2
22
o
44
o
Badanie zjawiska skręcenia płaszczyzny polaryzacji światła
4
1.2. Zjawisko aktywności optycznej.
a) Naturalna aktywność optyczna.
Oprócz zjawiska dwójłomności pewne kryształy mogą wykazywać w stosunku do światła liniowo
spolaryzowanego pewną inną właściwość. Aby to pokazać należy umieścić między skrzyżowanymi
polaryzatorami płytkę kwarcową wyciętą prostopadle do osi optycznej. Układ oświetlamy światłem
monochromatycznym. Zauważymy, że ciemne poprzednio pole widzenia rozjaśni się, jednak po obrocie
o pewien kąt polaryzatora znajdującego się za płytką (zwanego analizatorem) możemy wiązkę
przechodzącą całkowicie wygasić. Wnosimy stąd, że światło wychodzące z płytki kwarcowej jest
spolaryzowane liniowo, lecz jego płaszczyzna drgań jest skręcona o pewien kąt w stosunku do
płaszczyzny drgań fali padającej na płytkę. Kąt skręcenia płaszczyzny drgań jest oczywiście równy
kątowi o jaki należy skręcić analizator aby uzyskać wygaszenie wiązki po wstawieniu kwarcu pomiędzy
polaryzatory. A więc kwarc skręca płaszczyznę drgań światła biegnącego w kierunku jego osi
optycznej. Ciała zachowujące się w ten sposób nazywamy ciałami optycznie czynnymi, a samo zjawisko
nazywamy aktywnością optyczną.
Aktywność optyczną wykazują nie tylko kryształy, istnieją również ciecze skręcające
płaszczyznę polaryzacji np. terpentyna, nikotyna. Aktywność optyczną wykazują też roztwory ciał
stałych w cieczach optycznie nieczynnych np. roztwór cukru w wodzie. Kąt skręcenia płaszczyzny
drgań (
α
) jest proporcjonalny do stężenia roztworu (c) oraz do grubości warstwy roztworu (h). Tak
więc:
h
c
⋅
⋅
=
γ
α
(2)
Współczynnik (γ) nazywamy skręceniem właściwym lub zdolnością skręcającą roztworu.
Skręcenie właściwe zależy od długości fali padającego światła. Zjawisko zależności skręcenia
właściwego od długości fali światła nosi nazwę dyspersji skręcenia płaszczyzny drgań. Na ogół
skręcenie właściwe (γ) maleje wraz ze wzrostem długości fali światła.
b) Aktywność optyczna wywołana polem magnetycznym.
Zjawisko aktywności optycznej może też być wymuszone niektórymi czynnikami fizycznymi jak
np. polem magnetycznym. Ciała, które w nieobecności pola magnetycznego nie są aktywne optycznie,
po umieszczeniu w polu magnetycznym skręcają płaszczyznę polaryzacji. Zjawisko to zostało odkryte
przez Faradaya, który ustalił, że kąt skręcenia płaszczyzny polaryzacji jest proporcjonalny do indukcji
pola magnetycznego B i do długości drogi h światła przechodzącego przez badaną substancję.
Skręcenie płaszczyzny polaryzacji zależy od kąta pomiędzy kierunkiem propagacji światła a kierunkiem
wektora indukcji magnetycznej. Jest ono największe, gdy światło biegnie równolegle do kierunku
wektora indukcji magnetycznej. Eksperyment pokazuje, że dwukrotne przepuszczenie światła przez
próbkę (tam i z powrotem) w przeciwieństwie do naturalnej aktywności optycznej nie tylko nie znosi
ale powiększa go dwukrotnie.
Kąt skręcenia płaszczyzny polaryzacji w zjawisku Faradaya dla przypadku równoległego kierunku
wektora propagacji światła do kierunku wektora indukcji magnetycznej B można zapisać wzorem
fenomenologicznym:
B
h
V
⋅
⋅
=
α
(3a)
gdzie V jest współczynnikiem proporcjonalności zwanym stałą Verdeta.
Wartość stałej Verdeta zależy bardzo silnie od długości fali świetlnej. Zależy ona również od
gęstości ośrodka oraz od temperatury. Silna zależność stałej Verdeta od długości fali powoduje
konieczność używania w pomiarach światła monochromatycznego. Znak stałej Verdeta uważa się za
dodatni, jeżeli skręcenie płaszczyzny jest zgodne z krążeniem prądu w solenoidzie wytwarzającym
pole magnetyczne. Inaczej mówiąc, jeśli obserwator patrzący w kierunku pola magnetycznego widzi
skręcenie płaszczyzny polaryzacji w prawo, to takie materiały nazywamy prawoskrętnymi albo
dodatnimi. Gdy obrót następuje w lewo, to substancję nazywamy lewoskrętną albo ujemną. Dla
większości materiałów skręcenie płaszczyzny polaryzacji następuje w prawo. Zaliczają się do nich
wszystkie substancje diamagnetyczne i paramagnetyczne.
Zjawisko Faradaya jest wykorzystywane w technice laserowej oraz do modulacji światła, jak na
przykład w tzw. migawkach magnetooptycznych i urządzeniach przepuszczających światło w jednym
kierunku, a przeciwnym nie.
Badanie zjawiska skręcenia płaszczyzny polaryzacji światła
5
Dokładne przedstawienie teorii zjawiska Faradaya wymaga przeanalizowania ruchu elektronów
w substancji przez którą przechodzi światło i na które działa dodatkowo siła Lorentza pochodząca od
zewnętrznego pola magnetycznego B. Ten wymuszony przez pole B w obecności fali
elektromagnetycznej ruch elektronów zmienia własności dielektryczne substancji a tym samym wpływa
na zmianę współczynnika załamania, gdyż
ε
=
n
, gdzie n – współczynnik załamania oraz ε - względna
przenikalność dielektryczna substancji.
Rozkładając falę świetlną spolaryzowaną liniowo na dwie fale spolaryzowane kołowo i
przeciwskrętnie można wykazać, że ruchy elektronów pod wpływem tych dwóch fal oraz pola B
w konsekwencji dają dwa różne współczynniki załamania dla tych fal, a co za tym idzie wystąpienie
skręcenia płaszczyzny polaryzacji po przejściu światła przez substancję, wynikające z opóźnienia
jednej fali spolaryzowanej kołowo względem drugiej.
Pomiędzy falami spolaryzowanymi kołowo, na skutek przejścia przez warstwę ośrodka
magnetooptycznego o grubości h, powstaje różnica faz
'
δ
(patrz rozdział następny):
)
(
2
'
2
1
2
1
n
n
h
h
kn
h
kn
−
=
−
=
λ
π
δ
(3b)
gdzie:
h
kn
1
=
φ
- jest zmianą fazy fali spolaryzowanej prawoskrętnie, spowodowaną przejściem przez
próbkę,
h
kn
2
'
=
+
δ
φ
- jest zmianą fazy fali spolaryzowanej lewoskrętnie na skutek przejścia przez
próbkę,
2
1
n
i
n
- są współczynnikami załamania odpowiednio dla światła spolaryzowanego kołowo
prawoskrętnie i lewoskrętnie.
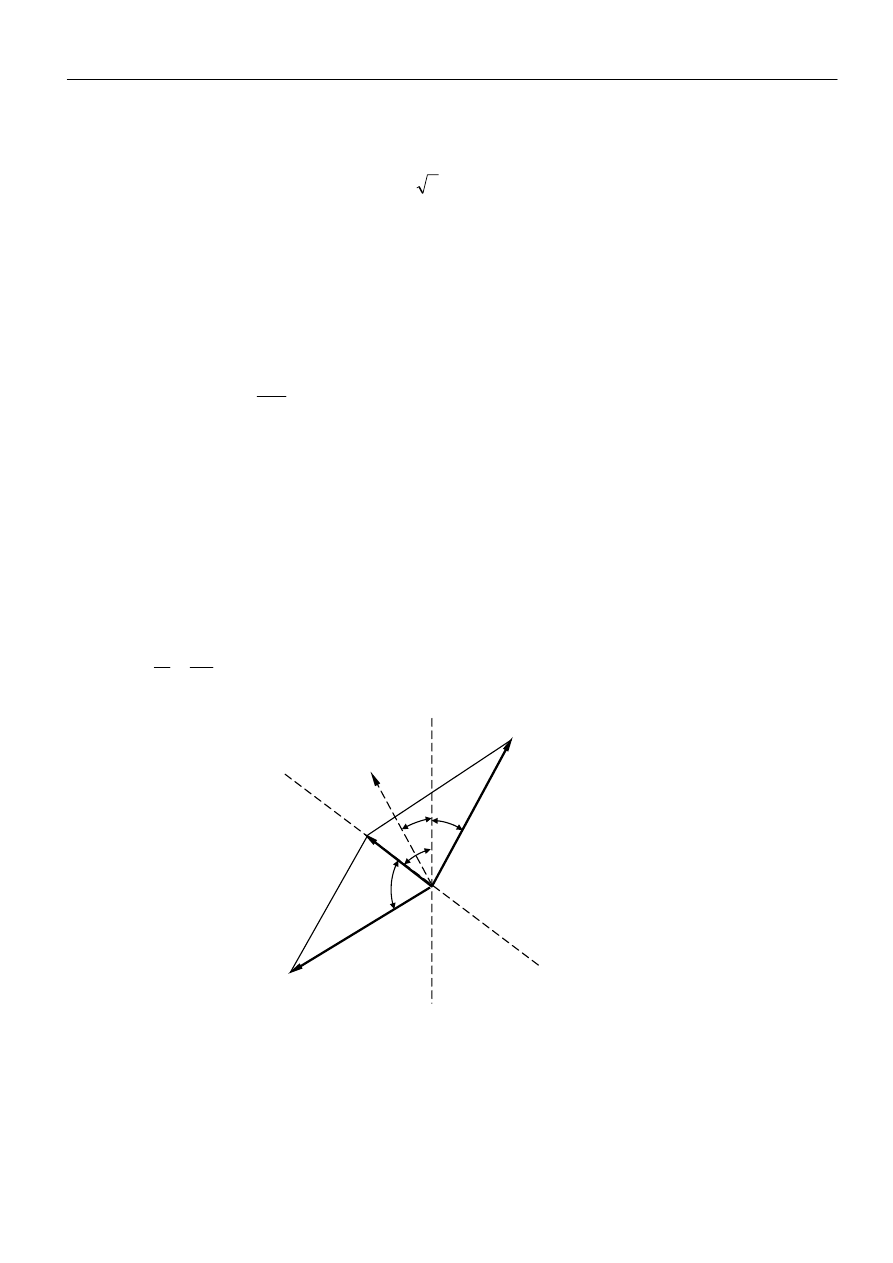
Po złożeniu fal spolaryzowanych kołowo na wyjściu z ośrodka magnetycznie czynnego
otrzymamy znów falę spolaryzowaną liniowo, której płaszczyzna polaryzacji obrócona jest względem
płaszczyzny polaryzacji fali padającej o kąt α (rys.5). Ponieważ wektory
2
1
E
i
E
r
r
wyznaczają
równoległobok będący rombem, zachodzi zatem związek:
)
(
'
φ
α
δ
φ
α
−
−
=
+
(przekątne rombu dzielą
jego kąty na połowy). Stąd:
)
(
2
'
2
1
n
n
h
−
=
=
λ
π
δ
α
.
(3c)
Rys.5 A – A’ - płaszczyzna polaryzacji światła wchodzącego do próbki,
1
E
r
- wektor fali spolaryzowanej prawoskrętnie po przejściu przez próbkę,
2
E
r
- wektor fali spolaryzowanej lewoskrętnie po przejściu przez próbkę,
2
1
E
E
r
r
+
- złożenie wektorów
2
1
E
i
E
r
r
, które wyznacza kierunek polaryzacji światła po przejściu
przez próbkę (płaszczyzna B – B’).
δ
’
φ
φ
α
B
A
B
’
A
’
1
E
r
2
E
r
2
1
E
E
r
r
+
Badanie zjawiska skręcenia płaszczyzny polaryzacji światła
6
Z teorii zjawiska Faradaya wynika, że stała Verdeta wyraża się wzorem:
λ
λ
d
dn
c
m
e
V
e
⋅
⋅
=
2
(3d)
gdzie:
e
m
- masa elektronu, c – prędkość światła,
λ
d
dn
- zmiana współczynnika załamania względem
długości fali.
Jeśli znana jest zależność współczynnika załamania od długości fali, wzór ten może posłużyć do
obliczenia
e
m
e
dla elektronu.
1.3. Zasada pomiaru kąta skręcenia płaszczyzny polaryzacji.
Do pomiaru kąta skręcenia płaszczyzny polaryzacji służą polarymetry. Najprostszym
polarymetrem mogłyby być dwa skrzyżowane polaryzatory. Jeśli skrzyżowane nikole oświetlimy
światłem monochromatycznym, wówczas ulega ono całkowitemu wygaszeniu. Po wstawieniu ciała
optycznie czynnego między nikole obraz ulegnie rozjaśnieniu, całkowite wygaszenie obrazu uzyskamy
obracając analizator o kąt równy kątowi skręcenia płaszczyzny polaryzacji przez kryształ optycznie
czynny.
Układ ten mimo prostoty ma tę zasadniczą wadę, że dokładność wyznaczenia położenia
całkowitego wygaszenia jest bardzo mała. Obecnie do pomiaru kąta skręcenia płaszczyzny polaryzacji
używamy prawie wyłącznie polarymetrów półcieniowych. Wykorzystują one właściwość oka polegającą
na dużej wrażliwości na różnice natężenia dwu sąsiadujących ze sobą obszarów. Schemat polarymetru
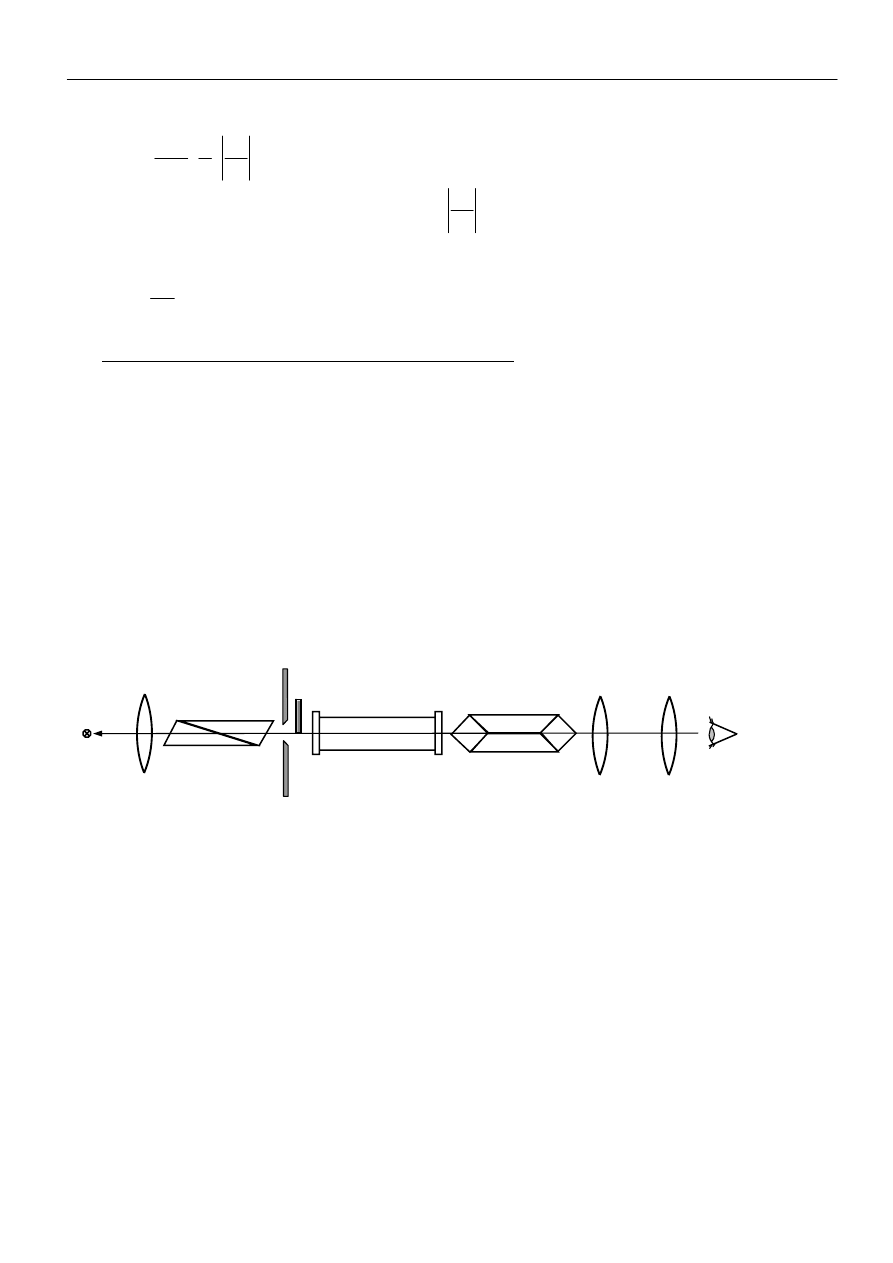
półcieniowego jest przedstawiony na rys.6. Światło lampy sodowej Z przechodzi przez polaryzator P
i pada na kolisty otwór w przesłonie D, którego połowa jest zasłonięta płytką kwarcową Laurenta L. T –
jest rurką wypełnioną badaną cieczą, A – zaś analizatorem. Ob. i Ok. - stanowią obiektyw i okular
lunetki, przez którą prowadzimy obserwacje.
Rys. 6 Schemat polarymetru półcieniowego.
Podział pola widzenia na dwie części uzyskuje się w polarymetrze przez zastosowanie płytki
Laurenta zwanej inaczej półfalówką. Laurent użył do wytworzenia dwóch rodzajów pól widzenia
prostokątnej płytki kwarcowej wyciętej równolegle do osi optycznej.
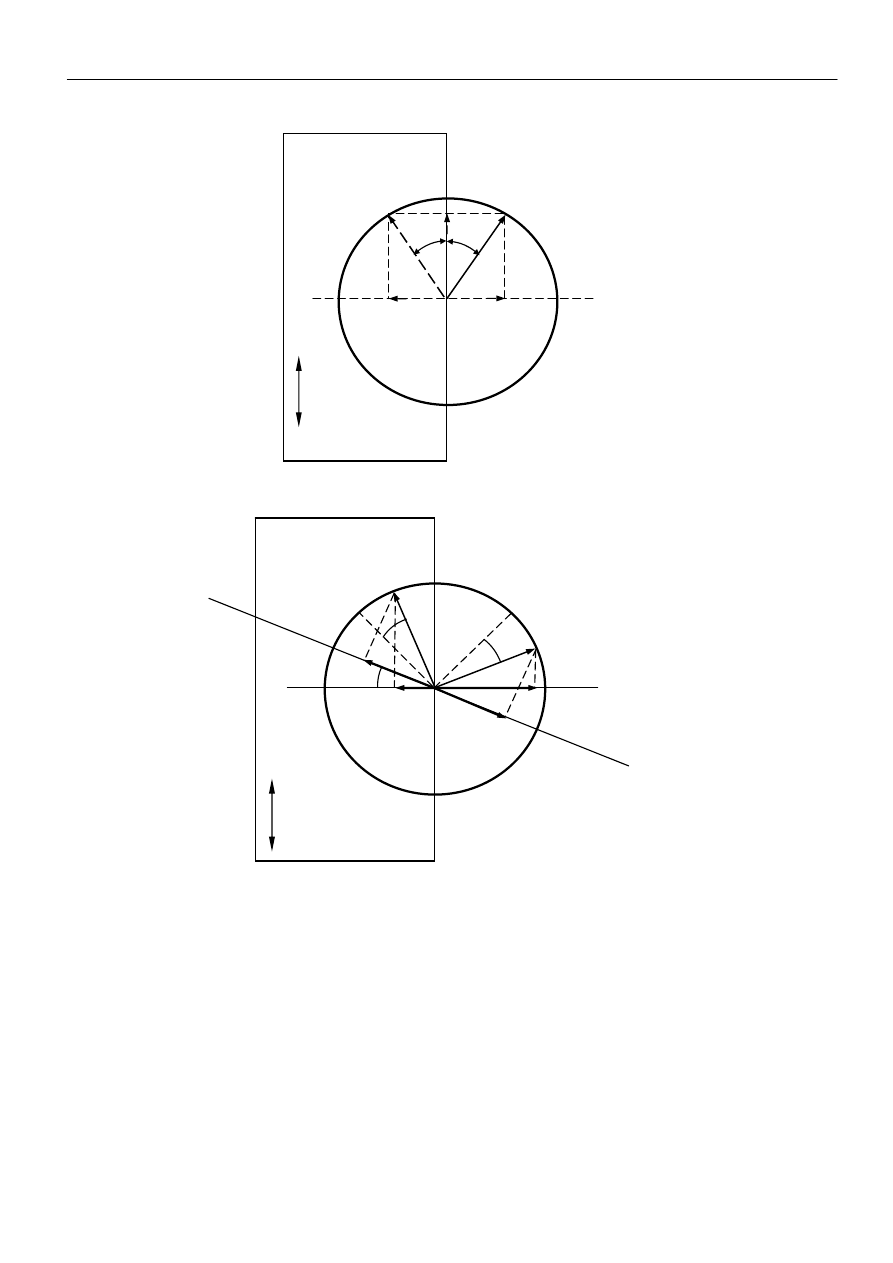
Oś optyczna skierowana jest równolegle do linii podziału pól MN. Kierunek ten zaznaczony jest
podwójną strzałką na rys. 7. Jeśli kierunek drgań padającego na płytkę światła tworzy z osią optyczną
kryształu kąt α (jak na przykład wiązka OA), wówczas ulega on w płytce podwójnemu załamaniu na
wiązkę zwyczajną i nadzwyczajną. Kierunkiem drgań wiązki zwyczajnej jest OC a nadzwyczajnej OD.
W omawianym przypadku kierunek rozchodzenia się wiązki świetlnej jest prostopadły do osi optycznej;
wówczas obie fale biegną w płytce tą samą drogą ale z różnymi prędkościami. Grubość płytki jest tak
dobrana, aby między falą zwyczajną i nadzwyczajną wytworzyła się różnica dróg równa połowie
długości fali, co odpowiada różnicy faz wynoszącej 180º. Wówczas, w chwili gdy drganie pionowe
w obu częściach pola widzenia ma kierunek OD, drganie poziome ma w części niezasłoniętej płytką
zwrot OC, a w części zasłoniętej zwrot OE. Składowe OD i OE po przejściu przez płytkę nałożą się,
dając drganie wypadkowe OB. Zatem płytka Laurenta (półfalówka) przekształca drganie OA na drganie
OB symetrycznie względem kierunku MN zwanego azymutem półfalówki.
Z
P
D
L
T
A
Ob
Ok
O
Badanie zjawiska skręcenia płaszczyzny polaryzacji światła
7
Rys. 7 Zasada działania półfalówki.
Rys. 8
Zmiana oświetlenia pól widzenia w polarymetrze wywołana przez ciało optycznie czynne.
Pomiar
kąta skręcenia przeprowadzamy w sposób następujący. Na początku usuwamy rurkę
z badaną cieczą i ustawiamy analizator w ten sposób, aby obie połowy pola widzenia były jednakowo
oświetlone. Skoro obie części pola widzenia są jednakowo jasne, to znaczy że płaszczyzna drgań
przepuszczanych przez analizator pokrywa się z kierunkiem PR na rys.7. Wtedy bowiem rzuty wektorów
drgań światła w obu częściach pola widzenia (OB i OA) na kierunek drgań przepuszczalnych przez
analizator są jednakowe i wynoszą OE = OC. Następnie wstawiamy rurkę z badaną cieczą, wskutek
czego jasności obu części pola widzenia stają się niejednakowe. Dzieje się tak dlatego, że z powodu
skręcenia o kąt β płaszczyzny polaryzacji przez ciecz optycznie czynną kierunki drgań świetlnych w obu
częściach pola widzenia są teraz OB’ i OA’, a ich rzuty na kierunek drgań przepuszczalnych przez
analizator, jak pokazano na rys. 8, wynoszące OE’ i OC’ nie są sobie równe w obu częściach pola
widzenia. Część lewa pola widzenia jest ciemniejsza od prawej. Jeśli obrócimy analizator tak, aby
płaszczyzna drgań przepuszczanych miała kierunek P’R’, wówczas obie części pola widzenia staną się
ponownie jednakowo jasne, gdyż rzuty wektorów OB’ i OA’ na ten kierunek będą jednakowe. Kąt
obrotu analizatora jest równy kątowi β skręcenia płaszczyzny polaryzacji przez ciecz optycznie czynną.
M
P
R
E
B A
C
D
N
α α
0
M
N
β
β
0
B
’
B
P
’
P
A
A
’
R
R
’
C
’
E
’
β
Badanie zjawiska skręcenia płaszczyzny polaryzacji światła
8
Mierząc zależność kąta skręcenia w funkcji stężenia roztworu lub w funkcji indukcji
magnetycznej B możemy na podstawie zależności (2) lub (3) wyznaczyć skręcenie właściwe cukru lub
stałą Verdeta V.
Polarymetry w technice są często stosowane do wyznaczenia stężenia ciał optycznie czynnych w
roztworach. Polarymetry do pomiaru stężenia cukru w roztworach nazywamy sacharymetrami. Ciała
skręcające płaszczyznę polaryzacji drgań w stanie ciekłym lub w roztworach zawdzięczają tę własność
budowie swoich cząsteczek, dlatego na podstawie pomiarów aktywności optycznej można uzyskać
informacje o strukturze nowych skomplikowanych cząstek.
2. Wykonanie ćwiczenia
I. Badanie naturalnej aktywności optycznej
1. Włączyć zasilanie lampy sodowej. Odczekać około 5 minut do uzyskania pełnej jasności świecenia
lampy. Ustawiamy okular polarymetru tak, aby obraz pola widzenia był ostry.
2. Zbiorniczek (kuwetę) napełniony wodą destylowaną umieszczamy w polarymetrze zwracając
uwagę, by korek nieodkręcany się był skierowany w dół. W zbiorniczku nie powinno być
pęcherzyków powietrza, a oba szkiełka muszą być suche i czyste.
3. Znajdujemy takie położenie analizatora, aby wszystkie trzy części pola widzenia (środkowy pasek
i dwa boczne pola) były jednakowo oświetlone (położenie półcienia).
4. Na skali analizatora odczytujemy kąt. Skala jest wycechowana w stopniach kątowych i wyposażona
w noniusz dziesiętny. Znajdujemy w ten sposób położenie zerowe analizatora α
0
dla wody.
Przygotowujemy sześć roztworów wodnych cukru o różnych stężeniach:
5. Odważamy 1g, 2g, 4g, 6g, 8g, 10g cukru i wsypujemy każdą z odważonych wielkości do zlewki.
6. Wlewamy do każdej zlewki 50ml wody destylowanej i dokładnie rozpuszczamy cukier.
7. Napełniamy kuwetę kolejno każdym z badanych roztworów. Przed dokonaniem pomiaru kąta
skręcenia dla danego stężenia należy dwukrotnie przepłukać kuwetę niewielką ilością roztworu
o tym stężeniu.
8. Umieszczamy zbiorniczek z roztworem w polarymetrze, znajdujemy położenie półcienia,
odczytujemy wartość analizatora
p
α
i obliczamy kąt skręcenia
0
α
α
α
−
=
p
9. Mierzymy długość kuwety, oceniamy błąd pomiaru długości.
10. Kuwetę napełniamy roztworem o nieznanym stężeniu, znajdujemy położenie półcienia.
II. Badanie zjawiska Faradaya
1. Włączyć zasilanie lampy sodowej. Odczekać około 5 minut do uzyskania pełnej jasności świecenia
lampy.
2. W polarymetrze wewnątrz solenoidu znajduje się pręt szklany. Ustawiamy położenie półcienia
w nieobecności pola magnetycznego, odczytujemy kąt analizatora
0
α
.
3. Włączamy zasilanie solenoidu i mierzymy dla co najmniej 6-ciu różnych natężeń prądu kąty
położenia analizatora, odpowiadające nowym położenia półcienia
p
α
. Obliczmy kąt skręcenia
0
α
α
α
−
=
p
.
3. Opracowanie wyników
Część I.
1. Sporządzić wykres zależności kąta skręcenia w zależności od stężenia roztworu. Korzystając
z metody najmniejszej sumy kwadratów liczymy współczynnik kierunkowy nachylenia prostej
h
a
⋅
=
γ
oraz błąd współczynnika
a
Δ
. Wyznaczamy skręcenie właściwe
γ
. Błąd skręcenia
właściwego
γ
Δ
liczymy metodą różniczki zupełnej.
2. Na podstawie wykresu wyznaczamy nieznane stężenie roztworu oraz jego błąd. Nieznane stężenie
można również wyznaczyć z zależności (2) w oparciu o wcześniej obliczoną wartość skręcenia
właściwego
γ
. Błąd w tym przypadku liczymy metodą różniczki zupełnej.
3. Na podstawie zależności wyprowadzonej w Dodatku (D12) wyznaczamy
2
1
n
n
n
−
=
Δ
różnicę
współczynników załamania fali spolaryzowanej prawo i lewoskrętnie w funkcji stężenia. Przyjąć
długość fali światła sodowego
nm
3
,
589
=
λ
.
Badanie zjawiska skręcenia płaszczyzny polaryzacji światła
9
Część II.
1. Sporządzamy wykres
α
w funkcji I (kąt należy przeliczyć na radiany!).
2. Korzystając ze wzoru
L
IN
B
0
μ
=
znajdujemy wartość indukcji magnetycznej, odpowiadającej
każdemu pomiarowi (
;
10
4
7
0
m
H
−
⋅
=
π
μ
N – ilość zwojów; L – długość solenoidu).
3. Korzystając z metody najmniejszych kwadratów znajdujemy stałą Verdeta przyjmując
h
V
a
B
x
y
⋅
=
=
=
,
,
1
1
1
1
α
(skorzystać z komputera). Obliczamy błąd stałej Verdeta.
4. Na podstawie wzoru (3d), w oparciu o obliczoną stałą Verdeta obliczamy wartość
e
m
e
. Występująca
w tym wzorze miara dyspersji
λ
d
dn
może być znaleziona jako wartość wyrażenia
2
1
2
1
λ
λ
−
− n
n
, gdzie
2
1
n
i
n
- są to współczynniki załamania fal λ
1
i λ
2
, pomiędzy którymi leży długość fali użytego
światła λ. Zależność n(λ) dla szkła podana jest na tabliczce obok ćwiczenia. Z tego wykresu należy
odczytać wartości współczynników załamania dla dwóch długości leżących symetrycznie względem
długości fali światła sodowego, np. dla długości 100 nm większej i mniejszej.
Uwaga! Wymiar stałej Verdeta policzonej teoretycznie według wzoru (3d) jest taki sam jak na
podstawie fenomenologicznego wzoru (3a) tylko wtedy, gdy we wzorze (3a)
α
wyrażone jest w
radianach. Należy więc przy liczeniu stosunku
e
m
e
stopnie zamienić na radiany.
Po obliczeniu błędu
e
m
e
należy ustosunkować się do otrzymanych wyników.
4. Pytania kontrolne
1. Jaka jest natura światła w zjawisku polaryzacji?
2. Co to jest światło spolaryzowane liniowo?
3. Jakie są metody otrzymywania światła liniowo spolaryzowanego?
4. Na czym polega naturalna i wymuszona aktywność optyczna?
5. Jaki może być stan polaryzacji światła będącego złożeniem dwóch drgań spolaryzowanych liniowo
zachodzących w kierunkach prostopadłych w zależności od różnicy faz między nimi?.
6. W oparciu o wnioski wynikające z punktu 5 wyjaśnić przyczyny powstawania zjawiska aktywności
optycznej.
7. Omówić zasadę działania polarymetru półcieniowego.
8. Jak płytka półfalowa oddziałuje na światło spolaryzowane liniowo?
9. Na czym polega efekt Faradaya?
5. Literatura
1. D. Halliday, R. Resnick; Fizyka dla studentów nauk przyrodniczych i technicznych, t.II Warszawa
PWN str.588 – 614
2. S. Szczeniowski; Fizyka doświadczalna cz.IV Optyka, PWN, Warszawa 1982 str. 359 – 459
3. W. Shurcliff, S. Billard; Światło spolaryzowane, PWN, Warszawa 1968 str. 11 - 34
4. Optyka i fizyka atomowa, pod red R.I. Sołuchina, PWN, Warszawa 1982 str. 328 – 338
5. J.R. Meyar-Arent, Wstęp do optyki, PWN Warszawa 1977 str. 237 – 263
Badanie zjawiska skręcenia płaszczyzny polaryzacji światła
10
Dodatek I
Fresnelowskie wytłumaczenie skręcenia płaszczyzny drgań.
Zajmiemy się na początku przypadkiem składania dwóch fal elektromagnetycznych o tej samej
częstości
)
(
ω
rozchodzących się w tym samym kierunku (oś 0z ). Amplitudy i fazy fal są różne. Kierunki
drgań wektora elektrycznego obu fal są wzajemnie prostopadłe. Niech A
1
i A
2
oznaczają amplitudy fal,
zaś
2
1
δ
δ
i
- fazy początkowe.
Niech jedno drganie zachodzi w kierunku osi 0x, a drugie w kierunku osi 0y. Oznaczymy wektory
natężenia pola elektrycznego obu fal przez X i Y. Przy tak przyjętych oznaczeniach fale wyrażają się
równaniami:
)
sin(
1
1
δ
ω
+
−
=
kz
t
A
X
(D1a)
)
sin(
2
2
δ
ω
+
−
=
kz
t
A
Y
(D1b)
gdzie k jest liczbą falową
λ
π
2
=
k
,
λ
- długością fali.
Aby znaleźć wynik superpozycji fal, należy te fale dodać. Rozpatrzymy wyłącznie rzuty
wektorów X i Y na płaszczyznę xy, podstawiając z = 0. Trzeba też wyeliminować czas z równań, co
pozwoli znaleźć tor zakreślany przez koniec wektora wypadkowego. Po wykonaniu przekształceń
otrzymamy:
δ
δ
2
2
2
2
2
1
2
1
2
sin
cos
2
=
+
−
A
Y
A
A
XY
A
X
(D2)
gdzie
δ
δ
δ
=
−
2
1
.
Wyrażenie to przedstawia równanie elipsy. W ogólności osie elipsy nie pokrywają się z osiami
układu współrzędnych 0x i 0y. Jednak dla δ=π/2, 3π/2, 5π/2 itd. równanie przybiera postać:
1
2
2
2
2
1
2
=
+
A
Y
A
X
(D3)
W tym przypadku mamy do czynienia z elipsą, której osie równe 2A
1
i 2A
2
pokrywają się z osiami
współrzędnych.
Gdy
π
π
δ
4
,
2
,
0
=
, wówczas
2
1
A
A
Y
X
=
; natomiast jeśli
π
π
π
δ
5
,
3
,
=
, wtedy
2
1
A
A
Y
X
−
=
. Są to
równania prostych przechodzących przez początek układu współrzędnych o współczynnikach nachylenia
2
1
2
1
i
A
A
A
A
−
. Gdy A
1
= A
2
= A i
2
5
,
2
3
,
2
π
π
π
δ
=
itd., wtedy zamiast elipsy otrzymujemy okrąg koła X
2
+
Y
2
= A
2
.
Z przeprowadzonych rachunków wynika, że złożenie dwóch drgań harmonicznych o różnych
fazach i amplitudach zachodzących w dwóch wzajemnie prostopadłych kierunkach, daje zazwyczaj
światło spolaryzowane eliptycznie. Jednak gdy różnica faz drgań
2
1
δ
δ
δ
−
=
wynosi
π
π
π
π
π
5
,
3
,
lub
,
4
,
2
,
0
, wynikiem tej superpozycji jest światło spolaryzowane liniowo.
Jeśli amplitudy drgań są jednakowe (A
1
= A
2
), a δ=π/2, 3π/2, 5π/2 itd., otrzymujemy światło
spolaryzowane kołowo. Jeśli δ=π/2, światło spolaryzowane jest kołowo prawoskrętnie, gdy δ=3π/2 -
lewoskrętnie. Tak wiec drganie kołowe prawoskrętne jest sumą dwóch następujących drgań
(przyjęliśmy
0
0
1
=
=
δ
i
z
):
t
A
X
ω
sin
1
=
t
A
t
A
Y
ω
π
ω
cos
2
sin
1
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
.
(D4)
Badanie zjawiska skręcenia płaszczyzny polaryzacji światła
11
Analogicznie drganie kołowe lewoskrętne jest sumą drgań:
t
A
X
ω
sin
2
=
t
A
t
A
Y
ω
π
ω
cos
2
3
sin
2
−
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
.
(D5)
W wyniku złożenia dwóch drgań kołowych o przeciwnych zwrotach otrzymamy:
t
A
X
X
X
ω
sin
2
2
1
=
+
=
(D6)
0
2
1
=
+
=
Y
Y
Y
(D7)
Drgania wzdłuż osi y znoszą się wzajemnie. Tak więc w wyniku dodania dwóch spójnych drgań
kołowych o przeciwnych zwrotach w rezultacie powstaje jedno drganie spolaryzowane liniowo o
amplitudzie 2A i tej samej częstotliwości ω. Zauważmy, że pojęcie fala zostało tu zastąpione przez
drganie, ponieważ wyeliminowaliśmy z równań (D1a) i (D1b) zmienną z, oznaczającą kierunek
rozchodzenia się fali i rozpatrując wyłącznie rzuty wektorów X i Y na płaszczyznę xy.
Opierając się na tym rozumowaniu Fresnel przyjął, że promień liniowo spolaryzowany padający
na kryształ optycznie czynny w kierunku jego osi optycznej ulega rozkładowi na dwie fale
spolaryzowane kołowo prawo- i lewoskrętnie. Fale te rozchodzą się w krysztale z różnymi
prędkościami. Fala spolaryzowana prawoskrętnie wychodząca z kryształu jest przesunięta w fazie
względem fali spolaryzowanej lewoskrętnie opuszczającej kryształ. Każde z drgań kołowych, jak już
wiemy, jest sumą dwóch drgań liniowych. Dlatego w momencie wyjścia z kryształu w punkcie z = h,
analogicznie do (D6) i (D7), drganie może być przedstawione w postaci:
2
1
X
X
X
+
=
2
1
Y
Y
Y
+
=
(D8)
gdzie X
1,
X
2,
Y
1,
Y
2
– są to drgania liniowe opuszczające kryształ:
)
sin(
1
1
h
kn
t
A
X
−
=
ω
)
cos(
1
1
h
kn
t
A
Y
−
=
ω
(D9)
)
sin(
2
2
h
kn
t
A
X
−
=
ω
)
cos(
2
2
h
kn
t
A
Y
−
−
=
ω
gdzie
2
2
1
1
v
v
c
n
i
c
n
=
=
są to współczynniki załamania fali spolaryzowanej prawo i lewoskrętnie, h
– grubość warstwy kryształu przebyta przez oba promienie, λ - długość fali w powietrzu wspólna dla
obu fal spolaryzowanych kołowo, v
1
i v
2
- są prędkościami światła dla polaryzacji prawo i lewoskrętnej.
Jednak na skutek innej niż miało to miejsce dla światła padającego różnicy faz między
drganiami Y
1
i Y
2
obecnie drganie Y nie jest równe zero. Drgania wzdłuż osi y nie znoszą się wzajemnie.
)]
sin(
)
[sin(
2
1
2
1
h
kn
t
h
kn
t
A
X
X
X
−
+
−
=
+
=
ω
ω
(D10)
)]
cos(
)
[cos(
2
1
2
1
h
kn
t
h
kn
t
A
Y
Y
Y
−
−
−
=
+
=
ω
ω
.
Przekształcając otrzymujemy:
⎥⎦
⎤
⎢⎣
⎡
+
−
−
=
2
)
(
sin
2
)
(
cos
2
2
1
2
1
h
n
n
k
t
h
n
n
k
A
X
ω
(D11)
⎥⎦
⎤
⎢⎣
⎡
+
−
−
=
2
)
(
sin
2
)
(
sin
2
2
1
2
1
h
n
n
k
t
h
n
n
k
A
Y
ω
.
Zatem na wyjściu z kryształu otrzymamy dwa drgania liniowe o tej samej częstotliwości i tej
samej fazie ale o różnych amplitudach, zachodzące w kierunkach wzajemnie prostopadłych. Zgodnie z
tym co zostało powiedziane wyżej na temat składania drgań, drganie będące wynikiem dodania tych
dwóch drgań będzie drganiem spolaryzowanym liniowo o tej samej fazie i częstotliwości co drgania
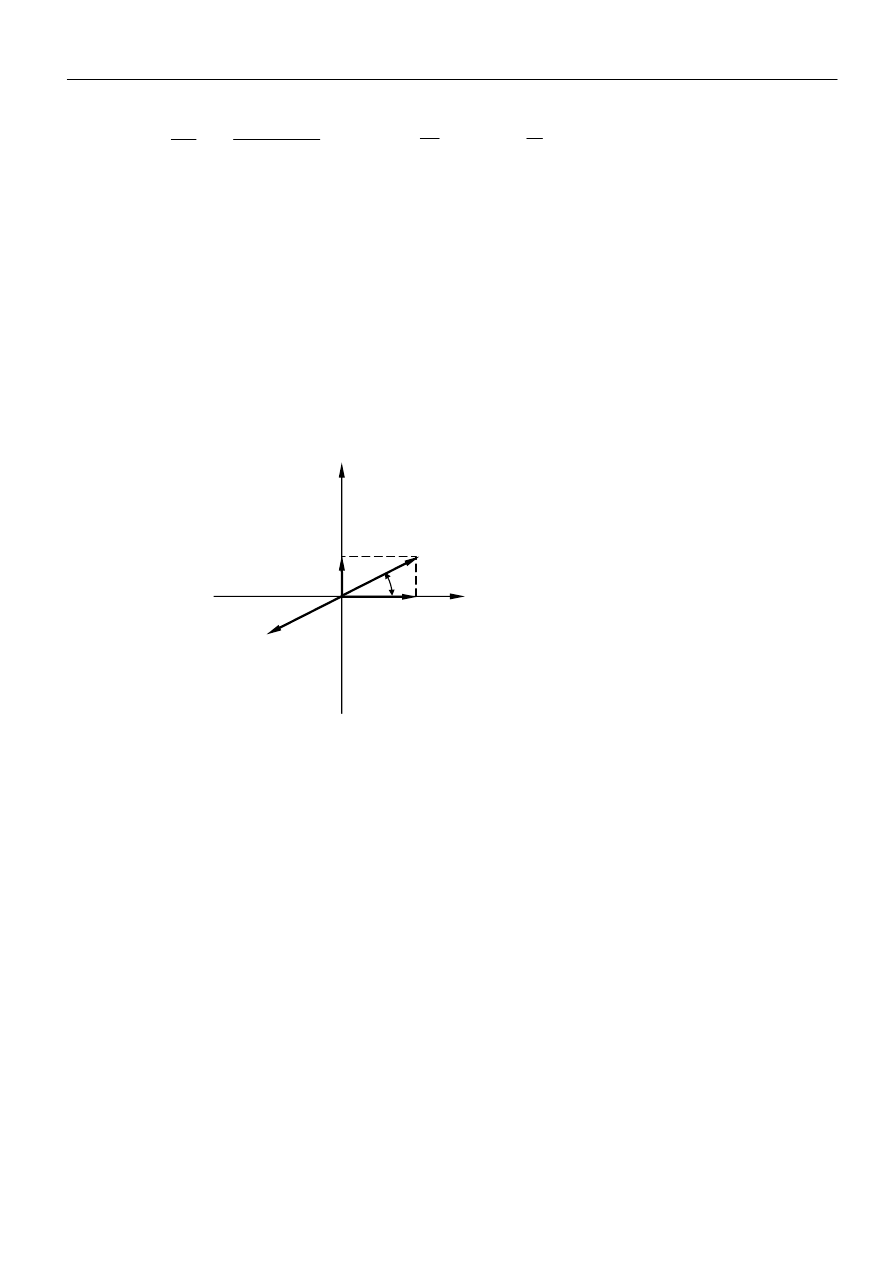
składowe. Jeśli amplitudę drgania X oznaczymy przez
0
X
a amplitudę drgania Y przez
0
Y
, wówczas
kierunek drgania opuszczającego kryształ tworzy z kierunkiem drgania padającego kąt α:
Badanie zjawiska skręcenia płaszczyzny polaryzacji światła
12
,
2
)
(
tg
tg
2
1
0
0
h
n
n
k
X
Y
−
=
=
α
skąd
2
'
)
(
2
2
1
δ
α
=
−
=
n
n
kh
(D12)
gdzie δ’ oznacza różnicę faz na wyjściu z próbki pomiędzy falą spolaryzowaną kołowo prawo i
lewoskrętnie (patrz (12)).
Jak widać skręcenie płaszczyzny drgań jest proporcjonalne do grubości h przebytej warstwy
ciała optycznie czynnego i odwrotnie proporcjonalne do długości fali padającego światła.
Wpływ ośrodka skręcającego uwidoczniony jest za pośrednictwem różnicy współczynników
załamania n
1
– n
2
. Gdy n
1
>n
2
wtedy α>0 skręcenie płaszczyzny polaryzacji następuje w lewo, gdy n
1
<n
2
wówczas α<0 i skręcenie następuje w prawo. W podobny sposób można wyjaśnić wywołane polem
magnetycznym skręcenie płaszczyzny drgań. Umieszczenie ciała w polu magnetycznym powoduje
zmianę jego własności optycznych, a w konsekwencji skręcenie płaszczyzny drgań. Tak jak
w przypadku naturalnej aktywności optycznej tak samo i teraz promień liniowo spolaryzowany
padający na ciało magnetycznie czynne ulega rozkładowi na dwie fale spolaryzowane kołowo prawo
i lewoskrętnie o różnych współczynnikach załamania i co za tym idzie o różnych prędkościach. Różnica
prędkości rozchodzenia się obu fal spolaryzowanych kołowo powoduje skręcenie płaszczyzny
polaryzacji w kierunku obrotu fali szybszej.
Rys.D1 Składanie drgań wzajemnie prostopadłych o tej samej fazie.
x
X
o
y
Y
o
α