Wykład 25

Płyty

1

1. Rodzaje płyt żelbetowych, siły przekrojowe, metody analizy
2. Płyty prostokątne oparte na całym obwodzie

2.1. Obliczanie sił wewnętrznych
2.2. Zasady konstruowania
2.3. Nośność graniczna płyt żelbetowych

Klasyfikacja ze względu na zasady projektowania i konstruowania. Tradycyjnie
rozróżnia się:

płyty jednokierunkowo zbrojone
płyty krzyżowo zbrojone
płyty oparte bezpośrednio na słupach, słupach z głowicami lub na
układach ścian i słupów.

Płyty jednokierunkowo zbrojone zostały już szczegółowo omówione w wykładach
20 i 21. Zasady konstruowania według wykładu 21 stosuje się do wszystkich płyt.
Z płyt krzyżowo zbrojonych omówi się tu tylko płyty prostokątne oparte na całym
obwodzie. W książkach można znaleźć także obszerne informacje o prostokątnych
płytach opartych na trzech krawędziach (występują najczęściej jako ściany
zbiorników) oraz o płytach kołowych (fundamenty kominów i wież).

Z punktu widzenia mechaniki wszystkie wymienione powyżej elementy konstrukcji
są płytami.

2

1. Rodzaje płyt żelbetowych, siły przekrojowe, metody analizy

Oczywiście, dwa pierwsze rodzaje są szczególnymi przypadkami trzeciego.
Wyróżnia się je dlatego, że do obliczania sił wewnętrznych w takich płytach
można zastosować teorię ustrojów prętowych (płyty jednokierunkowo zbrojone)
lub liczne tablice (prostokątne, kołowe, trójkątne płyty krzyżowo-zbrojone).

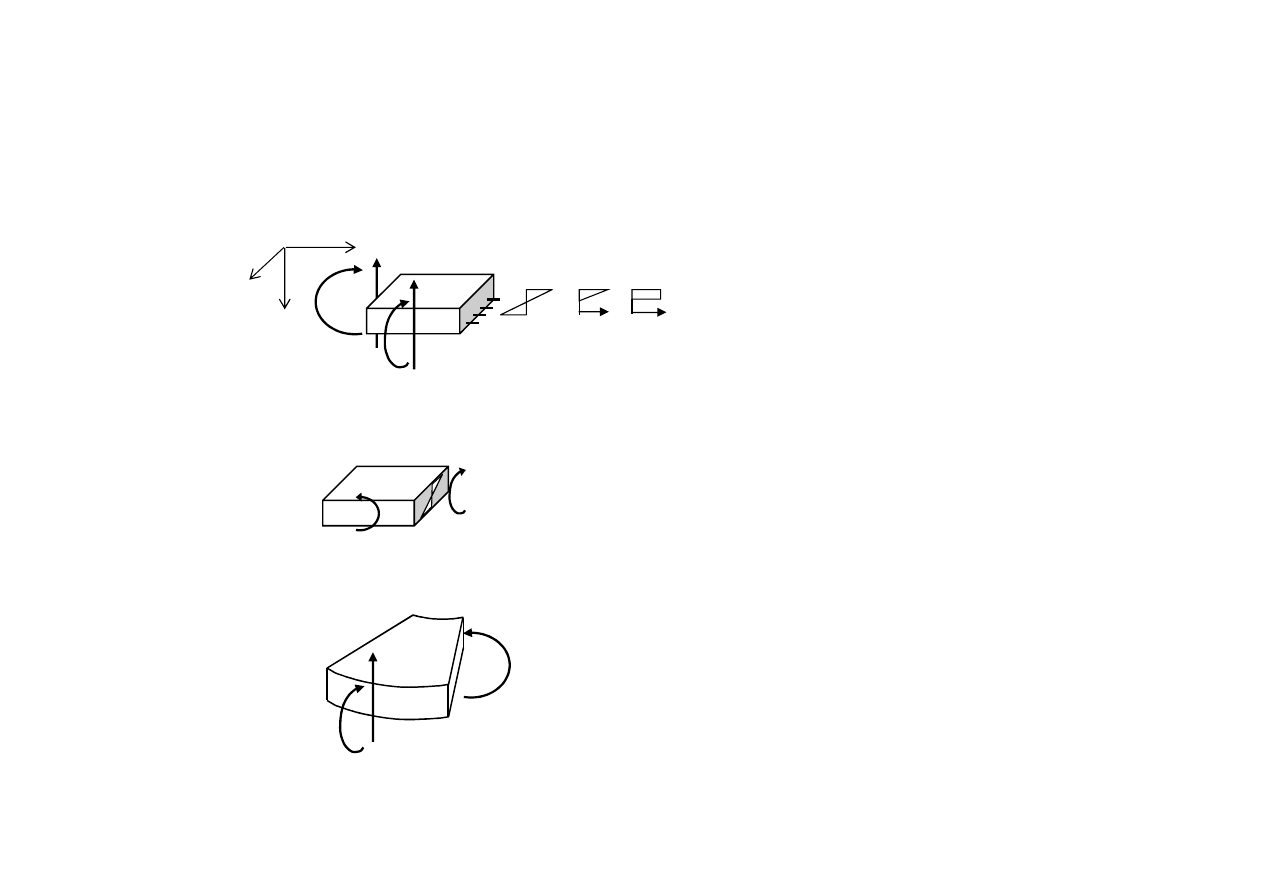
Siły przekrojowe w płytach (momenty zginające i skręcające oraz siły poprzeczne na
jednostkę szerokości przekroju)

x

M

y

V

y

V

x

y

M

x

I

II

III

Momenty wywołane naprężeniami
normalnymi i siły poprzeczne wywołane
naprężeniami stycznymi „jak w prętach”

M

xy

M

yx

Momenty skręcające M

xy

= M

yx

wywołane liniowo rozłożonymi
naprężeniami stycznymi

Płyty koliste rozpatruje się we współrzędnych
biegunowych

3

Między momentami M

x

M

y

i M

xy

i momentami głównymi M

1

i M

2

zachodzą zależności

analogiczne jak między naprężeniami σ

x

, σ

y

i τ

xy

i naprężeniami głównymi σ

1

i σ

2

w

płaskim stanie naprężenia.

Modele będące podstawą projektowania płyt żelbetowych

Teoria płyt sprężystych
Teoria plastyczności (teoria jednorodnych płyt a teoria płyt żelbetowych,
linie załomu)
Analiza nieliniowa
Modele a rzeczywistość

Obliczanie

Tablice oparte na t. płyt sprężystych lub uproszczeniach tej teorii
Przybliżone obliczanie płyt wieloprzęsłowych
Uproszczone zastosowania teorii plastyczności
Metody numeryczne
Metoda różnic skończonych

Zastosowania MES (przede wszystkim oparte na założeniu sprężystości) i
programy komputerowe

4

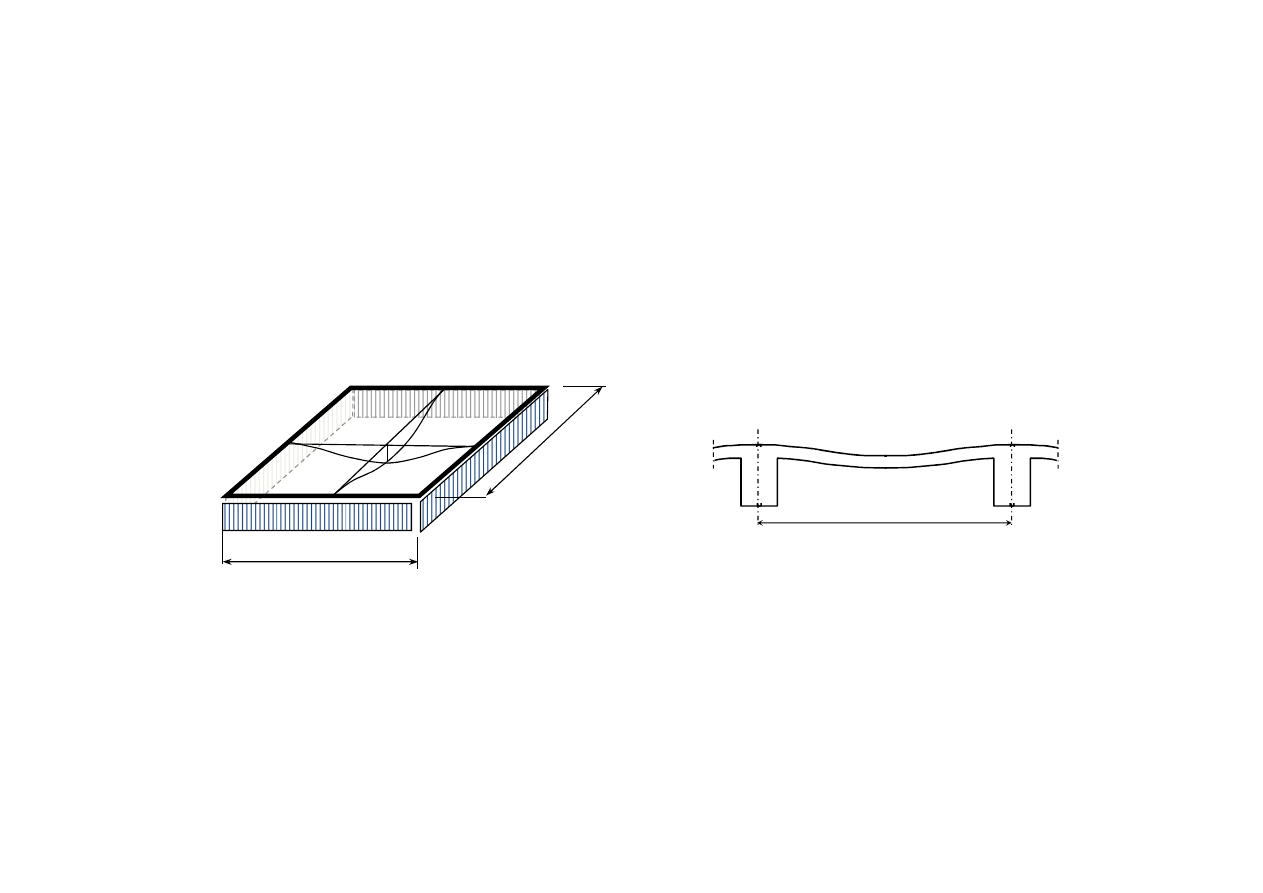
Płyta a układ gęsto rozmieszczonych, krzyżujących się belek (jakościowe
podobieństwo rozkładów momentów zginających). Jeżeli długości boków są
zbliżone (0,5 ≤ l

x

/l

y

≤ 2), to momenty M

x

i M

y

są tego samego rzędu – konieczne

jest zbrojenie dwukierunkowe (na ogół ortogonalne – stąd nazwa płyty krzyżowo-
zbrojone).

l

x

l

x

Jeżeli l

x

≤ 0,5l

y

, to dominuje moment

M

x

i płytę projektuje się jako

jednokierunkowo zbrojoną: wzdłuż
kierunku y umieszcza się zbrojenie
rozdzielcze.

5

2. Płyty prostokątne oparte na całym obwodzie

2.1. Obliczanie sił wewnętrznych

Jeżeli 0,5 < l

x

/l

y

< 2 , to momenty M

x

i

M

y

są tego samego rzędu i płytę

projektuje się jako krzyżowo zbrojoną.

l

y

6

Płyty jednoprzęsłowe można obliczać za pomocą tablic.

l

y

l

x

1

2

3

4

5

6

Tablice oparte są na rozwiązaniach sprężystych (wpływ współczynnika
Poissona powoduje, że można spotkać różne wartości) lub ich
przybliżeniach (np. metoda Marcusa). Przykłady wzorów:

2

x

x

x

pl

M

ϕ

=

2
y

y

y

pl

M

ϕ

=

7

Np. w płycie kwadratowej φ

x

= φ

y

= 0,0479 (w belce swobodnie podpartej 0,125).

Płyty krzyżowo zbrojone są zatem (ze względu na małe siły wewnętrzne) bardzo
korzystne.

Stosując tablice można także w przybliżeniu obliczyć momenty zginające w
wieloprzęsłowych, regularnych układach płyt krzyżowo zbrojonych (szczegóły
w książkach). Dziś jednakże do tego celu stosuje się na ogół MES.

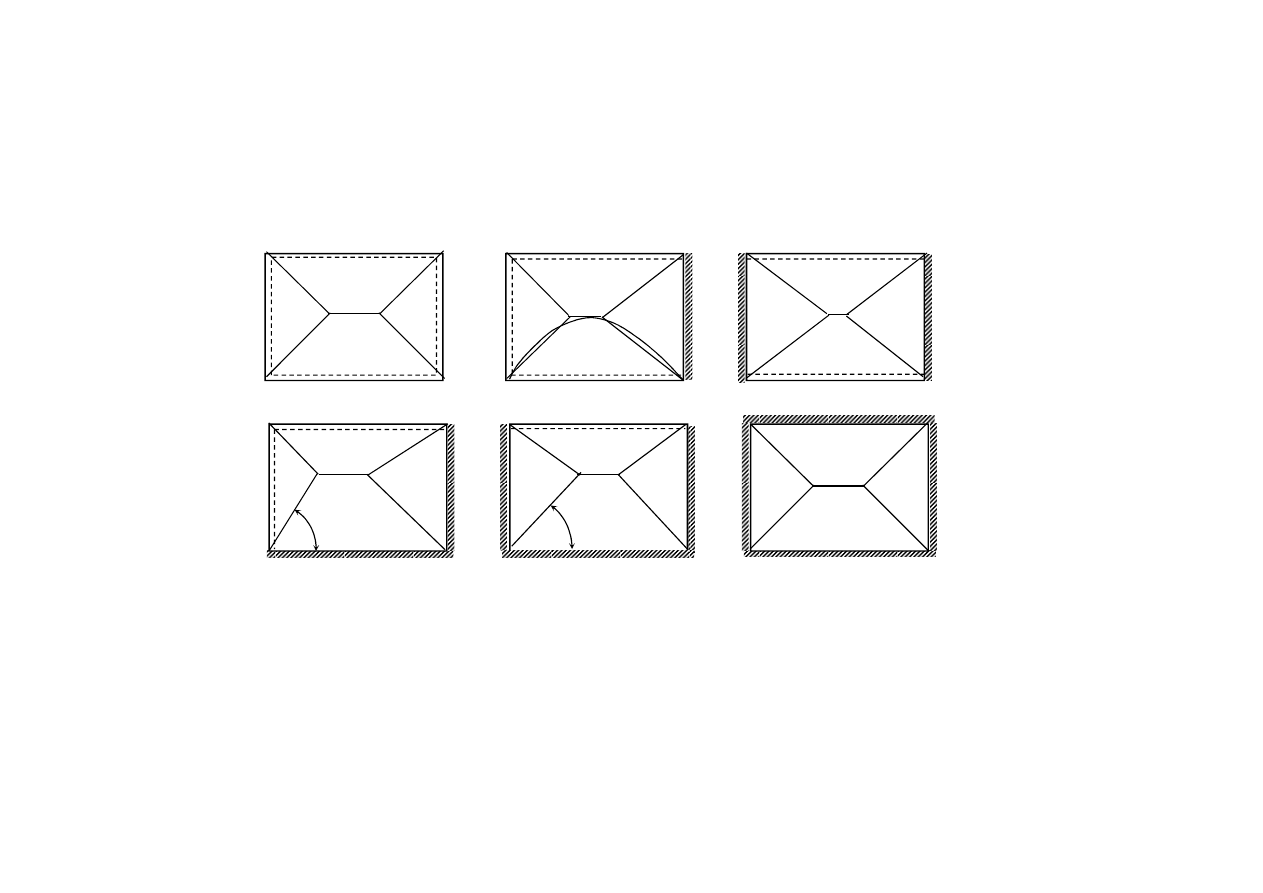
8

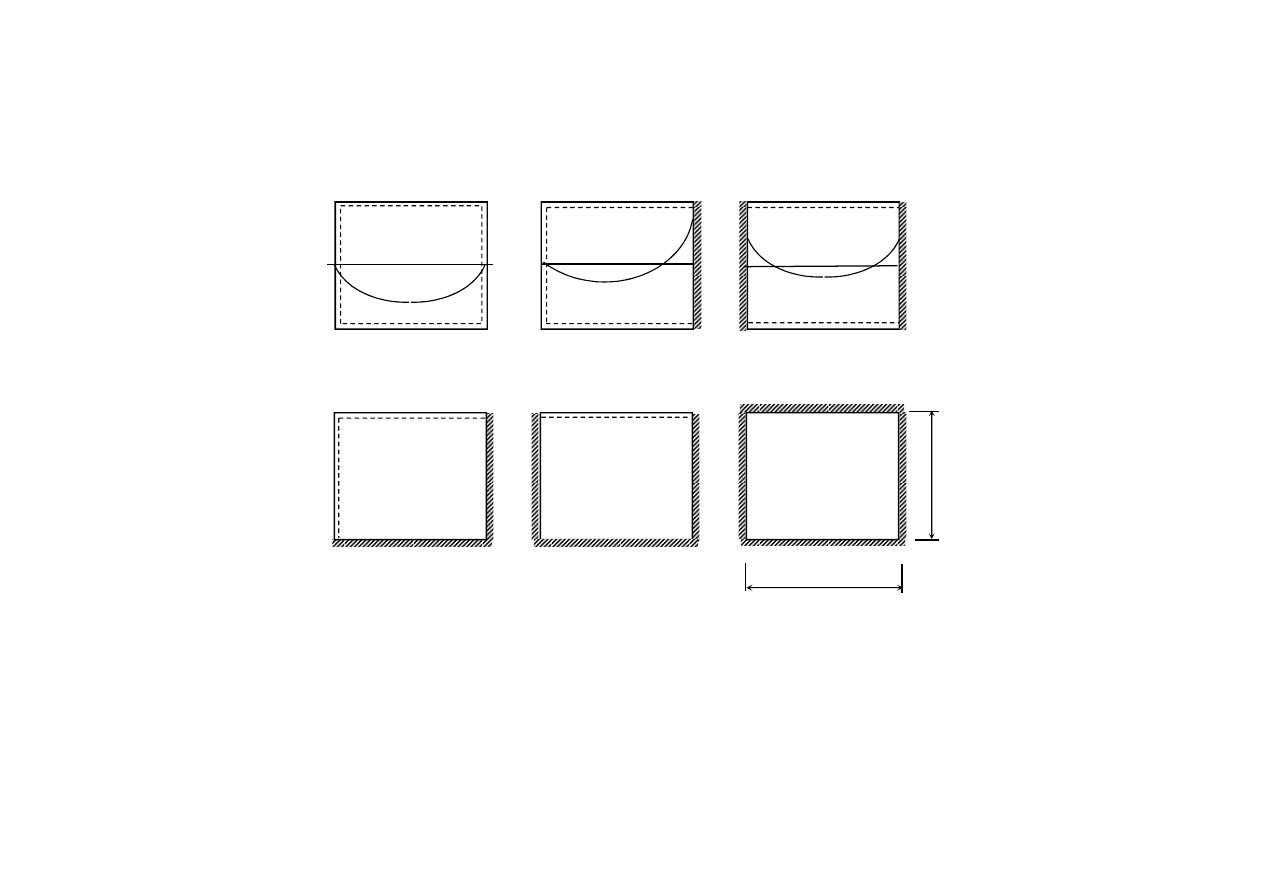
Siły poprzeczne i obciążenia belek podpierających płyty

60

0

45

0

W narożach, w których łączą się brzegi jednakowo podparte, linie podziału
prowadzi się pod kątem 45

0

, a w narożach, w których łączą się boki

niejednakowe, pod kątem 60

0

do boku „sztywniej” podpartego.

9

Stosuje się zasady przedstawione w wykładzie 21 (niektóre z nich przedstawiono
tu ponownie) oraz dodatkowe zalecenia (zaczerpnięte z podręczników – nie są
to przepisy normy) dotyczące zbrojenia narożników. Jeżeli momentyy zginające
obliczono za pomocą programu MES, to zbrojenie naroży można ustalić na
podstawie wyników tego obliczenia.

2.2. Zasady konstruowania

W płytach

swobodnie podpartych

połowę obliczonego zbrojenia przęsłowego

należy doprowadzić do podpór i zakotwić tam zgodnie z zasadami kotwienia
zbrojenia (takimi samymi, jak stosowane do belek).

Rozstaw prętów nie powinien przekraczać s

max,slabs

.

Wartość s

max,slabs

wynosi 3h i nie więcej niż 400 mm. W obszarach występowania

obciążeń skupionych lub w obszarach maksymalnego momentu należy
przyjmować rozstaw nie większy niż

2h i nie większy niż 250 mm.

Zbrojenie dolne w środkowej części płyty ma pola przekroju A

sx

i A

sy

– w

pasmach przy brzegach może być zredukowane do połowy (z wyjątkiem płyt,
które zaprojektowano na podstawie teorii plastyczności zakładając, że
zbrojenie ma stałą intensywność).

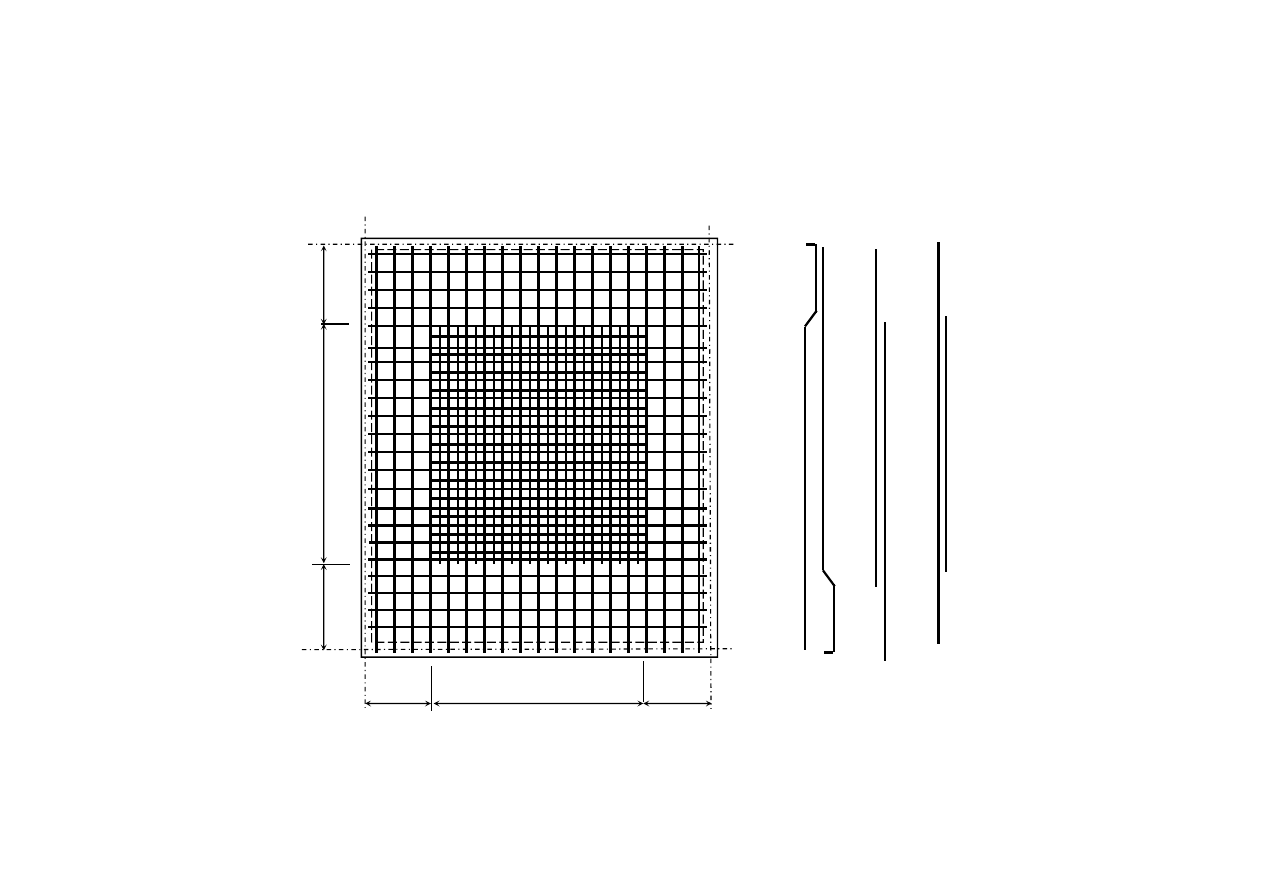
10

0,2

l

x

0,2

l

y

0,6

l

y

0,2

l

y

0,6

l

x

0,2

l

x

11

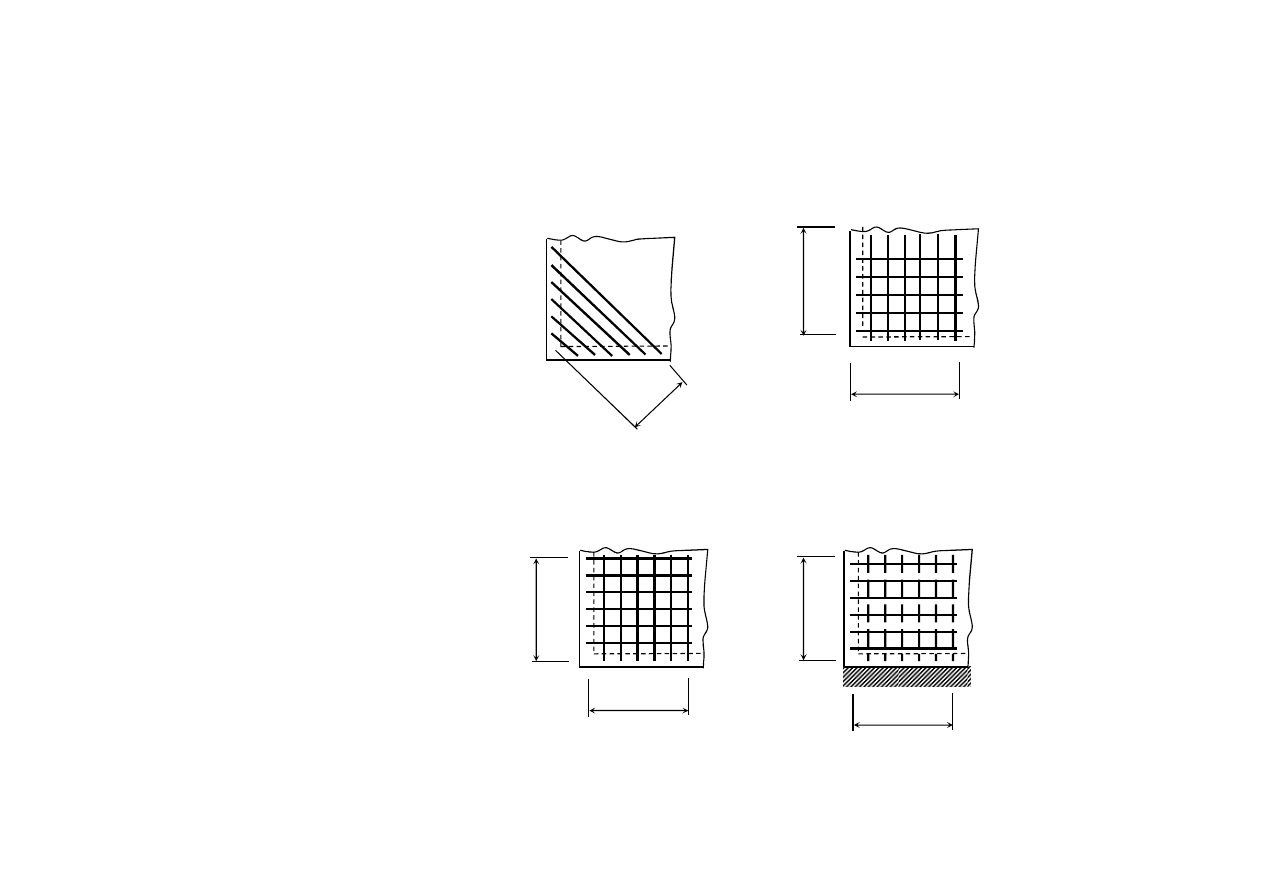
W narożach swobodnie podpartych umieszcza się u dołu zbrojenie o polu
przekroju na metr równym co najmniej A

s

, prostopadle do dwusiecznej naroża albo

zbrojenie ortogonalne

A

s

= max (A

sx

, A

sy

)

l = min (l

x

, l

y

)

0,2

l

0,3

l

0,3

l

Zbrojenie górne wynika z obliczeń i zasad konstruowania (por. wykład 21) –
ponadto w narożach umieszcza się zbrojenie prostopadłe do krawędzi
swobodnie podpartych:

A

s

≥ 0,5max(A

sx

, A

sy

)

0,3

l

0,3

l

0,3

l

0,3

l

Jeśli trzeba, to należy stosować zbrojenie przeciwdziałające unoszeniu się naroży.

12

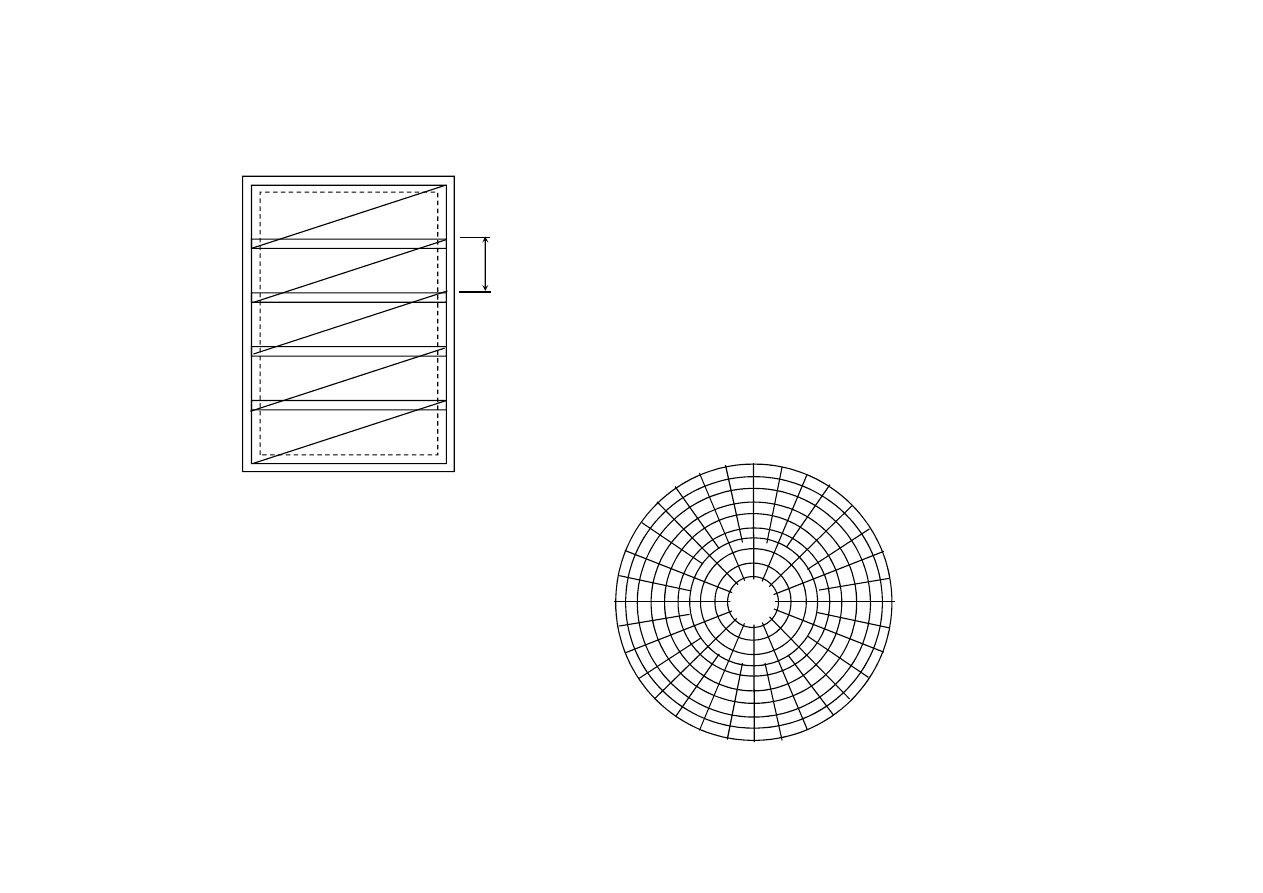
2400

Schemat zbrojenia siatkami
zgrzewanymi o szerokości 2400 mm.
Jeśli A

s

< 1200 mm

2

/m, to wolno

łączyć na zakład całe zbrojenie
w jednym przekroju.

Płyty koliste zbroi się
obwodowo i promieniowo

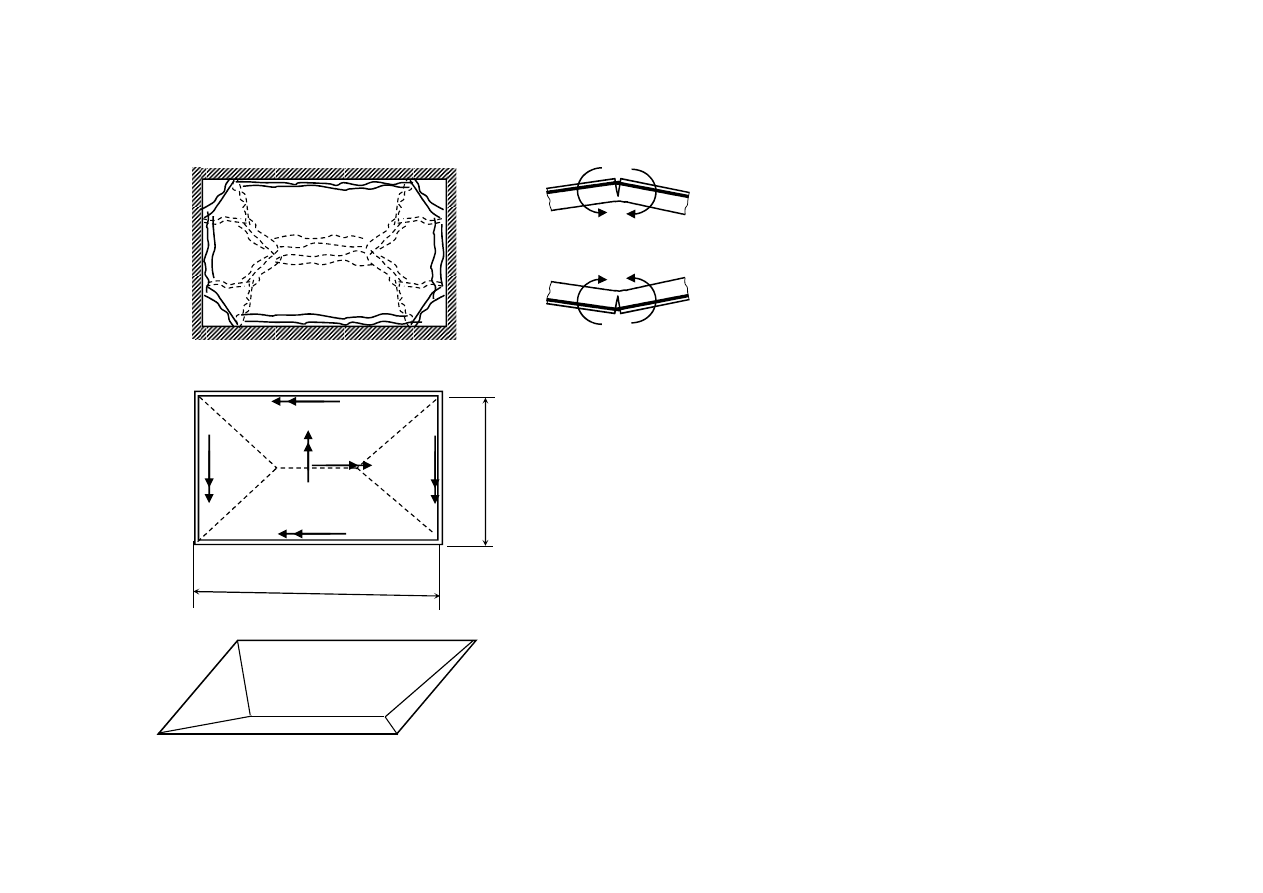
13

2.3. Nośność graniczna płyt żelbetowych

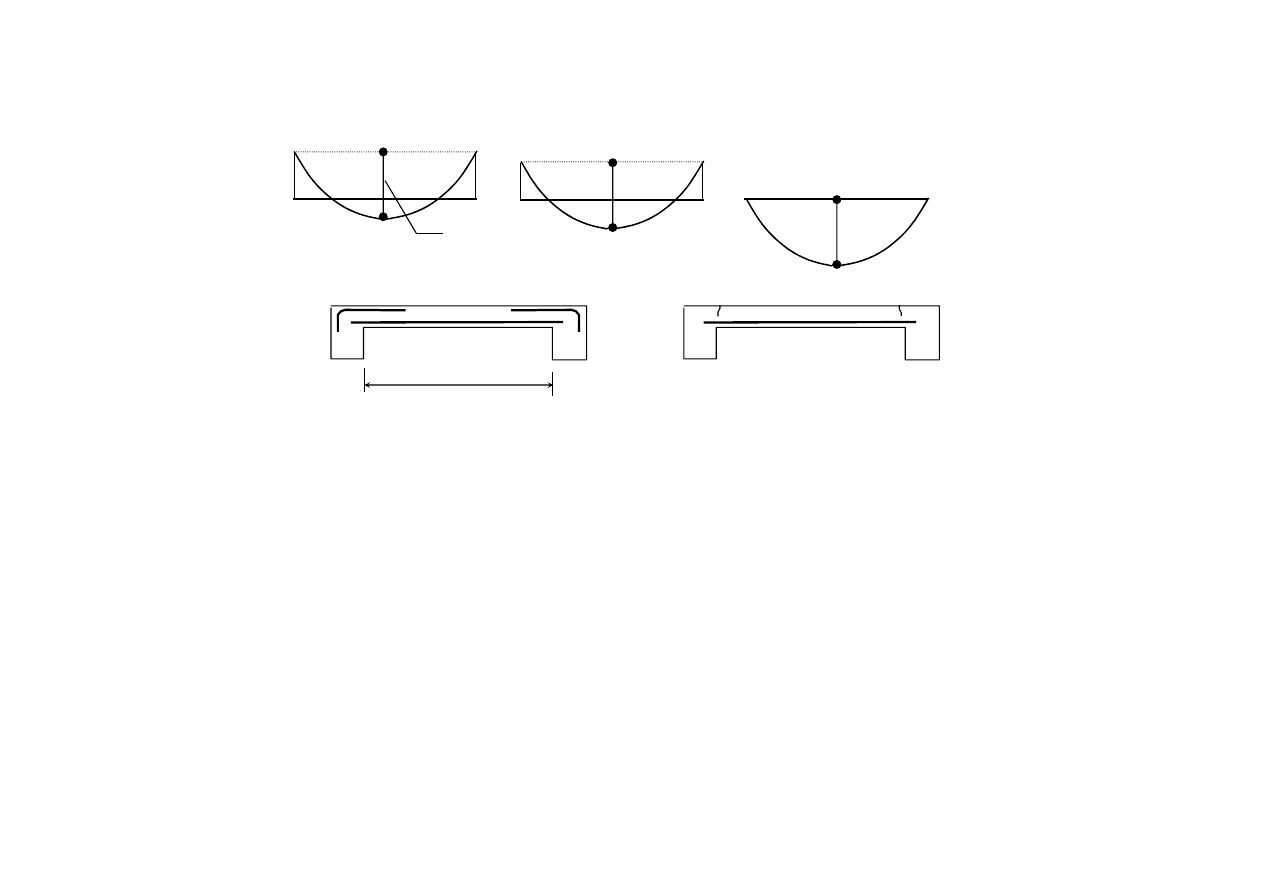
a

b

x

M

y

M

'
y

M

''

x

M

''

y

M

'

x

M

Linia ciągła – rysy na
górnej powierzchni

Linia przerywana – rysy
na dolnej powierzchni

Rysy w płycie utwierdzonej na brzegach –
układ rys i uproszczony schemat tego układu,
będący podstawą metody Gwozdiewa.

Wzdłuż linii załomu momenty zginające
osiągają wartości graniczne,
zależne od ilości zbrojenia. Jeśli bok jest
podparty przegubowo, to momentowi
granicznemu wzdłuż tego boku przypisuje
się wartość zerową

14

W stanie granicznym praca obciążenia związana z procesem plastycznego płynięcia
(proporcjonalna do objętości „daszka”) jest równa pracy wykonywanej przez
momenty graniczne w załomach. Na tej podstawie - jeśli zbrojenie dolne jest jednolitą
siatką (stała gęstość w kierunku x i stała w kierunku y) otrzymuje się wzór

(

)

(

) (

)

b

M

M

M

a

M

M

M

b

a

pb

x

x

x

y

y

y

"

'

''

'

2

2

2

12

3

+

+

+

+

+

=

−

Jeżeli zbrojenie w skrajnych pasmach 0,2a i 0,2b jest zredukowane do połowy (jak
na rysunku ilustrującym zasady konstruowania), to

(

)

b

M

M

M

a

M

M

M

b

a

pb

x

x

x

y

y

y













+

+

+













+

+

=

−

"

'

''

'

2

5

8

5

8

12

3

Inne możliwości np. u J.Kobiaka i W. Stachurskiego.

Projektowanie. Zakłada się wartości współczynników ortotropii i warstwowości

y

x

M

M

=

Λ

y

x

x

M

M

'

'

=

Λ

y

x

x

M

M

''

''

=

Λ

y

y

y

M

M

'

'

=

Λ

y

y

y

M

M

''

''

=

Λ

i po podstawieniu np. do odpowiedniej zależności (np. (1)) otrzymuje się równanie,
z którego można wyznaczyć M

y

(1)

(2)

(3)

15

(

)

(

)

(

)

b

M

a

M

b

a

pb

y

x

x

y

y

y

"

'

''

'

2

2

2

12

3

Λ

+

Λ

+

Λ

+

Λ

+

Λ

+

=

Następnie ze wzorów (3) wyznacza się pozostałe momenty graniczne i wymiaruje
zbrojenie. Wyniki silnie zależą od zakładanych dowolnie wartości współczynników
ortotropii i warstwowości.

Prosty przykład – symetryczna płyta „przechodząca w belkę”
Jeśli b jest małe w porównaniu z a, to można momenty M

x

są małe w porównaniu

z momentami M

y

i otrzymuje się

(

)

y

y

y

M

pb

''

'

2

2

12

3

Λ

+

Λ

+

=

Jeśli przyjąć, że każda ze zmiennych Λ jest równa 2, to

24

2

pb

M

y

=

12

2

''

'

pb

M

M

y

y

=

=

a jeśli każda ze zmiennych Λ jest równa zeru, to M

y

= 0,125pb

2

i momenty

podporowe są równe zeru. Dobierając wartości współczynników Λ można
otrzymać dowolne proporcje momentów podporowych do przęsłowych.

16

0,125

pl

2

l

Z rozpatrywanej tu teorii wynika, że jeśli zbrojenie zaprojektuje się ze względu
na nośność, to dla każdego z przedstawionych powyżej układów otrzyma się
takie same obciążenia graniczne. Czy doświadczenia to potwierdzają?
Projektując na podstawie teorii nośności granicznej mamy zatem znaczną
swobodę kształtowania proporcji zbrojenia w krytycznych przekrojach. Jeśli
zastosujemy rozwiązanie silnie odbiegające od „sprężysto-zgodnego”, to
powstaną bardzo szerokie rysy i nadmierne ugięcia (wymaga się sprawdzania
SGU). Z tego powodu (a także ze względu na ograniczenia kątów obrotu w
załomach) współczynniki ortotropii i warstwowości należy utrzymywać
w granicach zalecanych w podręcznikach.

17

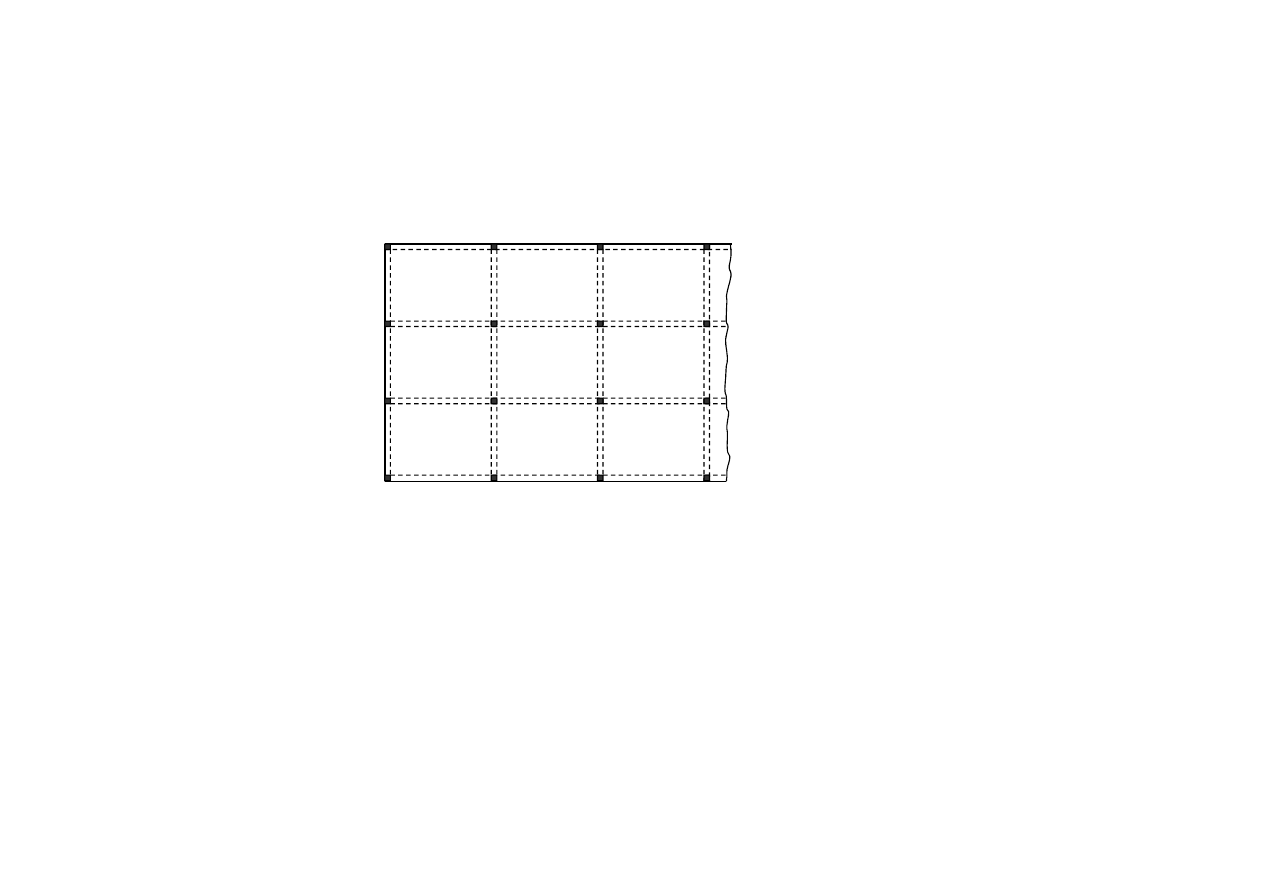
Obliczanie płyt wieloprzęsłowych

1

2

2

2

Zakładamy współczynniki Λ w płycie nr 1 i obliczamy momenty zginające
w tej płycie. Następnie obliczamy płyty nr 2 podstawiając do równań (1)
lub (2) wartości obliczone dla wspólnych krawędzi tych płyt i płyty nr 1
oraz potrzebne nowe współczynniki Λ. Proces kontynuujemy aż do
obliczenia wszystkich płyt.