1. Metody projektowania konstrukcji budowlanych (kryteria klasyfikacji)

Kryteria:

I. Niezawodność

 deterministyczne - (poziom 0), metody historyczne, w których miarą niezawodności jest globalny

(centralny) współczynnik bezpieczeństwa, czyli iloraz wartości nominalnych
nośności i efektów oddziaływań s = R/E. W zależności od wartości współczynnika
bezpieczeństwa stan konstrukcji ocenia się jako: zawodny s < 1, krytyczny
(graniczny) s = 1, niezawodny s> 1, i bezpieczny s > s

1

> 1

 probabilistyczne

o

półprobabilistyczne - (poziom I), w których miarą niezawodności są współczynniki częściowe,

tzn. mnożniki kwantyli losowych zmiennych stanu konstrukcji



i

, lub odstępy bezpieczeństwa



i

, tzn. różnice pomiędzy wartościami zmiennych stanu przyjmowanymi do obliczeń a ich

kwantylami (wartościami charakterystycznymi)

o

uproszczone - (poziom II), w których definiuje się miary niezawodności alternatywne w

stosunku do prawdopodobieństwa zniszczenia lub uszkodzenia konstrukcji, najczęściej w
postaci wskaźnika niezawodności



o

w pełni probabilistyczne - (poziom III), w których miarą niezawodności jest

prawdopodobieństwa zniszczenia lub przekroczenia wartości granicznych efektów
oddziaływań P

f

.

II. Poziom analizy

 1D – w punkcie - , (

R,



E

) odnoszone np. do zmęczenia (ULS) i do stanu granicznego naprężeń

beon sprężony (SLS

 2D – poziom podstawowy- przekrój poprzeczny , przekrój miarodajny (M

R,

M

E

)

 3D – poziom globalny – odnoszone np. do stanu granicznego równowagi statycznej – obrót,

przesunięcie (EQU)

III. Modele konstrukcji i oddziaływań

Model dobiera się do danego materiału:

 ST

 MES

2. Źródła, rodzaje i sposoby opisu niepewności w procesie budowlanym

Niemal wszystkie wielkości, którymi posługujemy się w obliczeniach i analizach inżynierskich są w

różnym stopniu niepewne (z wyjątkiem stałych fizycznych i matematycznych).

Źródła:

 zmienność oddziaływań i parametrów materiałów konstrukcyjnych

 niepełna wiedza dotycząca oddziaływań

 czynnik ludzki – niewiedza, terroryzm, zła wola, błędy ludzi

Rodzaje:

1. parametryczne – brak wiedzy dotyczącej ściśle określonych zjawisk, wartości

 opis losowy

wystarczający

2. systemowe – prawdziwość i adekwatność modelu

 opis losowy niewystarczający

o

fizyczne – opis zjawisk; związaną z naturalną zmiennością właściwości mechanicznych

materiałów budowlanych, oddziaływań i obciążeń oraz wymiarów geometrycznych elementów
i konstrukcji

o

statystyczne – ilość badań i informacji; wynikające z braku pełnej informacji o rzeczywistych

charakterystykach rozważanych wielkości i związane z metodami gromadzenia, opracowania i
analizy wyników obserwacji i badań doświadczalnych

o

modelowe – na ile model przystaje do rzeczywistego zachowania; wiążą się z modelami

matematycznymi opisującymi oddziaływania i reakcje konstrukcji na oddziaływania

Sposoby opisu niepewności:

Niepewność jest tradycyjnie kojarzona z losowym, przypadkowym charakterem zdarzeń i zmiennych.

W związku z tym, do opisu wielkości i zmiennych charakteryzujących się znaczącą niepewnością stosuje się
zmienne losowe lub procesy losowe.

3. Metoda współczynników częściowych wg Eurokodu (podstawowe założenia)

Należy wykazać, że we wszystkich odpowiednich sytuacjach obliczeniowych żaden istotny stan

graniczny nie zostaje przekroczony, jeżeli w modelach obliczeniowych przyjęto wartości obliczeniowe efektów
oddziaływań i nośności konstrukcji.
Metoda współczynników częściowych obejmuje III grupy:
GRUPA 1:

Wartości obliczeniowe właściwości materiałów lub wyrobów

Wartości obliczeniowe (Xd) właściwości materiału lub wyrobu można wyrazić w postaci ogólnej:

m

k

d

X

X









gdzie:X

k

- wartość charakterystyczna właściwości materiału lub wyrobu,

 - współczynnik konwersji

uwzględniający efekty: objętości i skali, wilgotności i temperatury i inne istotne parametry,



m

- współczynnik

częściowy dla materiału lub wyrobu, uwzględniający niekorzystne odchyłki ich właściwości od wartości
charakterystycznej, czyli losowa część współczynnika konwersji

.

Wartości obliczeniowe mogą być ustalane jako: zależności empiryczne, dotyczące zmierzonych
właściwości fizycznych lub na podstawie składu chemicznego, lub na podstawie uprzednio zebranych
doświadczeń, lub na podstawie wartości podanych w normach europejskich lub w innych właściwych
dokumentach.

GRUPA2:

Wartości obliczeniowe oddziaływań, efektów oddziaływań i współczynniki oddziaływań do kombinacji

Wartość obliczeniową oddziaływania Fmożna zapisać w ogólnej postaci:

rep

f

d

F

F







k

rep

F

F







gdzie: F

k

, F

rep

- wartość charakterystyczna i reprezentatywna oddziaływania,



f

- współczynnik częściowy dla

oddziaływania, uwzględniający możliwość niekorzystnychodchyleń wartości oddziaływania od wartości
reprezentatywnej,

 = 1,0 lub 

0

,



1,



2

- współczynniki do wartości kombinacyjnej, częstej i prawie stałej

oddziaływań zmiennych.
Wartości obliczeniowe efektów oddziaływań (E

d

) można wyrazić w postaci ogólnej:

1

}

;

{

,

,







i

a

F

y

E

E

d

i

rep

i

f

Sd

d



lub postaci uproszczonej:

1

}

;

{

,

,





i

a

F

y

E

E

d

i

rep

i

f

d

gdzie: a

d

- wartość obliczeniowa wielkości geometrycznej,



Sd

- współczynnik częściowy uwzględniający

niepewności modelu oddziaływań i, w niektórych przypadkach, modelowania oddziaływań,



F,i

=



Sd*



f,

.

Jeżeli rozróżnia się korzystne i niekorzystne efekty oddziaływań stałych, należy stosować dwa różne
współczynniki częściowe:



G,inf

i



G,sup

GRUPA3:

Wartości obliczeniowe danych geometrycznych

Wartości obliczeniowe danych geometrycznych, takich jak wymiary elementów konstrukcji, stosowane w
obliczeniach w celu wyznaczenia efektów oddziaływania, można wyrazić w postaci wielkości nominalnych:

nom

d

a

a



Jeżeli efekty odchyłek danych geometrycznych (np. niedokładność przyłożenia obciążenia albo miejsca
podpór) mają istotne znaczenie dla niezawodności konstrukcji (np. efekty drugiego rzędu), wartości
obliczeniowe danych geometrycznych ustala się jako:

a

a

a

nom

d







gdzie:

a uwzględnia: możliwość niekorzystnych odchyłek od charakterystycznych lub nominalnych wartości,

łączny efekt jednoczesnego wystąpienia kilku odchyłek geometrycznych.

Uwaga: a

d

może wyrażać także imperfekcje geometryczne, kiedya

nom

= 0, to jest gdy

a0

4. Wartości charakterystyczne i obliczeniowe zmiennych stanu konstrukcji

uwzględniane w metodzie częściowych współczynników (patrz wyżej)

Wartości charakterystyczne są kwantylami o złożonym rzędzie p i rozkładzie prawdopodobieństwa

rozważanej zmiennej losowej ( np. wytrzymałość charakterystyczna betonu na ściskanie jest definiowana jako
kwantyl rzędu p=0,95 zmiennej o rozkładzie normalnym) Wartości charakterystyczne są obliczane na podstawie
badań doświadczalnych wykonywanych wg ściśle określonych procedur.

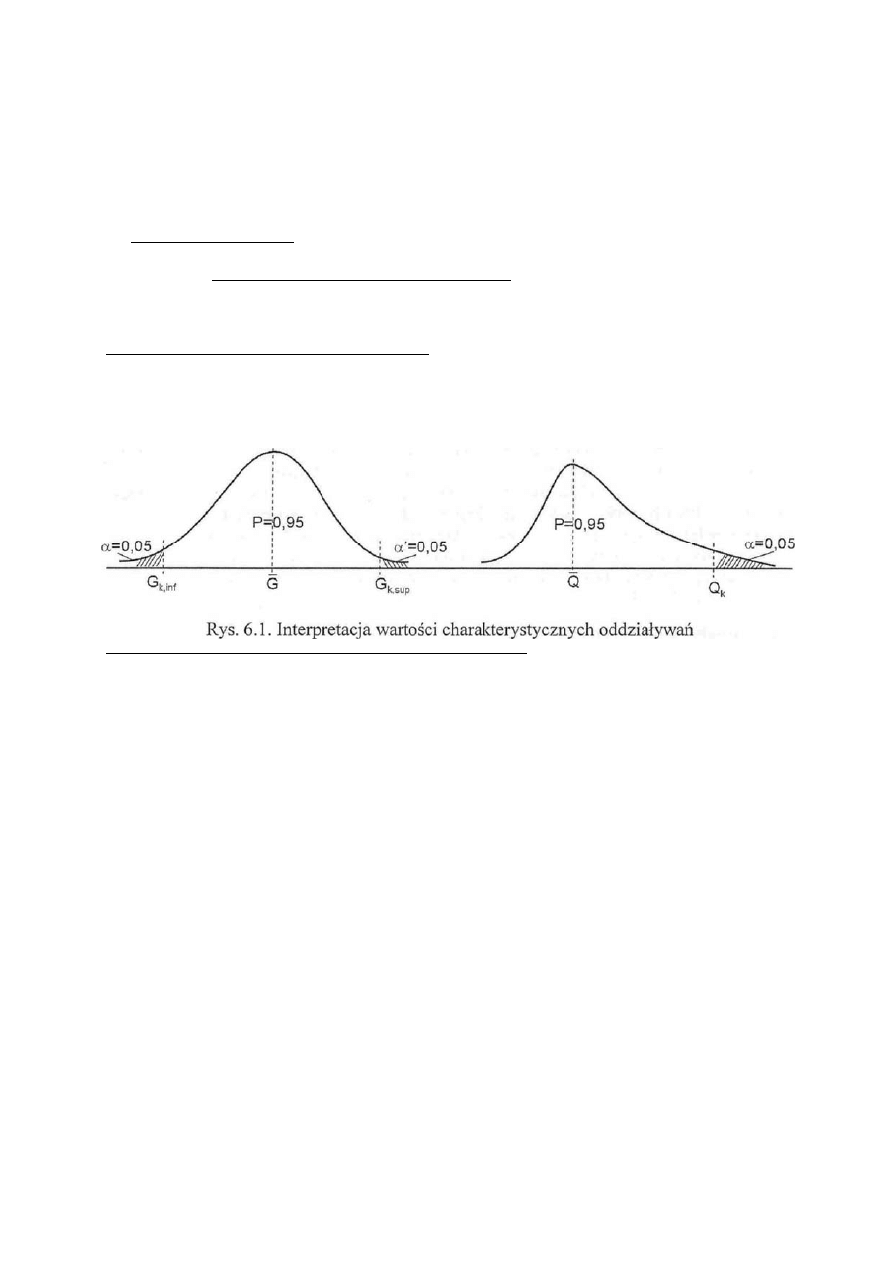
Wartość charakterystyczna oddziaływania jest główną wartością reprezentatywną określa się ją jako

wartość średnią górną lub dolną alb minimalną.

Wartości obliczeniowe używane są obliczeniach konstrukcji metodami półprobabilistycznymi PN-EN

1990 Zdefiniowano je w następujący sposób

- oddziaływania

k

F

d

F

F







- właściwości materiału

M

k

d

f

f









- dane geometryczne

a

a

a

k

d







5. Charakterystyka i opis oddziaływań (kryteria klasyfikacji, wartości

reprezentatywne, charakterystyczne, obliczeniowe, kombinacyjne)

Terminy

Oddziaływanie (F) - zbiór sił (obciążeń) przyłożonych do konstrukcji (oddziaływania bezpośrednie) lub zbiór
wymuszonych odkształceń albo przyśpieszeń, spowodowanych np. zmianami temperatury, zmiennością
wilgotności, różnicami osiadań lub trzęsieniem ziemi (oddziaływania pośrednie).

Oddziaływanie stałe (G) - oddziaływanie, które uważa się za działające przez cały okres odniesienia, a
zmienność jego wielkości w czasie jest pomijalna lub którego zmienność następuje zawsze w tym samym
kierunku (monotonicznie) do czasu osiągnięcia pewnej wielkości granicznej.

Oddziaływanie zmienne (Q) - oddziaływanie, którego zmienność wielkości w czasie nie jest ani pomijalna, ani
monotoniczna.

Oddziaływanie wyjątkowe

(A)

- oddziaływanie, zwykle krótkotrwałe, ale o znaczącej wielkości, którego

wystąpienie w przewidywanym okresie użytkowania konstrukcji uważa się za mało prawdopodobne.

Oddziaływanie sejsmiczne

(Ae) - oddziaływanie wywołane ruchami gruntu w czasie trzęsienia ziemi.

Podział

Oddziaływania dzielić należy ze względu na ich zmienność w czasie:

 oddziaływania stałe (G), np. ciężar własny konstrukcji, umocowane urządzenie, nawierzchnia jezdni,

oddziaływania pośrednie wywołane przez skurcz i nierównomierne osiadanie;

 oddziaływania zmienne (Q, np. obciążenie stropów w budynkach, belek i dachów, oddziaływania

wiatru lub obciążenie śniegiem;

 oddziaływania wyjątkowe (A), np. wybuchy lub uderzenia przez pojazd. Oddziaływania pośrednie

wywołane przez wymuszone odkształcenia mogą być stałe lub zmienne.

Oddziaływania należy również dzielić:

 ze względu na ich pochodzenie - na bezpośrednie i pośrednie;

 ze względu na ich zmienność w przestrzeni -na umiejscowione lub nieumiejscowione;

 ze względu na ich charakter i/lub odpowiedź konstrukcji - na statyczne i dynamiczne.

Oddziaływania są zazwyczaj traktowane jako niezależne od nośności konstrukcji na które działają, ale niekiedy
taka zależność ma charakter sprzężenia zwrotnego, na przykład w zagadnieniach wpływu tłumienia na rezonans
lub śledzącej siły ściskającej. Oddziaływania są najczęściej wyrażone następującymi wielkościami i ich
kombinacjami:

-

siła skupiona (kN), siły rozłożone (kN/m, kN/m

2

), parcie lub nacisk (MPa, lcN/m"), moment (kNm);

-

prędkość (m/s), przyśpieszenie (m/s

2

); na przykład ruchy skorupy ziemskiej, prędkość pojazdów na

łuku mostu;

-

pęd (kgm/s), energia kinetyczna (kgm /s ); na przykład uderzenie pojazdu w budynek lub podporę
mostu;

Kryteria podziału

Do

intensyw
(intensyw

Kom

którą mo
współrzęd

Wart

-

-

-

Wartość c

-

-

Innymi w

-

-

6. Sta

Stany gr
konstrukc
Jeżeli zac

a) E

j

b) S

o
ś
m

c) G

d

d) F

W

n

graniczne
inwestora

Przy spra

najważniejsz

wność, czas

wności, charak

mpletny opis o

żna wyrazić j

dnych przestr

tość charaktery

jako wa

Wart

jeżeli zm

jeżeli

charakterystyc

wartości g
dolnej z za

wartośc

wartościami re

wartość ko
granicznyc
wartość cz
nośności z
granicznyc

any granicz

raniczne nośn

cji.

chodzi potrzeb

EQU (equilib
jakiejkolwiek



małe

przyc



wytr

STR (strengt
odkształcenie
ścianami czę
materiałów ko
GEO (geotech
dla nośności k
FAT (fatigue)

niektórych ok

e dotyczące oc
a i właściwe w

awdzaniu rów

zych atrybut

działania, c

kterystyk geom
oddziaływań n
jako funkcję c

zennych, temp

ystyczna oddz

artość średnią,
tość charaktery

mienność G mo

zmienności G

czna oddziały

górnej z założo

ałożonym praw

i nominalnej,

prezentatywn

ombinacyjna,

ch nośności i n

zęsta, wyrażan

z uwzględnien

ch

zne konstru

ności (ULS)

ba należy spra

brium) – sta

k jej części, uw

e zmiany war

czynę są znac

rzymałość mat

th) – stan

m konstrukcj
ści podziemn

onstrukcji.

hnical) – czyl

konstrukcji ma
) – zniszczenie

kolicznościach
chrony zawart

władze).

wnowagi statyc

ów oddziały

charakterystyk

metrycznych)

na budowlę w

czasu (opis je

peratury, itp.)

ziaływania F

k

, wartość górn

ystyczną oddz

ożna uważać z

G nie można uw

wartością

ywania zmienn

onym prawdop

wdopodobień

którą przyjmo

ymi oddziaływ

wyrażona w

nieodwracalny

na jako iloczyn

niem oddziaływ

ukcji: podzi

– stany gran

awdzać następ
an graniczny

ważanej za cia

rtości lub roz

czące;

teriałów konst

graniczny zw

i lub element

nej, itp., w p

li zniszczenie

a wytrzymało
e zmęczeniow

h zaleca się,

tości budowli

cznej konstruk

ywań zalicza

ki geometryc

), prędkość zm

wymaga znajo

ednoparametro

).

jest główną w

ną lub dolną al

ziaływania sta
za małą, możn

ważać za mał

wyższą G

k,sup

nego (Q

k

) odp

podobieństwe
stwem jej osią

ować można w

zna

wania zmienn

w postaci ilocz

ych stanów gr
n



1

Qk, stoso

wań wyjątkow

iał, charak

niczne dotycz

pujące stany gr

związany z

ało sztywne, k

zkładu w prz

trukcyjnych lu

wiązany ze

tów konstrukc

przypadku kt

lub nadmiern

ość podłoża lub
we konstrukcji

aby zaliczać

(są to okolicz

kcji (EQU) na

się: możliw

czne (miejsc

mienności.

omości ich his

owy), lub jako

wartością repre

lbo jako warto

ałego należy u

na posługiwać

ą, należy posł

i wartością ni

powiada albo:

em, że nie zost

ągnięcia w ok

w przypadku,

any.

nego są:

zynu

Q

k

, st

ranicznych uż

owana przy sp

wych i przy sp

kterystyka,

zące bezpiecz

raniczne:

z utratą równ

iedy:

zestrzeni oddz

ub podłoża na

zniszczeniem

cji, łącznie ze

tórych decydu

ne odkształcen

b skały.

i lub elementu

ć do stanów

zności uzgodn

ależy wykazać

wość wystąp

ce, kierunek

storii w całym

o funkcję wie

ezentatywną i

ość nominalną

ustalać następu

ć się jedną poj

ługiwać się dw

iższą G

k,inf

tanie ona prze

kreślonym okre

kiedy rozkład

osowana przy

żytkowalności

rawdzaniu sta

prawdzaniu od

zasady wer

zeństwa ludzi

nowagi statyc

ziaływań, wyw

a ogół jest bez

m wewnętrzny

stopami fund

ujące znaczen

nie podłoża, k

u konstrukcji.

granicznych

nione dla okre

ć, że:

pienia, powta

k, zwrot), z

m okresie użyt

elu parametrów

i należy okreś
ą w dokument

ująco:

edynczą wart

wiema wartośc

ekroczona lub

resie powrotu;

d statystyczny

y sprawdzaniu
i;

anów graniczn

dwracalnych s

ryfikacji

i i/lub bezpie

cznej konstru

wołanych prz

z znaczenia.

nym lub nad

damentowymi

nie ma wytr

kiedy istotne z

nośności tak

eślonego proje

arzalność,

zmienność

tkowania,

w (czasu,

lać ją:

tacji

ością G

k

.

ciami:

b wartości

albo

y nie jest

u stanów

nych

stanów

eczeństwa

ukcji lub

zez jedną

dmiernym

i, palami,

rzymałość

znaczenie

kże stany

ektu przez

E

d,dst

- w

E

dstb

- wa

Przy sp
konstruk

E

d

- wart

kilka sił w

R

d

- warto

Stany gra

a) f

u

b) w

Zaleca się



u

m
n



d



u

W SGU n

C

d

- gran

E

d

- war

odpowied

7. Ko

SLS (SG
obliczeni
konstrukc
Ustala się

a

K

b

wartość oblicze

artość oblicze

rawdzaniu st

kcji lub połącz

tość obliczenio

wewnętrznych

ość obliczenio

aniczne użytk

funkcji kons
użytkowników

wyglądu kons

ę, aby przy sp
ugięć wpływa
maszyn i i
niekonstrukcy
drgań powodu
uszkodzeń, w

należy sprawd

niczna wartość

rtość obliczen

dniej kombina

mbinacje o

GU): Zaleca

iowych, odp

cji.

ę następujące
a) kombina

W której ko

Kombinacja c

b) kombina

eniowa efektu

niowa efektu

tanu graniczn

zenia (STR i/lu

owa efektu od
h lub moment

owa odpowied

kowalności (SL

strukcji lub

w;

strukcji (nieko

prawdzaniu sta

ających na wy

instalacji) lu

yjnych;

ujących dysko

wpływających n

dzić, czy:

ć obliczeniowa

niowa efektów

acji oddziaływ

oddziaływa

a się, aby

powiadały sp

kombinacje o

acja charakte

ombinacja odd

charakterystyc

acja częsta:

E

d

oddziaływań

oddziaływań

nego zniszcz

ub GEO) nale

ddziaływań, ta

tów,

dniej nośności

LS) dotyczą:

elementu ko

oniecznie estet

anów graniczn
ygląd, komfor

ub ugięć p

omfort ludzi lu

negatywnie na

E

a odpowiednie

w oddziaływań
wań.

ań w SLS i U

kombinacje

prawdzonym

oddziaływań:

erystyczna:

działywań pod

czna jest stoso

d,dst

< E

d,stb

destabilizując

destabilizując

zenia lub na

eży wykazać, ż

E

d

<R

d

akiego jak siła

i.

onstrukcji w

tyka, raczej du

nych użytkow

rt użytkownik

powodujących

ub ograniczają

a wygląd, trw

E

d

<C

d

ego kryterium

ń w jednostk

ULS

oddziaływań

wymaganiom

danych w naw

owana zazwyc

cych,

cych.

admiernego o
że:

a wewnętrzna,

warunkach

uże ugięcia, ry

walności posług

ków, funkcje k

h uszkodzeni

ących przydat

wałość lub funk

m użytkowalno

kach kryterium

ń, przyjmowa

m użytkowa

wiasach {…} m

czaj dla nieodw

odkształcenia

, moment lub

zwykłego uż

ysy itp.).

giwać się kryt
konstrukcji (w

ia wykończe

tność użytkow
kcjonowanie k

ości,

m użytkowaln

ane w odpo

alności i kr

może być wyr

wracalnych sta

a przekroju,

wektor, repre

żytkowania;

teriami dotycz

w tym funkcjo

enia lub el

wą konstrukcji

konstrukcji.

ności, wyznac

owiednich sy

ryteriom zac

rażona jako:

anów graniczn

elementu

ezentujący

komfortu

zącymi:

onowanie

lementów

i;

czona dla

ytuacjach
chowania

nych.

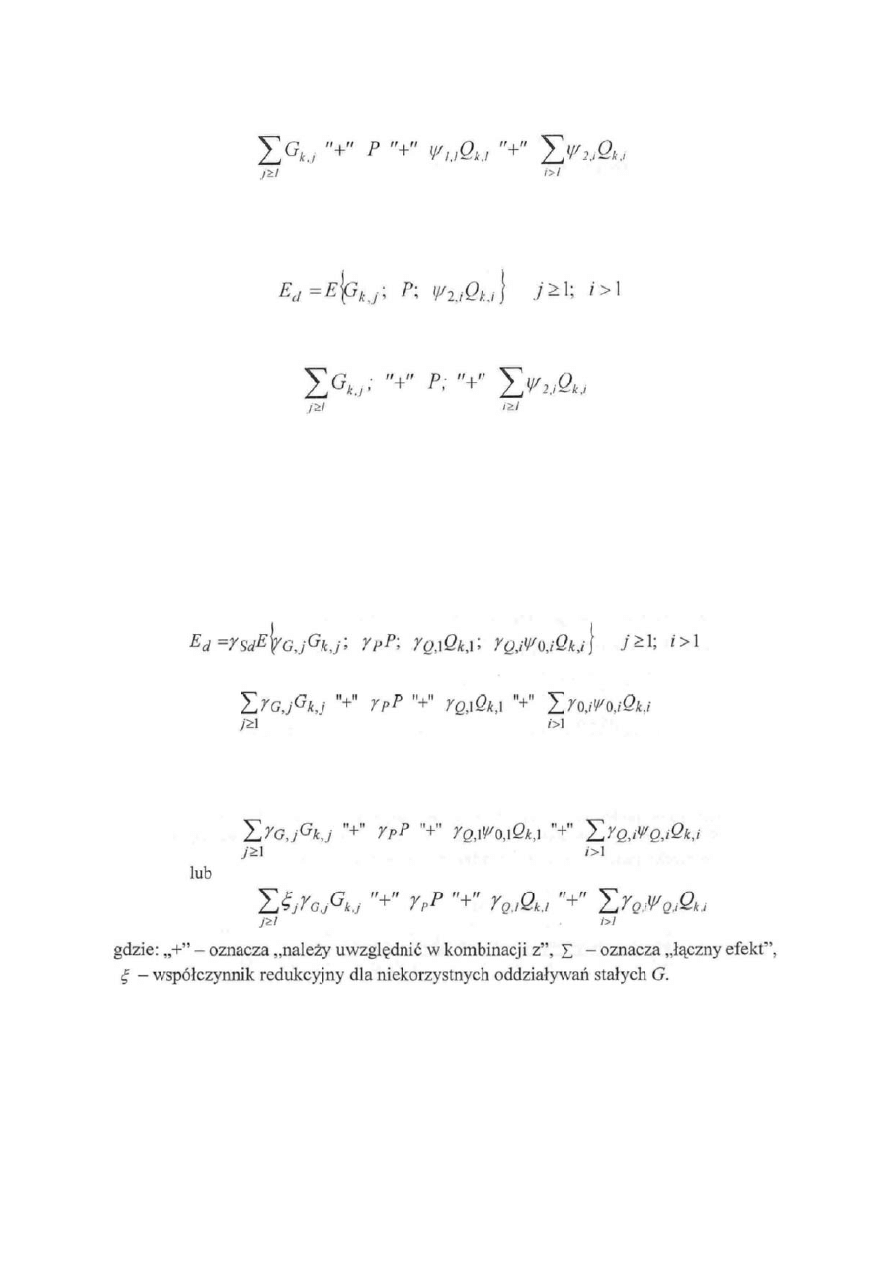
K

c

K

SLU (SG
oddziaływ

a) k

(

A

podanych

b) K

W której ko

Kombinacja c

c) kombina

W której ko

Kombinacja q

GN) - w każdy

wań (Ed) stosu

kombinacje
(kombinacje p

Kombinację

Albo alternaty

h niżej:

Kombinacje o

Ogólna posta

ombinacja odd

częsta stosowa

acja quasi-sta

ombinacja odd

quasi-stała sto

ym krytyczny

ując kombinac

oddziaływań

podstawowe):

oddziaływań

ywnie dla sta

oddziaływań w

ać efektu oddz

działywań pod

ana jest zwykl

ała:

działywań pod

sowana jest zw

ym przypadku

cje oddziaływ

w przypad

podanych w n

anów graniczn

w przypadku w

ziaływań:

danych w naw

le dla odwraca

danych w naw

wykle dla oce

u obciążenia w

wań, które mog

dku trwałych

nawiasach {..

nych STR i G

wyjątkowych

wiasach {…} m

alnych stanów

wiasach {…} m

eny efektów dł

wyznaczać nal

gą wystąpić je

h lub przejś

.} można wyr

GEO, jako m

sytuacji oblic

może być wyr

w granicznych.

może być wyr

ługotrwałych

leży wartości

ednocześnie. W

ciowych sytu

azić jako:

mniej korzystn

zeniowych

rażona jako:

.

rażona jako:

i wyglądu kon

obliczeniowe

Wyróżniamy:

tuacji oblicze

ne wyrażenie

nstrukcji.

e efektów

eniowych

z dwóch

8. Me

Anali

punkcie
globalnej

Rodzaje

a

b

c

d

e

f

g

h

i

9. Zas

czę

10. Ko

lini

Wskaźnik
E = 0. J
wartości
zdefiniow

0









etody analiz

iza konstrukcj

konstrukcji. A

j, analizy elem

analizy:

a) Analiza l

naprężen
odkształc

b) Analiza l

której siły
z zadany
obrotu.

c) Analiza

związek n

d) Analiza n

odkształc
sprężysto

e) Analiza

odkształc
idealnie p

f) Analiza

wykorzys
w część p

g) Analiza

odkształc
sprężystą

h) Analiza

moment/k
wzmocni
dotyczyć

i) Analiza s

twierdzen
uwzględn

sady szacow

ęściowych w

ncepcja i in

iowa i nieli

k niezawodno

Jest odwrotno

oczekiwanej o

wany jako:

g

g

g

g











zy konstruk

cji - procedur

Analizę konstr
mentu konstru

liniowo-spręży

ie/odkształcen

conej.

liniowo-spręży

y wewnętrzne

ymi oddziaływ

liniowo-spręż

naprężenie-od

nieliniowa 1

cona, uwzględ

o-plastyczna, l

nieliniowa 2

cona, uwzględ

plastyczna, lub

sprężysto-ide

stująca związe

plastyczną bez

sprężysto-ide

ceniem, wyko

ą przechodzącą

sprężysto-pla

krzywizna, op

ieniem lub be

także konstru

sztywno-plasty
nia teorii no

nienia odkszta

wania wart

współczynn

nterpretacj

niowa funk

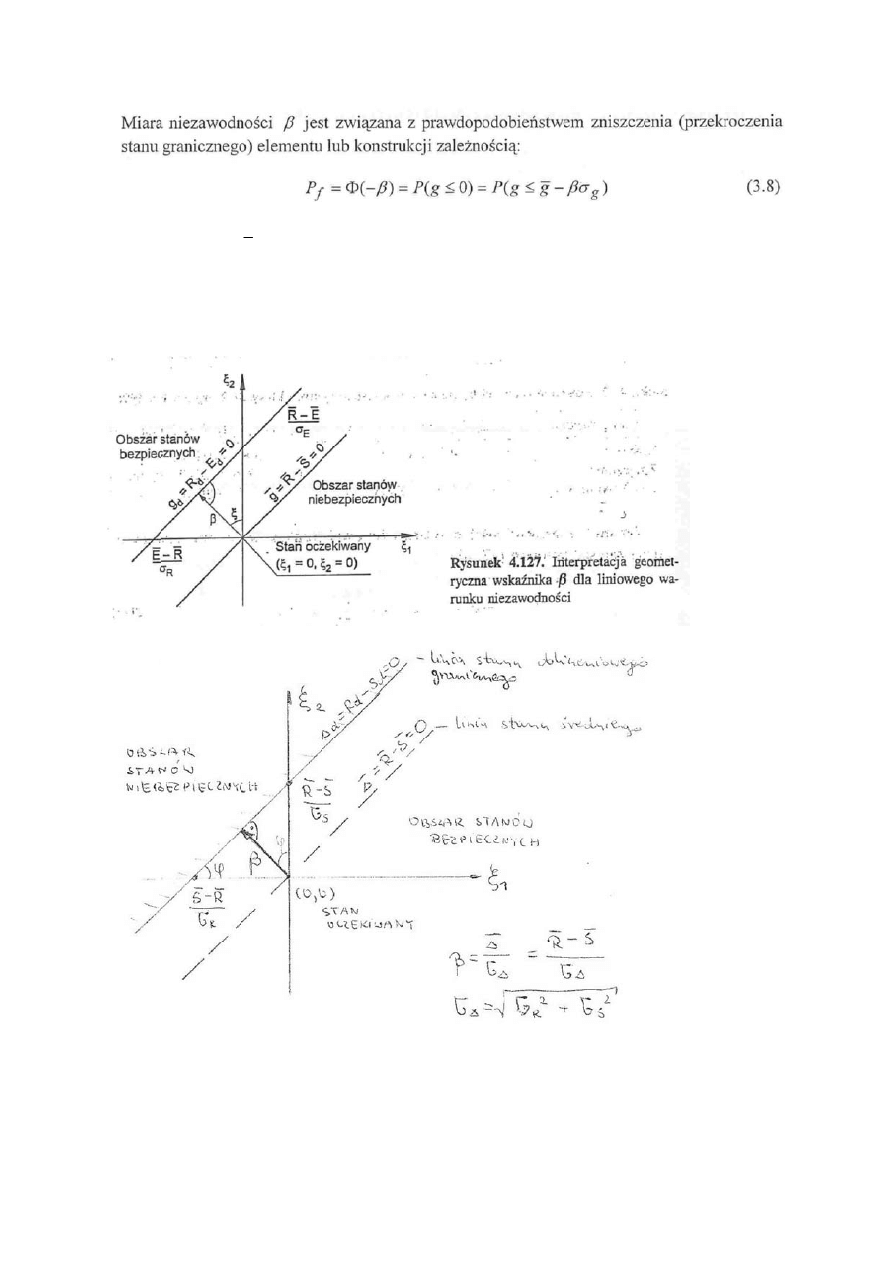
ości β - standa

ością współcz

odstępu bezpi

1

g



kcji:

a lub algorytm

rukcji można

ukcji i analizy

ysta 1 rzędu b

nie lub mom

ysta 1 rzędu z

e i momenty p

waniami zew

żysta 2 rzędu

dkształcenie i

rzędu - anal

dniająca niel

lub sztywno-p

2 rzędu - an

dniająca niel

b sprężysto-pl

ealnie plasty

ek moment/kr

z wzmocnieni

alnie plastycz

orzystująca z

ą w część plas

styczna (1 lu

pisany przez

ez wzmocnien

ukcji z przemi

yczna - analiz

ośności grani
ałceń sprężysty

tości oblicz

ników (patr

ja metody w

kcja stanu

ryzowana zm

zynnika zmie

eczeństwa do

tm służący do

przeprowadz

lokalnej.

bez redystryb

ment/krzywizn

z uwzględnien

podlegają redy

wnętrznymi, a

u - analiza

geometrię kon

liza przeprow
liniowe właśc

plastyczna).
naliza przepro

liniowe właśc

lastyczna).

yczna 1 rzę

rzywizna, opi

a.

zna 2 rzędu

związek mom

styczną bez w

ub 2 rzędu)

część liniowo

nia (zwykle d

ieszczeniem, l
za konstrukcji
icznej (związ

ych i bez wzm

zeniowych n

rz 3 i 4)

wskaźnika

mienna losowa

enności odstę

o odchylenia st

o wyznaczani

ać na trzech p

bucji - analiza

na i począt

niem redystryb

ystrybucji z z

ale bez dokła

sprężysta ko

nstrukcji odks

wadzona przy

ciwości mate

owadzona pr

ciwości mate

du - analiz
sany przez cz

- analiza ko

ment/krzywizn

wzmocnienia.

- analiza ko

o-sprężystą pr

dotyczy konst

lub odkształco

i nie odkształc

zek moment/k

mocnienia).

nośności i e

niezawodn

wyrażająca w

ępu bezpiecze

tandardowego

a efektów od

poziomach, st

a przy założen

kowej geom

bucji - analiza

achowaniem w

adniejszych o

onstrukcji, uw

ształconej.

założeniu, że

riałów (może

zy założeniu

riałów (może

a konstrukcj

zęść liniowo-s

onstrukcji z p

na opisany p

onstrukcji, wy

rzechodzącą w

trukcji nie od

onej).

conej, wykorz

krzywizna pr

efektów odd

ności

 wed

warunek stanu

eństwa v

g

, lu

o odstępu bezp

ddziaływań w

tosując model

niu liniowego

metrii konstru

a liniowo-sprę

warunków ró

obliczeń zdol

względniająca

e konstrukcja
e być ona s

u, że konstru

e być ona s

ji nie odksz

sprężystą prze

przemieszczen

przez część

ykorzystująca

w część plast

dkształconej,

zystująca bezp

rzyjmowany

działywań

dług Eurok

u granicznego

ub inaczej sto

pieczeństwa σ

w każdym

le analizy

związku

ukcji nie

ężysta, w

wnowagi
ności do

liniowy

a jest nie

sprężysta,

ukcja jest

sprężysto-

ztałconej,

echodzącą

niem lub

liniowo-

związek

tyczną ze

ale może

pośrednio

jest bez

metodą

odu:

g = ΔR –

osunkiem

σ

g

. Jest on

Wartość
niezawod

w szereg
otoczeni

W przypa
minimaln

oczekiwaną

dności β, moż

g Taylora i poz

iu rozwija się

adku dwóch z

ną odległość o

g

i odchylen

żna aproksymo

zostawiając ty

warunek niez

zmiennych po

od początku uk

ie standardow

ować rozwijaj

g = R – E

ylko człony lin

awodności w

dstawowych i

kładu współrz

we

g



zmienn

jąc nieliniową

E = g(X

1

, X

2

,…

niowe rozwin

szereg Taylor

interpretację g

zędnych do hip

nej losowej g,

ą funkcję
…,X

n

) = 0

ięcia. W zależ

ra uzyskuje si

geometryczną

perpowierzchn

, niezbędne do

żności od wyb

ę różne rozwi

ą wskaźnika m

ni granicznej:

o obliczenia w

boru punktu, w

iązania.

można przedst

β = ξ

d

= min.

wskaźnika

w którego

awić jako

.

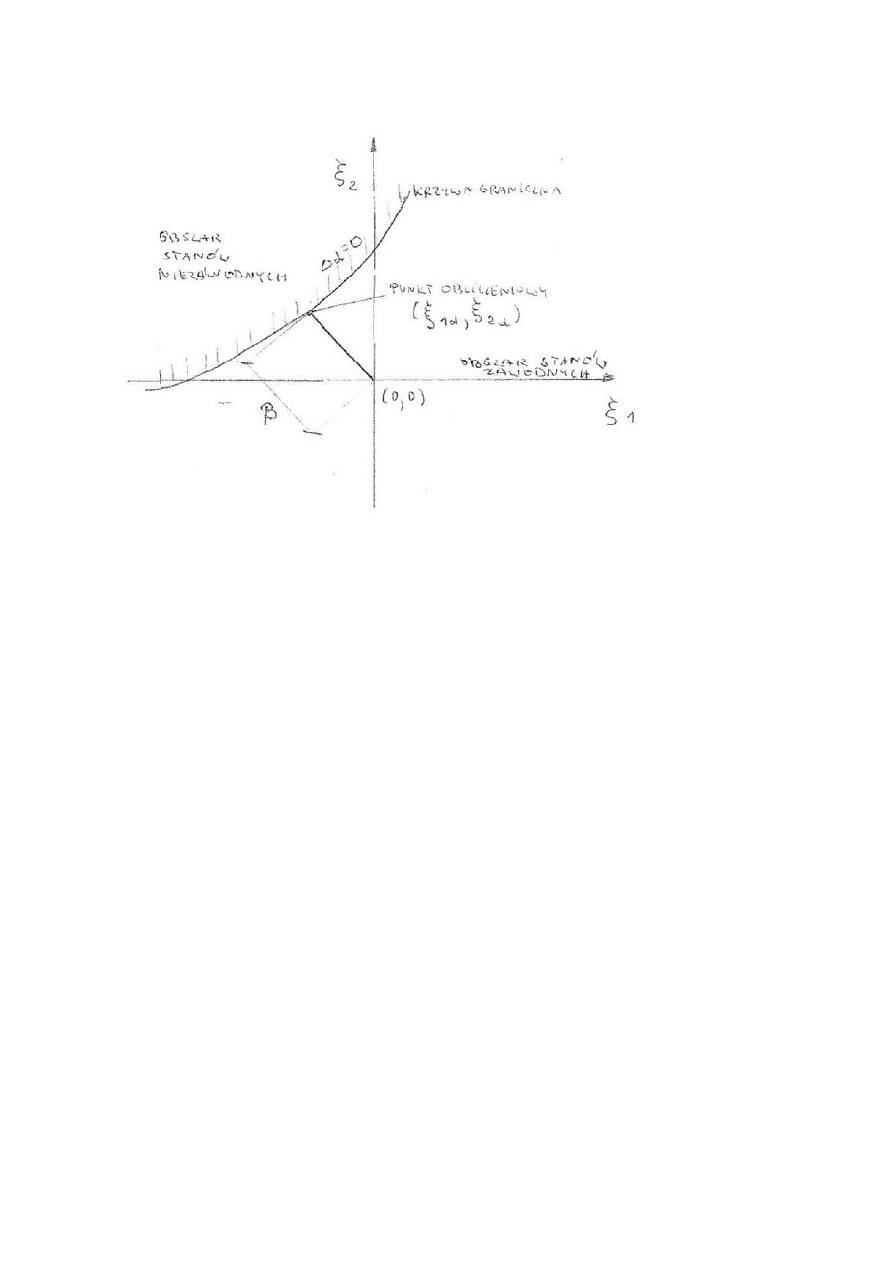
Warunek
W najpro
losowy e
stanów gr
Warunek
W przyp

bezpiecze
szereg Ta
otoczeniu
dwóch zm
jako mini

11. Ele

nie

W celu z
konstrukc
działań za
Jedną z m
Klasa CC
ekonomic
Klasa C
ekonomic
biurowyc
Klasa CC
W odnies
DSL 3 – N
DSL2 – N
DSL1 – N
Poziomy
IL 3 – Ins
IL2 – insp
IL1 inspe

k niezawodno

ostszym przyp

efekt oddziały

ranicznych od

k niezawodno

padku nielini

eństwa

σ

nie

aylora i pozos

u rozwija się w

miennych pod
imalną odległo

ementy zarz

zawodnośc

zapewnienia k

cji zalecają łą

apewniających

możliwości róż

C3 – stosow

cznych, społec

CC2 – stoso

cznych, społe

ch i użyteczno

C1 niskie zagro

sieniu do nadz

Nadzór zaostr

Nadzór norma
Nadzór norma

inspekcji w c

spekcja zaostr

pekcja norma

ekcja normaln

ości ma posta
padku, gdy ro

ywań konstruk

d początku ukł

ości ma posta

iowej postaci

ezbędne do ob

stawiając tylko

warunek niez

dstawowych i

ość od począt

ządzania n

ci, poziomy

konstrukcjom

ączenie odpo

h wymaganą j

żnicowania ni

wana w przy

cznych i środo

wana w prz

ecznych i środ

ości publicznej

ożenie życia l

zoru przy proj

rzony, sprawo

alny, sprawow
alny autokontr

czasie wykona

rzona, sprawo

lna zgodna z p

na, autoinspekc

ać liniową:

ozważa się dw

kcji. Geometr

ładu współrzę

ać nieliniową:

i warunku n

bliczenia β= Δ

o człony nielin

awodności w

interpretację g

tku układu wsp

iezawodno

y nadzoru p

„odpowiednie
wiednich met

jakość określa

iezawodności

ypadku wysok

owiskowych.
zypadku prze
dowiskowych

j

ludzi lub małe

ektowaniu de

owany przez st

wany zgodnie z

rola

ania zdefiniow

wana przez st

procedurami j
cja

wie nieskorel

ryczną interpr

ędnych repreze

:

niezawodnośc

Δ/

σ

można

niowe rozwin

szereg Taylo

geometryczną

półrzędnych d

ością konstr

przy projek

ego stopnia ni

tod i procedu

anych jako „za

jest podział e

kiego zagroż

eciętnego za

h. Do tej klasy

e albo znaczne

finiowano nas
tronę trzecią

z procedurami

wano następują

tronę trzecią
jednostki wyk

owane zmien

retację można

entującego sta

i wartość oc

a aproksymow

nięcia. W zale

ora, uzyskuje
ą wskaźnika n

do hiperpowie

rukcji: klas

ktowaniu i p

iezawodności

ur obliczeniow

arządzania nie

lementów kon

żenia życia l

agrożenia życ

y zalicza się

e skutki społec

stępujące pozi

i jednostki pro

ące poziomy

konawczej

ne podstawow

a przedstawić

an oczekiwany

czekiwaną Δ

wać, rozwijają

żności od wyb

się różne rozw

niezawodności

erzchni granic

sy konsekw

poziomy in

” współczesne

wych z podej

ezawodnością
nstrukcji na kl

ludzi lub ba

cia ludzi ub

większość bu

czne ekonomi

iomy

ojektowej

we – losową

jako odległo

y konstrukcji.

Δ i wariancję

ąc funkcję nie

boru punktu,

wiązania. W p

i β można pr

cznej.

wencji i

nspekcji

ne normy proj

ejmowaniem ś
ą”

lasy konsekw

ardzo dużych

b znacznych

udynków mie

iczne i środow

nośność i

ość prostej

ę odstępu

liniową w
w którego

przypadku

rzedstawić

ektowania

środków i

encji:

h skutków

skutków

eszkalnych

wiskowe

12. Mo

Niezawod
Projektow
postulatem
Najprosts
elementu
przypadk
wprowad
idealnych
Modele n
- dyskretn
-ciągłe.
Modele c
uwzględn
czasie jej
czasu. Ci
Modele d
sposób
-szeregow
-równoleg
-lub mies
model sze
niezawod
od nośno
jeden jeg

model rów
pozostaje

odele niezaw

dność konstr

wanym okresi

m formułowan

sze zadanie teo

u np. belki, gdy

ku gdy konstru
dza się modele

h elementów t

nośności konst

ne

ciągłe nośnośc

nieniem ciągło

użytkowania

ągłym modele

dyskretne - rz

wy,

gły

szany

eregowy- syst

dne, tzn zniszc

ści najsłabsze
o sposób znis

wnoległy - sy

e niezawodny

wodności k

rukcji – zdoln

e użytkowani
nym w odnies

orii losowej n

y efekt działan

ukcja składa si
e nośności. Rz

tak, aby uwzgl

trukcji można

ci są to model

ości materiału

a zmieniają się

em nośności j

zeczywista ko

tem szeregow

czenie jednego

ego elementu.

zczenia.

stem równole

. Nośność sys

konstrukcji

ność do bezaw

a – jest zasadn

sieniu do kons

nośności konst

nia S i nośnoś

ię z wielu elem

zeczywista kon

lędnić wszystk

a podzielić na:

le probabilisty

u i/lub czasu. W

ę w sposób cią

est model w p
nstrukcja jest

y pozostaje ni

o elementu po

Konstrukcje m

gły pozostaje

stemu równole

i: niezawod

waryjnego funk

niczym kryter

strukcji.
trukcji polega

ści elementu R

mentów i wys

nstrukcja jest

kie ważne me

:

yczne zachowa

Właściwości m
ągły. Nośność
postaci proces

zastępowana

iezawodny jeż

owoduje awari

możemy trakt

niezawodny j

egłego zależy

dność eleme

kcjonowania w
rium jakości i

a na obliczaniu

R można opisa

stępują różne m

zastępowana

echanizmy zni

ania się konstr

materiałowe w

konstrukcji je

su stochastycz

przez zespół

żeli wszystkie

ię całej konstr

tować jako uk

jeśli co najmn

od nośności n

entów i kon

w przewidzian

głównym (no

u niezawodnoś
ać dwoma zmi

możliwe mech

przez równow

iszczeń.

rukcji i jej noś

w różnych pun

est w wielu pr

nego.

elementów po

e jego element

rukcji. Nośnoś

ład szeregowy

niej jeden z jeg

najsilniejszego

nstrukcji

nym, tzw.

ormatywnym)

ści pojedyncz

iennymi losow

hanizmy znisz

ważny system

śności z

nktach konstru

rzypadkach fu

ołączonych ze

ty pozostają

ść konstrukcji
y jeśli jest mo

go elementów

o elementu.

zego

wymi. W

zczenia

ukcji i w

unkcją

e sobą w

i zależy

ożliwy

w

model mieszany- jest to model o strukturze szeregowo - równoległej

13. Ciągłe i dyskretne modele oddziaływań: zasady opisu oddziaływań

Praktyce ogólny i abstrakcyjny model zastępuje się prostymi i standardowymi modelami probabilistycznymi
dyskretnymi lub rzadziej ciągłymi.
Do modeli dyskretnych zalicza się
- losowy ciąg jednakowych sił, który może być modelem oddziaływań żywiołowych o katastrofalnych
skutkach(siły wywołane huraganowym wiatrem, pożarem, eksplozją). Wielkość sił nie jest w tym przypadku
istotna, a zasadnicze znaczenie ma sam fakt ich wystąpienia. Model ten jest nazywany strumieniem lub ciągiem
poissonowskim (prawdopodobieństwo wystąpienia sił w czasie opisuje rozkład Poissona).
- regularny ciąg losowych sił – może być używany do opisu oddziaływań użytkowych i środowiskowych
działających na konstrukcję (obciążenia stropów dachów w budynkach itp.) W modelu tym zakłada się, że różne
losowe siły działają w równych odstępach czasu lub w zagadnieniach statycznych, że różne są odstępy sił i
przestrzenie
- Model Ferry-Borgesa i Castanheta
Szeroko wykorzystywany w badaniach obciążeń grawitacyjnych, meteorologicznych i sejsmicznych. Model
oparty jest na koncepcji „przedziałów elementarnych” czasu trwania oddziaływania i rozkładzie wartości
ekstremalnych
- Probabilistyczna prognoza obciążeń jest nie tyle modelem oddziaływań lecz procedurą wykorzystującą
dyskretne zbiory wyników obserwacji na ogół bez przyjmowania konkretnego modelu

14. Metody symulacji Monte Carlo w projektowaniu i weryfikacji stanów granicznych

Symulacja to sztuczne eksperymentowanie z wykorzystaniem modelu matematycznego rzeczywistego systemu
(nośności oddziaływań zjawisk itp.) Podstawowa i najprostszą metodą symulacyjną jest metoda Monte Carlo.
Symulacja Monte Carlo polega na obliczeniu odpowiedzi konstrukcji na oddziaływania o ustalonych
wartościach, wielokrotnym powtórzeniu obliczeń dla różnych wartości oddziaływań, opracowaniu
przechowywaniu i interpretacji uzyskanego zbioru wyników

Koncepcje najprostszego sposobu oceny niezawodności konstrukcji metodą symulacji Monte Carlo można
przedstawić w postaci następującej procedury:

1. Należy wygenerować ciąg niezależnych liczb losowych dla każdej zmiennej losowej uwzględnionej w

analizie niezawodności

2. Następnie obliczyć wartości przyjętej miary niezawodności, traktowane jako wynik fizycznych

eksperymentów

3. Należy sprawdzić czy poszczególne wartości znajdują się w obszarze stanów niezawodnych czy

awaryjnych

4. Po wykonaniu odpowiednio dużej liczby takich operacji (N) obliczyć iloraz liczby wyników

znajdujących się w obszarze awaryjnym N

1

do ogólnej liczby wyników N

5. Wartość ilorazu Q=N1/Nd można potraktować jako miarę zawodności, gdy N dąży do nieskończoności

Metodę Monte Carlo można zastosować do obliczania dowolnych konstrukcji, szczególnie tych, dla których
wektor opisujący zachowanie konstrukcji jest funkcją nieliniową i metoda linearyzacji statystycznej może
prowadzić do znacznych błędów.

15. Statystyczne kontrola jakości materiałów i elementów konstrukcyjnych: koncepcja,

podstawowe metody i procedury

Statystyczna kontrola jakości.
Celem jest określenie przedziału ufności (zakresu), w którym mieści się badana cecha z prawdopodobieństwem z
góry określonym.
Zadania:

 Sprawdzenie czy właściwości gotowego wyrobu odpowiadają warunkom (np. normowym)

 Kontrola toku produkcji, tak aby przebiegał zgodnie w wytycznymi

SKJ przeprowadza się:

 W czasie produkcji

 W czasie odbioru gotowego produktu.

Podział metod SKJ:

 Metody kontroli na podstawie indywidualnych wartości cechy

 Metody kontroli na podstawie miary średnich wartości cechy

 Metody kontroli według oceny alternatywnej