LABORATORIUM MECHANIKI PŁYNÓW

Ć

wiczenie N 7

PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ

1. Cel ćwiczenia

Doświadczalne i teoretyczne wyznaczenie profilu prędkości w rurze prostoosiowej

2. Podstawy teoretyczne:

Kształt profilów prędkości przepływu płynu w rurociągu jest różny dla ruchu

laminarnego i turbulentnego.

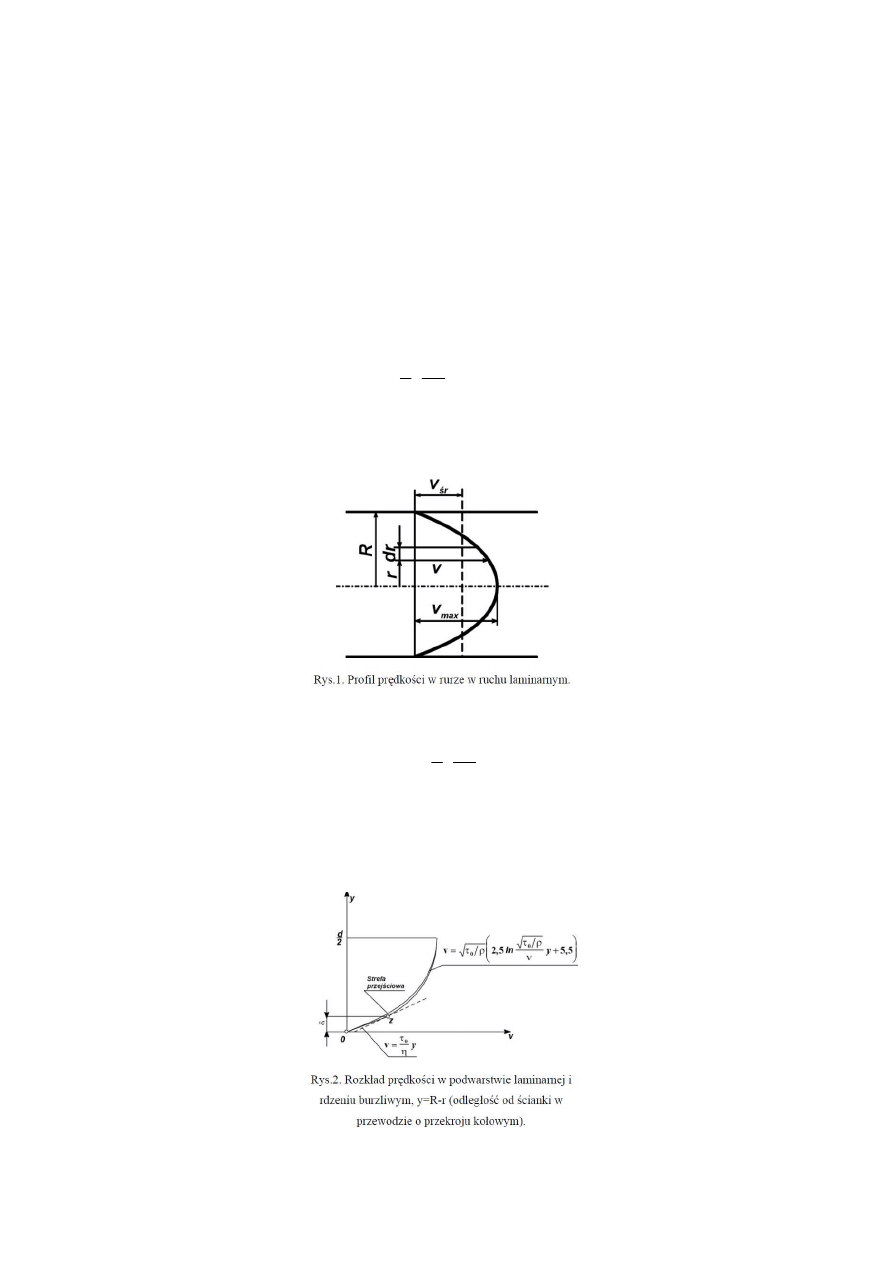
Dla przepływu laminarnego w rurze prostoosiowej profil prędkości przyjmuje kształt

paraboli (rys. 1) o równaniu:

(

)

2

2

4

1

r

R

l

p

−

⋅

∆

⋅

=

µ

υ

,

(1)

gdzie: p

∆

- spadek ciśnienia na odcinku przewodu o długości l,

µ

- dynamiczny współczynnik lepkości.

Prędkość maksymalna występuje w osi przewodu i wynosi:

2

max

4

1

R

l

p

⋅

∆

⋅

=

η

υ

.

(2)

W praktyce najczęściej występuje przepływ turbulentny. Aby określić zależność

opisującą profil prędkości przepływu należy rozwiązać równanie Reynolds’a.
Do wyznaczenia rozkładu prędkości w pobliżu ścian przewodu, przyjęto model
przedstawiony na rys. 2. W podwarstwie, o grubości

δ

, rozkład prędkości jest liniowy i

opisuje go równanie

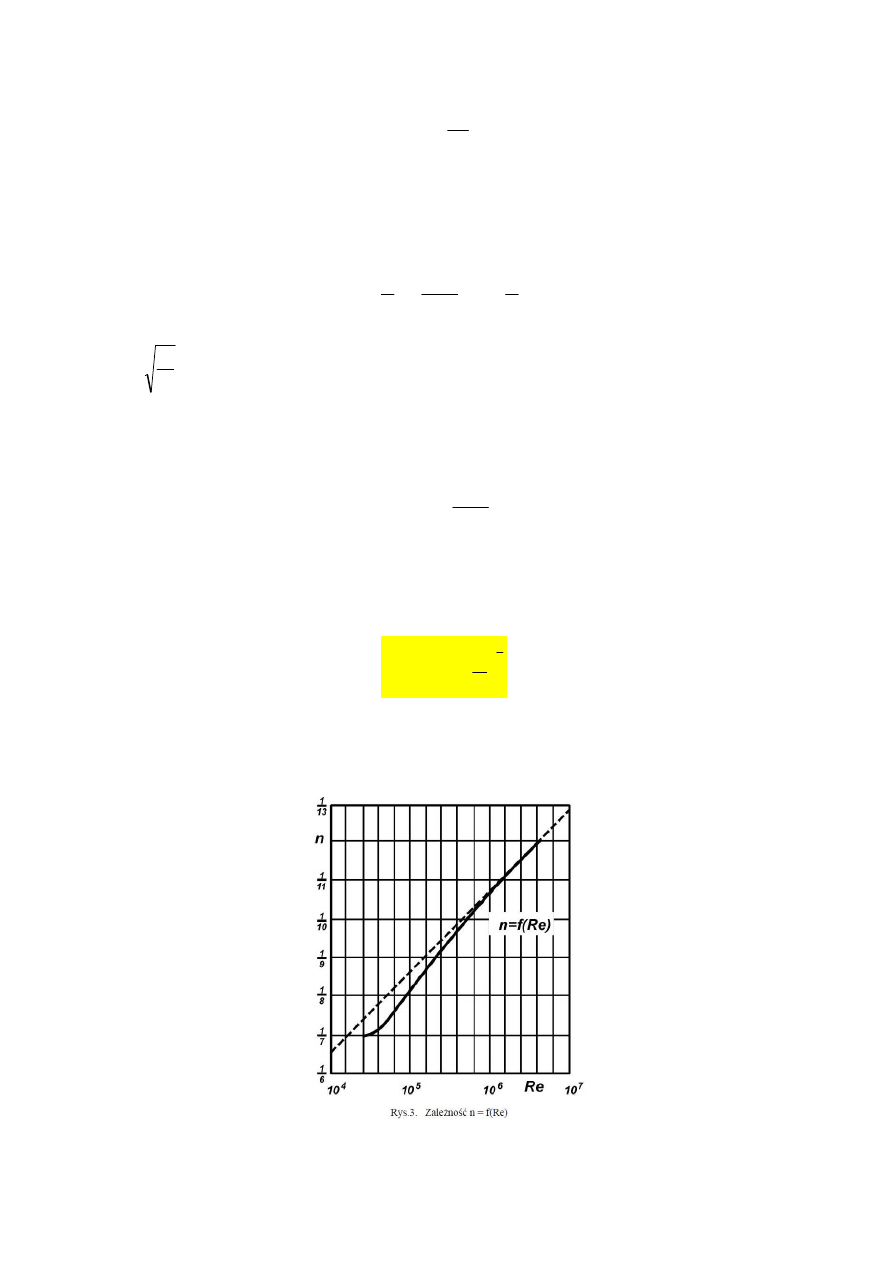
y

µ

τ

υ

0

=

,

(3)

gdzie:

0

τ

- naprężenie styczne na ścianie,

y

- odległość od ściany rury.

Po wprowadzeniu hipotezy Prandtla dotyczącej tzw. drogi mieszania uzyskuje się wzór
opisujący profil prędkości w rdzeniu turbulentnym:













−

+

=

β

κ

β

υ

υ

κ

υ

υ

ln

1

*

ln

1

*

y

,

(4)

gdzie:

ρ

τ

υ

0

*

=

- prędkość tarcia.

Stałe

κ

i

β

wyznaczane są eksperymentalnie, dla przewodu o przekroju kołowym wynoszą

odpowiednio około 0,4 i 11,5.
Po podstawieniu wartości współczynników

κ

i

β

otrzymamy równanie:













+

=

5

,

5

*

ln

5

,

2

*

υ

υ

υ

υ

y

.

(5)

Z równania (5) widać, że profil prędkości w rdzeniu turbulentnym jest logarytmiczny. Profil
opisanym powyższym równaniem nazywany jest uniwersalnym profilem prędkości.

W przybliżeniu rozkład prędkości dla przepływu turbulentnego można wyrazić równaniem:

n

R

r

1

max

1













−

=

υ

υ

.

(6)

R

– promień rurociągu,

[ ]

R

r

,

0

∈

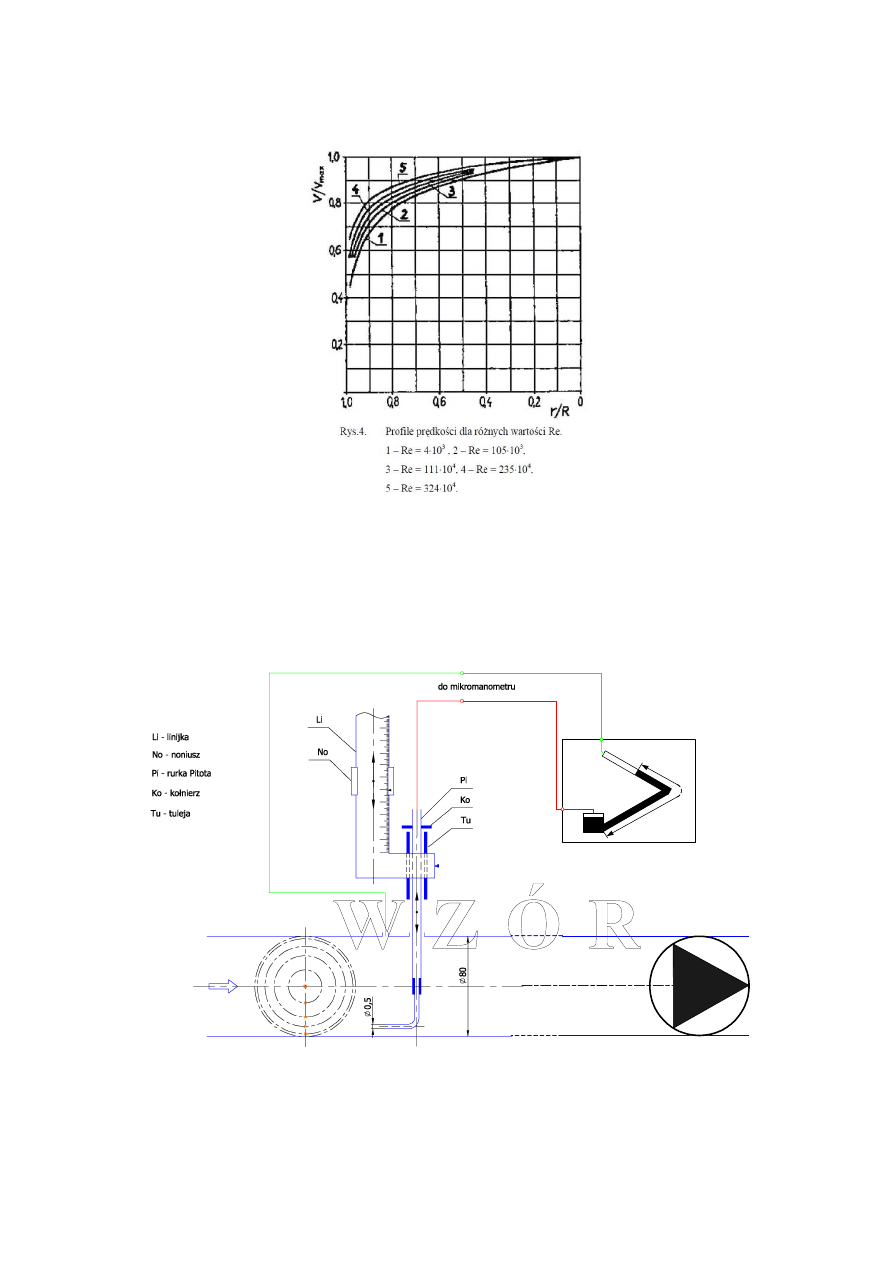
n

– współczynnik zależny od liczby Reynolds’a (

9

,

1

Re

log

1

,

2

−

⋅

=

n

)

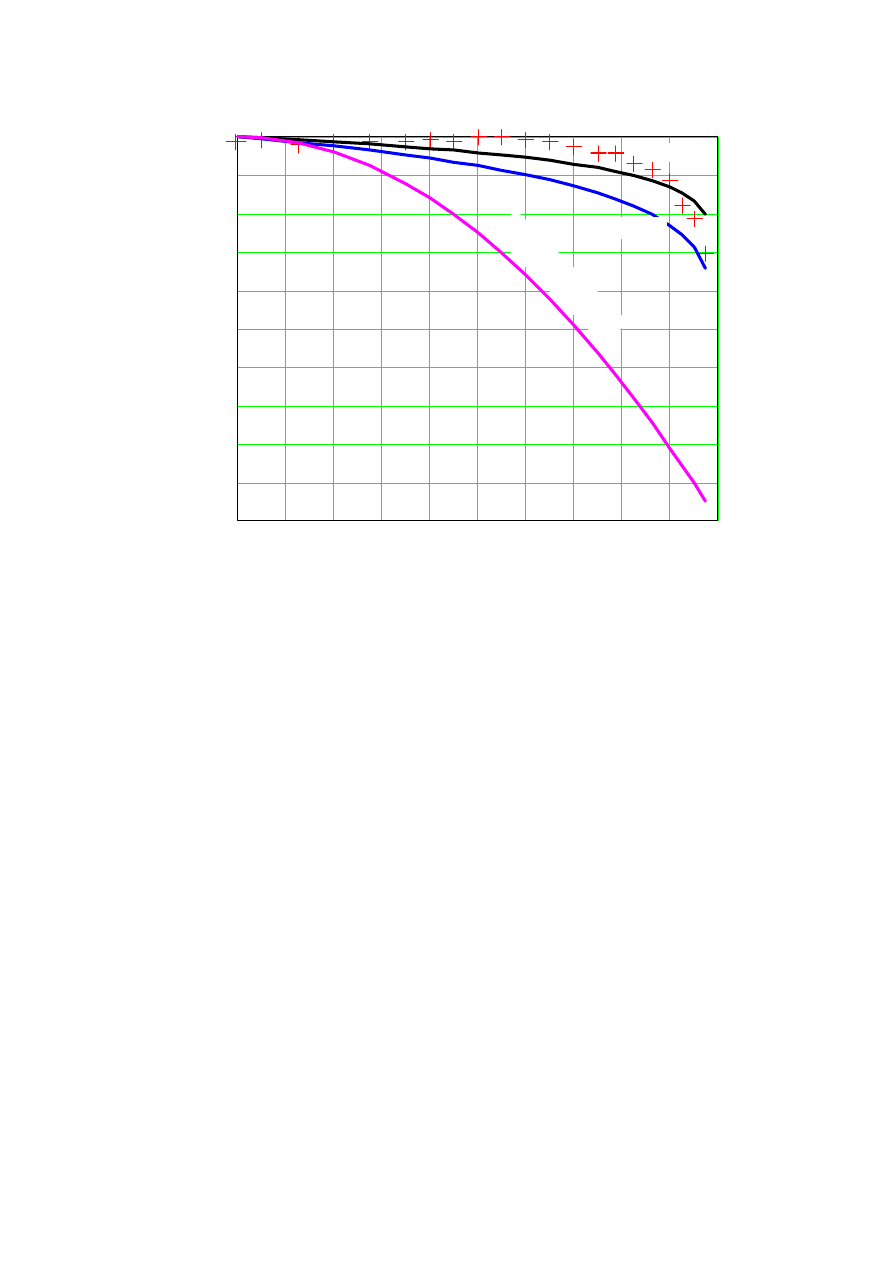
Zależność współczynnika n od liczby Reynolds’a przestawiono na rys. 3:

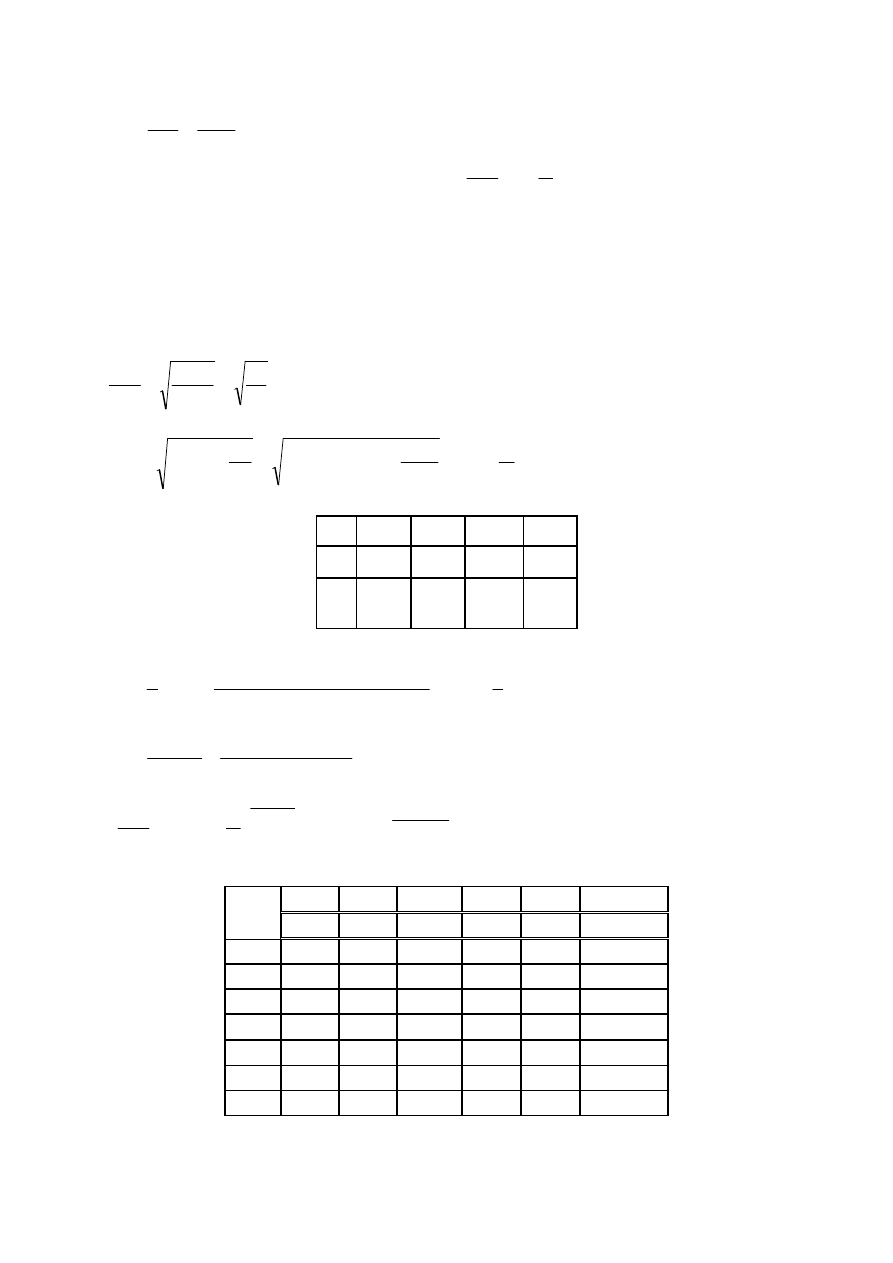
Na rys. 4 przedstawiono rozkład prędkości w zależności od liczby Reynolds’a.

Badania przepływów turbulentnych najczęściej przeprowadza się metodami

doświadczalnymi.

3. Stanowisko pomiarowe

Schemat stanowiska pomiarowego przedstawiono na rys. 5.

h

Rys. 5. Schemat stanowiska pomiarowego.

Stanowisko składa się następujących elementów:

−

rurociągu z przezroczystego tworzywa,

−

rurki Pitota,

−

mikromanometru,

−

termometru,

−

suwmiarki.

Rys. 6. Stanowisko pomiarowe

Rurociągiem przepływa powietrze o regulowanym strumieniu objętości q

v

, tłoczone przez

wentylator. Rurka Pitota służy do pomiaru ciśnienia całkowitego. Ciśnienie statyczne jest
mierzone na ścianie rurociągu. Przyjęto, że ciśnienie statyczne jest stałe w całym przekroju
rury. Uchwyt rurki Pitota umożliwia jej przesuwanie w kierunku pionowym oraz pomiar
rzędnej położenia osi tej rurki względem osi rury.

4. Przebieg i program ćwiczenia:

Pomiary rozkładu prędkości należy wykonać dla trzech różnych strumieni przepływu

płynu w rurociągu. Ciśnienie dynamiczne mierzyć w kilkunastu punktach, rozłożonych
wzdłuż średnicy. Pomiary należy przeprowadzić po ustaleniu się temperatury powietrza w
rurociągu. W celach kontrolnych obserwować termometr i odnotować ewentualne zmiany
temperatury.

Profil prędkości we współrzędnych bezwymiarowych













R

r

,

max

υ

υ

przedstawić graficznie.

Wykres powinien zawierać kilka profili prędkości otrzymywanych w wyniku własnych

pomiarów oraz profil porównawczy obliczony ze wzoru

n

R

r

1

max

1













−

=

υ

υ

. Dla każdego

profilu należy obliczyć wartość liczby Reynolds’a

v

R

v

D

s

s

υ

υ

2

Re

=

=

Prędkość średnią

s

υ

wyznacza się z wykresu













=

R

r

f

max

υ

υ

. W tym celu dzieli się pole

przekroju rury na co najmniej 4 pierścienie o równych polach i określa prędkość w środku
każdego z nich. Średnia arytmetyczna tych prędkości jest równa prędkości średniej

s

υ

.

5. Przykładowe obliczenia

Dla 1 punktu pomiarowego

697

,

0

37

18

max

max

=

=

∆

∆

=

h

h

υ

υ

s

m

h

g

p

w

81

,

24

179

,

1

1000

10

37

81

,

9

2

2

3

max

max

=

⋅

⋅

⋅

=

∆

=

−

ρ

ρ

υ

Li

r

∆

h

r/R

υ

/

υ

max

(

υ

/

υ

max

)teor

Lp

mm

mm

mm

−

−

−

1

1,0

39,0

18,0

0,975 0,697

0,658

2

3

…

19

20

21

i

1

2

3

4

r

i

/R 0,331 0,612 0,800 0,950

υ

i

m/s

24,48 24,61 23,55 23,58

4

1

1

23, 58 23, 55 24, 61 24, 48

24, 06

4

4

m

sr

i

s

i

υ

υ

=

+

+

+

=

=

=

∑

5

24, 06 0, 08 1,179

Re

122 500

1,808 10

sr

p

D

υ ρ

µ

−

⋅

⋅

=

=

=

⋅

(

)

1

2 ,1log Re 1,9

1

2 ,1log 122500 1,9

max

1

1 0, 975

0, 658

teor

r

R

υ

υ

−

−









= −

= −

=

















0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

P

rz

ep

ływ

la

m

in

arn

y

n=8,8

n=16,4

V

/V

m

a

x

r/R