Obliczenia sprężyn walcowych
Przykład:
Określić parametry sprężyn odsprężynowania I stopnia z łamaną charakterystyką sztywności dla
dwuosiowego wózka towarowego. Nad każdą maźnicą umieszczone są dwie pary sprężyn walcowych.
Na umieszczenie każdego pakietu sprężyn przewidziano przestrzeń w kształcie walca o średnicy D
v
=
210 mm, średnice prętów, z których wytwarzane są sprężyny są dostępne w rozmiarach
odpowiadających pełnej liczbie milimetrów, maksymalna wartość dopuszczalnego naprężenia
dynamicznego (ograniczona odbijakiem) wynosi
Ddop
= 720 MPa, moduł sprężystości G = 7,85·10
10
Pa.
Masa kompletnego zestawu kołowego m
d
= 1400 kg. Masa próżnego wagonu m
P
= 21 t, masa wagonu
ładownego m
L
= 80 t. Odkształcenie odsprężynowania pod maksymalnym użytecznym obciążeniem
z
u
= 35 mm. Przyjąć, że wewnętrzna średnica zewnętrznej sprężyny jest o 10 mm większa od
zewnętrznej średnicy wewnętrznej sprężyny.
Obciążenie jednej pary sprężyn dla wagonu próżnego i ładownego wynosi:
Przyjmuje się, że przypadku łamanej charakterystyki odsprężynowania wartość obciążenia
odpowiadająca zmianie nachylenia charakterystyki odpowiada połowicznemu ugięciu
odsprężynowania spowodowanemu przez maksymalne obciążenie użyteczne. Temu punktowi
odpowiada obciążenie sprężyn równe:
√
√
Sztywność głównej (zewnętrznej) sprężyny jest równa:
(
)
( )
Łączna sztywność pary sprężyn jest równa:
(
)
( )
Sztywność sprężyny wewnętrznej będzie równa:
Maksymalne obciążenie statyczne sprężyny zewnętrznej i wewnętrznej dla wagonu ładownego:
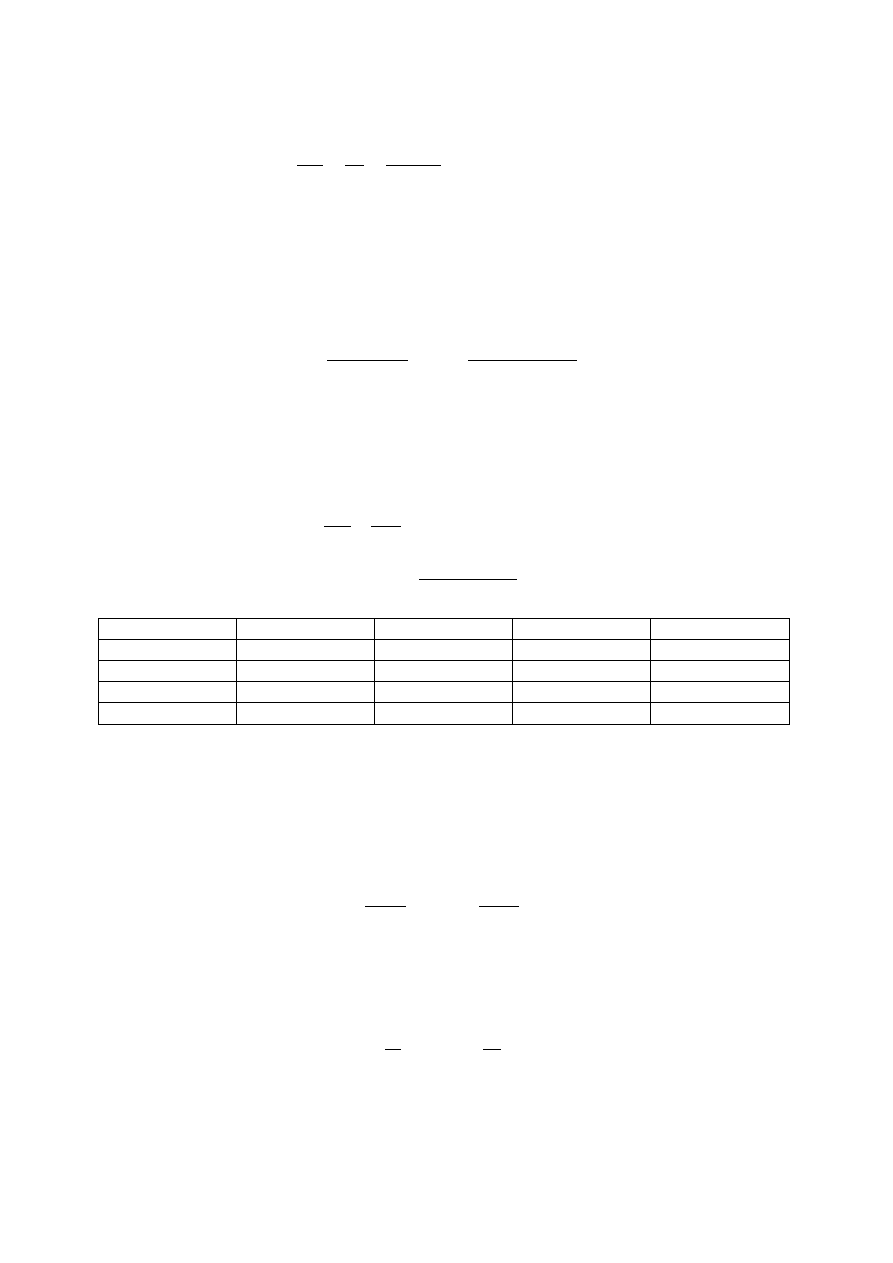
Ugięcie sprężyny zewnętrznej dla wagonu próżnego wyniesie:
Ugięcie zewnętrznej sprężyny dla wagonu ładownego:
Zakładając dodatkowe dynamiczne ugięcie sprężyny o ok. 25 mm uzyskamy w stanie ładownym
naprężenie w sprężynie zewnętrznej równe:
Średnia średnica sprężyny zewnętrznej D
1
w zależności od średnicy pręta sprężyny d
1
jest równa:
Przyjmujemy kilka różnych wartości średnicy pręta d
1
i korzystamy z zależności:
, gdzie (wzór Wahla)
d
1
[mm]
31
32
33
34
D
1
[mm]
179
178
177
176
D
1
/d
1
5,774
5,563
5,364
5,176
K
1,264
1,275
1,287
1,298
1L
[MPa]
619,9
565,5
517,4
474,8
Wymagania wytrzymałościowe spełnia sprężyna o średnicy drutu d
1
= 34 mm i ze średnią średnicą
D
1
= 176 mm
Maksymalne ugięcie dynamiczne sprężyny przy uwzględnieniu maksymalnego dopuszczalnego
naprężenia materiału sprężyny wynosi:
Przy obliczeniach sprężyny wewnętrznej przyjmuje się, że maksymalne obciążenie sprężyny nie może
powodować jej odkształcenia aż do odbijaka. Sprężyna wewnętrzna zaczyna działać od punktu
załamania charakterystyki, czyli w momencie, gdy sprężyna zewnętrzna odkształciła się o wartość:
Ugięcie sprężyny wewnętrznej przy maksymalnym obciążeniu dynamicznym (ograniczonym
odbijakiem) wynosi:
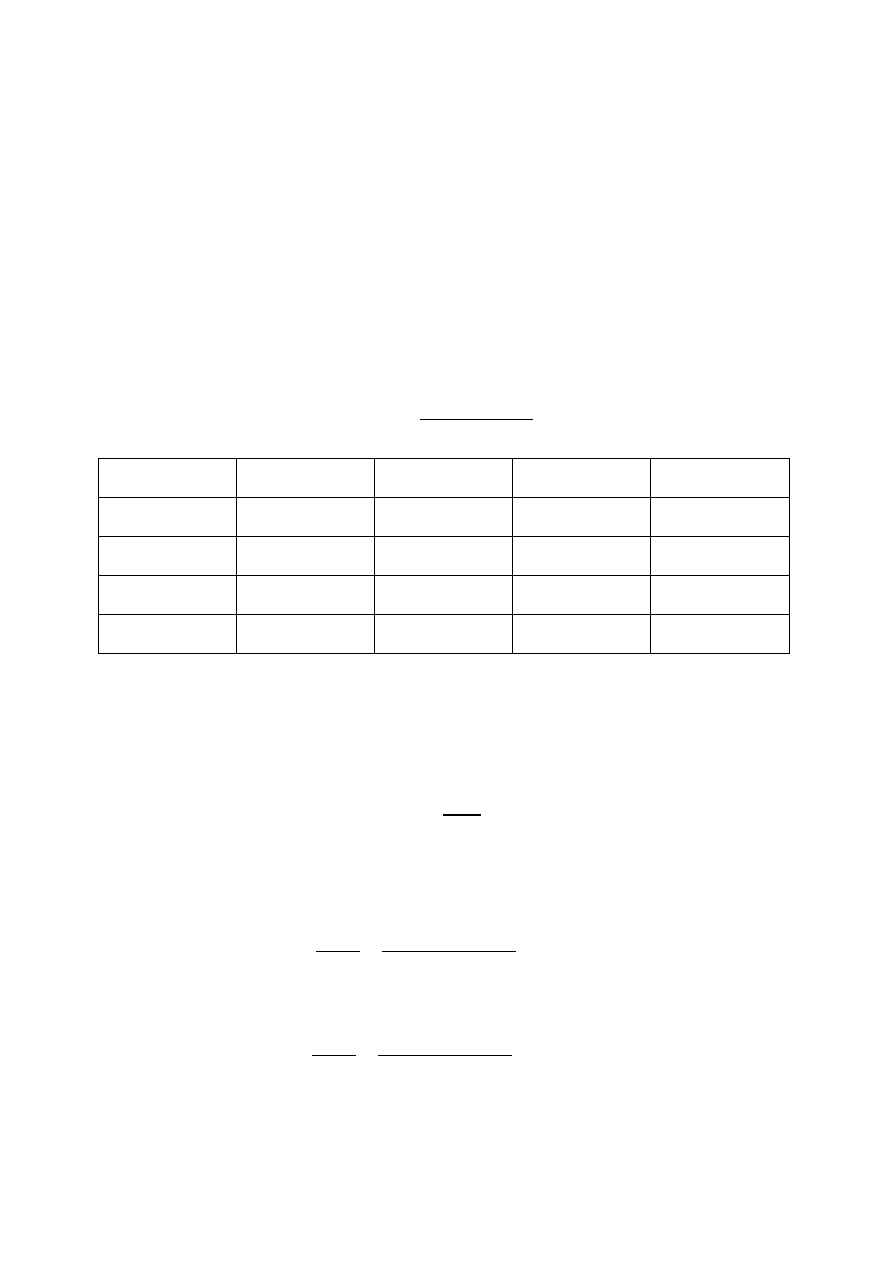
Powyższemu ugięciu sprężyny odpowiada maksymalne obciążenie dynamiczne:
Powyższą wartość wykorzystamy do obliczenia zasadniczych parametrów sprężyny wewnętrznej:
Maksymalna średnia średnica sprężyny wewnętrznej będzie równa:
Wybieramy kilka wartości średnicy drutu sprężyny wewnętrznej i wykorzystując wyżej podane wzory
obliczamy naprężenia w sprężynie:
d
2
[mm]
24
25
26
27
D
2
[mm]
108
107
106
105
D
2
/d
2
4,5
4,28
4,077
3,889
K
1,351
1,372
1,395
1,418
T
2dyn
[MPa]
897,2
798,7
715,2
643
Wymagania wytrzymałościowe spełnia sprężyna ze średnicą drutu d
2
= 26 mm i ze średnią średnicą
równą D
2
= 106 mm.
Liczba czynnych zwojów sprężyn będzie określona zależnością:
Na podstawie powyższego wzoru:
liczba czynnych zwojów sprężyny zewnętrznej będzie równa:
liczba czynnych zwojów sprężyny wewnętrznej będzie równa:
Minimalne swobodne wysokości sprężyn nieobciążonych:
sprężyna zewnętrzna:
(
)
( )
sprężyna wewnętrzna:
(
)
( )
Aby sprężyna wewnętrzna rozpoczęła działanie przy właściwej wartości ugięcia sprężyny
wewnętrznej konieczna jest modyfikacja jej wysokości swobodnej (przy założeniu jednakowych
powierzchni oporowych (czołowych).
W punkcie załamania charakterystyki ugięcie sprężyny zewnętrznej wyniesie:
Luz między powierzchnią czołową nieobciążonej sprężyny wewnętrznej a powierzchnią oporową musi
być przy takim obciążeniu równy:
Z powyższego wynika, że długość swobodna nieobciążonej sprężyny wewnętrznej musi być w
stosunku do obliczonej długości minimalnej zwiększona o 12,25 mm.
Aby zapobiec przeciążeniu sprężyny przy obciążeniach dynamicznych należy określić luz w odbijakach
odsprężynowania pionowego. Luz ten ze względów praktycznych oblicza się dla wagonu próżnego: