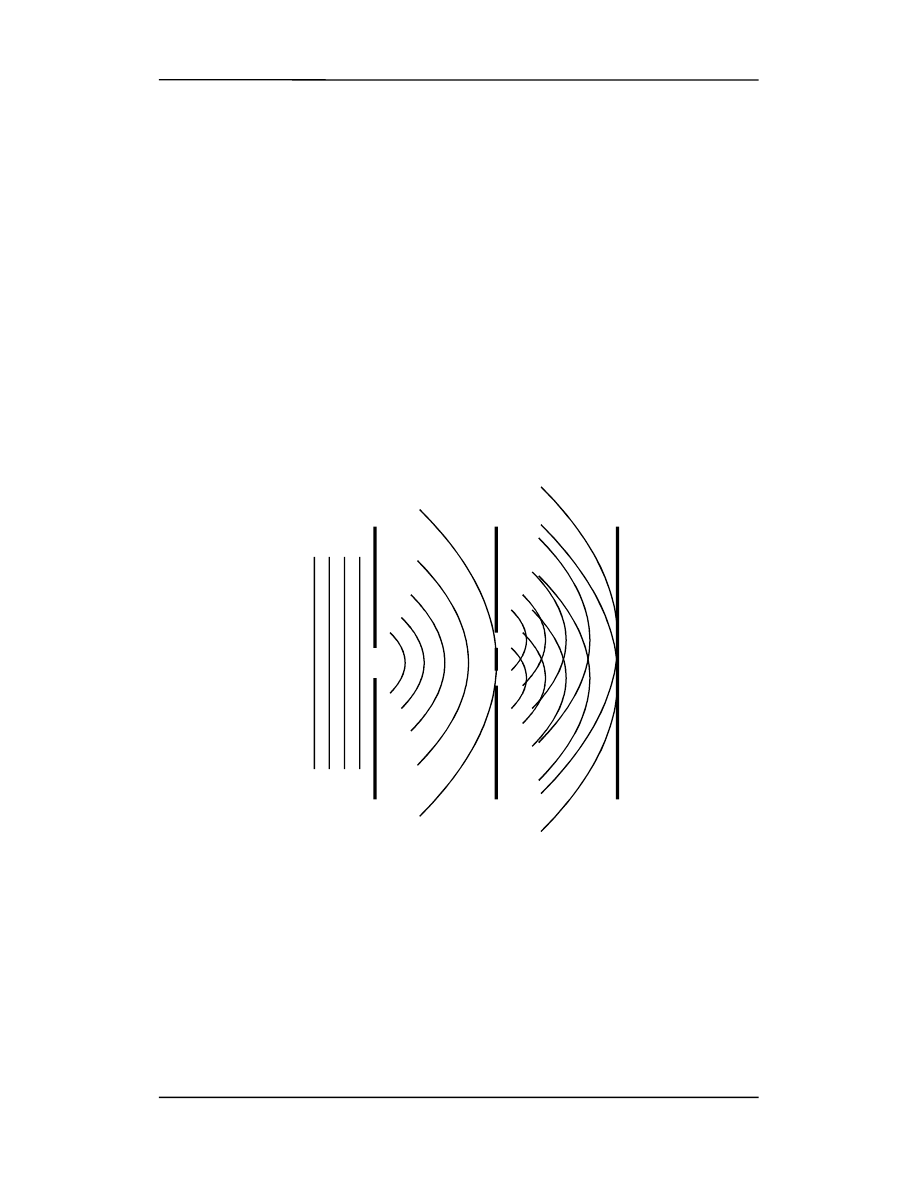
Z. Kąkol-Notatki do Wykładu z Fizyki

28-1

Wykład 28

28. Interferencja

28.1

Doświadczenie Younga

Na wykładzie dotyczącym fal w ośrodkach sprężystych omawiane było nakładanie

się fal. Wykazanie, przez Thomasa Younga (w 1801 r.) istnienia takiej

interferencji dla

światła było pierwszym eksperymentem wskazującym na falowy charakter światła

.

Young oświetlił światłem słonecznym ekran, w którym był zrobiony mały otwór S

0

.

Przechodzące światło padało następnie na drugi ekran z dwoma otworami S

1

i S

2

i roz-

chodzą się dalej dwie, nakładające się fale kuliste tak jak na rysunku. Warunki stoso-
walności optyki geometrycznej nie są spełnione i na szczelinach następuje ugięcie fal.
Mamy do czynienia z optyką falową. Jeżeli umieścimy ekran w jakimkolwiek miejscu,
tak aby przecinał on nakładające się na siebie fale to możemy oczekiwać pojawienia się
na nim ciemnych i jasnych plam następujących po sobie kolejno.

Przeanalizujmy teraz doświadczenie Younga ilościowo.
Zakładamy, że światło padające zawiera tylko jedną długość fali (jest monochromatycz-
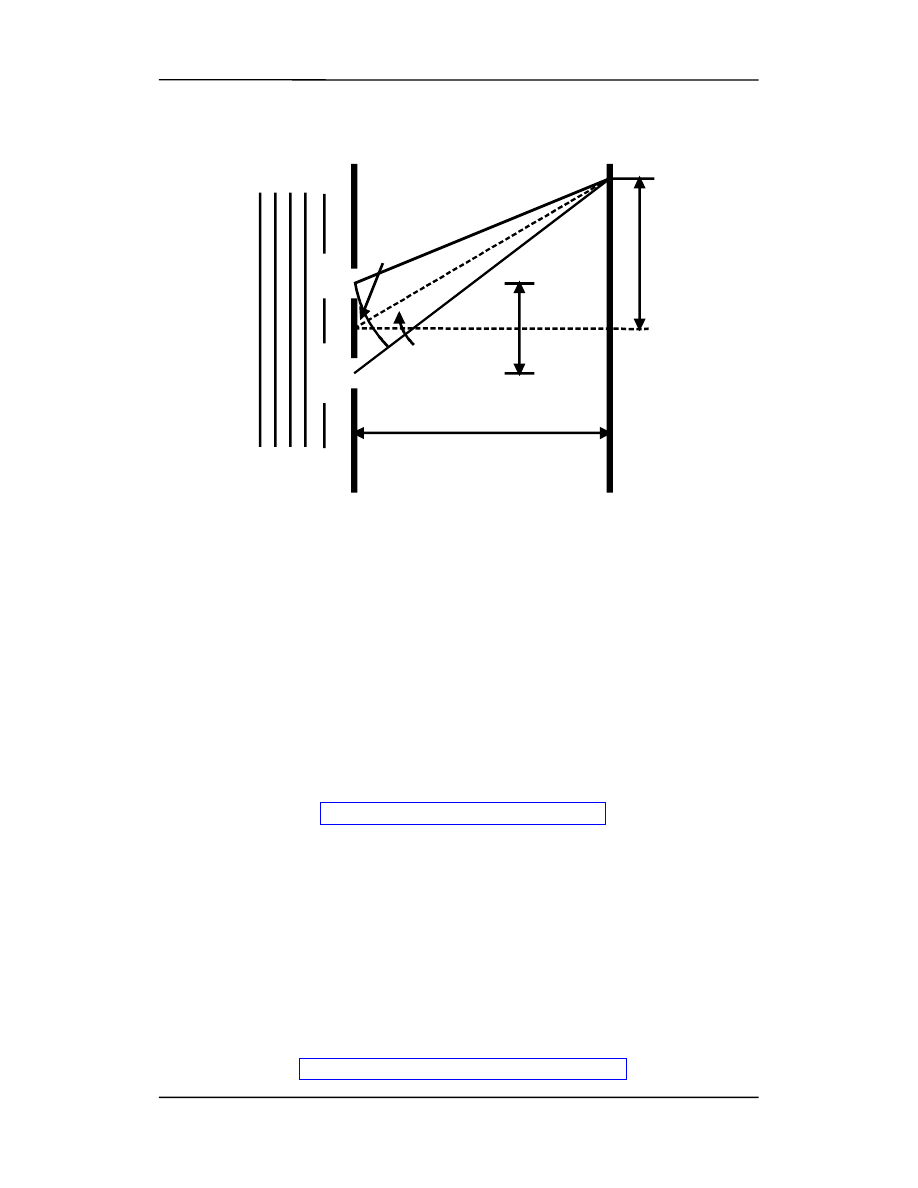
ne). Na rysunku poniżej punkt P jest dowolnym punktem na ekranie, odległym o r

1

i r

2

od wąskich szczelin S

1

i S

2

.

Linia S

2

b została poprowadzona tak, aby PS

2

= Pb. Trzeba zwrócić uwagę, że stosunek

d/D przedstawiony na rysunku jest dla większej jasności przesadnie duży. Naprawdę
d << D i wtedy kąt S

1

S

2

b jest równy

θ z dużą dokładnością.

S

0

S

2

S

1

Z. Kąkol-Notatki do Wykładu z Fizyki

28-2

Oba promienie wychodzące ze szczelin S

1

i S

2

są zgodne w fazie, gdyż pochodzą z tego

samego czoła fali płaskiej. Jednak drogi, po których docierają do punktu P są różne więc
i ich fazy mogą być różne. Odcinki Pb i PS

2

są identyczne (tak to skonstruowaliśmy)

więc o różnicy faz decyduje różnica dróg optycznych tj. odcinek S

1

b. Aby w punkcie P

było

maksimum

to odcinek S

1

b musi zawierać całkowitą liczbę długości fal. Jest tak dla-

tego, że po przebyciu odcinka równego

λ faza fali powtarza się więc dla drogi mλ fala

ma fazę taką jak na początku tej drogi; odcinek S

1

b nie wpływa na różnicę faz a ponie-

waż fale były zgodne w źródle (szczeliny S

1

i S

2

) więc będą zgodne w fazie w punkcie

P. Warunek ten możemy zapisać w postaci

S

1

b = m

λ, m = 0, 1, 2, ......,

lub

dsin

θ = mλ, m = 0, 1, 2, ......, (maksima)

(28.1)

Zauważmy, że każdemu maksimum powyżej punktu O odpowiada położone symetrycz-
nie maksimum poniżej punktu O. Istnieje też centralne maksimum opisywane przez
m = 0.
Dla uzyskania

minimum

w punkcie P, odcinek S

1

b musi zawierać połówkową liczbę

długości fal, to jest:

S

1

b = (m+1/2)

λ, m = 0,1,2,....,

lub

dsin

θ = (m+1/2) λ, m = 0, 1, 2, ......, (minima)

inaczej

dsin

θ = (2m+1)λ/2, m = 0, 1, 2, ......, (minima)

(28.2)

S

1

S

2

d

D

y

P

r

1

r

2

θ

θ

O

b

Z. Kąkol-Notatki do Wykładu z Fizyki

28-3

Przykład 1

Dwie szczeliny odległe od siebie o 1 mm oświetlono światłem zielonym (linia zielona
lampy rtęciowej) o długości

λ = 546 nm. Jaka jest odległość między sąsiednimi prążka-

mi interferencyjnymi obserwowanymi na ekranie umieszczonym w odległości 1 m od
szczelin?
Najpierw sprawdźmy położenie kątowe np. pierwszego maksimum.
Dla m = 1 otrzymujemy: dsin

θ = λ

skąd

sin

θ = λ/d = (546·10

-9

m)/(10

-3

m) = 0.000546

co daje

θ

≅

0.03

°

Dla tak małych kątów dobrym jest przybliżenie

sin

θ

≅

tg

θ

≅

θ

Z rysunku widać, że tg

θ = y/D. Podstawiając to wyrażenie zamiast sin

θ

w równaniu na

maksimum interferencyjne otrzymujemy dla m-tego prążka

d

D

m

y

m

λ

=

a dla następnego

d

D

m

y

m

λ

)

1

(

1

+

=

+

Odległość między nimi wynosi więc

mm

546

.

0

m

10

)

m

1

(

)

m

10

546

(

3

9

1

=

⋅

=

=

−

=

∆

−

−

+

d

D

y

y

y

m

m

λ

Uwaga: Jeżeli

θ jest małe to odległość między prążkami nie zależy od m, czyli prążki są

rozmieszczone równomiernie. Jeżeli mamy więcej niż jedną

λ to powstaną oddzielne

układy prążków (dla każdej z długości fal) o różnym odstępie między prążkami.

Równanie opisujące położenie kątowe maksimów może posłużyć do wyznaczenia dłu-
gości fali

m

d

θ

λ

sin

=

Z tej relacji T. Young wyznaczył długości fal światła widzialnego.

Z. Kąkol-Notatki do Wykładu z Fizyki

28-4

28.2

Koherencja

Podstawowym warunkiem powstania dobrze określonego obrazu interferencyjnego

jest, aby fale świetlne które przybywają z punktów S

1

i S

2

miały

dokładnie określoną

różnicę faz

ϕ stałą w czasie

. (Przypomnienie: faza jako określony stan fali w danym

miejscu i czasie, patrz równanie opisujące falę E = E

m

sin(kx-

ωt)). Np. jest miejsce na

ekranie, dla którego różnica faz wynosi

π co oznacza fizycznie, że fale docierające tam

wygaszają się (przy założeniu tej samej amplitudy); mamy ciemny prążek. I tak jest
zawsze o ile różnica faz się nie zmieni. Gdyby taka zmiana nastąpiła to w tym miejscu
natężenie światła nie będzie już równe zeru. Warunkiem stabilności obrazu jest więc
stałość w czasie różnicy faz fal wychodzących ze źródeł S

1

i S

2

. Mówimy, że te źródła

są

koherentne czyli spójne

.

Jeżeli szczeliny S

1

i S

2

zastąpimy przez dwa niezależne źródła fal (np. żarówki) to nie

otrzymamy prążków interferencyjnych, ekran będzie oświetlony prawie równomiernie.
Interpretujemy to w ten sposób, że różnica faz dla fal pochodzących z niezależnych źró-
deł zmienia się w czasie w sposób nieuporządkowany.
W krótkim czasie są spełnione warunki dla maksimum, a za chwile (b. krótką np. 10

-8

s)

dla minimum, a jeszcze za chwilę warunki pośrednie. I tak dla każdego punktu na ekra-
nie. Natężenie (w danym punkcie) jest więc sumą natężeń od poszczególnych źródeł.
Mówimy, że te źródła są

niespójne

,

niekoherentne

.

Podsumujmy więc podstawową różnicę w opisie, podyktowaną oczywiście przez fakty
doświadczalne:

•

dla fal spójnych najpierw dodajemy amplitudy (uwzględniając stała różnicę faz),
a potem celem obliczenia natężenia podnosimy otrzymaną amplitudę wypadkową do
kwadratu (przypomnienie dla ruchu harmonicznego: Energia

∼

A

2

).

•

dla fal niespójnych najpierw podnosimy do kwadratu amplitudy, żeby otrzymać na-
tężenia poszczególnych fal a potem dopiero sumujemy te natężenia.

Pozostaje jedynie pytanie jak wytworzyć światło spójne. Na tym etapie zapamiętajmy
tylko, że zwykłe źródła światła takie jak żarówki (żarzące się włókno) dają światło nie-
spójne dlatego, że emitujące atomy działają zupełnie niezależnie. Natomiast współcze-
śnie szeroko stosowanymi źródłami światła spójnego są

lasery

.

Szczegóły dotyczące emisji światła przez lasery jak i zasadę działania lasera poznamy
na dalszych wykładach.

28.3

Natężenie w doświadczeniu Younga

Załóżmy, że składowe pola elektrycznego obu fal w punkcie P zmieniają się następująco

E

1

= E

0

sin

ωt

E

2

= E

0

sin(

ωt+ϕ)

gdzie

ω = 2πv jest częstością kołową fal, a ϕ różnicą faz między nimi.

•

ϕ zależy od położenia punktu P a tym samym od kąta θ

•

załóżmy natomiast, że E

0

nie zależy od

θ (szczeliny są dostatecznie wąskie, tak że

światło ugięte na każdej ze szczelin oświetla środkową część ekranu równomiernie)

Z. Kąkol-Notatki do Wykładu z Fizyki

28-5

Wynika stąd, że wypadkowe pole elektryczne w punkcie P jest równe

E = E

1

+ E

2

Uwaga: Mówimy o polu E, a nie polu B (fali EM) ponieważ działanie tego drugiego na
detektory światła (w tym oko ludzkie) jest znikome. Równanie powyższe powinno być
wektorowe ale w tych przypadkach wektory E są do siebie równoległe więc wystarczy
równanie algebraiczne.
Podstawiając równania dla obu fal obliczamy pole wypadkowe

E = E

0

sin(

ωt+ϕ) + E

0

sin

ωt = 2E

0

cos(

ϕ/2) sin(ωt+ϕ/2)

lub

E = E

θ

sin(

ωt+β)

gdzie

β = ϕ/2 oraz E

θ

= 2E

0

cos

β

Teraz chcemy obliczyć natężenie fali wypadkowej

I

θ

∼

E

θ

2

Obliczmy stosunek natężeń dwu fal: fali wypadkowej i fali pojedynczej

2

0

0









=

E

E

I

I

θ

θ

czyli

β

β

θ

2

2

0

cos

cos

4

m

I

I

I

=

=

(28.3)

Natężenie zmienia się od zera (dla punktów, w których

ϕ = 2β = π) do maksymalnego

(dla punktów, w których

ϕ = 2β = 0).

Różnica faz wiąże się z różnicą dróg S

1

b poprzez prostą relację

różnica faz/2

π = różnica dróg/λ

(28.4)

czyli

λ

θ

π

ϕ

sin

2

d

=

Stąd

)

sin

(

2

θ

λ

π

ϕ

d

=

lub

θ

λ

π

β

sin

d

=

Poprzez to równanie mamy zależność natężenia od kąta

θ.

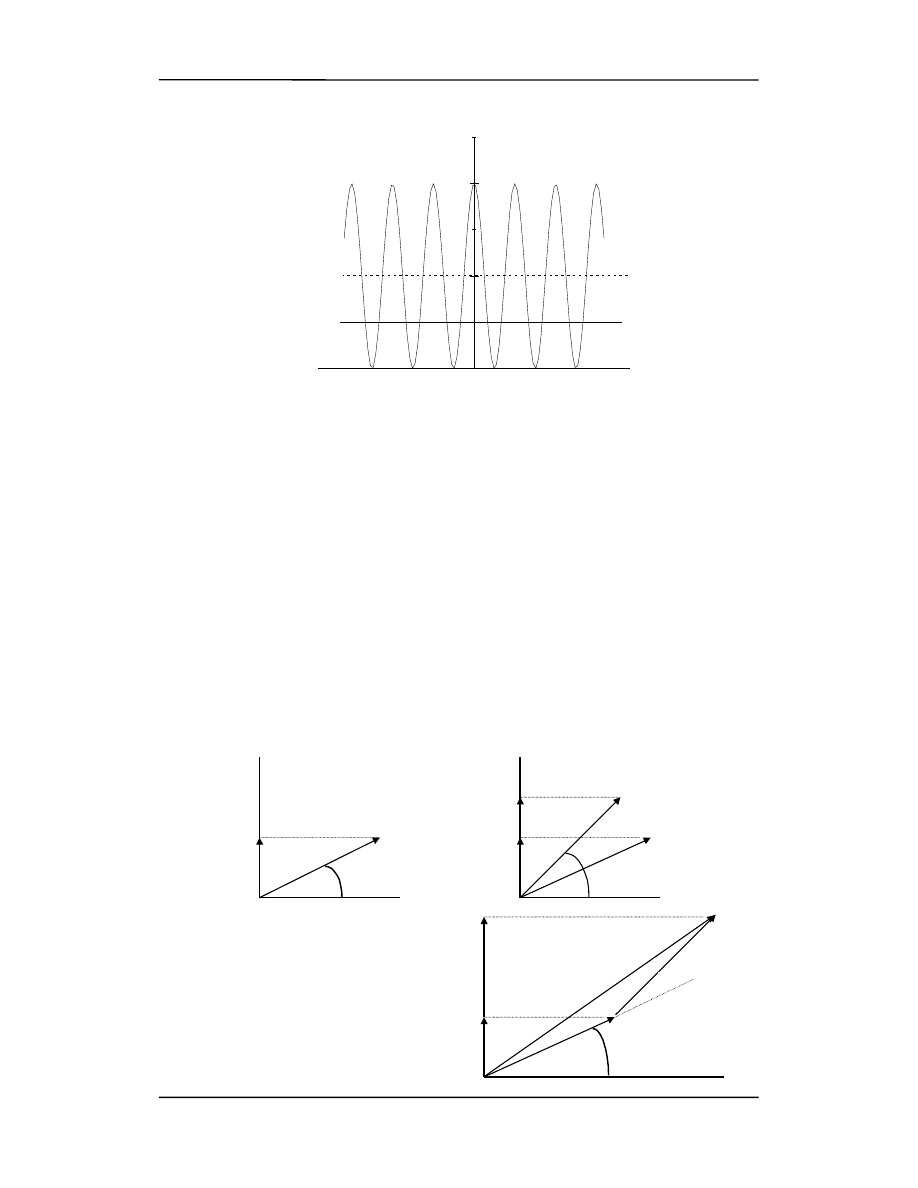
Narysujmy teraz rozkład natężeń dla interferencji przy dwóch szczelinach (rysunek po-
niżej) porównując z wynikiem dla pojedynczego źródła jak i dla źródeł niespójnych.

Z. Kąkol-Notatki do Wykładu z Fizyki

28-6

Aby wyliczyć wypadkowe natężenie światła w doświadczeniu Younga dodawali-

śmy dwa zaburzenia falowe postaci E

1

= E

0

sin

ωt, E

2

= E

0

sin(

ωt+ϕ), które miały tę samą

częstość i amplitudę, a różniły się fazą

ϕ. Wynik uzyskany został algebraicznie na pod-

stawie prostych wzorów trygonometrycznych. Jednak metody analityczne stają się
znacznie trudniejsze gdy dodajemy więcej zaburzeń falowych (funkcji typu sin, cos)
i dlatego wprowadzimy (głównie z myślą o następnych wykładach) prostą metodę gra-
ficzną.
Sinusoidalne zaburzenie falowe może być przedstawione graficznie jako obracający się
wektor, którego długość reprezentuje amplitudę. Taki wektor będziemy nazywać

strzał-

ką fazową

(wskazem). Zmienne zaburzenie falowe E

1

w chwili t przedstawione jest

przez rzut tej „strzałki” na oś pionową (odpowiada to pomnożeniu E

0

przez sin

ωt).

Drugie zaburzenie falowe E

2

, o tej samej amplitudzie E

0

, różni się od E

1

fazą

ϕ. Znajdu-

jemy je podobnie jako rzut „strzałki” na oś pionową. Teraz wystarczy dodać E

1

i E

2

że-

by otrzymać wypadkowe zaburzenie.

Widać to jeszcze lepiej gdy
umieści się początek jednej
strzałki na końcu poprzedniej
zachowując różnicę faz (rysunek
obok).

4I

0

źródła

spójne

I

0

jedno

źródło

2I

0

źródła

niespójne

2

λ

/d

λ

/d

2

λ

/d

λ

/d

0

sin

θ

n

a

tę

że

n

ie

E

2

E

1

E

1

E

0

E

0

E

0

ω

t

ω

t

ϕ

E

2

E

1

E

0

E

0

ω

t

ϕ

E

θ

Z. Kąkol-Notatki do Wykładu z Fizyki

28-7

Przykład 2

Znajdźmy

wypadkową

następujących

zaburzeń

falowych:

E

1

= 2sin

ωt,

E

2

= 2sin(

ωt+30

°

), E

3

= 2sin(

ωt+60

°

), E

4

= 2sin(

ωt+90

°

).

Jeżeli przyjmiemy np., że

ωt = 15

°

to E

M

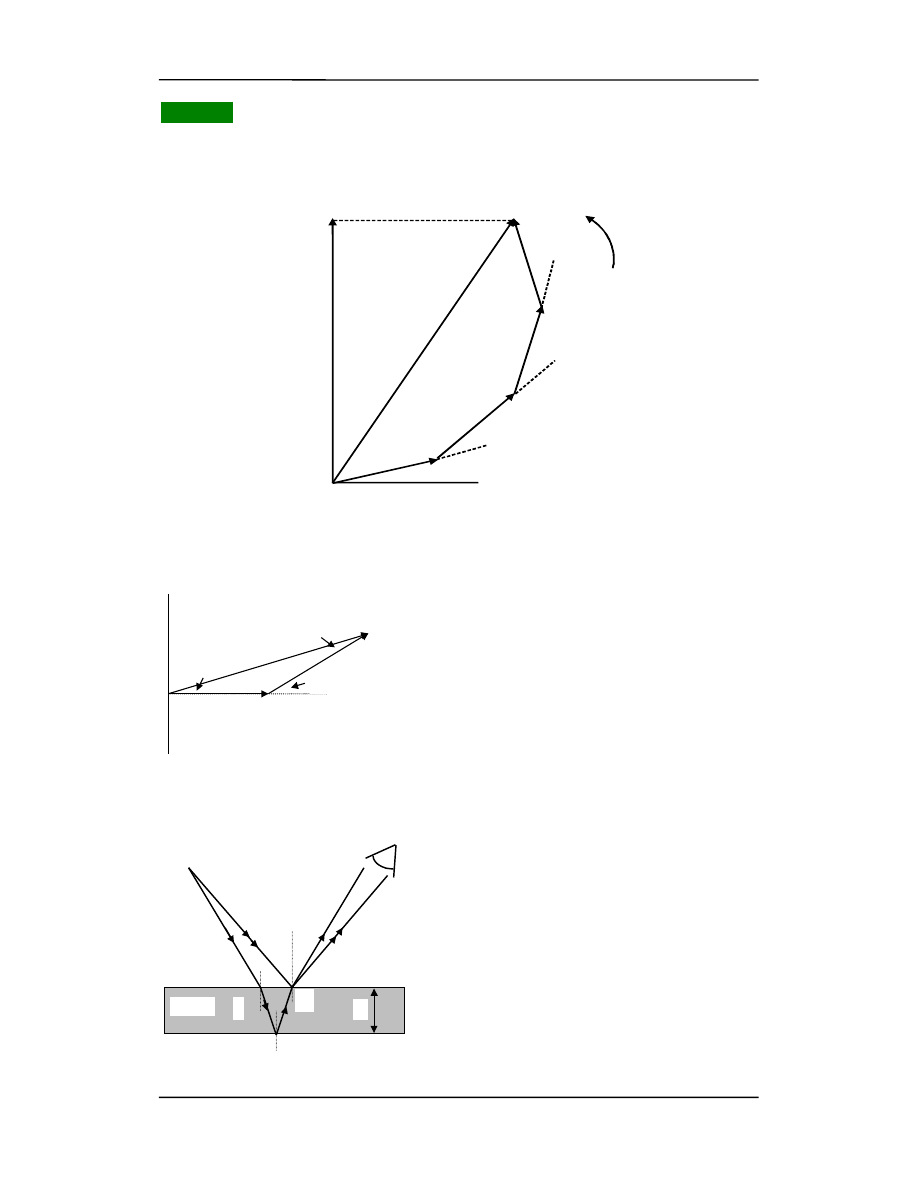
= 6.7, E = 5.8 (rysunek poniżej).

Na kolejnym rysunku pokazane są strzałki fazowe dla interferencji Younga (w chwili
t = 0).

E

θ

= 2E

0

cos

β = E

M

cos

β

Suma kątów w trójkącie wynosi 180

°

stąd wynika,

że: 2

β = ϕ (taki sam wynik jaki otrzymaliśmy al-

gebraicznie).
Maksimum amplitudy otrzymamy jak widać dla
ϕ = 0 (wektory równoległe), a minimum dla ϕ = π
(wektory antyrównoległe).

28.4

Interferencja w cienkich błonkach

Barwy cienkich błonek, baniek my-

dlanych, plam np. oleju na wodzie są wyni-
kiem interferencji. Na rysunku pokazana jest
warstwa o grubości d i współczynniku zała-
mania n. Błonka jest oświetlona przez roz-
ciągłe źródło światła monochromatycznego.
W źródle istnieje taki punkt S, że dwa pro-
mienie wychodzące z tego punktu mogą do-
trzeć do oka po przejściu przez punkt a.
Promienie te przebiegają różne drogi gdyż
jeden odbija się od górnej, a drugi od dolnej

ϕ

ϕ

ϕ

ω

t

E

E

M

E

0

E

0

E

0

E

0

E

0

E

0

β

β

ϕ

E

θ

oko

d

S

powietrze

powietrze

b

łonka

n

a

Z. Kąkol-Notatki do Wykładu z Fizyki

28-8

powierzchni błonki. To czy punkt a będzie jasny czy ciemny zależy od wyniku interfe-
rencji fal w punkcie a. Fale te są spójne, bo pochodzą z tego samego punktu źródła
światła. Jeżeli światło pada prawie prostopadle to geometryczna różnica dróg pomiędzy
obu promieniami wynosi prawie 2d. Można więc oczekiwać, że maksimum interferen-
cyjne (punkt a jasny) wystąpi gdy odległość 2d będzie całkowitą wielokrotnością długo-
ści fali. Okazuje się, że tak nie jest z dwu powodów

•

długość fali odnosi się do długości fali w błonce

λ

n

a nie do jej długości w powietrzu

λ. Oznacza to, że musimy rozważać drogi optyczne, a nie geometryczne (patrz wy-
kład 26 - zasada Fermata). Przypomnijmy, że prędkość fali jest związana z częstotli-
wością (barwą) i długością fali

v

=

λv

oraz, że przy przejściu do innego ośrodka

zmienia się prędkość i długość fali, a czę-

stotliwość pozostaje bez zmiany

. Ponieważ przy przejściu z powietrza do materiału o

współczynniku załamania n prędkość maleje n razy

v

= c/n

to długość fali też maleje n razy

λ

n

=

λ/n

•

okazuje się ponadto, że fala odbijając się od ośrodka optycznie gęstszego (większe n)

zmienia swoją fazę o

π

. Natomiast gdy odbicie zachodzi od powierzchni ośrodka

rzadszego optycznie fala odbija się

bez zmiany fazy

. Oznacza to, że promień odbity

od górnej powierzchni błonki zmienia fazę, a promień odbity od dolnej granicy nie.

Możemy teraz uwzględnić oba czynniki tj. różnice dróg optycznych oraz zmiany faz
przy odbiciu.
Dla dwóch promieni pokazanych na rysunku warunek na maksimum ma postać

2d = m

λ

n

+

λ

n

/2,

m = 0, 1, 2, ....,

Czynnik

λ

n

/2 opisuje zmianę fazy przy odbiciu (od górnej powierzchni) bo zmiana fazy

o 180

°

(

π

) jest równoważna różnicy dróg równej połowie długości fali (różnica

faz/2

π = różnica dróg/λ

)

. Ponieważ

λ

n

=

λ

/n otrzymujemy więc

λ











 +

=

2

1

2

m

dn

,

m = 0, 1, 2,..... (maksima)

Analogiczny warunek na minimum ma postać

λ

m

dn

=

2

,

m = 0, 1, 2,....(minimum)

Z. Kąkol-Notatki do Wykładu z Fizyki

28-9

Równania te są słuszne jeżeli współczynnik załamania błonki jest większy lub mniejszy
od współczynnika załamania ośrodków po obu stronach błonki.

Przykład 3

Błonka wodna (np. bańka mydlana, n = 1.33) znajdująca się w powietrzu ma grubość
320 nm. Jaki kolor ma światło odbite, gdy błonka jest oświetlona światłem białym pada-
jącym prostopadle?
Z warunku na maksimum obliczamy

λ

2

1

nm

850

2

1

33

.

1

nm

320

2

2

1

2

+

=

+

⋅

⋅

=

+

=

m

m

m

dn

λ

Obliczamy

λ dla kolejnych m:

m = 0,

λ = 1700 nm, poza zakresem widzialnym

m = 1,

λ = 567 nm, w zakresie widzialnym (żółtozielona)

m = 2,

λ = 340 nm, poza zakresem widzialnym

m = 3, 4, ...., poza zakresem widzialnym.