ROK WYD. LXVII

앫 ZESZYT 1/2008

Mgr in˝. Daniel Reclik i dr hab. in˝. Gabriel G. Kost, prof.

Pol. Âl., sà pracownikami Instytutu Automatyzacji Procesów
Technologicznych i Zintegrowanych Systemów Wytwa-
rzania Politechniki Âlàskiej w Gliwicach.

Definiowanie trajektorii robotów manipulacyjnych

realizowane jest zawsze z uwzgl´dnieniem Êrodowis-
ka, w którym pracujà. Wynika to z faktu, ˝e w oto-
czeniu technologicznym robota sà zdefiniowane
przestrzennie obiekty technologiczne stanowiàce
struktur´ systemu zrobotyzowanego [1]. Mo˝liwoÊç
w∏aÊciwego wyznaczenia optymalnego sposobu
przejÊcia robota pomi´dzy wyznaczonymi po∏o˝e-
niami poÊrednimi w przestrzeni zadaniowej jest
podstawà do oceny jakoÊci jego programu. W sytuacji
zag´szczenia jego przestrzeni zadaniowej obiektami
technologicznymi – przeszkodami, szczególnego
znaczenia nabiera kryterium optymalnego przejÊcia
robota z po∏o˝enia startowego do koƒcowego pla-
nowanej drogi. Wynika ono z koniecznoÊci bez-
wzgl´dnego spe∏nienia wymogu bezkolizyjnego
ruchu i wymusza wykorzystanie ró˝norakich dróg
obejÊcia, cz´sto eliminujàc drog´ geometrycznie
najkrótszà. Dwa podstawowe parametry ruchu robo-
ta, jakimi sà d∏ugoÊç drogi bezkolizyjnej i czas jej
realizacji, stanowià podstaw´ optymalizacji jego
programu [2, 3].

Dynamiczne planowanie trajektorii
robotów manipulacyjnych

DANIEL RECLIK
GABRIEL G. KOST

Planowanie bezkolizyjnej drogi robota

Coraz powszechniejsza integracja systemów wy-

twórczych realizowana jest g∏ównie na p∏aszczyênie
informacyjnej. W grupie Êrodków wspomagajàcych
prace z zakresu technologicznego przygotowania
produkcji systemy komputerowego programowania
off-line robotów przemys∏owych sà najmniej zaawan-
sowane technologicznie, przy wysokim zaawanso-
waniu informatycznym (dobrze rozbudowana p∏asz-
czyzna grafiki komputerowej). Szczególnie s∏abo
rozwini´ty w tych systemach jest obszar zagadnieƒ
dotyczàcych wyznaczania dróg bezkolizyjnych przejÊç
robota pomi´dzy obiektami znajdujàcymi si´ w jego
przestrzeni zadaniowej. Problem analizy planowa-
nego ruchu wynika z trudnoÊci rozwiàzania takich
kluczowych zagadnieƒ, jak [2 – 4]:

쐌 analiza trójwymiarowej przestrzeni zadanio-

wej robota, uwzgl´dniajàca rozmieszczenie obiektów-
-przeszkód,

쐌 sposób interpretacji struktury kinematycznej

robota przy analizie ruchu (∏aƒcuch kinematyczny,
przedmiot manipulowany, dynamiczna zmiana u∏o-
˝enia przestrzennego ∏aƒcucha kinematycznego ro-
bota w czasie ruchu w przestrzeni 3D),

쐌 ocena sposobu przemieszczania si´ robota w celu

wyznaczenia optymalnego przejÊcia bezkolizyjnego.

ROK WYD. LXVII

앫 ZESZYT 1/2008

2 4

Ze wzgl´du na z∏o˝onoÊç geometrycznà przestrzeni

zadaniowej robota, jego ruch bezkolizyjny musi si´
odbywaç etapami (krokami) wyznaczanymi pomi´dzy
kolejnymi napotykanymi miejscami mogàcymi po-
tencjalnie wywo∏aç kolizj´ [1 – 4]. Dlatego te˝ wszel-
kie próby komputerowego wspomagania procesu
wyznaczania bezkolizyjnego zachowania si´ robota
w Êrodowisku technologicznym opierajà si´ na roz-
wiàzaniach iteracyjnych. Jest to zagadnienie wielo-
etapowe, w którym ruch bezkolizyjny robota wyzna-
czany jest z u˝yciem specjalnie opracowanego pla-
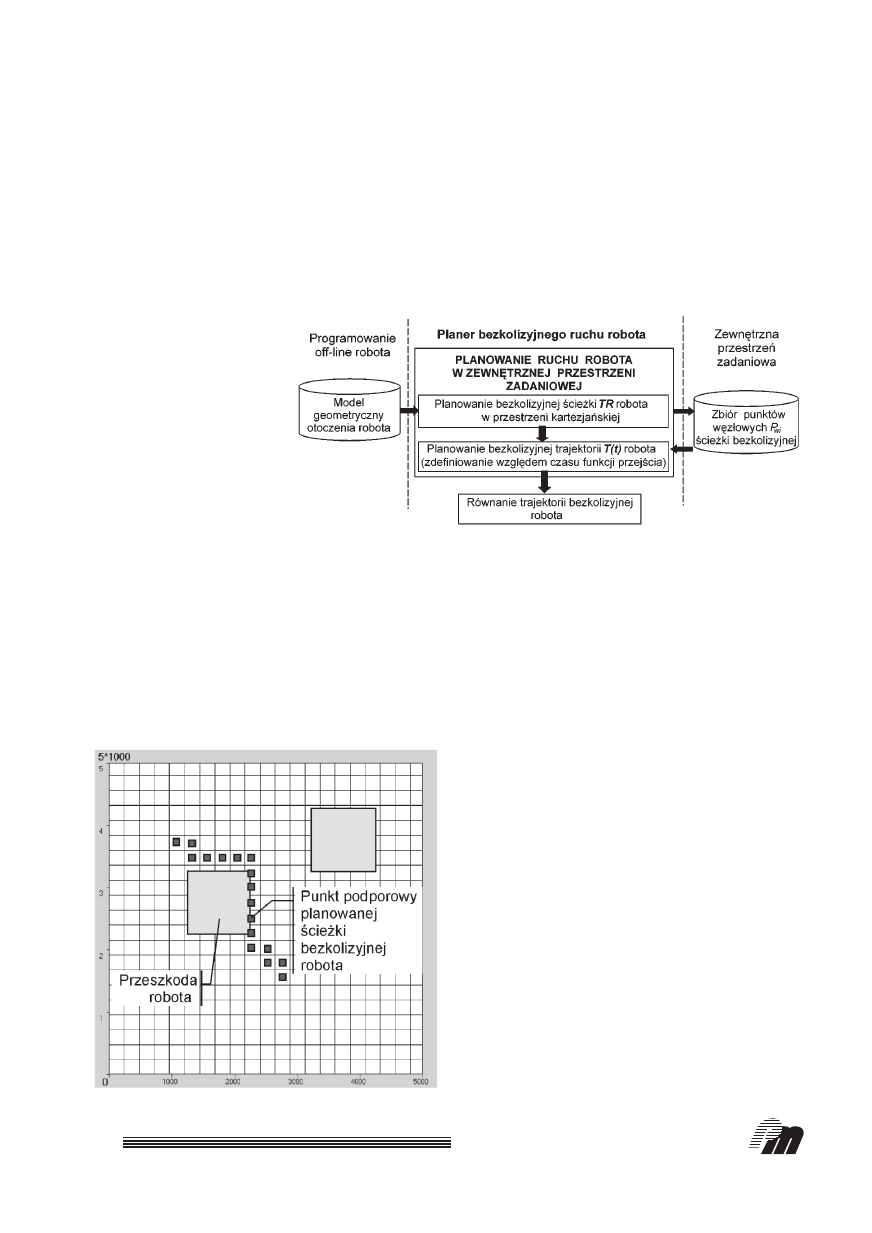
nera (rys. 1), którego kolejne etapy dzia∏ania dotyczà
[2 – 3]:

쐌 analizy przestrzeni zadaniowej robota w celu

wyznaczenia obszarów, w których ruch robota mo˝e
si´ odbywaç bezkolizyjnie,

쐌 wyznaczenia w przes-

trzeni zadaniowej robota
bezkolizyjnej Êcie˝ki robota,
rozumianej jako zbiór punk-
tów w przestrzeni, przez
które przebiega bezkolizyj-
na droga robota,

쐌 wyznaczenie bezkoli-

zyjnej trajektorii, jako spa-
rametryzowanego czasem

równania bezkolizyjnej drogi robota w przestrzeni
zadaniowej.

Zadaniem pierwszoplanowym dzia∏aƒ planera jest

wi´c analiza geometryczna otoczenia robota ze
szczególnym uwzgl´dnieniem przestrzeni zadaniowej
przy uwzgl´dnieniu konfiguracji przestrzennej oto-
czenia (obiektów-przeszkód) [2].

Na podstawie tej analizy planer typuje zbiór kolejno

osiàganych przez robota po∏o˝eƒ, tzw. punktów
podporowych. Punkty podporowe mogà byç przyj-
mowane tylko w cz´Êci przestrzeni zadaniowej wolnej
od przeszkód, dzi´ki czemu wyznaczajà one Êcie˝k´

bezkolizyjnà. Ze wzgl´du na sposób prowadzenia
analizy przestrzeni zadaniowej wyznaczona Êcie˝ka
bezkolizyjna jest ∏amanà, zdefiniowanà przez zbiór
kolejnych po∏o˝eƒ robota (punktów podporowych)
zwiàzanych z ka˝dym wytypowanym przez planer
pustym (bezkolizyjnym) fragmentem przestrzeni
(rys. 2). Uzyskana w ten sposób bezkolizyjna Êcie˝ka
(∏amana) nie mo˝e byç jednak wykorzystana przez
programator robota (system off-line). Jest to spo-
wodowane tym, ˝e ∏amanà tworzy zbyt liczny zbiór
punktów oraz to, ˝e ze wzgl´du na technik´ ich
uzyskania (metody rastrowe) [2, 5] nie jest ona g∏adka
w sensie geometrycznym, co oznacza, ˝e nie cechuje
si´ p∏ynnoÊcià zmiany przebiegu w przestrzeni. W wy-
niku tego, przejÊcie robota w przestrzeni po wyzna-

czonej Êcie˝ce charakteryzowa∏oby si´ ciàg∏à zmianà
kierunku przejÊcia (rys. 2). Z tego powodu konieczne
jest wyg∏adzenie uzyskanej Êcie˝ki poprzez wyeli-
minowanie ze zbioru punktów podporowych, które
nie powodujà zmiany kierunku przebiegu Êcie˝ki
w przestrzeni poza przyj´te kryteria. Tym samym
konieczne jest przeprowadzenie kolejnego etapu
planowania prowadzàcego do wyznaczenia podzbio-
ru punktów podporowych stanowiàcych podstaw´
wyznaczenia poszukiwanego równania drogi robota
w przestrzeni bezkolizyjnej [2, 3]. Uk∏ad przestrzenny
przeszkód robota oraz sposób ich omijania, po∏o˝enie
poczàtkowe, koƒcowe i wymagany kszta∏t planowa-
nej drogi powodujà, ˝e ustalenie jednoznacznych
kryteriów geometrycznych eliminacji bàdê typowania
punktów podporowych utrudniajà sformalizowanie
(zalgorytmizowanie) procedury ich typowania. Wyzna-
czenie równania krzywej geometrycznie g∏adkiej (bez
za∏amaƒ, p∏ynnie zmieniajàcej swój przebieg w wyz-
naczonym kierunku) umo˝liwia w koƒcowym etapie jej
sparametryzowanie czasem. Pozwala to na uzyskanie
równania bezkolizyjnej trajektorii robota w przestrzeni
spe∏niajàcej wymagane w robotyce kryteria g∏adkoÊci
(krzywa klasy C

2

z ciàg∏à pochodnà rz´du drugiego),

co umo˝liwia wyliczenie pochodnych przemieszczenia
wzgl´dem czasu, czyli okreÊlenie wartoÊci chwilo-
wych pr´dkoÊci i przyÊpieszeƒ kiÊci manipulatora.
Proces wyznaczania bezkolizyjnego równania Êcie˝ki
ruchu powtarzany jest dla ka˝dego kroku pracy
manipulatora. Wià˝e si´ to z koniecznoÊcià ciàg∏ego
monitorowania po∏o˝enia kiÊci robota i dynamicznym
wyznaczaniem kolejnych fragmentów bezpiecznego
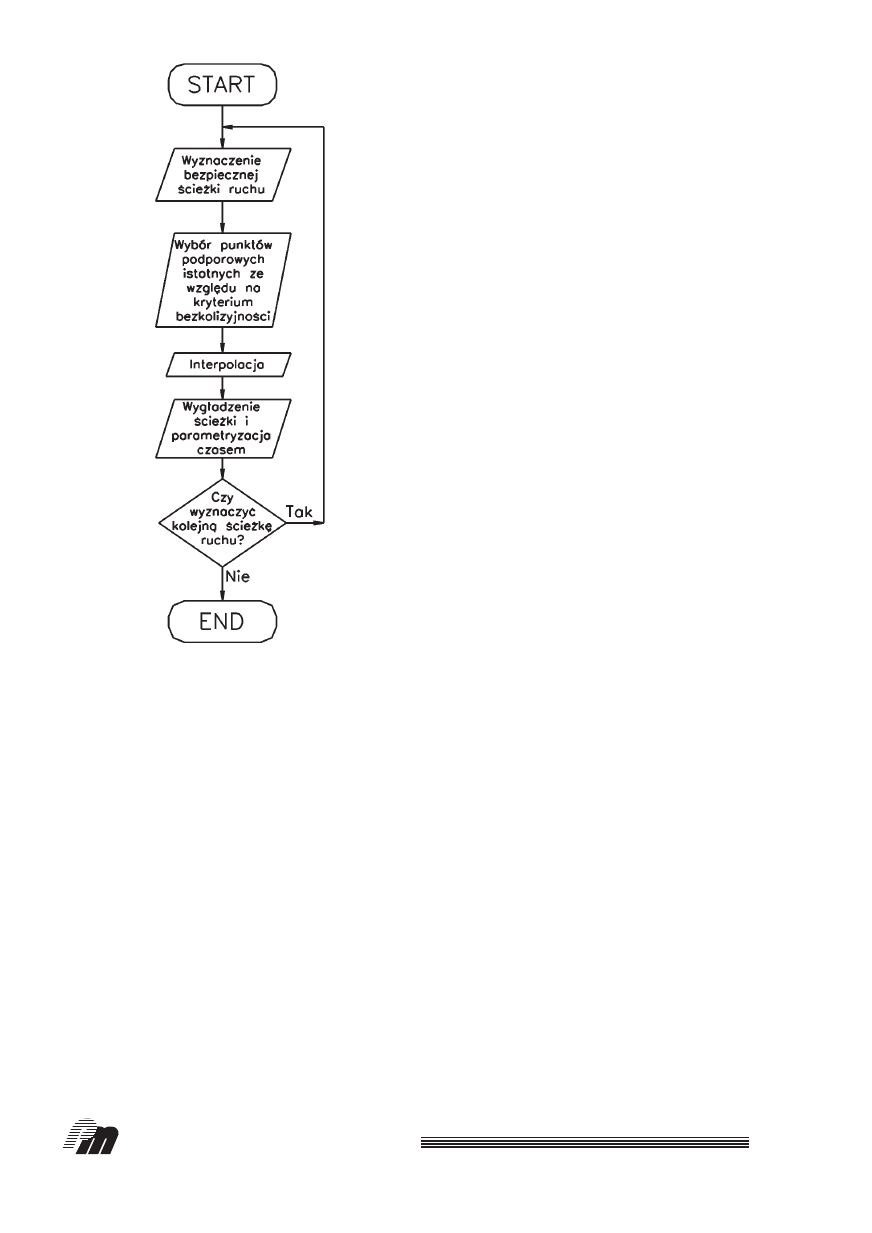
przejÊcia przez przestrzeƒ zadaniowà. Na rys. 3 po-
kazano algorytm dzia∏ania dynamicznego systemu
planowania bezpiecznych trajektorii ruchu robotów
manipulacyjnych.

Rys. 1. Zadanie planowania bezkolizyjnej
trajektorii robota [2]

Rys. 2. Przyk∏ad wygenerowanej Êcie˝ki bezkolizyjnej robota [3]

ROK WYD. LXVII

앫 ZESZYT 1/2008

2 5

Poszukiwanie równania

bezkolizyjnej krzywej w przestrzeni 3D

Wykorzystywane w robotyce techniki rozwiàzy-

wania zadania wyznaczania trajektorii robota opie-
rajà si´ na poszukiwaniu takich punktów podpo-
rowych, które pozwoli∏yby na uzyskanie metodami
interpolacyjnymi równania krzywej przybli˝ajàcej
kszta∏t uzyskanej Êcie˝ki bezkolizyjnej. Interpolacja
prowadzi jednak do odst´pstw przebiegu (kszta∏tu)
uzyskanej krzywej interpolowanej opartej na kilku
wybranych punktach podporowych w stosunku do
Êcie˝ki gwarantujàcej bezkolizyjnoÊç. Najprostszym
sposobem poprawy tego stanu jest zwi´kszenie liczby
wykorzystanych w procesie interpolacji punktów. To
jednak wyd∏u˝a czas niezb´dnych obliczeƒ [4 – 6].
Stosowane do rozwiàzywania tego zadania techniki
interpolacyjne wykorzystujà g∏ównie krzywe wielo-
mianowe. Z∏o˝onoÊç obliczeniowa problemów inter-
polacyjnych tego zadania powoduje, ˝e najcz´Êciej
wykorzystuje si´ do tego celu wielomiany niskich
stopni (trzeciego stopnia), które gwarantujà uzyskanie
ciàg∏ej pochodnej pierwszego rz´du w punktach
w´z∏owych (krzywe klasy C

1

) lub jedynie pozwalajà na

zdefiniowanie krzywej gwarantujàcej uzyskanie ciàg-
∏oÊci w sensie geometrycznym w tych punktach. Stàd
te˝ istotnym problemem jest znalezienie takiej

minimalnej liczby punktów podporowych, która przy
stosunkowo krótkim czasie prowadzonych analiz
umo˝liwi∏aby dostatecznie dok∏adne odwzorowanie
Êcie˝ki bezkolizyjnej i to wielomianem gwarantujàcym
uzyskanie ciàg∏ej pochodnej drugiego rz´du (C

2

).

Oprócz interpolacji wielomianowej w robotyce

proponuje si´ wykorzystanie krzywych

Béziera (wielo-

miany

Bernsteina-Béziera) i funkcji B-sklejanych [5 – 7]

oraz ich odmian wymiernych [6, 8], które pozwalajà
na nadawanie wagi punktom podporowym (liczby
wp∏ywu). Zmiana techniki interpolacyjnej nie wyni-
ka tylko z potrzeby w miar´ pe∏nego odwzorowania
posiadanej Êcie˝ki bezkolizyjnej, przy najmniejszej
liczbie wykorzystanych w procesie interpolacji
punktów podporowych. Oddzia∏uje ona równie˝
na sam proces sterowania robotem poprzez cha-
rakterystyk´ uzyskiwanego bezkolizyjnego toru ro-
bota [4].

쐌 Zastosowanie krzywych Béziera i B-sklejanych

w robotyce

PrzydatnoÊç procedur interpolujàcych opartych na

funkcjach wielomianowych, krzywych

Béziera czy

krzywych B-sklejanych nie zosta∏a w robotyce w szer-
szym zakresie zweryfikowana. G∏ównym powodem
takiego stanu jest czasoch∏onnoÊç procesów inter-
polujàcych, które dotyczà ka˝dorazowo krzywej
przestrzennej (przestrzeƒ 3D), oraz które muszà byç
poprzedzone z∏o˝onymi i bardzo czasoch∏onnymi, bo
odnoszàcymi si´ równie˝ do przestrzeni 3D, proce-
durami wyznaczania bezkolizyjnej Êcie˝ki w celu
jednoznacznego ustalenia zbioru punktów podpo-
rowych (rys. 3). Z tych powodów ostateczne ustalenie
sposobu przeprowadzenia procesu interpolacyjnego
nie jest proste i jednoznaczne [4, 5, 7, 8].

Metody interpolujàce oparte na wielomianach

Bernsteina-Béziera oprócz zalet majà równie˝ doÊç
istotne wady. Do g∏ównych nale˝y zaliczyç [7, 8]:

쐌 poszukiwanie optymalnego odwzorowania in-

terpolacyjnego istniejàcej Êcie˝ki robota wymaga
podejÊcia iteracyjnego, dodanie kolejnego punktu
poÊredniego w celu lepszego „dopasowania” krzywej
interpolowanej do wzorca Êcie˝ki wymaga przepro-
wadzenia kolejnych obliczeƒ interpolacyjnych,

쐌 trudnoÊci w odwzorowaniu typowych dla ruchu

robota kszta∏tów drogi, jakimi sà np. okr´gi, elipsy
typowe dla programowanych w robocie ruchów
interpolowanych,

쐌 niemo˝noÊç swobodnego manipulowania

punktami podporowymi w celu dok∏adnego od-
wzorowania posiadanej Êcie˝ki, mo˝na jedynie
do∏o˝yç kolejne w´z∏y, natomiast nie mo˝na ich
przesuwaç, gdy˝ powoduje to deformacj´ uzyskanej
ju˝ krzywej,

쐌 interpolowanie dróg o z∏o˝onych kszta∏tach

pociàga za sobà koniecznoÊç uzyskiwania krzywych
wysokich stopni, co znaczàco utrudnia bàdê nawet
uniemo˝liwia przeprowadzenie procesu interpolacji.

Ze wzgl´du na przytoczone wady proponuje si´

wykorzystaç w zadaniu interpolacji krzywe B-skle-
jane. Krzywe te spe∏niajà stawiane im podstawowe
wymagania na potrzeby interpolacji Êcie˝ki robota,
gdy˝ [7, 8]:

쐌 mo˝na je modyfikowaç fragmentami, bez ko-

niecznoÊci zmiany pozosta∏ych jej cz´Êci, co pozwa-
la na konstruowanie krzywych o kszta∏tach zgodnych
z oczekiwaniami (wymaganiami),

Rys. 3. Algorytm dzia∏ania systemu dynamicznego planowania
bezpiecznej Êcie˝ki robotów manipulacyjnych

ROK WYD. LXVII

앫 ZESZYT 1/2008

2 6

쐌 dla krzywych trzeciego stopnia mo˝na uzyskaç

ciàg∏oÊci drugiej pochodnej w w´z∏ach wspólnych
(punktach sklejania wielomianów rozpi´tych mi´dzy
kolejnymi punktami podporowymi), co jest warun-
kiem uzyskania krzywych klasy C

2

.

W przypadku zajÊcia koniecznoÊci zmiany krzywej

interpolujàcej z wielomianu B-sklejanego na krzywà
Béziera mo˝liwy jest do zastosowania niezmieniony
aparat matematyczny, poniewa˝ jednà z cech B-splaj-
nów jest fakt, ˝e ich stopieƒ nie mo˝e byç wi´kszy
ni˝ liczba punktów podporowych. Dla stopnia krzywej
B-sklejanej równej liczbie w´z∏ów interpolacji (wyb-
ranych punktów podporowych) matematyczna postaç
krzywej B-sklejanej jest to˝sama z opisem równania
krzywych

Béziera [7]. Zatem zamiana jednego typu

interpolacji w drugi polega na przyj´ciu w∏aÊciwego
stopnia B-splajnu równego liczbie w´z∏ów interpolacji
[7, 8].

쐌 Krzywe NURBS (wymierne wielomiany B-skle-

jane)

PrzydatnoÊç procedur interpolujàcych opartych na

funkcjach NURBS (Non Uniform Rational B-Spline)
jest znacznie wi´ksza ni˝ w przypadku konwencjo-
nalnych B-splajnów. Dzieje si´ tak dlatego, ˝e ka˝-
demu z punktów podporowych interpolacji mo˝na
przypisaç wag´, która okreÊla stopieƒ dopasowania
krzywej interpolujàcej do punktu. Aparat matema-
tyczny krzywych NURBS jest ponadto najbardziej
wszechstronny, poniewa˝ przypisanie jednakowej
wagi wszystkim punktom trajektorii bezkolizyjnej
podlegajàcym interpolacji spowoduje automatycznà
zamian´ równania drogi robota do postaci B-skejanej
(lub te˝, po przyj´ciu stopnia B-splajnu równego
liczbie punktów podporowych, przejÊcie do wielo-
mianów

Bernsteina-Béziera) [7].

Algorytm generowania krzywych

interpolujàcych

Krzywe interpolujàce oparte na wielomianach

Bernsteina-Béziera, jak i te˝ na NURBS i B-splajnach sà
funkcjami z∏o˝onymi. Podstawà generowania tych
krzywych sà funkcje bazowe, których odpowiednie
sklejenie ze sobà daje w rezultacie zamierzony kszta∏t
przestrzennej krzywej o zadanych parametrach. Po-
niewa˝ funkcje bazowe sà okreÊlone w dziedzinie
czasu, to mo˝na stwierdziç, ˝e powsta∏a z ich sklejenia
krzywa równie˝ jest poÊrednio okreÊlona w dziedzinie
czasu. Zatem aby móc wykreÊliç krzywà interpolujàcà
ruch robota po wyznaczonej Êcie˝ce bezkolizyjnej,
nale˝y w pierwszym etapie przewidzieç ca∏kowity czas
trwania ruchu. Czas ten w dalszej cz´Êci przyjmowany
jest jako umowna jednostka podstawowa, tzn. ruch
trwa w umownym przedziale czasowym od 0 do 1,
czyli od zera do 100% rzeczywistego czasu. Ponie-
wa˝ aparat matematyczny krzywych NURBS, jak ju˝
wspomniano, jest najbardziej wszechstronny, tote˝
w dalszej cz´Êci opisywany b´dzie tok post´powania
podczas realizacji tego w∏aÊnie algorytmu [7, 8].

W procesie tworzenia wielomianu interpolujàcej

funkcji gi´tkiej konieczne jest w pierwszej kolejnoÊci
wyznaczenie w´z∏ów interpolacji. Poniewa˝ ruch po
krzywej trwaç ma od 0 do 1, tote˝ w´z∏ami interpolacji
b´dà przedzia∏y czasowe z tego zakresu. Aby przyjàç
w∏aÊciwà liczb´ w´z∏ów interpolacji, musimy ustaliç
stopieƒ

n wielomianu interpolacyjnego oraz poznaç

liczb´ punktów podporowych interpolacji

Li. Ma-

tematycznie zbiór w´z∏ów mo˝na zapisaç w nast´-
pujàcy sposób [7]:

T = [t

0

,

t

1

,

t

2

, ...,

t

k

} (1)

przy czym liczba w´z∏ów

t

i

musi byç równa liczbie

U

[7]:

U = Li + n + 1 (2)

By przydzieliç w∏aÊciwe wartoÊci czasu z zakresu

od 0 do 1, nale˝y zastosowaç nast´pujàcy tok post´-
powania: Pierwsze

n + 1 w´z∏ów wype∏niç nale˝y war-

toÊciami 0, ostatnie

n + 1 w´z∏ów wartoÊciami 1, nato-

miast pozosta∏e w´z∏y wype∏niane sà proporcjonalnie
rosnàcymi wartoÊciami czasu. Przyk∏adowy zbiór
w´z∏ów interpolacji dla krzywej trzeciego stopnia
i 7 punktów podporowych ma postaç [7]:

T = {0; 0; 0; 0; 0,25; 0,5; 0,75; 1; 1; 1; 1} (3)

Majàc wyznaczone punkty w´z∏owe interpolacji

(punkty

T na osi czasu (3)), mo˝na wyznaczyç bazowe

funkcje sk∏adowe wymiernego wielomianu B-skle-
janego (NURBS). Wyznaczanie funkcji bazowych jest
procesem iteracyjnym, poniewa˝ aby wyznaczyç
funkcje bazowe danego stopnia, konieczne jest wyz-
naczenie wczeÊniej funkcji bazowych stopnia ni˝-
szego. W zwiàzku z tym ca∏y proces rozpoczyna si´ od
wyznaczenia funkcji bazowych stopnia zerowego,
które definiowane sà nast´pujàco: dla zadanego prze-
dzia∏u czasu sà równe 1, natomiast dla pozosta∏ych
okresów czasu przyjmujà wartoÊci 0, co mo˝na za-
pisaç [7]:

(4)

Funkcje bazowe stopni wy˝szych wyliczane sà na

podstawie nast´pujàcej zale˝noÊci [7]:

(5)

gdzie:

p przyjmuje kolejno wartoÊci: 1, 2, 3 a˝ do

wartoÊci stopnia wielomianu

n,

i przyjmuje kolejne wartoÊci od 0 a˝ do liczby

przedzia∏ów pomi´dzy w´z∏ami

Li + n.....

Majàc wyliczone wartoÊci funkcji bazowych, mo˝na

wyznaczyç wspó∏rz´dne punktów wielomianu inter-
polujàcego

X(t), Y(t), Z(t) jako superpozycji wartoÊci

poszczególnych wspó∏rz´dnych uk∏adu kartezjaƒ-
skiego. W przypadku konwencjonalnego wielomianu
B-sklejanego wartoÊci wspó∏rz´dnych liczone sà jako
suma iloczynów funkcji bazowych i wartoÊci wspó∏-
rz´dnych punktów podporowych

P, co mo˝na zapisaç

jako [7, 8]:

(6)

(7)

(8)

ROK WYD. LXVII

앫 ZESZYT 1/2008

2 7

Dla wyliczenia wymiernego wielomianu B-skle-

janego (NURBS) musimy uwzgl´dniç ponadto wagi
punktów podporowych

P oznaczone jako w. Znajàc

wagi punktów podporowych, mo˝na wyliczyç po-
szczególne wspó∏rz´dne wielomianu interpolujàcego
wykorzystujàc wzory [7, 8]:

(9)

(10)

(11)

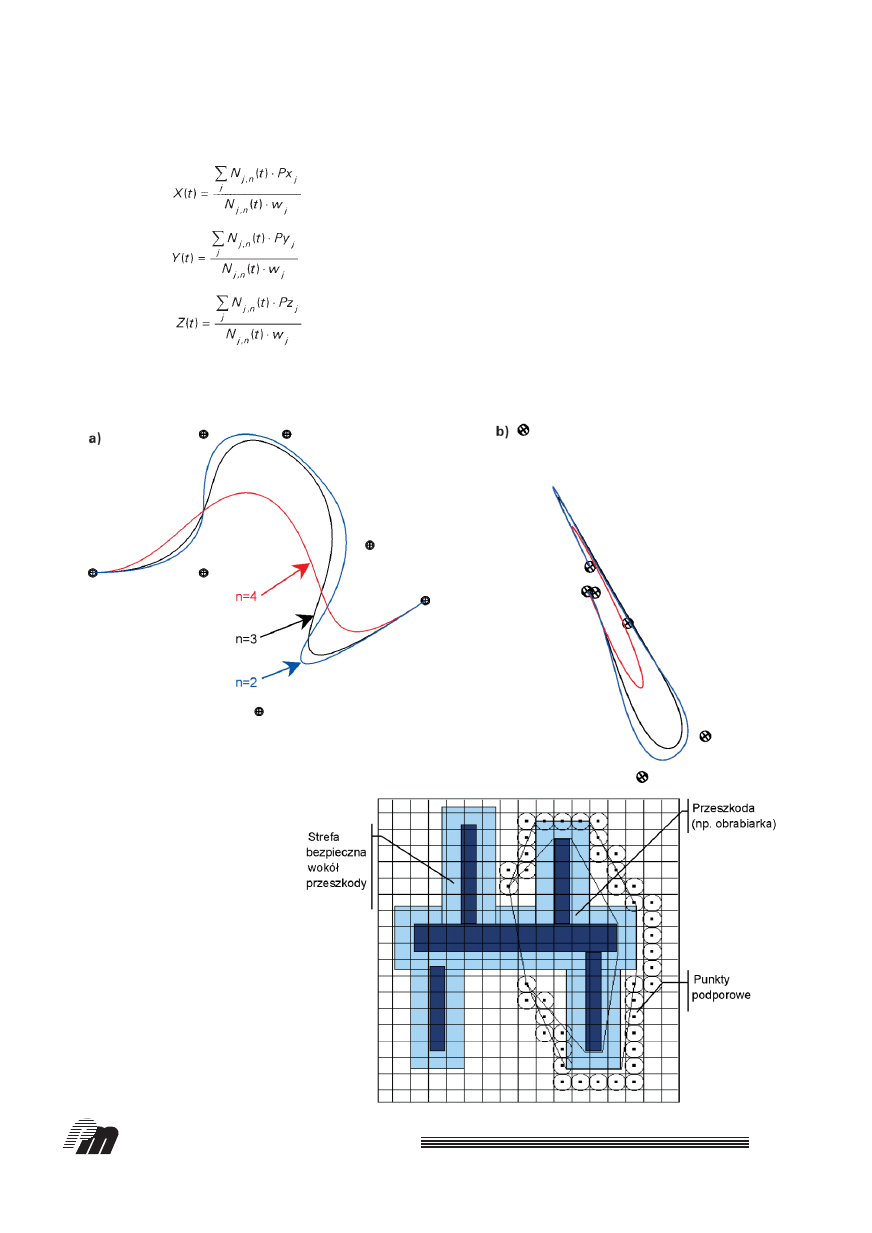
Aby zobrazowaç dzia∏anie algorytmu, pokazano

przyk∏adowo trajektorie utworzone z wykorzystaniem
losowo wytypowanych punktów podporowych. Na
rys. 4 pokazano wygenerowane przestrzenne trajek-

torie dla ró˝nych stopni wielo-
mianu interpolujàcego [7]. Istot-
nà w∏asnoÊcià wygenerowanych
krzywych jest stopieƒ dopaso-
wania do punktów podporowych.
Im wi´kszy stopieƒ wielomianu
interpolujàcego

n zostanie przy-

j´ty, tym bardziej odsuni´ta zosta-
je wygenerowana krzywa od wyz-
naczajàcych jà punktów podporo-
wych. Zwi´kszanie stopnia wielo-
mianu interpolujàcego powodu-
je równie˝ zmniejszenie przegi´ç
krzywej, co w rezultacie daje krzy-
wà o bardziej ∏agodnych zaokràg-
leniach.

Rys. 4. Ró˝ne uj´cia przestrzennych trajektorii B-sklejanych przy zró˝nico-
waniu stopnia wielomianu interpolacyjnego

Rys. 5. Scena robota z wygenerowanà
bezpiecznà Êcie˝kà wokó∏ przeszkody
(obrabiarki)

Zastosowanie aplikacyjne

krzywych B-sklejanych do interpolacji

bezpiecznych trajektorii robotów

w przestrzeniach zadaniowych

G∏ównym celem niniejszej publikacji by∏o przed-

stawienie próby zastosowania krzywych interpolu-
jàcych opartych na wielomianach NURBS do „wy-
g∏adzania” bezpiecznej trajektorii ruchu robotów
manipulacyjnych. Trajektorie poczàtkowe reprezen-
towane sà przez zbiór punktów podporowych tra-
jektorii ruchu robota. Przyj´ty przez autorów sposób
generowania trajektorii poczàtkowych implikuje
postaç krzywej opisanej na wynikowych punktach
podporowych [1 – 3]. Krzywa ta jest zawsze rów-
noleg∏a do jednej z osi kartezjaƒskiego uk∏adu wspó∏-
rz´dnych, przez co niemo˝liwe jest jej wykorzystanie
w sposób bezpoÊredni do zaprogramowania ruchu
robota. Na rys. 5 pokazano przyk∏adowà scen´
(przestrzeƒ roboczà) manipulatora przemys∏owego
wraz z rozmieszczeniem obrabiarek numerycznych.

Obrabiarki (kolor ciemnoniebieski) stanowià in-

frastruktur´ technicznà systemu zrobotyzowanego,

ROK WYD. LXVII

앫 ZESZYT 1/2008

2 8

jednak˝e sà zarazem przeszkodà w swobodnym
poruszaniu si´ robota. Opracowany planer trajektorii
potrafi, na podstawie zapisu matematycznego sceny
robota oraz wielkoÊci wymiarowych manipulowa-
nego przedmiotu, wyznaczaç trajektori´ bezpiecznà.
Aby uzyskaç pewnoÊç bezkolizyjnoÊci ruchów, pro-
gram przyporzàdkowuje ka˝dej obrabiarce stref´
niebezpiecznà (kolor jasnoniebieski), którà omija pod-
czas generowania trajektorii. Na podstawie danych
wymiarowych manipulowanego przedmiotu oblicza-
ny jest równie˝ wymiar siatki i Êrednica okr´gu
po∏o˝eƒ poÊrednich. Na rys. 5 pokazano wygenero-
wanà trajektori´ bezpiecznego przejÊcia z jednej
strony obrabiarek na drugà przy zachowaniu warunku
bezkolizyjnoÊci.

Po wygenerowaniu bezpiecznej trajektorii poczàt-

kowej nast´puje kolejny krok iteracyjnych obliczeƒ,
którego zadaniem jest dopasowanie mo˝liwie naj-
bardziej g∏adkiej trajektorii za pomocà sparametryzo-
wanej czasem funkcji interpolacyjnej bazujàcej na
aparacie matematycznym NURBS (uniwersalny apa-
rat matematyczny w zale˝noÊci od spe∏nienia za-
danych warunków logicznych automatycznie prze-
kszta∏ca si´ w wielomian B-sklejany lub te˝ w krzywà
Bernsteina-Béziera [7, 8]).

Jak wykaza∏y badania, niezb´dnym modu∏em do-

datkowym utworzonego oprogramowania jest algo-
rytm decyzyjny wielokrotnego selektywnego wyboru
punktów podporowych trajektorii poczàtkowej. Modu∏
ten w sposób automatyczny usuwa ze zbioru punktów
podporowych trajektorii poczàtkowej kolejne naro˝a,
sprawdzajàc ka˝dorazowo warunek bezkolizyjnoÊci
nowo utworzonej trajektorii. Zastosowany aparat
matematyczny zaprogramowany jest na minimalizo-
wanie iloÊci punktów podporowych. Zakoƒczenie
dzia∏ania do∏àczonego modu∏u powoduje rozpocz´cie
procesu maksymalizowania stopnia wielomianu in-
terpolacyjnego z mo˝liwoÊcià nadawania wag pozos-
ta∏ym punktom podporowym trajektorii poczàtko-
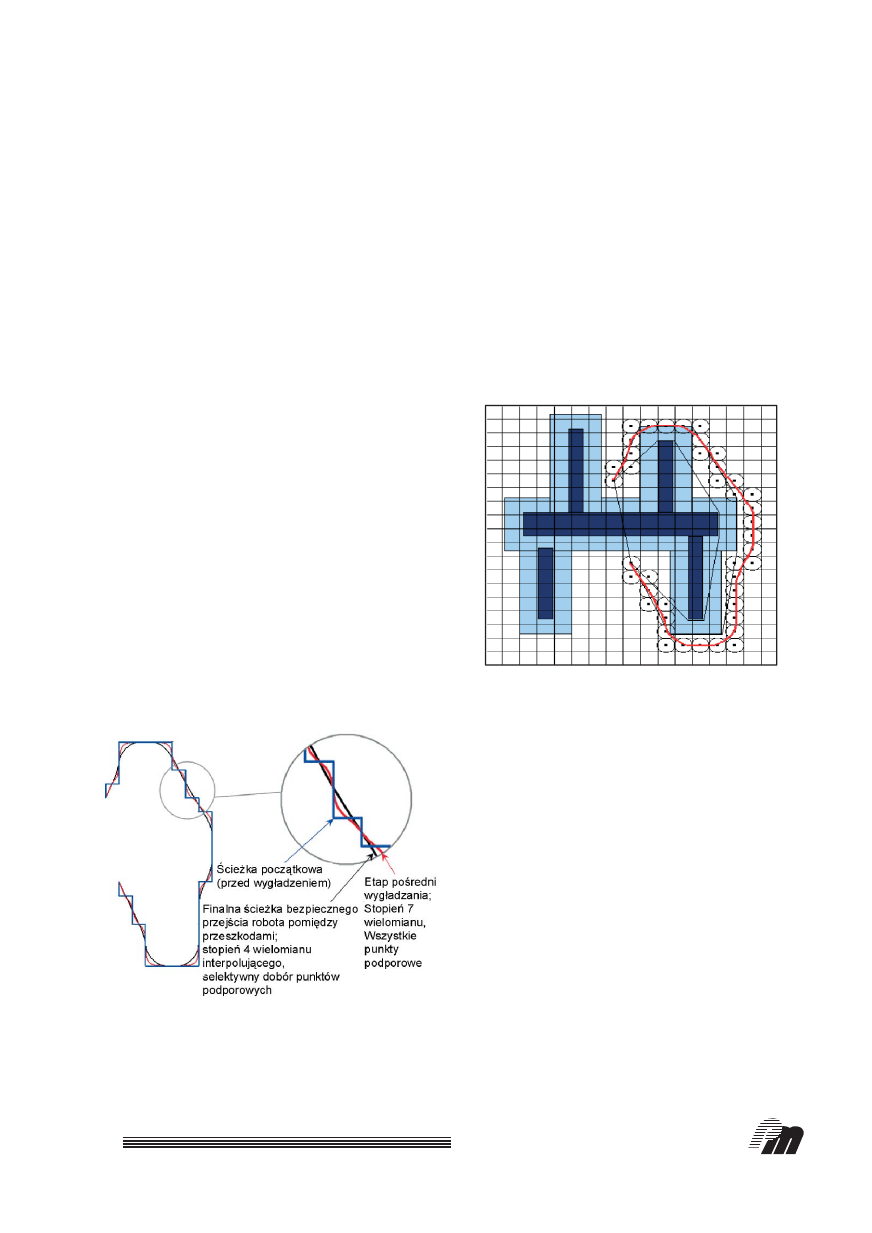
wej. Na rys. 6 pokazano kolejne stadia wyg∏adzania
trajektorii ruchu bezkolizyjnego robota w przestrzeni
zadaniowej.

ponowanà metodà. Ostateczna trajektoria (kolor
czarny) powsta∏a po selektywnym usuni´ciu 18 punk-
tów podporowych naro˝nych. Ostateczny stopieƒ
wielomianu ustalono na

n = 4 (warunkiem ciàg∏oÊci

drugiej pochodnej by∏o zachowanie stopnia wielo-
mianu interpolacyjnego wi´kszego ni˝ 2). O tym jak
wa˝ne jest selektywne usuwanie punktów, Êwiadczy
trzecia, poÊrednia trajektoria pokazana na rysunku
kolorem czerwonym. Trajektoria ta powsta∏a na bazie
wszystkich punktów podporowych i maksymalnie
wyg∏adzonego wielomianu interpolacyjnego (krzywa
Béziera – stopieƒ wielomianu równy liczbie punktów
podporowych trajektorii poczàtkowej). Jak widaç,
mimo zastosowania najwy˝szego z mo˝liwych stopni
wielomianu interpolacyjnego, nadal wyst´pujà oscy-
lacje wokó∏ przewidywanej trajektorii optymalnej. Po
zakoƒczeniu procesu optymalizacji i wyg∏adzania
bezpiecznej trajektorii ruchu robota w przestrzeni
zadaniowej mo˝liwe jest pokazanie wyników pracy
algorytmu na tle trajektorii poczàtkowej oraz sceny
robota (rys. 7).

Jak mo˝na zauwa˝yç w górnej cz´Êci rysunku,

nowa, wyznaczona trajektoria przecina stref´ bezpie-
czeƒstwa wokó∏ obrabiarki, a mimo to zosta∏a przez
system zaakceptowana. Dzieje si´ tak, poniewa˝ w po-
czàtkowych obliczeniach konieczne by∏o zastosowa-
nie obiektów technologicznych (w tym tak˝e stref bez-
pieczeƒstwa tych obiektów) o kraw´dziach równo-
leg∏ych. By∏o do podyktowane koniecznoÊcià ograni-
czenia czasu przeszukiwania przestrzeni zadanio-
wej, który by∏ znacznie krótszy w przypadku naro˝y
prostokàtnych [1 – 3]. W rzeczywistoÊci przestrzeƒ
bezpieczeƒstwa ma charakter ekwidystanty odsuni´-
tej na zewnàtrz konturu maszyny i d∏ugoÊci odsuni´-
cia równej Êrednicy kuli opisanej na manipulowa-
nym przedmiocie. Algorytm sprawdzajàcy popraw-
noÊç wykonywanej optymalizacji trajektorii pos∏u-
guje si´ rzeczywistym wyglàdem stref bezpieczeƒ-
stwa, których widok pokazano na rys. 8. Poniewa˝
modu∏ sprawdzajàcy ma zdefiniowany iteracyjny
algorytm kontroli znanej Êcie˝ki (aktualny poziom
wyg∏adzenia), to nie musi poszukiwaç jej w przestrze-
ni. Dlatego te˝ przyj´cie sprawdzania rzeczywistej
strefy bezpieczeƒstwa nie przynosi wyd∏u˝enia czasu
obliczeƒ (polega on tylko na sprawdzeniu dodat-
kowych warunków logicznych o sta∏ych parametrach
– pozycjach i wymiarach maszyn).

Kolejne stadia procesu optymalizowania bezpiecz-

nej trajektorii robota w przestrzeni zadaniowej po-
kazujà, jak mocne wyg∏adzenie poczàtkowej trajektorii
(kolor niebieski) jesteÊmy w stanie uzyskaç zapro-

Rys. 6. Kolejne stadia procesu wyg∏adzania bezpiecznej tra-
jektorii robota w przestrzeni zadaniowej

Rys. 7. Naniesiona trajektoria bezpieczna na scen´ robota

ROK WYD. LXVII

앫 ZESZYT 1/2008

2 9

Podsumowanie

Przedstawiony w niniejszej publikacji system po-

szukiwania bezkolizyjnych Êcie˝ek ruchu robotów
w ich przestrzeniach zadaniowych nie zosta∏ jeszcze
w pe∏ni ukoƒczony. Trwajà prace nad dalszà roz-
budowà systemu, a w szczególnoÊci nad do∏àczeniem
mechanizmów przestrzennych poszukiwaƒ optymal-
nego, sparametryzowanego czasem równania bez-
piecznego przemieszczania robota przemys∏owego
w jego przestrzeni zadaniowej. Docelowo autorzy
majà zamiar przygotowaç w pe∏ni funkcjonalny sys-
tem oparty na przestrzennych krzywych B-sklejanych,
jako modu∏ mogàcy byç przy∏àczany do jednego
z istniejàcych systemów programowania off-line
robotów przemys∏owych.

LITERATURA

1.

Kost G., Zdanowicz R.: Modeling of manufacturing systems
and robot motions. Journal of Materials Processing Techno-
logy, Vol. 164-165, (Special issue, Edt: M.J.S. Hashmi).
Elsevier, May 2005, pp. 1369 – 1378.

2.

Kost G.: Planowanie bezkolizyjnych Êcie˝ek manipulacyjnych
i stacjonarnych robotów przemys∏owych oparte na pro-
cesach decyzyjnych Markowa i funkcji ocen. Wydawnictwo
Politechniki Âlàskiej, Gliwice 2004.

3.

Kost G.: Planowanie bezpiecznych Êcie˝ek robotów oparte
na funkcji ocen. In˝ynieria Maszyn, T. 10, nr 1-2/2005. ss.
165 – 182.

4.

Boissonat J. D., Budrick J., Goldberg K.: Algorithmic Foun-
dations of Robotics V. Springer tracts in advanced robotics 7.
Springer-Verlag publishing. Berlin, Heidelberg 2004.

5.

Dul´ba I.: Metody i algorytmy planowania ruchu robotów
mobilnych i manipulacyjnych. Akademicka Oficyna Wy-
dawnicza EXIT, Warszawa 2001.

6.

Kiciak P.: Podstawy modelowania krzywych i powierzchni.
WNT, Warszawa 2005.

7.

Majchrzak E., Mochnacki B.: Metody numeryczne. Podstawy
teoretyczne. Aspekty praktyczne i algorytmy. Wydawnictwo
Politechniki Âlàskiej, Gliwice 2004.

8.

Fortuna Z., Macukow B., Wàsowski J.: Metody numeryczne.
Podr´czniki akademickie. Elektronika, Informatyka. Teleko-
munikacja. WNT, Warszawa 2001.

Rys. 8. Przeszkoda robota i jej rzeczywista strefa bezpieczeƒ-
stwa