Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
1
14.
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
14.1. Drgania poprzeczne pręta pryzmatycznego
Drgania poprzeczne są to takie drgania, które wywołują przemieszczenia w
x , t
prostopadłe do osi
pręta.
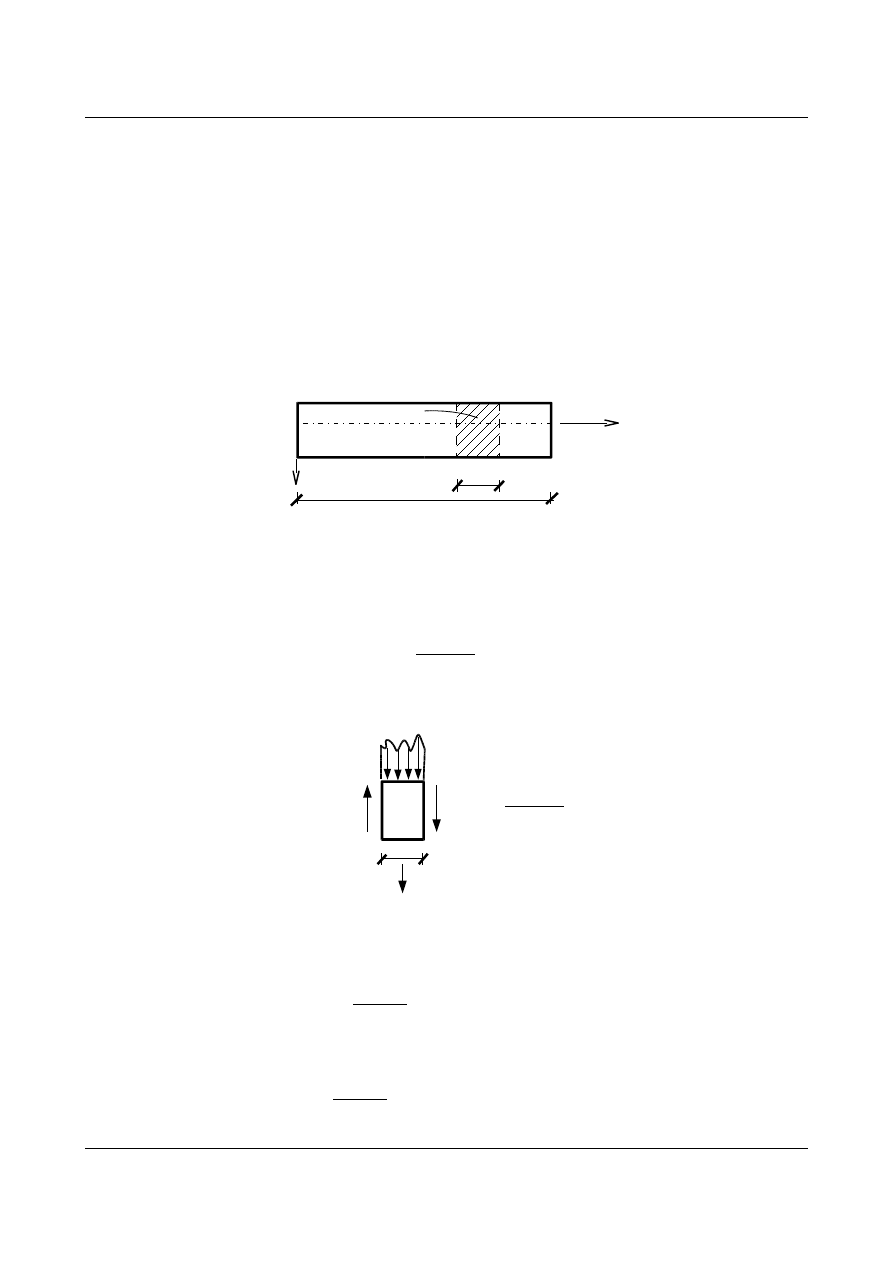
Rozpatrzmy nieskończenie mały wycinek pręta o długości dx , charakteryzujący się gęstością liniową
[
kg
/m
]
(rys. 14.1).
dx
l
dm=μ dx
x
y,w
Rys. 14.1. Element dx belki
Wszystkie wielkości fizyczne i geometryczne
q, M, T, r, ω są funkcjami położenia i czasu f
x , t
,
zależą od współrzędnej analizowanego punktu i od chwili czasu. Ponieważ wycinek pręta dx posiada masę
dm , to podczas ruchu działa na niego siła bezwładności:
r
x , t
=−dm
∂
2
w
x , t
∂t
2
Po wycięciu elementu dx z konstrukcji działają na niego siły:
dx
r(x,t)
T(x,t)
q(x,t)
∂
T
x , t
T
x , t
x
∂
Rys. 14.2. Siły działające na element dx
Zapisując równanie równowagi
∑
Y
=0 otrzymujemy:
T
x , t
−T
x , t
−
∂T
x , t
∂ x
dx
−q
x , t
dx
−r
x , t
=0
Dla pręta nieobciążonego (
q(x,t)=0) przy analizie drgań swobodnych mamy:
∂T
x , t
∂ x
dx
r
x , t
=0
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
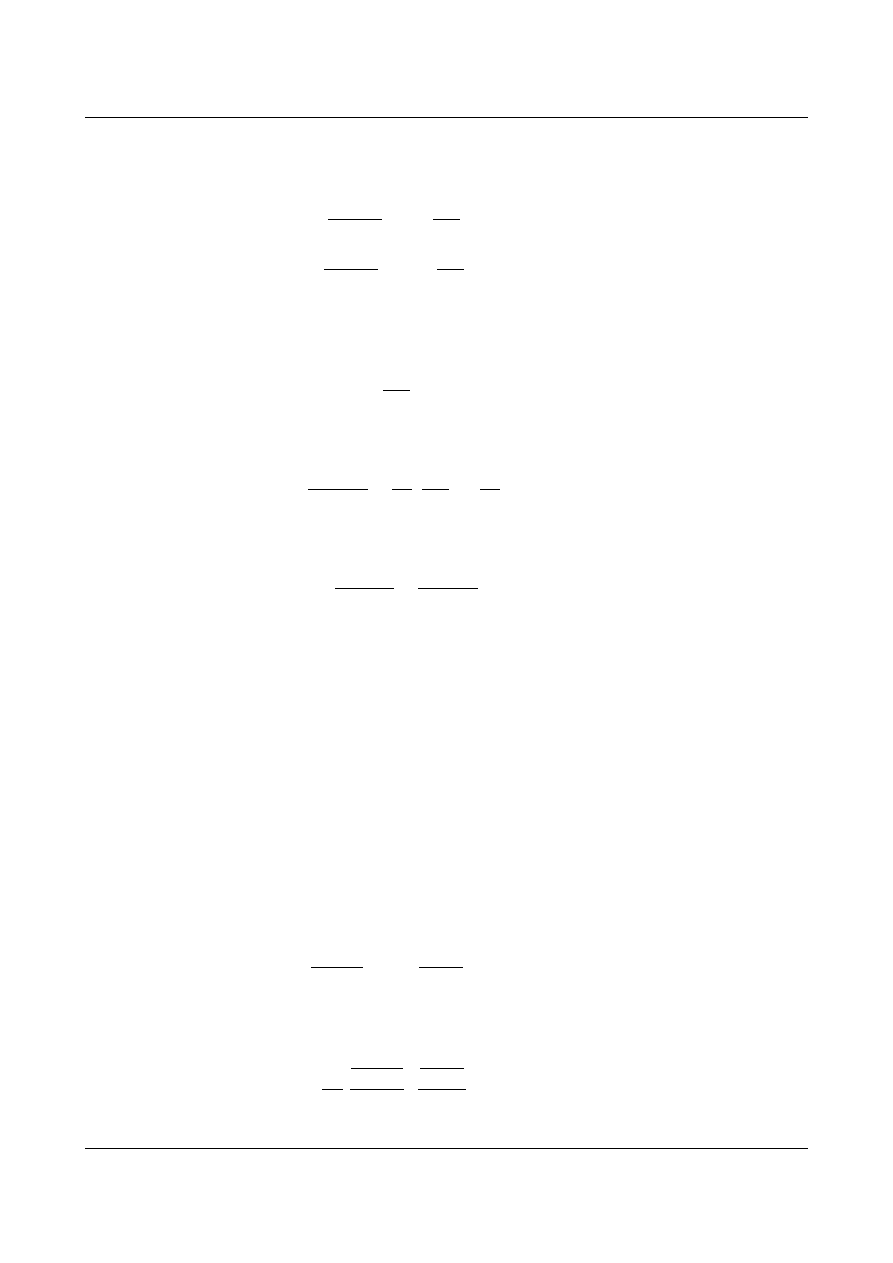
Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
2
a po podstawieniach wyrażeń na siłę bezwładności i masę:
∂T
x , t
∂ x
dx
−dm ∂
2
w
∂ t
2
=0
∂T
x , t
∂ x
dx
− dx ∂
2
w
∂t
2
=0
Dla pręta zginanego względem zmiennej
x obowiązuje zależność łącząca krzywiznę belki z momentem
zginającym:
EJ ∂
2
w
∂ x
2
=−M
Po dwukrotnym zróżniczkowaniu po zmiennej
x otrzymujemy:
EJ
∂
4
w
x , t
∂ x
4
=− ∂
∂ x
∂ M
∂ x
=− ∂
∂ x
T
Wykorzystując zależność na pochodną siły tnącej w równaniu równowagi mamy:
EJ
⋅
∂
4
w
x , t
∂ x
4
∂
2
w
x , t
∂t
2
=0
Upraszczając zapis:
EJ
⋅
IV
⋅ ¨=0
(14.1)
Należy zwrócić uwagę, względem której zmiennej wykonujemy różniczkowanie. Zgodnie z przyjętymi
oznaczeniami:
˙ – pochodne po czasie t,
I
– pochodne po współrzędnej przestrzennej
x.
Wprowadzamy do zapisu rozdział zmiennych. Przemieszczenie jest iloczynem funkcji
W zależnej tylko od
przestrzeni i funkcji
T zależnej tylko od czasu:
w
x , t
=W
x
⋅T
t
(14.2)
Pochodne liczymy po odpowiednich zmiennych:
EJ
⋅
d
4
W
x
d x
4
⋅T
t
d
2
T
t
d t
2
⋅W
x
=0
Po podzieleniu przez wyrażenie
⋅W
x
⋅T
t
otrzymujemy sumę:
EJ
⋅
d
4
W
x
d x
4
W
x
d
2
T
t
d t
2
T
t
=0
(14.3)
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
3
Aby równanie było spełnione, wyrażenia muszą być sobie równe, lecz z przeciwnym znakiem. Dla rozwiązań
różnych od zera każdy z członów przedstawia pewną skalarną wartość
2
.
EJ
⋅
d
4
W
x
d x
4
W
x
=−
d
2
T
t
d t
2
T
t
=
2
Następnie możemy rozwiązać oba równania niezależnie, najpierw dla zmiennej
t, a potem x.
−
d
2
T
t
d t
2
T
t
=
2
d
2
T
t
d t
2
2
⋅T
t
=0
Postępując analogicznie jak przy analizie ruchu punktu materialnego, po wstawieniu w równaniu (12.8) za
funkcję q
t
przemieszczenie T
t
otrzymujemy rozwiązanie:
T
t
=C
1
⋅sin tC
2
⋅cos t=
C
⋅sin
t
Stałe równania C
i
możemy wyznaczyć z warunków początkowych (czas).
EJ
⋅
d
4
W
x
d x
4
W
x
=
2
d
4
W
x
d x
4
−
2
⋅
EJ
⋅W
x
=0
Wprowadzając podstawienie
4
=
2
⋅
EJ
(14.4)
otrzymujemy
d
4
W
x
d x
4
−
4
⋅W
x
=0
(14.5)
Rozwiązaniem, całką ogólną równania różniczkowego (14.5) jest wielomian:
W
x
=A⋅sin xB⋅cos xC⋅sinh xD⋅cosh x
(14.6)
A, B, C i D to wielkości stałe niezależne od czasu, które możemy wyznaczyć z warunków brzegowych
(przestrzeń). Dalej będziemy poszukiwać rozwiązań dla konkretnych belek różniących się sposobem
podparcia.
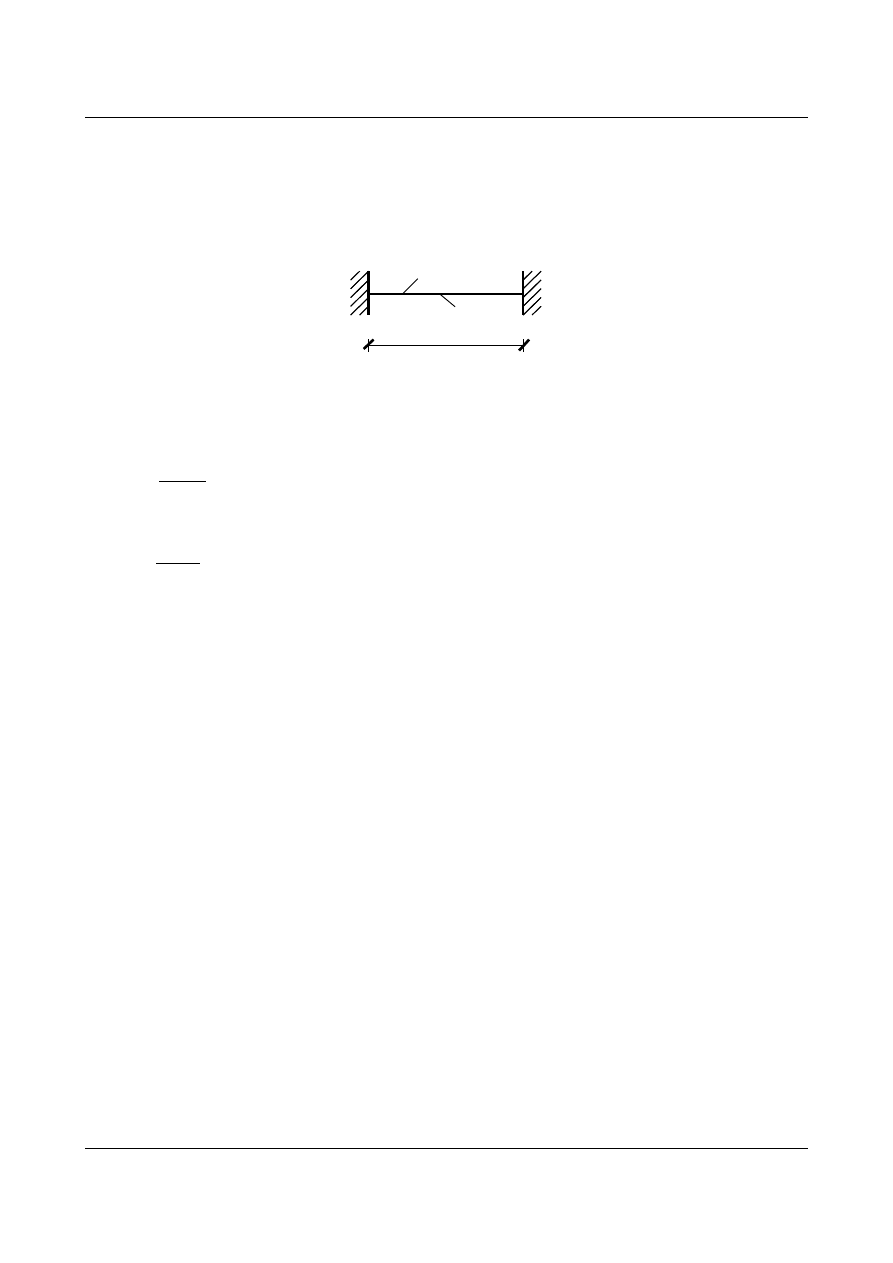
14.1.1. Belka swobodnie podparta
Zastanówmy się jak będą wyglądały drgania własne pręta, rozpatrując przypadek belki swobodnie
podpartej (rys. 14.3).
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater

Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
4
EJ [Nm²]
l
μ [kg/m]
Rys. 14.3. Belka swobodnie podparta
W układzie przedstawionym na rys. 14.3 przemieszczenia i momenty zginające nad podporami powinny być
równe zero:
1) W
x
=0
=0
2) M
x
=0
=W
II
0
=0
3) W
x
=l
=0
4) M
x
=l
=W
II
l
=0
Rozwiązaniem ogólnym jest wielomian:
W
x
=A⋅sin xB⋅cos xC⋅sinh xD⋅cosh x
którego druga pochodna wynosi:
W
II
x
=−
2
⋅A⋅sin x−
2
⋅B⋅cos x
2
⋅C⋅sinh x
2
⋅D⋅cosh x
Z warunków brzegowych otrzymujemy równania:
1)
B
D=0
2)
−BD=0
3)
A
⋅sin lB⋅cos lC⋅sinh lD⋅cosh l=0
4)
−
2
⋅A⋅sin l−
2
⋅B⋅cos l
2
⋅C⋅sinh l
2
⋅D⋅cosh l=0
−A⋅sin l−B⋅cos lC⋅sinh lD⋅cosh l=0
Z warunku
1) i 2) otrzymujemy wprost:
D
=0
B
=0
co wykorzystujemy w równaniach
3) i 4):
{
A
⋅sin lC⋅sinh l=0
−A⋅sin lC⋅sinh l=0
Sumowanie równań prowadzi do stałej:
C
=0
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater

Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
5
a ich odjęcie, do zależności:
2 A
⋅sin l=0
Równanie jest spełnione, gdy A
=0 lub sin l=0 . Funkcja sin x ma miejsca zerowe dla x=k , czyli:
l=k
a współczynnik:
=
k
l
Ponieważ przyjęliśmy podstawienie:
4
=
2
⋅
EJ
to:
2
=
4
EJ
Wobec tego:
2
=
k
4
4
l
4
⋅
EJ
=
k
2
2
l
2
⋅
EJ
Możemy wnioskować, że belka będzie miała nieograniczoną ilość częstości drgań własnych (
k jest liczbą
naturalną). Linia ugięcie będzie miała postać sinusoidy (rys. 14.4).
W
k
x
= A
k
⋅sin
k
l
x
k = 1
k = 2
k = 3
Rys. 14.4. Postacie drgań własnych belki wolnopodpartej dla różnych wartości k
Natomiast przemieszczenia będą się zmieniały w czasie według funkcji:
w
x , t
=
∑
k
=1
∞
sin
⋅
k
x
l
⋅
C
1 k
⋅sin
k
t
C
2 k
⋅cos
k
t
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
6
14.1.2. Belka obustronnie utwierdzona
Spróbujmy przeanalizować drgania własne belki o innym schemacie statycznym.
l
EJ [Nm²]
μ [kg/m]
Rys. 14.5. Belka obustronnie utwierdzona
Dla układu przedstawionego na rys. 14.5 możemy zapisać następujące warunki brzegowe:
1) W
0
=0
2)
0
=
dW
0
dx
=0
3) W
l
=0
4)
l
=
dW
l
dx
=0
Funkcję rozwiązującą przyjmujemy jak w 14.1.1. Jej pierwsza pochodna wynosi:
W
I
x
=⋅A⋅cos x−⋅B⋅sin x⋅C⋅cosh x⋅D⋅sinh x
Po podstawieniu otrzymujemy:
1)
B
D=0
2)
⋅A⋅C=0 AC=0
3)
A
⋅sin lB⋅cos lC⋅sinh lD⋅cosh l=0
4)
⋅A⋅cos l−⋅B⋅sin l⋅C⋅cosh l⋅D⋅sinh l=0
czyli:
A
⋅cos l−B⋅sin lC⋅cosh lD⋅sinh l=0
Układ równań jednorodnych rozwiązujemy przez przyrównanie wyznacznika det
∣W∣ do zera. Aby uprościć
rozwinięcie wyznacznika sprowadźmy układ do dwóch równań z dwoma niewiadomymi. Z dwóch pierwszych
równań wiemy, że:
B
=−D
A
=−C
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater

Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
7
podstawmy powyższe do równań
3) i 4)
{
−C⋅sin l−D⋅cos lC⋅sinh lD⋅cosh l=0
−C⋅cos l−−D⋅sin lC⋅cosh lD⋅sinh l=0
Po przekształceniach mamy:
{
C
sinh l−sin l Dcosh l−cos l =0
C
cosh l−cos l Dsinh l−sin l =0
Zatem wyznacznik tego układu to:
det
∣W∣=
∣
sinh l−sin l cosh l−cos l
cosh l−cos l sinh l−sin l
∣
det
∣W∣=−sin
2
lsinh
2
l−cosh l−cos l
2
=−sin
2
lsinh
2
l−cosh
2
l2 cos l cosh l−cos
2
l
Korzystając ze związków:
sin
2
lcos
2
l=1
cosh
2
l−sinh
2
l=1
po uproszczeniach otrzymujemy
det
∣W∣=cosh l⋅cos l−1=0
Rozwiązaniem są wartości (miejsca zerowe).
l=
2 k
1
2
⋅
gdzie
k jest liczbą naturalną. Podstawiając w miejsce k kolejne wartości
k=1,2 ,3 , ... otrzymujemy:
1
=
4,712
l
2
=
7,853
l
3
=
10,996
l
Częstości drgań własnych wyznaczymy ze wzoru:
=
i
2
⋅
EJ
Linię ugięcia opisuje wzór:
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
8
W
k
x
=A
k
⋅
sin
k
l
−sinh
k
l
⋅
[
sin
k
x
−sinh
k
x
sin
k
l
−sinh
k
l
−
cos
k
x
−cosh
k
x
cos
k
l
−cosh
k
l
]
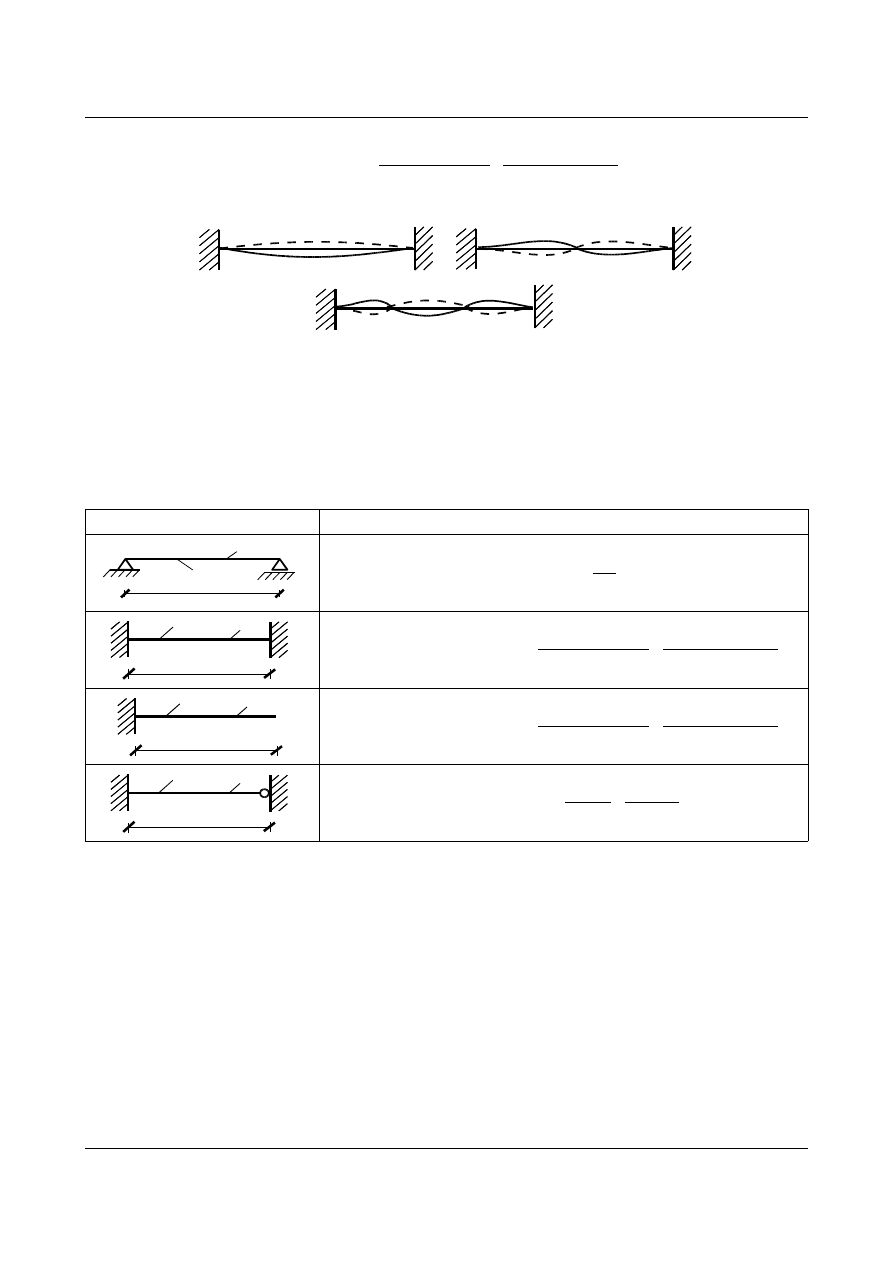
k = 1
k = 2
k = 3
Rys. 14.6. Postacie drgań własnych belki obustronnie utwierdzonej w zależności od k
Postępując analogicznie możemy wyznaczyć na podstawie warunków brzegowych postacie drgań
własnych prętów o różnych schematach statycznych. Wyniki obliczeń oraz schematyczne rysunki belek
zestawiono w tabeli 14.1.
Tabela 14.1. Postacie drgań własnych prętów
Schemat statyczny
Postać drgań własnych
EJ
l
μ
W
k
x
= A
k
⋅sin
k
l
x
l
EJ
μ
W
k
x
= A
k
⋅
sin
k
l
−sinh
k
l
⋅
[
sin
k
x
−sinh
k
x
sin
k
l
−sinh
k
l
−
cos
k
x
−cosh
k
x
cos
k
l
−cosh
k
l
]
l
EJ
μ
W
k
x
= A
k
⋅
sin
k
l
sinh
k
l
⋅
[
sin
k
x
−sinh
k
x
sin
k
l
sinh
k
l
−
cos
k
x
−cosh
k
x
cos
k
l
cosh
k
l
]
l
EJ
μ
W
k
x
=A
k
⋅sin
k
l
⋅
[
sin
k
x
sin
k
l
−
sinh
k
x
sinh
k
l
]
14.2. Wzory transformacyjne dla pręta zginanego (drgania poprzeczne)
Zakładamy, że belka charakteryzuje się ciągłym rozkładem masy. Gdy zaczyna drgać pojawiają się siły
bezwładności jako dodatkowe obciążenie układu.
Rozwiązując równanie różniczkowe równowagi drgającego pręta otrzymaliśmy całkę ogólną:
W
x
=A⋅sin xB⋅cos xC⋅sinh xD⋅cosh x
x
=⋅A⋅cos l−⋅B⋅sin l⋅C⋅cosh l⋅D⋅sinh l
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
9
Znając warunki brzegowe dla dowolnego pręta o dowolnym schemacie statycznym możemy wyznaczyć
funkcję przywęzłowego momentu zginającego lub siły poprzecznej, (wzory transformacyjne metody
przemieszczeń) w zależności od węzłowych przemieszczeń. Rozwiązań szczególnych poszukamy dla
konkretnych modeli pręta.
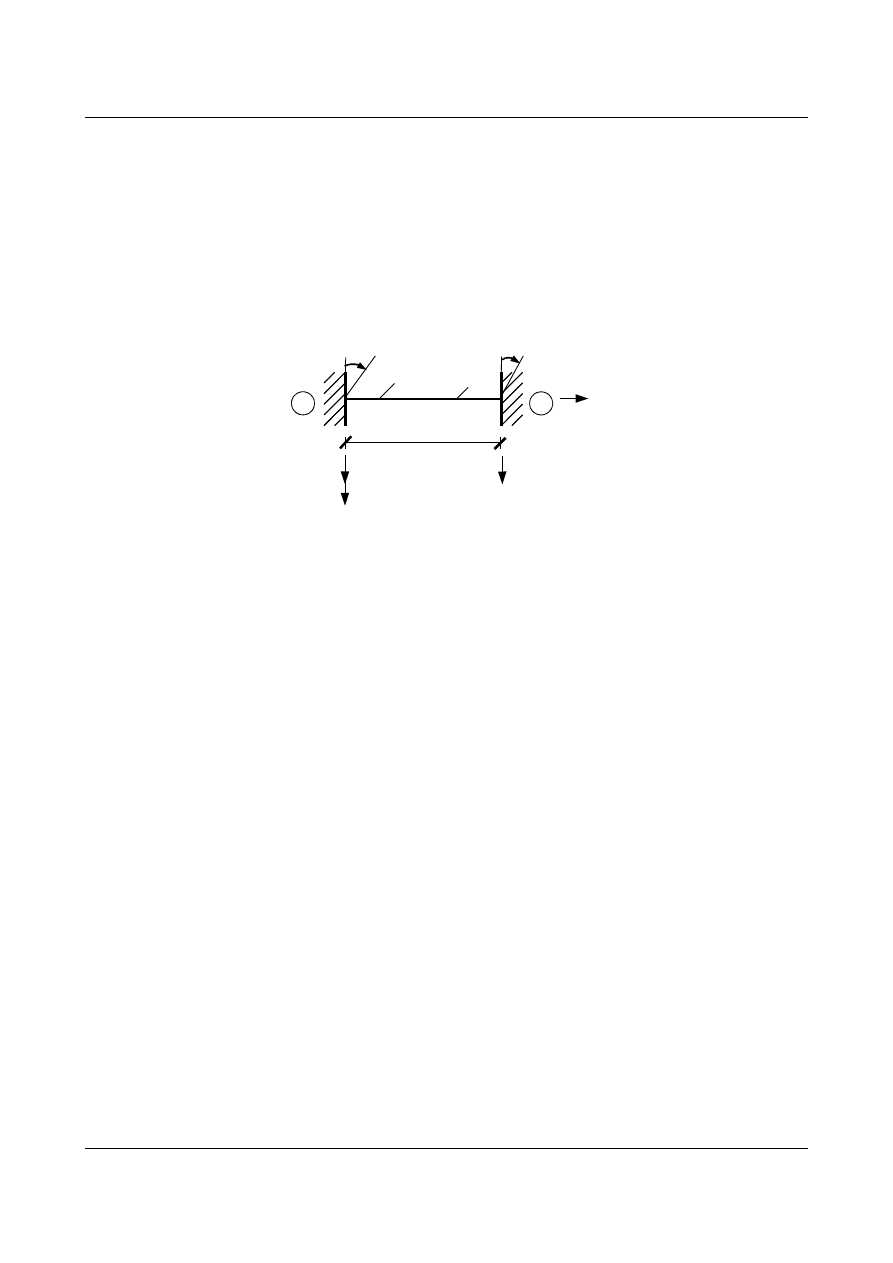
14.2.1. Pręt obustronnie utwierdzony
Dla pręta obustronnie utwierdzonego możemy zapisać następujące warunki brzegowe:
l
EJ
μ
v
i
v
k
φ
i
=1
φ
k
=1
i
k
w
x
Rys. 14.7. Pręt obustronnie utwierdzony
1) W
0
=v
i
2)
0
=
i
3) W
l
=v
k
4)
l
=
k
Warto zauważyć, że przy wyznaczaniu częstości drgań własnych (problem własny) przyjmowaliśmy
jednorodne (zerowe) warunki brzegowe.
Teraz musimy narzucić wartości przemieszczeń węzłowych aby uzależnić od nich siły wewnętrzne.
Wyznaczmy M
ik
i
,
k
, v
i
, v
k
. Uwzględniając powyższe warunki w rozwiązaniu ogólnym otrzymujemy
układ równań niejednorodnych:
1)
A
⋅sin 0B⋅cos 0C⋅sinh 0D⋅cosh 0=v
i
skąd:
B
D=v
i
2)
⋅A⋅cos 0−⋅B⋅sin 0⋅C⋅cosh 0⋅D⋅sinh 0=
i
skąd:
⋅A⋅C=
i
3)
A
⋅sin lB⋅cos lC⋅sinh lD⋅cosh l=v
k
4)
⋅A⋅cos l−⋅B⋅sin l⋅C⋅cosh l⋅D⋅sinh l=
k
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater

Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
10
{
B
D=v
i
AC=
i
A
⋅sin lB⋅cos lC⋅sinh lD⋅cosh l=v
k
A⋅cos l− B⋅sin lC⋅cosh l D⋅sinh l=
k
W rozważanym przykładzie na podstawie warunków brzegowych wyznaczono wartości stałych:
A
=−
[
sin coshsinh cos v
i
−sinsinhv
k
cos cosh sin sinh −1
i
cosh−cos
k
2
1−cos cosh
]
B
=
sinh sin−cosh cos 1v
i
cos −coshv
k
sin cosh−sinh cos
i
sinh−sin
k
2
1−cos cosh
C
=
sin coshsinh cosv
i
−sinsinh v
k
sin sinh −cos cosh1
i
cosh−cos
k
2
1−cos cosh
D
=
1−sinh sin−cosh cosv
i
cosh−cosv
k
sinh cos −sin cosh
i
sin −sinh
k
2
1−cos cosh
= l
Po wyznaczeniu stałych
A, B, C i D możemy zapisać wzory na siły wewnętrzne wykorzystując zależności
różniczkowe:
M
=−EJ ∂
2
w
∂ x
2
T
= ∂
M
∂ x
i dalej:
M
=−EJ
−
2
⋅A⋅sin x−
2
⋅B⋅cos x
2
⋅C⋅sinh x
2
⋅D⋅cosh x
T
=−EJ
−
3
⋅A⋅cos x
3
⋅B⋅sin x
3
⋅C⋅cosh x
3
⋅D⋅sinh x
Po podstawieniu stałych i przekształceniach można uzyskać ostateczne wzory wiążące siły wewnętrzne z
wielkościami amplitud przemieszczeń przywęzłowych:
M
x=0=M
ik
=
EJ
l
[
c
⋅
i
s⋅
k
−r
v
k
l
t
v
i
l
]
M
x=l =M
ki
=
EJ
l
[
s
⋅
i
−c⋅
k
−t
v
k
l
r
v
i
l
]
T
x=0=T
ik
=−
EJ
l
2
[
t
⋅
i
r⋅
k
−m
v
k
l
n
v
i
l
]
T
x=l =T
ki
=−
EJ
l
2
[
r
⋅
i
t ⋅
k
−m
v
i
l
n
v
k
l
]
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
11
We wzorach transformacyjnych zastosowano pewne współczynniki w celu uproszczenia zapisu, które
oznaczają:
c
=⋅
cosh
⋅sin−sinh ⋅cos
M
s
=⋅
sinh
−sin
M
r
=
2
⋅
cosh
−cos
M
t
=
2
⋅
sinh
⋅sin
M
m
=
3
⋅
sinh
⋅coscosh⋅sin
M
n
=
3
⋅
sinh
sin
M
= l
M
=M =1−cosh ⋅cos
Postępując analogicznie możemy zapisać podobne wzory dla belek o innych schematach statycznych.
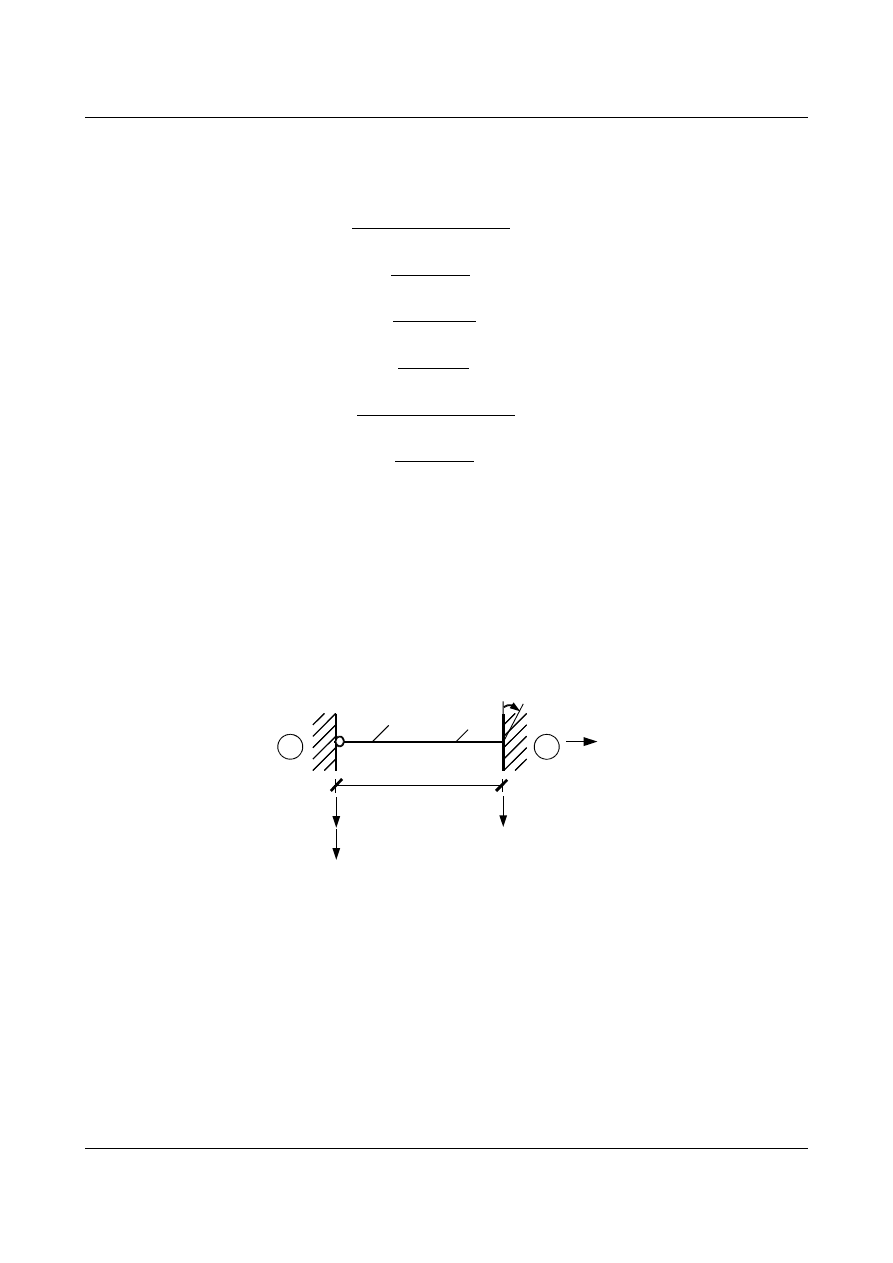
14.2.2. Pręt jednostronnie utwierdzony i podparty przegubowo
l
EJ
μ
v
i
v
k
φ
k
=1
i
k
w
x
Rys. 14.8. Pręt jednostronnie utwierdzony i podparty przegubowo
Warunki brzegowe:
1) W
0
=v
i
2) M
0
=0 W
II
0
=0
3) W
l
=v
k
4)
l
=
k
pozwalają sformułować układ równań, z którego wyznaczymy stałe. Następnie zapisujemy wzory
transformacyjne:
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
12
M
ik
=0
M
ki
=
EJ
l
[
c⋅
k
−t
v
k
l
r
v
i
l
]
T
ik
=−
EJ
l
2
[
r⋅
k
−n
v
k
l
m
v
i
l
]
T
ki
=−
EJ
l
2
[
t⋅
k
−p
v
i
l
n
v
k
l
]
w których poszczególne symbole oznaczają:
c=2 ⋅
sinh
⋅sin
M
t=
2
⋅
cosh
⋅sincos⋅sinh
M
r=
2
⋅
sinh
sin
M
n=
3
⋅
cosh
cos
M
m=
3
⋅
1
cosh⋅cos
M
p=2
3
⋅
sinh
⋅cos
M
= l
M
=
M
=cosh ⋅sin−cos ⋅sinh
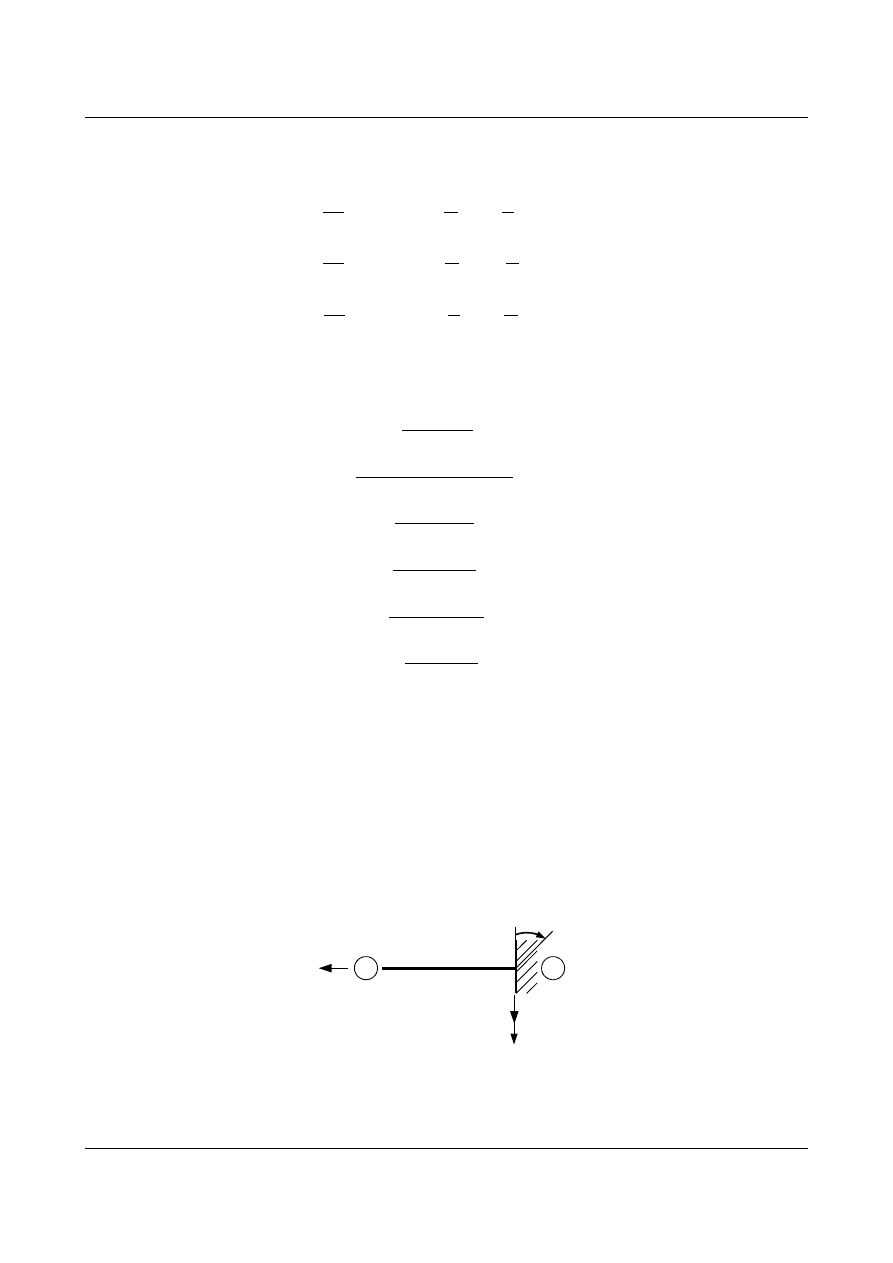
14.2.3. Wspornik
Jest to układ statycznie wyznaczalny. “Tradycyjne” wzory transformacyjne nie istnieją, gdyż
przemieszczenia
v
i
i φ
i
nie wywołują sił przywęzłowych. Inaczej jest w problemach dynamicznych.
v
k
φ
k
=1
i
k
y, w
x
Rys. 14.9 Wspornik
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
13
Dla wspornika zapiszemy:
1) W
0
=v
k
2)
0
=
k
3) M
l
=0 W
II
l
=0
4) T
l
=0 W
III
l
=0
W tym przypadku możemy określić wzory przy podporze
k:
M
ki
=
EJ
l
[
c ⋅
k
t
v
k
l
]
T
ki
=−
EJ
l
2
[
t ⋅
k
− m
v
k
l
]
gdzie:
c=⋅
sinh
⋅cos−cosh⋅sin
M
t =
2
⋅
sinh
⋅sin
M
m=
cosh
⋅sinsinh ⋅cos
M
M
=
M
=1cosh⋅cos
= l
14.2.4. Belka wolnopodparta
Podobnie jak w 14.2.3 mamy do czynienia z układem wyznaczalnym.
EJ
l
u
v
i
v
k
i
k
Rys. 14.10. Belka wolnopodparta
Na podporach momenty są zerowe, a przemieszczenia narzucone.
1) W
0
=v
i
2) M
0
=0 W
II
0
=0
3) W
l
=v
k
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater

Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
14
4) M
l
=0 W
II
l
=0
Wzory możemy wyprowadzić tylko na siły poprzeczne ( M
ik
=M
ki
=0 ).
T
ik
=−
EJ
l
2
[
n⋅v
k
m⋅v
i
]
T
ki
=−
EJ
l
2
[
m⋅v
k
n⋅v
i
]
gdzie:
m=
3
2
⋅
[
ctgh
−tg
]
n=
3
2
⋅
[
cosec
−cosech
]
Wyjaśnijmy jeszcze symbole
cosec (cosecans) i cosech (cosecans hiperboliczny):
cosec
=
1
sin
cosech
=
1
sinh
14.3. Ortogonalność układu drgającego
Zagadnienie ortogonalności udowodnimy rozpatrując dwie dowolne postacie drgań własnych
i oraz j.
Dla każdej z nich wyznacza się oddzielnie częstości drgań i amplitudy przemieszczeń z równań
różniczkowych:
Tabela 14.2. Dwie przykładowe postacie drgań
Postać drgań i
Postać drgań j
W
i
,
i
W
j
,
j
EJ
⋅
i
IV
−⋅
i
2
⋅W
i
=0
EJ
⋅
j
IV
−⋅
j
2
⋅W
j
=0
EJ
⋅
i
IV
=⋅
i
2
⋅W
i
EJ
⋅
j
IV
=⋅
j
2
⋅W
j
Dla belki zginanej obciążonej równomiernie q
x zapiszemy równanie różniczkowe równowagi:
EJ
⋅
IV
x
=q
x
Dla rozpatrywanych postaci drgań własnych
i oraz j układu możemy zapisać:
q
i
x
=⋅
i
2
⋅W
i
x
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater

Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
15
q
j
x
=⋅
i
2
⋅W
j
x
Warunek ortogonalności udowodnimy posiłkując się treścią twierdzenia Bettiego (o wzajemności prac):
Jeżeli na ustrój sprężysty działają dwa niezależne od siebie układy obciążeń, spełniające warunki
równowagi, to praca obciążeń jednego układu wykonana na przemieszczeniach wywołanych działaniem
drugiego układu równa się pracy obciążeń drugiego układu wykonanej na przemieszczeniach wywołanych
działaniem pierwszego układu obciążeń.
Na jego mocy zapiszemy:
∫
0
l
q
i
x
⋅W
j
x
dx
=
∫
0
l
q
j
x
⋅W
i
x
dx
(14.7)
Podstawiając równania różniczkowe równowagi do wyrażeń podcałkowych otrzymujemy:
∫
0
l
⋅
i
2
⋅W
i
x
⋅W
j
x
dx
−
∫
0
l
⋅
j
2
⋅W
j
x
⋅W
i
x
dx
=0
Po przekształceniu:
i
2
∫
0
l
⋅W
i
x
⋅W
j
x
dx
−
j
2
∫
0
l
⋅W
j
x
⋅W
i
x
dx
=0
i
2
−
j
2
∫
0
l
⋅W
i
x
⋅W
j
x
dx
=0
(14.8)
Możliwe są dwa przypadki rozwiązania:
1) Dla i
= j
i
2
−
j
2
=0 ,
2) Dla i
≠ j
∫
0
l
W
i
x
⋅W
j
x
dx
=0 .
Drugie rozwiązanie jest warunkiem ortogonalności dowolnych funkcji. Zostało udowodnione, że dwie
różne postacie drgań własnych układu są ortogonalne.
14.4. Drgania podłużne pręta pryzmatycznego
Z drganiami podłużnymi mamy do czynienia, gdy przemieszczenia odbywają się wzdłuż osi pręta.
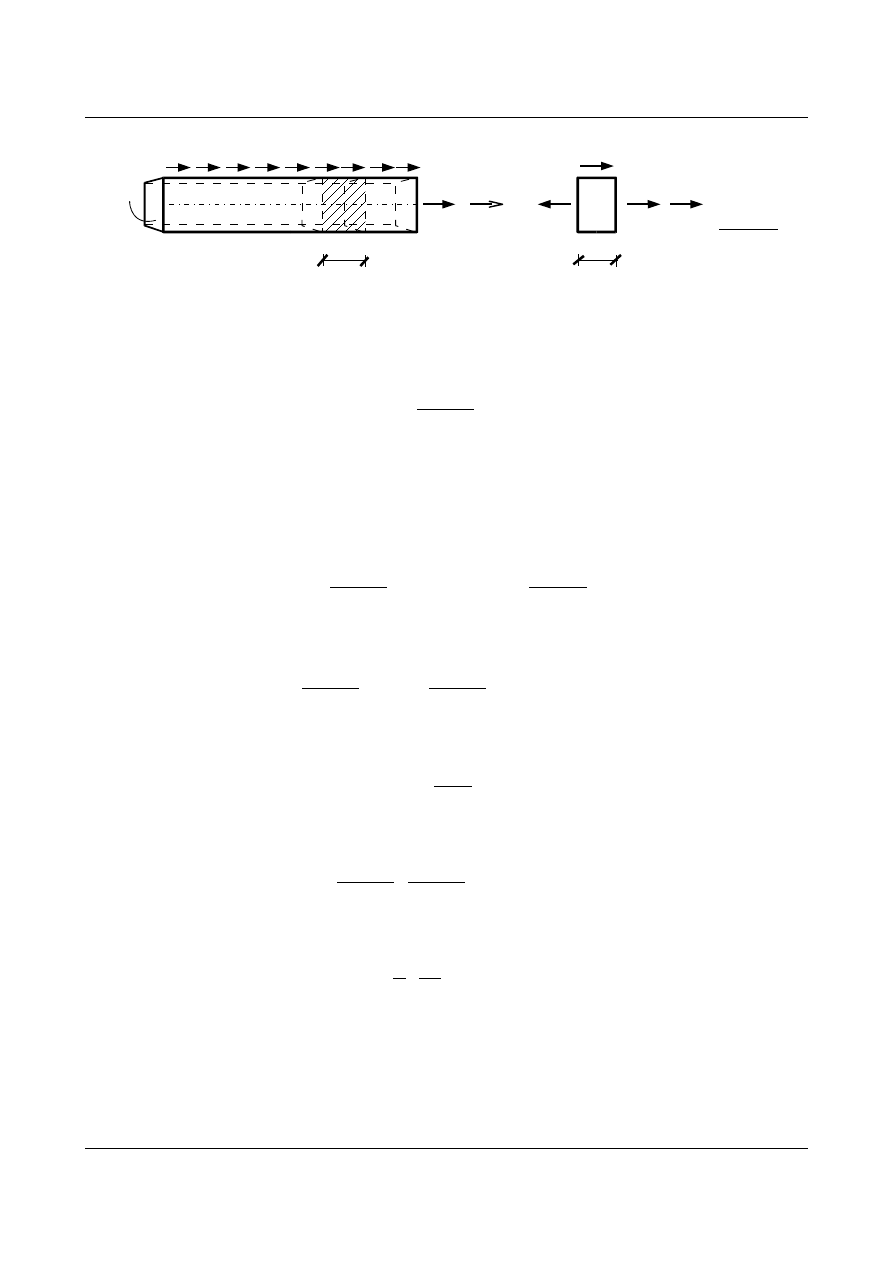
Rozpatrzmy nieskończenie mały wycinek pręta o długości dx , charakteryzujący się gęstością liniową
= A⋅ (A – powierzchnia przekroju, ρ – gęstość objętościowa
[
kg
/m
3
]
) (rys. 14.11).
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
16
dx
p(x,t)
u(x,t)
A,ρ
dx
r(x,t)
p(x,t)
N(x,t)
x
N
x , t
N
x , t
x
∂
∂
Rys. 14.11. Element dx belki
Wszystkie wartości sił
p, N, r, są funkcjami położenia i czasu f
x , t
. Opór ruchu, czyli siła
bezwładności wynosi:
r
x , t
=−dm
∂
2
u
x , t
∂t
2
Masę wycinka wyznaczamy mnożąc jego objętość przez gęstość:
dm
=A dx
Zapisując równanie równowagi
∑
X
=0 otrzymujemy:
−N
x , t
N
x , t
∂ N
x , t
∂ x
dx
p
x , t
dx
−A dx
∂
2
u
x , t
∂t
2
=0
Dla przypadku drgań swobodnych ( p
x , t
=0 ) mamy:
∂ N
x , t
∂ x
dx
− A dx
∂
2
u
x , t
∂t
2
=0
(14.9)
Wiedząc, że stan naprężeń wywołany działaniem siły podłużnej określa związek fizyczny:
N
=
x
⋅A=
x
⋅E A=
∂ u
x
∂ x
⋅EA
(14.10)
zapisujemy równanie falowe:
c
2
∂
2
u
x , t
∂ x
2
−
∂
2
u
x , t
∂t
2
=0
(14.11)
gdzie:
c
2
=
E
=
EA
(14.12)
Podobnie jak w przypadku drgań poprzecznych wprowadzamy do zapisu rozdział zmiennych. Przemieszczenie
jest iloczynem funkcji
U zależnej tylko od przestrzeni i funkcji T zależnej tylko od czasu:
u
x , t
=U
x
⋅T
t
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
17
Pochodne liczymy po odpowiednich zmiennych:
c
2
⋅
d
2
U
x
d x
2
⋅T
t
−
d
2
T
t
d t
2
⋅U
x
=0
Po podzieleniu przez wyrażenie U
x
⋅T
t
otrzymujemy różnicę:
EA
⋅
d
2
U
x
d x
2
U
x
−
d
2
T
t
d t
2
T
t
=0
Aby równanie było spełnione, wyrażenia muszą być sobie równe. Dla rozwiązań różnych od zera każdy z
członów przedstawia pewną skalarną wartość
2
.
EA
⋅
d
2
U
x
d x
2
U
x
=
d
2
T
t
d t
2
T
t
=−
2
Następnie możemy rozwiązać oba równania niezależnie, najpierw dla zmiennej
x, a potem t.
c
2
⋅
d
2
U
x
d x
2
−
d
2
T
t
d t
2
T
t
⋅U
x
=0
−
d
2
T
t
d t
2
T
t
=
2
c
2
⋅
d
2
U
x
d x
2
2
⋅U
x
=0
Dzieląc obustronnie równanie przez c
2
otrzymujemy:
d
2
U
x
d x
2
2
c
2
⋅U
x
=0
(14.13)
Wprowadzając podstawienie
2
c
2
=k
2
(14.14)
otrzymujemy
d
2
U
x
d x
2
k
2
⋅U
x
=0
(14.15)
Rozwiązaniem, całką ogólną równania różniczkowego jest wielomian:
U
x
= A⋅sin k xB⋅cos k x
(14.16)
A i B to wielkości stałe niezależne od czasu, które możemy wyznaczyć z warunków brzegowych (przestrzeń).
Wracając do równania falowego
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater

Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
18
EA
⋅
d
2
U
x
d x
2
U
x
⋅T
t
−
d
2
T
t
d t
2
=0
wykonujemy podstawienie
EA
⋅
d
2
U
x
d x
2
U
x
=−
2
−
d
2
T
t
d t
2
−
2
⋅T
t
=0
Dzieląc obustronnie równanie przez
−1 otrzymujemy:
d
2
T
t
d t
2
2
⋅T
t
=0
(14.17)
Rozwiązaniem, całką ogólną równania różniczkowego jest wielomian:
T
t
=C⋅sin tD⋅cos t
(14.18)
Stałe równania
C i D możemy wyznaczyć z warunków początkowych (czas).
Pręt doznaje przemieszczeń, które nazywamy drganiami własnymi (bez udziału siły wymuszającej) według
funkcji:
u
x , t
=
1
2
[
f
x
ct
f
x
−ct
]
1
2 c
∫
x
−ct
x
ct
g
d
Funkcja ta opisuje rozchodzenie się fali, przemieszczenia w nieskończonym pręcie. W dowolnej chwili
t
impuls fali rozejdzie się w obie strony pręta z prędkością
c.
14.4.1. Drgania własne pręta ściskanego
Wyznaczmy częstotliwość drgań własnych w pręcie ściskanym.
l
N
N
Rys. 14.12. Pręt ściskany
Zapiszmy warunki brzegowe, przemieszczenia poziome są równe zeru:
u
0
=0
u
l
=0
Przyjmujemy rozwiązania ogólne
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
19
u
x
=A⋅sin k xB⋅cos k x
z czego otrzymujemy układ równań:
{
B
=0
A sin kl
B cos kl=0
I odpowiadający mu wyznacznik
∣W∣=
∣
0
1
sin kl cos kl
∣
Wyznacznik tego układu równań musi być równy zeru det
∣W∣=0 , a zatem otrzymujemy:
sin k l
=0
Funkcja sin x ma miejsca zerowe dla x
=n , czyli:
k l
=n
Wtedy współczynnik:
k
=
n
l
Ponieważ przyjęliśmy podstawienie:
2
c
2
=k
2
oraz
c
=
E
to
=k⋅c
=
n
l
⋅
E
Możemy wnioskować, że belka będzie miała nieograniczoną ilość częstości drgań własnych (
n jest liczbą
naturalną). Postacie drgań opisuje funkcja:
U
x
= A⋅sin
n
l
x
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater

Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
20
14.4.2. Wzory transformacyjne dla pręta ściskanego
W oparciu o warunki brzegowe możemy zapisać wartości sił podłużnych dla pręta ściskanego.
l
N
N
u
i
u
k
i
k
u
0
=u
i
u
l
=u
k
Przyjmujemy rozwiązania ogólne
u
x
=A⋅sin k xB⋅cos k x
Ponadto ze związków fizycznych mamy:
N
x
=
x
⋅A=
x
⋅E A=
d u
x
d x
⋅EA
Po rozwiązaniu układu równań powstałego z warunków brzegowych wyznaczamy stałe
A i B. Po ich
podstawieniu do rozwiązania ogólnego obliczamy pochodną przemieszczenia. Wykorzystując ją w równaniu
fizycznym znajdujemy funkcje siły normalnej.
N
ik
= f u
i
, u
k
=N 0=
EA
l
[
a
⋅u
k
−b⋅u
i
]
N
ik
= f u
i
, u
k
=N l =
EA
l
[
b
⋅u
k
−a⋅u
i
]
gdzie:
a
=⋅cosec
b
=⋅ctg
=l⋅
EA
⋅
2
14.5. Drgania skrętne pręta pryzmatycznego
W celu wyprowadzenia równania ruchu pręta przyjmijmy następujące założenia:
–
drgania są harmoniczne (okresowe, periodyczne, czyli powtarzające się w regularnych odstępach
czasowych),
–
układ jest idealny (tzn. brak jakiegokolwiek tłumienia ruchu),
–
przemieszczenia pręta są małe w porónaniu z wymiarami układu,
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
21
–
rozpatrujemy ciągły, liniowy rozkład masy w pręcie,
–
pomijamy skrócenia bądź wydłużenia pręta,
–
zakładamy ponadto, że przekrój pręta nie ulega odkształceniom postaciowym, tzn. w procesie deformacji
zachowuje swój pierwotny kształt.
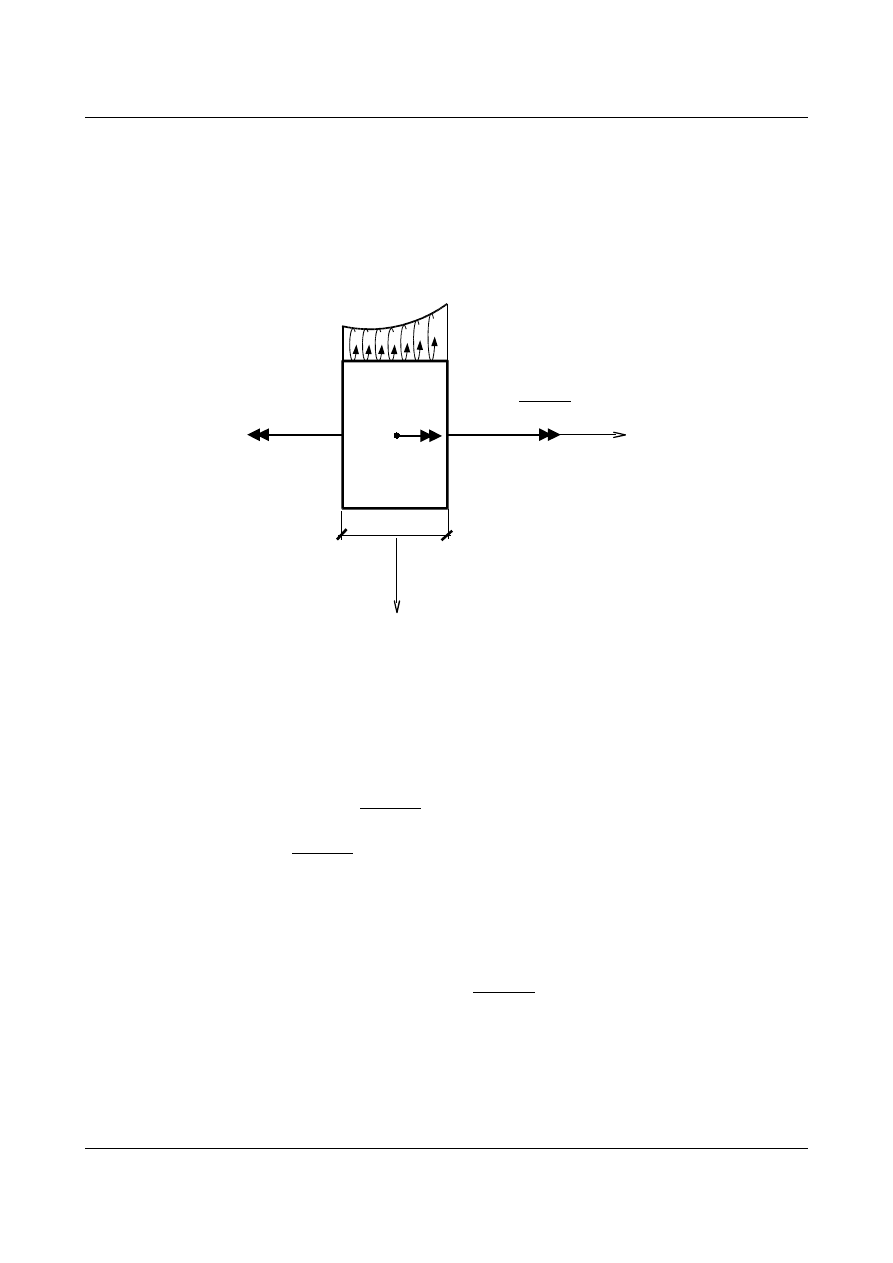
Obciążenia jak i siły wewnętrzne będą w postaci momentów działających w płaszczyznach prostopadłych do
osi pręta.
p(x,t)
Μ(x,t)
Μ(x,t) + dx
∂ Μ(x,t)
∂ x
0
r(x,t)
x
y
dx
Rys. 14.13. Wycięty myślowo element dx rozpatrywanego pręta wraz z działającymi na niego siłami
Zajmijmy się teraz wyprowadzeniem równania ruchu pręta wywołanego działaniem dowolnych sił skrętnych.
Dokonajmy na wstępie myślowego wycięcia elementu z nieskończenie długiego pręta (rys. 14.13). Z sumy
momentów względem środka ciężkości
O możemy zapisać:
M
0
=0
(14.19)
−M x , t M x , t
∂ M x , t
∂ x
dx
px , t dxrx , t =0
(14.20)
∂ M x , t
∂ x
dx
p x , t dxr x , t =0
(14.21)
gdzie:
r(x,t) - jest siłą oporu ruchu, wynikającą z drgań pręta (siłą bezwładności) i wynosi:
r
x , t =−⋅J
0
⋅ ¨x , t =−⋅J
0
⋅
∂
2
x , t
∂t
2
(14.22)
J
0
– biegunowy moment bezwładności względem środka ciężkości przekroju wynosi:
J
0
=J
x
J
y
(14.23
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater

Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
22
φ(x,t) - kąt skręcania w płaszczyźnie przekroju,
μ - gęstość masy rozpatrywanego elementu na powierzchni jego przekroju poprzecznego:
=
dm
A
=
dV
⋅
A
=
A
⋅dx⋅
A
=dx⋅
(14.24)
Znak “-” we wzorze (14.22), wynika z faktu przeciwnego zwrotu siły bezwładności do kierunku ruchu ją
wywołującego.
Po uwzględnieniu we wzorze (14.21) zależności (14.22) i (14.24), otrzymamy:
∂ M x , t
∂ x
dx
p x , tdx−J
0
⋅dx⋅⋅
∂
2
x , t
∂t
2
=0 /: dx
∂ M x , t
∂ x
p x , t −J
0
⋅⋅
∂
2
x , t
∂t
2
=0
(14.25)
Na podstawie definicji momentu skręcającego oraz po uwzględnieniu faktu, że rozpatrywany pręt jest
jednorodny i pryzmatyczny, możemy zapisać:
M
x , t =G⋅J
s
⋅x , t
(14.26)
gdzie:
γ – jednostkowy kąt skręcania równy:
x ,t =
∂x , t
∂ x
(14.27)
J
s
– moment bezwładności na skręcanie równy:
–
dla pręta o przekroju kołowym lub pierścieniowym:
J
s
=J
0
(14.28)
–
dla pręta o przekroju w kształcie trójkąta równobocznego o boku
2π:
J
s
=
a
4
⋅
3
5
(14.29)
–
dla pręta o przekroju w kształcie prostokąta o bokach
b i h (h>b):
J
s
≈
1
3
b
4
h
b
−0,63
0,052
h
/b
4
(14.30)
G – moduł Kirchhoffa (ścinania, odkształcenia postaciowego) równy:
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater

Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
23
G
=
E
2
1
(14.31)
Po uwzględnieniu zależności (14.27) we wzorze (14.26), oraz po zróżniczkowaniu uzyskanego w ten sposób
wyrażenia względem zmiennej
x otrzymamy:
M
x , t =G⋅J
s
⋅
∂ x ,t
∂ x
∂ M x , t
∂ x
=G⋅J
s
⋅
∂
2
x , t
∂ x
2
(14.32)
Następnie po podstawieniu wyrażenia (14.32) do wzoru (14.25) otrzymamy następujące równanie:
G
⋅J
s
⋅
∂
2
x , t
∂ x
2
−J
m
⋅
∂
2
x , t
∂t
2
=− px , t
(14.33)
gdzie:
J
m
- biegunowy moment masy, równy:
J
m
=J
0
⋅
(14.34)
Równanie (14.33) to równanie różniczkowe ruchu (tzw. równanie falowe) nieograniczonego pręta o liniowym
rozkładzie masy, gdy ruch ten spowodowany jest działaniem dowolnych, wymuszonych drgań skrętnych.
Gdy mamy do czynienia z drganiami swobodnymi (bez żadnych wymuszeń) wzór (14.33) przyjmuje
następującą postać:
p
x , t =0 ⇒ G⋅J
s
⋅
∂
2
x , t
∂ x
2
−J
m
⋅
∂
2
x , t
∂ t
2
=0
(14.35)
Zauważmy, że jeżeli mamy do czynienia z prętem o przekroju kołowym lub pierścieniowym (
J
s
=
J
0
), to
równanie falowe drgań własnych (14.35) przyjmie postać analogiczną jak dla drgań podłużnych:
c
2
∂
2
x , t
∂ x
2
−
∂
2
x , t
∂t
2
=0
(14.36)
Przy czym zmienia się interpretacja stałej
c:
c
2
=
G
(14.37)
Znajdźmy rozwiązanie ogólne (całkę ogólną) równania różniczkowego (14.35). Rozwiążmy to równanie
analogicznie jak dla drgań podłużnych metodą rozdzielenia zmiennych. Załóżmy, że istnieje taka funkcja
φ
(
x,t), która składa się z iloczynu dwóch funkcji, zależnych tylko i wyłącznie od jednej zmiennej, innej każda
tzn. od czasu “
t” (funkcja czasu T(t)), oraz od przestrzeni “x” (funkcja przestrzeni Φ
(
x)):
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater

Część 2
14. DRGANIA PRĘTÓW PROSTYCH O CIĄGŁYM ROZKŁADZIE MASY
24
x ,t =T t ⋅ x
Po uporządkowaniu
G
⋅J
s
⋅
∂
2
x
∂ x
2
⋅T t −J
m
⋅∂
2
T
t
∂ t
2
⋅ x=0 /:
T
t ⋅ x⋅J
m
otrzymujemy
G
⋅J
s
J
m
⋅
∂
2
x
∂ x
2
x
=
∂
2
T
t
∂ t
2
T
t
(14.38)
Aby lewa strona tego równania (funkcja przestrzenna) była równa prawej (funkcji czasu), w danym punkcie
czasoprzestrzeni, obie funkcje muszą osiągać w tym punkcie jakąś wartość stałą (skalar). Wartość tą
oznaczmy przez
ω
2
.
G
⋅J
s
J
m
⋅
∂
2
x
∂ x
2
x
=
∂
2
T
t
∂t
2
T
t
=
2
(14.39)
W ten sposób uzyskaliśmy następujący układ równań:
{
∂
2
T
t
∂ t
2
−
2
⋅T t =0
∂
2
x
∂ x
2
−
2
⋅ x=0
(14.40)
gdzie:
2
=
2
⋅J
m
G
⋅J
s
(14.41)
Po rozwiązaniu układu równań (14.40) dostaniemy:
T
t=C
1
⋅sin tC
2
⋅cos t
x=A⋅sin xB⋅cos x
(14.42)
Stąd rozwiązanie ogólne (całka ogólna) przyjmie postać:
x , t =T t ⋅x=[C
1
⋅sin t C
2
⋅cos t ]⋅[ A⋅sin xB⋅cos x]
(14.43)
Na podstawie powyższego ogólnego rozwiązania równania różniczkowego (całki ogólnej), postępując
analogicznie jak przy drganiach podłużnych, otrzymamy rozwiązanie szczególne.
Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.
AlmaMater
Wyszukiwarka
Podobne podstrony:
AiR 11 12 wyklad 14 20 01 2012 MDW
14 20
14 20 (2)
14 20 (3)
wyklad 14 20.02.2008, Administracja UŁ, Administracja I rok, Prawo konstytucyjne
14 20
GINEKOLOGIA 2 - opracowanie gieldy (pyt 14-20 fizjologia,cz[1].2), 14
wyklad 14 20.02.2008, wyklady - dr krawczyk
14 20
31.05. 14 20 rodzinna, 6 rok WOJSKOWO-LEKARSKI cały rok wszystkie materiały, materiały 6 rok woj-lek
14 20 86
14 (20)
PK, wykład 14, 20 01 2017
akumulator do opel astra h 14 20 t
więcej podobnych podstron