1. Wstęp.

Dla zadanych warunków gruntowych sprawdzić stateczność skarpy

gruntowej o nachyleniu 1:2 metodą Felleniusa przy zadanym obciążeniu q = 0,14
MPa. Obliczenia dokonane są sposobem normowym wg PN-81/B 03020 – Grunty
budowlane. Posadowienie bezpośrednie budowli na gruncie. Obliczenia statyczne i
projektowanie.

2. Opis obiektu

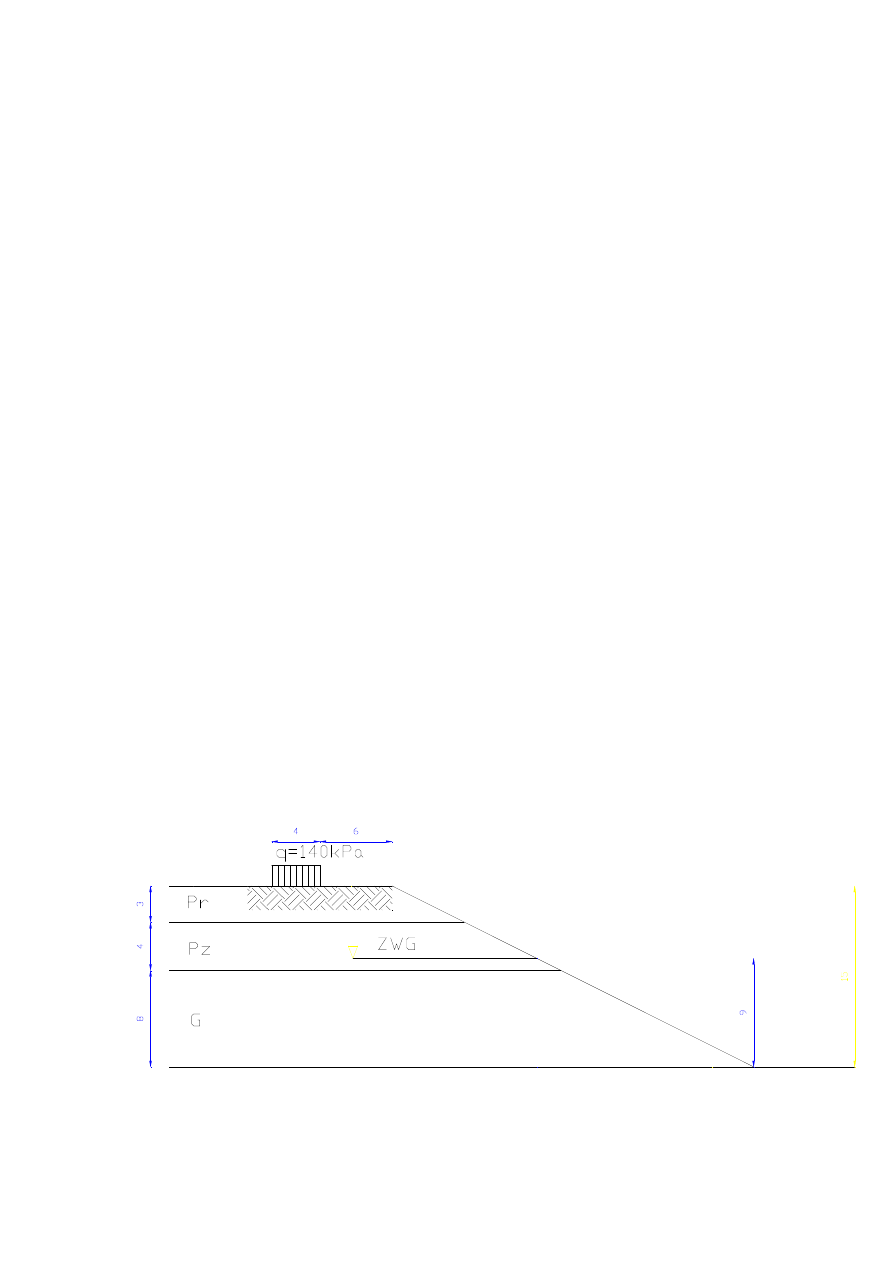
Sprawdzanym obiektem jest skarpa zbiornika wodnego, zalewu położonego w
Przewornie. Skarpa ma wysokość 15 m oraz nachylenie 1:2 .Zwierciadło wody
gruntowej znajduje się na wysokości 9 m od dolnej krawędzi skarpy. Skarpa nie jest
uszczelniona i woda wnika w głąb skarpy. W odległości 6 m od górnej krawędzi skarpy
znajduje się budynek „Wypożyczalni sprzętu wodnego”, który na długości 4 m
przekazuje obciążenie równomiernie rozłożone na grunt o wielkości q=0,14 Mpa.

3. Charakterystyka geotechniczna podłoża

W trakcie badań polowych wykonanych metoda sondowania dynamicznego
(końcówka cylindryczna, oraz na podstawie badań laboratoryjnych ustalono, iż
badana skarpa składa się z trzech warstw. Pierwszą z nich licząc od naziąbu jest
piasek gruby o miąższości 3 m o I

D

= 0,7. Druga to Glina zwięzła o miąższości 4 m

, o I

C

= 0,7. Następna warstwą jest glina pylasta o I

c

= 0,5.

W skarpie znajduje się ZWG na wysokości 9m, licząc od krawędzi dolnej skarpy.
Obiekt możemy zaliczyć do 2 kategorii geotechnicznej, gdyż badany skarpa wraz z
budynkiem zaliczają się do złożonych warunków gruntowych.

4. Warunki gruntowe .

?

Rys.1

5. Ustalenie wartości obliczeniowych parametrów wydzielonych warstw:

Tabela 1a. Podstawowe cechy fizyczne

GRUNT

w

n

[-]

ρ

[t/m

3

]

s

ρ

[t/m

3

]

d

ρ

[t/m

3

]

n

[-]

ρ

'

[t/m

3

]

ρ

sat

[kg/m

3

]

γ

[kN/m

2

]

γ

'

[kN/m

2

]

γ

sat

[kN/m

2

]

P

r

0,18

2.05

2,65

1,74

0,34

1,08

1,96

20,11

10,61

19,26

G

p

0,24

2.00

2,69

1,61

0,40

1,01

1,85

19,62

9,94

18,18

G

π

0,32

1.90

2,68

1,44

0,46

0,90

1,69

18,64

8,85

16,56

Tabela 1b. Parametry wytrzymałościowe

GRUNT

'

ϕ

]

[

kPa

c

U

]

[

' kPa

c

P

r

34

-

-

G

p

18

28

22,95

G

π

12

9

7,38

'

1, 2

u

c

c

=

Dla niespoistych c=0 i '

ϕ ϕ

=

'

ϕ

= '

1

2

u

ϕ ϕ

=

+ ° ÷ °

(grunty spoiste).

1

2

° ÷ °

- przyjmujemy w zależności od

c

I =0,70.Przyjmujemy 2

°

.

6. Analiza stateczności skarpy dla kołowo-cylindrycznej powierzchni poślizgu
metodą Felleniusa.

6.1. Założenia metody Felleniusa

-

płaski stan odkształcenia

-

kołowo-cylindryczna powierzchnia poślizgu

-

jednoczesne przemieszczenie punktów wzdłuż całej powierzchni poślizgu

(klin odłamu zachowuje się jak bryła sztywna).

-

zakłada się brak oddziaływań między elementami (paskami) klina odłamu.

-

rozpatruje się tylko jeden warunek równowagi – warunek momentu dla całego

klina odłamu

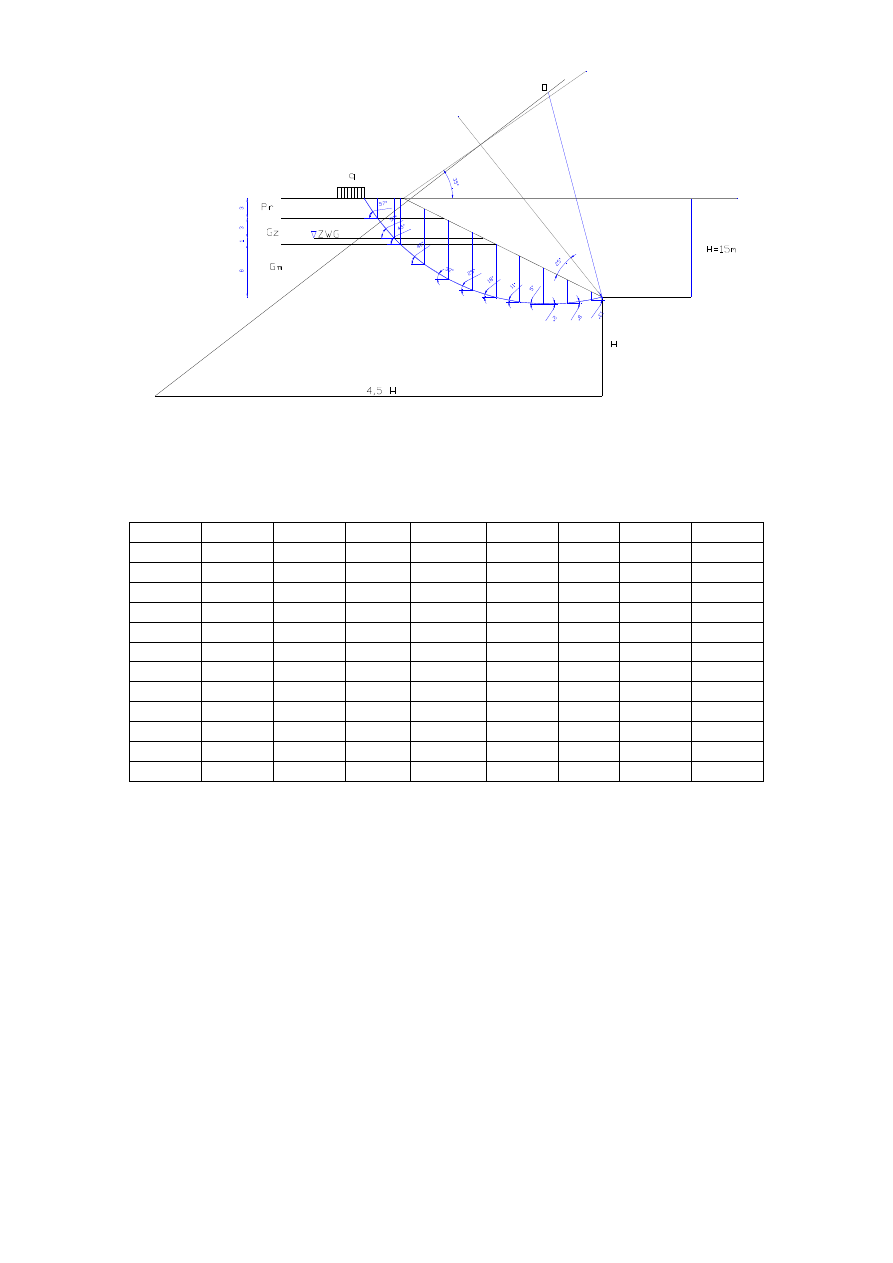
6.2. Obliczenie stateczności dla skarpy bez wody.

6.2.1 Wyznaczenie sił W

i

w paskach

i

i

i

G

W

∑

=

A1

A2a

A2b

A3

G1

G2a

G2b

G3

1

2,95

0

0,00

0

59,33

0,00

0,00

0,00

2

7,54

3,78

0,00

0

151,63

74,16

0,00

0,00

3

2,97

2,97

0,49

0

59,73

58,27

9,61

0,00

4

3,86

10,8

3,60

5,41

77,63

211,90

70,63

100,84

5

2,07

10,7

3,60

14,86

41,63

209,93

70,63

276,98

6

0

6,26

3,60

21,86

0,00

122,82

70,63

407,45

7

0

0,7

2,69

27,12

0,00

13,73

52,78

505,49

8

0

0

0,00

27,05

0,00

0,00

0,00

504,18

9

0

0

0,00

22,42

0,00

0,00

0,00

417,89

10

0

0

0,00

16,25

0,00

0,00

0,00

302,88

11

0

0

0,00

8,61

0,00

0,00

0,00

160,48

12

0

0

0,00

1,03

0,00

0,00

0,00

19,20

gdzie:

•

G

i

stanowi składową ciężaru właściwego pochodzącego od każdego rodzaju

gruntu w poszczególnych paskach;

∑

⋅

⋅

=

;

1m

A

G

i

i

i

γ

•

W

i

– wypadkowa obciążeń (sprowadzona do środka ciężkości bloku);

∑

=

i

i

G

W

•

B

i

= W

i

sinα;

•

N

i

– reakcja podłoża na składową normalną siły W

i

;

Ni = W

i

cosα

i

;

•

T

i

– opór tarcia i spójności (siła bierna, utrzymująca);

,

i

i

i

i

i

l

c

tg

N

T

⋅

+

⋅

=

ϕ

c

i

,φ

i

– dla gruntu w podstawie bloku;

6.2.2. Obliczanie współczynnika stateczności F.

[

]

∑

∑

⋅

⋅

+

⋅

⋅

=

i

i

i

i

i

Wi

l

c

tg

W

F

α

ϕ

α

sin

cos

gdzie:

W

i

– ciężar paska z uwzględnieniem obciążenia zewnętrznego

i

α

- kąt między powierzchnią poślizgu paska a poziomem (odczytane z rysunku);

l

i

– szerokość powierzchni poślizgu paska (odczytane z rysunku);

ϕ

– kąt tarcia wewnętrznego (odczytane z normy);

c –spójność (odczytana z normy);

nr paska

W

i

l

i

α

i

B

i

N

i

T

i

1

59,33

3,59

57,00

49,74

32,34

21,80

2

225,80

3,89

50,00

172,91

145,22

150,54

3

127,61

1,41

45,00

90,20

90,27

65,35

4

460,99

4,89

40,00

296,19

353,24

106,26

5

599,17

4,24

32,00

317,37

508,22

127,73

6

600,90

3,96

25,00

253,83

544,66

131,63

7

572,00

3,78

18,00

176,67

544,03

129,90

8

504,18

3,67

11,00

96,15

494,93

120,25

9

417,89

3,61

5,00

36,40

416,30

105,86

10

302,88

3,60

-2,00

-10,57

302,70

85,75

11

160,48

3,64

-8,00

-22,32

158,92

60,77

12

19,20

1,72

-13,00

-4,32

18,71

18,78

Przykładowe obliczenia:

kN

m

A

G

212

,

504

1

64

,

18

05

,

27

1

3

3

31

8

8

=

⋅

⋅

=

⋅

⋅

=

γ

=

8

W

G1

8

+G2

8

+ G’2

8

+G3

8

=0+0+0+504,212=504,212kN

kN

W

B

208

,

96

11

sin

212

,

504

sin

8

8

8

=

°

⋅

=

=

α

kN

W

N

95

,

494

11

cos

212

,

504

cos

8

8

8

=

°

⋅

=

=

α

.

302

,

120

67

,

3

9

10

95

,

494

8

8

8

8

8

kN

tg

l

c

tg

N

T

=

⋅

+

°

⋅

=

+

⋅

=

ϕ

;

26

,

1452

)

32

,

4

(

...

91

,

172

74

,

49

12

1

kN

Bi

i

=

−

+

+

+

=

∑

=

;

60

,

1124

78

,

18

...

54

,

150

8

,

21

12

1

kN

Ti

i

=

+

+

+

=

∑

=

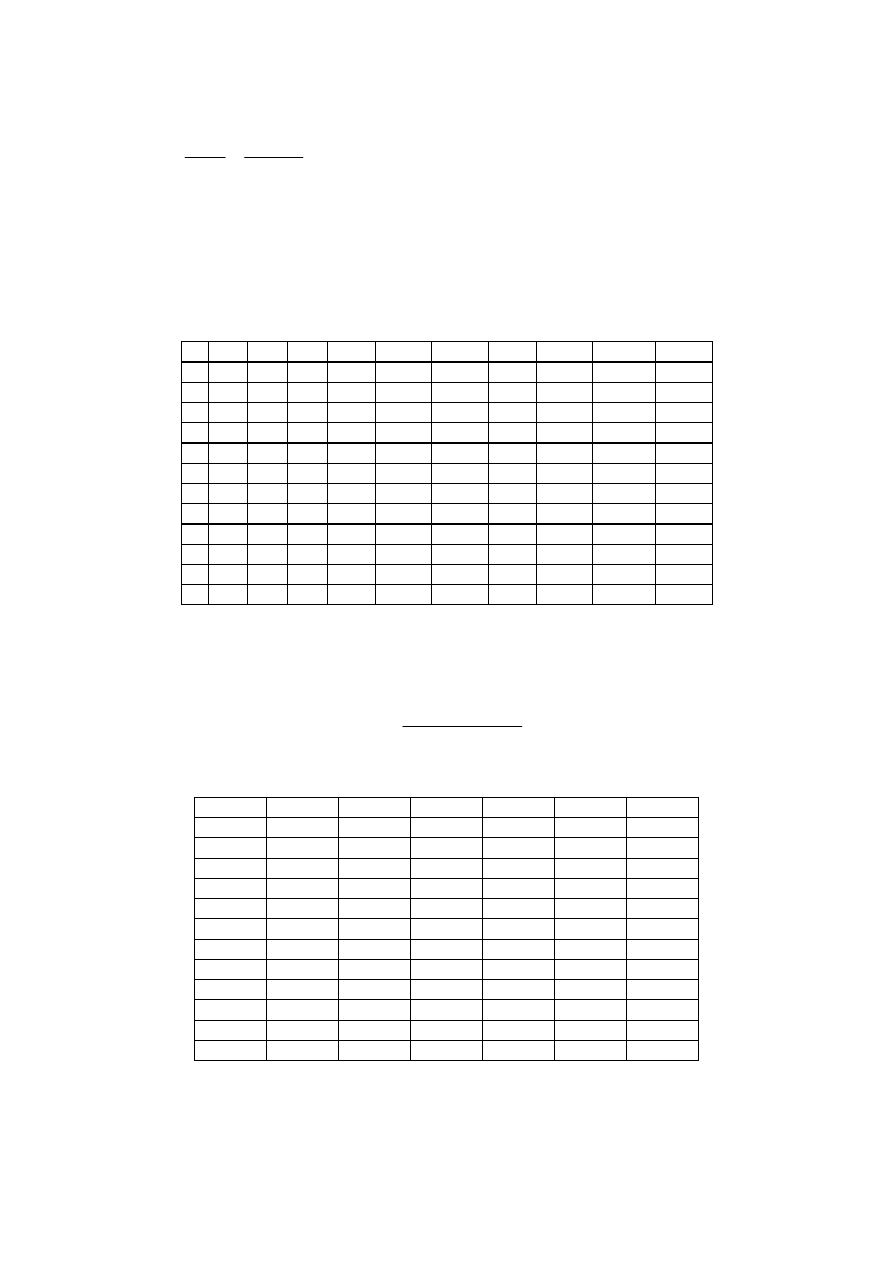
774

,

0

26

,

1452

60

,

1124

12

1

12

1

min

=

=

=

∑

∑

=

=

i

i

Bi

Ti

F

[

]

;

3

,

1

;

1

,

1

min

∉

F

6.3. Obliczanie stateczności dla skarpy z wodą

6.3.1 Wyznaczenie sił W

i

w paskach

A1 A2a A2b

A3

G1

G2a

G2b’

G3 '

G2b sat G3 sat

1 2,95

0

0,00

0

59,33

0,00

0,00

0,00

0,00

0,00

2 7,54 3,78 0,00

0

151,63 74,16

0,00

0,00

0,00

0,00

3 2,97 2,97 0,49

0

59,73

58,27

4,87

0,00

8,91

0,00

4 3,86 10,8 3,60 5,41

77,63 211,90 35,79 47,89

65,44

89,59

5 2,07 10,7 3,60 14,86 41,63 209,93 35,79 131,54

65,44 246,07

6

0

6,26 3,60 21,86

0,00

122,82 35,79 193,50

65,44 361,99

7

0

0,7 2,69 27,12

0,00

13,73 26,74 240,06

48,90 449,09

8

0

0

0,00 27,05

0,00

0,00

0,00 239,44

0,00 447,93

9

0

0

0,00 22,42

0,00

0,00

0,00 198,45

0,00 371,26

10

0

0

0,00 16,25

0,00

0,00

0,00 143,84

0,00 269,09

11

0

0

0,00 8,61

0,00

0,00

0,00

76,21

0,00 142,58

12

0

0

0,00 1,03

0,00

0,00

0,00

9,12

0,00

17,06

6.3.2. Obliczanie współczynnika stateczności F.

∑

∑

⋅

⋅

+

=

i

Wi

li

i

c

tg

W

F

i

α

φ

sin

'

'

'

Wi

W'i

l

σ

i

Bi

Ni

Ti

59,33

59,33

3,59

57,00

49,74

32,34

21,80

225,80

225,80

3,89

50,00

172,91

145,22

136,44

126,91

122,87

1,41

45,00

89,70

86,92

60,59

444,55

373,20

4,89

40,00

285,63

285,97

96,83

563,08

418,88

4,24

32,00

298,25

355,30

106,76

550,25

352,10

3,96

25,00

232,44

319,15

97,01

511,72

280,53

3,78

18,00

158,05

266,81

84,57

447,93

239,44

3,67

11,00

85,43

235,04

77,01

371,26

198,45

3,61

5,00

32,34

197,70

68,63

269,09

143,84

3,60

-2,00

-9,39

143,75

57,10

142,58

76,21

3,64

-8,00

-19,83

75,47

42,89

17,06

9,12

1,72

-13,00

-3,83

8,88

14,58

Przykładowe obliczenia:

kN

m

A

G

628

,

41

1

11

,

20

07

,

2

1

1

1

1

5

5

=

⋅

⋅

=

⋅

⋅

=

γ

kN

m

A

G

511

,

131

1

85

,

8

86

,

14

1

3

'

3

'

3

5

5

=

⋅

⋅

=

⋅

⋅

=

γ

;

101

,

243

1

56

,

16

68

,

14

1

3

3

3

5

5

kN

m

m

A

G

sat

sat

=

⋅

⋅

=

⋅

⋅

=

γ

kN

G

b

G

a

G

G

W

sat

sat

07

,

563

07

,

246

44

,

65

93

,

209

63

,

41

3

2

2

1

5

5

5

5

5

=

+

+

+

=

+

+

+

=

kN

G

b

G

a

G

G

W

89

,

418

54

,

131

79

,

35

93

,

209

63

,

41

3

2

2

1

5

'

5

'

5

5

'

5

=

+

+

+

=

+

+

+

=

kN

W

B

38

,

298

32

sin

07

,

563

sin

5

5

=

°

⋅

=

⋅

=

α

kN

W

N

24

,

355

32

cos

89

,

418

cos

'

5

5

=

°

⋅

=

⋅

=

α

kN

tg

N

l

c

tg

W

T

799

,

106

38

,

7

24

,

4

12

'

'

cos

5

5

5

'

5

5

=

⋅

+

°

⋅

=

⋅

+

⋅

=

φ

α

;

43

,

1371

)

83

,

3

(

...

91

,

172

74

,

49

12

1

kN

Bi

i

=

−

+

+

+

=

∑

=

;

19

,

864

8

5

,

14

...

44

,

136

80

,

21

12

1

12

1

kN

Ti

i

i

=

+

+

+

=

∑

∑

=

=

;

630

,

0

43

,

1371

19

,

864

12

1

12

1

min

=

=

=

∑

∑

=

=

i

i

Bi

Ti

F

[

]

;

3

,

1

;

1

,

1

min

∉

F

7. Wnioski

W obu rozpatrywanych przypadkach skarpę uznajemy za nie stabilna ponieważ

współczynnik stateczności nie mieści się w przedziale [1,1;1,3] (za Wiłun Z., Zarys

geotechniki, WKŁ, Warszawa, 1976,2001)

Zaleca się wprowadzenie środków podwyższających stateczność skarpy, np zmienieni

kąta nachylenia skarpy, lub wprowadzenie kotew umacniających zbocze.