13-06-2013
Kolokwium zaliczeniowe z KAP
1)
Dane jest równanie:
Niech A=
a)
2
1
0
3
b)
3
1
0
3
c)
2
0
0
3
d)
−
3
2
2
2
e)
−
3
1
1
1
Podaj, który z układów jest hiperboliczny i dlaczego.
2)
Niech A to macierz diagonalizowalna a f(x) i g(x) dwie dowolne funkcje.
Udowodnij, że:
e
(f(A) + g(A))
= e
f(A)
⋅
e
g(A)
3)
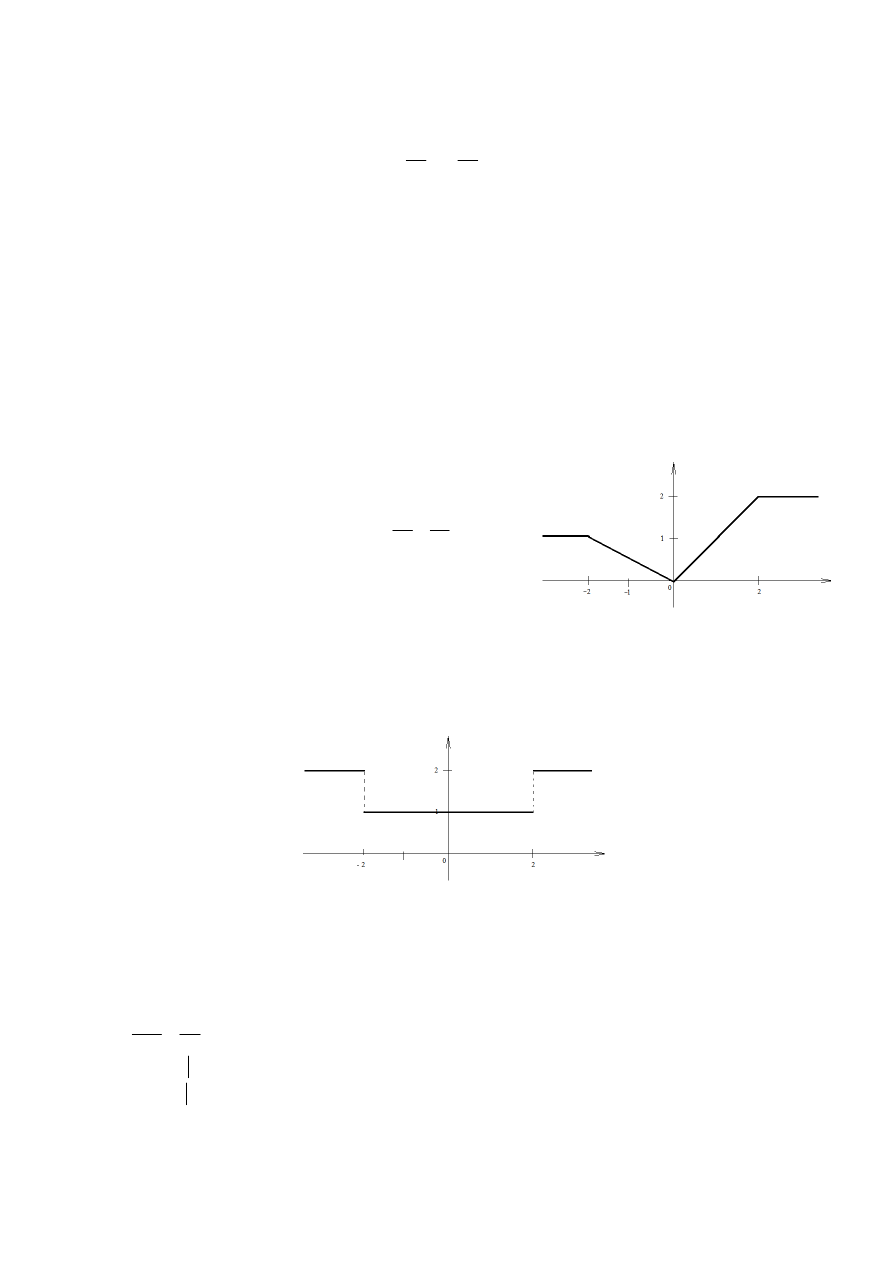
Dane jest nieliniowe równanie hiperboliczne:
u(x,t=0) = f(x)
Jak długo rozwiązanie będzie ciągłe? (t*)
Gdzie pojawi się nieciągłość?
(x*)
4)
Do równania z zadania 3ego i dla funkcji f(x):
Podaj rozwiązanie dla czasu t=1/5
5)
Dane jest nieliniowe zagadnienie brzegowe:
=
=
=
⋅
+
=
=
0
1
0
)
sin(
0
2
2
π
x
x
u
u
u
dx
du
dx
u
d
Przedstaw algorytm (quasilinearyzacji) Newtona.
0
=
∂
∂
+
∂
∂
x
u
A
t
u
( )
0
5
2
=
∂
∂
−
∂
∂
u
x
t
u