Dynamika punktu materialnego

1)

Winda o ciężarze Q=280 kG zaczyna opuszczać się w szybie ruchem
jednostajnie przyspieszonym i przebywa do chwili t=10 s drogę S=35
m. Wyznaczyć napięcie liny na której wisi klatka windy.

2)

Punkt materialny o masie m=0.5 kg porusza się wg równań:

x=2·t

2

+1

gdzie: x, y, z – (m)

y=t

2

-1

t

– (s)

z=t

3

-1

Określić wielkość siły w chwili t=1 s.

3)

Punkt materialny o masie m=2 kg opisuje krzywoliniową trajektorię wg równania: S=12·sin(t/2),
gdzie: S - (m), t - (s). W danej chwili punkt ten znajduje położenie M w którym osiąga prędkość
V

M

=3 m/s, przy czym promień krzywizny trajektorii w punkcie M równy jest

ρρρρ

=6 m. Znaleźć dla tej

chwili siły działające na ten punkt materialny.

4)

Punkt materialny o ciężarze P=1.96 N leżący na
poziomym stole, umocowany jest w punkcie O na
lince o długości l=35 cm. Punkt ten opisując na
stole okrąg ma prędkość początkową v

0

=4.9 m/s.

Znaleźć prędkość punktu i siły naciągu linki po
chwili t=1 s od początku ruchu, jeżeli
współczynnik

tarcia

między

rozważanym

punktem materialnym a stołem wynosi

µµµµ

=0.25.

5)

Ciało o ciężarze Q=10 kG porusza się pod działaniem zmiennej siły
F=10·(1-t), gdzie: F - (kG), t – (s). Po ilu sekundach ciało zatrzyma
się, jeżeli w chwili początkowej prędkość ciała wynosi v

0

= 20 cm/s, a

siła działała w kierunku ruchu. Jaką drogę przebędzie ciało do chwili
zatrzymania się.

6)

Punkt materialny o masie m porusza się prostoliniowo pod działaniem siły zmieniającej się wg
zależności: F=F

0

cos(

ω

ω

ω

ω

t), gdzie F

0

oraz

ω

ω

ω

ω

są stałe. W chwili początkowej punkt ma prędkość v

0

.

Znaleźć równanie ruchu punktu.

7)

Punkt materialny o masie m=0.5 kg porusza się prostoliniowo pod działaniem siły F=10 N. W chwili
początkowej prędkość punktu v

0

=2 m/s. Określić prędkość punktu w chwili, gdy przebędzie drogę

S=5 m.

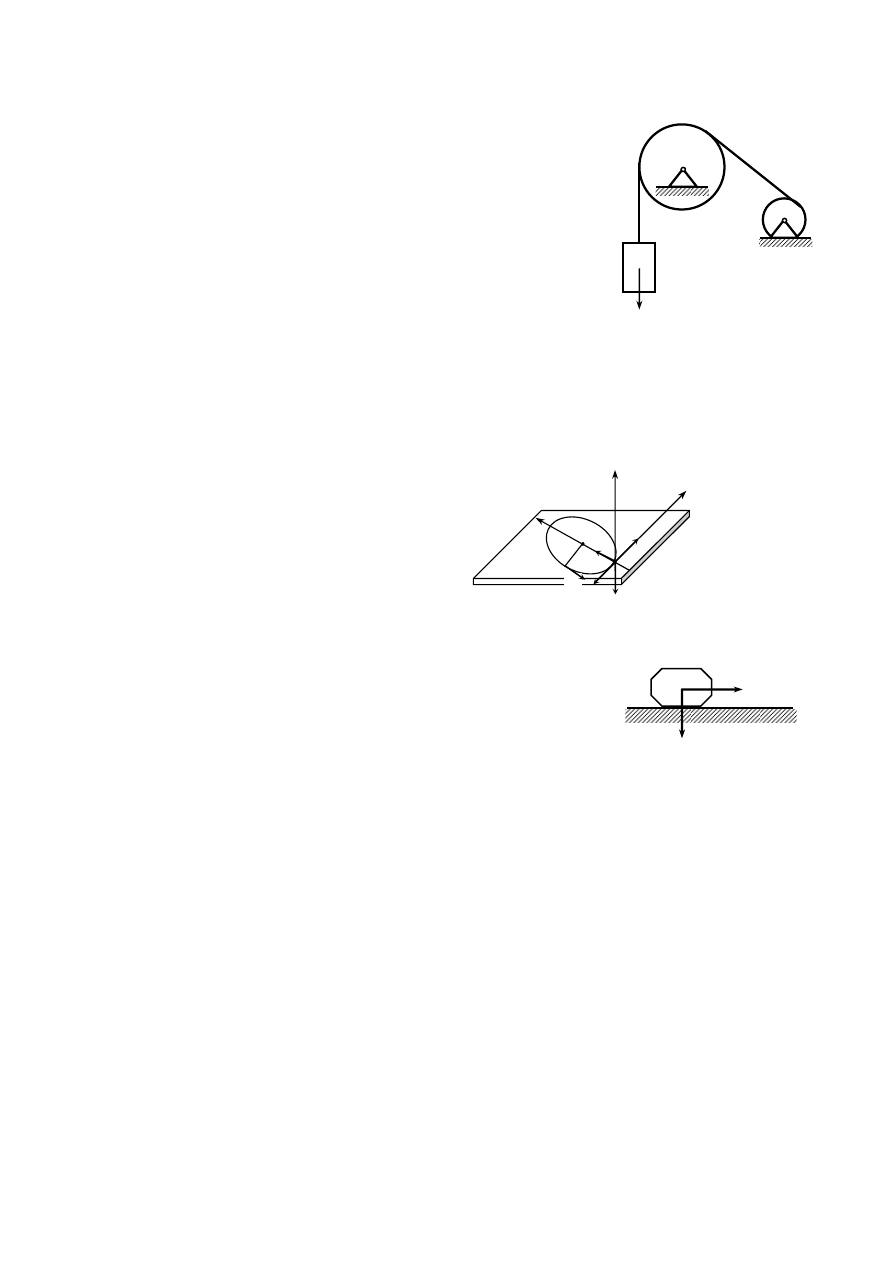
Q

Zad. 1

Q

F=10(1-t)

Zad. 5

ηηηη

ξξξξ

ψ

ψψ

ψ

l

l

O

v

0

v

S

T P

T – siła tarcia
S – siła naciągu linki

Zad. 4