121

Ć w i c z e n i e 15

Pomiar pola temperatur w przepływie turbulentnym

metodą termoanemometrii

1. Wprowadzenie

Pomiary pola temperatury w przepływie turbulentnym wykonuje się zwykle
termoanemometrem stałoprądowym [1]. Czujnikiem pomiarowym jest sonda
drucikowa o małej średnicy włókna (d

w

= 1 ÷ 3 µm) włączona w obwód mostka

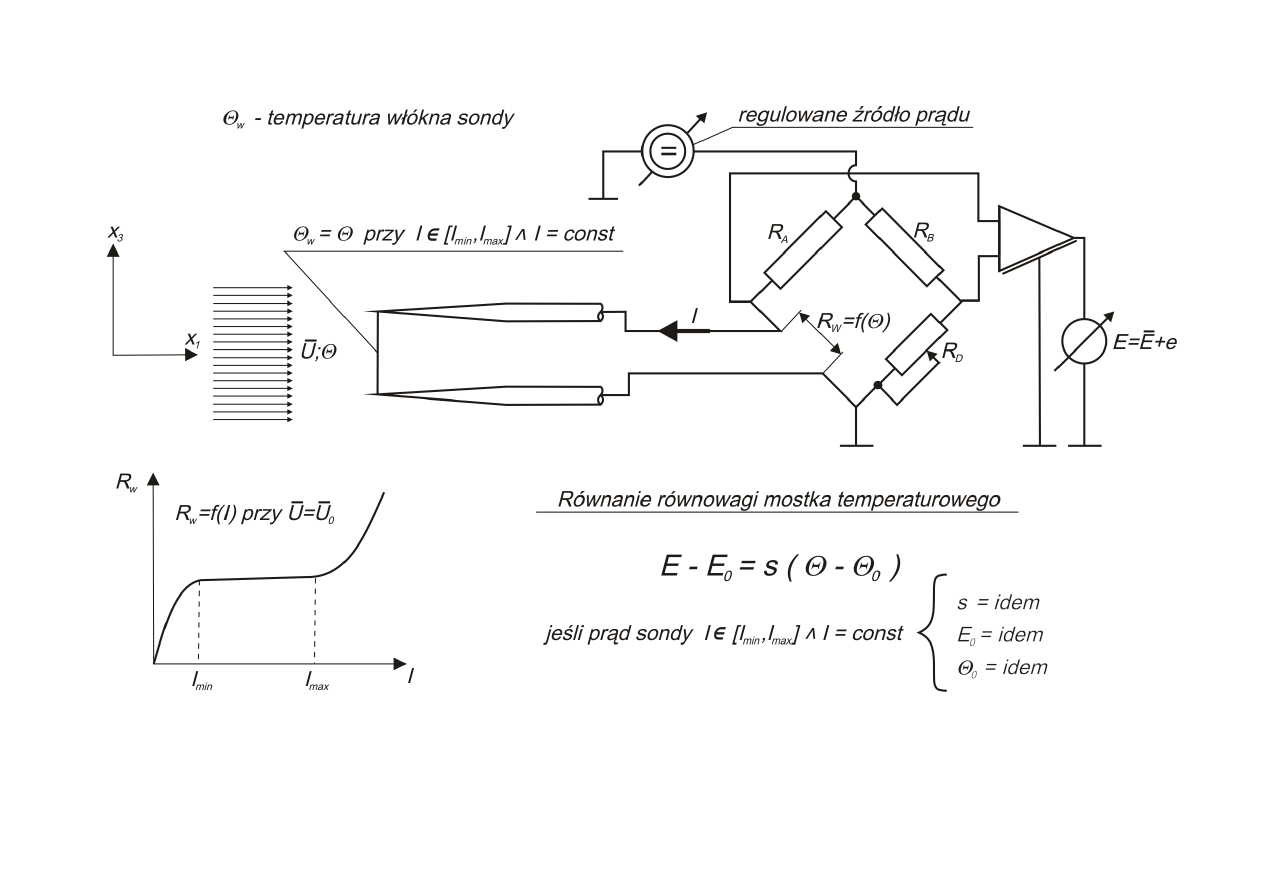
stałoprądowego (rys. 1). Przy bardzo małym natężeniu prądu włókno sondy działa jak
czuły termometr oporowy, nie wykazując praktycznie czułości na zmiany prędkości,
reaguje ono jedynie na zmiany temperatury płynącego medium. Zastosowany układ
mostkowy pozwala zmierzyć napięcie E, które jest związane z temperaturą czynnika Θ
zależnością:

(

)

0

Θ

Θ

s

E

E

−

+

=

0

(1)

w której E

0

oznacza napięcie mostka w ustalonej temperaturze odniesienia Θ

0

, a s jest

czułością układu pomiarowego na zmiany temperatury medium. Parametry równania
(1) E

0

, Θ

0

, s dla konkretnego czujnika i określonego układu pomiarowego wyznacza

się zwykle na drodze doświadczalnej.
Jeżeli przepływ turbulentny ma charakter stacjonarny, wówczas chwilową temperaturę
czynnika Θ traktować można jako sumę niezależnej od czasu wartości średniej Q oraz
wielkości fluktuacyjnej

ϑ

:

ϑ

+

= Θ

Θ

(2)

Również napięcie E wskazywane przez mostek pomiarowy uznać można za
superpozycję napięcia średniego E i zmiennego w czasie napięcia e:

e

E

E

+

=

(3)

Po wprowadzeniu związków (2) i (3) do równania (1) otrzymamy zależność:

(

)

ϑ

s

Θ

Θ

s

E

e

E

o

o

+

−

+

=

+

(4)

w której można wyróżnić składniki niezależne od czasu:

(

)

o

o

Θ

Θ

s

E

E

−

+

=

(5)

oraz składnik wiążący fluktuacje temperatury

ϑ

ze zmiennym w czasie napięciem e

ϑ

s

e

=

(6)

Równanie (5) wskazuje, że między średnią temperaturą czynnika Θ i napięciem
średnim E mostka stałoprądowego przy odpowiednio niskim prądzie płynącym przez
włókno sondy, istnieje zależność liniowa. Z równania (6) można wyznaczyć wariancję
temperatury, która jest wprost proporcjonalna do wartości średniokwadratowej
napięcia zmiennego:

2

2

1

e

s

=

ϑ

(7)

122

Rys. 1. Sonda pomiarowa w układzie mostka temperaturowego termoanemometru

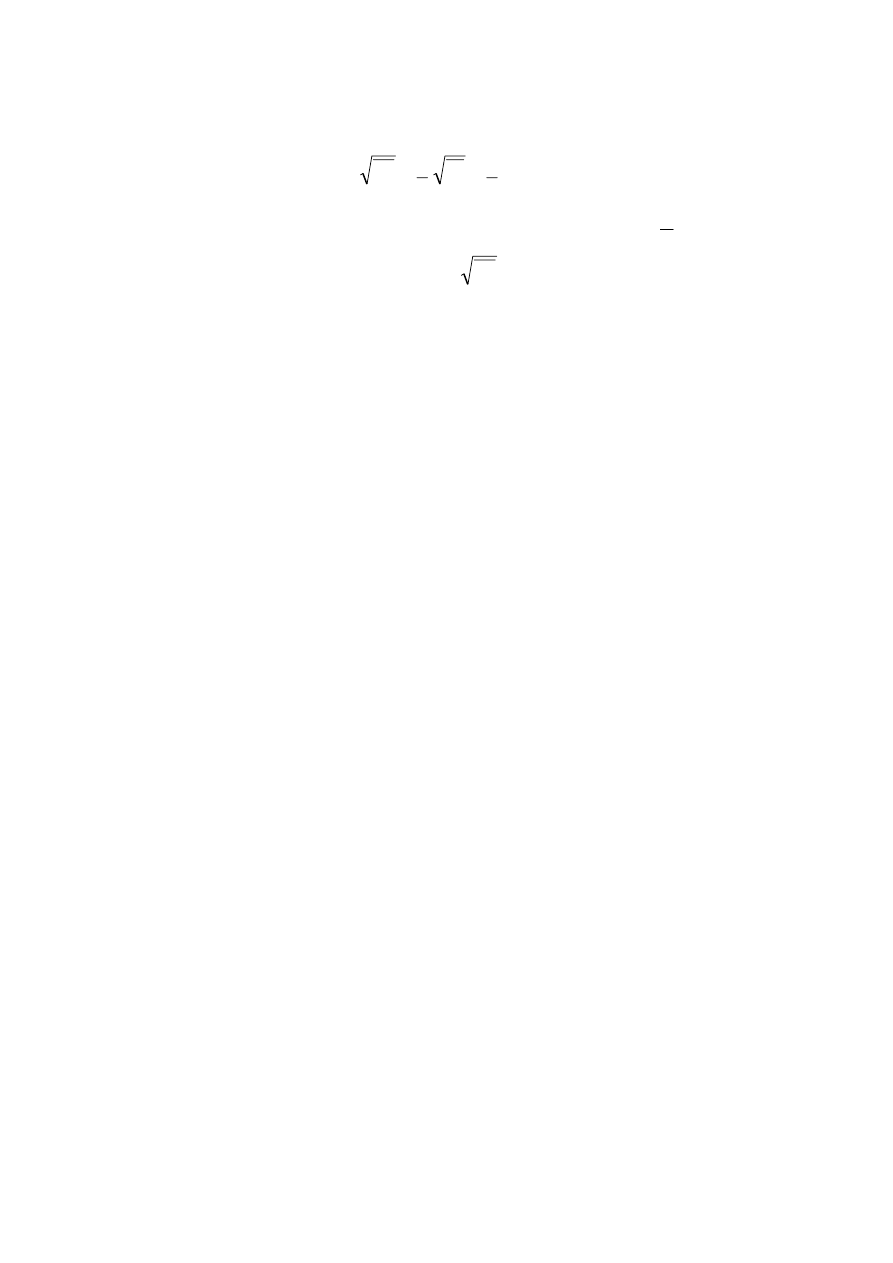
123

Za miarę poziomu fluktuacji temperatury medium przyjmuje się również wartość
skuteczną napięcia e(t):

( )

e

RMS

s

e

s

1

1

2

2

=

=

=

ϑ

ϑ

(8)

Badanie pola temperatur w nieizotermicznym przepływie turbulentnym polega na
określenia w wybranych punktach pomiarowych temperatury średniej Θ oraz wartości

skutecznej fluktuacji temperatury

( )

.

2

ϑ

ϑ

=

RMS

Przed wykonaniem badań zasadniczych należy wyznaczyć parametry E

o

, Θ

o

, s

występujące w równaniu (5) poprzez wzorcowanie układu pomiarowego.

2. Stanowisko badawcze

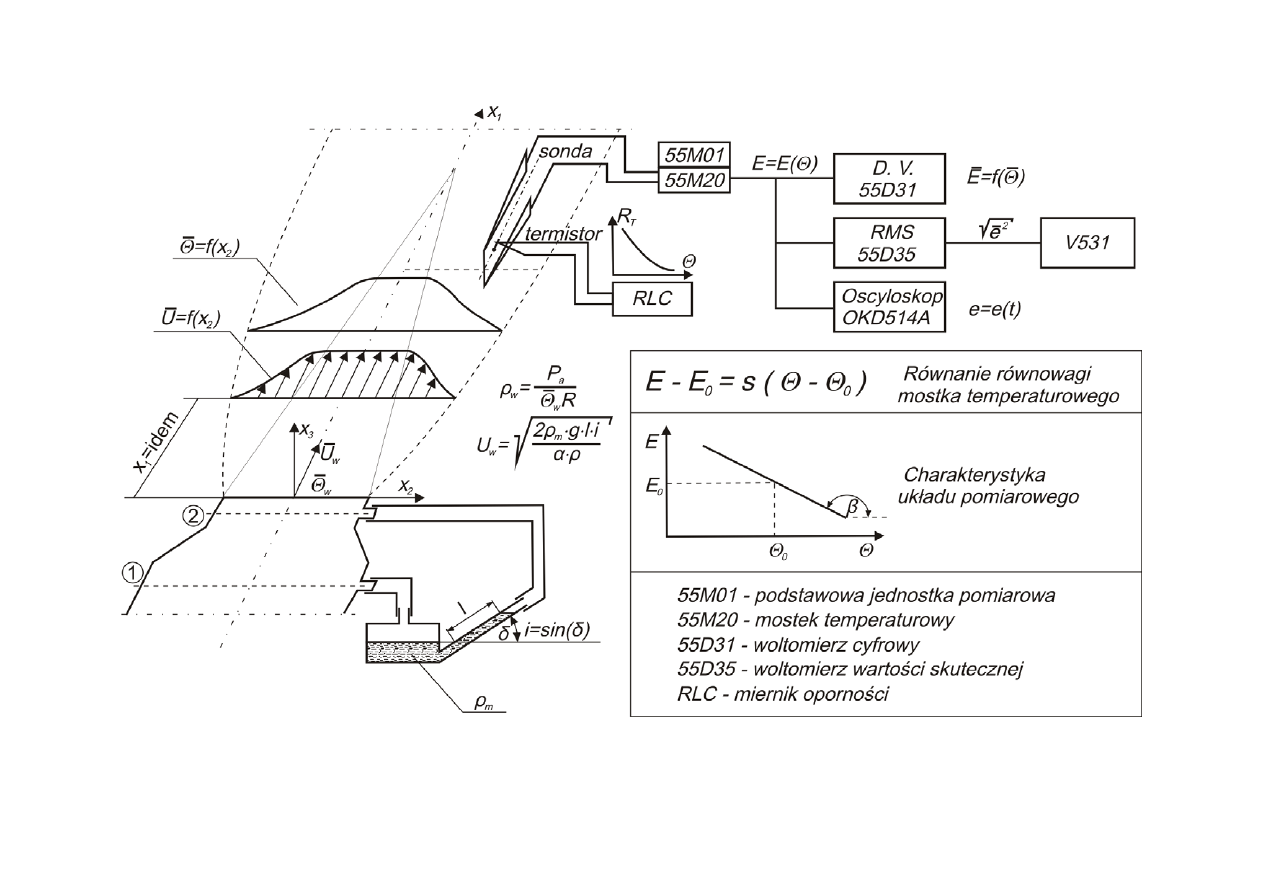
Stanowisko badawcze oraz zastosowana aparatura, pokazane w sposób

schematyczny na rys. 2, pozwalają wyznaczyć zarówno rozkłady temperatury średniej
i wartości skutecznej fluktuacji temperatury w kołowym nieizotermicznym przepływie
swobodnym, jak i parametry stałe E

o

, Θ

o

, s równania równowagi mostka

stałoprądowego termoanemometru.

124

Rys. 2. Schemat stanowiska badawczego

125

Z dyszy o średnicy d = 0.04 m, wypływa struga podgrzanego powietrza o
jednorodnym rozkładzie prędkości i temperatury w płaszczyźnie wylotowej, poza
warstwą przyścienną. Prędkość początkową strugi

w

U

można wyznaczyć z różnicy

ciśnień statycznych w dwóch przekrojach pomiarowych dyszy, wskazywaną przez
mikromanometr. Prędkość

w

U

można zmienić za pomocą pokrętła potencjometru

podłączonego do układu sterowania prędkością obrotową wentylatorów. W kanale
wylotowym z wentylatorów umieszczono grzejniki elektryczne, które zapewniają
ciągłe podgrzewanie przepływającego czynnika. Układ grzejny jest zasilany przez
autotransformatory umożliwiające regulację napięcia, a tym samym temperatury
wypływającego z dyszy powietrza

w

Θ

.

Sonda pomiarowa jest podłączona do mostka stałoprądowego termoanemometru CCA
55M20, którego napięcie wyjściowe jest zależne od temperatury chwilowej czynnika
(1). Włączony w tor pomiarowy woltomierz cyfrowy 55D31 posiada układ całkujący z
regulowanym czasem uśredniania. Układ taki pozwala zmierzyć składową stałą
napięcia E , która zgodnie z zależnością:

(

)

o

o

Θ

Θ

s

E

E

−

⋅

+

=

jest funkcją temperatury średniej Θ .
Woltomierz RMS 55D35 umożliwia pomiar wartości skutecznej składowej zmiennej
sygnału napięciowego, która jest miarą poziomu fluktuacji temperatury:

2

2

s

e

ϑ

=

(9)

Podłączony do mostka CCA 55M20 oscyloskop pozwala obserwować przebiegi
czasowe napięcia e(t).

3. Metodyka pomiarów i obliczeń

Ćwiczenie składa się z dwóch części. W części pierwszej należy wykonać

wzorcowanie układu pomiarowego, natomiast część druga obejmuje badanie pola
temperatur w kołowej, nieizotermicznej strudze swobodnej.

3.1. Wzorcowanie układu pomiarowego

Wzorcowanie

układu pomiarowego mostka stałoprądowego termoanemometru

przygotowanego do pomiaru temperatury (tzn. przy bardzo małym prądzie płynącym
przez włókno sondy), polega na wyznaczeniu jego odpowiedzi napięciowej na zmiany
temperatury czynnika i określeniu wartości parametrów stałych równania (5).
Stanowisko badawcze opisane w rozdziale 2 pozwala na zmianę temperatury średniej
jednorodnej strugi powietrza w płaszczyźnie wylotowej dyszy, w zakresie od
temperatury otoczenia do około 80

o

C, jednak ze względu na dużą bezwładność

cieplną układu przepływowego tunelu aerodynamicznego, czas ustalania się określonej
temperatury czynnika Θ jest bardzo długi (około 3 godziny). Należy więc zastosować
inny sposób zmiany temperatury średniej w bezpośrednim otoczeniu włókna sondy.
Liniowy charakter zależności E(Θ) wskazuje, że fluktuacje temperatury czynnika nie
wpływają na wartość napięcia średniego (równanie (5)). Znaczy to, że poziom
turbulencji przepływu nie ma istotnego znaczenia podczas cechowania układu mostka

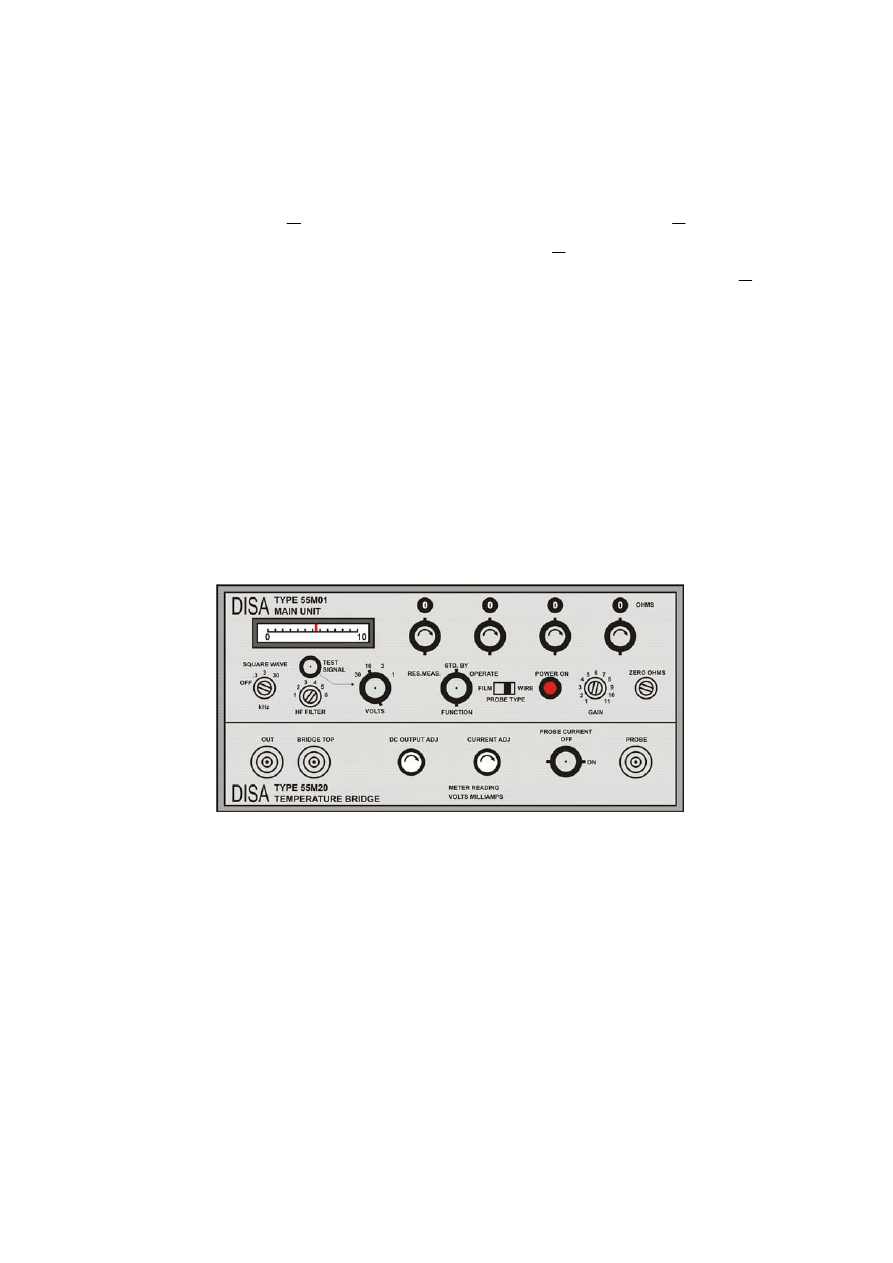
126

temperaturowego. Wystarczy więc zapewnić jednorodny rozkład temperatury wzdłuż
włókna sondy i możliwość pomiaru temperatury średniej w jego bezpośrednim
otoczeniu. Z dostateczną dokładnością warunek jednorodności można zrealizować
ustawiając włókno sondy (o długości

1

≅

l

mm) prostopadle do kierunku prędkości

średniej, w płaszczyźnie prostopadłej do promieniowego kierunku strugi (rys. 2). Przy
określonej prędkości

w

U

oraz ustalonej temperaturze początkowej

w

Θ

powietrza

wypływającego z dyszy, zmiany temperatury średniej

i

Θ

uzyskuje się przesuwając

wzorcowaną sondę wzdłuż promienia strugi. Pomiar temperatury średniej

i

Θ

w

otoczeniu drucika sondy realizuje się czujnikiem termistorowym o znanej
charakterystyce Θ = Θ(R) (gdzie R [kΩ] – rezystancja termistora), umieszczonym w
niewielkiej odległości za włóknem (~ 1 mm).

3.1.1. Przygotowanie

termoanemometru do pomiarów

Przygotowanie termoanemometru stałoprądowego wymaga wyboru właściwego

prądu płynącego przez włókno sondy oraz odpowiedniego doboru napięcia
wyjściowego mostka CCA 55M20, przy określonej rezystancji nastawionej na
dekadzie jednostki podstawowej 55M01.
Czynności przygotowawcze można wykonać według niżej podanej instrukcji
(opracowanej według [3]) oraz w oparciu o rys. 3.

1. Włączyć zasilanie wszystkich jednostek układu pomiarowego.
2. Nastawy

wstępne:

SQUARE

WAVE

:OFF

HF

FILTER

:1

VOLTS

:10

FUNCTION

:STD.BY

PROBE

TYPE

:WIRE

GAIN

:1

Oporność dekady

:00,000 OHMS

PROBE

CURRENT

:OFF

3. Styki uchwytu sondy zewrzeć końcówką zerującą.

Rys. 3. Płyta czołowa termoanemometru stałoprądowego

127

4. Kompensacja

oporności przewodów:

a) przełącznik FUNCTION ustawić w położenie RES.MEAS.
b) wyregulować ZERO OHMS tak, aby wskazówka miernika wychyliła się do

czerwonej kreski,

c) przełącznik FUNCTION ustawić w położenie STD.BY, zdjąć końcówkę i

podłączyć sondę drucikową do pomiaru temperatury.

5. Dobór

prądu sondy:

a) umieścić sondę w przepływie
b) ustawić przełącznik FUNCTION w położenie OPERATE,
c) nastawić przełącznik METER w położenie 3,
d) nastawić przełącznik PROBE CURRENT w położenie CURRENT ADJ,
e) wyregulować potencjometrem CURRENT ADJ. tak, aby prąd wynosił 3 mA,
f) ustawić przełącznik PROBE CURRENT w położenie OFF,
g) przełącznik METER ustawić w położenie 10, a przełącznik GAIN w

położenie 11,

h) regulować potencjometrem DC OUTPUT ADJ tak, aby wskazówka miernika

wychyliła się do czerwonej kreski,

i) przełącznik PROBE CURRENT ustawić w położenie ON,
j) dobrać nastawę dekady tak, aby wskazania miernika były identyczne dla obu

położeń (ON; OFF) przełącznika PROBE CURRENT; NASTAWA
DEKADY WSKAZUJE TERAZ OPORNOŚĆ CZUJNIKA,

k) zmierzyć oporność czujnika także przy innych prędkościach przepływu,
l) powtórzyć czynności c) do k) kilka razy dla coraz niższych prądów tak, aby

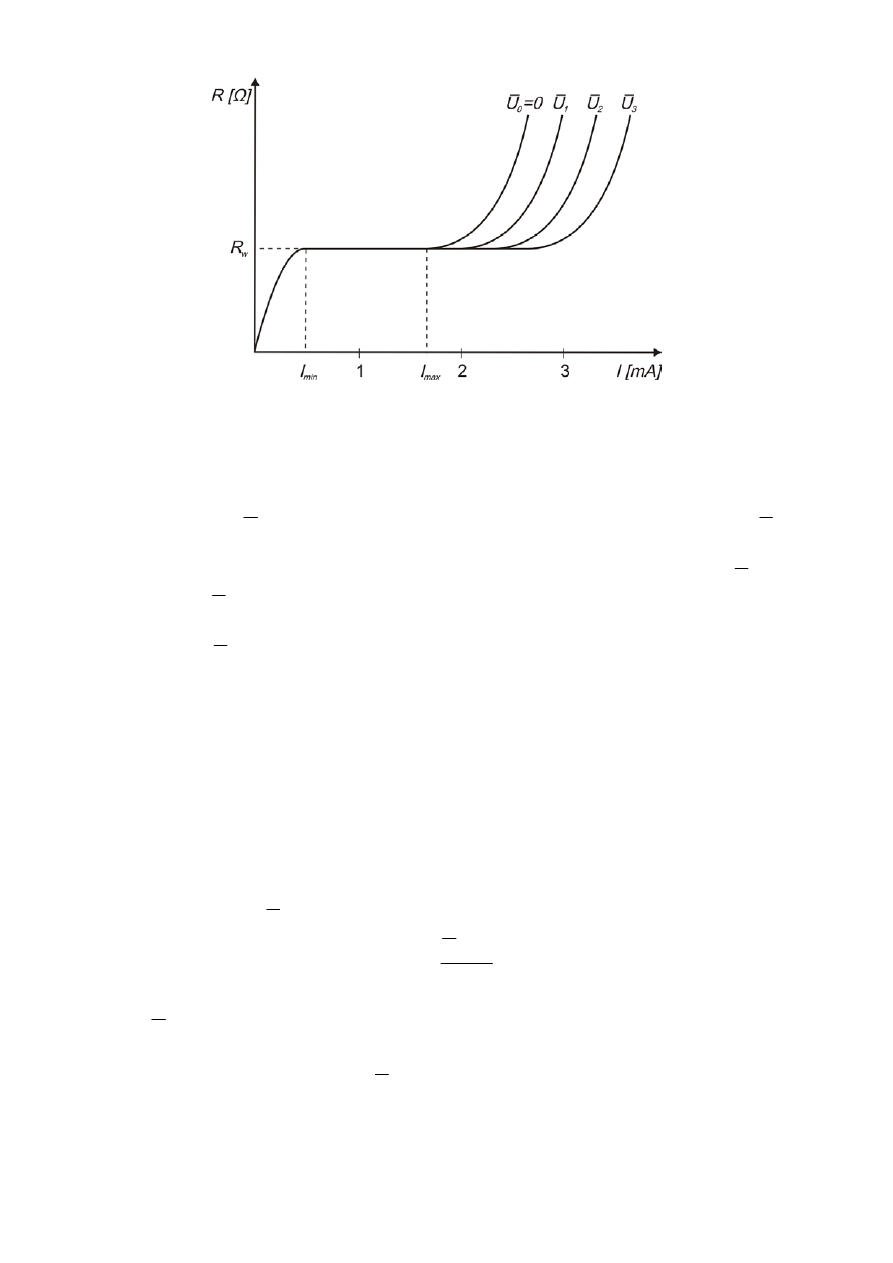
móc sporządzić wykresy zmian rezystancji czujnika w funkcji prądu sondy
(rys. 4),

m) na podstawie wykresów wybrać najwyższy dopuszczalny prąd sondy,
n) nastawić wybrany prąd sondy.

6. Regulacja wzmocnienia i napięcia wyjściowego:

a) wyregulować napięcie pokrętłem DC OUTPUT ADJ. do odpowiedniego

poziomu
- podczas pomiarów dodatnich zmian temperatury wskazówkę miernika

ustawić w prawej połowie skali,

- podczas pomiarów ujemnych zmian temperatury wskazówkę miernika

ustawić w lewej części zakresu,

- podczas pomiarów zarówno dodatnich jak i ujemnych zmian temperatury

– pośrodku skali,

b) wyregulować GAIN tak, aby cały stojący do dyspozycji zakres zmian

napięcia (0 ÷ 20 V) odzwierciedlał maksymalny zakres zmian temperatury w
przepływie.

7. Woltomierz 55D31, przy właściwie wybranym czasie uśredniania, wskazuje

napięcie średnie E , woltomierze 55D35 i V531 (rys. 2) rejestrują wartość

skuteczną napięcia zmiennego

2

e

, oscyloskop przedstawia przebieg czasowy

e(t).

128

3.1.2. Pomiar temperatury średniej i napięcia średniego

W czasie wzorcowania układu pomiarowego CCA prędkość wypływającego z

dyszy powietrza

w

U

można ustalić na poziomie 10 ÷ 20 m/s, a jego temperatura

w

Θ

winna wynosić około 70

o

C. Włókno sondy należy ustawić w osi strugi w odległości

około x

1

= 2,5 d od wylotu z dyszy. W punkcie tym temperatura powietrza Θ jest

zbliżona do

w

Θ

tzn. do maksymalnej temperatury w przepływie. Należy odczytać

oporność R

T

wskazywaną przez miernik RLC, a z charakterystyki termistora

temperaturę

i

Θ

. Wyniki pomiaru należy wpisać do Tabeli 1. Następne punkty

pomiarowe można ustalać w taki sposób, aby po każdym przesunięciu sondy w
kierunku promieniowym temperatura zmniejszała się o około 4 deg.
Na podstawie wyników wzorcowania można wyznaczyć parametry E

o

, Θ

o

, s równania

równowagi układu mostka temperaturowego CCA 55M20 (vide rozdział 4).

3.2. Pomiar pola temperatur

W wybranym przekroju pomiarowym x

1

= idem turbulentnej, nieizotermicznej

swobodnej strugi kołowej (rys. 2) należy wyznaczyć rozkład temperatury średniej oraz
rozkład wartości skutecznej fluktuacji temperatury.
Warunki początkowe przepływu określone są przez liczbę Reynoldsa Re oraz stopień
przegrzewu strugi

w

Θ

∆

. Liczba Re oparta jest na średnicy dyszy i wyraża się wzorem:

w

w

d

U

Re

ν

⋅

=

(10)

w którym:

w

U

, m/s - prędkość przepływu w płaszczyźnie wylotowej dyszy,

w

ν

, m/s - kinematyczny

współczynnik lepkości obliczony dla powietrza o

temperaturze

w

Θ ,

d, m

- średnica dyszy.

Rys. 4. Zależność rezystancji włókna sondy od prądu mostka stałoprądowego

129

Przez stopień przegrzewu strugi należy rozumieć nadwyżkę temperatury

średniej w płaszczyźnie wylotowej dyszy

w

Θ

nad temperaturą otoczenia

ot

Θ

:

ot

w

w

Θ

Θ

∆Θ

−

=

(11)

Prędkość powietrza wypływającego z dyszy można wyznaczyć ze wskazań
mikromanometru podłączonego do króćców pomiarowych, wykorzystując wzór:

,

2

w

m

w

i

l

g

U

ρ

α

ρ

⋅

⋅

⋅

⋅

=

m/s (12)

w którym:

m

ρ

, kg/m

3

- gęstość cieczy manometrycznej w temperaturze otoczenia,

i -

przełożenie mikromanometru,

g, m/s

2

-

przyspieszenie

ziemskie,

w

ρ

, kg/m

3

- gęstość powietrza w temperaturze

w

Θ

,

α -

stała dyszy pomiarowej,

l, m

- długość słupa cieczy manometrycznej równoważącego różnicę

ciśnień statycznych istniejącą między przekrojami dyszy.

Występującą we wzorze (12) gęstość powietrza można wyliczyć z zależności:

3

kg/m

,

w

w

Θ

R

p

⋅

=

ρ

(13)

w której:

p, N/m

2

-

ciśnienie statyczne w strudze,

w

Θ

, K

- temperatura powietrza w przekroju wylotowym dyszy,

R, J/kg·K - stała gazowa powietrza R = 287,04.

Ciśnienie statyczne w przepływie swobodnym p można uznać za równe ciśnieniu
atmosferycznemu p

a

. Wyliczona ze wzoru (13) gęstość dotyczy powietrza

traktowanego jako gaz doskonały. Przyjęcie takiego uproszczenia jest dopuszczalne,
ponieważ zakres zmian parametrów przepływu w przypadku prowadzonego
eksperymentu jest stosunkowo niewielki.
Dynamiczny współczynnik lepkości gazu o temperaturze Θ K i ciśnieniu 1 bar (10

5

Pa) można wyznaczyć z dostateczną dokładnością według wzoru Sutherlanda [5]:

273

1

273

1

Θ

Θ

C

C

o

t

+

+

=

µ

µ

(14)

w którym:

o

µ

- dynamiczny

współczynnik lepkości gazu przy 0

o

C i 1 bar,

Θ

- temperatura gazu według skali bezwzględnej,

C

- stała Sutherlanda.

Kinematyczny współczynnik lepkości w warunkach prowadzonego eksperymentu
można więc wyznaczyć ze związku:

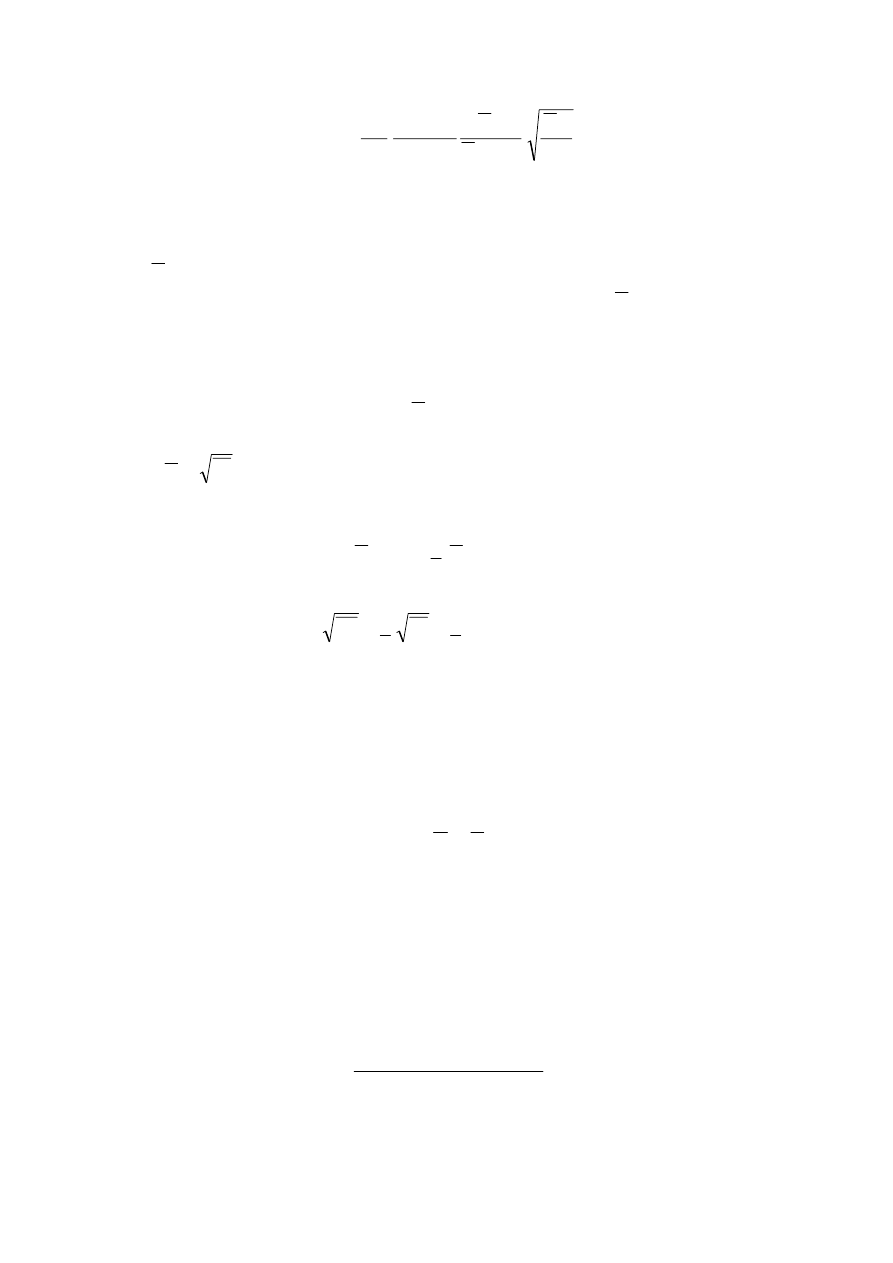
130

273

Θ

C

Θ

Θ

C

ν

w

w

w

w

o

w

+

+

=

273

273

ρ

µ

(15)

gdzie:

µ

o

,

kg/m

⋅ s - dynamiczny współczynnik lepkości powietrza suchego w

temperaturze 0

o

C i przy ciśnieniu 1 bar, µ

o

=17,08ּ10

-6

C -

stała Sutherlanda dla powietrza, C = 112

w

Θ

, K -

temperatura

powietrza,

w

ρ

, kg/m

3

- gęstość powietrza o temperaturze

w

Θ

, obliczona wg

wzoru (13).

3.2.1. Rozkład temperatury

Rozkład temperatury średniej Θ oraz fluktuacji temperatury RMS )

(

ϑ

w

kierunku promieniowym strugi można wyznaczyć w oparciu o pomiary wielkości

napięć E i

2

e

.

Odpowiednie wzory obliczeniowe mają postać:

- temperatura średnia

(

)

K

,

1

o

o

E

E

s

Θ

Θ

−

+

=

(16)

- wartość skuteczna RMS )

(

ϑ

K

,

1

1

2

2

W

K

s

e

s

RMS

=

=

ϑ

(17)

K

RMS

oznacza wybrany zakres woltomierza RMS 55D35, a W [V] wskazanie

woltomierza V531.
Występujące w powyższych wzorach wielkości E

o

, Θ

0

, s należy wyznaczyć w sposób

opisany w rozdziale 4.

4. Szczegółowy program ćwiczenia

Kolejność postępowania podczas realizacji ćwiczenia jest następująca:
1. Po ustaleniu parametrów przepływu

w

w

Θ

U ,

i przygotowaniu termoanemometru

stałoprądowego według instrukcji zawartej w rozdziale 3 do pomiarów
temperatury, przeprowadza się wzorcowanie w kolejnych punktach wybranego
przekroju kontrolnego (x

1

= idem). Uzyskane dane pomiarowe zamieszcza się w

kolumnach 2 ÷ 6 Tabeli 1.

2. Wyniki zawarte w kolumnach 5 ÷ 6 są podstawą do wykreślenia charakterystyki

układu pomiarowego mostka w układzie

).

,

(

E

Θ

3. Czułość układu pomiarowego mostka oblicza się metodą najmniejszych kwadratów

wg wzoru:

(

)(

)

(

)

∑

∑

∑

∑

∑

−

−

=

i

i

i

i

i

i

x

x

n

y

x

y

x

n

s

2

(18)

4. Parametr b prostej regresji wyraża się wzorem:

131

n

x

s

n

y

b

i

i

∑

∑

−

=

(19)

z

którego

wynika,

że estymatorami parametrów odniesienia E

o

i Θ

o

mogą być

średnie arytmetyczne z uzyskanych pomiarów:

n

E

E

i

o

∑

=

(20)

n

Θ

Θ

i

o

∑

=

(21)

5. Ocenę dokładności wyznaczonej czułości układu pomiarowego można dokonać

poprzez obliczenie odchylenia standardowego

( )

∑

∑

∑

∑

∑

−

−

−

−

=

2

2

2

2

i

i

i

i

i

i

s

x

x

n

y

b

y

x

s

y

n

n

S

(22)

i określenie przedziału ufności dla przyjętego poziomu istotności α przy n
niezależnych pomiarach

α

α

α

−

=

+

≤

≤

−

1

}

{

,

.

,

s

n

rzeczyw

s

n

S

t

s

s

S

t

s

P

(23)

Wielkość t

n,α

jest zmienną losową rozkładu Studenta, której wartość dla znanego n

i przyjętego α można odczytać z tabel statystycznych.

6. Miarą odchyleń punktów pomiarowych od prostej regresji:

(

)

o

o

Θ

Θ

s

E

E

−

+

=

jest odchylenie standardowe obliczone ze wzoru [4]:

(

)

2

2

2

o

S

E

E

Θ

Θ

S

S

S

o

−

+

=

(24)

w którym

2

o

E

S

jest miarą niepewności jednego punktu prostej regresji o

współrzędnych (Θ

o

, E

o

); wartość

2

o

E

S

można wyliczyć ze związku:

(

)

(

)

∑

∑

∑

−

−

−

=

i

i

i

i

E

y

b

y

x

s

y

n

n

S

o

2

2

2

1

(25)

Dla małej próby należy zastosować rozkład Studenta i odczytać współczynnik t

n,α

z

tablic dla odpowiedniego n oraz przyjętego poziomu istotności α. Wówczas
przedział ufności dla wartości E wyraża się następująco:

α

α

α

−

=

+

≤

≤

−

1

}

{

,

.

,

n

rzeczyw

E

n

t

E

E

S

t

E

P

(26)

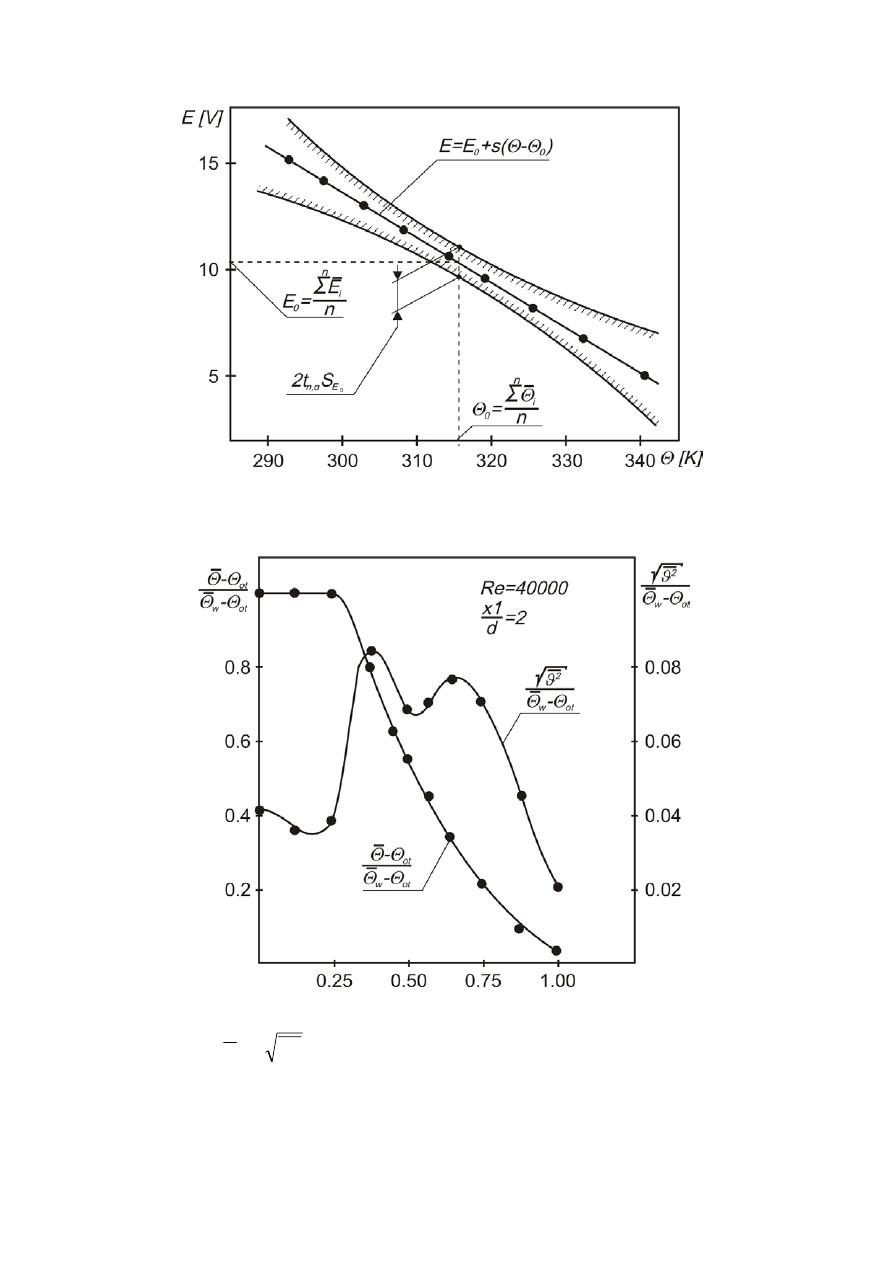
Przykładową charakterystykę termoanemometru stałoprądowego przystosowanego
do pomiaru temperatury wraz z naniesionymi krzywymi ufności pokazano na rys.
5.

7. Po wycechowaniu termoanemometru przeprowadza się pomiar rozkładów

wielkości Θ i

2

ϑ

w płaszczyźnie x

1

= idem, przy ustalonych parametrach

początkowych

w

U

i

w

Θ powietrza wypływającego z dyszy. Wyniki zamieszcza

się w kolumnach 1, 2, 3, 4 Tabeli 2.

132

8. Wielkości Θ i

2

ϑ

oblicza się z zależności (16) i (17). Otrzymane wyniki w

postaci zredukowanej przedstawia się w formie graficznej. Przykładowe rozkłady
temperatury średniej i wartości skutecznej fluktuacji temperatury przy Re = 40000
i ∆Θ

w

= 40 deg pokazano na rys. 6.

Uzyskane wyniki badań pozwalają odpowiedzieć na następujące pytania:

Rys. 5. Charakterystyka temperaturowa termoanemometru stałoprądowego

Rys. 6. Rozkład temperatury średniej i fluktuacji temperatury w przekroju strugi kołowej

133

−

jak zmienia się temperatura średnia w kierunku promieniowym w swobodnej,
nieizotermicznej strudze kołowej?

−

jaki jest rozkład poziomu turbulencji termicznej w przekroju promieniowym?

Literatura

1. Elsner J.W.: Turbulencja przepływów, PWN, Warszawa 1987
2. Hinze J.O.: Turbulence, 2nd ed. New York, Mc Graw-Hill 1975
3. Instruction Manual DISA 55M System with 55M20 Temperature Bridge
4. PN-65/M-53950 Pomiar natężenia przepływu płynów za pomocą zwężek
5. Szydłowski H.: Teoria pomiarów, PWN, Warszawa 1981

134

Tabele pomiarowo – obliczeniowe

Tabela 1

Dane ogólne:

Temp. medium w płaszczyźnie wylotowej dyszy

w

Θ

= ................. K

Temp. otoczenia

Θ

ot

= ................. K

Odległość przekroju kontrolnego od wylotu z dyszy

x

1

= ................. mm

Prąd sondy

I =

................. mA

Oporność włókna sondy w temp. Θ

o

R

w

= ................. Ω

Nastawa oporności na dekadzie mostka CCA

R

D

= R

w

Lp.

r

mm

R

T

kΩ

t

o

C

i

i

Θ

x

=

K

i

i

E

y

=

V

x

i

y

i

2

i

x

2

i

y

1
2
3

.
.
.
.

n

∑

=

n

i 1

135

Tabela 2

Parametry stałe układu pomiarowego:

s

=

............V/K

E

o

= ...............V

Θ

o

= ............ K

Temp. otoczenia

Θ

ot

= ................. K

Ciśnienie otoczenia

p

ot

= ................. N/m

2

Parametry czynnika w płaszczyźnie wylotowej dyszy:

Temperatura czynnika

Θ

w

= ................. K

Ciśnienie statyczne

p

w

= ................. N/m

2

Średnica dyszy

d =

................. m

Stała dyszy pomiarowej

α = .................

Gęstość cieczy manometrycznej

ρ

m

= ................. kg/m

3

Przełożenie manometru

i = .................

Stała gazowa czynnika

R = ................. J/kg·K

Gęstość czynnika

ρ

= ................. kg/m

3

Kinematyczny współczynnik lepkości

ν

w

= ................. m

2

/s

Prędkość czynnika

w

U

= ................. m/s

Liczba Reynoldsa

Re

= .................

Współrzędna płaszczyzny pomiarowej

x

1

= ................. m

Zredukowana odległość płaszczyzny od wylotu dyszy x

1

/d = .................

x

2

mm

E

V

K

RMS

W

V

Θ

K

2

ϑ

K

x

2

/d

ot

w

ot

Θ

Θ

Θ

Θ

−

−

ot

w

Θ

Θ

−

2

ϑ

1 2 3 4 5 6 7 8

9