Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–1

Skalowanie w systemach naturalnych

Skalowanie – mno enie przez całkowit pot g podstawy

β

k

.

•

skalowania mo na składa poniewa

β

k

X =

β

…

ββ

X

•

mno enie przez ka d dodatni pot g podstawy

daje w wyniku cykliczne przemieszczenie cyfr w lewo, poniewa

∑

∑

∑

=

+

−

=

−

−

=

−

=

+

−

=

−

=

=

=

k

i

m

i

i

i

k

i

m

i

i

i

k

i

m

i

i

i

x

x

x

1

1

1

1

1

β

β

β

β

•

mno enie przez ka d ujemn pot g podstawy

daje w wyniku cykliczne przemieszczenie cyfr w prawo, poniewa

∑

∑

∑

−

=

−

−

=

+

−

=

−

=

−

−

=

−

=

−

=

=

2

1

1

1

1

1

1

k

i

m

i

i

i

k

i

m

i

i

i

k

i

m

i

i

i

x

x

x

β

β

β

β

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–2

Skalowanie w systemach uzupełnieniowych i dopełnieniowych

Je li najwy sz pozycj liczby nie jest cyfra rozszerzenia

)

1

)(

(

1

−

=

−

β

ϕ

k

k

x

x

,

to w wyniku mno enia przez

β

wyst pi nadmiar.

Je li k najwy szych pozycji liczby nie jest cyframi rozszerzenia,

to w wyniku mno enia przez

β

k

wyst pi nadmiar.

W systemie uzupełnieniowym – rozszerzenie:

)

1

)(

(

1

−

=

−

β

ϕ

k

k

x

x

– otrzymamy

}

0

,

,...,

,

{

}

,...,

,

),

1

)(

(

{

2

1

e

2

1

1

e

m

k

k

m

k

k

k

x

x

x

x

x

x

x

−

−

−

−

−

−

−

=

⇒

−

=

X

X

β

β

ϕ

,

W systemie dopełnieniowym nast pi cykliczne przemieszczenie cyfr

)}

1

)(

(

,

,...,

,

{

}

,...,

,

),

1

)(

(

{

1

2

1

e

2

1

1

e

−

=

⇒

−

=

−

−

−

−

−

−

−

−

β

ϕ

β

β

ϕ

k

m

k

k

m

k

k

k

x

x

x

x

x

x

x

x

X

X

Wynik skalowania odwrotnego (mno enia przez

β

−1

) jest zawsze poprawny

}

,...,

,

),

1

)(

(

{

}

,

,...,

,

{

1

2

1

1

e

1

1

2

1

e

+

−

−

−

−

−

−

+

−

−

−

−

=

⇒

=

m

k

k

k

m

m

k

k

x

x

x

x

x

x

x

x

β

ϕ

β

X

X

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–3

Skalowanie w dwójkowym systemie uzupełnieniowym i dopełnieniowym

Wynikiem dodawania liczby do niej samej jest na ka dej pozycji:

i

i

i

i

i

s

c

c

x

x

+

=

+

+

+

1

2

⇒

i

i

x

c

=

+

1

,

i

i

c

s

=

⇒

i

i

x

s

=

+

1

W systemie uzupełnieniowym, u ywaj c rozszerzenia, otrzymamy

}

0

,

,

,...,

,

{

}

,

,...,

,

,

{

1

2

1

e

e

1

2

1

1

e

m

m

k

k

m

m

k

k

k

x

x

x

x

x

x

x

x

x

−

+

−

−

−

−

+

−

−

−

−

=

+

⇒

=

X

X

X

,

•

(

×2

)

U

= przesuni cie logiczne (logical shift)

W systemie dopełnieniowym pojawi si przeniesienie okr

ne o warto ci x

k–1

}

,

,

,...,

,

{

}

,

,...,

,

,

{

1

1

2

1

e

e

1

2

1

1

e

−

−

+

−

−

−

−

+

−

−

−

−

=

+

⇒

=

k

m

m

k

k

m

m

k

k

k

x

x

x

x

x

x

x

x

x

x

X

X

X

•

(

×2

)

D

= przemieszczenie cykliczne, rotacja (rotation)

Wynikiem skalowania odwrotnego (mno enia przez

2

−1

) jest zawsze

}

,...,

,

,

{

}

,

,...,

,

{

1

2

1

1

e

2

1

1

2

1

e

+

−

−

−

−

−

+

−

−

−

=

⇒

=

m

k

k

k

m

m

k

k

x

x

x

x

x

x

x

x

X

X

•

(

×2

−1

) = przesuni cie arytmetyczne (arithmetic shift).

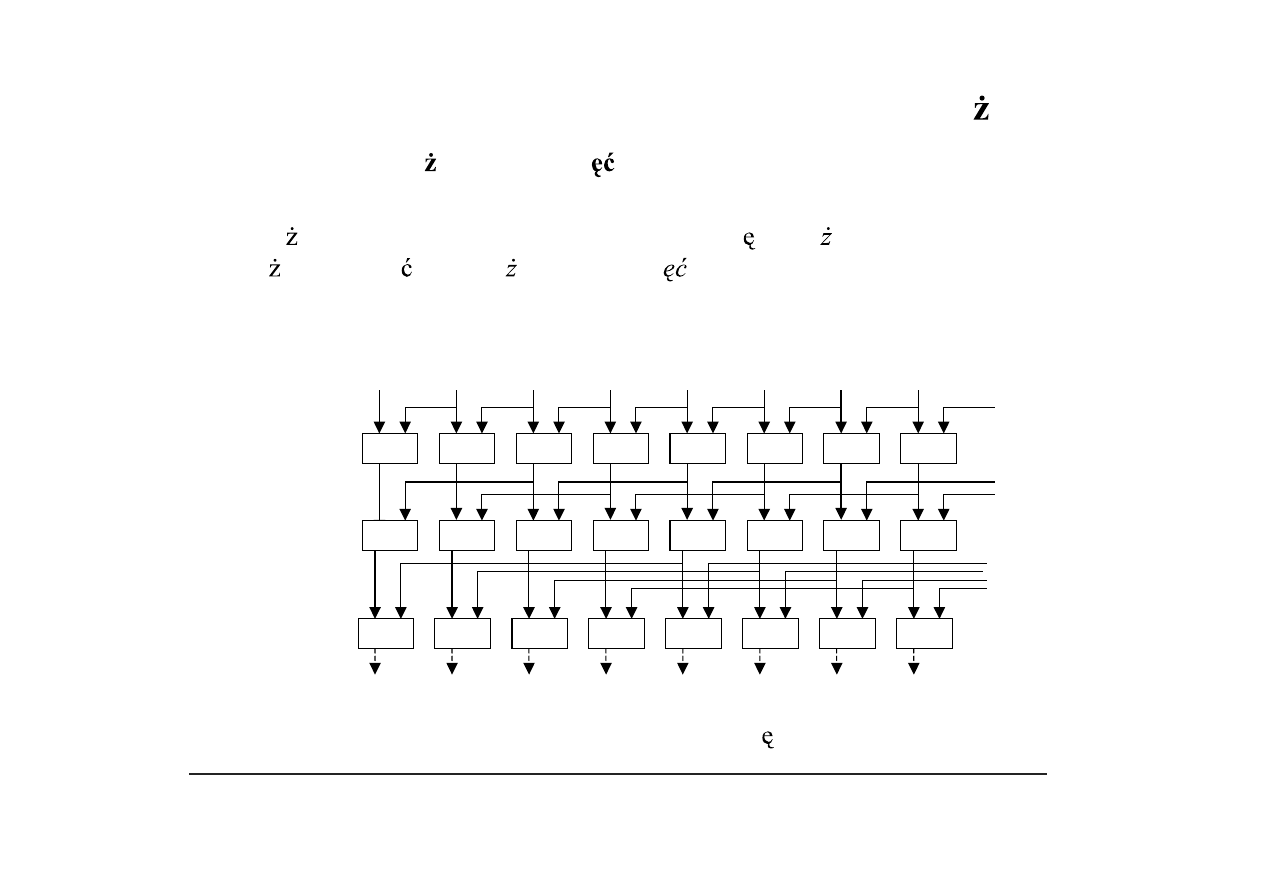
Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–4

Skalowanie jako zło enie przesuni

Poniewa

β

k

= (

β

a

β

2

b

β

4c

…)

−1

(a, b, c, … = 0, 1) , wi c mno enie przez

β

k

mo na wykona jako zło enie przesuni

o 2

i

pozycji

•

w lewo gdy k > 0

•

w prawo gdy k < 0

L P

←

←

1

L P

L P

L P

L P

L P

L P

L P

L P

←

←

2

L P

L P

L P

L P

L P

L P

L P

L P

←

←

4

L P

L P

L P

L P

L P

L P

L P

Schemat skalowania przez przesuni cie w lewo

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–5

Sekwencyjny algorytm mno enia w systemie naturalnym

Mno na (multiplicand)

|

}

,

,...,

{

|

1

1

β

p

p

s

a

a

a

A

−

+

−

−

=

,

Mno nik (multiplier)

|

}

,

,...,

{

|

1

1

β

m

m

k

x

x

x

X

−

+

−

−

=

,

∑

∑

−

−

=

−

−

=

=













⋅

=

⋅

1

1

)

(

k

m

i

i

i

k

m

i

i

i

A

x

x

A

X

A

β

β

Algorytm pisemny – akumulacja skalowanych iloczynów cz ciowych

i =

−

m,

−

m+1,...,k

−

1,

0

=

−

m

S

)

(

1

A

x

S

S

i

i

i

i

β

+

=

+

,

X

A

S

k

⋅

=

Algorytm dodaj-przesu (add-and-shift) – skalowanie sum cz ciowych

i

i

i

S

P

−

=

β

)

(

1

1

A

x

P

P

i

i

i

+

=

−

+

β

X

A

x

A

P

P

k

m

i

i

i

m

k

k

⋅

=

+

=

∑

−

−

=

−

1

}

{

β

β

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–6

Mno enie sekwencyjne w systemach uzupełnieniowych i dopełnieniowych

Warto ci znakowanego mno nika jest

∑

−

−

=

−

+

−

=

1

1

)

(

k

m

i

i

i

k

x

R

x

X

β

ϕ

,

gdzie

))

1

2

(

sgn

1

(

)

(

1

2

1

1

β

ϕ

−

+

+

=

−

−

k

k

x

x

– funkcja znaku liczby,

R = Q +ulp =

β

k

w systemie pełnym, R = Q =

β

k

−

β

–m

– w niepełnym

Mamy zatem (

δ

= 0 w systemie pełnym (U

β

), 0 – w systemie niepełnym (D

β

)):

m

k

k

m

i

i

i

k

k

k

x

x

x

x

X

−

−

−

−

=

−

−

−

+

+

−

=

∑

β

δϕ

β

β

ϕ

β

)

(

))

(

(

1

2

1

1

1

Je eli najwy sz cyfr jest cyfra rozszerzenia

)

(

)

1

(

1

1

−

−

−

=

k

k

x

x

ϕ

β

, to wtedy

A

x

A

x

A

x

x

x

x

A

X

A

m

k

k

m

i

i

i

k

k

m

k

k

m

i

i

i

k

k

−

−

−

−

=

−

−

−

−

−

−

=

−

−

+

+

−

=

=













+

+

−

⋅

=

⋅

∑

∑

β

δϕ

β

β

ϕ

β

δϕ

β

β

ϕ

)

(

)

(

)

(

)

(

)

(

1

2

1

1

1

2

1

1

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–7

Interpretacja

Funkcja

)

(

1

1

1

−

−

−

−

=

k

k

k

x

x

z

ϕ

β

opisuje przekształcenie zbioru

D = {0, 1, …,

β

−

1}

na nieredundantny zbiór cyfr znakowanych

}

1

,...,

1

,

0

,

1

,...,

{

2

1

2

1

−

−

−

=

β

β

S

D

W

NIOSKI

:

W mno eniu w systemach uzupełnieniowych rozszerzenie mno nika zapewnia,

e warto ci najwy szej cyfry jest zawsze 0 albo –1 („

β

−

1”).

W mno eniu przez k-cyfrowy mno nik nale y u y k cyfr lewostronnego

rozszerzenia mno nej

W dwójkowym systemie uzupełnieniowym równowa n interpretacji liczby

jako stałobazowej z ujemn wag pozycji najwy szej (–2

k–1

), jest jej

traktowanie jako liczby z ujemn cyfr (–x

k–1

) i dodatni wag (2

k–1

)

∑

∑

∑

−

=

−

=

−

−

−

=

−

=

−

−

−

=

−

=

−

−

+

−

=

+

−

=

+

−

2

1

1

2

1

1

2

1

1

2

2

)

(

2

)

2

(

2

2

k

i

m

i

i

i

k

k

k

i

m

i

i

i

k

k

k

i

m

i

i

i

k

k

x

x

x

x

x

x

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–8

Mno enie pisemne w systemie uzupełnieniowym – przykład

bez rozszerzenia mno nika

A

=−124

9 9 9 9 9 8 7 6

A

=124

0 1 2 4

X

=−21

7 7 9

X

=−21

7 7 9

x

0

=9

9 9 9 9 8 8 8 4

x

0

=9

0 0 0 0 1 1 1 6

x

1

=7

9 9 9 9 1 3 2

x

1

=7

0 0 0 0 8 6 8

x

2

=−3

−3

A 0 0 0 3 7 2

x

2

=−3

−3

A 9 9 9 6 2 8

X

⋅

A

0 0 0 2 7 4 0 4

X

⋅

A

9 9 9 7 2 5 9 6

z rozszerzeniem mno nika

A

=−124

9 9 9 9 9 8 7 6

A

=124

0 0 0 0 0 1 2 4

X

=−21

9 7 7 9

X

=−21

9 7 7 9

x

0

=9

9 9 9 9 8 8 8 4

x

0

=9

0 0 0 0 1 1 1 6

x

1

=7

9 9 9 9 1 3 2

x

1

=7

0 0 0 0 8 6 8

x

2

=7

9 9 9 1 3 2

x

2

=7

0 0 0 8 6 8

x

3

=−1

−

A

0 0 1 2 4

x

3

=−1

−

A

9 9 8 7 6

X

⋅

A

0 0 0 2 7 4 0 4

X

⋅

A

9 9 9 7 2 5 9 6

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–9

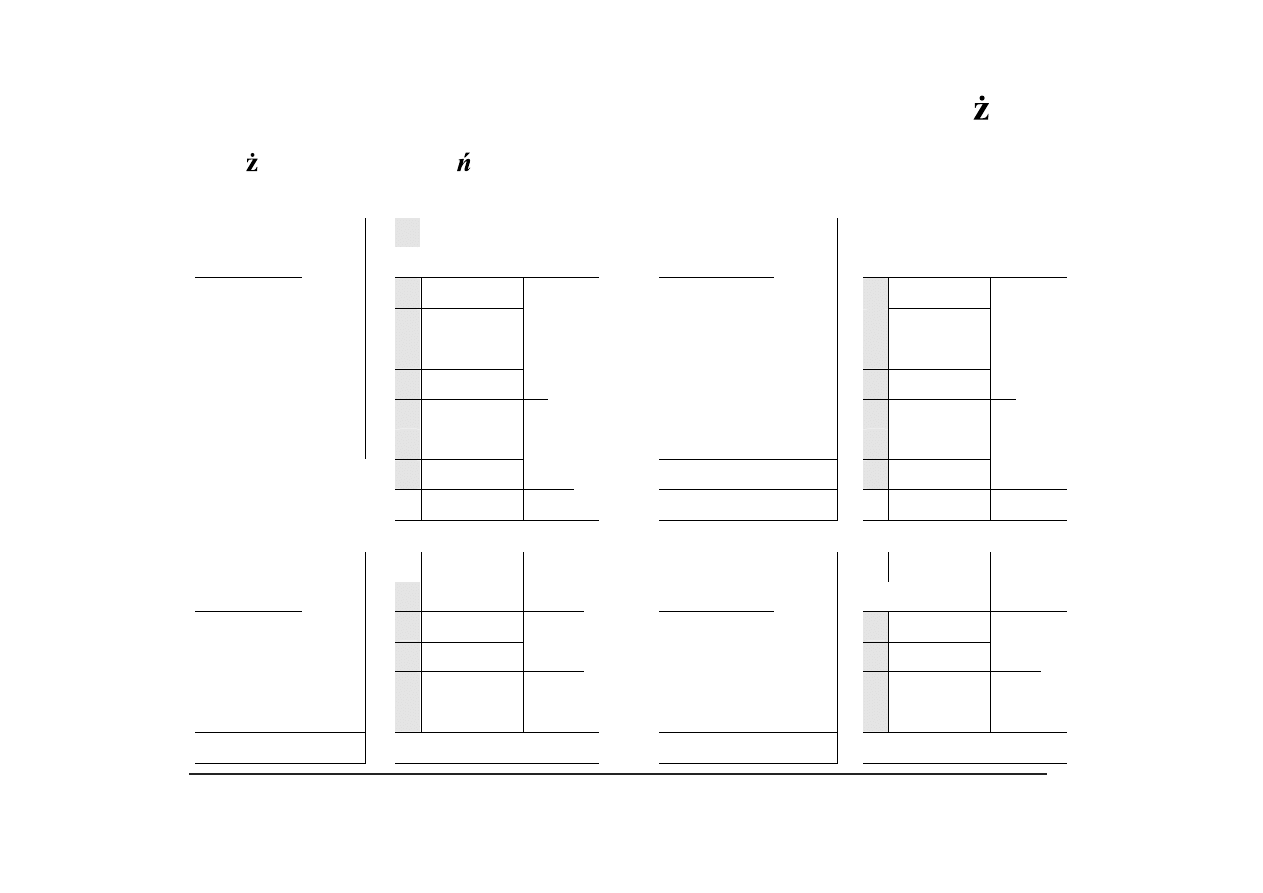
Algorytm mno enia sekwencyjnego w systemach uzupełnieniowych

Algorytm mno enia dodaj-przesu (add-and-shift) – [

)

(

)

1

(

1

1

−

−

−

=

k

k

x

x

ϕ

β

]

0.

if

)

(

)

1

(

1

1

−

−

−

≠

k

k

x

x

ϕ

β

then

a)

)

(

)

1

(

1

−

−

=

k

k

x

x

ϕ

β

; dopisz pozycj rozszerzenia

b) k ++

; zwi ksz k

1.

A

x

P

k

m

)

(

1

−

−

=

δϕ

; (

δ

=1 w s. niepełnym, 0 w pełnym)

2. i = –m
3.

A

x

M

i

i

=

; oblicz iloczyn cz ciowy

4.

)

(

1

1

i

i

i

M

P

P

+

=

−

+

β

; przeskaluj (przesu ) sum cz ciow

5. i ++

; zwi ksz i

6.

if i < k–1 goto 3

; powtarzaj do przedostatniego

7.

))

)(

(

(

1

1

1

A

x

P

P

k

k

k

−

+

=

−

−

−

ϕ

β

; dodaj dopełnienie mno nej lub 0

8.

k

k

P

X

A

β

=

⋅

; iloczyn

!! UWAGA: Wszystkie sumy cz ciowe s przesuwane w prawo

wi c musz by obliczane z lewostronnym rozszerzeniem

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–10

Mno enie dodaj-przesu w systemie uzupełnieniowym – przykład

A

=−124

9 9 8 7 6

A

=124

0 1 2 4

X

=−21

7 7 9

X

=−21

7 7 9

x

0

=9

+9A

9 8 8 8 4

x

0

=9

+9A 0 1 1 1 6

→

9 9 8 8 8 4

→

0 0 1 1 1 6

x

1

=7

+7A

9 9 1 3 2

x

1

=7

+7A 0 0 8 6 8

9 9 0 2 0 4

0 0 9 7 9 6

→

9 9 9 0 2 0 4

→

0 0 0 9 7 9 6

x

2

=−3

−3

A

0 0 3 7 2

x

2

=−3

−3

A 9 9 6 2 8

0 0 2 7 4 0 4

9 9 7 2 5 9 6

X

⋅

A

→

0 0 0 2 7 4 0 4

X

⋅

A

9 9 9 7 2 5 9 6

… …

… …

→

9 9 9 0 2 0 4

→

0 0 0 9 7 9 6

x

2

=7

+7A

9 9 1 3 2

x

2

=7

+7A 0 0 8 6 8

9 9 0 3 4 0 4

0 0 9 6 5 9 6

→

9 9 9 0 3 4 0 4

→

0 0 0 9 6 5 9 6

x

3

=−1

−

A

0 0 1 2 4

x

3

=−1

−

A

9 9 8 7 6

X

⋅

A

0 0 0 2 7 4 0 4

X

⋅

A

9 9 9 7 2 5 9 6

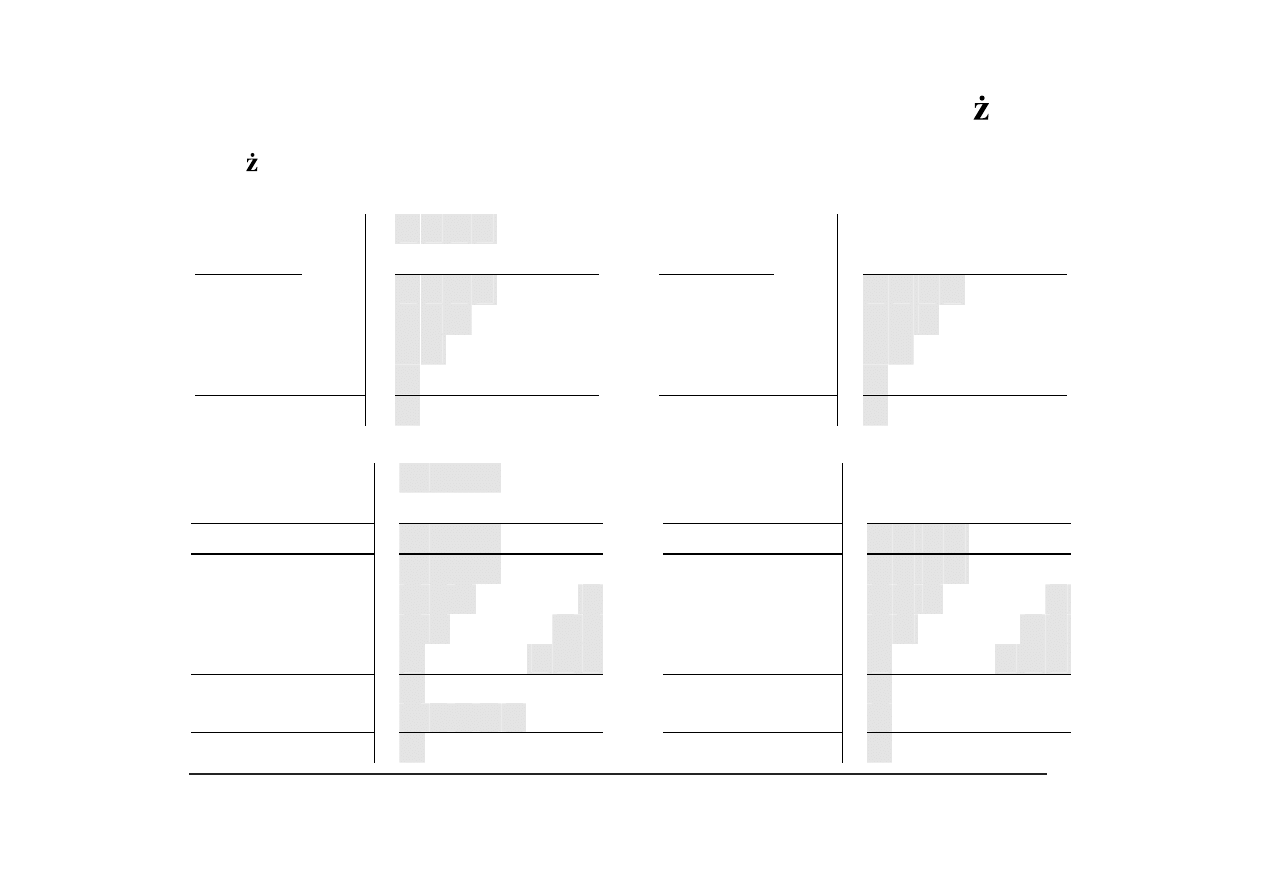
Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–11

Mno enie pisemne w dwójkowych systemach uzupełnieniowych U2 i U1

U2

A

=−7

1 1 1 1 1 0 0 1

A

=+5

0 1 0 1

X

=−5

1 0 1 1

X

=−3

1 1 0 1

x

0

=1

1 1 1 1 1 0 0 1

x

0

=1

0 0 0 0 0 1 0 1

x

1

=1

1 1 1 1 0 0 1

x

1

=0

0 0 0 0 0 0 0 0

x

2

=0

0 0 0 0 0 0

x

2

=1

0 0 0 1 0 1

x

3

=1

(−

A)

0 0 1 1 1

x

3

=1

(−

A) 1 1 0 1 1 0 0 0

X

⋅

A

=

35

0 0 1 0 0 0 1 1

X

⋅

A

=−

15

1 1 1 1 0 0 0 1

U1

A

=−7

1 1 1 1 1 0 0 0

A

=+5

0 1 0 1

X

=−4

1 0 1 1

X

=−2

1 1 0 1

P

0

=

x

3

A

1 1 1 1 1 0 0 0

P

0

=

x

3

A

0 0 0 0 0 1 0 1

x

0

=1

1 1 1 1 1 0 0 0

x

0

=

1

0 0 0 0 0 1 0 1

x

1

=1

1 1 1 1 0 0 0 1

x

1

=0

0 0 0 0 0 0 0 0

x

2

=0

0 0 0 0 0 0 0 0

x

2

=1

0 0 0 1 0 1 0 0

x

3

=

1

(−

A) 0 0 1 1 1 0 0 0

x

3

=1

(−

A) 1 1 0 1 0 1 1 1

0 0 0 1 1 0 0 1

1 1 1 1 0 1 0 1

e-a-c = 11

0 0 0 0 0 0 1 1

e-a-c = 0

0 0 0 0 0 0 0 0

X

⋅

A

=28

0 0 0 1 1 1 0 0

X

⋅

A

=−10

1 1 1 1 0 1 0 1

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–12

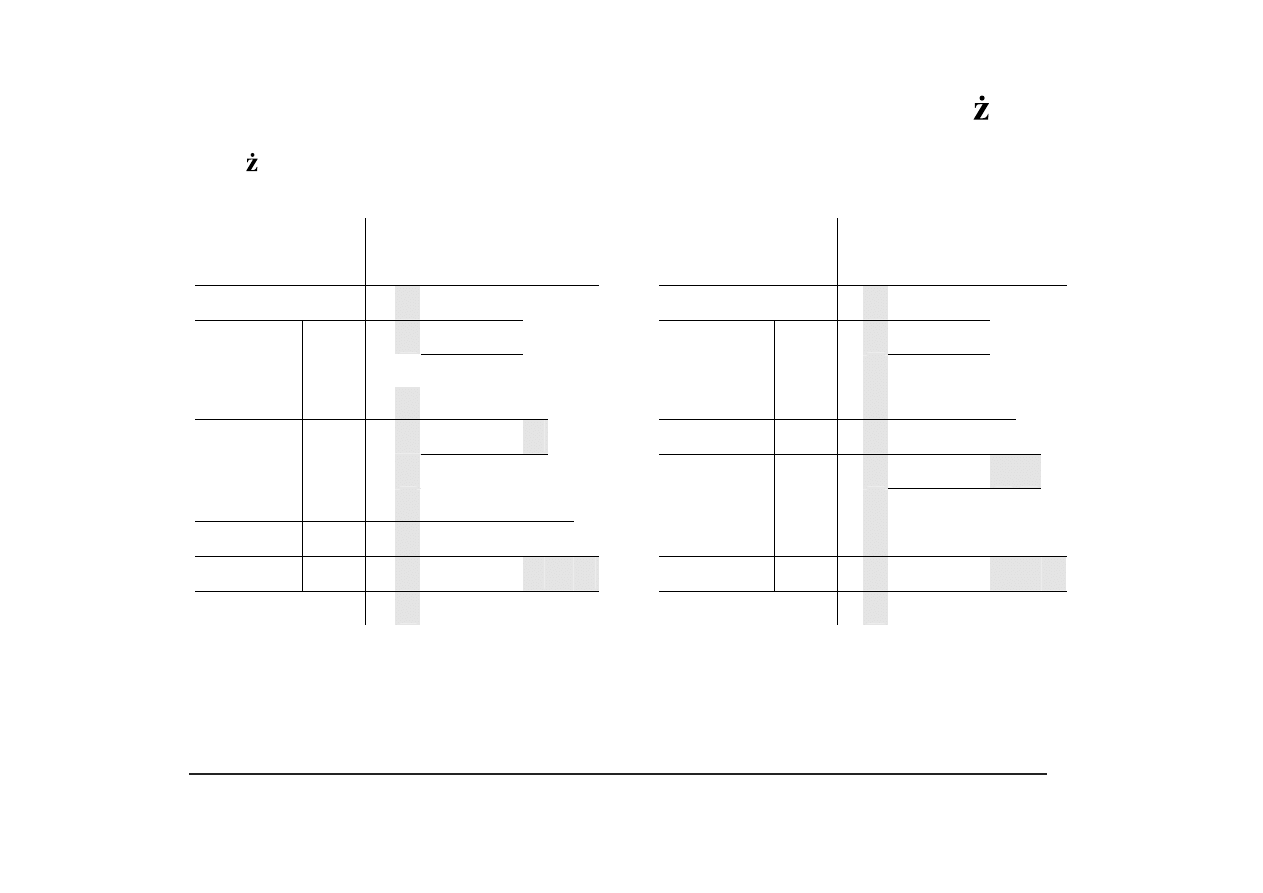
Mno enie maszynowe w dwójkowych systemach uzupełnieniowych

W dwójkowych systemach uzupełnieniowych

1

1

1

)

(

2

−

−

−

−

=

−

k

k

k

x

x

x

ϕ

m

k

k

m

i

i

i

k

k

x

x

x

X

−

−

−

−

=

−

−

+

+

−

=

∑

2

2

2

1

2

1

1

δ

1.

A

x

P

k

m

1

−

−

=

δ

; (x

k–1

A) 0 w systemie (nie)pełnym

i = –m

2.

A

x

M

i

i

=

; oblicz iloczyn cz ciowy

3.

i

i

i

M

P

S

+

=

+

1

; oblicz sum cz ciow

4. if

δ

= 1 then

+

+

+

+

=

c

S

S

i

i

1

1

;

δ

= 1

→

skoryguj sum przeniesieniem

5.

1

1

1

2

+

−

+

=

i

i

S

P

; przeskaluj sum (przesu w prawo)

6. i ++

; zwi ksz i

7. if i < k–1 goto 3

; powtarzaj do przedostatniego

8.

))

(

(

2

1

1

1

A

x

P

P

k

k

k

−

+

=

−

−

−

; dodaj dopełnienie mno nej lub 0

9.

k

k

P

X

A

2

=

⋅

; iloczyn

•

działania na wszystkich pozycjach sum cz ciowych

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–13

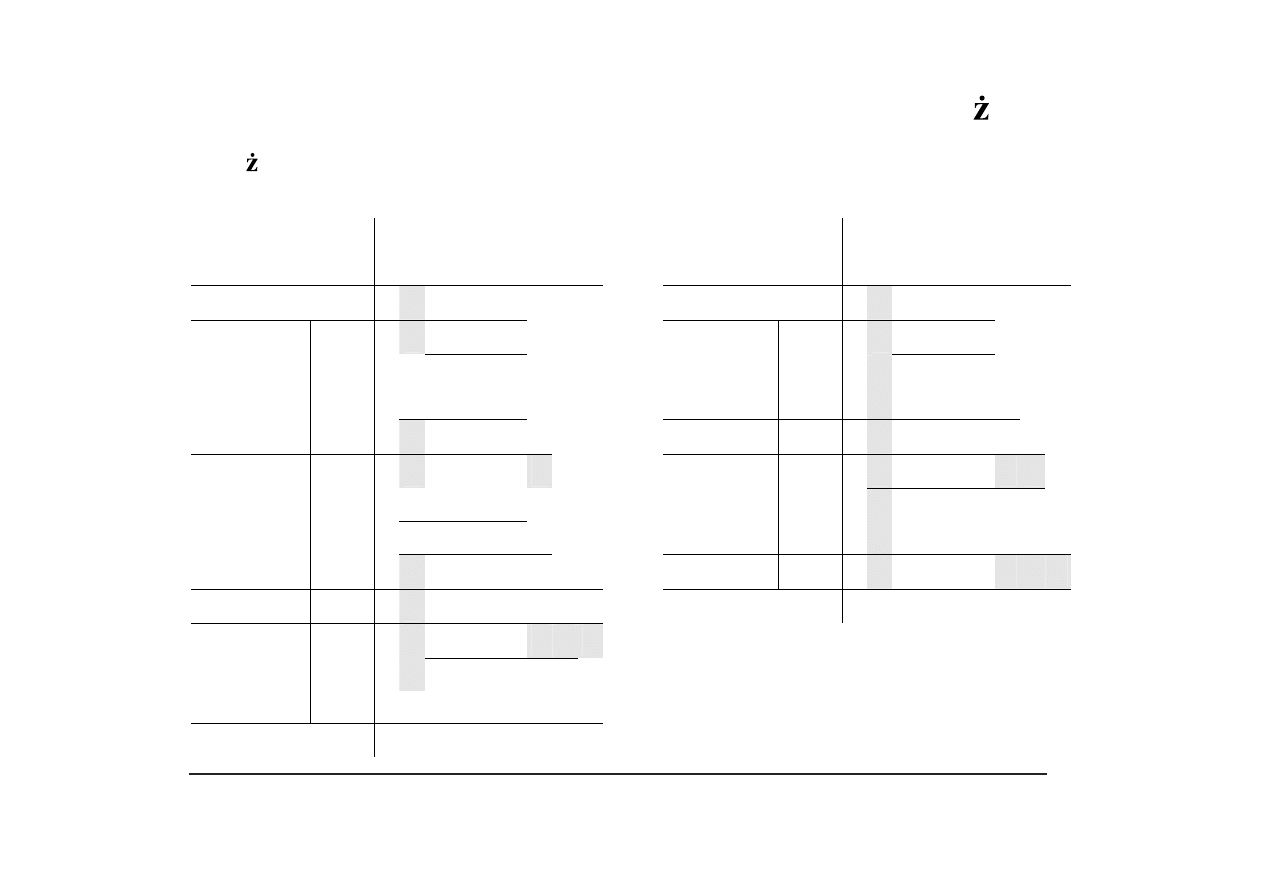
Mno enie maszynowe w systemie U2 – przykład

A

=−7

1 0 0 1

A

=+5

0 1 0 1

X

=−5

1 0 1 1

X

=−3

1 1 0 1

P

0

=0

0 0 0 0 0

P

0

=0

0 0 0 0 0

x

0

=1

+A

+ 1 1 0 0 1

x

0

=1

+A

0 0 1 0 1

1 1 0 0 1

0 0 1 0 1

ShR 1 1 1 0 0 1

ShR 0 0 0 1 0 1

x

1

=1

+A

+ 1 1 0 0 1 0

x

1

=0

ShR 0 0 0 0 1 0 1

1 0 1 0 1 1

x

2

=1

+A

+ 0 0 1 0 1 0 0

ShR 1 1 0 1 0 1 1

0 0 1 1 0 0 1

x

2

=0

ShR 1 1 1 0 1 0 1 1

ShR 0 0 0 1 1 0 0 1

x

3

=1

−

A

+ 0 0 1 1 1 0 0 0

x

3

=1

−

A

+ 1 1 0 1 1 0 0 0

X

⋅

A

=

35

0 0 1 0 0 0 1 1

X

⋅

A

=−

15

1 1 1 1 0 0 0 1

Uwaga: W polach zacienionych wpisano cyfry rozszerzenia znakowego.

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–14

Mno enie maszynowe w systemie U1 – przykład

A

=−7

1 0 0 0

A

=+5

0 1 0 1

X

=−4

1 0 1 1

X

=−2

1 1 0 1

P

0

=

x

3

A

1 1 0 0 0

P

0

=

x

3

A

0 0 1 0 1

x

0

=1

+A

+ 1 1 0 0 0

x

0

=

1

+A

0 0 1 0 1

+1

1 0 0 0 0

0 1 0 1 0

1 0 0 0 1

ShR 0 0 1 0 1 0

ShR 1 1 0 0 0 1

x

1

=0

ShR 0 0 0 1 0 1 0

x

1

=1

+A

+ 1 1 0 0 0 1

x

2

=1

+A

+ 0 0 1 0 1 0 0

+1

1 0 0 0 1 0

0 0 1 1 1 1 0

1 0 0 0 1 1

ShR 0 0 0 1 1 1 1 0

ShR 1 1 0 0 0 1 1

x

3

=1

−

A

+ 1 1 0 1 0 1 1 1

x

2

=0

ShR 1 1 1 0 0 0 1 1

X

⋅

A

=−10

1 1 1 0 1 0 1

x

3

=

1

−

A

+ 0 0 1 1 1 0 0 0

+1

0 0 0 1 1 0 1 1

+ 1

X

⋅

A

=28

0 0 0 1 1 1 0 0

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–15

Uproszczenie mno enia w dwójkowym systemie uzupełnieniowym

Je li do liczby danej w dwójkowym systemie uzupełnieniowym o k pozycjach
cz ci całkowitej dodamy 2

k–1

to otrzymamy liczb dodatni

∑

∑

−

−

=

−

−

−

−

−

=

−

−

+

−

=

+

+

−

2

1

1

1

2

1

1

2

2

)

1

(

2

2

2

k

m

i

i

i

k

k

k

k

m

i

i

i

k

k

x

x

x

x

Je li zatem do ka dego iloczynu cz ciowego x

i

A dodamy i odejmiemy 2

k–1

(waga najwy szego bita mno nej), to iloczyn b dzie sum dodatnich
skalowanych iloczynów cz ciowych z dopełnieniem najwy szej cyfry

pomniejszon o sum kolejnych pot g dwójki

poczynaj c od pot gi odpowiadaj cej najwy szej cyfrze mno nej.

UWAGA:
Uproszczenie jest istotne w rozwi zaniach układowych, ale tak e

umo liwia uproszczenie realizacji programowej.

Intuicja (inne systemy)

Je li do liczby w systemie uzupełnieniowym o k pozycjach cz ci całkowitej
dodamy

1

2

1

−

k

β

, to otrzymamy liczb dodatni , ale … algorytm si komplikuje

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–16

Akumulacja iloczynów cz ciowych w kodzie U2

W systemie U2 mamy

+

−

−

=

−

−

−

−

=

−

−

+

−

=

+

−

+

−

=

+

−

=

∑

∑

Z

z

z

z

z

Z

k

k

i

i

i

k

k

k

k

i

i

i

k

k

1

2

0

1

1

1

2

0

1

1

2

2

2

)

1

(

2

2

2

Iloczyny cz ciowe (x

i

A, –x

m–1

A) maj te przypisane wagi, wi c:

∑

∑

−

=

−

+

−

+

−

−

−

=

−

−

−

+

−

−

=

+

−

=

1

0

1

1

1

1

1

0

1

1

)

2

(

2

)

2

)

(

(

2

2

2

m

i

k

i

i

k

m

m

m

i

i

i

m

m

A

x

A

x

A

x

A

x

AX

.

a zatem:

1

1

1

0

1

1

2

2

]

)

(

2

)

)

(

(

2

[

−

−

+

−

=

+

+

−

−

+

−

+

−

=

∑

k

k

m

m

i

i

i

m

m

A

x

A

x

AX

→

algorytm

•

zast pi bit znaku iloczynu cz ciowego (mno nej, jej uzupełnienia lub 0)

jego dopełnieniem (0

→

10...00)

•

doda stał korekcyjn

1

1

2

2

−

+

−

−

k

m

k

(„1” na pozycji najwy szego bitu

mno nej i pozycjach wy szych od najwy szego bitu ostatniego iloczynu)

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–17

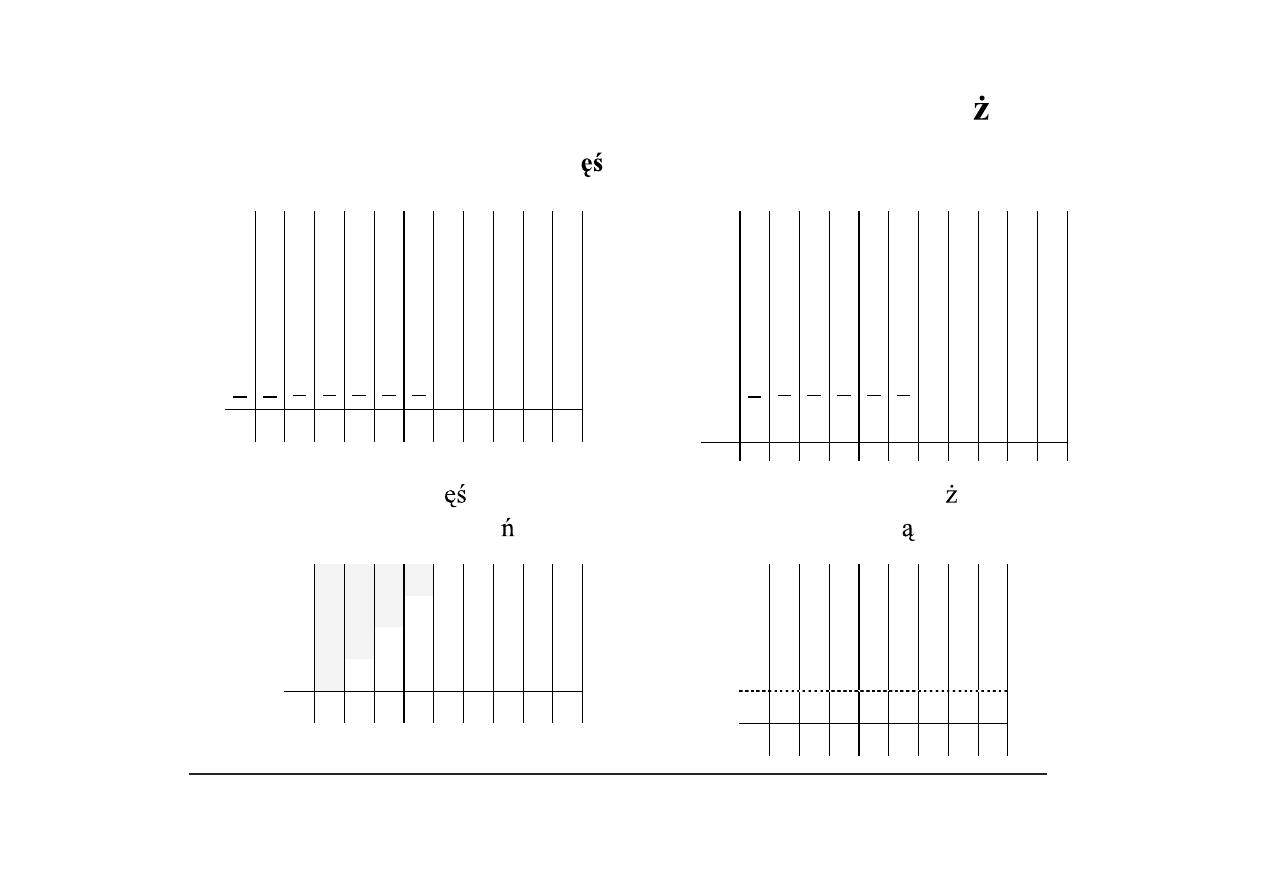
Schemat dodawania iloczynów cz ciowych w kodzie U2

a) A 9 8 7 6 5 4 3 2 1 0

b)

A 9 8 7 6 5 4 3 2 1 0

∗∗∗∗

∗∗∗∗

∗∗∗∗

∗∗∗∗

∗∗∗∗

∗∗∗∗

∗∗∗∗

o o o o o

•

o o o o o

∗∗∗∗

∗∗∗∗

∗∗∗∗

∗∗∗∗

∗∗∗∗

∗∗∗∗

o o o o o

•

o o o o o

∗∗∗∗

∗∗∗∗

∗∗∗∗

∗∗∗∗

∗∗∗∗

o o o o o

•

o o o o o

∗∗∗∗

∗∗∗∗

∗∗∗∗

∗∗∗∗

o o o o o

•

o o o o o

∗∗∗∗

∗∗∗∗

∗∗∗∗

o o o o o

•

o o o o o

∗∗∗∗

∗∗∗∗

o o o o o

•

o o o o o

+ (1) 0 0 0 0 0 1

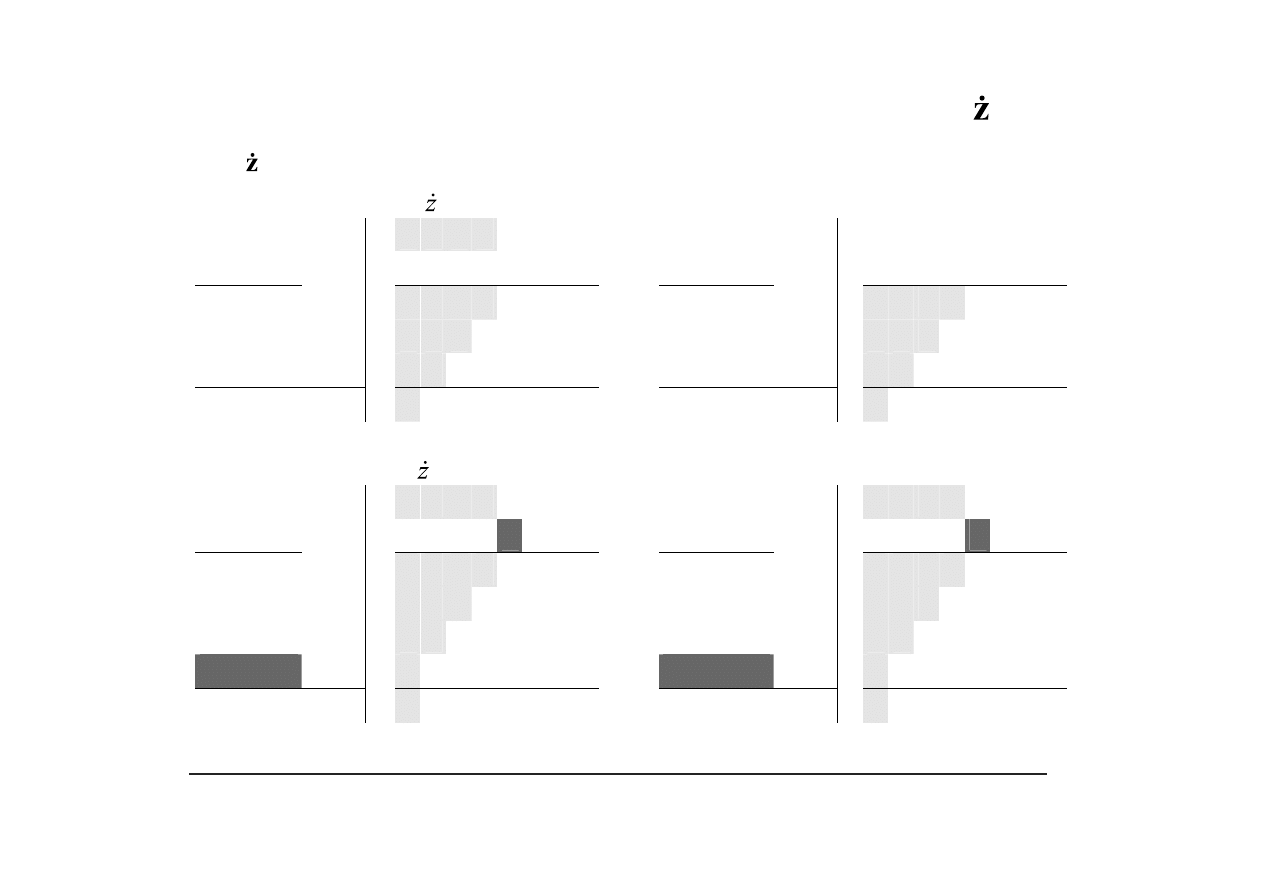
Matryca iloczynów cz ciowych: a) z rozszerzeniem (

∗∗∗∗

– bit najwy szy i jego

kopia), b) bez rozszerze (

•

– dopełnienie najbardziej znacz cego bitu)

1 1 1 1 1 0 1 1 0 1

0 0 1 1 0 1

0 0 0 0 0 0 0 0 0

1 0 0 0 0 0

1 1 1 0 1 1 0 1

0 0 1 1 0 1

1 0 1 0 0 1 1

1 1 0 0 1 1

0 0 0 1 1 1 0 0 1 (1) 0 0 0 1
(0) 0 0 0 1 1 1 0 0 1

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–18

Nadmiar w mno eniu w systemie naturalnym i uzupełnieniowym

Wynik mno enia k-pozycyjnej mno nej przez p-pozycyjny mno nik

mo na zawsze zapisa na k+p pozycjach iloczynu.

2

2

1

1

1

1

2

2

2

2

,

2

2

−

+

−

+

−

−

−

−

≤

<

−

⇒

<

≤

−

<

≤

−

p

k

p

k

p

p

k

k

AX

X

A

(A oraz X s argumentami przeskalowanymi do warto ci całkowitych)

W układach cyfrowych wymaga si cz sto,

aby operandy (argumenty i wynik działania) były takiego samego rozmiaru.

Przekroczenie zakresu odpowiadaj cego rozmiarowi operandu jest zwykle

sygnalizowane jako nadmiar.

Wyró nia si ponadto:
mno enie dolne – wynikiem jest ni sza cz

(połowa bitów) iloczynu

sygnalizacja nadmiaru je li wy sze bity nie s rozszerzeniem

mno enie górne – wynikiem jest wy sza cz

(połowa bitów) iloczynu,

odpowiada mno eniu ułamków z obci ciem ni szych bitów,
nadmiar nie mo e wyst pi

mno enie z normalizacj – ustalona liczba bitów cz ci całkowitej

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–19

Algorytm mno enia równoległego

mno na

|

}

,

,...,

{

|

1

1

β

p

p

s

a

a

a

A

−

+

−

−

=

, mno nik

|

}

,

,...,

{

|

1

1

β

m

m

k

x

x

x

X

−

+

−

−

=

system naturalny

∑

∑

∑

∑

=

+

−

+

−

−

=

−

−

=

−

−

=

=

























=

⋅

r

j

i

i

j

k

s

p

m

r

r

k

m

i

i

i

s

p

j

j

j

x

a

x

a

X

A

2

1

1

β

β

β

algorytm

→

obliczenie wszystkich iloczynów elementarnych

i

j

x

a

→

akumulacja czynników o tej samej wadze

∑

=

+

r

j

i

i

j

x

a

problem

– szybkie dodawanie wieloargumentowe

system uzupełnieniowy do 2 – niektóre iloczyny elementarne maj ujemne wagi

∑

∑

∑

∑

=

+

−

+

−

−

=

−

−

=

−

−

−

−

=

−

−

−

=













+

−













+

−

=

⋅

r

j

i

p

i

j

k

s

p

m

r

r

k

m

i

i

i

k

k

s

p

j

j

j

s

s

x

a

x

x

a

a

X

A

)

1

(

2

2

2

2

2

2

2

1

1

2

1

1

p = 0 gdy j

≠

s–1 oraz i

≠

k–1 lub i+j = s+k–2, w przeciwnym razie p = 1

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–20

Algorytm mno enia liczb dwójkowych w kodzie NB

Krok 0. A

←

A, X/P

←

X, C||S/P

←

0. Podstaw i = 1.

Krok 1. C||S/P

←

(S/P) + x

i

(A)

Krok 2. C||S/P||X/P

←

2

–1

(C||S/P||X/P) = ShR(C||S/P||X/P)

Krok 3. i = i +1. Je li i < k+m, wró do kroku 1.

Wynik: A

⋅

X = (S/P||X/P)

Σ

ShR

C

S/P

X/P

A

S

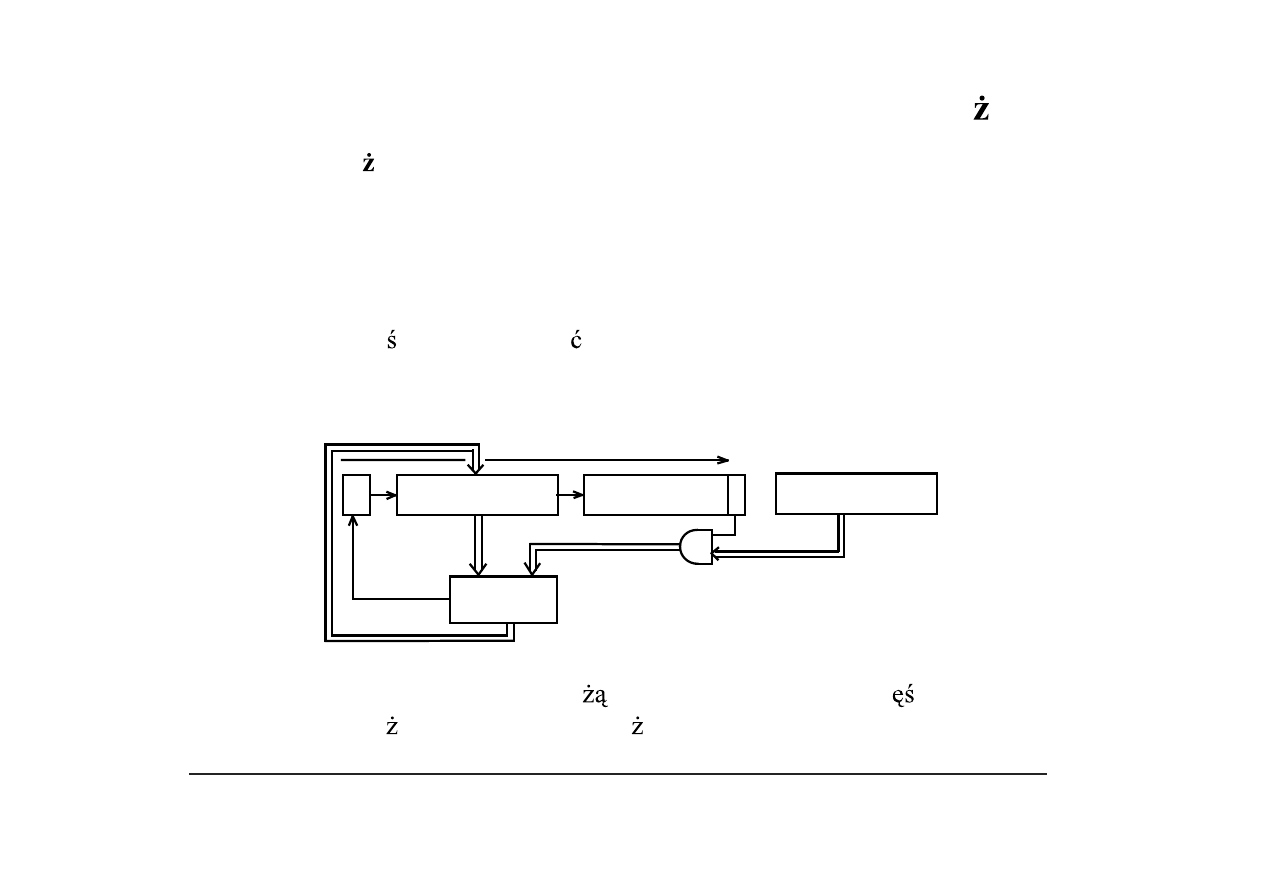
Schemat blokowy układu mno

cego: S/P – rejestr sum cz ciowych,

X/P – rejestr mno nika, A – rejestr mno nej, C – rejestr przeniesienia

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–21

Redukcja liczby iloczynów cz ciowych – przekodowanie kanoniczne

Minimaln dla danego mno nika liczb dodawa lub odejmowa okre la waga

|)

|

...

|

|

|

|

(

0

2

1

y

y

y

n

n

+

+

+

−

−

jego minimalnej reprezentacji w kodzie SD.

}

,

,...,

{

0

1

1

x

x

x

n

−

=

X

U2

→

}

,

,...,

{

0

1

1

min

y

y

y

n

−

=

Y

SD

– przekodowanie kanoniczne

Przekodowanie kanoniczne –algorytm sekwencyjny (p

0

=0)

x

i–1

x

i

p

i

p

i+1

y

i

Komentarz

0

0

0

0

0

ci g zer

0

1

0

0

1

izolowana jedynka

1

0

0

0

0

ci g zer

1

1

0

1

1

pocz tek ci gu jedynek

0

0

1

0

1

koniec ci gu jedynek

0

1

1

1

0

ci g jedynek

1

0

1

1

1

izolowane zero

1

1

1

1

0

ci g jedynek

Skomplikowana i czasochłonna procedura przekodowania

→

rzadko stosowane

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–

22

Przekodowanie Bootha

•

zast pienie serii dodawa jednym odejmowaniem i jednym dodawaniem

l

s

l

l

s

s

2

2

2

2

...

2

2

1

2

1

−

=

+

+

+

+

+

−

−

|{...0[11...11]0... }

U2

| = |{...1[00...00]0... }

U2

| – |{...0[00...01]0...}

U2

,

|{...0[11...11]0... }

SD

| = |{

...

0

]

1

0

...

00

[

1

...

}

SD

|

→

reguła Bootha

≡

przekodowanie mno nika na kod SD

•

reprezentacja w systemie NB lub U2 jest reprezentacj w systemie SD, ale

przekodowanie

według reguły Bootha:

•

U2

→

SD – wykonalne, bo [x1...11]0... = [(1

−

x

)0...00]0...

−

[00...01]0...

•

NB

→

SD – niewykonalne bez rozszerzenia gdy {1,1,… ,1,0, x ,…}, bo

x

≥

0

∧

z

≠

1 ⇒ |{1, x,..., x, x}

SD

| > |{z, y, y,..., y}

SD

|

⇒ konieczne rozszerzenie {1,…,1,0, x ,…}

NB

= {0,1, … ,1,0, x ,…}

U2

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–

23

Algorytm Bootha

Uzasadnienie teoretyczne – równowa no X = 2X

−

X

1

1

0

1

2

0

1

1

1

2

0

1

2

)

(

2

2

2

2

−

−

=

−

−

=

−

−

+

−

=

−

−

−

=









+

−

−









+

−

=

∑

∑

∑

x

x

x

x

x

x

x

X

i

n

i

i

i

i

n

i

i

n

n

i

n

i

i

n

n

}

1

,

0

{

∈

i

x

⇒

}

1

,

0

,

1

{

1

−

∈

−

=

−

i

i

i

x

x

y

(x

–1

= 0)

|{x

n–1

, x

n–2

, x

n–1

, …, x

1

, x

0

}

U2

| = |{(x

n–2

– x

n–1

), (x

n–3

– x

n–2

), …, (x

0

– x

1

), (x

– 1

– x

0

)}

SD

|

Przekodowanie Bootha (

i

i

i

x

x

y

−

=

−

1

)

x

i

x

i–1

y

i

operacja komentarz

0

0

0

—

ci g zer

0

1

1

+

A

koniec ci gu jedynek

1

0

1

−

A

pocz tek ci gu jedynek

1

1

0

—

ci g jedynek

Wady

:

– zmienna liczba działa arytmetycznych, zale na od kodu liczby,
– nieefektywne kodowanie izolowanych jedynek –...010101(0)

→

1

1

1

1

1

1

...

.

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–

24

Alternatywne przekodowanie Bootha

0

2

0

1

1

1

0

1

2

)

(

2

2

)

(

x

x

x

x

x

x

X

i

n

i

i

i

i

n

i

i

i

−

−

=

−

−

=

∑

∑

−

=

+

−

−

=

−

.

⇒ alternatywne przekodowanie mno nika

}

,

,...,

{

0

1

1

y

y

y

n

−

=

Y

1

0

,

1

−

≤

≤

−

=

+

n

i

x

x

y

i

i

i

,

Poniewa

0

2

x

Y

X

−

=

, wi c

•

warto ci pocz tkow akumulowanej sumy iloczynów jest

A

x

0

−

,

•

zamiast mno nej A nale y w algorytmie u y jej podwojenia 2A,

•

y

i

(przekodowanie alternatywne) = y

i+1

(przekodowanie proste)

Przekodowanie alternatywne NB/U2

→

SD zawsze wykonalne:

•

U2

→

SD – rozszerzenie

1

−

=

n

n

x

x

, ⇒

0

1

=

−

n

y

•

NB

→

SD – rozszerzenie

0

=

n

x

⇒

1

1

−

−

=

n

n

x

y

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–25

Przekodowanie rozszerzone (w bazie 2

2

) – algorytm Bootha-McSorleya

1

2

1

0

1

2

2

1

2

1

2

1

0

1

2

2

2

1

2

1

1

2

1

0

1

2

2

2

1

0

2

1

2

1

1

2

0

1

2

)

2

(

2

)

2

2

(

2

)

(

2

)

(

2

)

(

−

−

=

−

+

−

−

=

+

−

−

+

−

=

+

−

=

−

−

−

=

−

−

+

+

−

=

−

−

+

−

=

=

−

−

+

−

=

−

−

=

∑

∑

∑

∑

∑

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

X

i

k

i

i

i

i

i

k

i

i

i

i

i

i

k

i

i

i

i

k

i

i

i

j

k

j

j

j

Poniewa je li

}

1

,

0

{

∈

i

x

to

}

2

,

1

,

0

,

1

,

2

{

2

1

2

2

1

2

+

+

−

−

∈

+

+

−

−

+

i

i

i

x

x

x

(x

−

1

=0), wi c

istnieje jednoznaczne przekształcenie

X

U2

→

Y

SD

:

}

0

1

,

1

0

,

0

0

,

1

0

,

0

1

{

}

,

{

}

,

,

{

}

1

,

0

{

2

1

2

1

2

2

1

2

3

∈

→

∋

+

−

+

i

i

i

i

i

y

y

x

x

x

Wynik przekształce :

SD

0

1

1

}

,

,...,

{

y

y

y

n

−

=

Y

})

1

,

0

,

1

{

(

#

∈

y

takie, e

i

i

i

i

i

y

y

x

x

x

2

1

2

1

2

2

1

2

2

2

+

=

+

+

−

+

−

+

,

0

2

1

2

=

+

i

i

y

y

•

połowa cyfr

Y to zera

•

mo liwe zmniejszenie liczby zer mno nika (00101010

→

0

1

1

0

1

010

).

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–

26

Algorytm Bootha-McSorleya – praktyczna realizacja

Analizowane s pary bitów ⇒ rozszerzenie mno nika do parzystej liczby bitów

•

ka da z kolejnych par bitów mno nika zawiera co najmniej jedno 0

⇒ liczba iloczynów cz ciowych

≤

n

2

1

•

dla pary

i

i

x

x

2

1

2

,

+

iloczynem jest

A

x

x

x

i

i

i

)

2

(

1

2

1

2

2

+

−

−

+

o wadze 2

2i

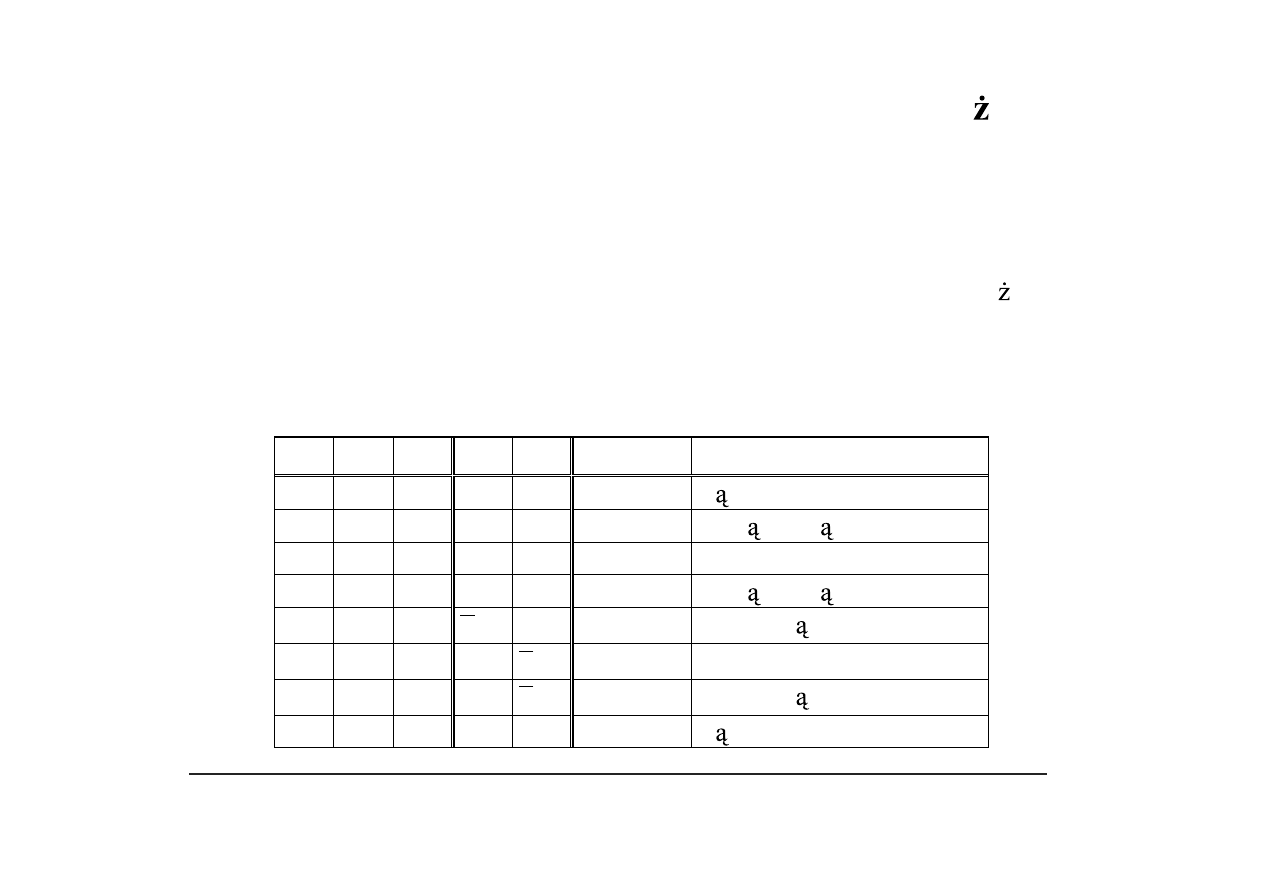
Przekodowanie rozszerzone (Bootha-McSorleya)

x

2i+1

x

2i

x

2i–1

y

2i+1

y

2i

działanie komentarz

0

0

0

0

0

—

ci g zer

0

1

0

0

1

+A

izolowana jedynka

1

0

0

1

0

−

2A

pocz tek ci gu jedynek

1

1

0

0

1

−

A

pocz tek ci gu jedynek

0

0

1

0

1

+A

koniec ci gu jedynek

0

1

1

1

0

+2A

koniec ci gu jedynek

1

0

1

0

1

−

A

izolowane zero

1

1

1

0

0

—

ci g jedynek

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–

27

Alternatywne przekodowanie Bootha-McSorleya

0

2

2

1

2

2

2

1

0

0

2

2

0

1

2

)

2

(

2

2

)

(

2

x

x

x

x

x

x

x

X

i

i

i

i

k

i

j

k

j

j

j

−

+

+

−

=

−

−

=

+

+

−

=

−

=

+

∑

∑

.

}

2

,

1

,

0

,

1

,

2

{

)

2

(

2

1

2

2

2

−

−

∈

+

+

−

+

+

i

i

i

x

x

x

→

wynik przekodowania: Y

SD

taka, e

i

i

i

i

i

y

y

x

x

x

2

1

2

2

1

2

2

2

2

2

+

=

+

+

−

+

+

+

oraz

0

2

1

2

=

+

i

i

y

y

Alternatywne przekodowanie Bootha-McSorleya

x

2i+2

x

2i+1

x

2i

y

2i+1

y

2i

działanie komentarz

0

0

0

0

0

—

ci g zer

0

0

1

0

1

+2A

pocz tek ci gu jedynek

0

1

0

0

1

+2A

izolowana jedynka

0

1

1

1

0

+4A

pocz tek ci gu jedynek

1

0

0

1

0

−

4A

koniec ci gu jedynek

1

0

1

0

1

−

2A

izolowane zero

1

1

0

0

1

−

2A

koniec ci gu jedynek

1

1

1

0

0

—

ci g jedynek

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–

28

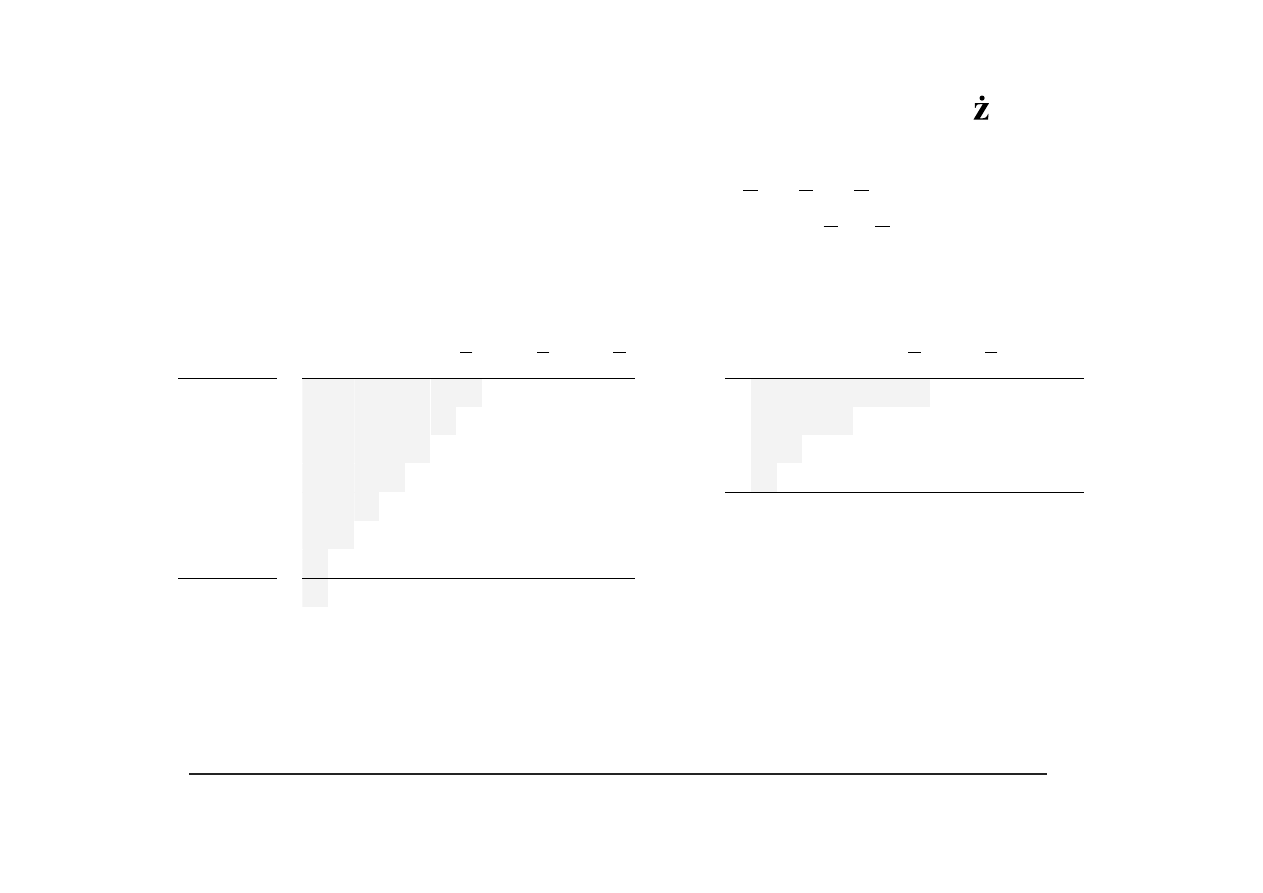
Algorytm Bootha/Bootha-McSorleya – przykłady

X

= {(1),1,0,1,1,0,0,1}

U2

– w bazie 2 –

}

1

,

1

,

0

,

1

,

0

,

1

,

1

{

=

Y

,

– alternatywne w bazie 4 –

}

01

,

0

1

,

10

,

1

0

{

=

Y

A

=−19

1 0 1 1 0 1

1 0 1 1 0 1

X

=−39

1 1 0 1 0 1 1

0 1 1 0 1 0 0 1

–A 0 0 0 0 0 0 0 0 1 0 0 1 1

A 1 1 1 1 1 1 1 1 0 1 1 0 1

+A 1 1 1 1 1 1 1 0 1 1 0 1

–2A 0 0 0 0 0 1 0 0 1 1

0 0 0 0 0 0 0 0 0 0 0 0

2A 1 1 1 0 1 1 0 1

–A 0 0 0 0 0 1 0 0 1 1

–A 0 0 1 0 0 1 1

0 0 0 0 0 0 0 0 0 0

0 0 0 1 0 1 1 1 0 0 1 0 1

+A 1 1 1 0 1 1 0 1

–A 0 0 1 0 0 1 1

XA

=741

0 0 0 1 0 1 1 1 0 0 1 0 1

Uwaga

: W polach zacienionych wpisano cyfry rozszerzenia znakowego.

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–

29

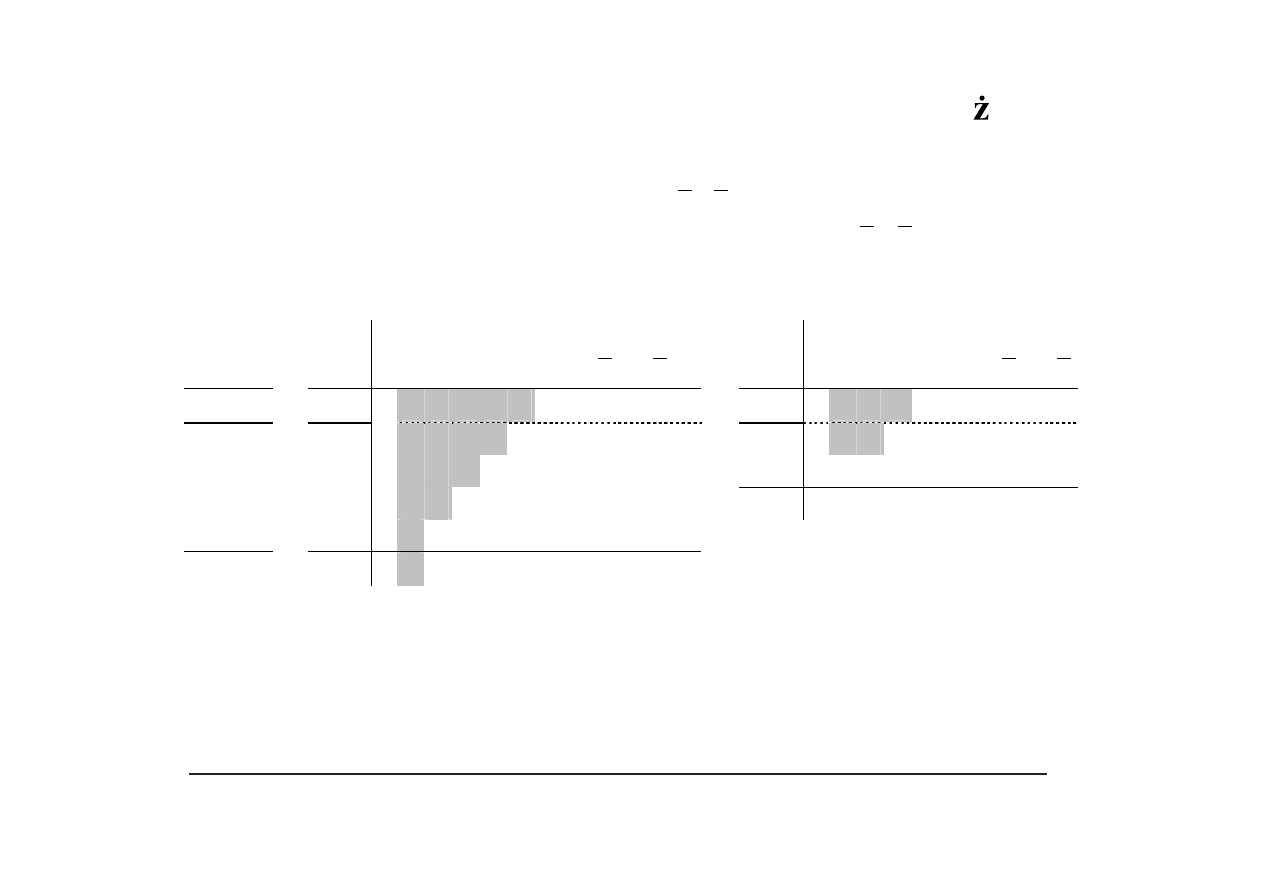
Alternatywny algorytm Bootha/Bootha-McSorleya – przykłady

X

= {1,1,0,1,0,1}

U2

– w bazie 2 –

}

1

,

1

,

1

,

1

,

0

{

=

Y

,

– alternatywne w bazie 4 –

}

1

0

,

1

0

,

00

{

=

Y

, P

0

=–x

0

A

Y

(2R)

Y

(4R)

A

=−3

1 1 1 1 0 1

1 1 1 1 0 1

X

=−11

0

1

1

1

1

0 0 0

1

0

1

P

0

=

–x

0

A

0 0 0 0 0 0 0 0 0 1 1

–x

0

A

0 0 0 0 0 0 0 1 1

+2A 1 1 1 1 1 1 1 1 0 1

–2A 0 0 0 0 0 0 1 1

–2A 0 0 0 0 0 0 0 1 1

–2A 0 0 0 0 1 1

+2A 1 1 1 1 1 1 0 1

0 0 0 1 0 0 0 0 1

–2A 0 0 0 0 0 1 1

XA

=

33

0 0 0 0 0 1 0 0 0 0 1

Uwaga

: W polach zacienionych wpisano cyfry rozszerzenia znakowego.

Mno enie

© Janusz Biernat, 03-06-Mnozenie.doc, 4 pa

ź

dziernika 2006

MUL–

30

Przekodowanie mno nika w systemie uzupełnie do 1

W systemie U1, na podstawie równowa no ci X = 2X

−

X

mamy









+

−

−

−









+

−

−

=

∑

∑

−

=

−

−

+

−

=

−

i

n

i

i

n

n

i

n

i

i

n

n

x

ulp

x

x

ulp

x

X

2

)

2

(

2

)

2

2

(

2

0

1

1

1

2

0

1

,

sk d wynika

ulp

x

x

x

x

X

n

i

n

i

i

i

1

1

1

0

1

2

)

(

−

−

−

=

−

+

−

−

=

∑

.

Poniewa ulp = 1, a rozszerzeniem liczby w kodzie U1 jest

1

1

−

−

=

n

x

x

, zatem

i

n

i

i

i

x

x

X

2

)

(

1

0

1

∑

−

=

−

−

=

.

Podobnie

)

(

2

)

(

2

0

1

2

0

1

x

x

x

x

X

n

i

n

i

i

i

−

+

−

=

−

−

=

+

∑

.

•

algorytm analogiczny jak w U2, lecz inna warto pocz tkowa akumulacji

•

sumowanie z uwzgl dnieniem rozszerze prawo- i lewostronnych