Bazy danych – wykład dwunasty

Wykonywanie i optymalizacja zapyta ´n SQL

Konrad Zdanowski

Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

1 / 36

Model kosztów

Paremtry okre´slaj ˛

ace rozmiar relacji R:

B(R) – liczba bloków jakie zajmuje R (b ˛edziemy zakłada´c, ˙ze
relacja jest sklastrowana),

T (R) – liczba krotek w relacji R,

V (R, A) – liczba

róznych warto´sci atrybutu A w R,

V (R[a

1

, . . . ,

a

k

])

– liczba

róznych krotek o warto´sci atrybutów

a

1

, . . . ,

a

k

w R

Szacuj ˛

ac koszty wykonania zapytania minimalizujemy liczb ˛e operacji

I/O.

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

2 / 36

Model kosztów

Dla sklastrowanej relacji R koszt wczytania relacji to B(R).

Koszt sortowania relacji R, je´sli ta mie´sci si ˛e w cało´sci w pami ˛eci
operacyjnej, to równie˙z B(R).

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

3 / 36

Podstawowe operacje na relacjach – przypomnienie

Niech R(A

1

, . . . ,

A

k

),

S(B

1

, . . . ,

B

n

)

dane relacje.

Rzutowanie

π

A

1

,...,

A

m

(

R) = {(a

1

, . . . ,

a

m

)

:

istniej ˛

a a

m+1

, . . . ,

a

k

, takie, ˙ze (a

1

, . . . ,

a

m

,

a

m+1

, . . . ,

a

k

) ∈

R}.

Oczywi´scie, mo˙zemy wybra´c w rzutowaniu dowolne atrybuty.

Dla warunku C na krotki relacji R,

σ

C

(

R) = {(a

1

, . . . ,

a

k

) :

C(a

1

, . . . ,

a

k

)}.

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

4 / 36

Podstawowe operacje na relacjach – przypomnienie

Niech R(A, B, C, D), S(C, D, E ) dane relacje.

Zł ˛

aczenie

R o

n S = {(a, b, c, d , e) : (a, b, c, d ) ∈ R ∧ (c, d , e) ∈ S}.

Zł ˛

aczenie warunkowe dla warunku Θ,

R o

n

Θ

S = {(a, b, c, d , e) : (a, b, c, d ) ∈ R ∧ (c, d , e) ∈ S∧

Θ(

a, b, c, d , e)}.

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

5 / 36

Koszt pewnych operacji jednoargumentowych

Uwaga. Zajmiemy si ˛e kosztem operacji jednoprzebiegowych. Tzn.
tylko raz wczytujemy dan ˛

a krotk˛e i cały wynik albo zmie´sci si ˛e w

pami ˛eci operacyjnej albo mo˙zemy go generowa´c “online”.

Algorytm naiwny – dla ka˙zdej nowej krotki sprawdzamy, czy ju˙z
nie wyst ˛

apiła – ma koszt n

2

(dla n – krotek wyniku – to problem

cho´c oczywi´scie nie zmieniamy ilo´sci operacji I/O).

Tablice z haszowaniem optymalizuj ˛

a ten koszt wymagaj ˛

ac

dodatkowej pami ˛eci.

Operacje agreguj ˛

ace – mo˙zemy oblicza´c podczas tworzenia

kolejnych krotek wynikowej relacji.

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

6 / 36

Koszt operacji dwuargumentowych

Rozwa˙zmy operacje sumy, iloczyny, ró˙znicy dla wielozbiorów i zbiorów
(bez powtórze ´n).

Niech M liczba wolnych buforów w pami ˛eci operacyjnej.

Suma wielozbiorów dla relacji R i S to B(R) + B(S).

Dla róznicy i iloczynu musimy wczyta´c mniejsz ˛

a relacj ˛e do

pami ˛eci operacyjnej, czyli musi by´c spełniony warunek
min(B(R), B(S)) ¬ M(−1).

Dla operacji na zbiorach (bez powtórze ´n) musimy wczyta´c
mniejsz ˛

a relacj ˛e i zarezerwowa´c dodatkow ˛

a pami ˛e´c na struktury

pomocnicze (jak tablice haszuj ˛

ace). W przybli˙zeniu mamy wi ˛ec

wymóg min(B(R), B(S)) ¬ M.

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

7 / 36

Koszt zł ˛

aczenia

Rozpatrzmy zł ˛

aczenie R(A, B) o

n S(B, C).

Naiwny algorytm wymaga B(R)B(S) operacji wczytania.

Je´sli mamy M buforów, mo˙zemy wczytywa´c po M − 1 bloków
relacji R i nast ˛epnie wczytywa´c po jednym bloku z S aby stworzy´c
zł ˛

aczenie.

Koszt wyniesie około B(R)B(S)/M.

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

8 / 36

Koszt operacji dwuargumentowych

Zauwa˙zmy, ˙ze koszt tych operacji mo˙zemy istotnie zmniejszy´c
przy zastosowaniu dodatkowyc struktur danych (np. tablic
haszuj ˛

acych, indeksów).

Np. je´sli na B jest nało˙zony indeks w R lub S, mo˙zemy efektywnie
znajdowa´c krotki, które wejd ˛

a do zł ˛

aczenia. Koszt zł ˛

aczenia

b ˛edzie wtedy optymalny.

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

9 / 36

Przetwa˙zanie zapytania SQL

Elementy procesu wykonywania zapytania:

kompilacja zapytania (przedstawienie zapytania w “optymalnej”
postaci logicznej,

wykonywanie zapytania.

Aby wykonanie przebiegło efektywnie potrzebujemy zdefiniowa´c
cz ˛esto dodatkowe struktury danych (np. indeksy).

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

10 / 36

Kompilowanie zapytania SQL

Elementy procesu kompilowania zapytania:

zapisanie zapytania w postaci wyra˙zenia algebry relacji (drzewo
zapytania),

wybranie optymalnej, z równowa˙znych, postaci zapytania,

wybranie algorytmów przetwa˙zania bazy danych.

Aby wykonanie przebiegło efektywnie potrzebujemy zdefiniowa´c
cz ˛esto dodatkowe struktury danych (np. indeksy).

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

11 / 36

Drzewo zapytania – przykład

select tytul from Ksiazki where rok == 2011;

π

tytul

σ

rok=2011

Ksiazki

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

12 / 36

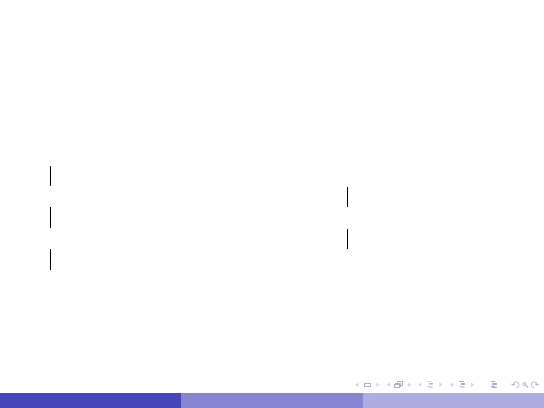
Drzewo zapytania – przykład

select tytul from Ksiazki where rok = 2011 and wydawca = ’Znak’;
Które z drzew da efektywniejsze wykonanie?

π

tytul

σ

rok=2011

σ

rok=’Znak’

Ksiazki

π

tytul

σ

rok=2011∧rok=’Znak’

Ksiazki

Oba plany s ˛

a równowa˙zne, bo σ

C∧D

(

R) = σ

C

(σ

D

(

R)).

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

13 / 36

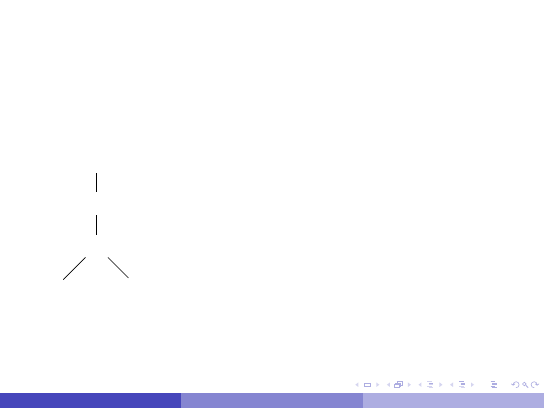
Drzewo zapytania – przykład

select nazwisko, tytul from Ksiazki, Autorzy where Ksiazki.autor_id =
Autorzy.id;

π

nazwisko, tytul

σ

Ksiazki.autor_id=Autorzy.id

×

Ksiazki

Autorzy

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

14 / 36

Drzewo zapytania – przykład

select nazwisko, tytul from Ksiazki, Autorzy where Ksiazki.autor_id =
Autorzy.id and rok=2011;

Które plan jest lepszy? Ci zmienia (prawdopodobna) obecno´s´c
indeksu na atrybucie, po którym zł ˛

aczamy?

π

nazwisko, tytul

σ

Ksiazki.autor_id=Autorzy.id∧rok=2011

×

Ksiazki

Autorzy

π

nazwisko, tytul

σ

Ksiazki.autor_id=Autorzy.id

×

σ

rok=2011

Ksiazki

Autorzy

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

15 / 36

Optymalizacja zapytania

Stworzenie reprezentacji algebraicznej.

Eliminacja (je´sli mo˙zliwa) podzapyta ´n.

Transformacje algebraiczne w algebrze relacji.

Zdefiniowanie porz ˛

adku wykonywania zł ˛

acze ´n i innych operacji.

Po tych krokach nast ˛epuj ˛e wybór konkretnych algorytmów
operuj ˛

acych na bazie danych.

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

16 / 36

Analiza semantyczna zapytania

Po stworzeniu reprezentacji algebraicznej mo˙zemy upro´sci´c
zapytanie korzystaj ˛

ac z praw logicznych oraz arytmetycznych.

W szczególno´sci mo˙zemy wyeliminowac warunki (i zapytania)
sprzeczne.

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

17 / 36

Transformacja zapytania

Korzystaj ˛

ac z praw algebry relacji mo˙zemy upro´sci´c i

zoptymalizowa´c dane zapytanie

Oprócz metod “aksjomatycznych” stosowa´c mo˙zna te˙z analizy
statystyczne, szacowanie kosztów w oparciu o statystyki działania
bazy danych (pracochłonne i kosztowne).

Operacje unarne (filtruj ˛

ace) przesuwamy w dół drzewa zapytania.

Operacje binarne przesuwamy w góre.

Zł ˛

aczenia najlepiej definiowa´c na atrybutach, na których mamy

zdefiniowany indeks.

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

18 / 36

Przykładowe prawa algebry relacji

R o

n (S o

n T ) = (R o

n S) o

n T ,

R o

n (S ∪ T ) = (R o

n S) ∪ (R o

n T ),

σ

C∧D

(

R) = σ

C

(σ

D

(

R)) = σ

C

(

R) ∩ σ

D

(

R),

σ

C∨D

(

R) = σ

C

(

R) ∪ σ

D

(

R),

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

19 / 36

Przykładowe prawa algebry relacji

σ

C

(

R − S) = σ

C

(

R) − S,

je´sli C zawiera tylko predykaty z R to

σ

C

(

R o

n S) = σ

C

(

R) o

n S,

je´sli M = N ∪ Q, gdzie N to atrybuty z R a Q to atrybuty z S (i N i
Q zawieraj ˛

a atrybuty, po których obliczamy zł ˛

aczenie), to

π

M

(

R o

n S) = π

N

(

R) o

n π

Q

(

S),

je´sli M nie zawiera atrybutów Z , po których obliczamy zł ˛

aczenie,

to

π

M

(

R o

n S) = π

N∪Z

(

R) o

n π

Q∪Z

(

S).

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

20 / 36

Przykłady

Niech dane R(A, B) i S(B, C).

Czy lepsze jest σ

A=a

(

R o

n S) czy σ

A=a

(

R) o

n S?

Czy lepsze jest σ

A=a∧C=c

(

R o

n S) czy σ

A=a

(

R) o

n σ

C=c

(

S)?

Czy σ

A=a∨C=c

(

R o

n S), czy σ

A=a

(

R o

n S) ∪ σ

C=c

(

R o

n S), czy

(σ

A=a

(

R) o

n S) ∪ (R o

n σ

C=c

(

S)?

Czy co´s mog ˛

a zmieni´c indeksy na atrybutacie C?

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

21 / 36

Optymalizacja podzapyta ´n

Podzapytanie wymaga obliczenia dla ka˙zdej krotki, która mo˙ze
nale˙ze´c do wyniku.

Trudno optymalizowa´c razem zapytanie i podzapytanie.
Optymalizuj ˛

ac je oddzielnie mo˙zemy pomin ˛

a´c pewne mo˙zliwo´sci

uproszczenia.

Zmniejszenie kosztów mo˙zna (czasem) osi ˛

agn ˛

a´c przez

eleminacje podzapytania.

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

22 / 36

Przykład - optymalizacja podzapyta ´n

Jak zooptymalizowa´c to zapytanie?

s e l e c t a . nazwisko , a . mi as t o

from A u t o r z y a
where a . r o k _ u r o d z e n i a >1980 and

a . i d

i n ( s e l e c t k . a u t o r _ i d

from K s i a z k i k
where k . rok_wydania < 2000 ) ;

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

23 / 36

Przykład - optymalizacja podzapyta ´n

s e l e c t a . nazwisko , a . mi as t o

from A u t o r z y a , K s i a z k i k
where a . r o k _ u r o d z e n i a >1980

and

k . rok_wydania < 2000

and a . i d = k . a u t o r _ i d ;

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

24 / 36

Przykład - optymalizacja podzapyta ´n

s e l e c t a . nazwisko , a . mi as t o

from A u t o r z y a
where a . p l e c = ’ F ’

and

k . r o k _ u r o d z e n i a <=

ALL ( s e l e c t b . r o k _ u r o d z e n i a

from A u t o r z y b
where b . p l e c = ’ F ’

and a . m i a s t o _ u r o d z e n i a =

b . m i a s t o _ u r o d z e n i a ) ;

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

25 / 36

Przykład - optymalizacja podzapyta ´n

Obliczmy zbiór “nie najmłodszych” autorek:

s e l e c t a . nazwisko , a . mi as t o

from A u t o r z y a
where a . p l e c = ’ F ’

and

k . r o k _ u r o d z e n i a >

SOME ( s e l e c t b . r o k _ u r o d z e n i a

from A u t o r z y b
where b . p l e c = ’ F ’

and a . m i a s t o _ u r o d z e n i a =

b . m i a s t o _ u r o d z e n i a ) ;

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

26 / 36

Przykład - optymalizacja podzapyta ´n

Zoptymalizujmy ostatnie zapytanie:

s e l e c t a . nazwisko , a . mi as t o

from A u t o r z y a , A u t o r z y b
where a . p l e c = ’ F ’

and b . p l e c = ’ F ’

and a . m i a s t o _ u r o d z e n i a = b . m i a s t o _ u r o d z e n i a
and a . r o k _ u r o d z e n i a > b . r o k _ u r o d z e n i a ;

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

27 / 36

Przykład - optymalizacja podzapyta ´n

Odejmijmy:

(

s e l e c t a . nazwisko , a . mi as t o

from A u t o r z y a
where a . p l e c = ’ F ’ )

except

(

s e l e c t a . nazwisko , a . mi as t o

from A u t o r z y a , A u t o r z y b
where a . p l e c = ’ F ’

and b . p l e c = ’ F ’

and a . m i a s t o _ u r o d z e n i a = b . m i a s t o _ u r o d z e n i a
and a . r o k _ u r o d z e n i a > b . r o k _ u r o d z e n i a ; )

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

28 / 36

Przesuwanie predykatów

π

nazwisko, tytul

σ

rok=2011

o

n

Ksiazki.autor_id=Autorzy.id

Ksiazki

Autorzy

π

nazwisko, tytul

o

n

Ksiazki.autor_id=Autorzy.id

σ

rok=2011

Ksiazki

Autorzy

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

29 / 36

Przesuwanie predykatów

s e l e c t w . nazwa , Min ( a . r o k _ u r o d z e n i a )

from Wydawnictwa w, A u t o r z y a
where w . a u t o r _ i d = a . i d
group by w . nazwa
having Min ( a . r o k _ u r o d z e n i a ) <=1939;

s e l e c t w . nazwa , Min ( a . r o k _ u r o d z e n i a )

from Wydawnictwa w, A u t o r z y a
where w . a u t o r _ i d = a . i d

and a . r o k _ u r o d z e n i a <=1939
group by w . nazwa ;

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

30 / 36

Przesuwanie predykatów

Czy tak te˙z mo˙zna?

s e l e c t w . nazwa , Min ( a . r o k _ u r o d z e n i a )

from Wydawnictwa w, A u t o r z y a
where w . a u t o r _ i d = a . i d
group by w . nazwa
having Min ( a . r o k _ u r o d z e n i a ) >1939;

s e l e c t w . nazwa , Min ( a . r o k _ u r o d z e n i a )

from Wydawnictwa w, A u t o r z y a
where w . a u t o r _ i d = a . i d

and a . r o k _ u r o d z e n i a >1939
group by w . nazwa ;

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

31 / 36

Optymalizacja zapytania – heurystyka

Selekcje opart ˛

a na warunku, σ

C

(

R) warto przenie´s´c w dół drzewa,

je´sli to mo˙zliwe.

Podobnie post ˛epujemy z projekcjami.

Usuwanie powtórze ´n cz ˛esto lepiej zrobi´c wy˙zej w drzewie (je´sli
trzeba) aby operowa´c na mniejszych relacjach.

Przed zł ˛

aczeniem lepiej wykona´c selekcj ˛e na obu relacjach

składowych (je´sli wogle chcemy wykona´c selekcj ˛e).

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

32 / 36

Fizyczny plan realizacji zapytania

Po dokonaniu optymalizacji logicznej trzeba wybra´c algorytmy
realizacji zapytania:

kolejno´s´c wykonania operacji przemiennych jak zł ˛

aczenia, sumy,

. . . ,

algorytmy dla operatorów logicznych (haszowanie, zagnie˙zd˙zone
p ˛etle, . . . ),

realizacja operatorów sortowania, grupowania, . . . ,

sposób przekazywania argumentów i wyników podzapyta ´n (przez
dysk, pami ˛e´c operacyjna, po jednej krotce, . . . ).

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

33 / 36

Szacowanie kosztów

Aby wybra´c odpowiednie algorytmu nale˙zy oszacowa´c ich koszty,
czyli przede wszystkim oszacowa´c wielko´s´c po´srednich wyników.
Stosuje si ˛e tutaj:

I

przewidywanie przypadków najgorszych,

I

rachunek prawdopodobie ´nstwa by wyliczy´c oczekiwane warto´sci
rozmiaru relacji

I

obliczanie okresowo statystyk bazy danych.

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

34 / 36

Szacowanie kosztów – rozmiar projekcji

Je´sli dane maj ˛

a rozkład jednostajny, to oczekiawna wielko´s´c projekcji

σ

A=a

(

R) wynosi T (R)/V (R, A).

W praktyce wiele danych ma np. rozkład Zipfa (np. rozmiar populacji
miast - podzielony na przedziały). W rozkładzie Zipfa i-ta najcz ˛estsza

warto´s´c wyst ˛epuje z cz ˛estotliwo´sci ˛

a 1/

√

i. Otrzymujemy wtedy ci ˛

ag

stosunków cz ˛esto´sci 1, 0.71, 0.58, . . .

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

35 / 36

Szacowanie kosztów

Szacowanie rozmiaru sumy, iloczynu, ró˙znicy do´s´c łatwe cho´c
niekoniecznie dokładne.

Np. rozmiar ró˙znicy R − S zawiera si ˛e w T (R) a T (R) − T (S).

´

Srednio mo˙zemy przyj ˛

ac

(

T (R) + (T (R) − T (S)))/2 = T (R) − T (S)/2.

Zł ˛

aczenie R(A, B) is S(B, C) mo˙ze mie´c w wyniku

I

0 krotek,

I

T (R) krotek, je´sli B jest kluczem obcym w R pobieranym z S,

I

rz ˛edu T (R)T (S) krotek, je´sli warto´s´c atrybutu B jest w obu
relacjach taka sama i mało zmienna.

Przy pewnych dodatkowych zało˙zeniach (V (R, B) ¬ V (S, B)) i
V (R o

n S, A) = V (R, A)) mo ˙

zemy szacowa´c rozmiar zł ˛

aczenia

jako T (R)T (S)/ max(V (R, B), V (S, B)).

Konrad Zdanowski ( Uniwersytet Kardynała Stefana Wyszy ´nskiego, Warszawa)

Bazy danych – wykład dwunasty Wykonywanie i optymalizacja zapyta ´n SQL

36 / 36