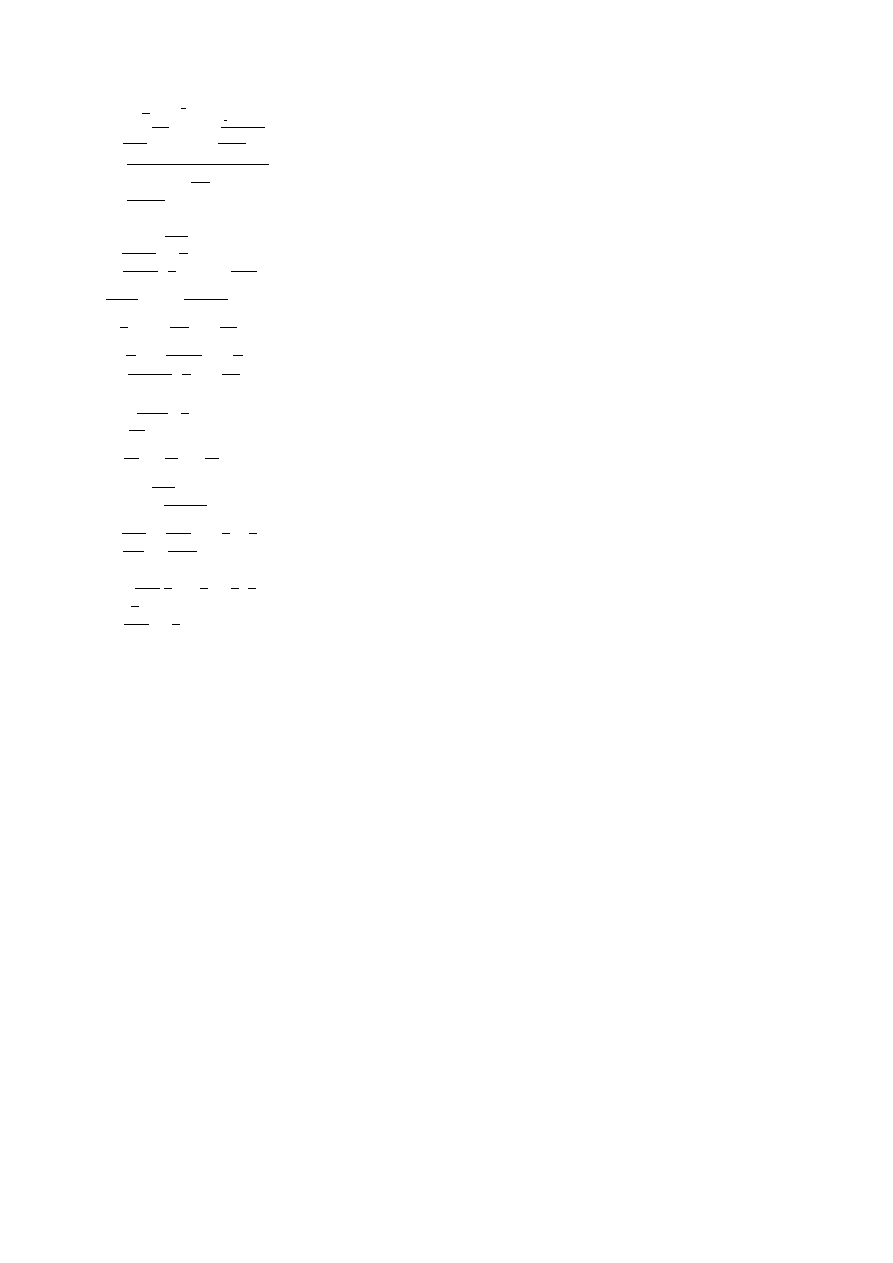
𝑒

𝑥

𝑡 = 𝑛

𝑥

𝑑𝑓𝑖

𝑑𝑡

𝑄 = 𝑎 𝑃 a –wypełnienei żelazem, P moc

𝑅

𝑤

= 𝑅

𝑤𝑡 ó𝑟

+

𝑅

𝑝𝑖𝑒𝑟𝑤

𝑛

2

𝑈

𝑤

=

2𝑈

𝑠𝑘

sin ⁡

(𝑤𝑡 +𝑓𝑖 )

𝑛

𝑘

𝑡

=

𝑈

𝑡𝑒𝑡𝑛𝑖𝑒𝑛

𝑈

ś𝑟 𝑤𝑦𝑝

𝑈

𝑡

=

𝑈

𝑤𝑦𝑗 𝑚𝑎𝑥

2 𝑓𝑅

0

𝐶

𝑰

𝑪𝑸

=

𝑬

𝑩

− 𝑼

𝑩𝑬𝑸

𝑩 + 𝑰

𝑪𝟎

𝑩 + 𝟏 (𝑹

𝑪

+ 𝑹

𝑩

+ 𝑹

𝑬

)

𝟏 + 𝑩 𝑹

𝑬

+ 𝑹

𝑪

+ 𝑹

𝑩

𝑼

𝑪𝑬𝑸

= 𝑬

𝑪

− 𝑰

𝑪𝑸

− 𝑰

𝑪𝟎

𝑩 + 𝟏

𝑩

(𝑹

𝑪

+ 𝑹

𝑬

)

𝑰

𝑪𝑸

=

𝑬

𝑪

− 𝑼

𝑪𝑬(𝑸)

𝑹

𝑪

+ 𝑹

𝑬

𝑈

𝐵𝐸

𝑡

1

= 𝑈

𝐵𝐸

𝑇

0

− 𝑐 𝑇

1

− 𝑇

0

𝑐 = 1,5 − 2,5𝑚𝑉/𝐾

𝐵 𝑇

1

= 𝐵 𝑇

0

1 − 𝑔𝑎𝑚𝑚𝑎 𝑇

1

− 𝑇

0

5 − 10 1/𝑘𝐾

𝐼

𝐶0

= 𝐼

𝐶0

𝑇

0

exp

𝑇

1

− 𝑇

0

𝑏

𝑏 = 14𝐾

𝑠

𝑖

=

𝑅

𝐵

+ 𝑅

𝐸

𝑅

𝐸

+ 𝑅

𝐵

/𝐵

= 1 +

𝑅

𝐵

𝑅

𝐸

𝑅

𝐸

↑

𝑠

𝑢

=

1

𝑅

𝐸

+ 𝑅

𝐵

/𝐵

=

1

𝑅

𝐸

𝑅

𝐵

↓ 𝑠

𝐵

=

𝑅

𝐵

+ 𝑅

𝐸

𝑅

𝐸

∗ 𝐵

𝐵 ↑

Ograniczenie R
𝐸

𝐶

− 𝑈

𝐶𝐸𝑄

𝐼

𝐶𝑄

< 𝑅

𝐸

+ 𝑅

𝐶

<

𝐸

𝐶𝑚𝑎𝑥

− 𝑈

𝐶𝐸𝑄

𝐼

𝐶𝑄

Ilość diod potrzebnych do skompens.

𝑛 =

𝑅

2

𝑅

1

+ 1 𝑎 =

𝐵

𝐵 + 1

𝐵 =

𝑎

1 − 𝑎

Model hybryd PI

𝑔

𝑚

=

𝐼

𝐶𝑄

𝑓𝑖

𝑇

𝑔

𝑐𝑒

=

𝐼

𝐶𝑄

𝑈

𝐸𝑌

+ 𝑈

𝐶𝐸𝑄

𝑔

𝑏

′

𝑒 =

𝑔

𝑚

𝐵

𝑔

𝑏

′

𝑐 =

𝐼

𝑐𝑄

𝐵(𝑈

𝐸𝑌

+ 𝑈

𝐵𝐸

)

=

𝑔

𝑖𝑒

𝐵

𝑐

𝑏𝑒

=

𝑔

𝑚

2𝑝𝑖𝑓

𝑇

− 𝑐

𝑏𝑐

𝑟

𝑤𝑒𝑗

= 𝑅

1

𝑅

2

{𝑟

𝑏𝑒

+ 𝑅

𝐸

(𝐵 + 1)}

𝑟

𝑤𝑦𝑗

= 𝑟

𝑐𝑒

||𝑅

𝑐

≈ 𝑅

𝐶

𝑗𝑒𝑠𝑙𝑖 𝑟

𝑐𝑒

≫ 𝑅

𝐶

𝑘

𝑢𝑠𝑘

= −

𝑔

𝑚

𝑅

𝑐

1 + 𝑔

𝑚

𝑅

𝐸

≈

𝑅

𝐶

𝑅

𝐸

𝑐

𝑤𝑒𝑗

=

𝑔

𝑚

2𝜋𝑓

𝑇

𝑐

𝑤𝑦𝑗

= 𝑐

𝑏𝑒

+ 𝑐

𝑏𝑐

(1 − 𝑘

𝑢

)

𝑘

𝑢

=

𝑈

𝑤𝑦𝑗

𝑈

𝑤𝑒𝑗

𝑘

𝑖

=

𝐼

𝑤𝑦𝑗

𝐼

𝑤𝑒𝑗

𝑘

𝑝

=

𝑃

𝑤𝑦𝑗

𝑃

𝑤𝑒𝑗

(10𝑙𝑜𝑔)

Dynamiczna prosta pracy DC

𝒊

𝒄𝒎𝒂𝒙

= 𝑰

𝑪𝑸

+

𝑼

𝑪𝑬𝑸

𝑹

𝑪

||𝑹

𝟎

𝒖

𝒄𝒆𝒎𝒂𝒙

= 𝑼

𝑪𝑬𝑸

+ 𝑱

𝑪𝑸

(𝑹

𝑪

||𝑹

𝟎

)

𝑨𝑪 𝒊

𝒄𝒎𝒂𝒙

= 𝑰

𝑪𝑸

+

−𝑼

𝑪𝑬

+ 𝑼

𝑪𝑬𝑸

𝑹

𝑪

||𝑹

𝟎

Tw Millera

𝐼

1

=

𝑈

1

− 𝑈

2

𝑍

, 𝐼

2

=

𝑈

2

− 𝑈

1

𝑍

=> 𝐼

1

=

𝑈

1

𝑍

1

, 𝐼

2

=

𝑈

2

𝑍

2

𝑍

1

=

𝑍

1 − 𝑘

𝑢

𝑍

2

=

𝑍

1 − 1/𝑘

𝑢

Wzmacniacze
Wzmacniacz operacyjny

𝑈

𝑤𝑒𝑗

=

𝑅

1

+ 𝑅

2

𝑅

3

+ 𝑅

4

𝑅

4

𝑅

1

𝑈

𝑤𝑒𝑗 2

−

𝑅

1

𝑅

2

𝑗𝑒𝑠𝑙𝑖

𝑅

2

𝑅

1

=

𝑅

4

𝑅

3

𝑈

𝑤𝑦𝑗

=

𝑅

2

𝑅

1

𝑈

𝑤𝑒𝑗 2

− 𝑈

𝑤𝑒𝑗 1

𝑗𝑒𝑠𝑙𝑖 𝑅

1

= 𝑅

2

𝑘

𝑈

=

𝑅

1

+ 𝑅

2

𝑅

1

= 1 +

𝑅

2

𝑅

1

STAŁE
Fi(t)=25 – 26 mV – pot. Term elekt Uces=0,2-0,3V
Kompensacja zmian Ic0 poprzez wpięcie C między B i E