
Opracował i wykonał: Stanisław Zoń
1
/
5
2013-04-27, godz. 14:43
6.1 Punkty osobliwe. Residua
Punkty zerowe funkcji holomorficznej
Def. Punkt
0
z nazywamy punktem zerowym funkcji
)
(z
f
, jeżeli
0
)
(
0
=
z
f
.
Def. Punkt
0
z nazywamy k-krotnym (
1
≥
k
) punktem zerowym funkcji
)
(z
f
, jeżeli w jej rozwinięciu
w szereg Taylora o środku w
0
z , współczynnik
0
≠
k
a
, natomiast
0
1
1
0
=
=
=
=
−
k
a
a
a
L
,
czyli gdy
∑
∞
=
+
+
−
⋅
=
+
−
⋅
+
−
⋅
=
k
n
n
n
k
k
k
k
z
z
a
z
z
a
z
z
a
z
f
)
(
)
(
)
(
)
(
0
1
0
1
0
L
.
(1)
Przykład 1. Funkcja
)
1
(
−
z
z
ma w
0
=
z
1-krotny punkt zerowy, ponieważ
2
)
1
(
z
z
z
z
+
−
=
−
.
Własności.
1. Punkt
0
z jest k-krotnym punktem zerowym funkcji
)
(z
f
wtedy i tylko wtedy gdy:
0
)
(
0
)
(
≠
z
f
k
, natomiast
0
)
(
)
(
)
(
)
(
0
)
1
(
0
0
0
=
=
=
=
=
−
z
f
z
f
z
f
z
f
k
L
"
'
.
(2)
2. Punkt
0
z jest k-krotnym punktem zerowym funkcji
)
(z
f
wtedy i tylko wtedy gdy:
)
(
)
(
)
(
0
z
z
z
z
f
k
ϕ
⋅
−
=
, a
)
(z
ϕ
jest funkcją holomorficzną i
0
)
(
0
≠
z
ϕ
.
(3)
3. Jeżeli
0
z jest punktem zerowym funkcji holomorficznej, to jest on punktem
odosobnionym,
tzn. istnieje takie otoczenie
0
z w którym nie ma innych punktów zerowych.
4. Jeżeli funkcja jest holomorficzna w obszarze, to albo jest tożsamościowo równa zeru, albo
każdy jej punkt zerowy jest odosobniony.
Przykład 2. Funkcja
)
(z
f
=
)
cos(
1
z
−
ma punkty zerowe w
π
k
z
2
=
. Są to 2-krotne punkty zerowe,
ponieważ,
(
)
0
2
)
sin(
2
)
cos(
1
=
=
=
=
−
π
π
k
z
z
k
z
z '
,
ale
(
)
(
)
0
1
2
)
cos(
2
)
sin(
2
)
cos(
1
≠
=
=
=
=
=
=
−
π
π
π
k
z
z
k
z
z
k
z
z
'
"
.
Punkty osobliwe
Def. Punkt
0
z w którym funkcja
)
(z
f
jest holomorficzna nazywamy punktem regularnym tej funkcji.
Def. Punkt
0
z nazywamy punktem osobliwym odosobnionym funkcji
)
(z
f
, jeżeli funkcja f
nie jest
holomorficzna w punkcie
0
z , ale jest holomorficzna w sąsiedztwie tego punktu.
Przykłady 3. Funkcja
)
1
(
1
−
z
z
ma punkty osobliwe odosobnione
0
=
z
i
1
=
z
,
funkcja z
z
e ma punkt osobliwy odosobniony
0
=
z
.
Założenie. Niech
)
(z
f
ma rozwinięcie w szereg Laurenta w sąsiedztwie
punktu osobliwego odosobnionego
0
z , zatem:
)
(z
f
=
∑
∞
−
=
−
1
0
)
(
n
n
n
z
z
a
+
∑
∞
−
=
0
0
)
(
n
n
n
z
z
a
(4)
Def. Punkt
0
z nazywamy punktem pozornie osobliwym funkcji
)
(z
f
, jeżeli w jej rozwinięciu
w szereg Laurenta o środku w
0
z nie ma części osobliwej.
Przykład 4. Punkt
0
=
z
jest punktem pozornie osobliwym funkcji
z
z)
sin(
ponieważ
L
L
−
−
+
−
=
−
+
−
=
!
5
!
3
1
!
5
/
!
3
/
)
sin(
4
2
5
3
z
z
z
z
z
z
z
z
(nie ma części osobliwej).
część osobliwa
rozwinięcia

6. Punkty osobliwe. Residua
Opracował i wykonał: Stanisław Zoń
2
/
5
2013-04-27, godz. 14:43
Wniosek. Jeżeli
0
z jest punktem pozornie osobliwym funkcji
)
(z
f
, to
)
(z
f
=
∑
∞
−
=
0
0
)
(
n
n
n
z
z
a
,
zatem
)
(
lim
0
z
z
f
z
→
=
(
)
0
2
0
2
0
1
0
)
(
)
(
lim
0
a
z
z
a
z
z
a
a
z
z
=
+
−
+
−
+
→
K
.
Def. Punkt
0
z nazyw. biegunem k-krotnym (
1
≥
k
) funkcji
)
(z
f
, jeżeli część osobliwa rozwinięcia
ma skończoną liczbę wyrazów i
0
≠
−
k
a
czyli
)
(z
f
=
1
0
1
0
)
(
)
(
z
z
a
z
z
a
k
k
−
+
+
−
−
−
L
+
∑
∞
−
=
0
0
)
(
n
n
n
z
z
a
.
(5)
Przykład 5. Punkt
0
=
z
jest biegunem 1-krotnym funkcji
z
z
z
f
)
cos(
)
(
=
ponieważ
L
L
−
+
−
=
+
+
−
=
=
!
4
!
2
1
!
4
/
!
2
/
1
)
cos(
)
(
3
4
2
z
z
z
z
z
z
z
z
z
f
.
Przykład 6. Punkt
0
=
z
jest biegunem 2-krotnym funkcji
2
)
cos(
)
(
z
z
z
f
=
ponieważ
L
L
−
+
−
=
+
+
−
=
=
!
4
!
2
1
1
!
4
/
!
2
/
1
)
cos(
)
(
2
2
2
4
2
2
z
z
z
z
z
z
z
z
f
.
Def. Punkt
0
z nazywamy punktem istotnie osobliwym funkcji
)
(z
f
, jeżeli część osobliwa rozwinięcia
ma nieskończenie wiele wyrazów.
Przykład 7. Punkt
0
=
z
jest punktem istotnie osobliwym funkcji
z
z
f
/
1
e
)
(
=
ponieważ
∑
∑
∞
=
∞
=
=
=
=
0
0
1
!
1
!
)
/
1
(
/
1
e
)
(
n
n
n
z
n
n
n
z
z
z
f
Uwaga. Weryfikację punktów osobliwych odosobnionych funkcji f można przeprowadzić bez
rozwijana funkcji f w jej szereg Laurenta.
Tw. Punkt
0
z jest:
•
punktem pozornie osobliwym funkcji
)
(z
f
, gdy istnieje
skończona granica
)
(
lim
0
z
f
z
z
→
.
•
biegunem funkcji
)
(z
f
wtedy i tylko wtedy gdy
=
→
)
(
lim
0
z
f
z
z
∞
.
•
biegunem k-krotnm funkcji
)
(z
f
wtedy i tylko wtedy gdy
(
)
0
)
(
)
(
lim
0
0
≠
⋅
−
→
z
f
z
z
k
z
z
oraz
(
)
0
)
(
)
(
lim
1
0
0
=
⋅
−
+
→
z
f
z
z
k
z
z
.
(6)
•
punktem istotnie osobliwym funkcji
)
(z
f
, gdy
nie istnieje granica
)
(
lim
0
z
f
z
z
→
.
Jeżeli punkt
0
z jest k-krotnym zerem funkcji f, to dla funkcji 1/f jest on k-krotnym biegunem.
Jeżeli punkt
0
z jest k-krotnym biegunem funkcji f, to dla funkcji 1/f jest on k-krotnym zerem.
Przykład 8. Funkcja
)
1
(
1
)
(
−
=
z
z
z
f
ma 1-krotne bieguny w
0
=
z
i
1
=
z
, ponieważ
funkcja
)
1
(
)
(
1
−
=
z
z
z
f
ma 1-krotne zera w tych punktach.
lub inaczej
...)
1
(
1
1
1
1
1
1
1
)
1
(
1
)
(
2
+
+
+
−
−
=
−
−
−
≡
−
+
−
≡
−
=
z
z
z
z
z
z
z
z
z
z
f
szereg zbieżny gdy |z|<1.

6. Punkty osobliwe. Residua
Opracował i wykonał: Stanisław Zoń
3
/
5
2013-04-27, godz. 14:43
Residua
Założenie. Niech
)
(z
f
będzie funkcją holomorficzną w sąsiedztwie punktu
0
z . Niech C będzie
dowolną, kawałkami gładką, dodatnio skierowaną krzywą Jordana zawartą w tym sąsiedztwie.
Def. Residuum funkcji
)
(z
f
w punkcie
0
z , oznaczane przez
)
(
res
0
z
f
z
, nazywamy liczbę równą
∫
C
z
z
f
i
d
)
(
2
1
π
(7)
Tw.
1
)
(
res
0
−
=
a
z
f
z
,
gdzie
1
−
a
jest współczynnikiem rozwinięcia funkcji
)
(z
f
w szereg Laurenta w sąsiedztwie
0
z :
+
−
+
=
−
2
0
2
)
(
)
(
z
z
a
z
f
K
)
(
0
1
z
z
a
−
−
...
)
(
)
(
2
0
2
0
1
0
+
−
⋅
+
−
⋅
+
+
z
z
a
z
z
a
a
(8)
Dowód. Podstawiając szereg (8) do wzoru na residuum (7) i całkując wyraz po wyrazie otrzymujemy
wszystkie całki równe zero, z wyjątkiem całki z wyrazu o współczynniku
1
−
a
, ponadto
1
0
1
0
1
d
1
2
d
2
1
d
)
(
2
1
−
−
−
=
⌡
⌠
−
=
⌡
⌠
−
=
∫
a
z
z
z
i
a
z
z
z
a
i
z
z
f
i
C
C
C
π
π
π
.
cbdo
Wniosek. Residuum funkcji w punktach regularnych i pozornie osobliwych jest równe zero.
Sposoby wyznaczania residuum.
1.
Jeżeli
0
z jest punktem istotnie osobliwym funkcji f, to jej residuum w
0
z należy wyznaczać
z rozwinięcia funkcji f w szereg Laurenta.
2.
Jeżeli punkt
0
z jest biegunem k-krotnym funkcji
)
(z
f
, to
[
]
)
(
)
(
d
d
lim
)!
1
(
1
)
(
res
0
1
1
0
0
z
f
z
z
z
k
z
f
k
k
k
z
z
z
⋅
−
−
=
−
−
→
.
(9)
3.
Jeżeli punkt
0
z jest biegunem 1-krotnym funkcji
)
(
)
(
)
(
z
h
z
g
z
f
=
gdzie funkcje g(z) i h(z) są
holomorficzne
w otoczeniu punktu
0
z , przy czym
0
)
(
0
=
z
h
,
0
)
(
0
≠
z
h
'
, to
)
(
)
(
)
(
res
0
0
0
z
h
z
g
z
f
z
'
=
.
(10)
Tw. Jeżeli funkcja
)
(z
f
jest holomorficzna w obszarze jednospójnym D z wyjątkiem co najwyżej
punktów
n
z
z
z
,
,
,
2
1
K
, a C jest krzywą Jordana kawałkami gładką, dodatnio zorientowaną, leżą-
cą w tym obszarze i zawierającą te punkty w swoim wnętrzu, to
∫
∑
=
=
n
j
z
C
z
f
i
z
z
f
j
1
)
(
res
2
d
)
(
π
.
(11)
Przykład 9. (por. przykł.5) Obliczyć całkę
⌡
⌠
−
C
z
z
z
d
)
cos(
1
3
, gdzie C jest dodatnio zorientowanym
okręgiem
2
|
1
|
=
−
z
.
Rozwiązanie.
(
)
L
L
+
−
=
+
+
−
−
=
−
!
4
!
2
1
!
4
/
!
2
/
1
1
)
cos(
1
3
4
2
3
z
z
z
z
z
z
z
,
czyli z = 0 jest (punktem osobliwym) biegunem 1-krotnym, więc
2
1
)
cos(
1
res
3
0
=
−
z
z
,
zatem
i
i
z
z
i
z
z
z
C
π
π
π
=
⋅
=
−
⋅
=
⌡
⌠
−
2
1
2
)
cos(
1
res
2
d
)
cos(
1
3
0
3
.
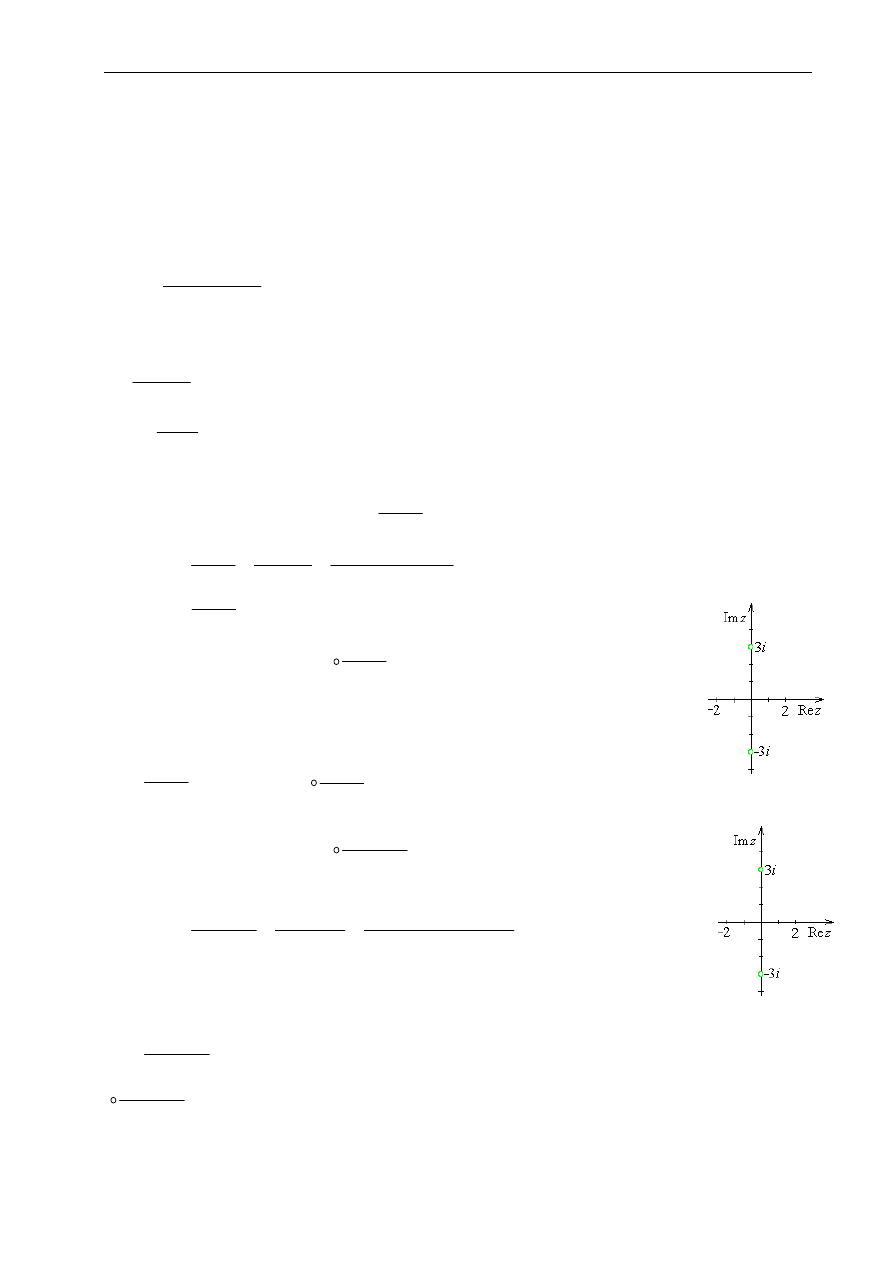
6. Punkty osobliwe. Residua
Opracował i wykonał: Stanisław Zoń
4
/
5
2013-04-27, godz. 14:43
Zadania na ćwiczenia 6.
1
Punkty zerowe i osobliwe
Zad. 1.
Znaleźć wszystkie punkty zerowe funkcji
3
2
2
)
1
(
)
(
z
z
z
f
⋅
+
=
i zbadać ich krotność.
Odp
.
±
=
z
….. – punkty zerowe …-krotne,
=
z
…. – punkt zerowy …-krotny.
Zad. 2.
(~133)
Wyznaczyć punkty osobliwe i określić ich rodzaj:
3
)
2
)(
(
1
−
+
z
i
z
Odp
.
i
z
−
=
biegun …-krotny,
2
=
z
biegun …-krotny.
Zad. 3.
(135)
Wyznaczyć punkty osobliwe i określić ich rodzaj:
A)
2
)
cos(
1
z
z
−
=………………………..……………..
Odp
.A) z = …. punkt …………… osobliwy
B)
( )
i
z
2
1
sin
−
= …………………………………….
Odp
.B) z = … punkt …………… osobliwy.
Residuum funkcji i całki
Zad. 4.
Wyznaczyć residuum funkcji
9
1
2
+
z
w punkcie z = 3i.
Rozwiąznie
.
)
(
)
(
1
9
1
9
1
2
2
2
+
⋅
−
=
−
=
+
z
z
i
z
z
, więc z = 3i jest ……………………………:
zatem
(9)
wzór
2
3
9
1
res
=
+
z
i
……………………………….……………
Odp
. 1
/(6i).
Zad. 5.
(
108
.1). Obliczyć całkę
∫
+
C
z
z
d
9
1
2
,
gdzie C jest dodatnio zorientowanym okręgiem |z-2i| = 2.
Odp
.
3
/
π
.
Rozwiąznie
. Okrag |z-2i| = 2 zawiera punkt z = …. w którym
=
+
9
1
res
2
3
z
i
.…,
.zatem
)
11
(
2
d
9
1
=
+
∫
C
z
z
……………………………………..
Zad. 6.
(
108
.1). Obliczyć całkę
∫
+
C
z
z
d
)
9
(
1
2
2
,
gdzie C jest dodatnio zorientowanym okręgiem |z-2i| = 2.
Odp
.
54
/
π
.
Rozwiąznie
.
2
2
2
2
2
2
)
(
)
(
1
)
9
(
1
)
9
(
1
+
⋅
−
=
−
=
+
z
z
i
z
z
Okrag |z-2i| = 2 zawiera punkt z = ….. który jest ………..…………….……
zatem :
=
+
2
2
3
)
9
(
1
res
z
i
………………………………………………….……..…………………
(9)
wzór
2
2
d
)
9
(
1
=
+
∫
C
z
z
………………………………………………………………………………..
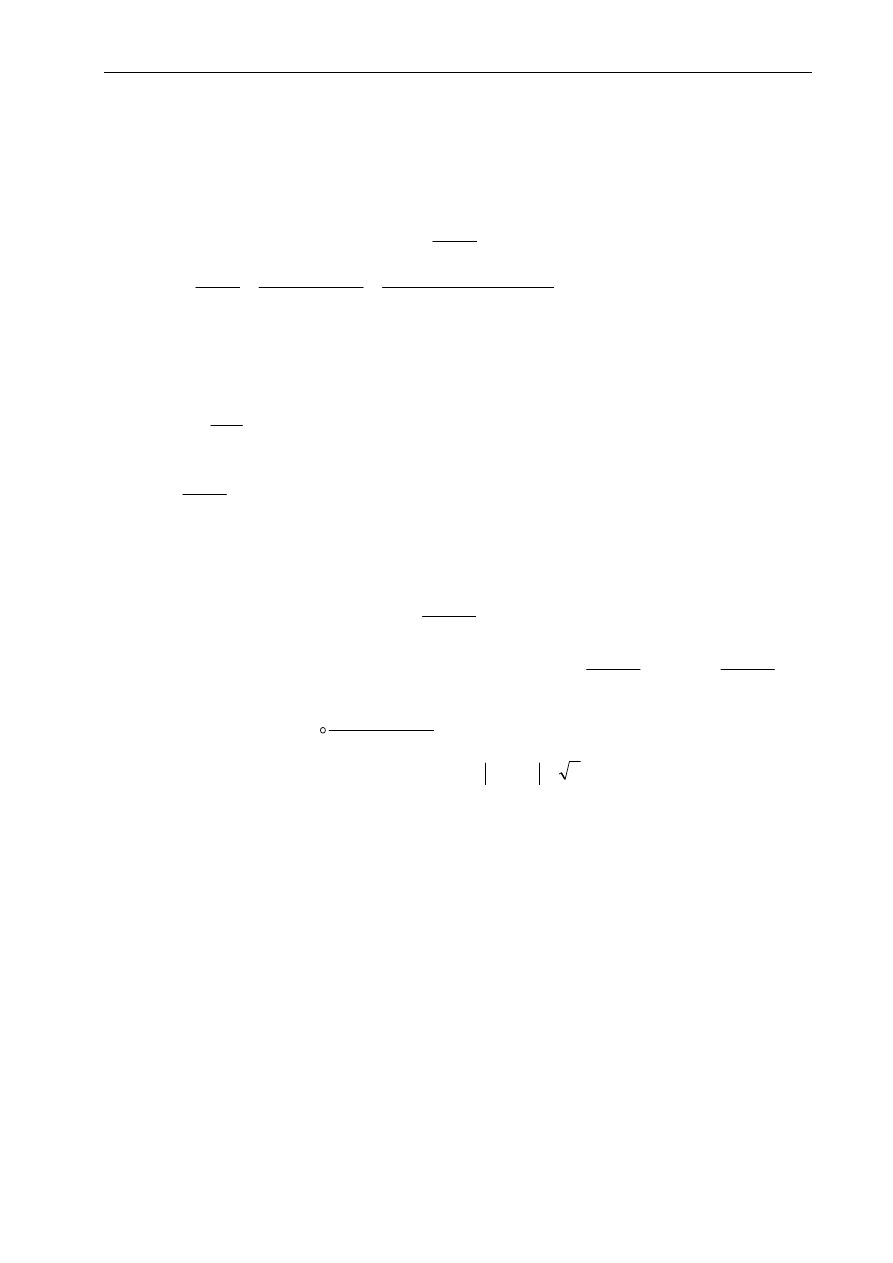
6. Punkty osobliwe. Residua
Opracował i wykonał: Stanisław Zoń
5
/
5
2013-04-27, godz. 14:43
Zadania domowe 6.1
Punkty zerowe i osobliwe
Zad. 1.
Znaleźć wszystkie punkty zerowe funkcji
)
sin(
)
(
z
z
z
f
=
i zbadać ich krotność.
Odp
.
0
=
z
– punkt zerowy 2-krotny, oraz (gdy
0
≠
k
)
π
k
z
=
– punkty zerowe 1-krotne.
Zad. 2.
Wyznaczyć punkty osobliwe funkcji
1
4
2
−
+
z
z
z
i określić ich rodzaj.
Wskazówka
.
)
)(
)(
1
)(
1
(
)
1
(
)
1
)(
1
(
)
1
(
1
2
2
4
2
i
z
i
z
z
z
z
z
z
z
z
z
z
z
z
+
−
+
−
+
=
+
−
+
=
−
+
Odp
.
i
z
±
=
– biegun 1-krotny,
1
=
z
– biegun 1-krotny,
1
−
=
z
– punkt pozornie osobliwy.
Zad. 3.
(135)
Wyznaczyć punkty osobliwe funkcji i określić ich rodzaj.
3)
( )
i
z
+
1
cos
,
Wskazówka
. Rozłożyć na szereg Laurenta
Odp
.
i
z
−
=
punkt istotnoie osobliwy.
5)
)
sin(
1
z
Wskazówka
. Skorzystać z rozw. przykładu 1 materiałów do ćwiczeń .
Odp
.
π
k
z
=
, gdzie k liczby całkowite, – bieguny 1-krotne.
Residuum funkcji i całki
Zad. 4.
(136.3)
Wyznaczyć residuum funkcji
)
1
(
e
−
z
z
z
w punktach: z = 0, z = 1.
Odp
.
1
)
1
(
e
res
0
−
=
+
z
z
z
,
e
)
1
(
e
res
1
=
+
z
z
z
.
Zad. 5.
(
143
)
. Obliczyć całkę
∫
+
−
C
z
z
z
d
)
1
(
)
1
(
1
2
2
.
gdzie C jest dodatnio zorientowanym okręgiem
2
1
=
−
−
i
z
.
Odp
.
2
/
π
i
−
.
Wyszukiwarka
Podobne podstrony:
Asymptoty ekstrema punkty przegiecia szkic zadania domowe
Asymptoty ekstrema punkty przegiecia szkic zadania domowe
Asymptoty ekstrema punkty przegiecia szkic zadania domowe
Balonowy bieg, zuchy, zadania na punkty
Zagubiony meldunek, zuchy, zadania na punkty
Rozrzucone sylaby, zuchy, zadania na punkty
Łańcuch skojarzeniowy(1), zuchy, zadania na punkty
Gra hula hop, zuchy, zadania na punkty
Gra pamięciowa, zuchy, zadania na punkty
Historyjka, zuchy, zadania na punkty
Kolekcjoner osobliwości, zuchy, zadania na punkty
Puzzle, zuchy, zadania na punkty
Pułapka, zuchy, zadania na punkty
Żarłacze, zuchy, zadania na punkty
Pamiętnik, zuchy, zadania na punkty
Gwizdek, zuchy, zadania na punkty
więcej podobnych podstron