
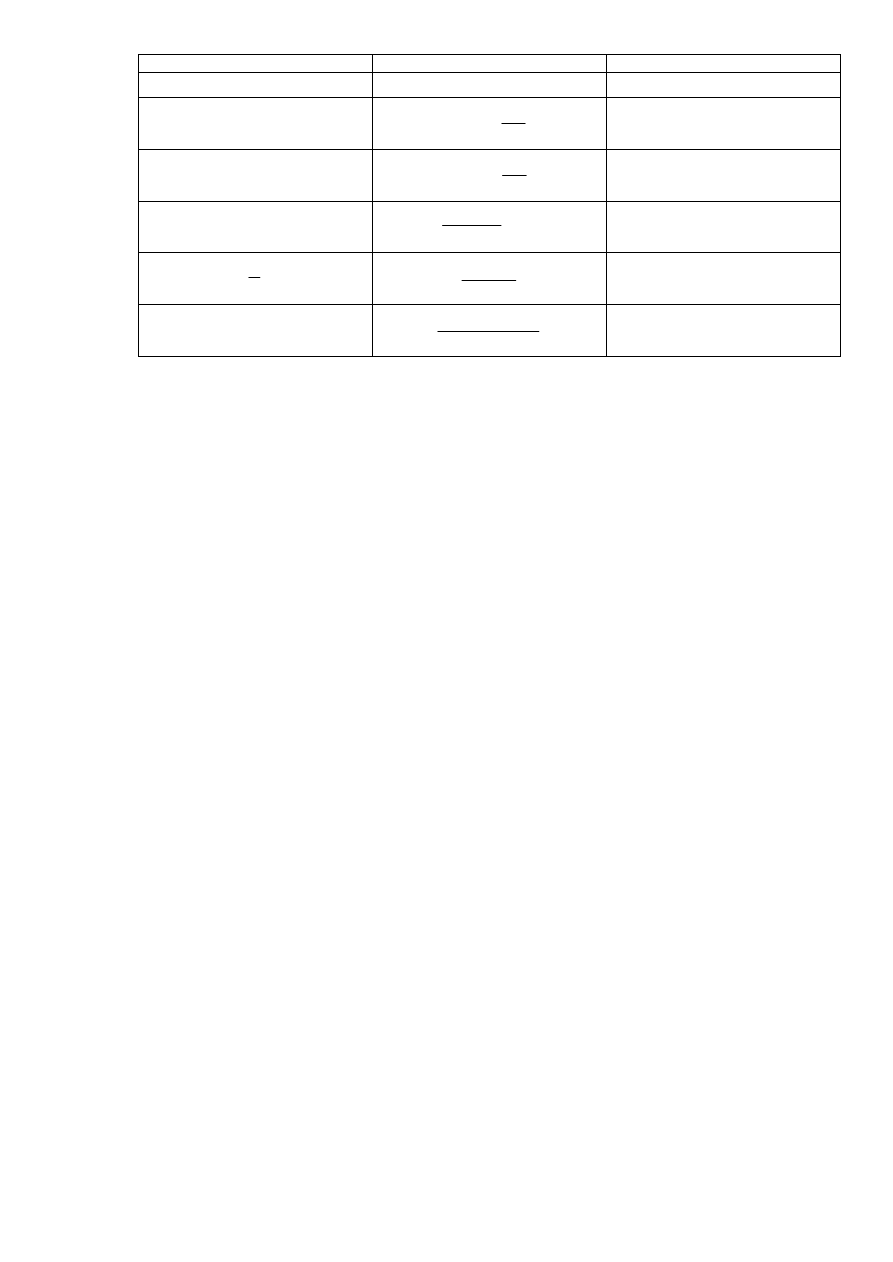
Fakt 4.1.4 (pochodne ważniejszych funkcji elementarnych)
Funkcja
Pochodna
Zakres zmienności
c
0
R
c
Î
n
x
1
-
n
nx
n
Î N, x Î R
p
x
1
-
p
px
p
Î {-1, -2, -3, ...}, x ¹ 0
a
x
1
-
a
ax
a Î R, x > 0
x
sin
x
cos
R
x
Î
x
cos
x
sin
-
R
x
Î
Funkcja
Pochodna
Zakres zmienności
x
tg
x
x
2
2
tg
1
cos
1
+
=
Z
k
gdzie
k
x
Î
+
¹
,
2
p
p
x
ctg
x
x
2
2
ctg
1
sin
1
-
-
=
-
Z
k
gdzie
k
x
Î
¹
,
p
x
a
a
a
x
ln
0 < a
¹ 1, x Î R
x
e
x
e
R
x
Î
x
sh
x
ch
R
x
Î
x
ch
x
sh
R
x
Î
x
th
x
2
ch
1
R
x
Î
x
cth
x
2
sh
1
-
x
¹ 0
x
sin
arc
2
1
1
x
-
1
<
x
x
arccos
2
1
1
x
-
-
1
<
x
x
arctg
2
1
1
x
+
R
x
Î
x
arcctg
2
1
1
x
+
-
R
x
Î
x
a
log
a
x ln
1
0 < a
¹ 1, x Î R
x
ln
x
1
x > 0
Uwaga. Do obliczania pochodnych funkcji postaci
g
f
oraz
g
f
log
stosujemy wzory:
f
g
g
e
f
ln
=
f
g
g
f
ln
ln
log
=
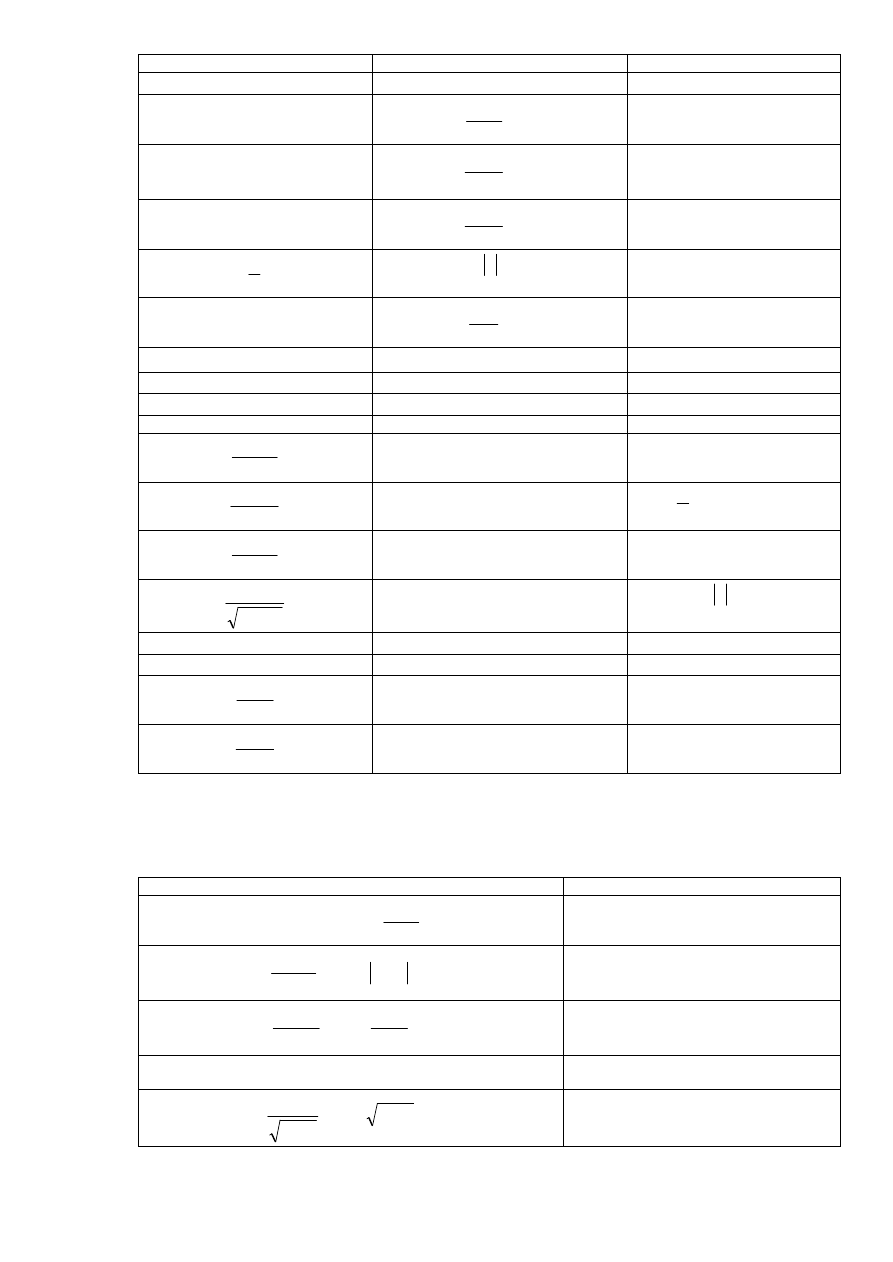
Fakt 4.5.3 (pochodne wyższych rzędów ważniejszych funkcji)
Funkcja
n-ta pochodna
Zakres zmienności
x
e
x
e
R
x
Î
x
sin
÷
ø
ö
ç
è
æ +
2
sin
p
n
x
R
x
Î
x
cos
÷
ø
ö
ç
è
æ +
2
cos
p
n
x
R
x
Î
m
x
n
m
x
n
m
m
-
- )!
(
!
R
x
m
n
Î
£ ,
x
1
1
!
)
1
(
+
-
n
n
x
n
0
¹
x
x
ln
n
n
x
n
)!
1
(
)
1
(
1
-
-
-
0
>
x
Fakt 7.2.4 (całki nieoznaczone ważniejszych funkcji elementarnych)
Funkcja
Całka nieoznaczona
Zakres zmienności
0
C
R
x
Î
n
x
C
n
x
n
+
+
+
1
1
n
Î N È {0}, x Î R
p
x
C
p
x
p
+
+
+
1
1
p
Î {-2, -3, -4, ...}, x ¹ 0
a
x
C
x
+
+
+
1
1
a
a
0
},
1
{
\
>
-
Î
x
R
a
x
1
C
x
+
ln
0
¹
x
x
a
C
a
a
x
+
ln
0 < a
¹ 1, x Î R
x
e
C
e
x
+
R
x
Î
x
sin
C
x
+
- cos
R
x
Î
x
cos
C
x
+
sin
R
x
Î
Funkcja
Całka nieoznaczona
Zakres zmienności
x
2
sin
1
C
x
+
- ctg
Z
k
gdzie
k
x
Î
¹
,
p
x
2
cos
1
C
x
+
tg
Z
k
gdzie
k
x
Î
+
¹
,
2
p
p
2
1
1
x
+
C
x
+
arctg
lub
C
x
+
arcctg
-
R
x
Î
2
1
1
x
-
C
x
+
sin
arc
lub
C
x
+
-
cos
arc
1
<
x
x
sh
C
x
+
ch
R
x
Î
x
ch
C
x
+
sh
R
x
Î
x
2
sh
1
C
x
+
- cth
0
¹
x
x
2
ch
1
C
x
+
th
R
x
Î
Uwaga. W powyższej tabeli symbol C oznacza dowolną stałą rzeczywistą.
Fakt 7.2.5 (tabela całek ważniejszych typów funkcji)
Wzór
Zakres zmienności
ò
+
+
=
+
C
n
f
dx
x
f
x
f
n
n
1
)
(
)
(
1
/
{ }
0
È
Î N
n
C
x
f
dx
x
f
x
f
+
=
ò
)
(
ln
)
(
)
(
/
0
)
(
¹
x
f
C
x
f
dx
x
f
x
f
+
-
=
ò
)
(
1
)
(
)
(
2
/
0
)
(
¹
x
f
C
e
dx
x
f
e
x
f
x
f
+
=
ò
)
(
/
)
(
)
(
f
D
x
Î
C
x
f
dx
x
f
x
f
+
=
ò
)
(
2
)
(
)
(
/
0
)
(
>
x
f
Uwaga. Powyższe wzory wynikają bezpośrednio z reguł różniczkowania funkcji złożonych oraz definicji całki nieoznaczonej.

Document Outline
Wyszukiwarka
Podobne podstrony:
6 - spr pochodne i calki (2) dla ZSZ-PF34 - pl 4[1], Pomoce naukowe SGSP, Moje Dokumenty, Matematyka
Pochodne, całki
Pochodne i całki wzory
Pochodne Całki
zestaw 2 pochodne, całki
granice, ciagi, pochodzne, calki
Matematyka - pochodne + całki + liczby zespolone, STUDIA
ściąga pochodne i całki wzory, pwr
pochodne i calki
pochodne i całki wzory przypomnienie
pochodne i całki wzory przypomnienie
Matematyka pochodne, całki, miejsca zerowe (wzory)
Wektory, pochodne, całki Wiesława Korczak, Marianna Trajdos
pochodne i calki
więcej podobnych podstron