Informatyka I – Lab 09, r.a. 2011/2012

prow. Sławomir Czarnecki

Zadania na laboratorium nr. 9

Po utworzeniu nowego projektu, dołącz bibliotekę

bibs.h

.

1. Zadanie problemowe z równań różniczkowych zwyczajnych – wstęp.

Algorytm Runge-Kutta rozwiązywania układu dwóch równań różniczkowych zwyczajnych
pierwszego rzędu:

( )

( ) ( )

( )

( ) ( )

'

,

,

,

'

,

,

u x

f x u x v x

v x

g x u x v x

= 







= 







z dwoma znanymi funkcjami

(

)

(

)

3

3

:

;

, ,

,

:

;

, ,

f R

R f

f x u v

g R

R g

g x u v

→

=

→

=

oraz z dwoma nieznanymi i poszukiwanymi funkcjami

( )

( )

,

u

u x

v

v x

=

=

które spełniać mają warunki początkowe

( )

( )

0

0

0

0

,

u x

u

v x

v

=

= .

Dane wejściowe i parametry algorytmu

• punkt początkowy (chwila początkowa x = x

0

):

x

0

• warunek początkowy dla funkcji u = u(x):

u

0

• warunek początkowy dla funkcji v = v(x):

v

0

• długość kroku (czasowego):

θ

• liczba dyskretnych punktów (liczba chwil czasowych)

n

w których obliczane będą wartości funkcji:

u = u(i ·

θ

) , v = v(i ·

θ

) (i = 0,1,...,n – 1)

• wskaźnik do funkcji typu

double

f (

double

,

double

,

double

):

*f

• wskaźnik do funkcji typu

double

g (

double

,

double

,

double

):

*g

• wektor punktów, w których obliczamy numerycznie rozwiązanie:

X[n]

• wektor wartości funkcji u = u(x):

U[n]

• wektor wartości funkcji v = v(x):

V[n]

Algorytm Runge-Kutta – pseudo-kod

1.

zainicjalizuj pierwsze składowe:

X[0] = x0
U[0] = u0
V[0] = v0

2

. dla każdej chwili czasowej

(

)

0

1

i

i

n

≤ < − , obliczaj

{

F =

θ

· f (X[i] , U[i] , V[i])

G =

θ

· g (X[i] , U[i] , V[i])

dU =

θ

· f (X[i] + 0.5

θ

, U[i] + 0.5 F , V[i] + 0.5 G)

dV =

θ

· g (X[i] + 0.5

θ

, U[i] + 0.5 F , V[i] + 0.5 G)

X[ i + 1 ] = X[i] +

θ

U[ i + 1 ] = U[i] + dU

V[ i + 1 ] = V[i] + dV

}

Na podstawie powyższego algorytmu, zdefiniuj funkcję

void

runge_kutta(

double

x0 ,

double

u0 ,

double

v0 ,

double

θ

,

int

n,

double

(*f )(

double

x ,

double

u ,

double

v),

double

(*g)(

double

x ,

double

u ,

double

v),

double

* X ,

double

* U ,

double

* V )

i znajdź następnie rozwiązanie numeryczne

( )

u

u t

=

,

( )

v

v t

=

układu dwóch równań

różniczkowych zwyczajnych:

'

3

'

4

u

u v

v

u v

=

−

=

−

z warunkami początkowymi

( )

( )

0

0.2

0

0.5

u

v

=

=

w przedziale

[

]

0 , 2

T =

wywołując funkcję runge_kutta(…) dla kroku czasowego

0.05

θ

=

.

Sprawdź poprawność rozwiązania numerycznego, konfrontując otrzymane wartości dyskretne
funkcji

( )

( )

,

u

u t

v

v t

=

=

z wartościami dyskretnymi, znanego w tym przypadku,

rozwiązania analitycznego:

( )

5

10

t

t

e

t e

u t

=

−

,

( )

2

5

t

t

e

t e

v t

=

−

.

Sporządź wykres (np. w Excel) funkcji wektorowej

( )( )

( ) ( )

2

,

,

T

u v t

u t v t

=

∈









ℝ , który

powinien wyglądać tak jak na zamieszczonym poniżej rysunku rys.1.

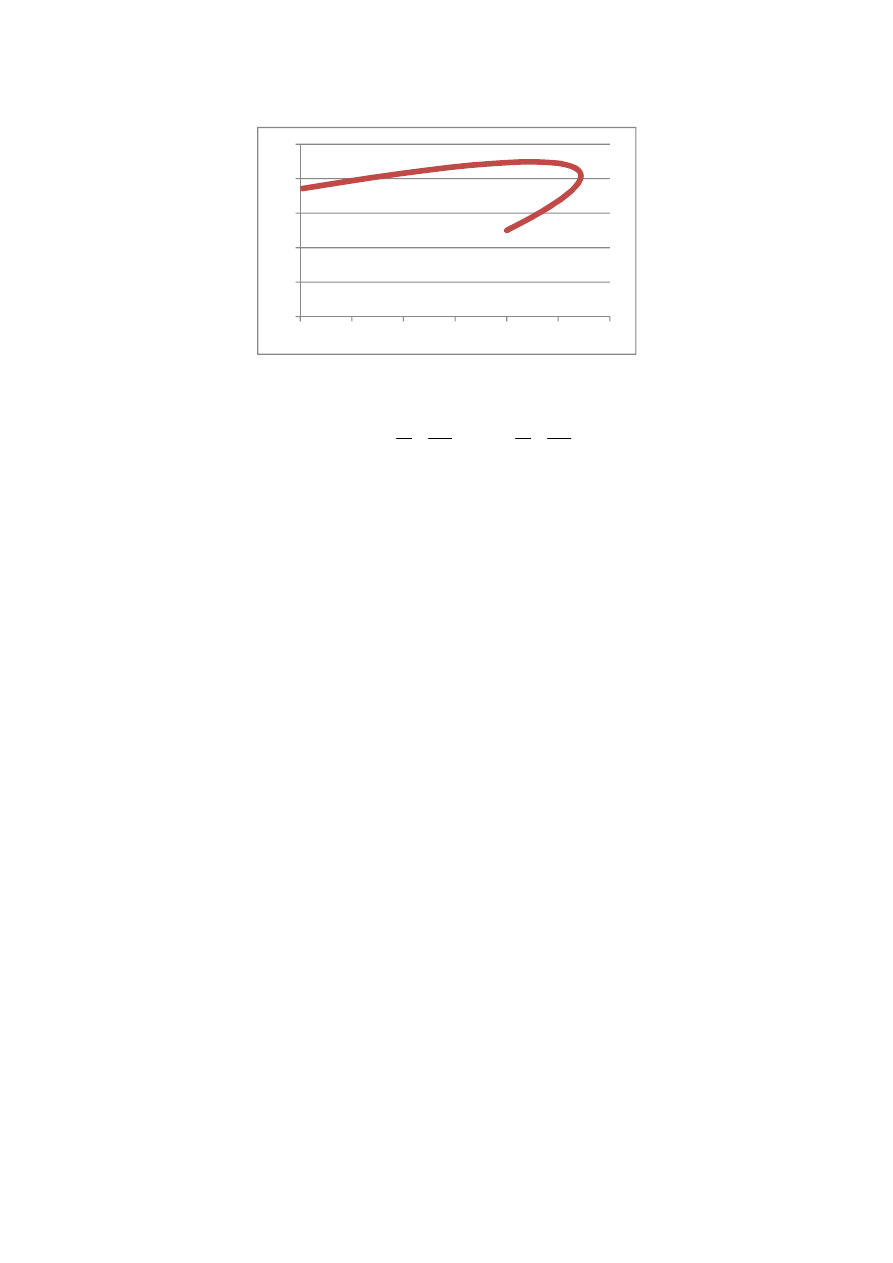
Rys.1. Wykres funkcji wektorowej

( )( )

( ) ( )

2

,

,

T

u v t

u t v t

=

∈









ℝ

dla

( )

5

10

t

t

e

t e

u t

=

−

,

( )

2

5

t

t

e

t e

v t

=

−

Algorytm poszukiwania rozwiązania równania różniczkowego zwyczajnego

rzędu drugiego

Zadanie numerycznego rozwiązania równania różniczkowego zwyczajnego drugiego rzędu

( )

( ) ( )

"

,

, '

y

x

h x y x

y x

= 







ze znaną funkcją

3

:

h R

R

→

oraz nieznaną i poszukiwaną funkcją

:

y R

R

→

spełniającą warunki początkowe

( )

( )

0

0

0

0

, '

y x

y

y x

v

=

=

gdzie

0

0

0

,

,

x

y

v są znanymi wartościami, można z reguły odpowiednio przedefiniować w

terminach zadania rozwiązywania układu dwóch równań różniczkowych zwyczajnych (

x

0

jest

najczęściej początkową chwilą czasu,

y

0

jest najczęściej wartością współrzędnej uogólnionej

Lagrange’a definiującej położenie punktu materialnego lub układu materialnego o jednym
stopniu swobody w chwili początkowej

x

0

, natomiast

v

0

jest wtedy prędkością uogólnioną w

chwili początkowej

x

0

).

0

0.2

0.4

0.6

0.8

1

0

0.05

0.1

0.15

0.2

0.25

0.3

Algorytm

• zdefiniuj funkcję

3

:

f R

R

→ ,

(

)

, ,

f x u v

v

=

oraz funkcję

3

:

g R

R

→ ,

(

)

(

)

, ,

, ,

g x u v

h x u v

=

gdzie

u i v są odpowiednio wartościami funkcji:

( )

( )

:

,

u R

R

u x

y x

→

=

i

( )

( )

:

,

'

v R

R

v x

y x

→

=

• Znajdź rozwiązania

( )

u

u x

=

i

( )

v

v x

=

układu dwóch równań różniczkowych

zwyczajnych pierwszego rzędu

( )

( ) ( )

( )

( ) ( )

'

,

,

'

,

,

u x

f x u x v x

v x

g x u x v x

= 







= 







przy warunkach początkowych

( )

( )

0

0

0

0

,

u x

y

v x

v

=

=

wykorzystując na przykład opisany powyżej algorytm Runge-Kutta.

Zadanie problemowe – wahadło matematyczne

Rozważmy równanie różniczkowe ruchu wahadłowego punktu materialnego o masie

m,

poruszającego się na końcu nieważkiej linki o długości

L, w polu grawitacyjnym ziemi

(

a = 9.81 [m/s

2

]). Zakładamy dodatkowo, że istnieje siła tłumienia ruchu, która jest

proporcjonalna do prędkości kątowej ruchu linki. Współczynnik tłumienia oznaczmy przez

c.

Przemieszczenie punktu w każdej chwili czasu

t określa kąt y = y(t). Prędkością kątową ruchu

obrotowego linki będzie zatem

y’ = y’(t).

( )

( )

( )

2

0

2

sin

0,

0

,

0

0

d y

c dy

a

dy

y

y

dt

mL dt

L

dt

ϕ

+

+

=

=

=

Równanie różniczkowe zapiszemy w postaci

( )

2

2

sin

d y

a

c dy

y

dt

L

mL dt

= −

−

i definiujemy funkcje

(

)

3

:

;

, ,

f R

R f t u v

v

→

=

(

)

( )

3

:

;

, ,

sin

a

c

g R

R g t u v

u

v

L

mL

→

= −

−

Ponadto załóżmy, że

a = 9.81[m/s

2

] ,

m = 1.0 [kg] , L = 10.0 [m] , c = 3.0 [N s]

chwila początkowa:

0

0

t

=

warunek początkowy dla funkcji

u = u(t):

0

2

u

π

=

,

tj.

( )

0

0

2

y t

π

ϕ

=

=

warunek początkowy dla funkcji

v = v(t):

0

0

v

= ,

tj.

( )

0

0

dy

t

dt

=

długość kroku (czasowego):

θ

= 0.001

liczba chwil czasowych:

n = 30000

Znajdź rozwiązanie numeryczne

( )

y

y t

=

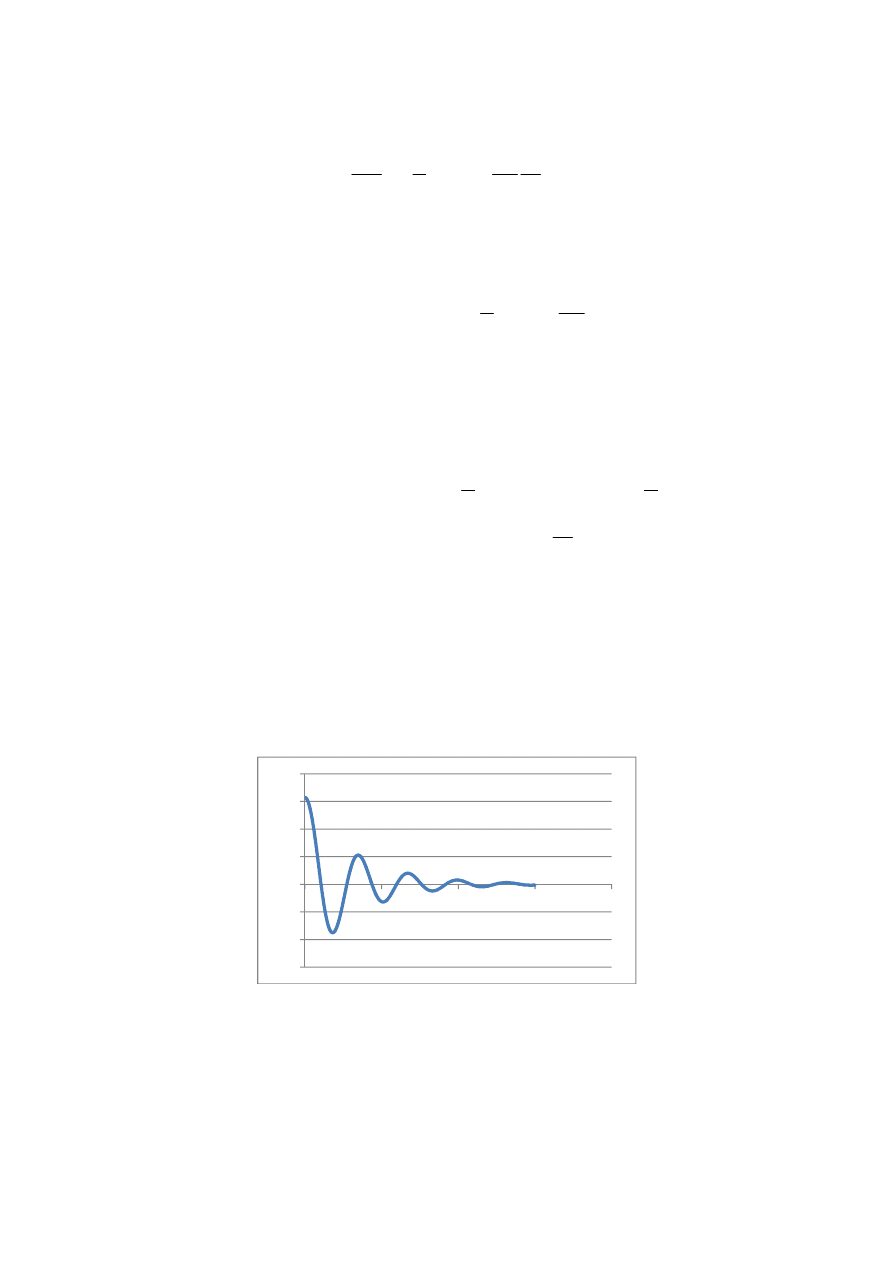
wywołując funkcję

Runge_Kutta(…), której

wykres jest pokazany na rys.2.

Rys. 2. Wykres funkcji

( )

y

y t

=

dla wahadła matematycznego.

-1.5

-1

-0.5

0

0.5

1

1.5

2

0

10

20

30

40

Zadanie problemowe - oscylator harmoniczny

Rozważmy równanie różniczkowe ruchu punktu materialnego o masie

m, z warunkami

początkowymi na przemieszczenie

y = y(t) i prędkość y’ = y’(t)

( )

( )

( )

2

2

0

0 ,

0

0

d y

m

ky

F t

dt

dy

y

dt

+

=

=

=

F = F(t)

y = y(t)

k

m

Umieszczony na końcu sprężyny o stałej

k punkt ma masę m. Do punktu materialnego

przyłożona jest, zależna tylko od czasu

τ

, siła

F = F(

τ

). Pomijamy tarcie pomiędzy punktem a

podłożem.
Nietrudno wykazać, że całka ogólna tego równania (jego rozwiązanie) dana jest wzorem

( )

(

) ( )

0

1

sin

,

0

t

y

y t

t

F

d

t

m

ω ωτ

τ τ

ω

=

=

−

≥

∫

.

gdzie zdefiniowano nową wielkość, tzw. częstość kołową drgań

k

m

ω

=

Dla siły

F = F(t) danej wzorem

( )

[

]

0,

const

const

const

const

const

F

t

t

F

F

t

τ τ

τ

τ



∈



= 



≥



t

const

F

const

F(

<

)

<

całkę ogólną równania różniczkowego możemy przedstawić w postaci następującego wzoru:

( )

( )

[

]

(

)

( )

sin

1

0,

1

1

sin

sin

const

const

STAT

const

const

const

t

t

t

t

t

y t

y

t

t

t

t

t

t

ω

ω

ω ω

ω

ω







−

∈













=



 +

−

−

≥











gdzie

2

const

const

STAT

F

F

y

k

m

ω





=

= 







jest rozwiązaniem statycznym równania różniczkowego, dla stałego w czasie obciążenia
F

const

.

W celu sprawdzenia skuteczności algorytmu Runge-Kutta rozwiązywania układu dwóch
równań różniczkowych zwyczajnych, dopasujmy najpierw oznaczenia i zdefiniujmy
poprawnie wszystkie funkcje, które są parametrami naszej procedury. Najpierw równanie

( )

2

2

d y

m

ky

F t

dt

+

=

zapiszmy w postaci

( )

2

2

F t

ky

d y

dt

m

−

=

i zgodnie z podanymi wzorami oraz po uwzględnieniu faktu, że rolę zmiennej

x, odgrywa

teraz parametr

t, mamy następujące definicje funkcji f i g:

(

)

3

:

;

, ,

f R

R f t u v

v

→

=

(

)

(

)

3

:

;

, ,

, ,

g R

R g t u v

h t u v

→

=

gdzie dla zdefiniowanej wcześniej funkcji

F = F(t)

(

)

( )

, ,

F t

ku

h t u v

m

−

=

Wartości pozostałych parametrów są następujące:
chwila początkowa:

x

0

= 0

warunek początkowy dla funkcji

u = u(t):

u

0

= 0

warunek początkowy dla funkcji

v = v(t):

v

0

= 0

długość kroku (czasowego):

θ

= 0.001

liczba chwil czasowych

n,

n = 500 ÷ 2000

Dla przyjętych danych, przeprowadź symulację numerycznego rozwiązania naszego równania
oscylatora, dla kilku różnych wartości chwili czasowej

t

const

charakteryzującej moment, w

którym narastająca liniowo siła

F = F(t) osiąga stałą wartość F

const

= 1000.0 [N]. Przyjmij

ponadto stałą sprężyny

k = m ·

ω

2

dla

m = 1.0 [kg] i

ω

= 50.0 [1/s]. Chwilę czasową

t

const

zdefiniuj następująco:

const

t

T

ξ

= ⋅

gdzie

2

T

π

ω

=

natomiast

ξ

jest dowolną, ale ustaloną liczbą dodatnią. Wykresy sporządź nie dla funkcji

y =

y(t), ale dla ilorazu

( )

STAT

y t

y

gdzie

[ ]

[ ]

2

2

2

1000.0 N

0.4[m]

1

1.0 kg 50.0

s

const

const

STAT

F

F

y

k

m

ω





=

=

=

=





 





⋅

 

 

.

Przypadek 1 (

θ

= 0.001,

ξ

= 0.5,

n = 500)

Przypadek 2 (

θ

= 0.001,

ξ

= 1.0 ,

n = 500)

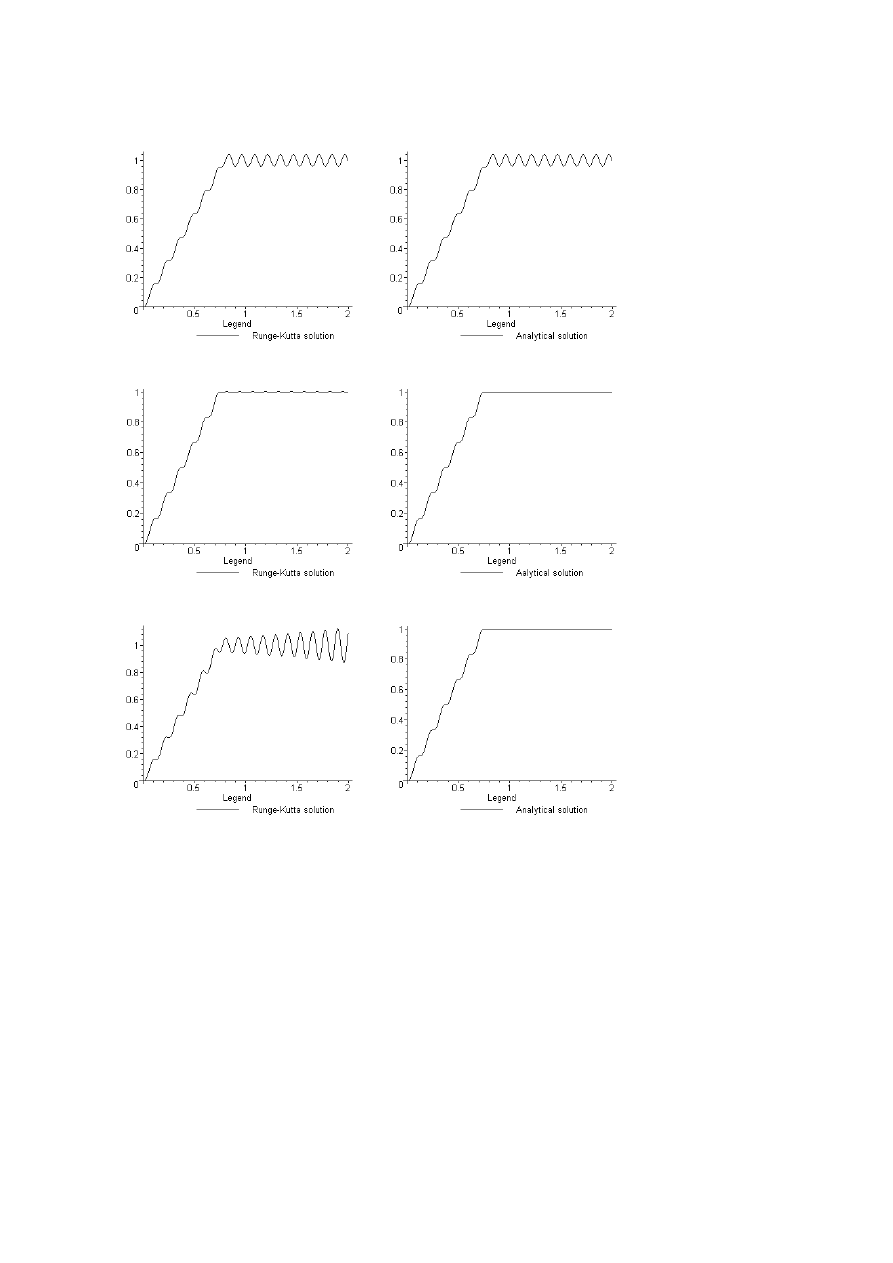
Przypadek 3 (

θ

= 0.001,

ξ

= 6.3 ,

n = 2000)

Przypadek 4 (

θ

= 0.001,

ξ

= 6.0 ,

n = 2000)

Przypadek 5 (

θ

= 0.01

,

ξ

= 6.0 ,

n = 200)

W przykładzie tym widzimy, jak przyjęcie zbyt dużego kroku czasowego

θθθθ

powoduje na

tyle znaczące pogorszenie dokładności rozwiązania numerycznego, że w praktyce nie
mogłoby być ono zaakceptowane.

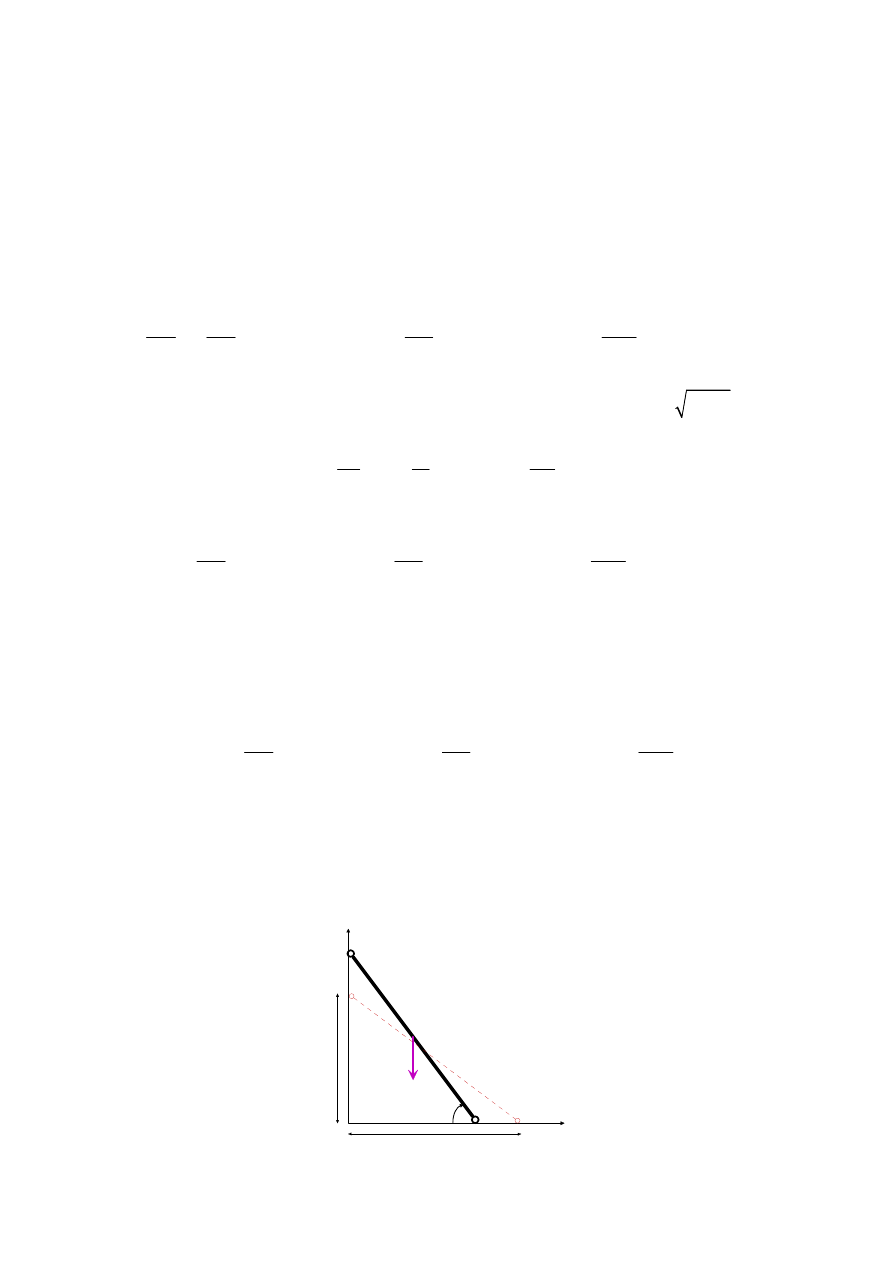
Zadanie problemowe – drgania pręta

Jednorodny pręt

AB o masie m jest obciążony w środku geometrycznym dodatkową pionową

siłą

( )

Q

Q t

=

. Końce

A i B mogą przemieszczać się bez poślizgu odpowiednio wzdłuż osi y i

x. Punkty O, A oraz O, B połączone są odpowiednio pionową sprężyną o stałej k

y

i poziomą

sprężyną o stałej

k

x

, których długości w stanie naturalnym (nierozciągniętym) wynoszą

odpowiednio

l

y

,

l

x

. Przyjmując kąt

( )

t

φ φ

=

jako współrzędną uogólnioną Lagrange’a,

wyprowadź równanie różniczkowe ruchu pręta z równania Lagrange’a II-go rodzaju:

( )

( )

( )

( )

( )

2

2

3

3

3

sin

cos

cos

sin

cos

2

y

x

y

x

k

k

d

l

l

l

l

P

dt

m l

m l

m l

φ

φ

φ

φ

φ

φ





= −

−

−

−

−













(

•)

gdzie

( )

( )

P

P t

G

Q t

=

= +

(

G

m g

=

,

g oznacza przyśpieszenie ziemskie),

2

2

x

y

l

l

l

=

+

.

Dopasowując się do oznaczeń argumentów i funkcji przyjętych w opisanych powyżej

algorytmach:

t

x

= ,

u

φ

=

,

d

v

dt

φ

=

,

( ) ( )

...

... '

d

dt

=

,

( ) ( )

2

2

...

... "

d

dt

=

ostateczna postać

równania różniczkowego (

•) będzie zatem następująca:

( )

( )

( )

( )

( )

3

3

3

''

sin

cos

cos

sin

cos

2

y

x

y

x

k

k

u

l

u

l

u

l

l

u

u

P

u

m l

m l

m l





= −

−

−

−

−













(

••)

która z kolei jest równoważna układowi dwóch równań różniczkowych zwyczajnych

(

)

'

'

, ,

u

v

v

h x u v

=

=

gdzie

(

)

( )

( )

( )

( )

( )

3

3

3

, ,

sin

cos

cos

sin

cos

2

y

x

y

x

k

k

h x u v

l

u

l

u

l

l

u

u

P

u

m l

m l

m l





= −

−

−

−

−













.

Znajdź numeryczne rozwiązanie równania różniczkowego funkcją

Runge_Kutta(...) dla

następujących danych:

(

)

(

)

(

)

0

0

0

0 ,

0.12435499454676195 ,

0 ,

0.003 ,

31999

, ,

,

, ,

, ,

1.0 ,

2.0 ,

2.0 ,

4.0 ,

3.0 ,

10.0

x

y

x

y

x

u

v

n

f x u v

v g x u v

h x u v

m

k

k

l

l

g

θ

=

=

=

=

=

=

=

=

=

=

=

=

=

x

y

P

k

y

k

x

l

x

l

y

φ

Α

Β

Ο

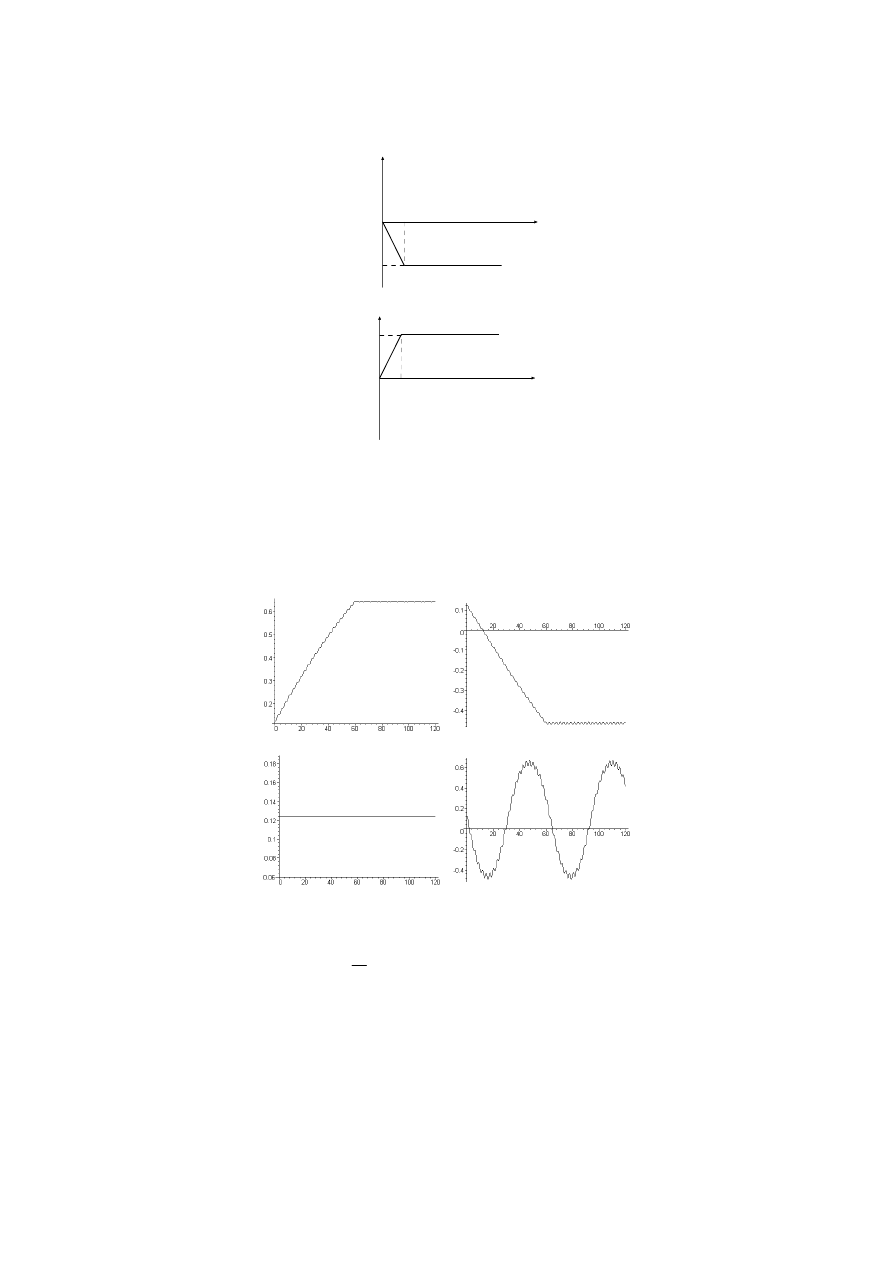
Siłę

(

)

Q

Q t

x

=

=

zdefiniuj na cztery sposoby:

I przypadek:

- G

t

Q

t

0

II przypadek:

G

t

Q

t

0

III przypadek:

( )

0

Q t

const

= =

IV przypadek:

( )

(

)

sin 0.1

Q t

G

t

=

⋅

gdzie

0

60

t =

.

Wartości składowych wektorów

[

]

1

x n +

,

[

]

1

U n +

zapisz do pliku tekstowego i porównaj

wczytane wartości z tymi podanymi na poniższych rysunkach.

Zależność kąta

( )

t

φ φ

=

kolejno dla I, II, III i IV przypadku

Kąt

[

]

0.643501

arctan

y

x

l

rad

l

φ

 

≈

=

 

 

definiuje położenie równowagi pręta dla przypadku

0

P

= (położenie w którym sprężyny są w stanie naturalnym).

Kąt

[

]

0.463648 rad

φ

≈ −

definiuje położenie równowagi pręta dla przypadku

2

P

G

=

.

Kąt

[

]

0.124355 rad

φ

≈

definiuje położenie równowagi pręta dla przypadku P

G

=

.