Informatyka I – Lab 10, r.a. 2011/2012
prow. Sławomir Czarnecki
Zadania na laboratorium nr. 10
Po utworzeniu nowego projektu, dołącz bibliotekę bibs.h.
1. Zdefiniuj dwie wersje funkcji „silnia” n! = n ⋅ ( n − ) 1 ⋅ ( n − 2) ⋅...⋅ 2 ⋅1 dla dowolnego n ≥ 0 .
Pierwszą wersję rekurencyjną:
unsigned long silnia(unsigned long n) i drugą wersję iteracyjną
unsigned long SILNIA(unsigned long n) Przetestuj działanie obu tych funkcji dla n nie większego od 12.
2. Zdefiniuj (bardzo niewydajną) rekurencyjną wersję unsigned long binomial(unsigned long n, unsigned long k) funkcji na współczynnik dwumianowy
n
n!
=
dla 0 ≤ k ≤ n
k
k (
! n − k )!
korzystając z następującej prostej do udowodnienia indukcyjnie zależności rekurencyjnej
n −1 n −1
n
+
0 < k < n
=
k −1
k
k
1
k = 0
lub
k = n
która pozwala wyeliminować konieczność obliczania wyrażenia typu n! lub k ! .
n
n
Algorytm rekurencyjny oblicza aż 2
−1
wyrazów w celu obliczenia wartości .
k
k
=
=
(
, gdzie składowa B [ i][ j] ( i 0,1,..., n, j
0,1,..., k )
n+ )
1 × ( k + )
1
i
będzie zawierała wartość możliwe jest „skonstruowanie” znacznie wydajniejszej j
iteracyjnej wersji algorytmu
unsigned long BINOMIAL(unsigned long n, unsigned long k) Definiowanie składowych macierzy B oparte jest rekurencyjną zależność
[ ][ ] B[ i − ]1[ j − ]1+ B[ i − ]
1 [ j] 0 < j < i
B i
j =
1
j = 0
lub
j = i
oraz o realizację w porządku wstępującym, rozpoczynającym się od pierwszego wiersza i wyliczającym po kolei wartości w wierszach tablicy B. Każda kolejna składowa wiersza (od lewej do prawej) jest wyliczana na podstawie wartości składowych w wierszu poprzedzającym przy wykorzystaniu powyższej zależności rekurencyjnej. Ostatnia obliczana
n = 4
wartość, to [ ][ ]
n
B n k = . Np. przy obliczaniu
mamy
k
k = 2
B[0][0] = 1
(wartość B[0][0] nie jest potrzebna w dalszych obliczeniach) B[1][0]
=
1
B[1][1]
=
1
B[2][0]
=
1
B[2][1]
=
B[1][0] + B[1][1] = 1 + 1 = 2
B[2][ k=2]
=
1
B[3][0]
=
1
B[3][1]
=
B[2][0] + B[2][1] = 1 + 2 = 3
B[3][ k=2]
=
B[2][1] + B[2][2] = 2 + 1 = 3
B[ n=4][0]
=
1
B[ n=4][1]
=
B[3][0] + B[3][1] = 1 + 3 = 4
B[ n=4][ k=2] =
B[3][1] + B[3][2] = 3 + 3 = 6
(Uwaga ! możliwych jest jeszcze szereg wielu dodatkowych ulepszeń). Przetestuj działanie obu tych funkcji.
3. Zdefiniuj dwie, odpowiednio rekurencyjną i iteracyjną wersję double bisection(double ( * f )(double), double a, double b, double eps) double BISECTION(double ( * f )(double), double a, double b, double eps) funkcji poszukiwania pierwiastka ciągłej funkcji jednej zmiennej rzczywistej f : ℝ → ℝ w przedziale domkniętym I = [ a, b] ⊂ ℝ z dokładnością eps > 0, w oparciu o algorytm metody bisekcji. Zakładamy, że wartości funkcji f na końcach przedziału I są różne od zera i mają różne znaki.
W wersji rekurencyjnej mamy:
• Pre: x lewy < x prawy , eps > 0. Znaki f( x) w punktach x lewy i x prawy muszą być różne, co wystarcza do stwierdzenia, że w przedziale [ x lewy , x prawy] znajduje się co najmniej jeden pierwiastek.
• Rozpoczynamy od wyznaczenia punktu środkowego x srodek = ( x lewy + x prawy) / 2.
• Należy wyróżnić dwa przypadki elementarne: x prawy – x lewy < eps lub f( x srodek) = 0 dla których pierwiastek = x srodek.
• Nie spełnienie żadnego z przypadków elementarnych prowadzi do rekurencyjnego wywołania funkcji:
bisection( f, x lewy, x srodek, eps) jeśli f( x lewy) f( x srodek) < 0
lub
bisection( f, x srodek, x prawy, eps) jeśli f( x lewy) f( x srodek) > 0.
f(x prawy )
pierwiastek
x lewy
x prawy
x srodek
f(x lewy )
f(x prawy )
pierwiastek
x lewy
x prawy
x srodek
f(x lewy )
f(x prawy )
x
x
lewy
prawy
x srodek
pierwiastek
f(x lewy )
W wersji iteracyjnej strategia polega poszukiwaniu pierwiastka od skrajnego lewego punktu przedziału I w kierunku prawym lub od skrajnego prawego punktu przedziału I w kierunku lewym, w zależności od tego, w którym z tych punktów wartość funkcji jest ujemna. Każdy kolejny przyrost (dodatni lub ujemny) jest połową wartości ostatniego przyrostu, przy czym nie dopuszczamy do sytuacji, w której wartość funkcji w nowo sprawdzanym punkcie byłaby dodatnia (zawsze jesteśmy po ujemnej stronie). Szczegóły będą omówione na laboratorium.
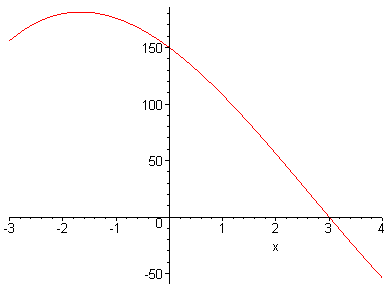
Przetestuj działanie obu tych funkcji dla funkcji f ( x) 3
2
= x − 8 x − 35 x +150 w przedziale
[-3 , 4], której wykres przedstawiono na poniższym rysunku.
4. Sortowanie tablicy a[ dim] przez wstawianie (por. np. Cormen T., Leiserson C., Rivest R., Wprowadzenie do algorytmów, Wyd. Naukowo-Techniczne, Warszawa 1997). Algorytm jest analogiczny do czynności porządkowania talii kart. Zaczynamy od „pustej” lewej ręki, po czym bierzemy ze stołu kolejne karty i wstawiamy je we właściwe miejsca w posortowanej już części talii kart trzymanej w lewej ręce. Aby znaleźć właściwe miejsce dla danej karty trzymanej w prawej ręce, porównujemy ją (od strony prawej do lewej) z posortowanymi już
kartami, które mamy w lewej ręce. Przykład:
lewa ręka
stół z nieposortowanymi kartami
5 2 4 6 1 3
talia na stole do posortowania
5
2 4 6 1 3
bierzemy pierwszą kartę 5 ze stołu do lewej ręki 5 2
4 6 1 3
bierzemy drugą kartę
2 ze stołu do lewej ręki
2 5
4 6 1 3
szukamy dla karty
2 właściwego miejsca w lewej ręce
2 5 4
6 1 3
bierzemy trzecią kartę
4 ze stołu do lewej ręki
2 4 5
6 1 3
szukamy dla karty
4 właściwego miejsca w lewej ręce
2 4 5 6
1 3
bierzemy czwartą kartę 6 ze stołu do lewej ręki
2 4 5 6 1
3
bierzemy piątą kartę
1 ze stołu do lewej ręki
2 4 5 1 6
3
szukamy dla karty
1 właściwego miejsca w lewej ręce
2 4 1 5 6
3
szukamy dla karty
1 właściwego miejsca w lewej ręce
2 1 4 5 6
3
szukamy dla karty
1 właściwego miejsca w lewej ręce
1 2 4 5 6
3
szukamy dla karty
1 właściwego miejsca w lewej ręce
1 2 4 5 6 3
bierzemy szóstą kartę
3 ze stołu do lewej ręki
1 2 4 5 3 6
szukamy dla karty
3 właściwego miejsca w lewej ręce
1 2 4 3 5 6
szukamy dla karty
3 właściwego miejsca w lewej ręce
1 2 3 4 5 6
szukamy dla karty
3 właściwego miejsca w lewej ręce
Uwaga ! Elementy tablicy mogą być sortowane w miejscu, tzn. nie jest konieczne definiowanie żadnej innej dodatkowej tablicy pomocniczej i wszystkie operacje można przeprowadzać na elementach sortowanej tablicy.
5. Porównanie dwóch algorytmów sortowania: insert_sort(...) oraz quick_sort(...).
Utwórz dość dużą tablicę v typu double (np. v[100000]) inicjalizując ją dowolnymi liczbami losowymi (na przykład z przedziału [–1000.0,1000.0]).
Przeprowadź dla tablicy v test szybkości działania obu algorytmów sortowania insert_sort(...) i quick_sort(...).
6. Zaimplementuj algorytm poszukiwania binarnego w posortowanej tablicy a[dim] jako funkcję int binary_search(double* a, double x, int dim). Funkcja binary_search(...) ma zwracać najmniejszy indeks i (0 ≤ i < dim) , dla którego x = a[ i] lub –1, jeśli nie istnieje składowa wektora a równa x. Idea (dobrze znanego i bardzo prostego) algorytmu poszukiwania binarnego przedstawiona będzie w czasie zajęć.
Wyszukiwarka
Podobne podstrony:
Lab 02 2011 2012
Lab 06 2011 2012
Lab 09 2011 2012
Lab 06 2011 2012 NWD
więcej podobnych podstron