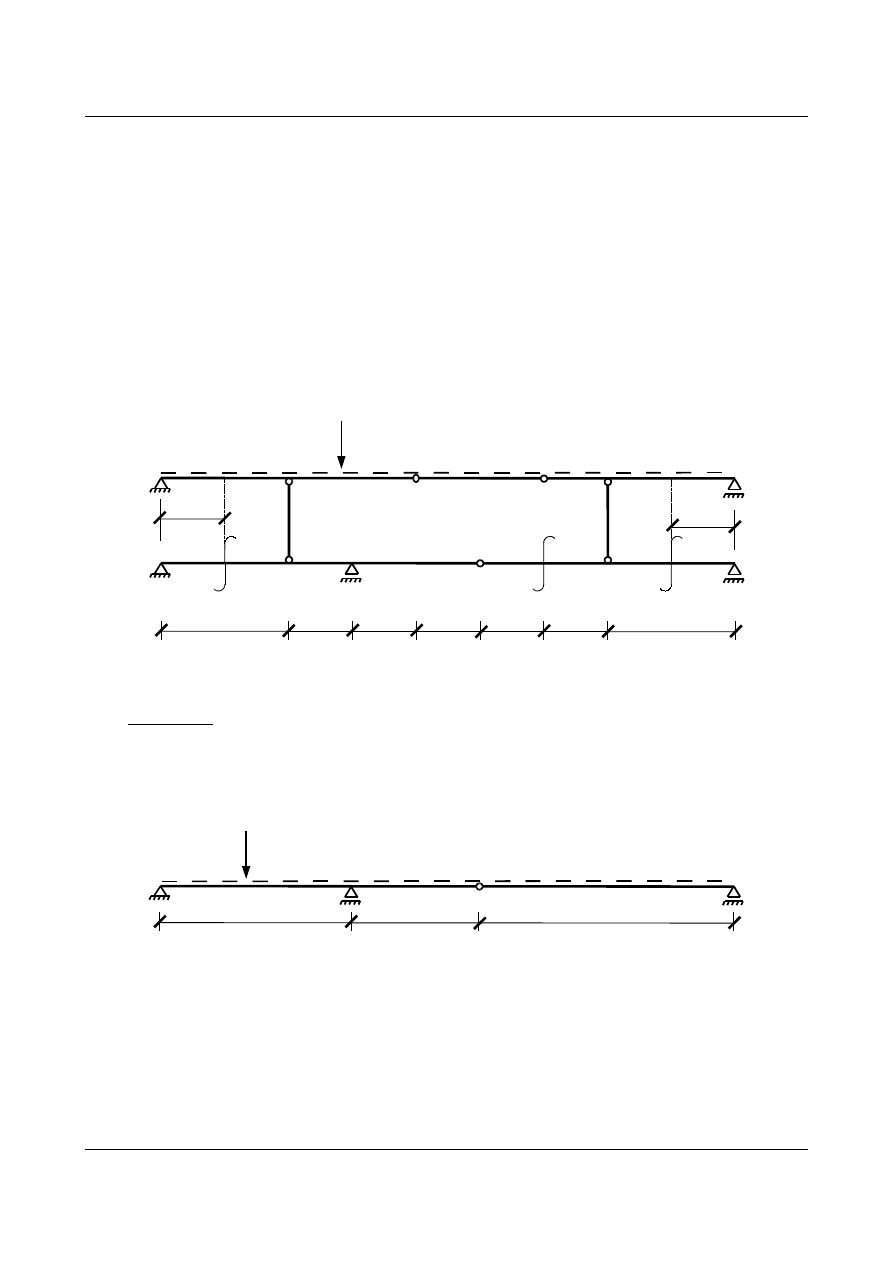
Część 1
1. LINIE WPŁYWOWE W UKŁADACH STATYCZNIE WYZNACZALNYCH
1
1.
1. LINIE WPŁYWOWE W UKŁADACH
STATYCZNIE WYZNACZALNYCH
1.1. Zadanie 1
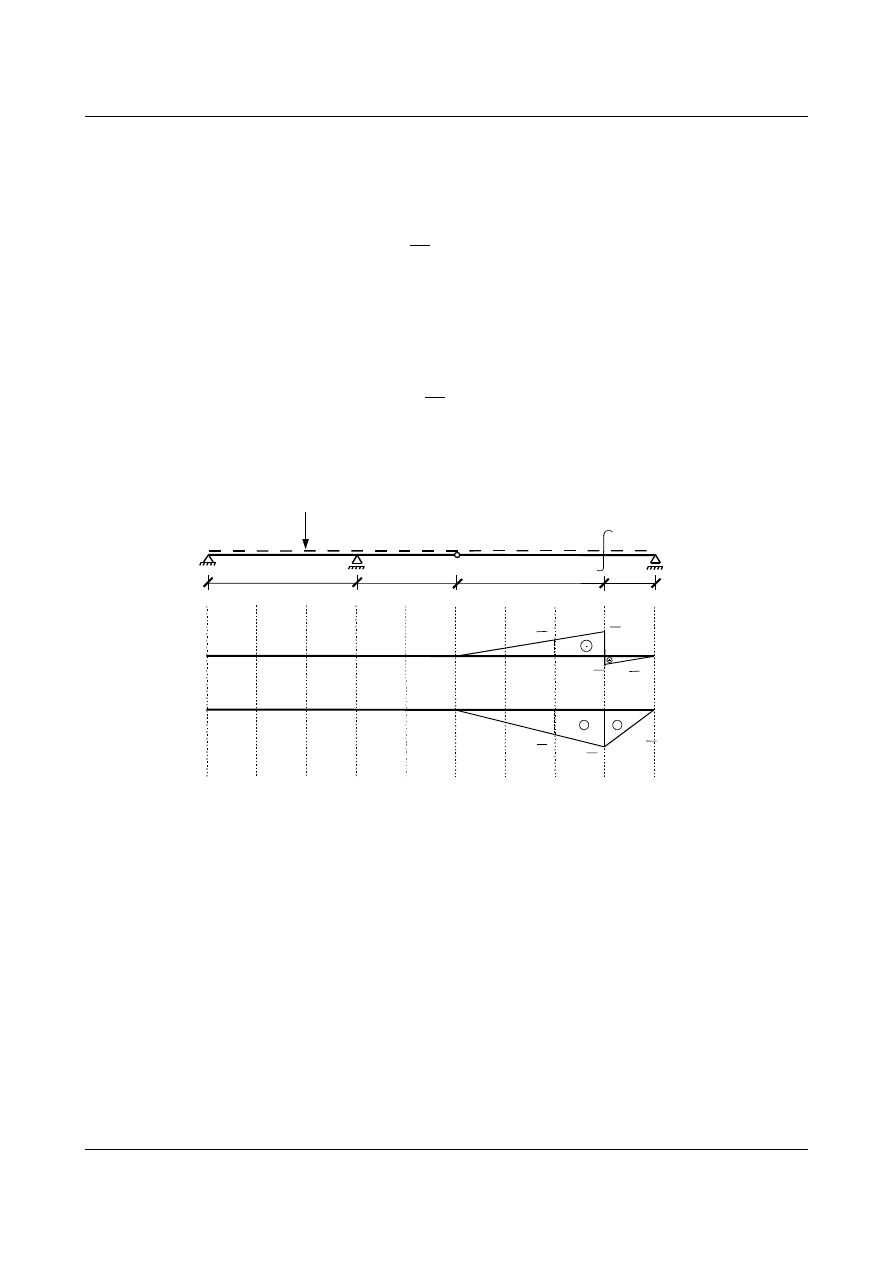
Dla belki przedstawionej na poniższym rysunku wyznaczyć linie wpływowe zaznaczonych wielkości
statycznych (linie wpływowe reakcji podporowych oraz sił wewętrznych w zaznaczonych przekrojach
− , − , − ,−
).
P=1 [-]
2a
2a
a
a
a
a
a
A
B
C
D
a
a
α
γ
α
γ
β
β
Rys. 1.1.
Rozwiązanie
Wyznaczając linie wpływowe wielkości statycznych dla belki z pomostem pośrednim na którym
porusza się jednostkowa siła P=1 [-] początkowo rozpatrzyć należy analogiczną belkę bez pomostu (rys. 1.2)
P=1 [-]
4a
A
B
C
D
2a
3a
Rys. 1.2.
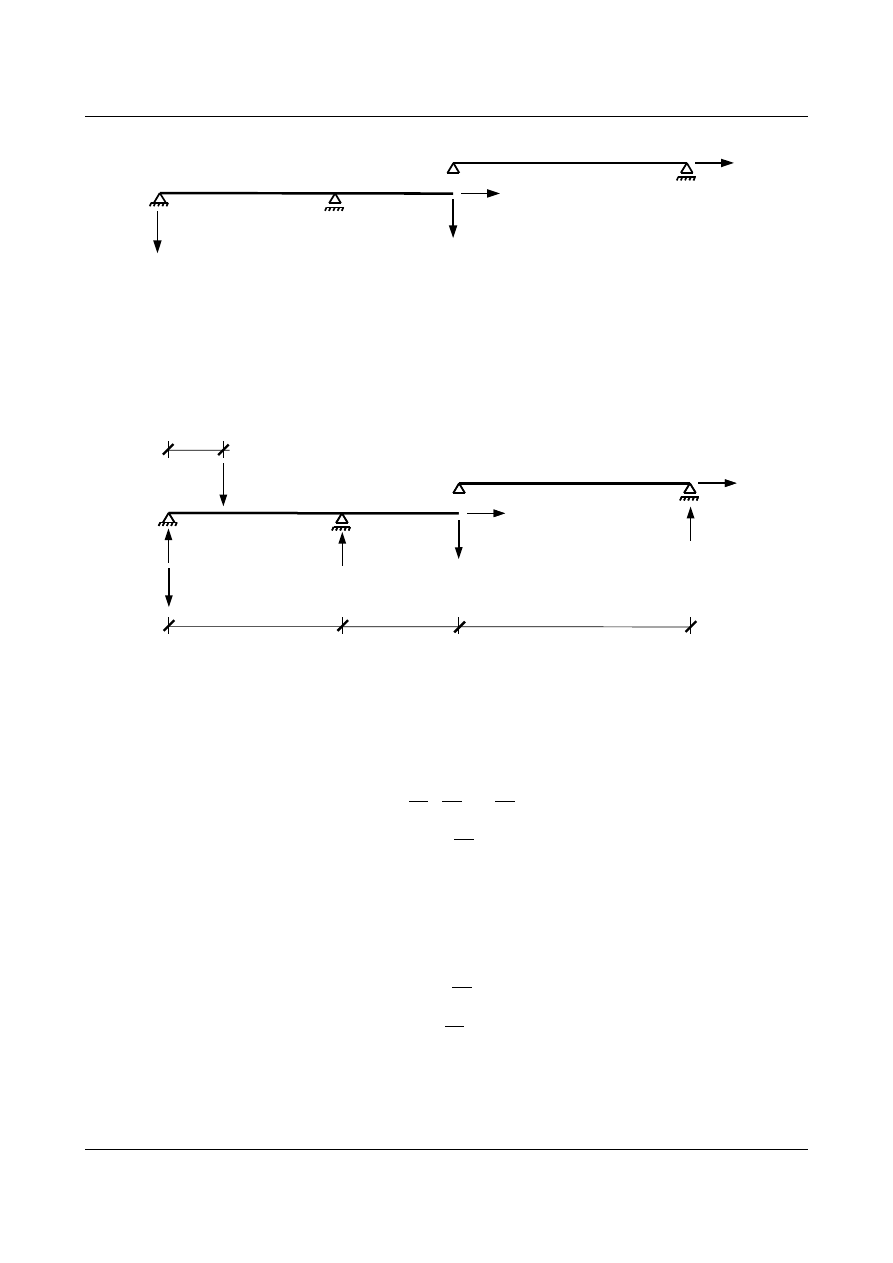
Daną belkę złożoną należy rozdzielić na dwie belki proste dla których przyjmujemy odpowiednie
układy współrzędnych (rys. 1.3).
Dominik Kretschmer, Łukasz Lewiński – gr.2
AlmaMater
Część 1
1. LINIE WPŁYWOWE W UKŁADACH STATYCZNIE WYZNACZALNYCH
2
x
1
y
1
x
2
y
2
A
B
C
D
Rys.1.3.
1. Wyznaczenie funkcji reakcji podporowych w zależności od położenia poruszającej się siły P=1 [-].
a)
x
∈〈 A ;C 〉
- położenie siły P=1[-] określa współrzędna
x
1
x
1
x
2
P=1 [-]
A
B
C
D
x
1
y
1
x
2
y
2
P=1 [-]
A
B
C
D
V
A
(x)
V
D
(x)
V
B
(x)
x
1
4a
2a
3a
Rys. 1.4.
Wyznaczenie linii wpływu reakcji podporowej
V
A
-
lw V
A
∑
M
B
=0
V
A
⋅3 a−1⋅3 a−x
1
=0
V
A
=
3 a
3 a
−
x
1
3 a
=1−
x
1
3 a
lwV
A
=1−
x
1
3 a
[ − ]
Wyznaczenie linii wpływu reakcji podporowej
V
B
-
lw V
B
∑
M
A
=0
−V
B
⋅3 a1⋅x
1
=0
V
B
=
x
1
3 a
lwV
B
=
x
1
3 a
[ − ]
Dominik Kretschmer, Łukasz Lewiński – gr.2
AlmaMater
Część 1
1. LINIE WPŁYWOWE W UKŁADACH STATYCZNIE WYZNACZALNYCH
3
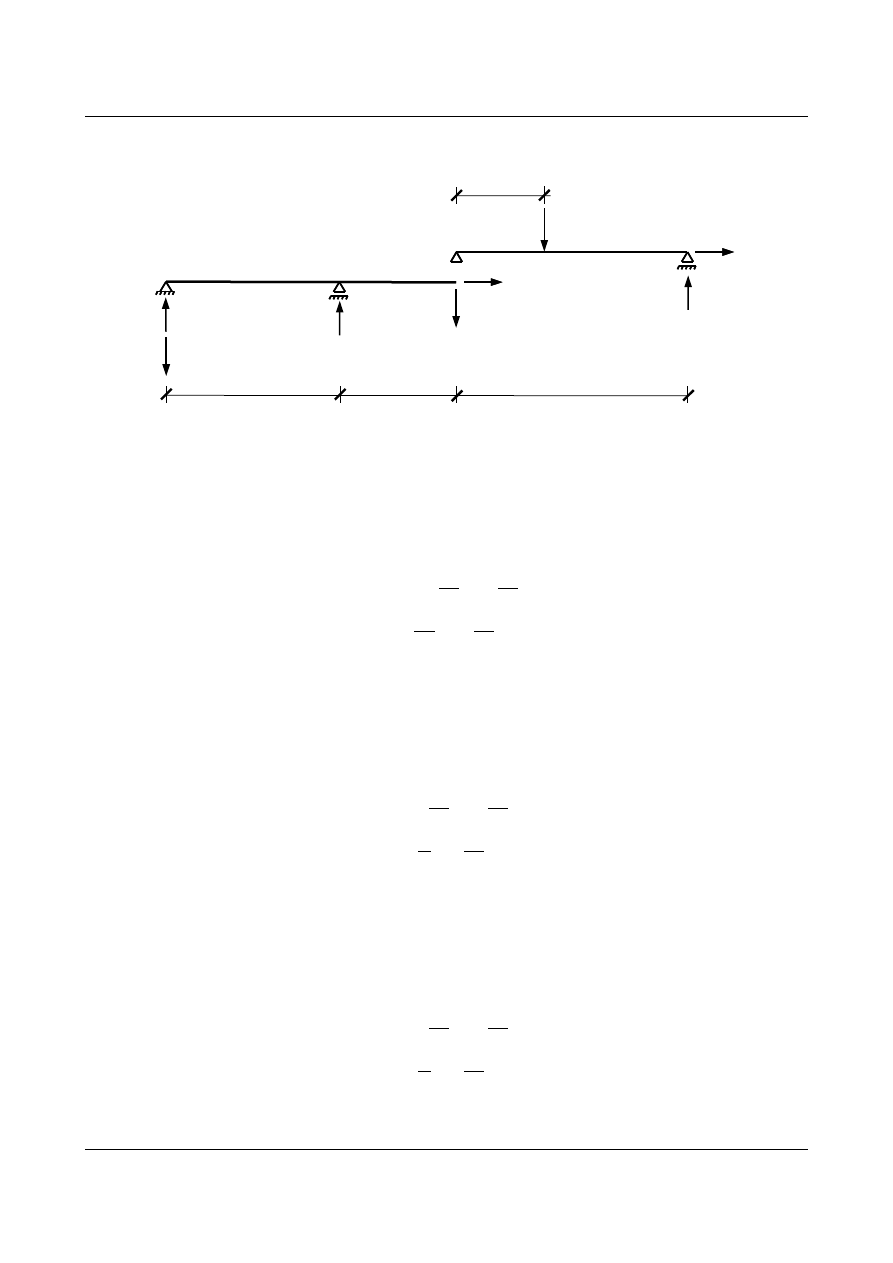
b)
x
∈〈C ; D〉
- położenie siły P=1[-] określa współrzędna
x
2
x
1
x
2
P=1 [-]
A
B
C
D
x
1
y
1
x
2
y
2
P=1 [-]
A
B
C
D
V
A
(x)
V
D
(x)
V
B
(x)
x
2
4a
2a
3a
Rys. 1.5.
Wyznaczenie linii wpływu reakcji podporowej
V
A
-
lw V
A
lwV
A
=lwV
A
C ⋅lwV
C
lwV
A
=lwV
A
5 a⋅lwV
C
lwV
A
=
1
−
5 a
3 a
⋅
1
−
x
2
4 a
lwV
A
=
−2
3
⋅
1
−
x
2
4 a
[ − ]
Wyznaczenie linii wpływu reakcji podporowej
V
B
-
lw V
B
lwV
B
=lwV
B
C ⋅lwV
C
lwV
B
=lwV
B
5 a⋅lwV
C
lwV
B
=
5 a
3 a
⋅
1
−
x
2
4 a
lwV
B
=
5
3
⋅
1
−
x
2
4 a
[ − ]
Wyznaczenie linii wpływu reakcji podporowej
V
B
-
lw V
B
lwV
B
=lwV
B
C ⋅lwV
C
lwV
B
=lwV
B
5 a⋅lwV
C
lwV
B
=
5 a
3 a
⋅
1
−
x
2
4 a
lwV
B
=
5
3
⋅
1
−
x
2
4 a
[ − ]
Dominik Kretschmer, Łukasz Lewiński – gr.2
AlmaMater
Część 1
1. LINIE WPŁYWOWE W UKŁADACH STATYCZNIE WYZNACZALNYCH
4
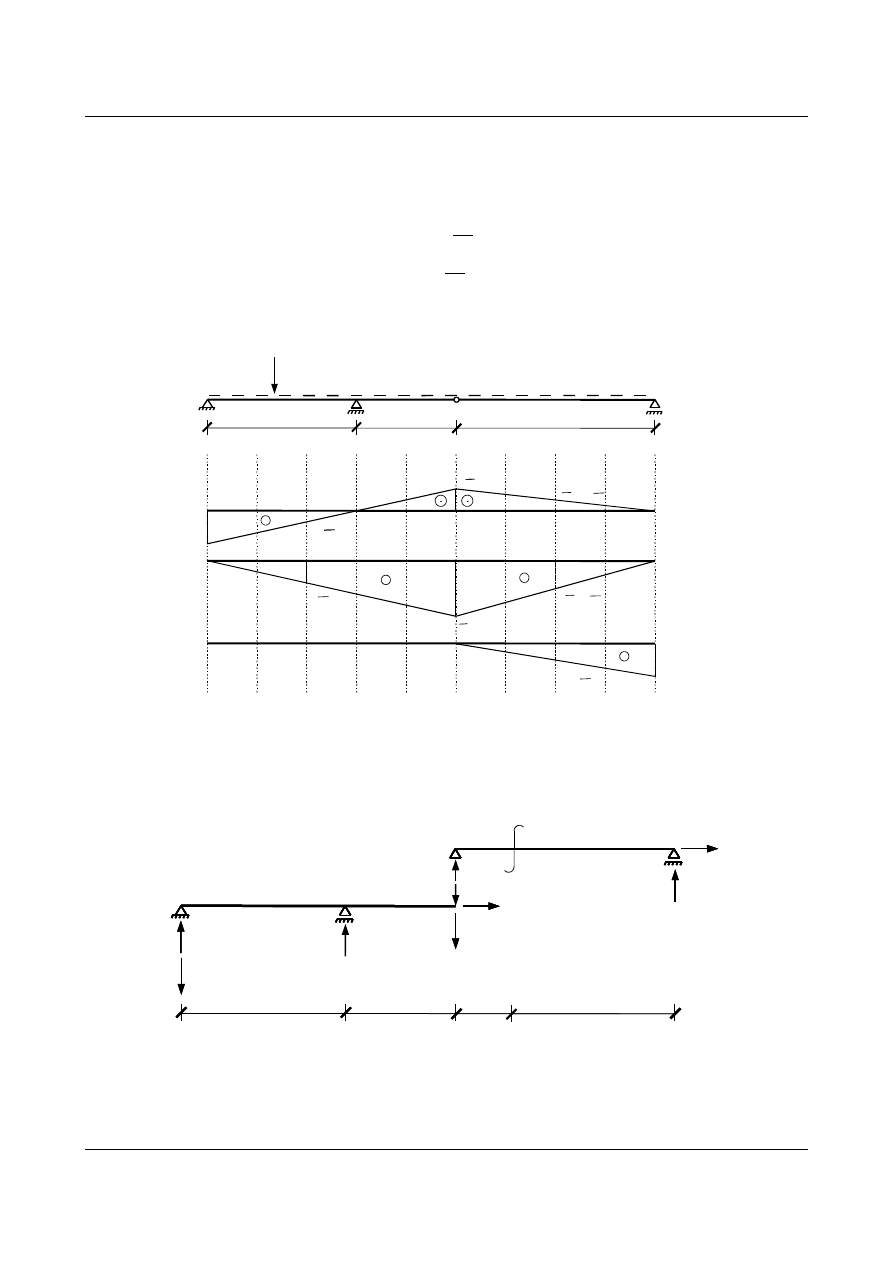
Wyznaczenie linii wpływu reakcji podporowej
V
D
-
lw V
D
∑
M
C
=0
−V
D
⋅4 a1⋅x
2
=0
V
D
=
x
2
4 a
lwV
D
=
x
2
4 a
[ − ]
Wykres linii wpływu reakcji podporowych przedstawiono na poniższym rysunku.
1
1
P=1 [-]
4a
A
B
C
D
2a
3a
lw V
A
lw V
D
[-]
[-]
lw V
B
[-]
1 -
x
1
3a
+
+
+
+
2
3
-
(1 - )
x
2
4a
2
3
(- )
5
3
x
1
3a
x
2
4a
5
3
(1- )
x
2
4a
1-
Rys. 1.6.
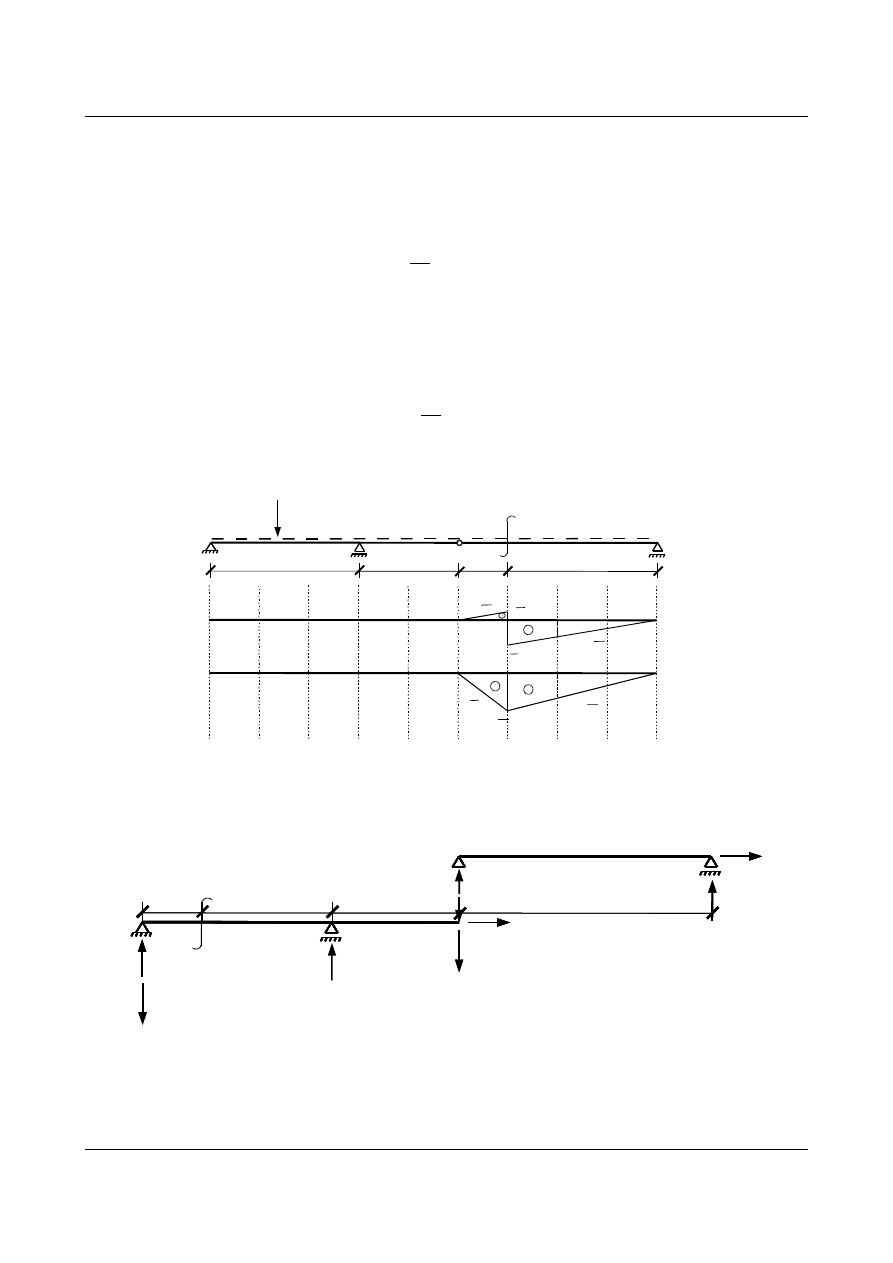
2. Wyznaczenie funkcji sił wewnętrznych w przekroju α-α.
x
2
A
B
C
D
y
1
y
2
D
V
A
(x)
V
D
(x)
V
B
(x)
2a
3a
D
x
1
D
2a
3a
V
C
(x)
V
C
(x)
a
α
α
3a
Rys. 2.1.
Dominik Kretschmer, Łukasz Lewiński – gr.2
AlmaMater
Część 1
1. LINIE WPŁYWOWE W UKŁADACH STATYCZNIE WYZNACZALNYCH
5
a)
x
∈〈 A ;C 〉
- położenie siły P=1[-] określa współrzędna
x
1
lwT
=0 [ − ]
lwM
=0 [m]
b)
x
∈〈C ; D〉
- położenie siły P=1[-] określa współrzędna
x
2
•
0
≤x
2
a
W celu uproszczenia obliczeń warto skorzystać z równań równowagi części położonej na prawo
od przekroju α-α, gdyż nie uwzględnia się wtedy poruszającej się siły.
3a
T
α
V
D
M
α
Rys. 2.2.
∑
Y
=0
−T
−V
D
=0
T
=−V
D
lwT
=−lwV
D
lwT
=−
x
2
4 a
[ − ]
∑
M
−
=0
−V
D
⋅3 aM
=0
M
=3 a⋅V
D
lwM
=3 a⋅lwV
D
=3 a⋅
x
2
4 a
lwM
=
3
4
x
2
[m]
•
a
x
2
≤4 a
W celu uproszczenia obliczeń warto skorzystać z równań równowagi części położonej na lewo
od przekroju α-α, gdyż nie uwzględnia się wtedy poruszającej się siły.
a
M
α
V
D
T
α
Rys. 2.3
Dominik Kretschmer, Łukasz Lewiński – gr.2
AlmaMater
Część 1
1. LINIE WPŁYWOWE W UKŁADACH STATYCZNIE WYZNACZALNYCH
6
∑
Y
=0
−T
V
C
=0
T
=V
C
lwT
=lwV
C
lwT
=1−
x
2
4 a
[ − ]
∑
M
−
=0
V
C
⋅a−M
=0
M
=a⋅V
C
lwM
=a⋅lwV
C
lwM
=a⋅
1
−
x
2
4 a
[m]
Wykres linii wpływu sił wewnętrznych w przekroju α-α przedstawiono na poniższym rysunku.
P=1 [-]
3a
A
B
C
D
2a
3a
α
α
a
lw M
α
lw T
α
[-]
[m]
x
2
4a
-
1
4
-
3
4
x
2
4a
1-
3
4
x
2
a(1- )
x
2
4a
+
+
+
3
4
a
Rys. 2.4.
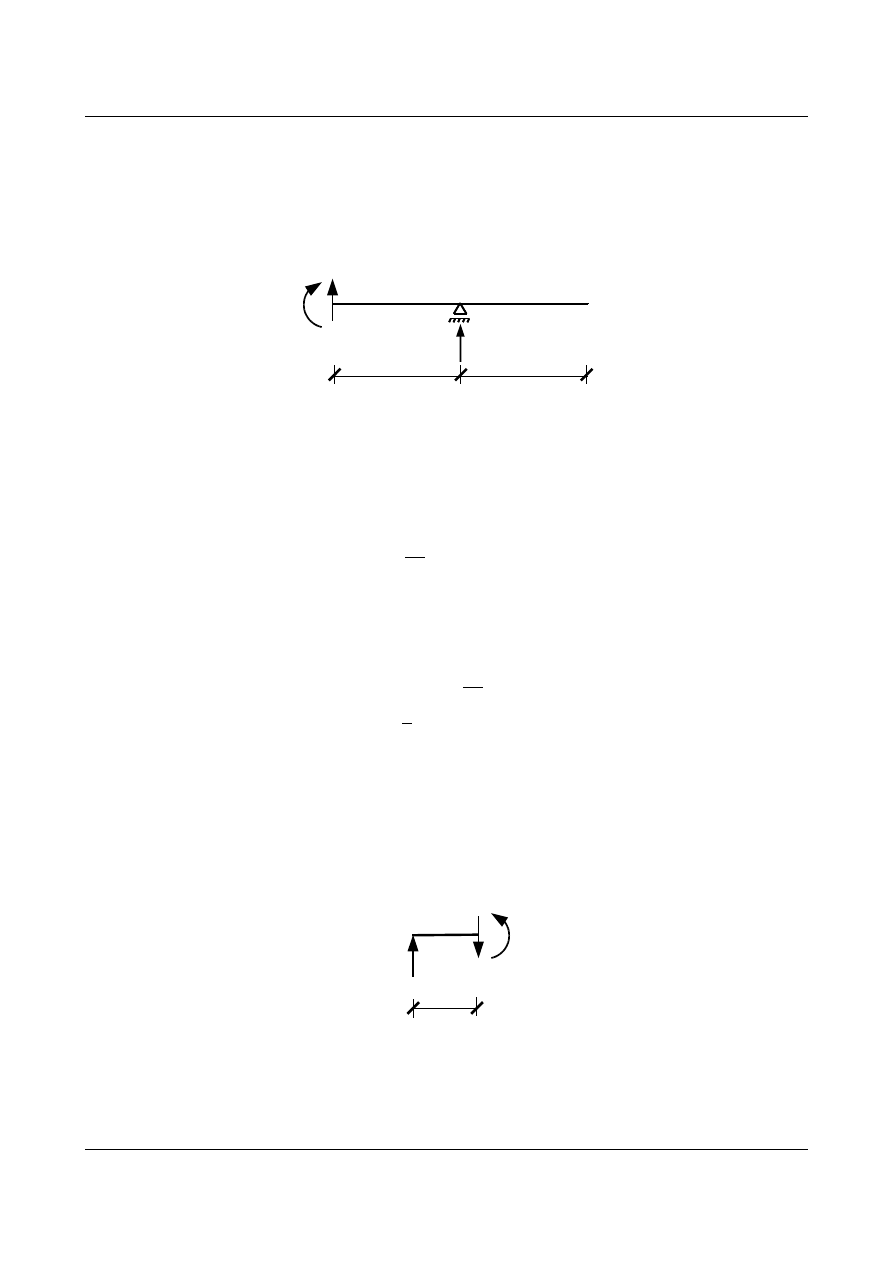
3. Wyznaczenie funkcji sił wewnętrznych w przekroju β-β.
β
x
2
A
B
C
D
y
1
y
2
V
A
(x)
V
D
(x)
V
B
(x)
2a
x
1
2a
V
C
(x)
V
C
(x)
a
3a
β
Rys. 3.1.
Dominik Kretschmer, Łukasz Lewiński – gr.2
AlmaMater
Część 1
1. LINIE WPŁYWOWE W UKŁADACH STATYCZNIE WYZNACZALNYCH
7
•
0
≤x
1
a
W celu uproszczenia obliczeń warto skorzystać z równań równowagi części położonej na prawo
od przekroju β-β, gdyż nie uwzględnia się wtedy poruszającej się siły.
V
B
2a
2a
T
β
M
β
Rys. 3.2.
∑
Y
=0
−T
−V
B
=0
T
=−V
B
lwT
=−lwV
B
lwT
=−
x
1
3 a
[ − ]
∑
M
−
=0
−V
B
⋅2 aM
=0
M
=2 a⋅V
B
lwM
=2 a⋅lwV
B
=2 a⋅
x
1
3 a
lwM
=
2
3
x
1
[m]
•
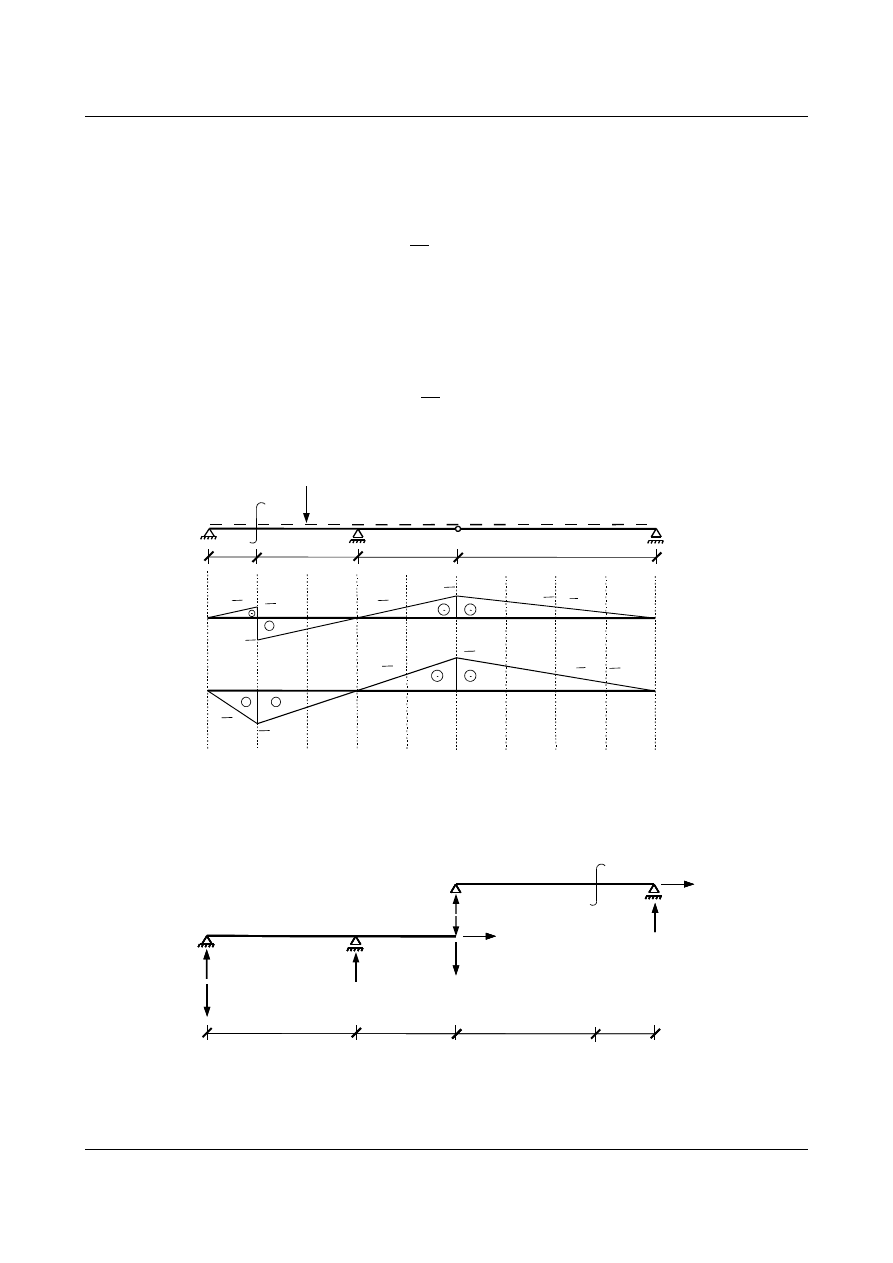
a
x
1
≤5 a
W celu uproszczenia obliczeń warto skorzystać z równań równowagi części położonej na lewo
od przekroju β-β, gdyż nie uwzględnia się wtedy poruszającej się siły.
a
V
A
M
β
T
β
Rys. 3.3.
.
Dominik Kretschmer, Łukasz Lewiński – gr.2
AlmaMater
Część 1
1. LINIE WPŁYWOWE W UKŁADACH STATYCZNIE WYZNACZALNYCH
8
∑
Y
=0
T
−V
A
=0
T
=V
A
lwT
=lwV
A
lwT
=1−
x
1
3 a
[ − ]
∑
M
−
=0
V
A
⋅a−M
=0
M
=a⋅V
A
lwM
=a⋅lwV
A
lwM
=a⋅
1
−
x
1
3 a
[m]
Wykres linii wpływu sił wewnętrznych w przekroju β-β przedstawiono na poniższym rysunku.
P=1 [-]
4a
A
B
C
D
2a
2a
β
a
β
lw M
β
lw T
β
[-]
[m]
x
1
3a
-
1
3
-
2
3
x
1
3a
1 -
2
3
-
x
2
4a
2
3
(- )(1- )
2
3
x
1
2
3
a
2
3
- a
a(1- )
x
1
3a
x
2
4a
2
3
(- a)(1- )
+
+
+
Rys. 3.4.
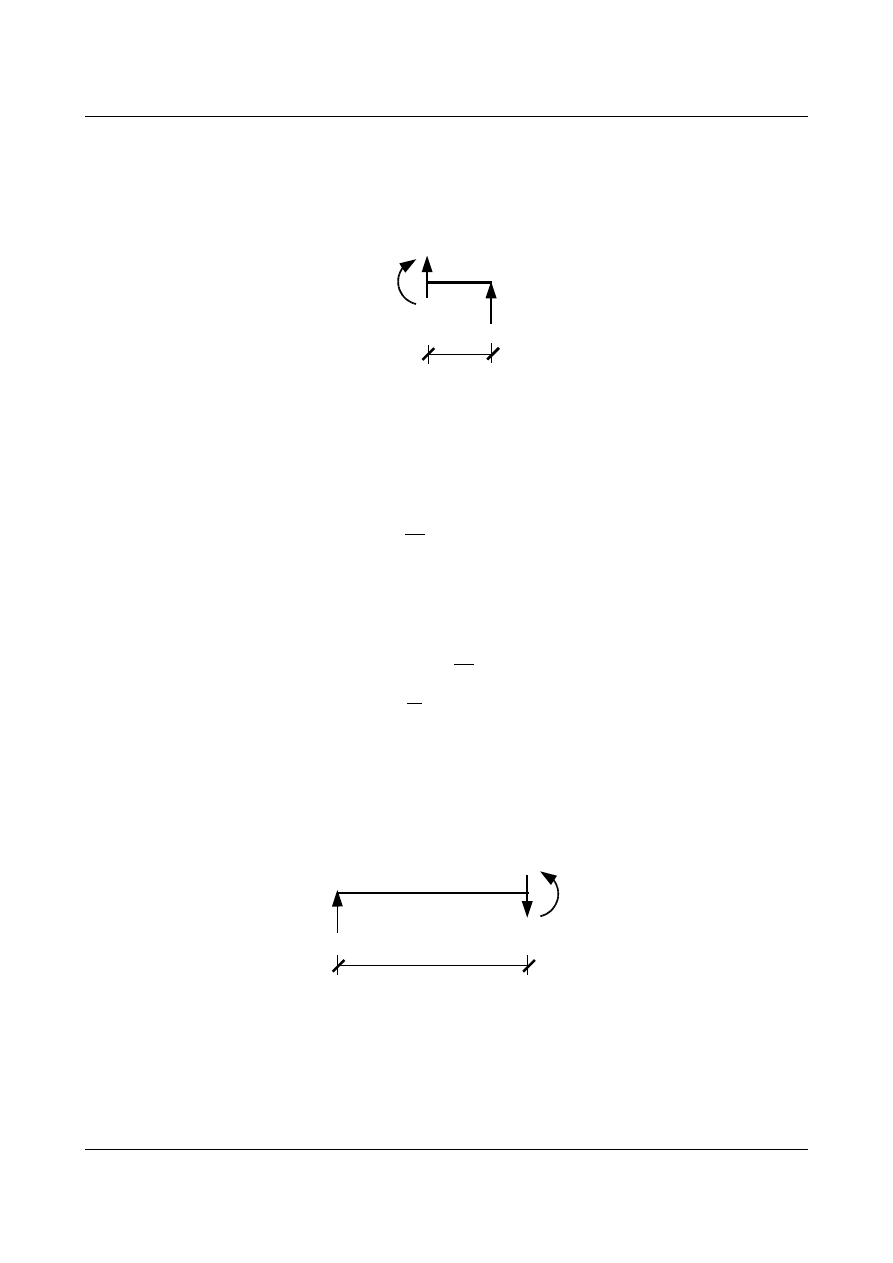
4. Wyznaczenie funkcji sił wewnętrznych w przekroju γ-γ.
x
2
A
B
C
D
y
1
y
2
D
V
A
(x)
V
D
(x)
V
B
(x)
2a
D
x
1
D
3a
V
C
(x)
V
C
(x)
a
3a
γ
γ
Rys. 4.1.
Dominik Kretschmer, Łukasz Lewiński – gr.2
AlmaMater
Część 1
1. LINIE WPŁYWOWE W UKŁADACH STATYCZNIE WYZNACZALNYCH
9
•
0
≤x
2
3 a
W celu uproszczenia obliczeń warto skorzystać z równań równowagi części położonej na prawo
od przekroju γ-γ, gdyż nie uwzględnia się wtedy poruszającej się siły.
V
D
a
T
γ
M
γ
Rys. 4.2.
∑
Y
=0
−T
−V
D
=0
T
=−V
D
lwT
=−lwV
D
lwT
=−
x
2
4 a
[ − ]
∑
M
−
=0
−V
D
⋅aM
=0
M
=a⋅V
D
lwM
=a⋅lwV
D
=a⋅
x
2
4 a
lwM
=
x
2
4
[m]
•
0
≤x
2
3 a
W celu uproszczenia obliczeń warto skorzystać z równań równowagi części położonej na lewo
od przekroju γ-γ, gdyż nie uwzględnia się wtedy poruszającej się siły.
V
C
3a
M
γ
T
γ
Rys. 4.3.
Dominik Kretschmer, Łukasz Lewiński – gr.2
AlmaMater
Część 1
1. LINIE WPŁYWOWE W UKŁADACH STATYCZNIE WYZNACZALNYCH
10
∑
Y
=0
−T
V
C
=0
T
=V
C
lwT
=lwV
C
lwT
=1−
x
2
4 a
[ − ]
∑
M
−
=0
V
C
⋅3 a−M
=0
M
=3 a⋅V
C
lwM
=3 a⋅lwV
C
lwM
=3 a⋅
1
−
x
2
4 a
[m]
Wykres linii wpływu sił wewnętrznych w przekroju γ-γ przedstawiono na poniższym rysunku.
P=1 [-]
3a
A
B
C
D
2a
3a
γ
a
lw M
γ
lw T
γ
[m]
[-]
γ
+
+
3
4
-
1
4
x
2
4a
-
x
2
4a
1-
x
2
4a
3
4
a
3a(1- )
x
2
4a
Rys. 4.4.
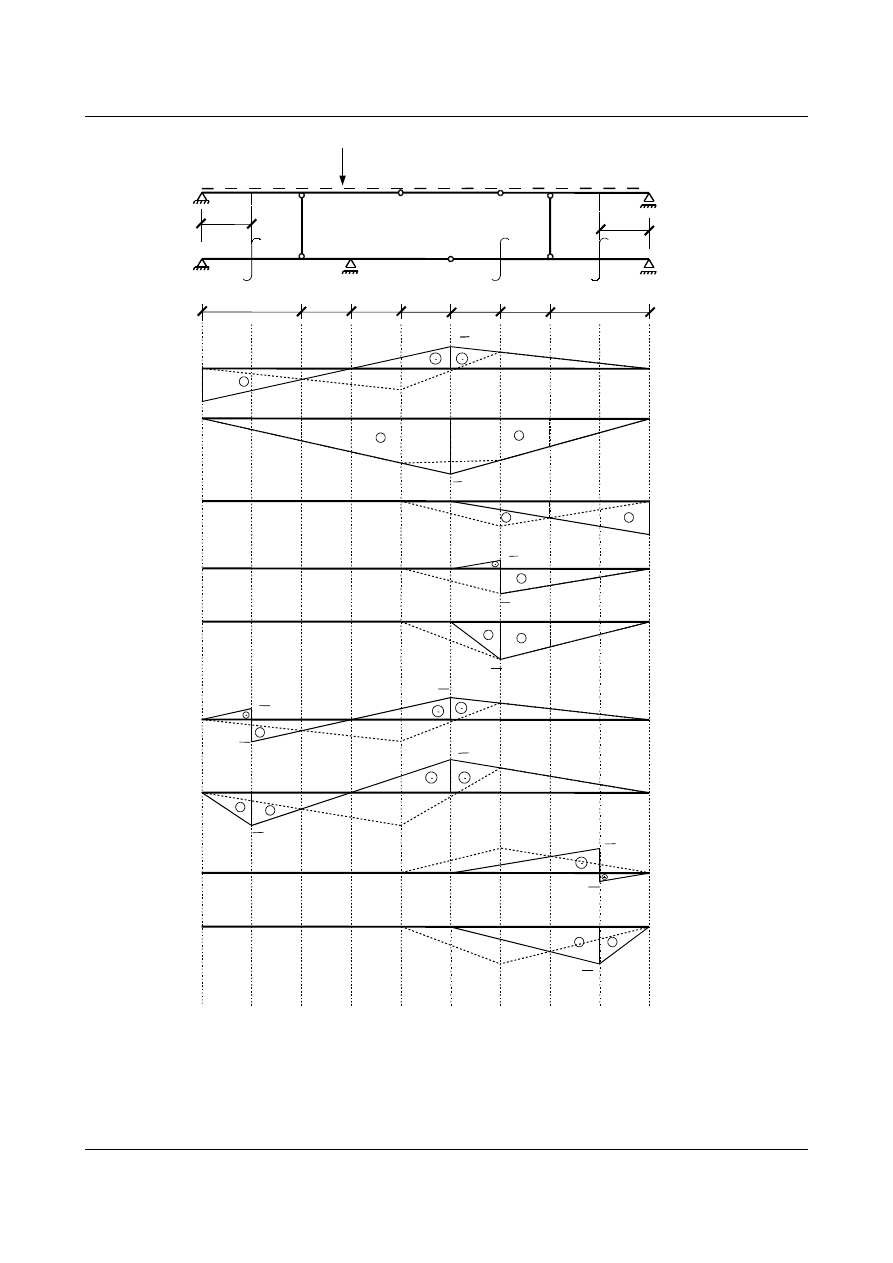
5. Wykres linii wpływu zadanych wielkości statycznych dla układu wyjściowego (belki z pomostem
pośrednim) przedstawiono na poniższym rysunku.
Na poniższym rysunku zaznaczono linią ciągłą wykresy zadanych wielkości statycznych dla belki
bez pomostu pośredniego, a linią przerywaną naniesiono na nie linie wpływowe wielkości statycznych
dla belki z pomostem pośrednim. Właściwy wykres dla całego układu belek tworzymy łącząc
odpowiednie wartości rzędnych w punktach połączenia belki z pomostem pamiętając o tym, że w
podporach wartość linii wpływu wielkości statycznej jest równa zero. Proste prowadzimy do miejsca w
którym na pomoście znajduje się przegub.
Dominik Kretschmer, Łukasz Lewiński – gr.2
AlmaMater
Część 1
1. LINIE WPŁYWOWE W UKŁADACH STATYCZNIE WYZNACZALNYCH
11
P=1 [-]
2a
2a
a
a
a
a
a
A
B
C
D
a
a
α
γ
α
γ
β
β
1
1
lw M
α
lw T
α
[-]
[m]
lw V
A
lw V
D
[-]
[-]
lw V
B
[-]
+
+
+
+
2
3
-
5
3
1
4
-
3
4
+
+
+
3
4
a
lw M
β
lw T
β
[-]
[m]
lw M
γ
lw T
γ
[m]
[-]
1
3
-
2
3
2
3
-
2
3
a
2
3
- a
+
+
+
+
+
3
4
-
1
4
3
4
a
+
Rys. 5.1.
Dominik Kretschmer, Łukasz Lewiński – gr.2
AlmaMater