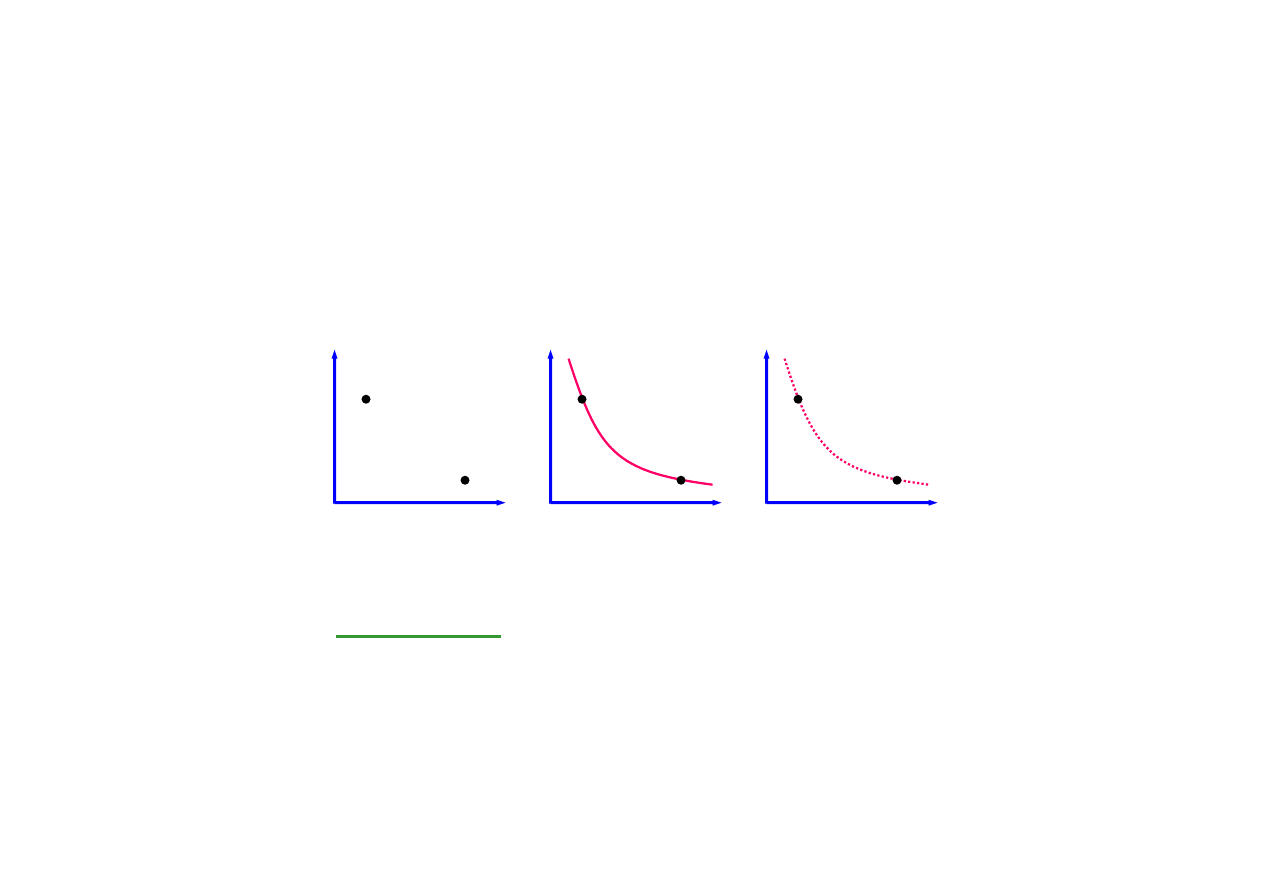
II

ga

zasada termodynamiki

y

procesy odwracalne i nieodwracalne

p

1

p

1

p

1

2

V

2

V

2

V

odwracalny: nieskończenie mała zmiana

t ó

ż

d

ó ić

parametrów może odwrócić proces

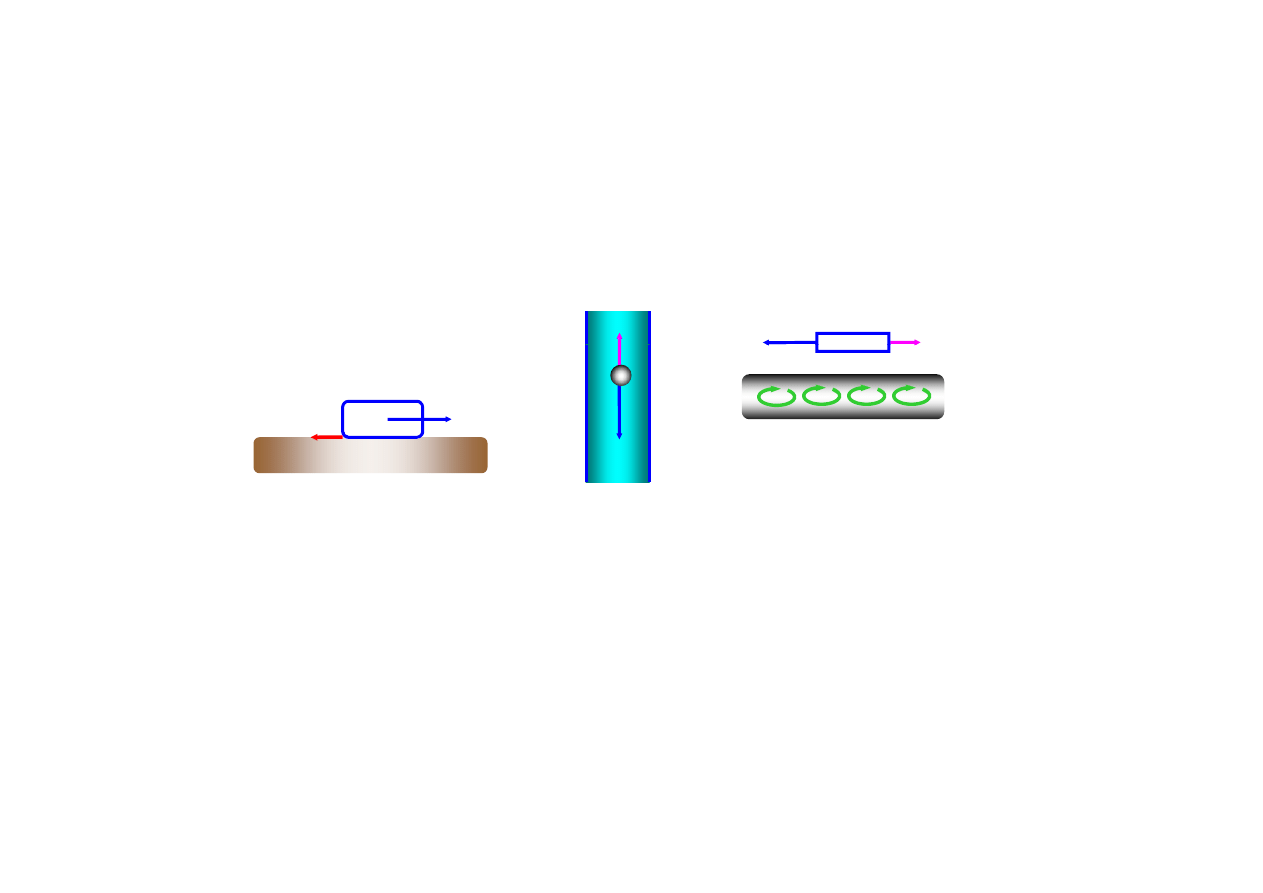
procesy nieodwracalne

p

y

siła

N

S

siła tarcia

siła
lepkości

N

S

prądy wirowe w metalu

prądy wirowe w metalu

żaden proces rzeczywisty
nie może być w pełni odwracalny

nie może być w pełni odwracalny

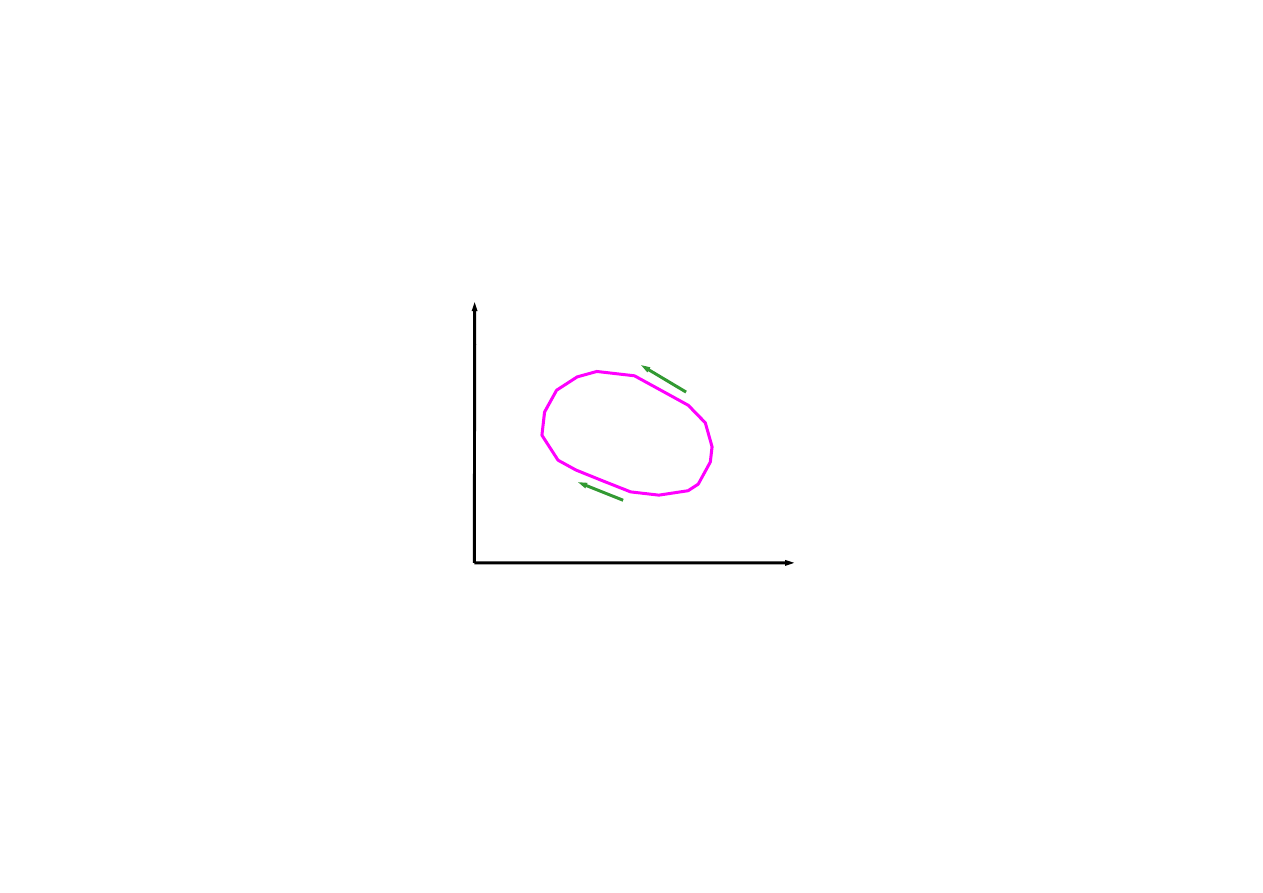
cykl termodynamiczny

y

y

y

p

chłodziarka

chłodziarka

maszyna cieplna

V

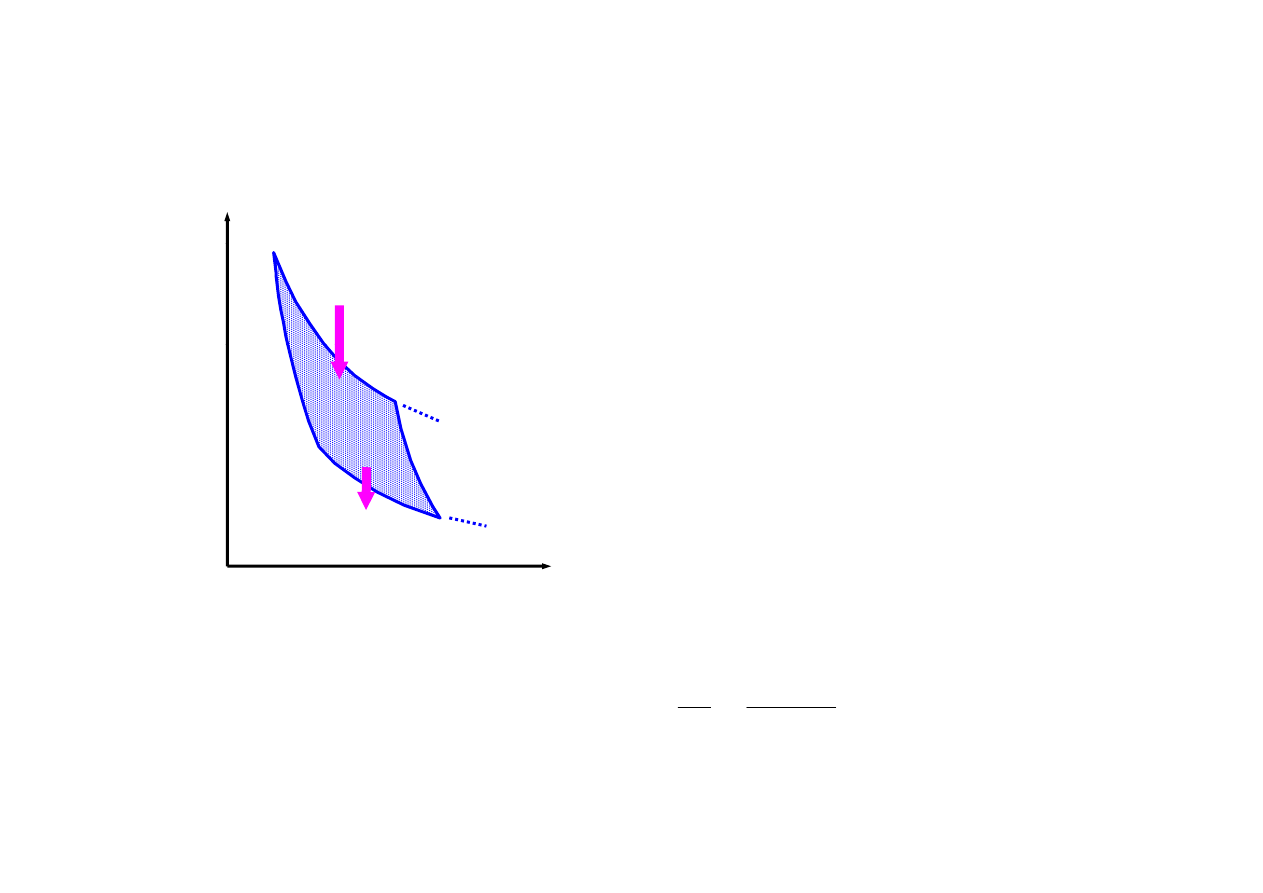
cykl Carnota

y

p

1

p

1

Q

W

U

W

Q

→

→

→

→

3

,

2

2

,

1

3

2

2

1

T

2

U

W

Q

W

→

→

→

→

∗

1

,

4

4

,

3

1

4

4

3

Q

∗

T

∗

3

4

∗

−

−

+

=

Q

Q

W

W

W

W

W

W

W

1

,

4

4

,

3

3

,

2

2

,

1

V

3

∗

−

=

−

=

Q

Q

W

W

4

,

3

2

,

1

Q

Q

Q

Q

W

def

∗

−

=

=

η

sprawność:

sprawność

p

Q

Q

W

def

∗

−

ść

1

ln

−

′

∗

T

T

V

RT

Q

d

k

ł

Q

Q

Q

Q

=

=

η

sprawność:

1

ln

<

=

→

=

T

V

RT

Q

C

η

ν

gaz doskonały:

przykładowo:

p

T

%

25

K

400

=

⎬

⎫

=

η

T

przykładowo:

T

ma

x

d

l

i

kl

(

d C

)

%

25

K

300

=

⎭

⎬

=

∗

η

T

T

min

dowolny inny cykl:

η ≤ η

C

(zasada Carnota)

nieodwracalny cykl Carnota:

η´

C

≤ η

C

V

T

min

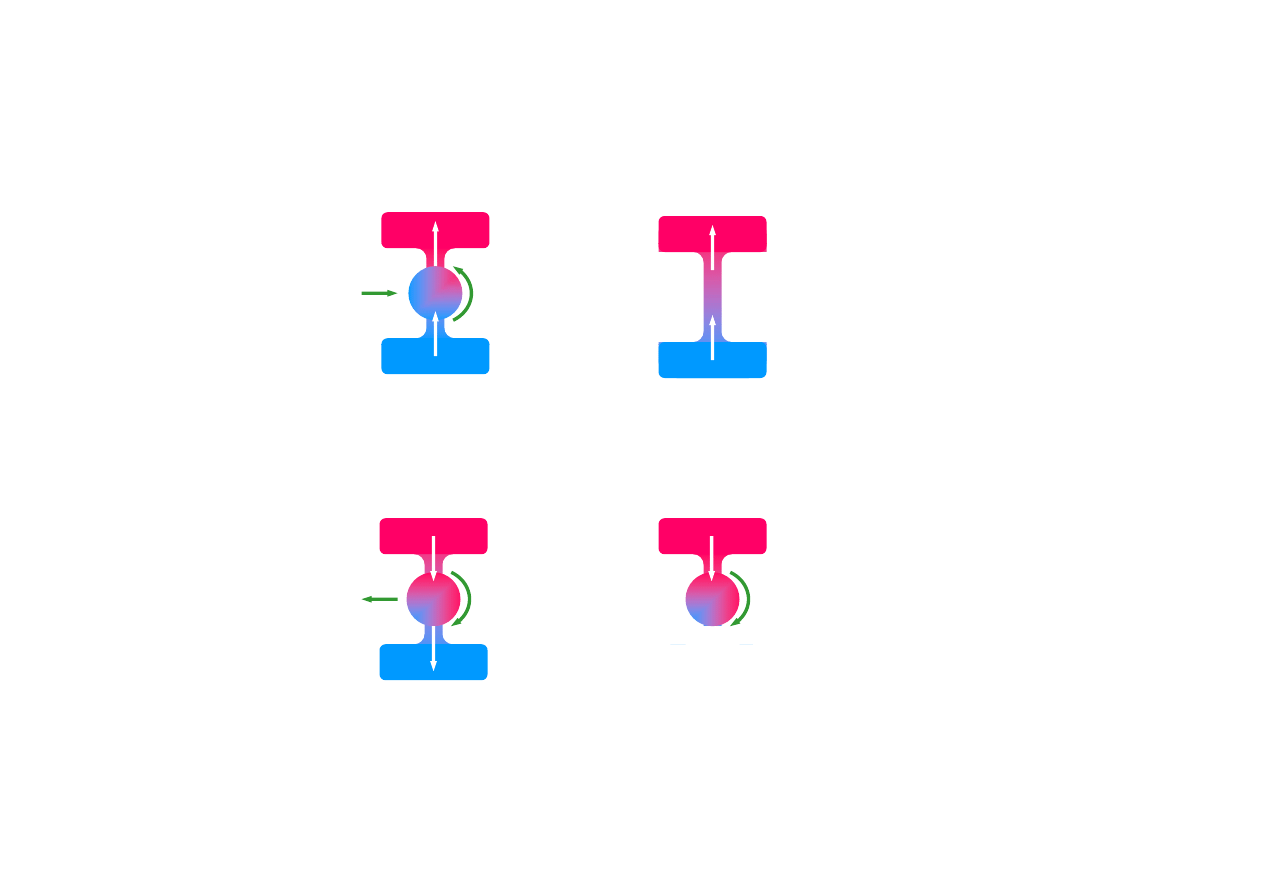
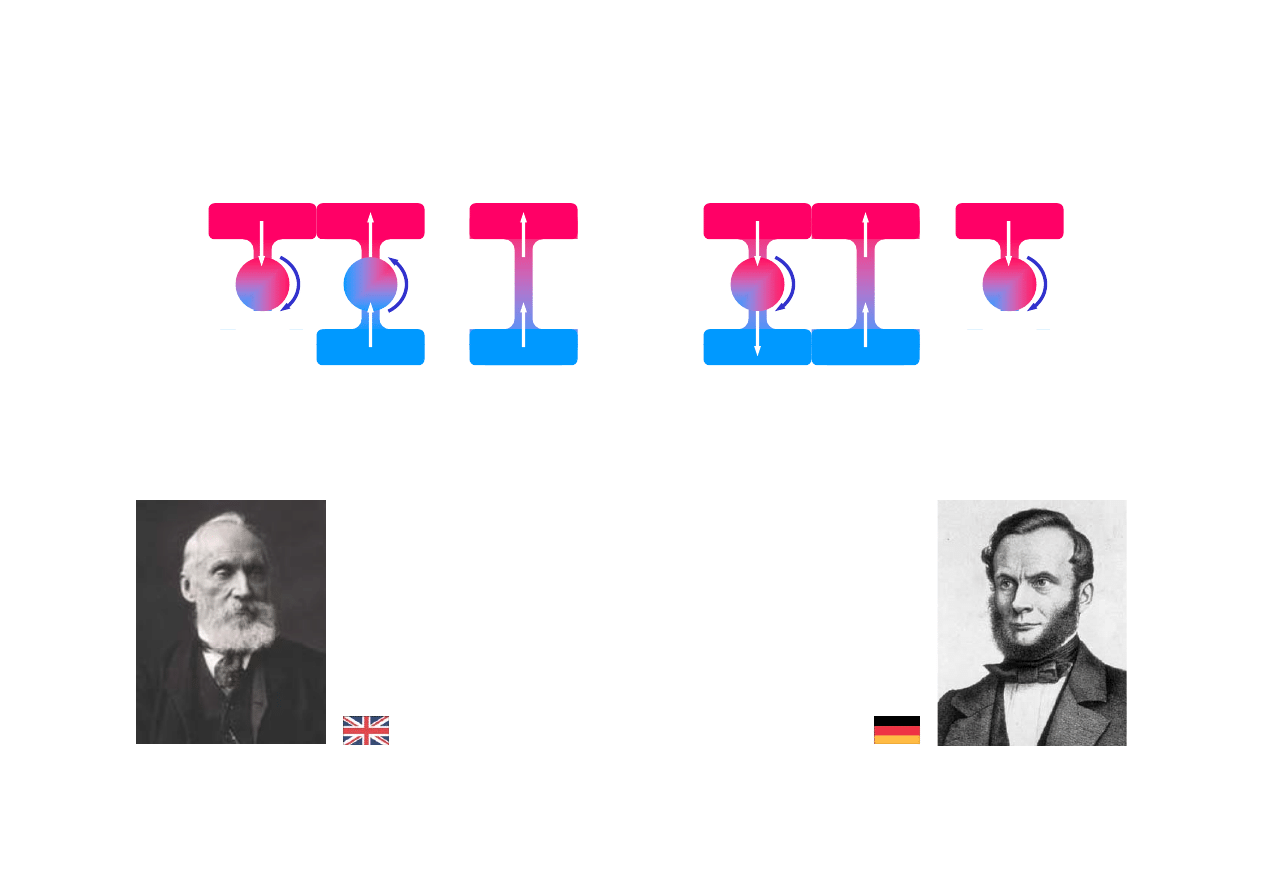
II zasada termodynamiki

y

T

1

> T

2

Q

1

Q

1

T

1

Clausius 1850

1

Q

1

= Q

2

W = Q

1

- Q

2

1

T

niemożliwy jest proces, którego jedynym rezultatem jest

Q

2

Q

2

T

2

przekazanie ciepła od ciała zimniejszego do cieplejszego

Q

1

Q

1

T

1

1

W = Q

1

- Q

2

1

W = Q

1

Kelvin 1851

Q

2

niemożliwy jest proces, którego jedynym rezultatem
j t

i

i

ł

ó

ż

T

2

jest zamiana ciepła na równoważną mu pracę

cd.

Q

1

Q

1

Q

1

Q

1

Q

1

Q

1

Q

Q

Q

⇒

⇒

Q

...również zasada Carnota jest równoważna

Q

2

Q

2

Q

2

Q

2

j

lord Kelvin, William Thomson
(1824 - 1907)

Rudolf Emanuel Clausius
(1822 - 1888), ur. w Koszalinie

entropia

p

funkcja stanu związana z I:

energia wewnętrzna U

funkcja stanu związana z II:

entropia S

1

2

1

g.d.

1

2

1

T

T

T

Q

Q

Q

−

=

−

0

2

2

1

1

=

+

T

Q

T

Q

T

Q

0

=

∫

T

Q

δ

- ciepło zredukowane

ogólniej:

stąd:

dS

T

Q =

δ

różniczka zupełna

∫

=

−

=

Δ

2

1

1

2

T

Q

S

S

S

δ

ilościowe ujęcie II zasady

termodynamiki

termodynamiki

η

η

<

∗

0

2

2

1

1

>

+

T

Q

T

Q

w procesie nieodwracalnym ( )

0

>

∫

T

Q

δ

ogólniej w procesach nieodwracalnych:

każdemu procesowi nieodwracalnemu towarzyszy wzrost entropii

0

=

ΔS

tylko w procesie odwracalnym i adiabatycznym

np.

p

zmiana entropii przy przepływie (nieodwracalnym) ciepła
od ciała cieplejszego (T

1

) do ciała zimniejszego (T

2

)

1

0

2

T

T

T

←

→

2

2

1

0

T

T

T

+

=

1

0

2

2

0

0

1

ln

0

0

T

T

C

T

dT

C

T

Q

S

T

T

=

=

=

Δ

∫

∫

δ

0

2

1

1

ln

0

0

1

1

T

T

C

T

dT

C

T

Q

S

T

T

T

T

T

T

T

=

=

=

Δ

∫

∫

∫

∫

δ

2

2

2

T

T

T

T

T

∫

∫

ln

ln

0

0

2

1

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

Δ

+

Δ

=

Δ

T

T

T

T

C

S

S

S

(

)

0

4

ln

ln

2

1

2

2

1

2

1

2

0

2

1

>

+

=

=

⎠

⎝

T

T

T

T

C

T

T

T

C

T

T

1

2

1

2

1

>

43

42

1

x

izotermiczne rozprężanie (neodwracalne) gazu

izotermiczne rozprężanie (neodwracalne) gazu

V

1

V

V

2

0

ln

ln

1

2

2

2

>

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

Δ

=

=

Δ

∫

V

V

R

V

V

RT

T

T

Q

T

Q

S

ν

ν

δ

1

1

1

⎟

⎠

⎜

⎝

∫

V

V

T

T

T

przykład

p y

obliczyć przyrost entropii gazu doskonałego

pdV

dT

C

Q

V

+

=

δ

RT

pV

ν

=

obliczyć przyrost entropii gazu doskonałego

p

V

p

V

T

V

RdV

T

dT

C

T

pdV

T

dT

C

T

Q

S

V

V

+

=

+

=

=

Δ

∫

∫

∫

∫

∫

ν

δ

0

0

0

0

ln

ln

ln

ln

ln

ln

S

V

C

p

C

S

V

R

T

C

V

V

R

T

T

C

p

V

V

V

′

+

+

=

+

+

=

+

=

ν

ν

p

entropia S jest zdefiniowana z dokładnością do stałej

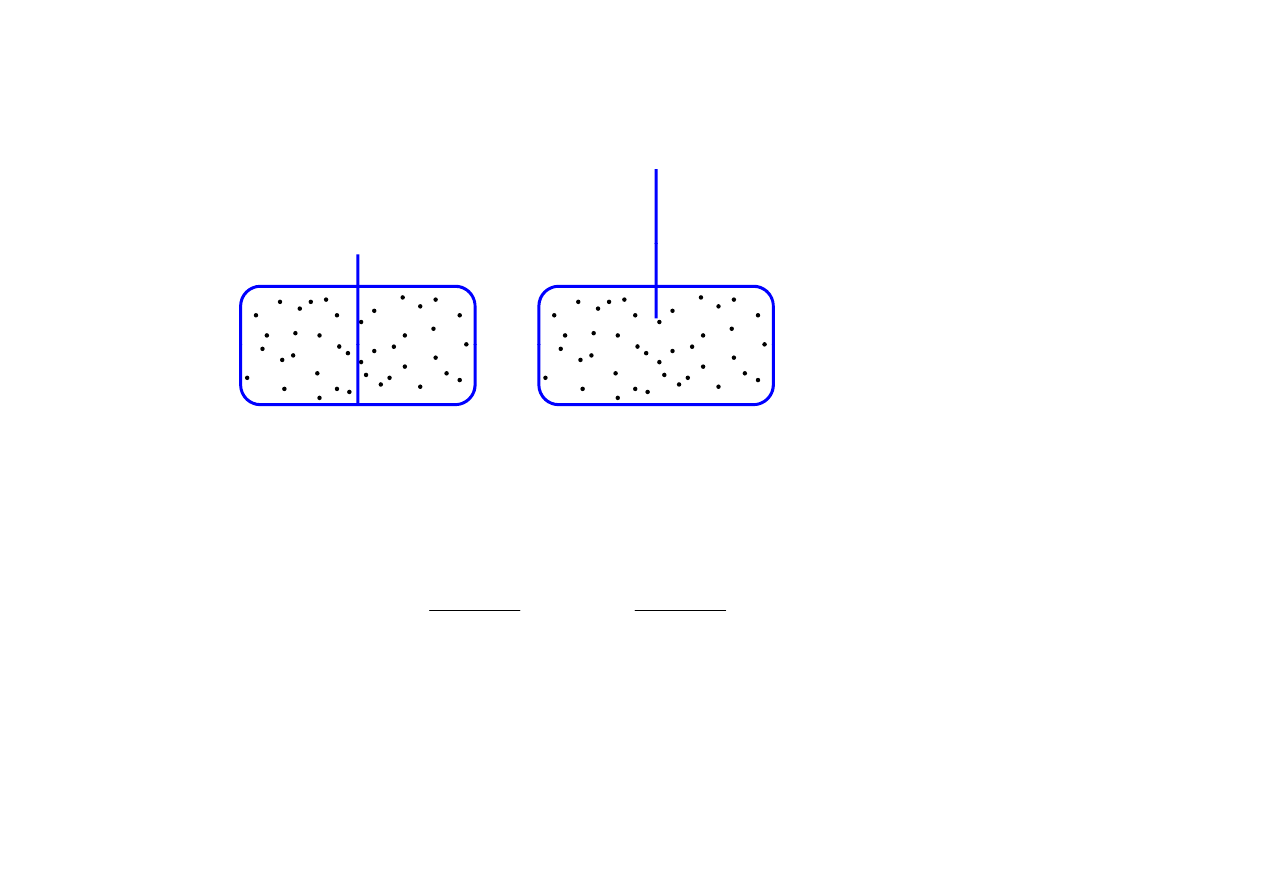
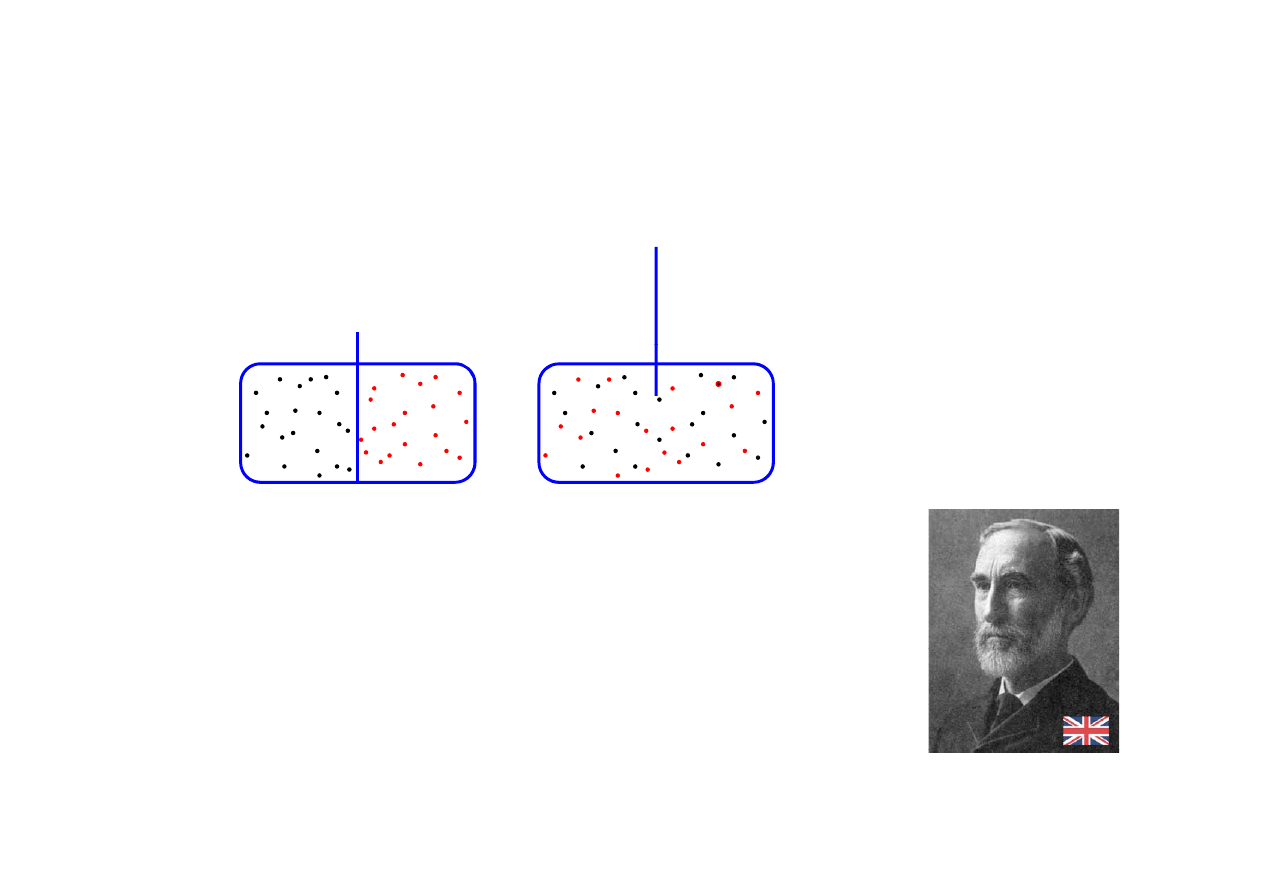
paradoks Gibbsa

p

identyczny gaz z lewej i z prawej

2

2

1

2

1

2

1

1

ln

ln

V

V

V

R

V

V

V

R

S

+

+

+

=

Δ

ν

ν

izotermicznie

2

1

0

2

ln

2

2

1

>

=

Δ

⎭

⎬

⎫

=

=

R

S

V

V

V

ν

ν

ν

ν

!?

2

1

⎭

=

=

V

V

V

x

Josiah Willard Gibbs (1839 - 1903)

III zasada termodynamiki

y

entropia układu w temperaturze zera bezwzględnego równa się zero

( )

0

lim

0

=

→

T

S

T

( )

0

lim

0

=

→

T

C

T

T

dT

( )

∫

=

T

T

dT

T

C

S

0

i

ż

i

ć t

t

T

0

≡ nie można osiągnąć temperatury T = 0 w

skończonej liczbie kroków (W.Nernst - 1905)

zweryfikowano eksperymentalnie…

Walther Hermann Nernst (1864 - 1941)
1920

tk P lk

1920, matka Polka

ver-01