termodynamika

termodynamika

termodynamika fenomenologiczna

y

g

własności termiczne ciał makroskopowych

uogólnienie licznych badań doświadczalnych

układ termodynamiczny
wielkości termodynamiczne

(parametry) np : T V p

opis makro i mikro
rezygnacja z przyczynowości
znaczenie praktyczne

(parametry) np.: T, V, p

stan układu
równanie stanu
stan stacjonarny

znaczenie praktyczne

p

stan stacjonarny
stan zrównoważony
proces kwazistatyczny

d

l

proces odwracalny

V

temperatura

p

istnieje wielkość skalarna „temperatura” będąca własnością
układu termodynamicznego, która ma jednakową wartość dla
układów w równowadze termodynamicznej

równość temperatur jest warunkiem koniecznym i
wystarczającym równowagi termodynamicznej

relacja przechodnia:

C

A

C

B

B

A

~

~

~

⇒

∧

ilościowe określenie temperatury poprzez własności termometryczne

ilościowe określenie temperatury poprzez własności termometryczne
(objętość cieczy, opór elektryczny, rozmiary liniowe ciał, etc.)

energia wewnętrzna

g

ę

podstawowa funkcja stanu U:

energia kin. i pot. molekuł
energia atomowa, jądrowa itd…
b

i ki

i

t

kł d j k

ł ś i

·

bez energi kin. i pot. układu jako całości

określa stan termodynamiczny układu

istotny do opisu procesów jest przyrost

ΔU

(można przyjąć, że w T =0 również U = 0)

W – praca: sposób przekazu energii (makroskopowy)
Q – ciepło; inny sposób przekazu energii (mikroskopowy)

y

g (

y)

I zasada termodynamiki:
ogólniejsza zasada zachowania energii

{ {

od

do

W

Q

U

−

=

Δ

od

do

cd.

Julius Robert von Mayer (1814 - 1878) D

1842

f

ł

i

1842 – sformułowanie

James Prescott Joule (1818 - 1889) GB

1843 d ś i d

i

1843 - doświadczenie

Hermann Ludwig Ferdinand von Helmholtz (1821 - 1894)

1847 matematyczne

1847 - matematyczne

energia wewnętrzna

g

ę

W

Q

dU

δ

δ

−

=

d - różniczka zupełna, zależy od stanu pocz. i końc.

δ

- przyrost infinitezymalny, zależy od procesu

∫

=

Δ

2

dU

U

δ

przyrost infinitezymalny, zależy od procesu

∫

1

∫

Γ

=

W

W

δ

∫

Γ

=

Q

Q

δ

Γ

δW - praca wykonana przez układ
δQ - ciepło dostarczone do układu

równanie Clapeyrona

p y

równanie stanu gazu doskonałego

RT

pV

ν

=

A

N

N

=

ν

ν

– liczba moli

N

A

– liczba Avogadra

mol

1

10

022

,

6

23

⋅

=

def

A

N

A

R

– stała gazowa

p

– ciśnienie

K

mol

J

31

,

8

=

R

S

F

p

def

=

[ ]

Pa

m

N

2

ozn

p

=

=

paskal

SI

Benoît Pierre Émile Clapeyron (1799 - 1864)

p y

(

)

Amadeo Avogadro di Quaregna (1776 - 1856)

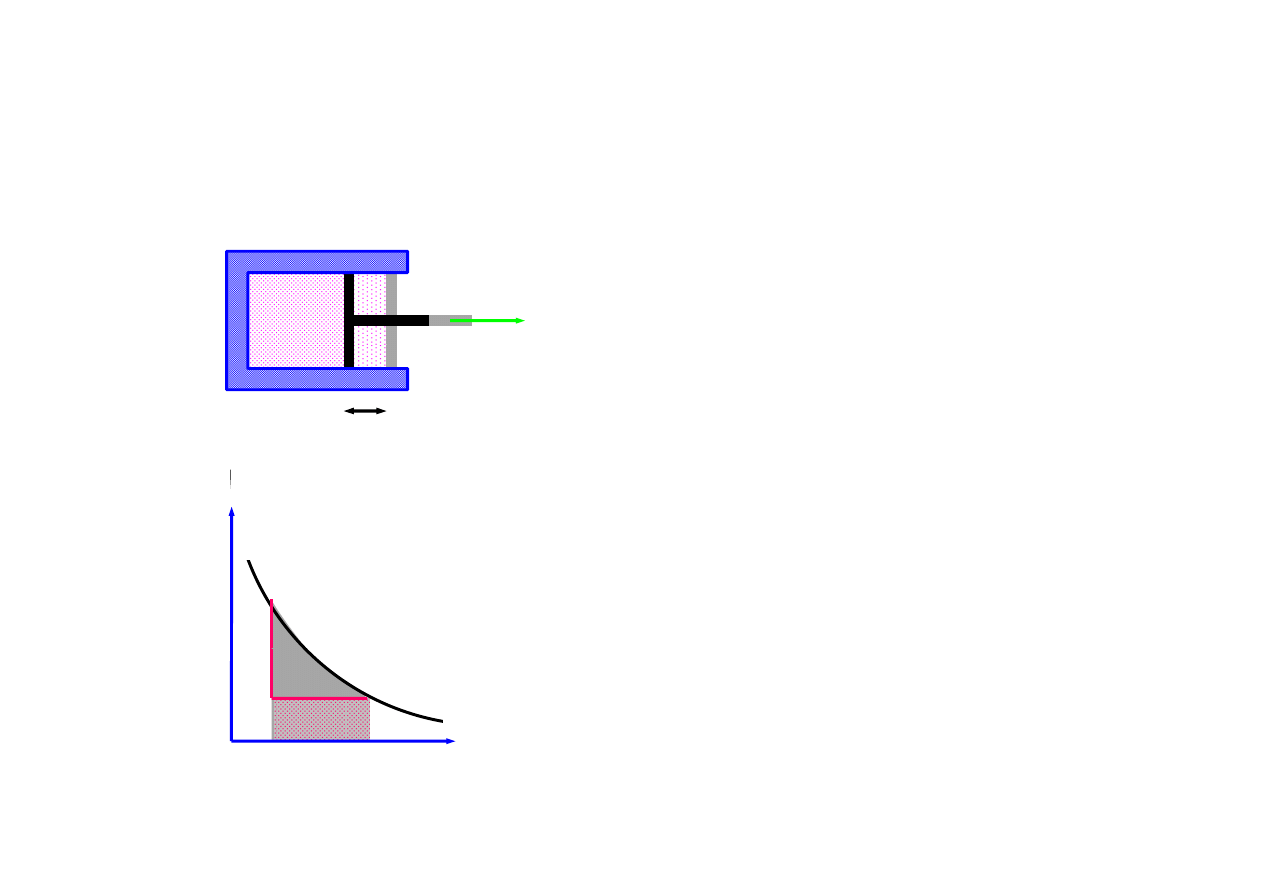
praca

p

F

pdV

pSdl

Fdl

W

=

=

=

δ

pdV

W

=

δ

F

dl

pdV

W

=

δ

( )

∫

2

V

dV

V

p

W

dl

( )

∫

=

1

V

dV

V

p

W

p

2

,

3

,

1

2

,

1

W

W

≠

1

( )

V

p

– funkcja zależna od procesu

,

,

,

2

3

V

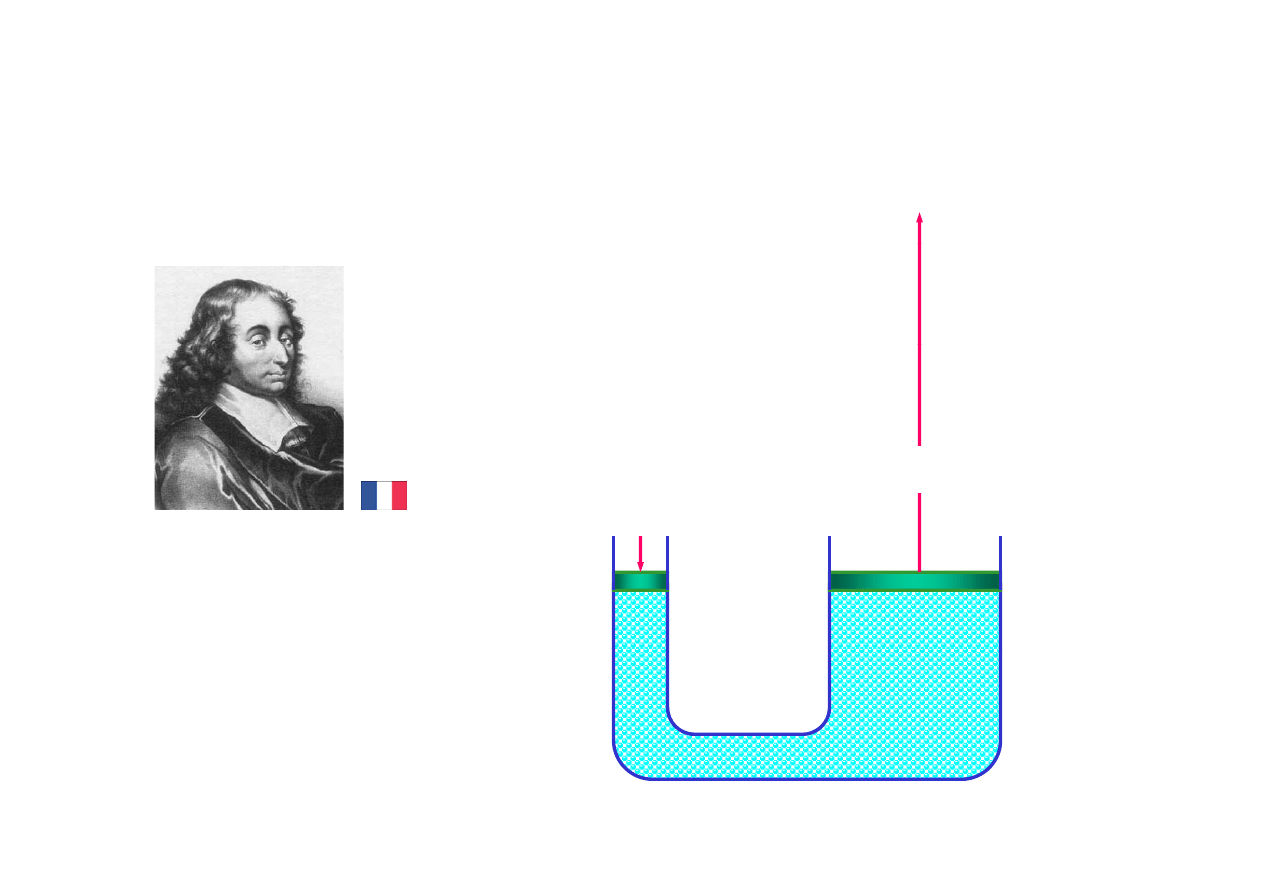
prasa hydrauliczna Pascala

p

y

F

1

F

2

=

(S

2

/S

1

)F

1

Blaise Pascal (1623 1662)

Blaise Pascal (1623 - 1662)

pojemność cieplna

p j

p

Q

δ

zależy od procesu (

δ

Q)

dT

Q

C

def

δ

=

CdT

Q

=

δ

Q

C

δ

ilość ciepła potrzebna do ogrzania o 1 K

proces izochoryczny

const

=

=

V

V

dT

Q

C

δ

Q

C

δ

– proces izochoryczny

i b

const

=

=

p

p

dT

Q

C

pdV

CdT

dU

i

I

d t

d

iki

– proces izobaryczny

pdV

CdT

dU

−

=

Q

def

δ

1

więc I zasada termodynamiki:

dT

Q

m

c

δ

1

=

NB: ciepło właściwe

proces izochoryczny

p

y

y

dU

dT

C

0

W

δ

V

=

const

p

dU

dT

C

V

=

0

=

W

δ

T

T

∫

∫

2

2

p

↑

T

C

dT

C

dU

U

V

T

V

T

Δ

=

=

=

Δ

∫

∫

1

1

prawo Charlesa

↑

ogrzewanie
↓ oziębianie

więc teraz I zasada termodynamiki:

prawo Charlesa

V

V

0

pdV

dT

C

CdT

V

+

=

(w dowolnym procesie)

Jaques Alexandre César Charles (1746 - 1823)

proces izobaryczny

p

y

y

p

p

p

=

const

p

0

dT

C

Q

=

δ

→ ogrzewanie

← oziębianie

dT

C

Q

p

δ

pdV

dT

C

dT

C

+

=

V

pdV

dT

C

dT

C

V

p

+

=

(

)

2

V

V

p

W

W

V

=

=

∫

δ

(

)

1

2

1

V

V

p

W

W

V

−

=

=

∫

δ

prawo Gay - Lussaca

y

L

i J

h G

L

(1778 1850)

Louis Joseph Gay-Lussac (1778 - 1850)

równanie Mayera

y

RT

pV

ν

=

RdT

pdV

ν

=

⇒

p

R

C

C

V

p

ν

=

−

V

p

C

C

>

μ

R

c

c

V

p

=

−

lub:

ν

μ

m

def

=

masa molowa:

(

)

T

R

W

RT

pV

V

V

p

W

p

Δ

=

⎭

⎬

⎫

=

−

=

⇒

=

ν

ν

1

2

const

praca jaką 1 mol gazu wykonuje rozszerzając się

K

mol

J

3

,

8

=

Δ

=

T

W

R

ν

praca jaką 1 mol gazu wykonuje rozszerzając się
izobarycznie przy

Δ

T

=

1 K (interpretacja stałej gazowej R)

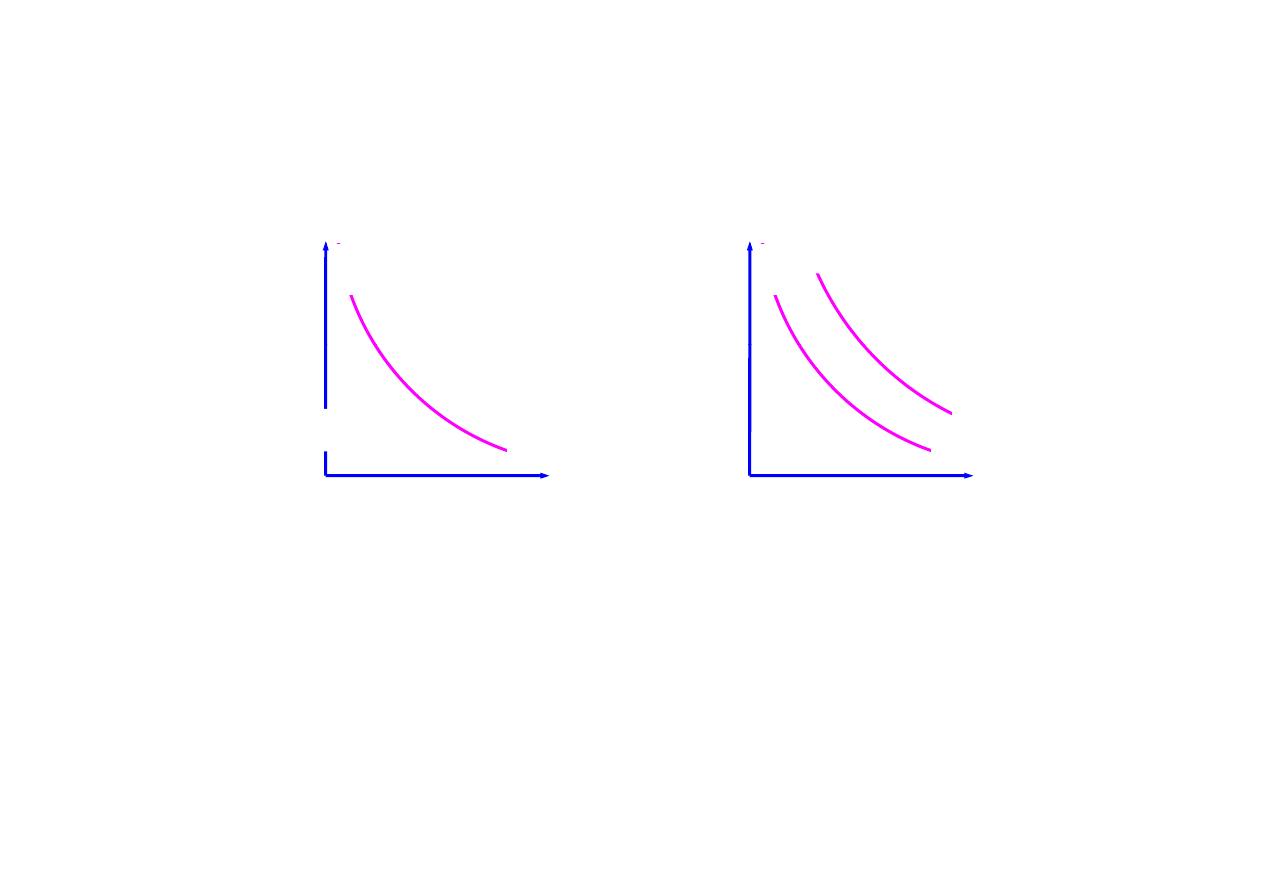
proces izotermiczny

p

y

p

T

2

T

1

< T

2

p

É

oddawanie

ciepła

T

1

pobieranie

Ì

ciepła

ciepła

pV = const

V

V

prawo Boyla–Mariotte’a: w stałej temperaturze (pV = const) podczas

ż

i dl

i

i

t ł j t

t

i b ć d

t

rozprężania dla zapewnienia stałej temperatury musi być dostarczane
ciepło, kosztem którego zostaje wykonana praca bez zmiany energii
wewnętrznej

cd.

const

=

T

const

=

U

dT

C

dU

V

=

W

Q

δ

δ

= W

Q

δ

δ

2

ln

2

2

V

RT

m

dV

RT

m

pdV

Q

V

V

=

=

=

Δ

∫

∫

1

ln

1

1

V

RT

V

RT

pdV

Q

V

V

μ

μ

=

=

=

Δ

∫

∫

V

RT

m

p

μ

=

Robert Boyle (1627 - 1691)
Edmé Mariotte (1620 - 1684)

Edmé Mariotte (1620 1684)

proces adiabatyczny

p

y

y

0

Q

δ

i l j

i

0

=

Q

δ

izolacja termiczna

zmieniają się trzy parametry: p V T

0

=

+ W

dU

δ

zmieniają się trzy parametry: p, V, T

RdT

Vdp

pdV

ν

=

+

0

+ pdV

dT

C

równanie Clapeyrona:

0

=

+ pdV

dT

C

V

R

C

C

V

p

ν

=

−

oraz:
oraz:

V

p

C

C

Vdp

pdV

dT

−

+

=

(

)

0

=

+

+

−

pdV

Vdp

pdV

C

C

C

V

p

V

p

cd.

d f

C

0

=

+ Vdp

pdV

C

C

V

p

V

p

def

C

C

=

κ

współczynnik Poissona

0

=

+

p

dp

V

dV

κ

const

ln

ln

=

+ p

V

κ

const

ln

=

κ

pV

const

=

κ

pV

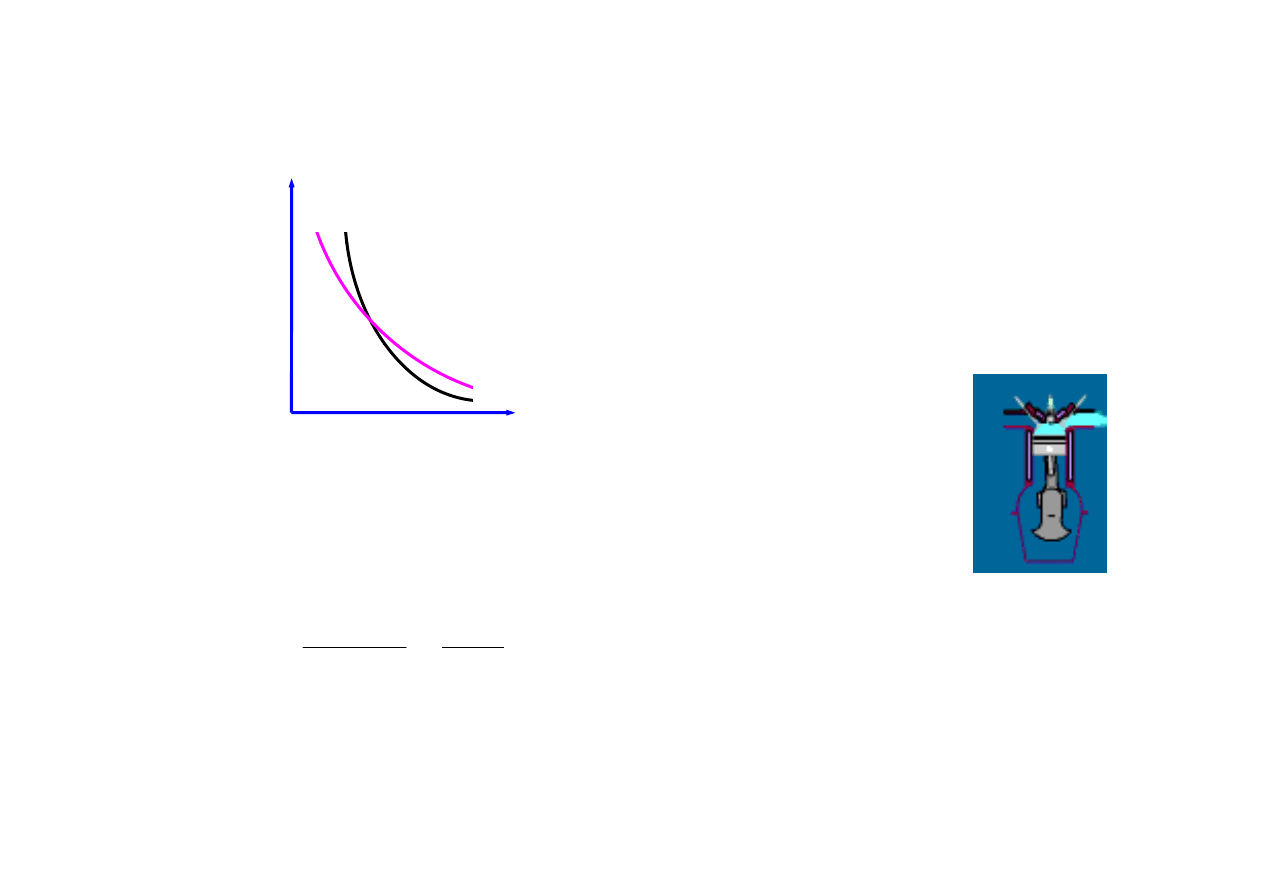
równanie Poissona

p

pV = const

const

=

κ

pV

1

>

κ

V

V

adiabatyczne rozprężanie – gaz ochładza się (CO

2

)

adiabatyczne sprężanie gaz ogrzewa się (Diesel)

temperatura sublimacji: -78,5 °C

=

=

=

pV

pV

C

T

C

U

V

(

)

T

C

C

RT

pV

−

=

=

ν

adiabatyczne sprężanie – gaz ogrzewa się (Diesel)

gdyż:

1

−

=

−

=

=

κ

C

C

T

C

U

V

p

V

(

)

T

C

C

RT

pV

V

p

=

=

ν

gdyż:

Siméon Denis Poisson (1781 - 1840) F
Rudolf Diesel (1858 - 1913) D

proces politropowy

p

p

p

y

const

=

C

⎧

⎧

+ W

dU

Q

δ

δ

⎩

⎨

⎧

=

+

+

=

RdT

Vdp

pdV

pdV

dT

C

CdT

V

ν

⎩

⎨

⎧

=

+

=

RT

pV

W

dU

Q

ν

δ

δ

(

)

(

)

R

pdV

Vdp

pdV

C

C

V

ν

=

+

−

(

)

(

)

0

=

−

+

−

−

Vdp

C

C

pdV

R

C

C

V

V

ν

p

C

(

)

(

)

mpV

Vdp

C

C

pdV

C

C

V

p

1

0

=

−

+

−

(

)

(

)

(

)

(

)

0

=

−

+

−

dp

C

C

dV

C

C

V

(

)

(

)

const

ln

ln

=

−

+

−

p

C

C

V

C

C

V

p

(

)

(

)

0

+

p

C

C

V

C

C

V

p

cd.

– politropa

const

=

n

pV

V

p

C

C

C

C

n

−

−

=

1

−

−

=

n

C

nC

C

p

V

n

C

izobaryczna

0

C

p

izotermiczna

1

∞

izotermiczna

1

∞

adiabatyczna

κ

0

izochoryczna

∞ C

V

y

V

ver-01