„Matematyka jest językiem.”

Josiah Willard Gibbs

SKALA, MAPA, PLAN.

Mapy i plany są odbiciem rzeczywistego
świata na papierze. Każda mapa oprócz
legendy niezbędnej do jej odczytania opisana
jest także skalą, która informuje nas w jak
wielkim pomniejszeniu przedstawia dany
teren. Nie bez powodu skala na mapie i skala
w podobieństwie noszą tę samą nazwę…

SKALA.

Skala informuje nas ile razy dany przedmiot
został pomniejszony (w przypadku dużych
obiektów) lub też powiększony(w przypadku
bardzo małych obiektów), aby można go było
przedstawić na mapie lub planie.

Istnieje kilka standardów zapisu skali na
mapach i planach, najpopularniejsza jest
skala liczbowa. Np. zapis 1 : 25000
oznacza, że odległości przedstawione na
rysunku wykonanym w tej skali są 25000
razy mniejsze niż w rzeczywistości, czyli, że
1 cm na mapie odpowiada 25000 cm w
rzeczywistości.

SKALA.

Zapis 5 : 1 oznacza, że przedmiot
przedstawiony na rysunku jest 5 razy
większy niż w rzeczywistości.

Zapis 1 : 1 oznacza, że dany przedmiot
został

przedstawiony

w

rzeczywistych

rozmiarach.

Często stosuje się także:

• Skalę mianowaną, np. 1 cm – 1 km lub 1
cm → 1 km

• Podziałkę liniową

PRZYKŁADY.

PRZYKŁAD 1.
Dany jest prostokąt o wymiarach 28 cm na
36 cm. Jakie wymiary ma ten prostokąt w
poszczególnych skalach?

Skala

Wymiary prostokąta

1 : 1

28 cm

36 cm

1 : 2

28 cm : 2 = 14 cm

36 cm : 2 = 18 cm

1 : 4

28 cm : 4 = 7 cm

36 cm : 4 = 9 cm

2 : 1

28 cm ∙ 2 = 56 cm

36 cm ∙ 2 = 72 cm

3 : 1

28 cm ∙ 3 = 84 cm

36 cm ∙ 3 = 108 cm

PRZYKŁADY.

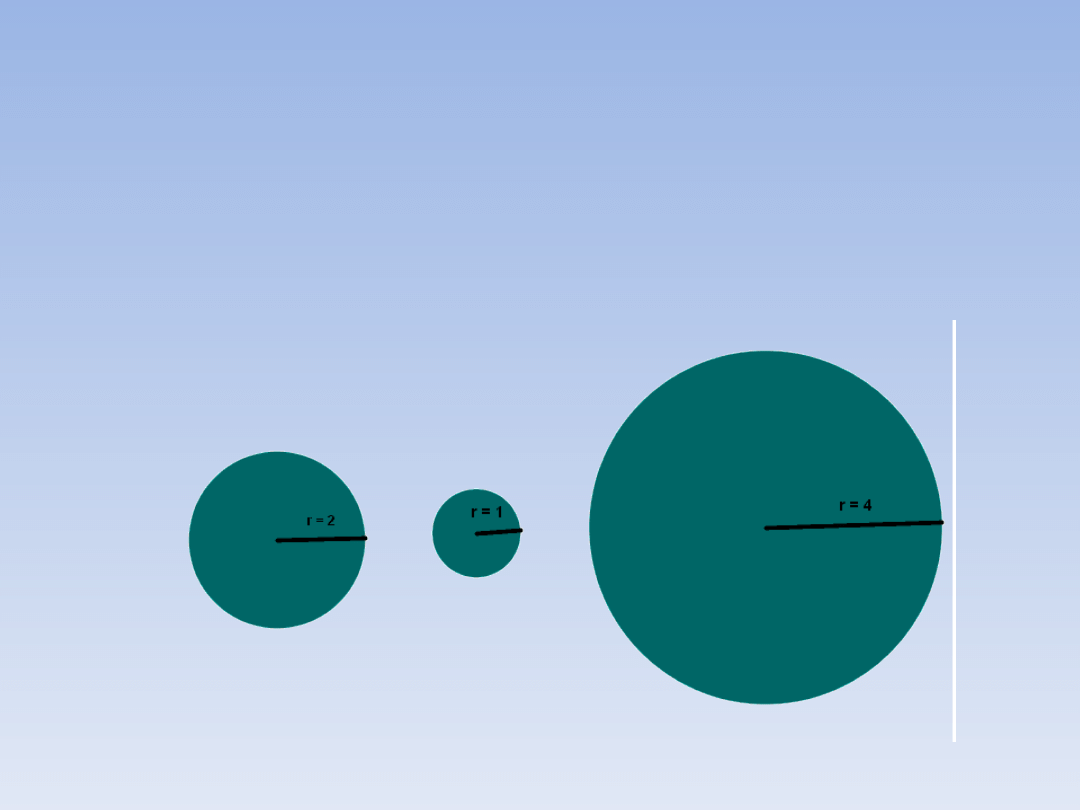
PRZYKŁAD 2.
Okrąg o promieniu r = 2 cm narysuj w skali 1
: 2 oraz w skali 2 : 1.
W skali 1 : 2 promień jest dwa razy mniejszy,
a

w

skali

2 : 1 dwa razy większy.

1 : 1

1 : 2

2 : 1

PRZYKŁADY.

PRZYKŁAD 3.
Jakiej skali liczbowej odpowiadają podane
skale mianowane?
1 cm – 20 km ; 1 cm – 350 km; 1cm – 2,5 km
1 km to 1000 m a więc 100000 cm, stąd:
skali 1 cm – 20 km odpowiada skala 1 :
2000000
(20 ∙ 100000 cm = 2000000 cm)
skali 1 cm – 350 km odpowiada skala 1 :
35000000
(350 ∙ 100000 cm = 35000000 cm)
skali 1cm – 2,5 km odpowiada skala 1 :
250000
(2,5 ∙ 100000 cm = 250000 cm)

PRZYKŁADY.

PRZYKŁAD 4.
Na mapie wykonanej w skali 1 : 500000
odległość między Ciepielowem a Baranowem
wynosi 4 cm, jaka to odległość w terenie? Od
Ciepielowa do Kąkolewa w linii prostej jest 35
km, jaka to odległość na mapie?

Skala 1 : 500000 oznacza, że jednemu
centymetrowi na mapie odpowiada 500000
cm = 5000 m = 5 km w terenie, stąd:
4 cm na mapie to 4 ∙ 5 km = 20 km w
terenie
35 km w terenie to 35 : 5 = 7 cm na mapie

PRZYKŁADY.

PRZYKŁAD 4 – ciąg dalszy.
Jeżeli przeliczanie jednostek sprawia Ci
trudność i nie możesz zapamiętać, kiedy
należy mnożyć a kiedy dzielić odległości,
korzystaj z proporcji:

x = 4 ∙ 500000 cm = 2000000 cm = 20 km

500000y = 3500000 cm |: 500000
y = 7 cm

mapa

teren

skala

1 cm

500000 cm

dane

4 cm

x

mapa

teren

skala

1 cm

500000 cm

dane

y

3500000 cm

PRZYKŁADOWE ZADANIA.

ZADANIE 1.
Podaj w jakiej skali wykonano mapę, jeżeli
odległość między dwoma miejscowościami na
mapie wynosi 6 cm, a w rzeczywistości 180 km.

180 km = 180 ∙ 100000 cm = 18000000 cm
Posłużymy się proporcją:

6x = 18000000 | : 6
x = 3000000
Odpowiedź: Mapę wykonano w skali 1 :
3000000.

mapa

teren

skala

1 cm

x

dane

6 cm

18000000 cm

PRZYKŁADOWE ZADANIA.

ZADANIE 2.
Świnoujście i Ustrzyki Górne to najbardziej

oddalone od siebie miejscowości w Polsce.

Odległość między nimi mierzona w linii prostej

wynosi ok. 800 km. Jaka będzie odległość

między nimi na mapie wykonanej w skali

1 : 16000000?
800 km = 80000000 cm

16000000x = 80000000 cm | : 16000000
x = 5 cm
Odpowiedź: Na takiej mapie odległość ta będzie

wynosić 5 cm

mapa

teren

skala

1 cm

16000000 cm

dane

x

80000000 cm

PRZYKŁADOWE ZADANIA.

ZADANIE 3.
Odległość między Brukselą a Sofią na mapie o

skali

1 : 40000000 wynosi 4,25 cm. Ile wynosi ta

odległość na mapie o skali 1 : 20000000?
Wbrew pozorom nie musimy liczyć odległości w

terenie żeby rozwiązać to zadanie. Zauważmy, że

druga mapa jest wykonana w skali dwa razy

większej niż pierwsza (druga mapa pomniejsza

20000000 razy a pierwsza 40000000 razy), a

więc odległości na niej są dwa razy większe niż

na pierwszej.
2 ∙ 4,25 cm = 8,5 cm
Odpowiedź: Na mapie o skali 1 : 20000000 ta

odległość wynosi 8,5 cm.

PRZYKŁADOWE ZADANIA.

ZADANIE 4.
Jaka jest skala mapy, na której jednemu
hektarowi odpowiada kwadrat o boku 2 cm?
Uwaga: mamy tu do czynienia z polami
powierzchni, należy więc pamiętać, że
stosunek pól jest równy kwadratowi skali
(patrz lekcja „Pola figur podobnych”).
1 ha = 10 000 m

2

= 100 000 000 cm

2

4 cm

2

(mapa) = 100 000 000 cm

2

(teren) | : 4

1 cm

2

(mapa) = 250 000 000 cm

2

(teren)

Po wyciągnięciu pierwiastka dostajemy:
1 cm (mapa) = 5 000 cm

(teren)

Odpowiedź: Skala tej mapy wynosi 1 : 5000.

PRZYKŁADOWE ZADANIA.

ZADANIE 4.
Podłoga pokoju ma powierzchnię 25 m

2

. Jaką

powierzchnię zajmuje ta podłoga na planie
wykonanym w skali 1 : 500?
Pamiętajmy,

że

działamy

na

polach

powierzchni, podobnie jak w poprzednim
zadaniu.
25 m

2

= 250 000 cm

2

1 cm (plan) = 500 cm (teren)
Po podniesieniu do kwadratu mamy:
1 cm

2

(plan) = 250 000 cm

2

(teren)

250 000 cm

2

: 250 000 = 1 cm

2

Odpowiedź: Na planie ten pokój zajmuje 1
cm

2

.

PRZYKŁADOWE ZADANIA.

ZADANIE 5.
Pewien układ scalony mieści się na
prostokątnej płytce o powierzchni 6 cm

2

. W

jakiej skali wykonano plan na którym płytka
ta ma wymiary 8 cm na 12 cm?
Obliczmy pole tej płytki na planie:
8 cm ∙ 12 cm = 96 cm

2

Zauważmy, że plan został wykonany w
powiększeniu.
96 cm

2

(plan) = 6 cm

2

(w rzeczywistości) |: 6

16 cm

2

(plan) = 1 cm

2

(w rzeczywistości)

Wyciągamy pierwiastek:
4 cm (plan) = 1 cm (w rzeczywistości)
Odpowiedź: Plan ten wykonano w skali 4 : 1.