TEORETYCZNE

PODSTAWY

INFORMATYKI

Prowadzący:

ppor. mgr inż. Mariusz

CHMIELEWSKI

e-mail:

[e-mail]

Temat 4:

Temat 4:

Automaty skończone,

Automaty skończone,

gramatyki, wyrażenia regularne

gramatyki, wyrażenia regularne

ppor. mgr inż. Mariusz CHMIELEWSKI

2

Deterministyczny Automat

Skończony (DAS)



Deterministyczny automat skończony (ang.
Deterministic Finite-state Automaton) to abstrakcyjna
maszyna o skończonej liczbie stanów, która zaczynając w
stanie początkowym czyta kolejne symbole pewnego
słowa, po przeczytaniu każdego zmieniając swój stan na
stan będący wartością funkcji jednego przeczytanego
symbolu oraz stanu aktualnego.



Jeśli po przeczytaniu całego słowa maszyna znajduje się w
którymś ze stanów oznaczonych jako akceptujące
(końcowe), słowo należy do języka regularnego, do
rozpoznawania którego jest zbudowana.



Deterministyczny automat skończony, podobnie jak inne
automaty skończone może być reprezentowany za
pomocą tabeli przejść pomiędzy stanami lub diagramu
stanów

ppor. mgr inż. Mariusz CHMIELEWSKI

3

Deterministyczny Automat

Skończony (DAS)



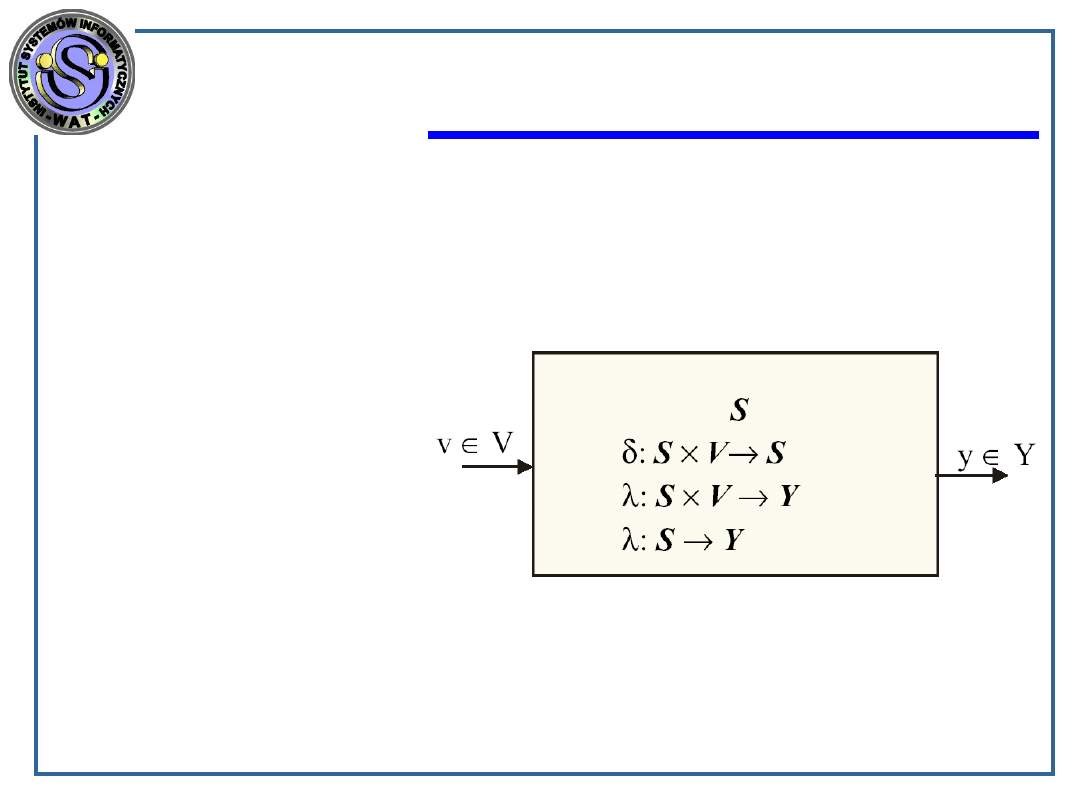
Automat jest definiowany przez określenie:

a) zbioru liter wejściowych V (X) i wyjściowych

Y,

e) zbioru stanów wewnętrznych S,
f) funkcji przejść (),
g) funkcji wyjść ().
Funkcja przejść:
: S X S
Funkcja wyjść:
: S  X Y (tzw. automat Mealy’ego)
: S Y (tzw. automat Moore’a)

ppor. mgr inż. Mariusz CHMIELEWSKI

4

Deterministyczny Automat

Skończony (DAS)

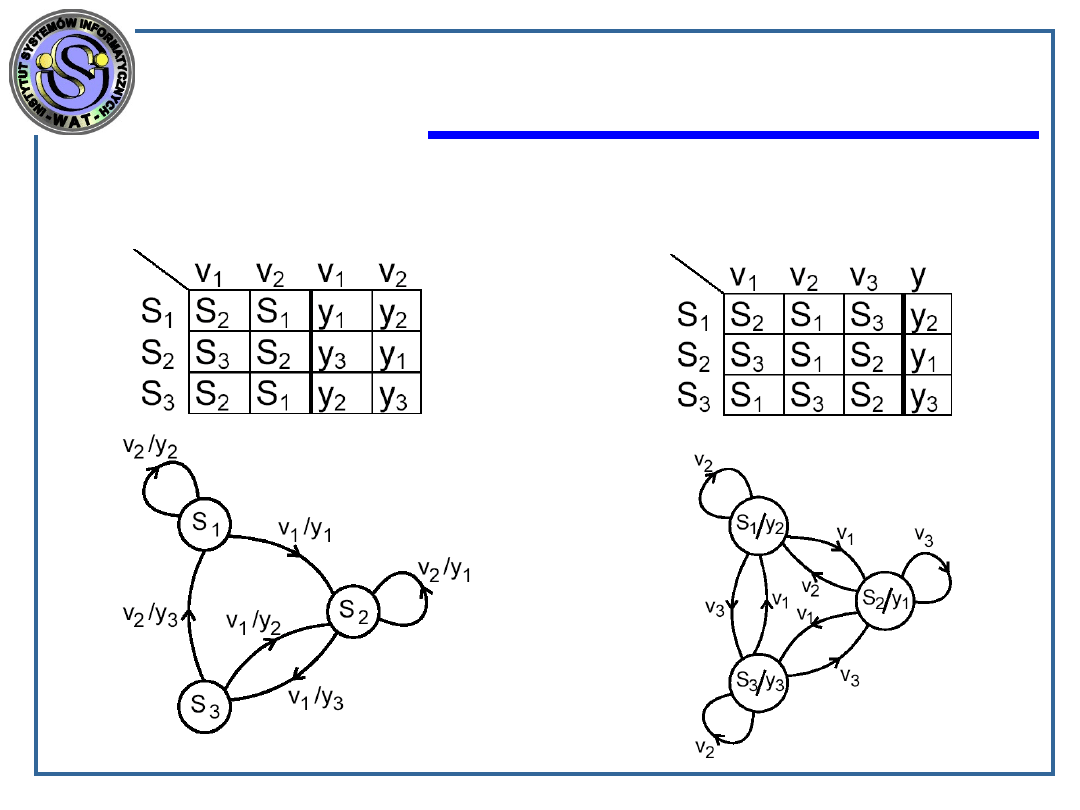
Mealy’ego

Moore’a

ppor. mgr inż. Mariusz CHMIELEWSKI

5

Automat skończony przedstawiamy formalnie jako

uporządkowaną piątkę:

< Q, , , q

o

, F>

gdzie:



Q - jest skończonym zbiorem stanów,



 - jest skończonym alfabetem symboli wejściowych,

q

0

należące do Q jest stanem początkowym od którego

automat rozpoczyna działanie,



F Q - jest zbiorem stanów końcowych (stan

akceptacji lub nieakceptacji),



 - jest funkcją odwzorowującą Q x  w Q czyli 

określa każdemu stanowi q i każdemu symbolowi na
wejściu nowy stan automatu.

ppor. mgr inż. Mariusz CHMIELEWSKI

6



W danej chwili automat odczytuje symbol wejściowy i
przechodzi do kolejnego stanu. Jeżeli stan ten jest
stanem akceptacji to znaczy, że dotychczasowy ciąg
symboli na taśmie jest zaakceptowany przez AS.



Jeżeli głowica przesunęła się na koniec taśmy, a ostatni
stan jest stanem zaakceptowanym przez AS to AS
zaakceptował cały łańcuch.



Formalnie przyjmuje się, że łańcuch jest akceptowany
przez automat M, jeżeli  (q

o

,x)= p dla jakiegoś p

należącego do F.



Język akceptowany przez dany automat M oznaczany
L(M), to zbiór {x | (q

o

,x) należy do F}.



Język nazywamy zbiorem regularnym, jeżeli jest on
językiem akceptowanym przez pewien automat
skończony.

ppor. mgr inż. Mariusz CHMIELEWSKI

7

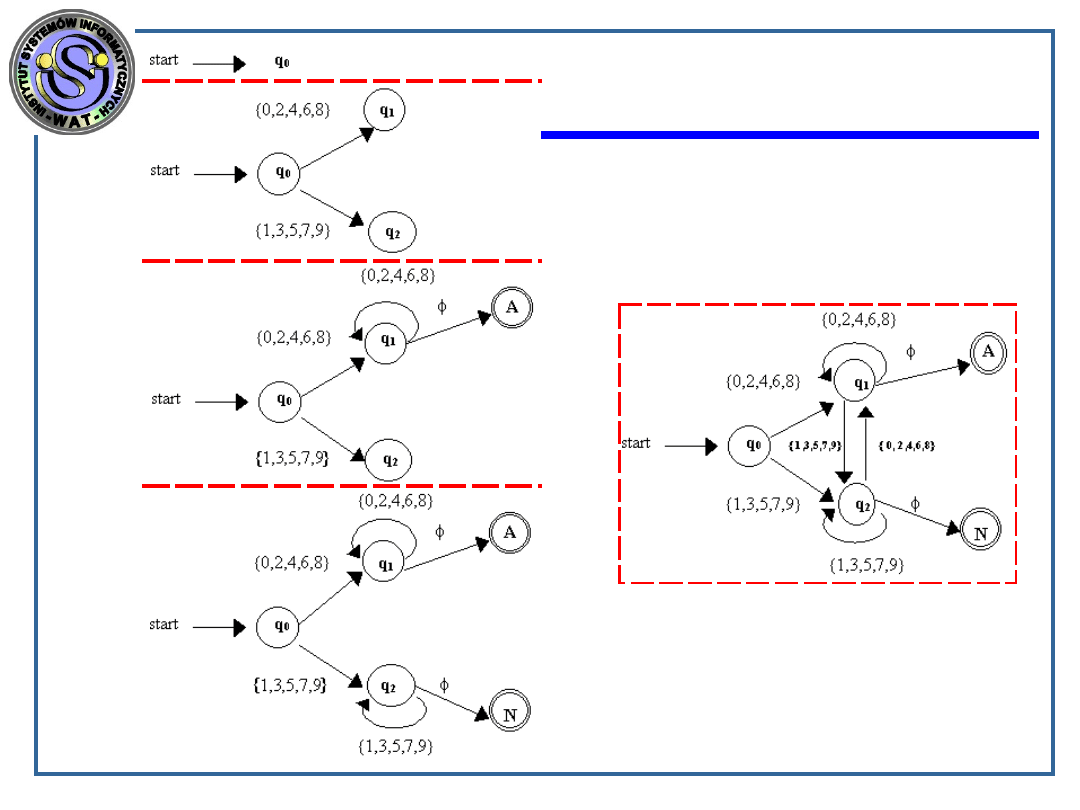
Automat skończony akceptujący liczby podzielne

przez 2



Dla automatu zbiór symboli wejściowych będzie złożony z cyfr od 0..9 czyli

= {0,1,2,3,4,5,6,7,8,9}.



liczba jest parzysta, gdy ostatnia jej cyfra jest podzielna bez reszty przez 2.



Jeżeli pojawi się na wejściu cyfra podzielna przez 2 to zaznaczmy to na

grafie jako przejście do stanu q

1

, jeżeli pojawi się na wejściu cyfra

niepodzielna przez 2 to zaznaczmy to jako przejście do stanu q

2



jeżeli AS jest w stanie q

1

i kolejna cyfra na wejściu jest podzielna przez dwa

to automat pozostaje nadal w tym samym stanie co zaznaczamy na grafie

łukiem wychodzącym z stanu q

1

opatrzonego etykietą {0,2,4,6,8},



jeżeli pozostając w stanie q

2

AS odczyta wszystkie symbole (co umownie

oznaczamy pojawieniem się symbolu  lub # ) wówczas AS przechodzi do

stanu akceptacji A



jeżeli AS jest w stanie q

1

i kolejna cyfra na wejściu jest nieparzysta to AS

pozostaje nadal w tym samym stanie co zaznaczamy na grafie łukiem

wychodzącym i wchodzącym do stanu q

2

opatrzonego etykietą {1,3,5,7,9},



jeżeli pozostając w stanie q

2

AS odczyta wszystkie symbole to wówczas AS

przechodzi do stanu nieakceptacji N



istnieje możliwość pojawienia się na wejściu przemiennie liczb parzystych i

nieparzystych a tym samym przejścia z stanu q

1

do stanu q

2

ppor. mgr inż. Mariusz CHMIELEWSKI

8

Automat skończony akceptujący

liczby podzielne przez 2

Diagram przejść stanów automatu

Diagram przejść stanów automatu

ppor. mgr inż. Mariusz CHMIELEWSKI

9

Automat skończony akceptujący liczby podzielne

przez 3



Dla tego automatu zbiór symboli wejściowych będzie
złożony z cyfr od 0..9 czyli = {0,1,2,3,4,5,6,7,8,9}.



Wiadomo też, że liczba jest podzielna bez reszty przez 3,
gdy suma cyfr danej liczby jest podzielna przez 3.



Musimy więc rozpatrzyć następujące przypadki tego
zadania:



jeżeli liczba złożona jest z cyfr 0,3,6,9 to jest ona na
pewno podzielna przez 3.



dla cyfr 1,4,7 i 2,5,8 rozpatrza się dodatkowe warunki :
pojawienie się cyfr 1,4,7 musi wystąpić trzykrotnie bądź
musi wystąpić cyfra 2,5,8 by liczba była podzielna przez
3.



pojawienie się cyfr 2,5,8 musi wystąpić trzykrotnie bądź
po pojawieniu się jednej z nich musi wystąpić cyfra 1,4,7.

ppor. mgr inż. Mariusz CHMIELEWSKI

10

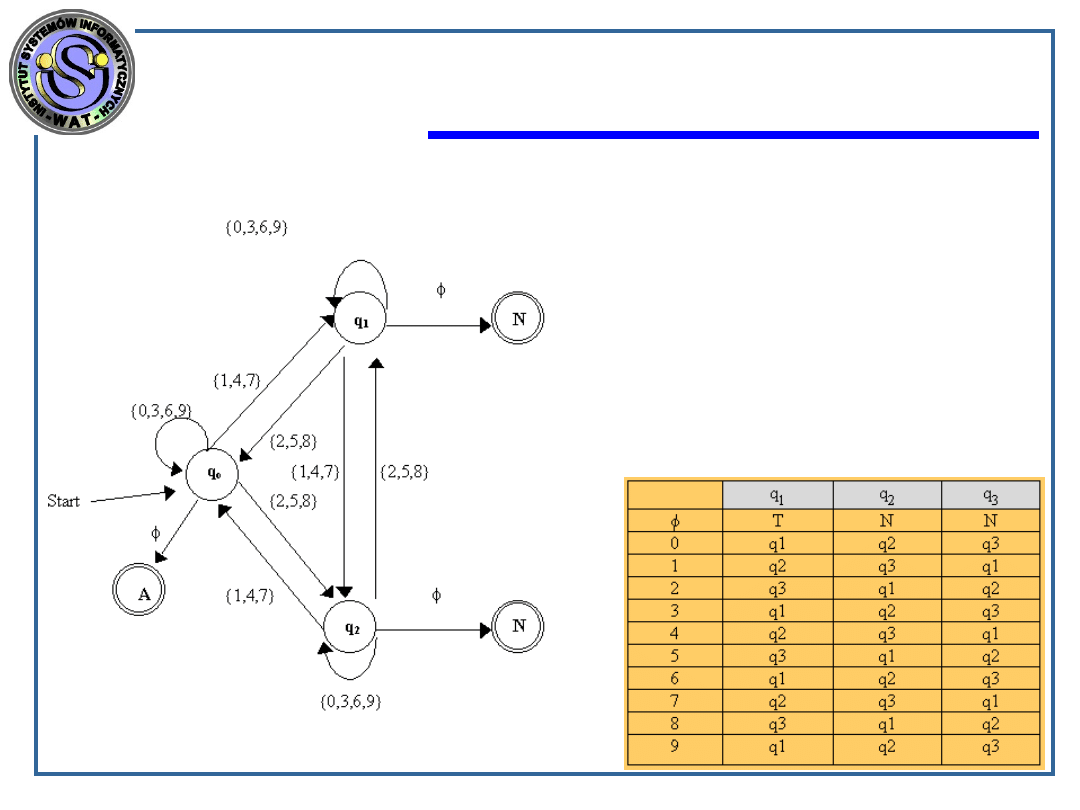
Automat skończony akceptujący liczby podzielne

przez 3

Badanie czy dana liczba jest podzielna przez

n sprowadza się do operacji modulo
(badanie reszty z dzielenia liczby przez
n).

W tym celu tworzymy tabelę stanów,

obrazującą przejścia między stanami w
zależności od rozpatrywanej cyfry.

Tabelę taką tworzymy w następujący sposób:

1.

liczba kolumn jest równa n, czyli
liczbie przez którą dana liczba
wejściowa ma być podzielna,

2.

natomiast liczba wierszy jest równa
liczbie cyfr (0-9) uzupełniona o 1
dla symbolu pustego .

ppor. mgr inż. Mariusz CHMIELEWSKI

11

Niedeterministyczny automat

skończony



Dany symbol wejściowy może wymusić przejście do różnych stanów
DAS, stąd wprowadźmy modyfikację modelu automatu skończonego,
polegającą na istnieniu kilku przejść ze stanu przy tym samym
symbolu wejściowym. Taka modyfikacja pozwala zdefiniować model
niedeterministycznego automatu skończonego (NAS), który
formalnie jest definiowany jako uporządkowana piątka:

<Q, , , q

o

, F>

gdzie:



Q - jest skończonym zbiorem stanów,



 - jest skończonym alfabetem symboli wejściowych, q

0

należące do Q

jest stanem początkowym od którego automat rozpoczyna działanie,



F Q - jest zbiorem stanów końcowych (stan akceptacji lub

nieakceptacji),



- jest odwzorowaniem Q x  w 2

Q

. (2

Q

- jest zbiorem potęgowym Q,

czyli zbiorem wszystkich podzbiorów Q), czyli  (q,a) jest zbiorem

wszystkich stanów p, dla których istnieje przejście ze stanu q do p o
etykiecie związanej z symbolem wejściowym a.

ppor. mgr inż. Mariusz CHMIELEWSKI

12

Niedeterministyczny automat

skończony



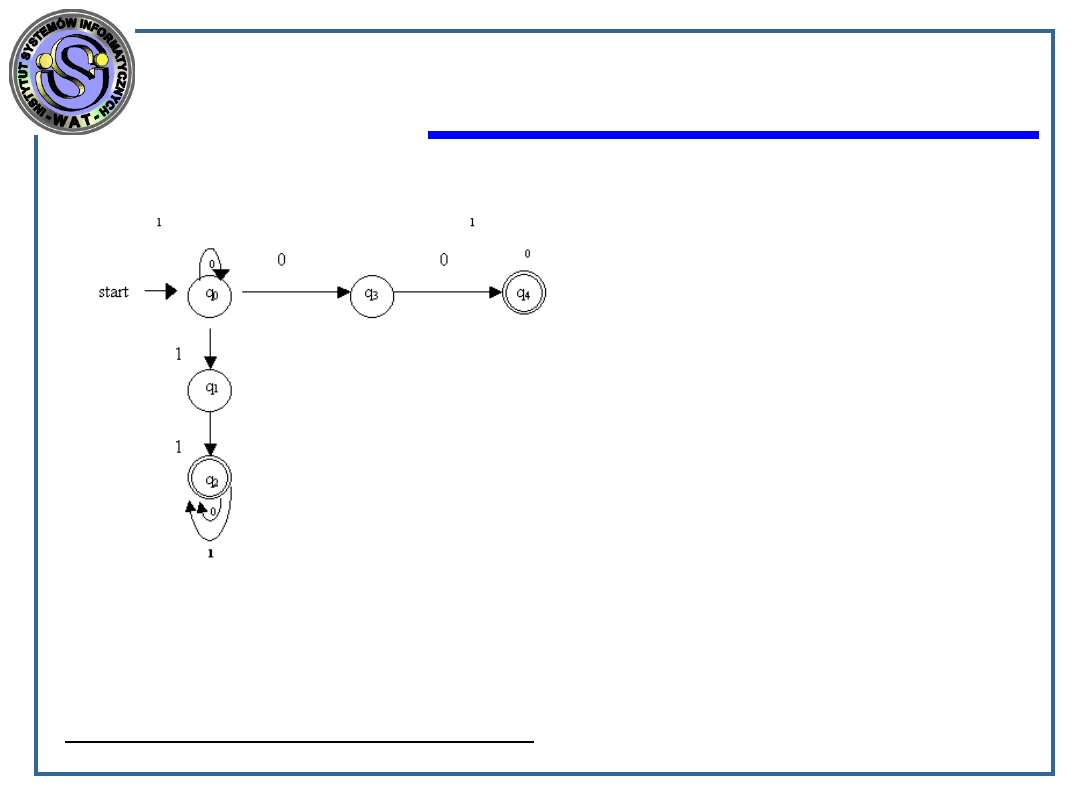
Ze

stanu

q

0

wychodzą

dwie

krawędzie (drogi) o etykiecie 0, czyli

w momencie pojawienia się zera na

wejściu istnieje możliwość przejścia

ze stanu q

0

do stanu q

1

lub q

3

.



Taka właśnie możliwość wyboru

stanów przy tym samym symbolu

wejściowym wyróżnia NAS od DAS.



Automat będzie akceptował ciąg

symboli

a

1

,a

2

...a

n

,

dla

którego

istnieje ciąg przejść prowadzący od

stanu początkowego do stanu

końcowego.

Dla przykładu ciąg 101001 zostanie zaakceptowany przez powyższy NAS
ponieważ istnieje ciąg przejść: q

0

, q

0

, q

0

, q

3

, q

4

, q

4

; natomiast dla ciągu 10101

nie istnieje żadne przejście ze stanu początkowego do końcowego, gdyż
automat w wyniku pojawienia się symboli 10101 pozostanie w stanie q

0

czyli

wyrażenie nie zostanie zaakceptowane.

ppor. mgr inż. Mariusz CHMIELEWSKI

13```````````

Przykład – NAS



Deterministyczny

automat

skończony

jest

szczególnym przypadkiem NAS, w którym dla
każdego stanu istnieje dokładnie jedno przejście
ze stanu do stanu czyli każdy DAS jest NAS

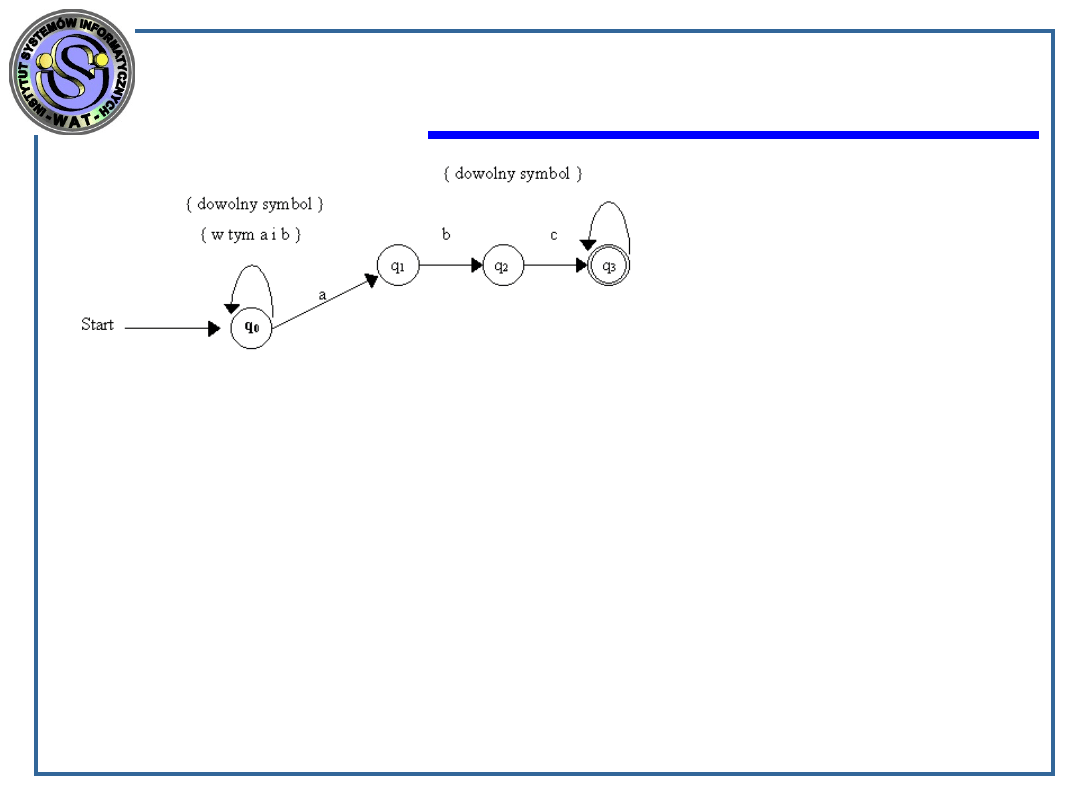
NAS akceptujący ciągi

NAS akceptujący ciągi

wyrazowe,

wyrazowe,

w których wystąpiła

w których wystąpiła

przynajmniej

przynajmniej

raz sekwencja symboli

raz sekwencja symboli

a,b,c

a,b,c

ppor. mgr inż. Mariusz CHMIELEWSKI

14

Automat skończony z  - ruchami



Modyfikacją niedeterministycznego automatu skończonego

jest automat skończony z - ruchami.



Model automatu w tym przypadku dopuszcza przejście ze

stanu do stanu przy pustym wejściu .



Formalnie niedeterministyczny automat skończony z -

ruchami jest definiowany jako uporządkowana piątka:

< Q, , , q

o

, F>

gdzie:



Q - jest skończonym zbiorem stanów,



 - jest skończonym alfabetem symboli wejściowych, q

0

należące do Q jest

stanem początkowym od którego automat rozpoczyna działanie,



F Q - jest zbiorem stanów końcowych (stan akceptacji lub

nieakceptacji),



- odwzorowuje Q x ( {}) w 2

Q

. Czyli  jest zbiorem wszystkich stanów

p takich, że istnieje przejście o etykiecie a ze stanu q do p, natomiast a

jest słowem pustym  lub symbolem ze zbioru .

ppor. mgr inż. Mariusz CHMIELEWSKI

15

Automat skończony z  - ruchami



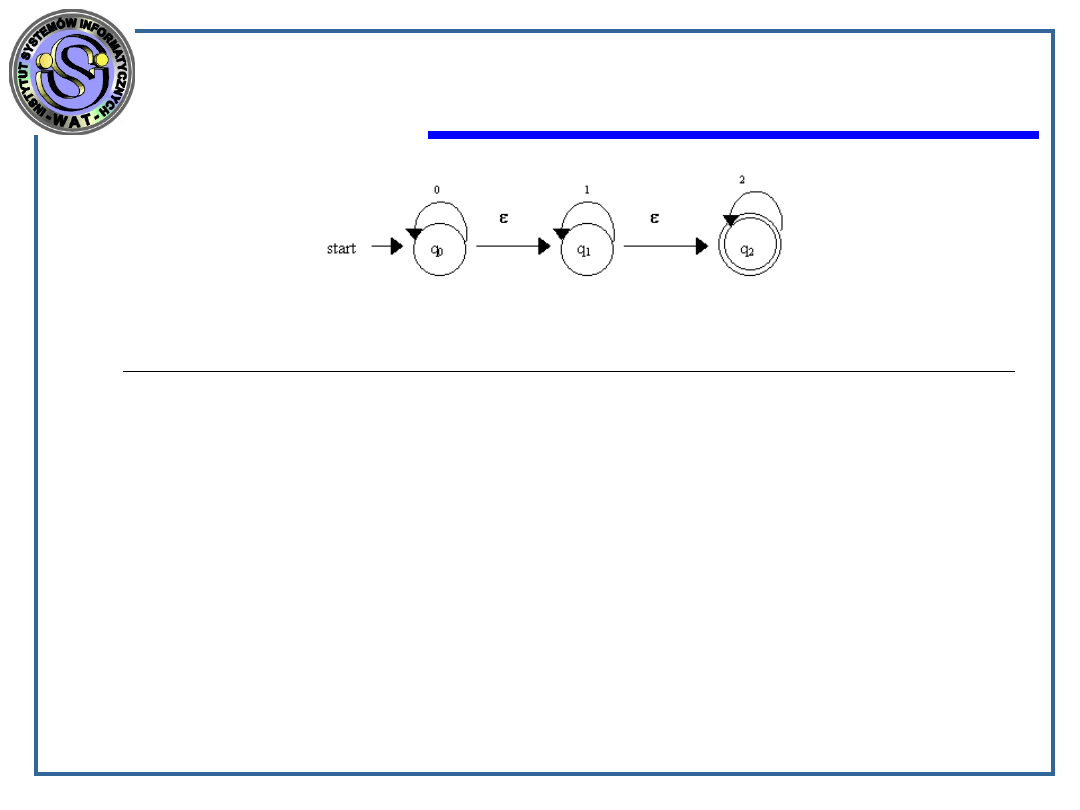
Rozpatrzmy diagram przejść AS z - ruchami, który

akceptuje ciąg symboli zawierających dowolna liczbę zer,
po których następuje dowolna liczba jedynek, a następnie
dowolna liczba dwójek. Oczywiście zgodnie z definicją
dowolna liczba poszczególnych symboli może wynosić 0
czyli nastąpi przejście przy pustym wejściu .



Słowo 002 zostanie zaakceptowane, gdyż istnieje droga od
stanu początkowego do stanu końcowego: q

0

, q

0

, q

0

, , , q

2

,

o łukach etykietowanych 0 ,0, , , 2.

ppor. mgr inż. Mariusz CHMIELEWSKI

16

Wyrażenia regularne



Języki

akceptowane

przez

automaty

skończone

można

opisać

prostymi

wyrażeniami

zwanymi

wyrażeniami

regularnymi.

Niech:  będzie skończonym zbiorem symboli,

L, L

1

, L

2

będą zbiorami łańcuchów z 

*

.

Złożeniem L

1

i L

2

, oznaczanym jako L

1

L

2

, nazywamy

{xy | x należy do L

1

i y należy do L

2

}

oznacza to, że łańcuchy należące do L

1

L

2

tworzone są poprzez wypisanie łańcucha

z L

1

, a następnie łańcucha z L

2

, we wszystkich możliwych kombinacjach

np. niech L

1

={0,1} i L

2

={01,101} wtedy złożenie

L

1

L

2

= {001,0101, 101,1101}.

Niech L

0

={} i L

i

=Ll

i-1

dla i  0.

ppor. mgr inż. Mariusz CHMIELEWSKI

17

Wyrażenia regularne

Domknięciem Kleene’ego (domknięciem) L, oznaczanym symbolem L

*

, nazywamy

zbiór:

Domknięciem dodatnim L, oznaczanym symbolem L

+

, nazywamy zbiór:

L

*

jest zbiorem wszystkich słów otrzymanych w wyniku złożenia dowolnej liczby

słów z L,

L

+

wyklucza przypadek zera słów, których złożenie określa się - ;

np. domknięciem Kleene’ego {1,0}

*

= {, 1, 0, 11,10,01,00....} ,

zaś domknięciem dodatnim {1,0}

+

= {1, 0, 11,10,01,00....}.









0

*

i

i

L

L











1

i

i

L

L

ppor. mgr inż. Mariusz CHMIELEWSKI

18

Wyrażenia regularne - definicja



Wyrażenia regularne i zbiory przez nie reprezentowane definiujemy
w następujący sposób:

1.

0 jest wyrażeniem regularnym reprezentującym
zbiór pusty.

.

2

 jest wyrażeniem regularnym reprezentującym

zbiór {}.

3.

Dla każdego a z , a jest wyrażeniem regularnym

reprezentującym zbiór {a}.

4.

Jeżeli r i s są wyrażeniami regularnymi
reprezentującymi odpowiednio języki R i S, to (r+s),
(rs)

i

(r

*

)

są

wyrażeniami

regularnymi

reprezentującymi odpowiednio zbiory RS, RS i R

*

.

ppor. mgr inż. Mariusz CHMIELEWSKI

19

Wyrażenia regularne - przykład

1.

00 jest wyrażeniem regularnym, reprezentującym {00}

2.

(0+1) opisuje zbiór wszystkich łańcuchów złożonych z zer i

jedynek

3.

(0+1)

*

00(0+1)

*

opisuje zbiór wszystkich zer i jedynek, w

których przynajmniej raz wystąpiło podwojenie zer

4.

(1+10)

*

reprezentuje zbiór wszystkich zer i jedynek

rozpoczynających się od 1 i nie zawierajęcych podwojonych

symboli 0.

5.

(0+1)

*

011 opisuje wszystkie łańcuchy zer i jedynek

kończące się sekwencją 011

6.

0

+

1

+

2

+

jest wyrażeniem reprezentującym dowolna liczbę zer

po których następuje dowolna liczba jedynek, a następnie

dowolna liczba dwójek (domknięcie dodatnie - czyli łańcuchy

końcowe

muszą

zawierać

przynajmniej

po

jednym

reprezentancie powyższych symboli).

Zadanie: Podaj po 4 przykłady do podpunktów 3- 6

ppor. mgr inż. Mariusz CHMIELEWSKI

20



Wyrażenia regularne reprezentują języki
akceptowane przez automaty skończone co
oznacza, że dla

dowolnego

wyrażenia

regularnego

istnieje odpowiadający mu NAS z -

ruchami

,



Wprowadzono

gotowe

konstruktory

dla

diagramów

przejść

pozwalające

dla

dowolnego wyrażenia regularnego stworzyć
mechanicznie

konstrukcję

automatu

skończonego.

ppor. mgr inż. Mariusz CHMIELEWSKI

21

Podstawowe postacie wyrażeń

regularnych

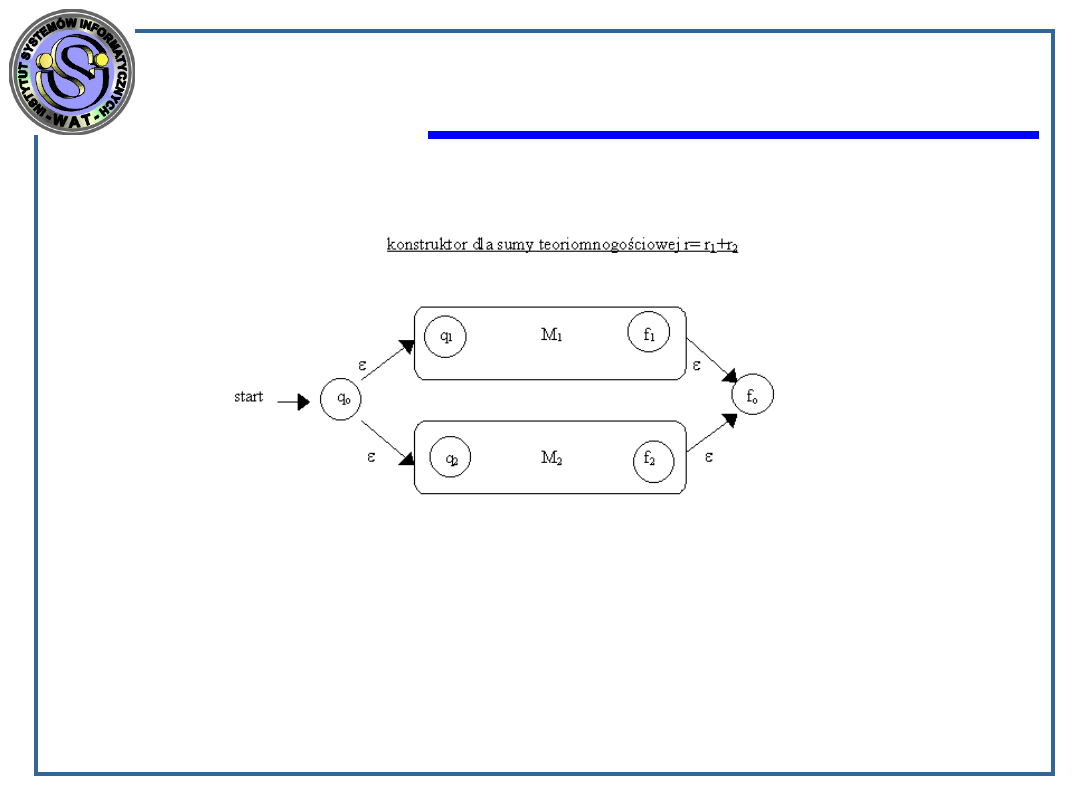
1.

suma teoriomnogościowa: r = r

1

+ r

2

2.

złożenie: r = r

1

r

2

3.

domknięcie: r = r

1

*

ppor. mgr inż. Mariusz CHMIELEWSKI

22

Podstawowe postacie wyrażeń

regularnych



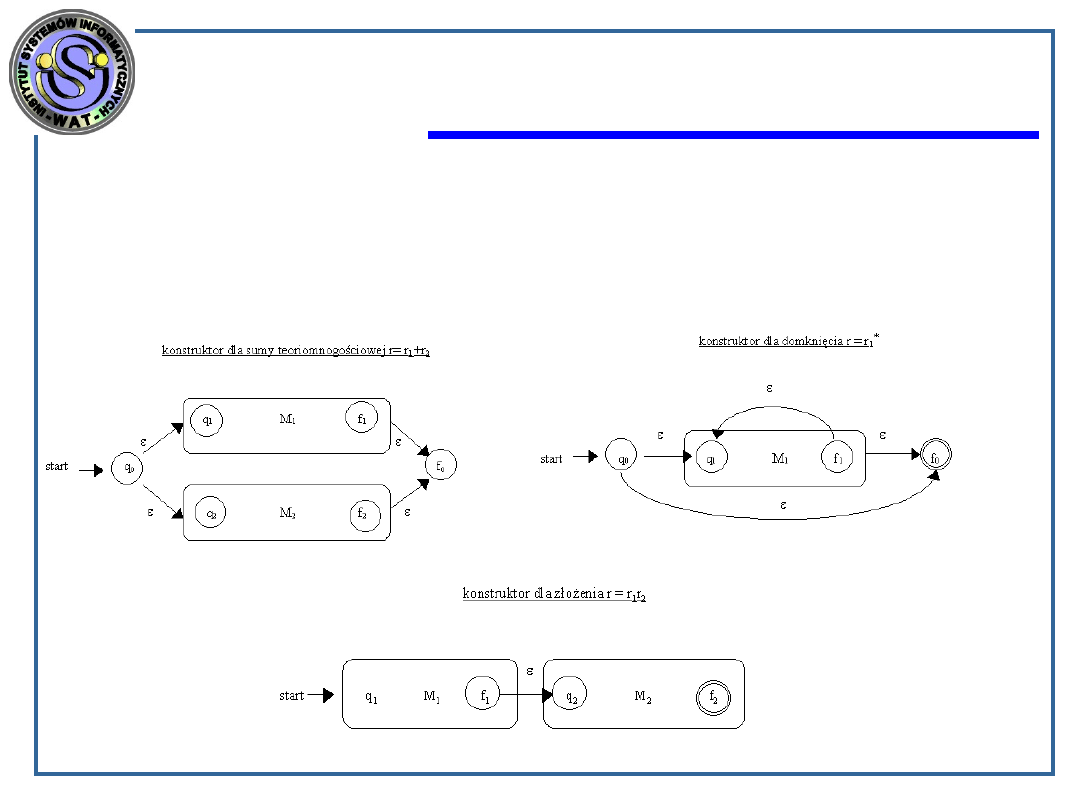
suma teoriomnogościowa: r = r

1

+ r

2

Każda droga na diagramie automatu M musi rozpoczynać się od przejścia do

stanu q1 lub do stanu q2 przy pustym wejściu .

Jeżeli droga prowadzi do q1, to następnie może dowolnie przebiegać w

automacie M1, aż do osiągnięcia stanu f1, potem następuje przejście do
stanu fo, przy pustym wyjściu .

Jeżeli droga rozpoczęła się przejściem ze stanu q0 do q2 to następnie może

przebiegać dowolną trasą w automacie M2, aż do osiągnięcia stanu f2, a
następnie przejście do stanu f0.

ppor. mgr inż. Mariusz CHMIELEWSKI

23

Podstawowe postacie wyrażeń

regularnych



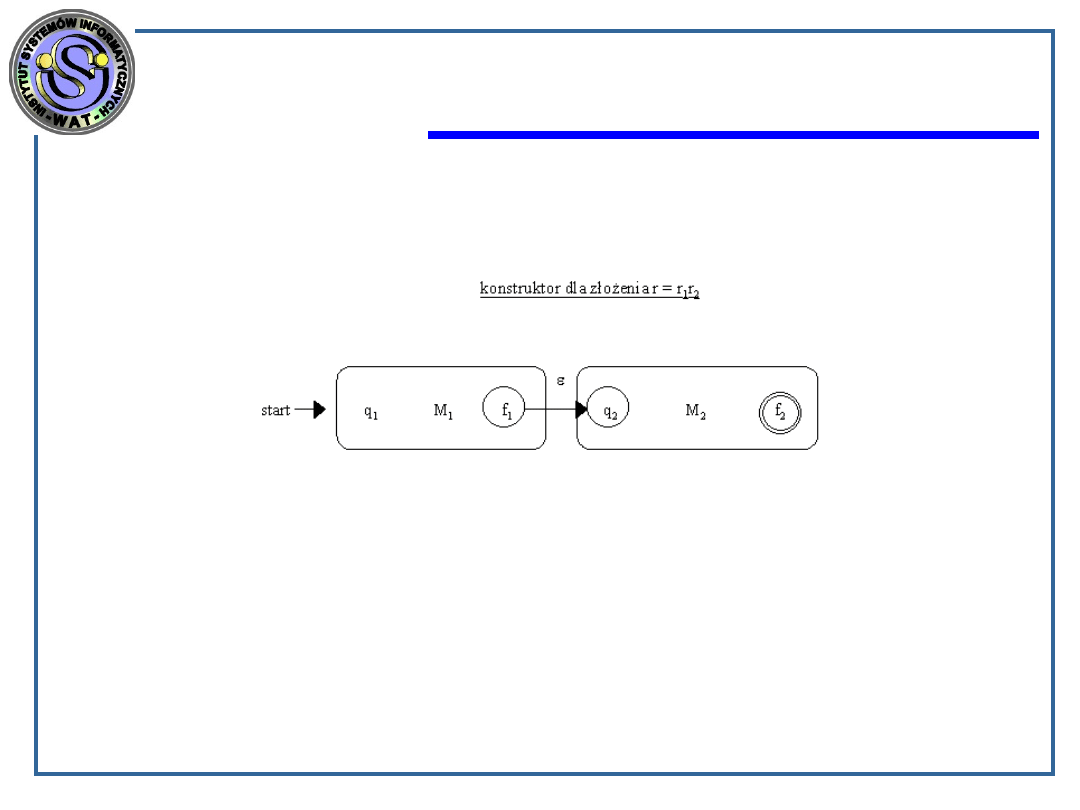
złożenie: r = r

1

r

2



Każda droga z q1 do f2 w automacie M składa się z
drogi etykietowanej jakimś łańcuchem x prowadzącej z
q1 do f1, po której następuje przejście ze stanu f1 do
stanu q2 przy pustym wejściu , a następnie następuje

droga z q2 do f2 etykietowana jakimś łańcuchem y.

ppor. mgr inż. Mariusz CHMIELEWSKI

24

Podstawowe postacie wyrażeń

regularnych



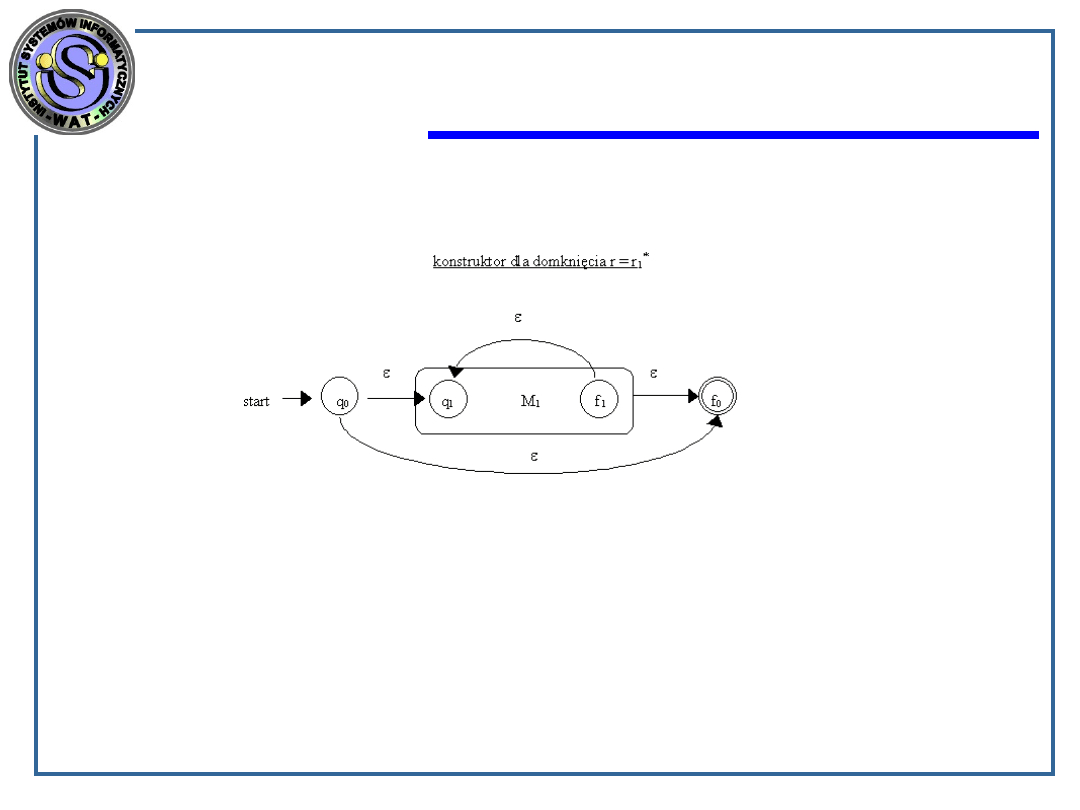
domknięcie: r = r

1

*



Dowolna droga prowadząca z q0 do f2 składa się albo z
drogi z q0 do f0 o etykiecie , albo też z drogi od q0 do q1

przy , po których następuje pewna liczba (w

szczególnym przypadku 0) dróg z q1 do f1, potem znowu
do q1 przy , następnie znów droga z q1 do f1, aż w

końcu droga z f2 do f0 przy .

ppor. mgr inż. Mariusz CHMIELEWSKI

25

Podstawowe postacie wyrażeń

regularnych



Konstrukcję takiego automatu rozpoczynamy od rozłożenia

Konstrukcję takiego automatu rozpoczynamy od rozłożenia

wyrażenia regularnego na elementarne składowe, dla których

wyrażenia regularnego na elementarne składowe, dla których

tworzymy automaty, te z kolei na podstawie konstruktorów łączymy

tworzymy automaty, te z kolei na podstawie konstruktorów łączymy

w logiczną całość.

w logiczną całość.

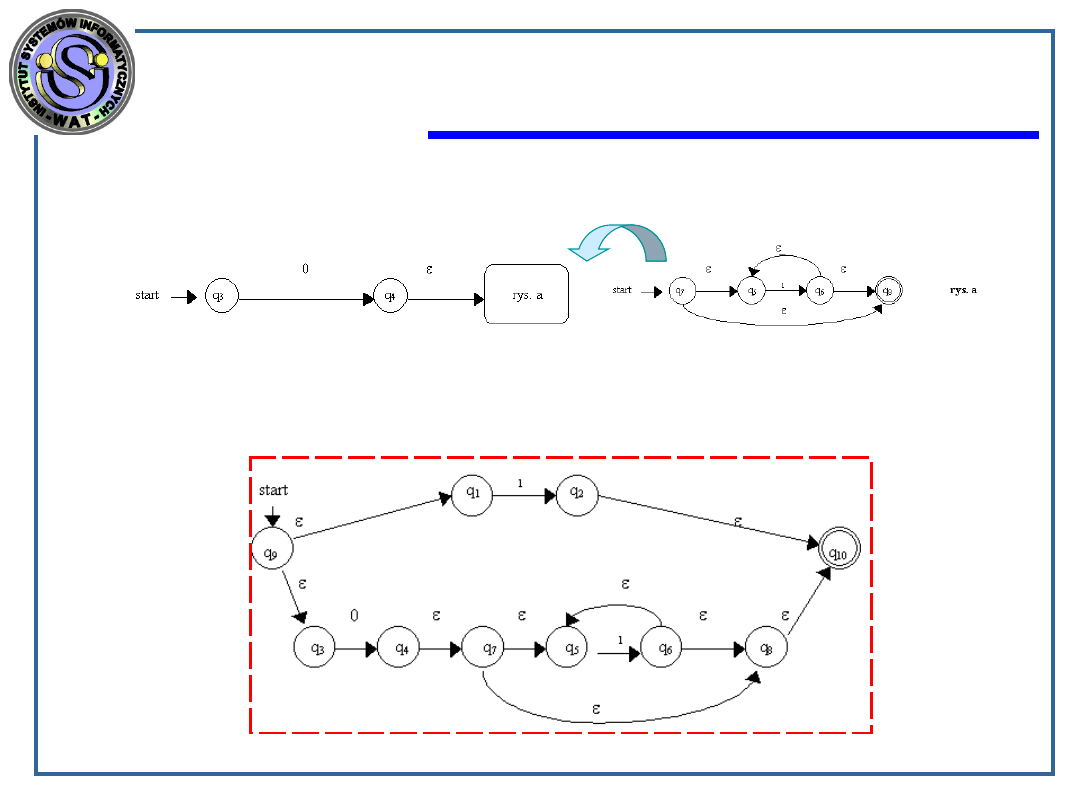
Przykład:

Przykład: automat akceptujący wyrażenie regularne postaci: 01

*

+1.

wyrażenie jest postaci r = r

1

+ r

2

gdzie: r

1

=01

*

; r

2

= 1.

wyrażenie r

1

możemy zapisać jako r

1

= r

3

+ r

4

gdzie r

3

= 0; r

4

=1

*

wyrażenia r

2

postać automatu

automat
dla r

3

wyrażenie r

4

możemy zapisać jako r

4

= r

*

5

gdzie r

5

to 1, a

NAS dla r

5

to

r

4

=

1*

(

konstruktor

domknięcia)

ppor. mgr inż. Mariusz CHMIELEWSKI

26

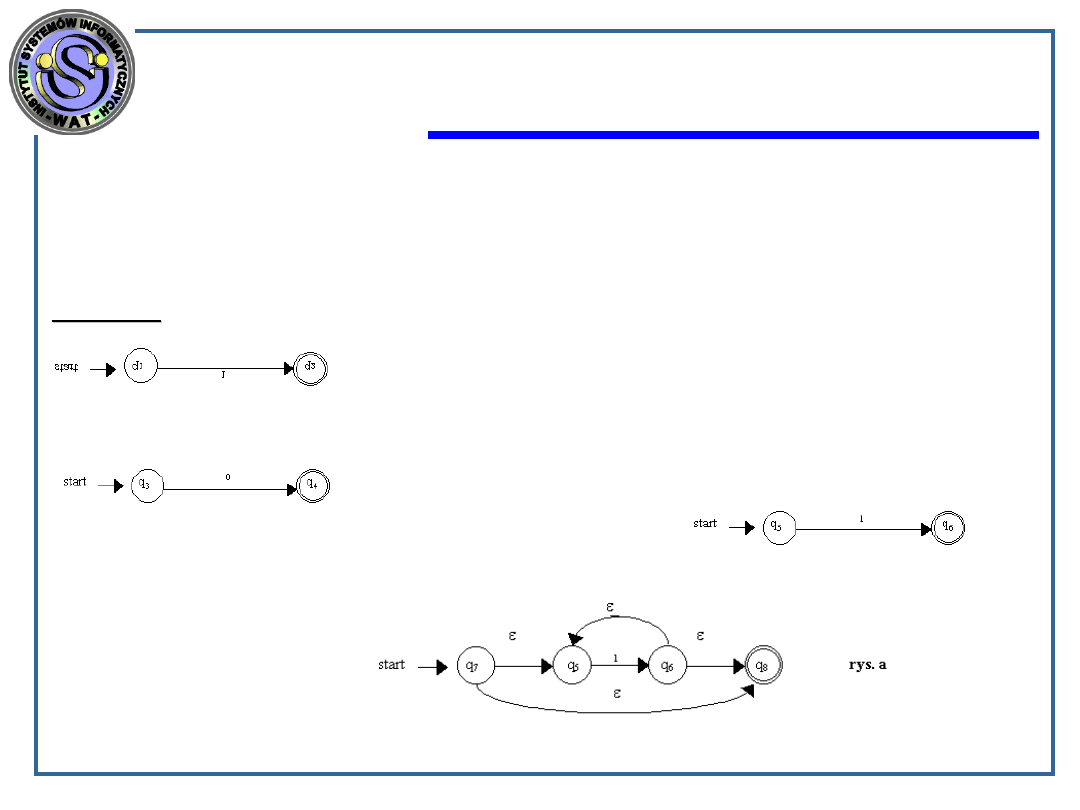
dla r

1

=r

3

r

4

(r= 01

*

) wykorzystujemy konstruktor złożenia dokładając do rys. a

następującą konstrukcję

dla wyrażenia r= r

1

+ r

2

(r=01

*

+1) tworzymy konstrukcję wykorzystując

konstruktor sumy teoriomnogościowej

ppor. mgr inż. Mariusz CHMIELEWSKI

27

Analizatory leksykalne



Tokeny (czyli bazowe kategorie syntaktyczne) języka programowania dają się
niemal bez wyjątku przedstawić w postaci wyrażeń regularnych. I tak na
przykład, identyfikatory ALGOLu, będące ciągami liter i cyfr rozpoczynającymi się
od litery (małej czy dużej), bez ograniczenia co do długości ciągu, można wyrazić
w postaci

( litera ) ( litera + cyfra )

*

Gdzie:

litera oznacza A + B +... + Z + a + b + .. z, a cyfra – 0 + 1 + .. + 9



Identyfikatory w Fortranie, których długość jest ograniczona do sześciu znaków i
które nie mogą zawierać innych liter niż duże oraz znak $ mogą być
przedstawione jako

( litera ) (  + litera + cyfra )

5



Niektóre generatory analizatorów leksykalnych przyjmują jako wejście ciąg
wyrażeń regularnych opisujących tokeny i wytwarzają pojedynczy automat
skończony, rozpoznający dowolny token.



Zazwyczaj przekształcają one wyrażenia regularne na NAS z -przejściami, a

następnie konstruują podzbiory zbioru stanów, aby otrzymać DAS w sposób
bezpośredni, zamiast wyeliminować najpierw -przejścia.

ppor. mgr inż. Mariusz CHMIELEWSKI

28

Automaty skończone z wyjściem



Główne ograniczenia AS – binarne wyjście (akceptuję/nie akceptuję)

Automat Moore’a:

< Q, , , , , q

o

>

gdzie:



Q - jest skończonym zbiorem stanów,



 - jest skończonym alfabetem symboli wejściowych, q

0

należące do Q jest stanem początkowym od którego automat

rozpoczyna działanie,





- jest alfabetem wejściowym





- jest odwzorowaniem Q w



zadającym wyjście związane z każdym ze stanów.



Wyjściem M odpowiadającym wejściu a

1

a

2 ...

a

n ,

n0, jest

(q

1

) (q

2

) ... (q

n

),

gdzie q

0

, q

1...

q

n

jest ciągiem stanów, takim

że

(q

i-1

,a

i

)=q

i

, dla 1<=i<=n.

Automat Mealy’ego:

< Q, , , , , q

o

>

gdzie:



Q - jest skończonym zbiorem stanów,



 - jest skończonym alfabetem symboli wejściowych, q

0

należące do Q jest stanem początkowym od którego automat

rozpoczyna działanie,





- jest alfabetem wejściowym





- jest odwzorowaniem Q   w



. Inaczej mówiąc

(q,a)

podaje wyjście związane z przejściem ze stanu q przy wejściu a.



Wyjściem M odpowiadającym wejściu a

1

a

2 ...

a

n

, jest

(q

0,

a

1

) (q

1,

a

2

) ... (q

n-1,

a

n

),

gdzie q

0

, q

1...

q

n

jest ciągiem stanów,

takim że

(q

i-1

,a

i

)=q

i

, dla 1<=i<=n.

ppor. mgr inż. Mariusz CHMIELEWSKI

29

Język formalny

ppor. mgr inż. Mariusz CHMIELEWSKI

30

Generator - akceptor

ppor. mgr inż. Mariusz CHMIELEWSKI

31

Gramatyki

ppor. mgr inż. Mariusz CHMIELEWSKI

32

Generowanie języka przez

gramatykę

ppor. mgr inż. Mariusz CHMIELEWSKI

33

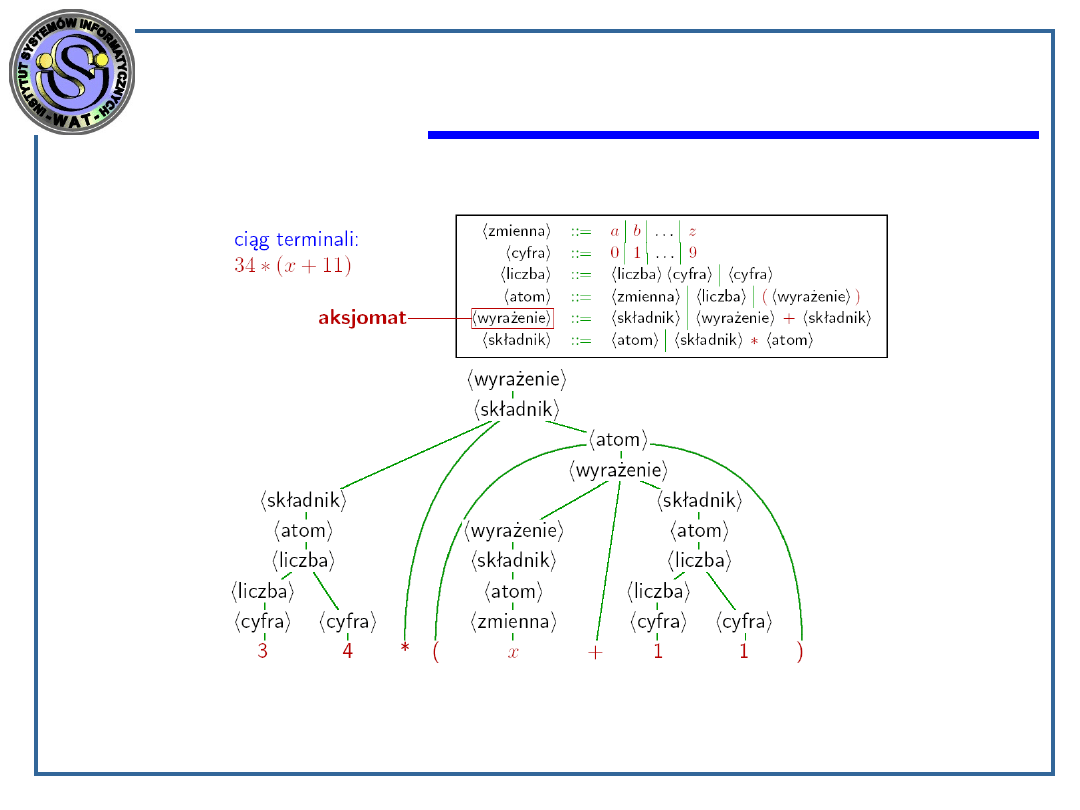
Drzewa wywodu

ppor. mgr inż. Mariusz CHMIELEWSKI

34

Drzewa wywodu

ppor. mgr inż. Mariusz CHMIELEWSKI

35

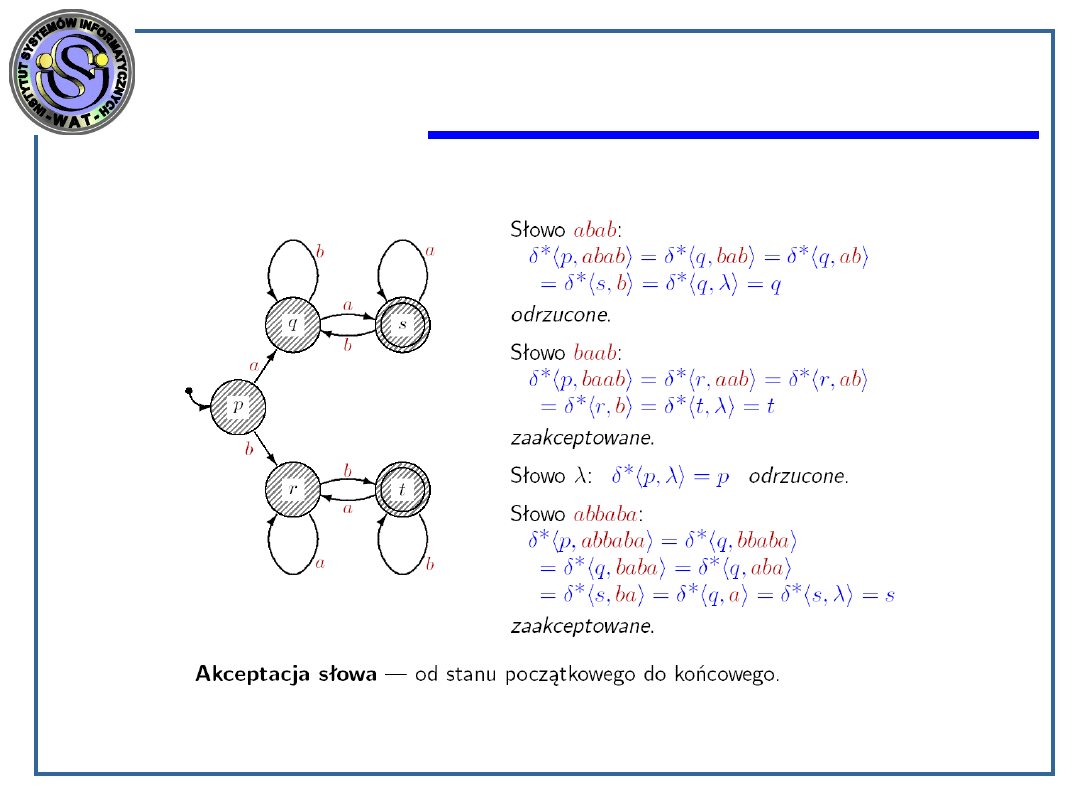
Drzewo wywodu a struktura słowa

ppor. mgr inż. Mariusz CHMIELEWSKI

36

Akceptor