Łukasz Przywarty 171018 (sprawozdanie)

Data wykonania układów: 5.11.2009 r.

Szymon Miazga

Prowadzący: dr inż. Dariusz Banasiak

Sprawozdanie z zajęć laboratoryjnych:

Logika Układów Cyfrowych

Temat: „Komputerowa realizacja automatów skończonych”

(208)

I. Cel ćwiczenia

Celem ćwiczenia jest praktyczne zapoznanie się ze sposobem programowej realizacji na

komputerze lub mikrokomputerze automatów skończonych (na przykładzie automatów

typu Moore`a).

II. Opis programu komputerowego

Ponieważ program pochodzi z roku 1990, przed rozpoczęciem pracy należało uruchomić

emulator systemu DOS – DOSBox.

W oknie konsoli wpisaliśmy kolejno:

mount c c:/labluc //'zamontowanie' katalogu jako partycji c

c:

//przejście do katalogu

new

//uruchomienie programu

Po wykonaniu powyższych instrukcji możliwe było korzystanie z programu. Aby

poprawnie zasymulować automat skończony musimy wprowadzić następujące dane:

–

alfabet wejściowy (czyli co podajemy na wejście automatu),

–

stany wewnętrzne,

–

alfabet wyjściowy (wyjście automatu),

–

funkcja przejść (np. G

i

+

=

0

(q

0

1

(z

3

q

3

, z

2

q

2

, z

1

q

1

2

(z

3

q

3

, z

1

q

4

, z

2

q

2

3

(z

2

q

4

, z

1

q

1

, z

3

q

3

4

(z

1

q

1

, z

2

q

2

, z

3

q

4

5

(z

1

q

4

, z

2

q

4

, z

3

q

4

)

5

)

4

)

3

)

2

)

1

)

0

- q

r

reprezentuje wierzchołek grafu

natomiast wyrażenie z

j

q

s

oznacza wychodzącą z niego krawędź. Cyfry przy

nawiasach to indeksy.)

–

funkcja wyjść (przyporządkowanie stanom wewnętrznym wyjścia).

Dane wprowadzamy korzystając z menu Edycja

Po wprowadzeniu wszystkich danych możemy zasymulować automat – w sposób krokowy

lub ciągły. Wynik symulacji widoczny jest w części Symulacja.

III. Automaty zaprojektowane i zrealizowane na zajęciach

a) automat sprawdzający czy suma liczb jest podzielna przez 5. Na wejście możemy

podać liczby 1,2 lub 3

–

Alfabet wejściowy: Z = {z

0

, z

1

, z

2

}

–

Alfabet wyjściowy: liczba jest lub nie jest podzielna przez 5 dlatego mamy

możliwość otrzymania 2 stanów wyjściowych Y = {y

0

, y

1

}

Ilustracja 1: Okno programu do realizacji automatu skończonego po uruchomieniu

–

Zbiór stanów wewnętrznych Q = {s

0

, s

1

, s

2

, s

3

, s

4

} s

0

oznacza, że reszta z dzielenia

sumy cyfr jest równa 0 (liczba jest podzielna prze 5), natomiast kolejne indeksy

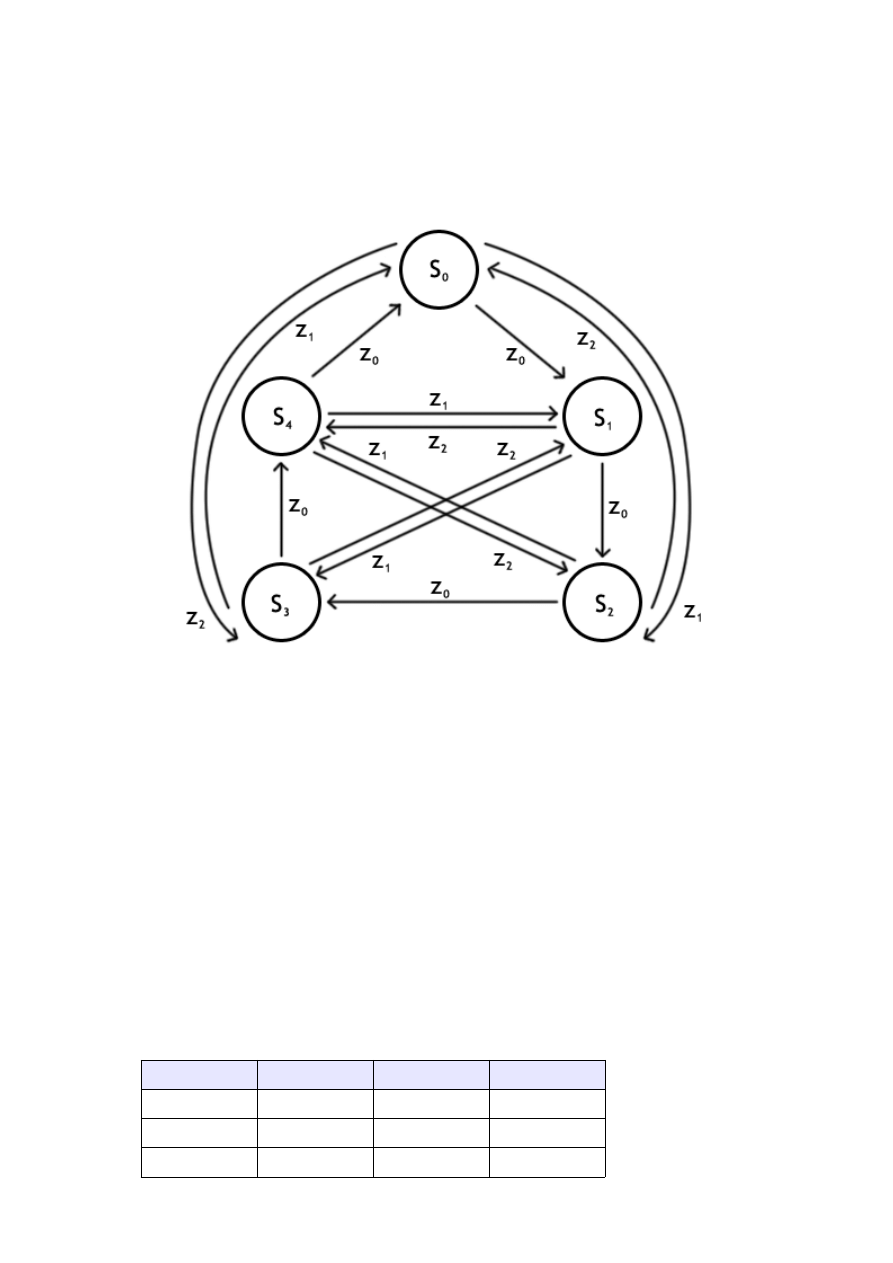
przy s oznaczają kolejne reszty z dzielenia przez 5. (1,2,3 lub 4)

–

Diagram stanów

–

Funkcja wyjść

s

0

y

→

1

s

1

y

→

0

s

2

y

→

0

s

3

y

→

0

s

4

y

→

0

–

Funkcja przejść

G

i

+

=

0

(s

0

1

(z

2

s

3

, z

1

s

2

, z

0

s

1

2

(z

2

s

4

, z

1

s

3

, z

0

s

2

3

(z

2

s

2

, z

1

s

4

, z

0

s

3

4

(z

2

s

1

, z

1

s

0

, z

0

s

4

5

(z

2

s

2

,

z

1

s

1

, z

0

s

0

)

5

)

4

)

3

)

2

)

1

)

0

–

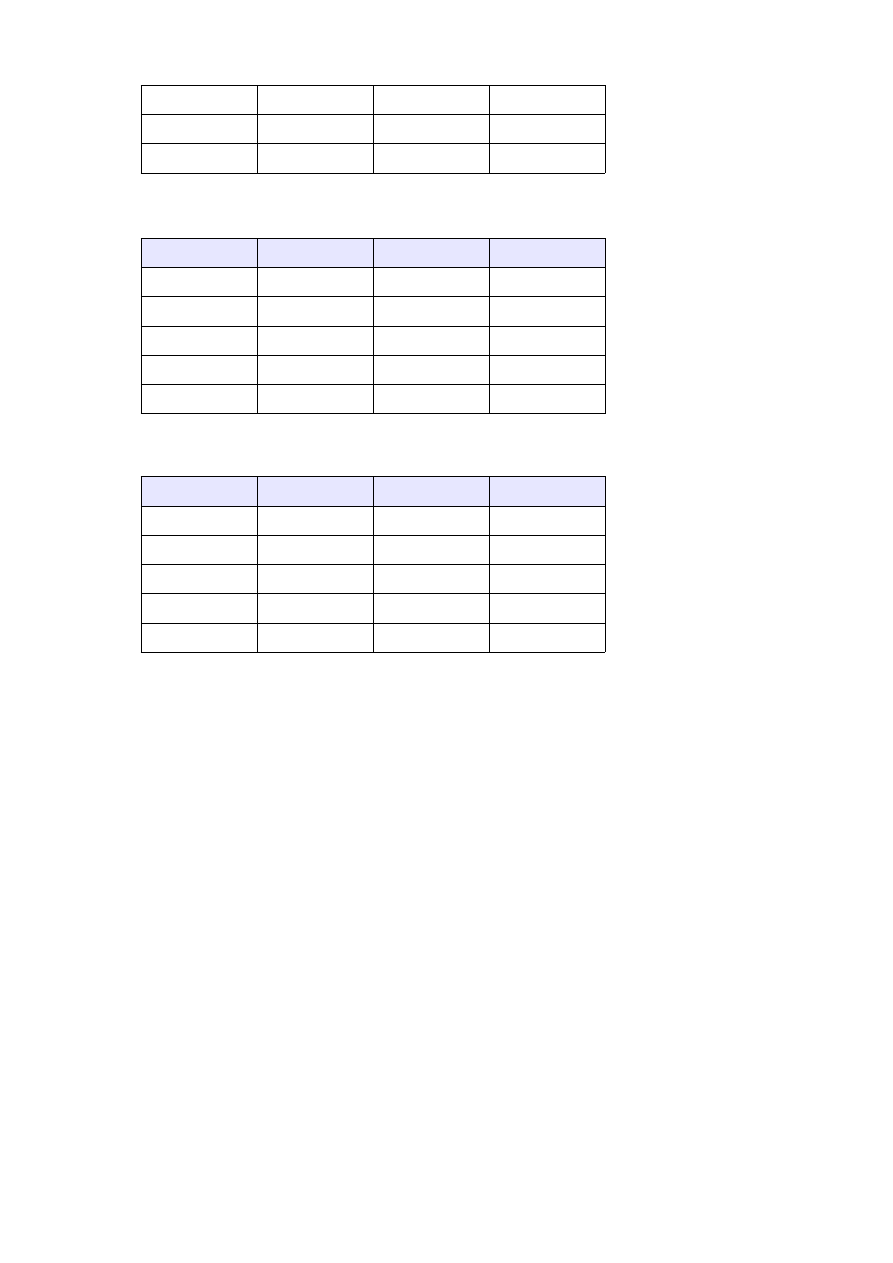
Symulacja:

Słowo wejściowe: z

0

, z

1

, z

2

, z

0

, z

1

, z

2

Q(t)

x(t)

Q(t+1)

Y(t+1)

s

0

z

0

s

1

y

0

s

1

z

1

s

3

y

0

s

3

z

2

s

1

y

0

s

1

z

0

s

2

y

0

s

2

z

1

s

4

y

0

s

4

z

2

s

2

y

0

–

Słowo wejściowe: z

0

, z

1

, z

1

, z

2

, z

0

Q(t)

x(t)

Q(t+1)

Y(t+1)

s

0

z

0

s

1

y

0

s

1

z

1

s

3

y

0

s

3

z

1

s

0

y

1

s

0

z

2

s

3

y

0

s

3

z

0

s

4

y

0

Słowo wejściowe: z

0

, z

2

, z

2

, z

1

, z

0

Q(t)

x(t)

Q(t+1)

Y(t+1)

s

0

z

0

s

1

y

0

s

1

z

2

s

4

y

0

s

4

z

2

s

2

y

0

s

2

z

1

s

4

y

0

s

4

z

0

s

0

y

1

b) Podajemy ciąg składający się z cyfr 1,2,3 a akceptujemy te ciągi, w których obok

siebie nie ma powtarzających się cyfr.

–

Alfabet wejściowy: Z = {z

1

, z

2

, z

3

}

–

Alfabet wyjściowy: ciąg może być poprawny lub nie więc na wyjściu możemy

otrzymać dwa stany wyjściowe Y = {y

0

, y

1

}

–

Zbiór stanów wewnętrznych: Q = {q

1

, q

2

, q

3

, q

4

} gdzie q

0

oznacza stan początkowy

a q

4

błąd

–

Funkcja przejść G

i

+

=

0

(q

0

1

(z

3

q

3

, z

2

q

2

, z

1

q

1

2

(z

3

q

3

, z

1

q

4

, z

2

q

2

3

(z

2

q

4

, z

1

q

1

, z

3

q

3

4

(z

1

q

1

, z

2

q

2

, z

3

q

4

5

(z

1

q

4

, z

2

q

4

, z

3

q

4

)

5

)

4

)

3

)

2

)

1

)

0

–

Funkcja wyjść:

q

0

y

→

1

q

1

y

→

1

q

2

y

→

1

q

3

y

→

1

q

4

y

→

0

–

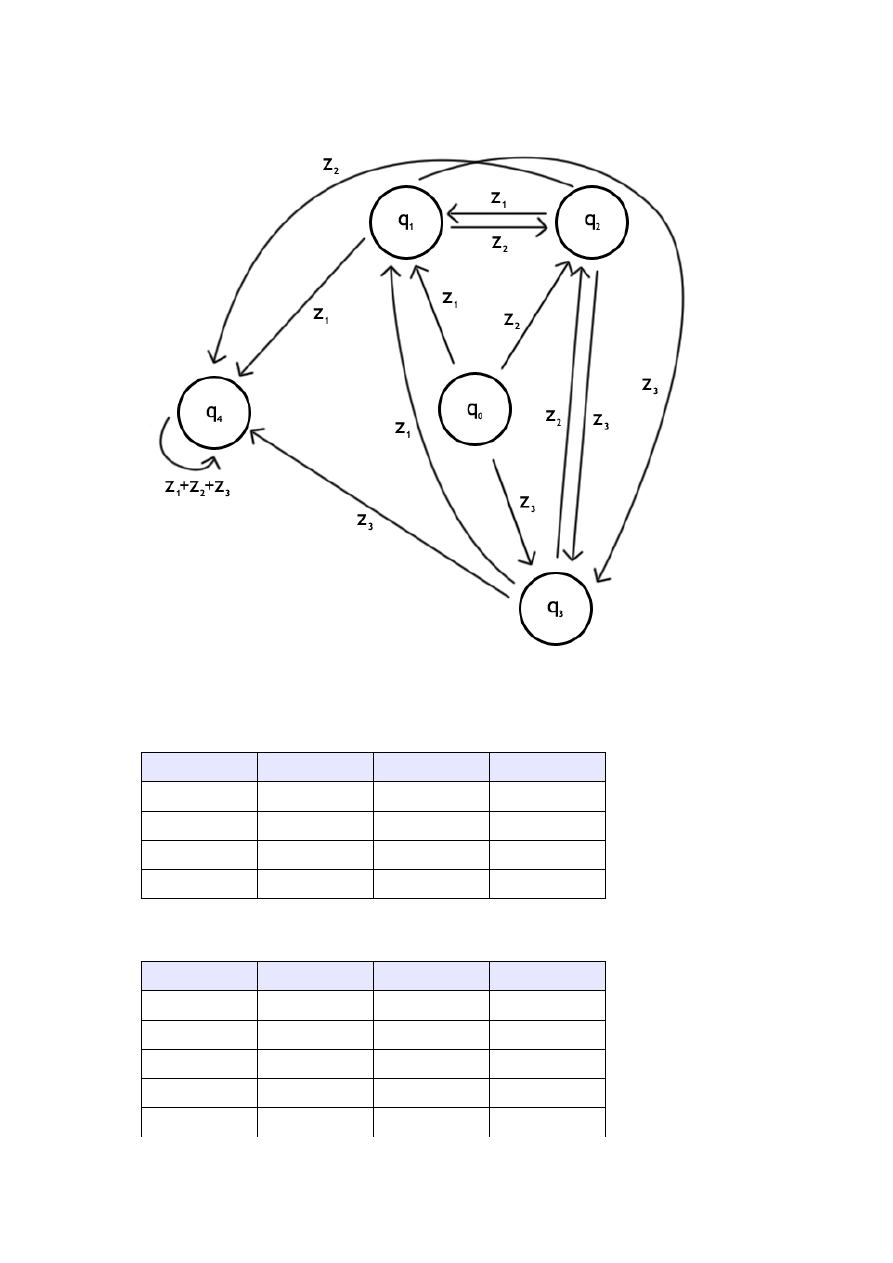
Diagram stanów:

–

Symulacja

Słowo wejściowe: z

1

, z

3

, z

2

, z

2

Q(t)

x(t)

Q(t+1)

Y(t+1)

q

0

z

1

q

1

y

1

q

1

z

3

q

3

y

1

q

3

z

2

q

2

y

1

q

2

z

2

q

4

y

0

Słowo wejściowe: z

1

, z

3

, z

2

, z

1

, z

3

Q(t)

x(t)

Q(t+1)

Y(t+1)

q

0

z

1

q

1

y

1

q

1

z

3

q

3

y

1

q

3

z

2

q

2

y

1

q

2

z

1

q

1

y

1

q

1

z

3

q

3

y

1