Sortowanie tablic

dr inż. Andrzej Obuchowicz
Algorytmy i struktury danych

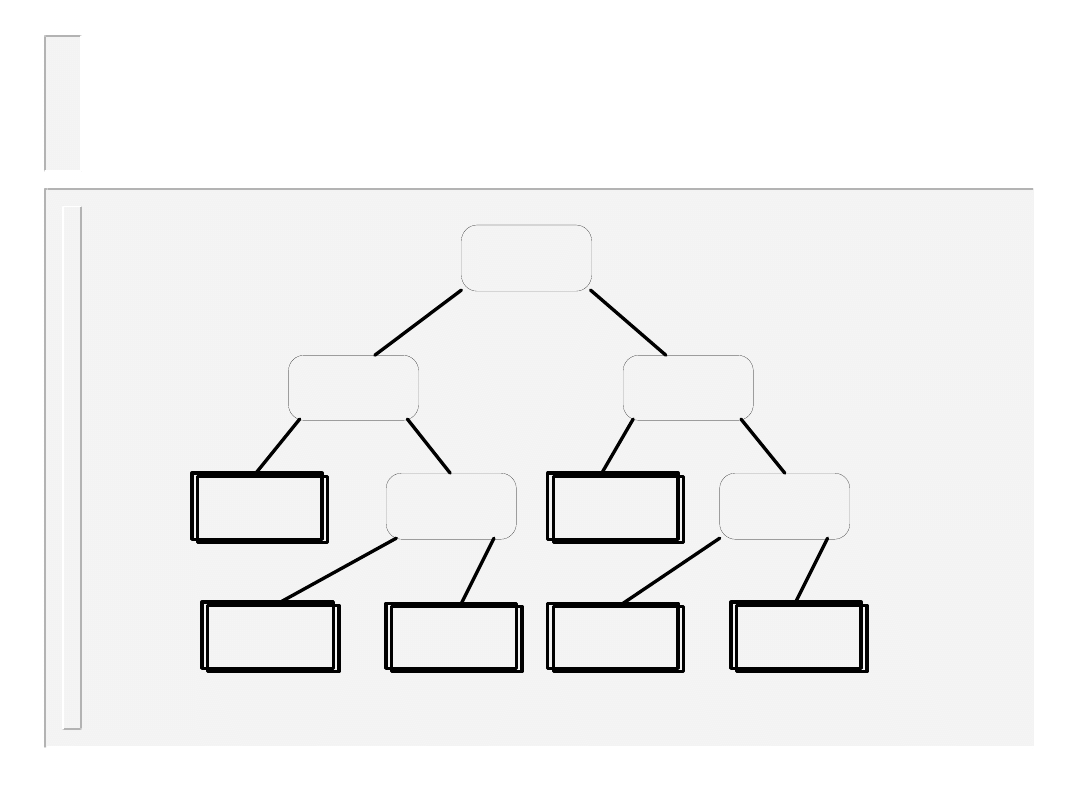
Drzewo decyzyjne
sortowania

a

b



b

c



a

c



b

c



a

c



a

b

c





c

b

a





b

a

c





b

c

a

 

c

a

b





a

c

b

 

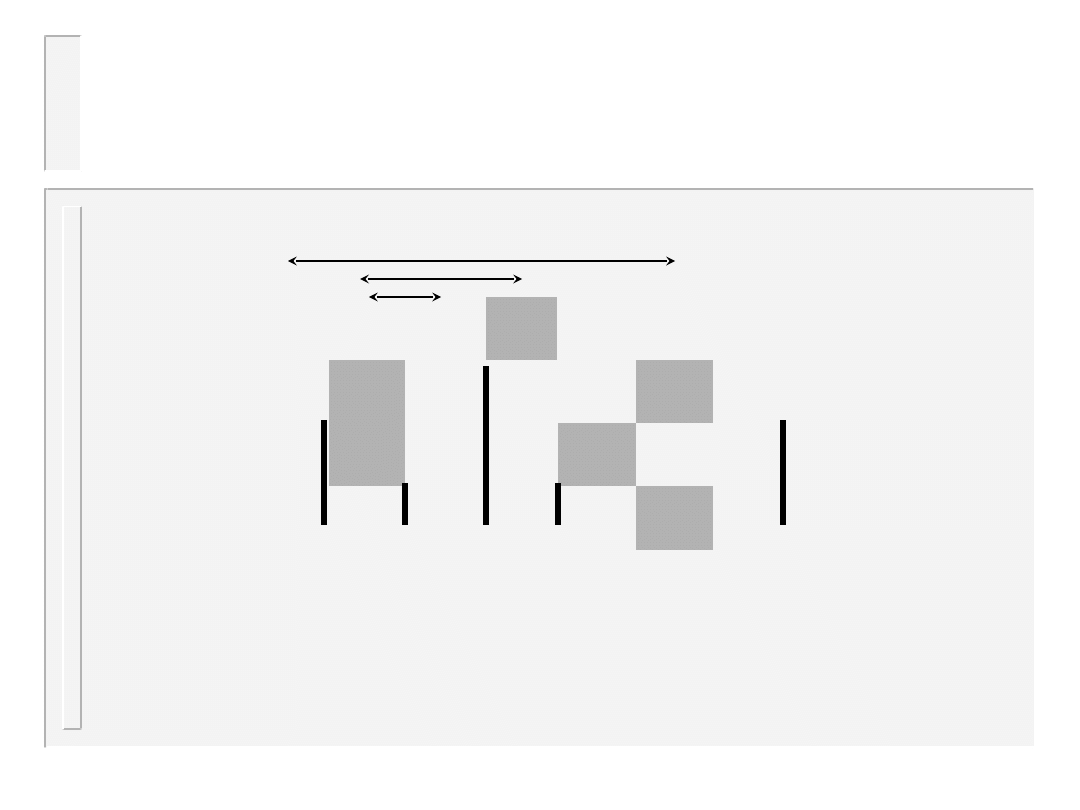
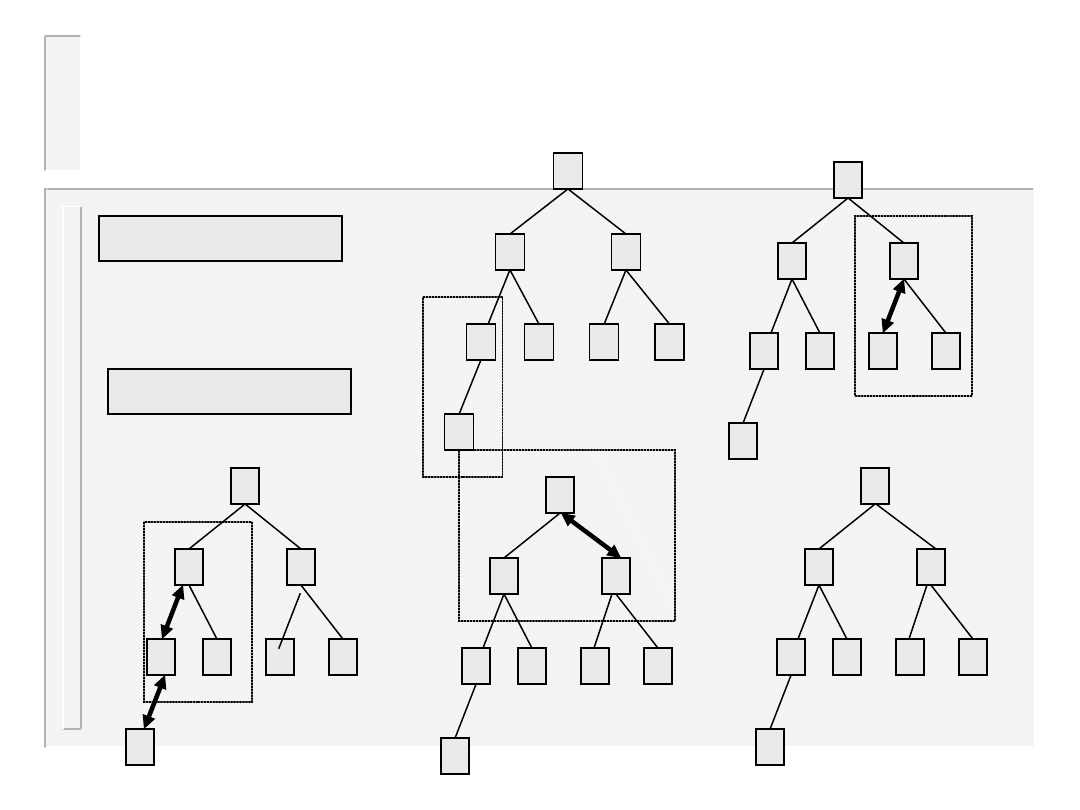
Dolne ograniczenie
złożoności

L e m a t : K a ż d e d r z e w o b i n a r n e o w y s o k o ś c i h m a c o n a j w y ż e j 2

h

l i ś c i .

D o w ó d : P r z e z i n d u k c j ę

h = 0 t o m a m y p o j e d y n c z y e l e m e n t c z y l i 2

h

= 2

0

= 1 ;

n i e c h d l a w y s o k o ś c i h d r z e w o b i n a r n e p o s i a d a c o n a j w y ż e j 2

h

l i ś c i

t o

d r z e w o b i n a r n e o w y s o k o ś c i h + 1 m o ż n a p o d z i e l i ć n a k o r z e ń i d w a p o d d r z e w a o

w y s o k o ś c i h o c o n a j w y ż e j 2

h

l i ś c i a c h , m a m y z a t e m 2 * 2

h

= 2

h + 1

l i ś c i .

T w i e r d z e n i e : K a ż d e d r z e w o d e c y z y j n e s o r t u j ą c e n r ó ż n y c h e l e m e n t ó w m a w y s o k o ś ć c o n a j m n i e j

l o g !

n .

D o w ó d : P o n i e w a ż w y n i k i e m p o s o r t o w a n i a m o ż e b y ć k a ż d a z n ! p e r m u t a c j i c i ą g u w e j ś c i o w e g o ,

w i ę c d r z e w o d e c y z y j n e p o s i a d a ć m u s i n ! l i ś c i , s t ą d

2

2

h

n

h

n







!

l o g

!

W n i o s e k : K a ż d y a l g o r y t m s o r t u j ą c y c i ą g n - e l e m e n t o w y z a p o m o c ą p o r ó w n a ń w y k o n u j e c o

n a j m n i e j c n

n c

l o g

(

)

 0 p o r ó w n a ń d l a d o s t a t e c z n i e d u ż e g o n .

D o w ó d : Z a u w a ż m y , ż e :

































 

n

n

n n

n

n

n

n

n

n

n

n

n

n

 

















1

1

2

2

2

2

2

4

2

2

!

. . .

/

/

l o g !

l o g

/

/

l o g

/

/

l o g

/

/

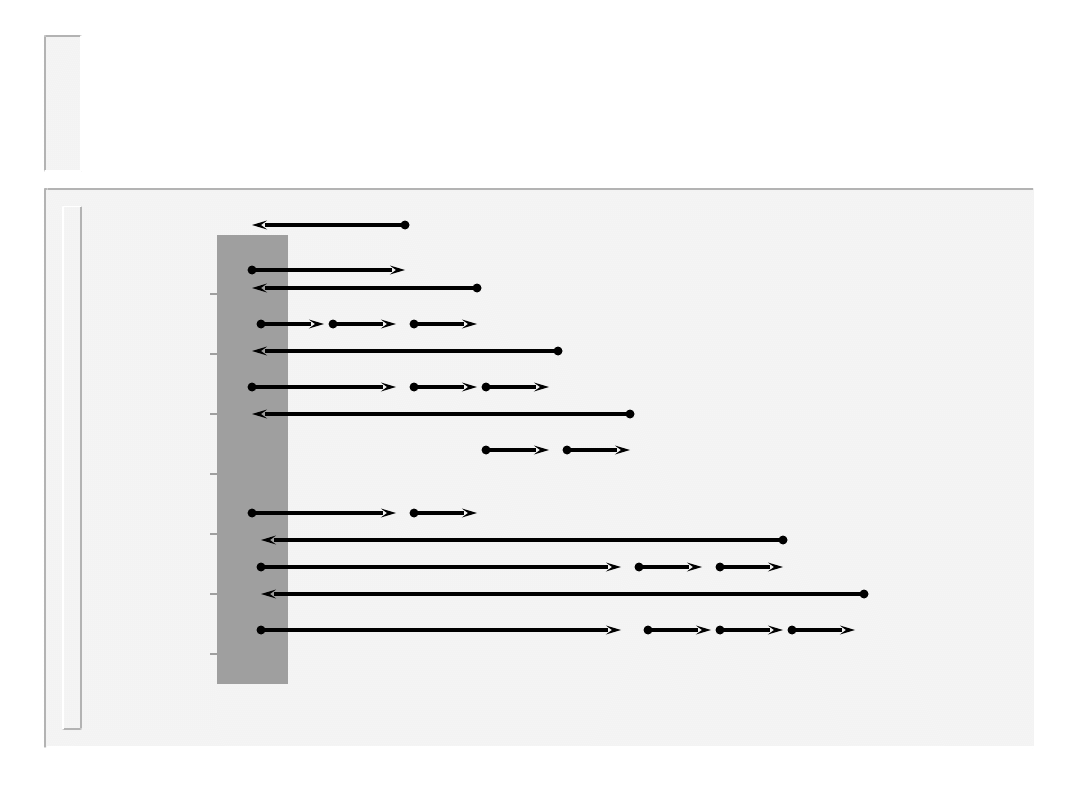
Sortowanie przez
wstawianie

9

8

9

1

3

4

2

6

5

1

8

9

1

3

4

2

6

5

3

1

8

9

3

4

2

6

5

4

1

3

8

9

4

2

6

5

2

1

3

4

8

9

2

6

5

6

1

2

3

4

8

9

6

5

5

1

2

3

4

6

8

9

5

1

2

3

4

5

6

8

9

Sortowanie przez
wstawianie c.d.

begin
for i:=2 to n do begin
t[0]:=t[i]; j:=i-1;
while t[0].klucz<t[j].klucz

do begin

t[j+1]:=t[j]; j:=j-1
end;
t[j+1]:=t[0]
end
end;

P

RZESTAWIENIA

P

ORÓWNANIA

M

IN

n-1

2(n-1)

Ś

R

.

(n

2

+n-2)/4

(n

2

+9n-10)/4

M

AX

(n

2

+n)/4 - 1

(n

2

+3n-4)/2

Sortowanie przez wstawianie
połówkowe

begin
for i:=2 to n do begin
t[0]:=t[i]; l:=1; p:=i-1;
while l<=p do begin
m:=(l+p) div 2;
if t[0].klucz<t[m].klucz

then p:=m-1 else l:=m+1

end;
for j:=i-1 downto l do t[j+1]:=t[j];
t[l]:=t[0]
end
end;

P

RZESTAWIENIA

P

ORÓWNANIA

M

IN

n-1

n(logn-loge±0.5)

Ś

R

.

(n

2

+n-2)/4

n(logn-loge±0.5)

M

AX

(n

2

+n)/4 - 1

n(logn-loge±0.5)

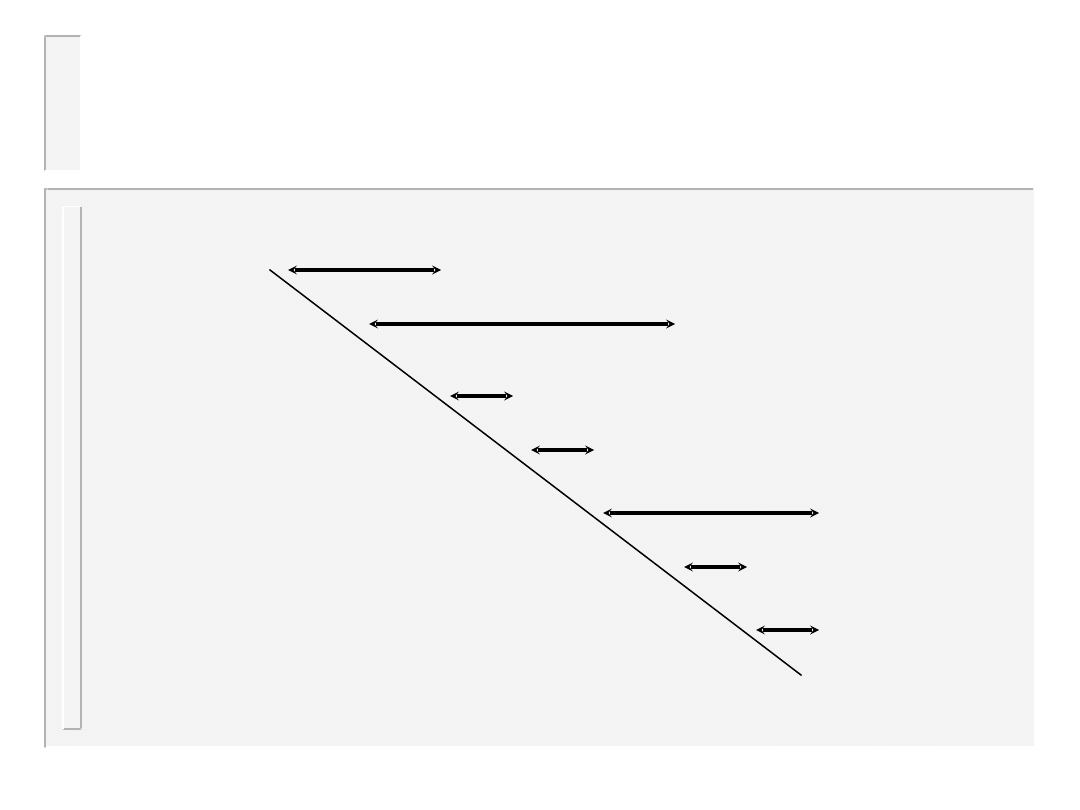
Sortowanie przez
wybieranie

8

9

1

3

4

2

6

5

1

9

8

3

4

2

6

5

1

2

8

3

4

9

6

5

1

2

3

8

4

9

6

5

1

2

3

4

8

9

6

5

1

2

3

4

5

9

6

8

1

2

3

4

5

6

9

8

1

2

3

4

5

6

8

9

Sortowanie przez
wybieranie c.d.

begin
for i:=1 to n-1 do begin
k:=i; t[0]:=t[i];
for j:=i+1 to n do
if t[j].klucz<t[0].klucz then begin
k:=j; t[0]:=t[j]
end;
t[k]:=t[i]; t[i]:=t[0]
end
end;

P

RZESTAWIENIA

P

ORÓWNANIA

M

IN

3(n-1)

(n

2

-n)/2

Ś

R

.

?

(n

2

-n)/2

M

AX

trunc(n

2

/4)+ 3(n-1)

(n

2

-n)/2

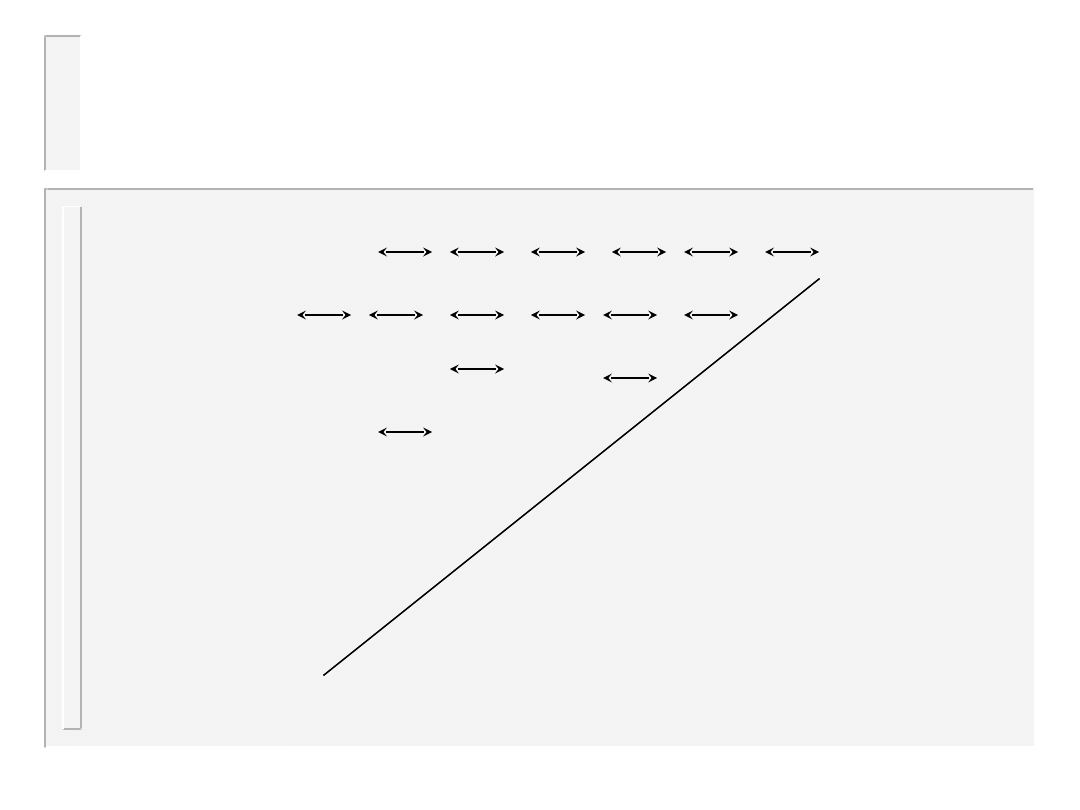
Sortowanie bąbelkowe

8

9

1

3

4

2

6

5

8

1

3

4

2

6

5

9

1

3

4

2

6

5

8

9

1

3

2

4

5

6

8

9

1

2

3

4

5

6

8

9

1

2

3

4

5

6

8

9

1

2

3

4

5

6

8

9

1

2

3

4

5

6

8

9

Sortowanie bąbelkowe
c.d.

begin
for i:=n-1 downto 1 do
for j:=1 to i do
if t[j].klucz>t[j+1].klucz then begin
t[0]:=t[j]; t[j]:=t[j+1]; t[j+1]:=t[0]
end;
end;

P

RZESTAWIENIA

P

ORÓWNANIA

M

IN

0

(n

2

-n)/2

Ś

R

.

3(n

2

-n)/4

(n

2

-n)/2

M

AX

3(n

2

-n)/2

(n

2

-n)/2

Sortowanie szybkie
(quicksort)

8

9

1

3

4

2

6

5

2

1

3

9

4

8

6

5

1

2

3

5

4

6

8

9

1

2

3

4

5

6

8

9

Sortowani
e
szybkie
c.d.

Procedure podzial(f,l:integer);
i,j,:integer; pomoc: {typ elementu tablicy}
begin

pomoc:=t[(f+l)div 2]; i:=f; j:=l;
repeat
while t[i]<pomoc do i:=i+1;
while t[j]>pomoc do j:=j-1;
if i<=j then begin
t[0]:=t[i]; t[i]:=t[j]; t[j]:=t[0];
i:=i+1; j:=j-1;
end;
until i>j

if f<j then podzial(f,j);
if i<l then podzial(i,l);
end;

Startujemy od

podzial(1,n);

Sortowanie stogowe
(heapsort)

9,8,7,6,3,5,2,4

7

6

8 3

9

2

4

5

7

6

8 3 9 2

4

5

7

4

6 3 5 2

8

9

7

6

8 3 5 2

4

9

7,4,5,8,3,9,2,6

9

4

6 3 5 2

8

7

Sortowanie stogowe c.d.
(1)

Procedure przeczesz(r,b);
var ok:boolean; mc:integer
begin

ok:=false;
while (2*r<=b) and not ok do begin
if 2*r=b then mc:=2*r else
if t[2*r]>t[2*r+1] then mc:=2*r else mc:=2*r+1;
if t[r]<t[mc] then begin
t[0]:=t[r]; t[r]:=t[mc]; t[mc]:=t[0]; r:=mc end;
else ok:=true
end;

end;

Sortowanie stogowe c.d.
(2)

Procedure heapsort;
var i:integer;
begin

for i:=(n div 2) downto 1 do przeczesz(i,n);
for i:=n downto 2 do begin

t[0]:=t[1]; t[1]:=t[i]; t[i]:=t[0];
przeczesz(1,i-1)

end;

end;