ALGORYTMY I STRUKTURY DANYCH
©Lisek89
-> odczyt z Kozackich fotek
11.02.2010r.
E
GZAMIN
-
Wersja
A
Strona 1
1. (2 pkt) Dany jest algorytm, który dla dowolnej liczby naturalnej n, powinien wyznaczyd sumę
kolejnych liczb naturalnych mniejszych od n. Wynik algorytmu jest zapisany w zmiennej suma.
Algorytm
i=1; suma=0;
while(i!=n){
suma+=i;
i+=2;
}
Czy powyższy algorytm jest:
poprawny całkowicie,
poprawny częściowo,
nie jest poprawny ani całkowicie ani częściowo
2. (3 pkt) Dane są trzy funkcje:
f
1
(n) = 0,01 4
𝑛
+ 100𝑛
2
,
𝑓
2
(n) = logn
n
+ 0,1𝑛
2
,
𝑓
3
(𝑛) = 2
log
2
𝑛
+ 𝑙𝑜𝑔𝑛
100
oraz następujące rzędy funkcji:
(n),
(logn),
(2
n
),
(4
n
),
(n
2
),
(n
1/2
),
(nlogn),
(n
100
),
(n!),
(n
n
)
Przyporządkuj każdej z funkcji odpowiedni rząd:
f
1
n =
𝑓
2
n =
𝑓
3
𝑛 =
3. (2 pkt) Dana jest następująca funkcja:
int F(int n){
if(n==0 || n==1)
return 1;
return F(n-1)+F(n-2);
}
Jaki jest co do rzędu, pesymistyczny koszt czasowy powyższej funkcji. Zakładamy, że rozmiarem
zadania jest n, a operacją elementarną dodawanie.
ODP: …………………………………………………………………………………………
4. (2 pkt) Dana jest następująca funkcja:
int G(int n, int k){
if(n==k || k==0) return 1;
return G(n-1, k-1)+G(n-1,k);
}
Ile razy wywoła się powyższa funkcja dla danych n=4 i k=2?
ODP: …………………………………………………………………………………………
5. Z którymi elementami tablicy uporządkowanej będzie porównany element x=1 w algorytmie
wyszukiwania binarnego. Wynik zapisz w kolejności wykonywanych porównao.
tablica: 1, 5, 20, 25, 30, 50, 80, 100, 200
ODP: …………………………………………………………………………………………
ALGORYTMY I STRUKTURY DANYCH
©Lisek89
-> odczyt z Kozackich fotek
11.02.2010r.
E
GZAMIN
-
Wersja
A
Strona 2
6. (2 pkt) Pewien problem o rozmiarze n został rozwiązany przy użyciu strategii „dziel i zwyciężaj”. Jego
czasowa złożonośd pesymistyczna została następnie zapisana w postaci poniższego równania
rekurencyjnego:
𝑇
𝑚𝑎𝑥
𝑛 =
2 𝑑𝑙𝑎 𝑛 ≤ 2
2𝑇
𝑚𝑎𝑥
𝑛
2
+ 𝑛 𝑑𝑙𝑎 𝑛 > 2
Jaki jest rząd funkcji kosztu tego algorytmu:
(nlogn)
(n
2
)
(logn)
Inny koszt. Jak?: …………………………………………………………………………………
7. (3 pkt) Dany jest zbiór n przedmiotów o wagach wyrażonych w kg będących liczbami naturalnymi.
Chcemy załadowad możliwie najpełniej przyczepę o ładowności m kg. Czy tak zdefiniowany problem
można rozwiązad strategią zachłanną, stosując w pierwszym kroku algorytmu sortowanie
przedmiotów nierosnąco po wagach?
Tak.
Nie. Podaj kontrprzykład (tzn. przykład danych wejściowych, dla których rozwiązanie
algorytmem zachłannym nie będzie optymalne):
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………
8. (1 pkt) Które z poniższych zdao są prawdziwe?
Wszystkie problemy posiadające własnośd optymalnej podstruktury można optymalnie
rozwiązad strategią zachłanną
Wszystkie problemy posiadające własnośd wyboru zachłannego można rozwiązad optymalnie
strategią zachłanną
Problemy posiadające obie własności: optymalnej podstruktury i wyboru zachłannego,
można rozwiązad optymalnie strategią zachłanną.
Żadne z powyższych zdao nie jest prawdziwe.
9. (1 pkt) Wskaż algorytmy wykorzystujące programowanie dynamiczne:
Algorytm Dijkstry
Algorytm Forda-Bellmana
Algorytm wyszukiwania binarnego
Żaden z powyższych algorytmów nie wykorzystuje techniki programowania dynamicznego
10. (2 pkt) W tablicy liczb został zbudowany kopiec zupełny. Zawartośd kopca jest następująca: 10, 8, 7,
5, 3, 6. Do kopca dodano następnie liczbę 9. Jaka jest kolejnośd liczb w kopcu po dodaniu tej
wartości:
ODP: …………………………………………………………………………………………
11. Nie mam treści zadania widad koniec pierwszej linijki: „ciągu uporządkowanym:”
Jak ktoś może niech dopisze to zadanie na forum.
ALGORYTMY I STRUKTURY DANYCH
©Lisek89
-> odczyt z Kozackich fotek
11.02.2010r.
E
GZAMIN
-
Wersja
A
Strona 3
12. (2 pkt) Jaki jest koszt pesymistyczny wyszukiwania elementu w następujących strukturach danych,
zawierających w momencie wyszukiwania n elementów? Wystarczy podad rząd funkcji kosztu.
Lista nieuporządkowana:
……………………………………………
Tablica posortowana:
……………………………………………
Drzewo BST:
……………………………………………
Drzewo AVL:
……………………………………………
13. (2 pkt) Ile co najwyżej elementów może zawierad drzewo binarne składające się z n poziomów?
Zakładamy, że drzewo posiadające tylko jeden element składa się z jednego poziomu. Podaj
dokładny wynik.
ODP: …………………………………………………………………………………………
14. (2 pkt) Zbuduj drzewo BST wstawiając kolejno elementy: 8, 12, 25, 1, 6, 20, 10. Jaki element może
zastąpid wartośd 8 w procesie usuwania tej wartości z drzewa.
ODP: …………………………………………………………………………………………
15. (2 pkt) Do początkowo pustego drzewa AVL wstawiono kolejno elementy: 15, 5, 10, 25, 35, 12.
Etykietą korzenia utworzonego w ten sposób drzewa jest:
10
25
15
Żadna z wartości. Podaj poprawną odpowiedź: …………………………………………………......
16. (1 pkt) Jaki jest optymalny koszt algorytmu wyświetlającego zawartośd drzewa BST w porządku
rosnącym?
ODP: …………………………………………………………………………………………
17. (1 pkt) Które z poniższych zdao są prawdziwe:
Algorytm Dijkstry zawsze działa skutecznie w grafach o ujemnych wagach.
Algorytm Forda-Bellmana można zastosowad tylko do grafów z wagami dodatnimi.
Algorytm Floyda-Warshalla służy do wyznaczania najkrótszych ścieżek między wszystkimi
odległościami wierzchołków.
Żaden z powyższych algorytmów nie daje dobrych wyników w grafach z cyklami o ujemnych
wagach.
Żadne z powyższych zdao nie jest prawdziwe.
18. (2 pkt) Dany jest graf o następujących listach incydencji:
1: 2, 4
2: 1, 3, 5
3: 2, 5, 6
4: 1
5: 2, 3, 6
6: 3, 5, 7
Wypisz kolejno odwiedzane wierzchołki w wyniku przeglądania tego grafu „wszerz” rozpoczynając od
wierzchołka nr 1.
ODP: …………………………………………………………………………………………
19. (3 pkt) Określ kolory poszczególnych wierzchołków ustalone w algorytmie aproksymacyjnym
kolorowania opartym o maksymalne zbiory niezależne dla grafu o następujących listach incydencji:
1: 2, 3, 4
2: 1, 3, 4
3: 1, 2, 6
4: 1, 2, 6
5: 6
6: 3, 4, 5
ALGORYTMY I STRUKTURY DANYCH
©Lisek89
-> odczyt z Kozackich fotek
11.02.2010r.
E
GZAMIN
-
Wersja
A
Strona 4
Zakładamy, że jeżeli w trakcie realizacji algorytmu dochodzi do wyboru wierzchołków według
ustalonego kryterium i kilka wierzchołków spełnia to kryterium to wybierany jest wierzchołek o
najniższym numerze.
nr wierzchołka
1
2
3
4
5
6
nr koloru
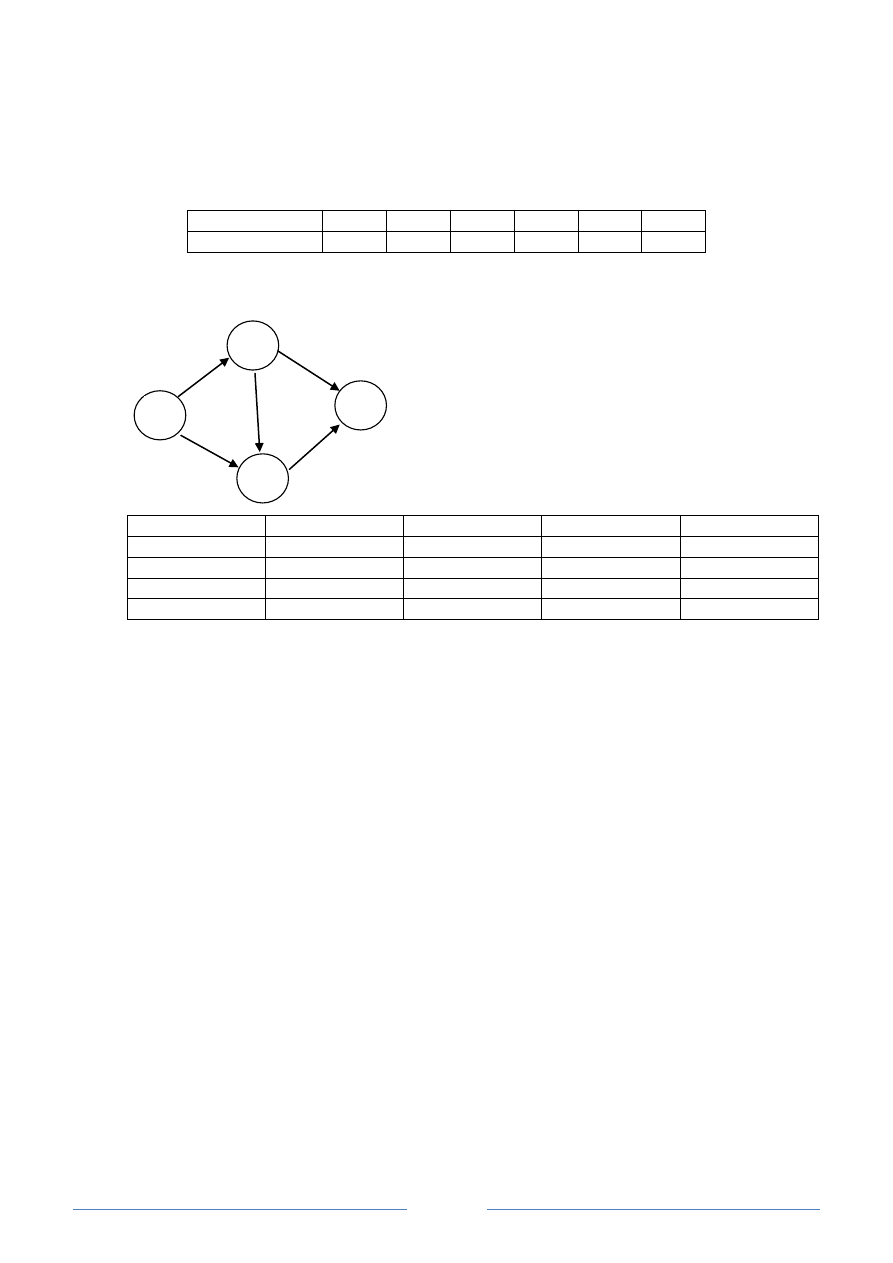
20. (3 pkt) Ustal zawartośd tabeli odległości d (tabeli odległości minimalnych) po każdym kroku
algorytmu Dijkstry dla następującego grafu. Wierzchołek startowy s=
tablica d
d[1]
d[2]
d[3]
d[4]
po inicjalizacji
po I kroku
po II kroku
ostatecznie
21. (2 pkt) Mamy dany problem maksymalnego wypełnienia różnymi towarami windy o ładowności 1000
kilogramów. W rozwiązaniu optymalnym udało się wypełnid kabinę windy maksymalnie. Algorytm
przybliżony (bazujący na strategii zachłannej) posiada ograniczenie względne błędu
aproksymacyjnego równe 2. Oznacza to, że:
Algorytm ten zdoła zapełnid windę przynajmniej 998 kilogramami towaru.
Algorytm ten zdoła zapełnid windę przynajmniej do połowy jej ładowności.
Algorytm ten zdoła zapełnid windę co najwyżej do połowy jej ładowności.
Algorytm ten załaduje do windy jedynie 2kg towaru.
Żadna z powyższych odpowiedzi nie jest poprawna.
22. (1 pkt) Które z poniższych zdao jest prawdziwe:
Każdy problem NP-zupełny posiada rozwiązanie działające w czasie wielomianowym.
Żaden problem NP-zupełny nie posiada rozwiązania działającego w czasie wielomianowym.
Nie wiadomo, czy problemy NP-zupełne mają rozwiązanie działające w czasie
wielomianowym.
Żadne z powyższych zdao nie jest prawdziwe.
23. (2 pkt) Który z poniższych problemów jest NP-zupełny?
problem domina
problem sortowania topologicznego grafu
problem cyklu Hamiltona
problem komiwojażera
Żaden z powyższych problemów
2
1
5
4
2
1
2
3
4
ALGORYTMY I STRUKTURY DANYCH
©Lisek89
-> odczyt z Kozackich fotek
11.02.2010r.
E
GZAMIN
-
Wersja
A
Strona 5
24. (2 pkt) Który z cykli Hamiltona wygeneruje się jako pierwszy dla grafu z zadania nr 19. Wierzchołek
startowy cyklu ma numer 1.
ODP: …………………………………………………………………………………………
25. (3 pkt) Do tablicy z haszowaniem T o długości m=11 wstawiamy kolejno klucze 11, 23, 34, 4, 15, 25,
22, używając adresowania otwartego typu liniowego do rozwiązywania problemu kolizji. Funkcja
haszująca ma wzór 𝑥, 𝑖 =
′
𝑥 + 𝑖 %𝑚, gdzie
′
𝑥 = 𝑥%𝑚. Wyznacz zawartośd tablicy T.
T = [
]
0
1
2
3
4
5
6
7
8
9
10