Grafika w programie

MATLAB

dr inż. Henryk Olszewski

PWSZ, 2006

2

Wykresy 2D - ćwiczenie 1

Wykres liniowy
Napisać skrypt rysujący wykres funkcji:

dla:

Wykonać dwa wykresy: dla A=2, B=3 (czarna linia ciągła) oraz dla A=1, B=-3 (niebieska
linia kropkowana). Na wykresie umieścić siatkę linii pomocniczych, podpisy pod osiami
(oś x - t, oś y - y(t)). Nadać tytuł wykresu: Wykres funkcji oraz legendę.

 

)

t

sin(

B

Ae

y 



 20

,

0

t

)

t

sin(

B

Ae

y 

PWSZ, 2006

3

Wykresy 2D - ćwiczenie 1

Wykres liniowy
Napisać skrypt rysujący wykres funkcji:

dla:

t=0:0.1:20;
A=2;B=3; y1=A*exp(B*sin(t));
A=1;B=-3; y2=A*exp(B*sin(t));
plot(t,y1,’k-’,t,y2,’b:’)
xlabel(‘t’)
ylabel(‘y(t)’)
title(‘Wykres funkcji y=Ae^{Bsin(t)}’)
legend(‘A=2, B=3’,’A=1, B=-3’)
grid on

)

t

sin(

B

Ae

y 



 20

,

0

t

PWSZ, 2006

4

Wykresy 3D

Wyświetlenie funkcji dwóch zmiennych
W celu wyświetlenia funkcji dwóch zmiennych z = f (x,y), należy wygenerować dwie macierze X i Y
zawierające współrzędne wierszy i kolumn macierzy dziedziny funkcji. Powyższe macierze służą do
obliczenia i wyświetlenia funkcji. Funkcja meshgrid przekształca dziedzinę określoną poprzez pojedynczy
wektor lub dwa wektory x i y w macierze X i Y wykorzystywane w obliczeniach funkcji dwóch zmiennych.
Wiersze macierzy X są kopiami wektora x, zaś kolumny macierzy Y są kopiami wektora y.

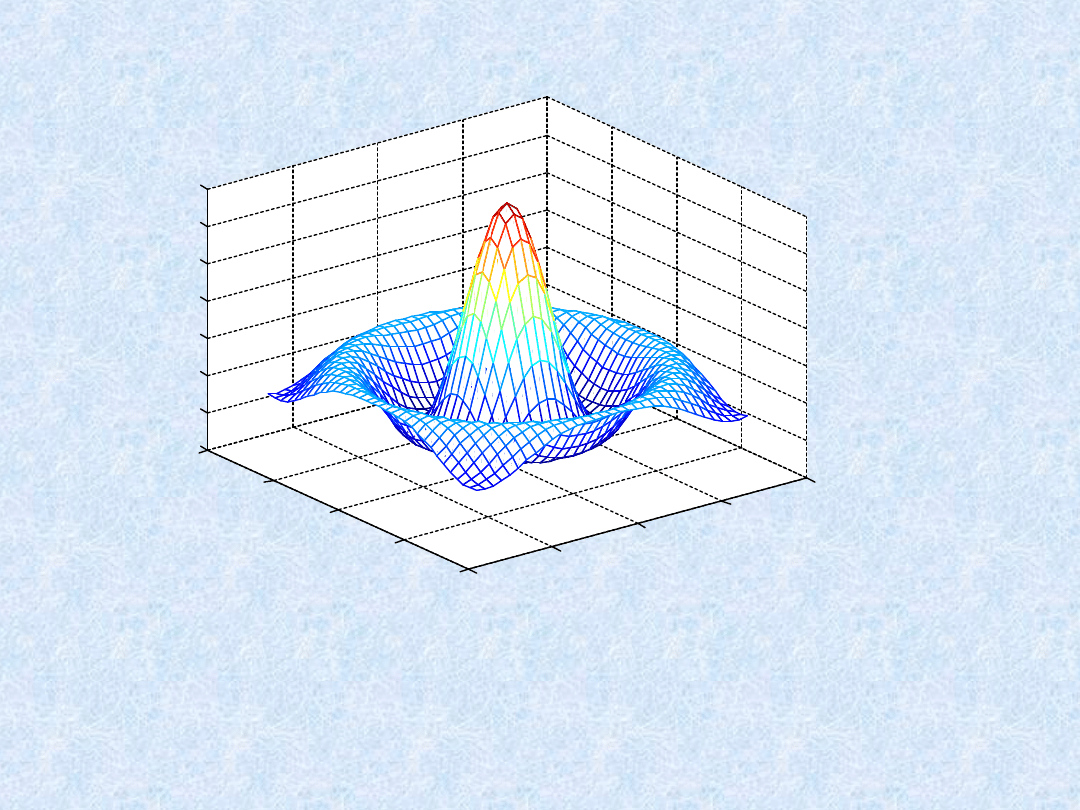
W celu obliczenia dwuwymiarowej funkcji sinc, sin(r)/r, dwóch argumentów x i y należy wydać

następujące polecenia:
 

» [X,Y] = meshgrid(-8:.5:8);
» R = sqrt(X.^2 + Y.^2) + eps;
» Z = sin(R)./R;
» mesh(X,Y,Z)

PWSZ, 2006

5

Wykresy 3D

W powyższym przykładzie R jest odległością od początku układu współrzędnych, który
jest środkowym elementem macierzy. Dodanie elementu eps zabezpiecza przed
dzieleniem 0/0 w początku układu współrzędnych.

-10

-5

0

5

10

-10

-5

0

5

10

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

PWSZ, 2006

6

-10

-5

0

5

10

-10

-5

0

5

10

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

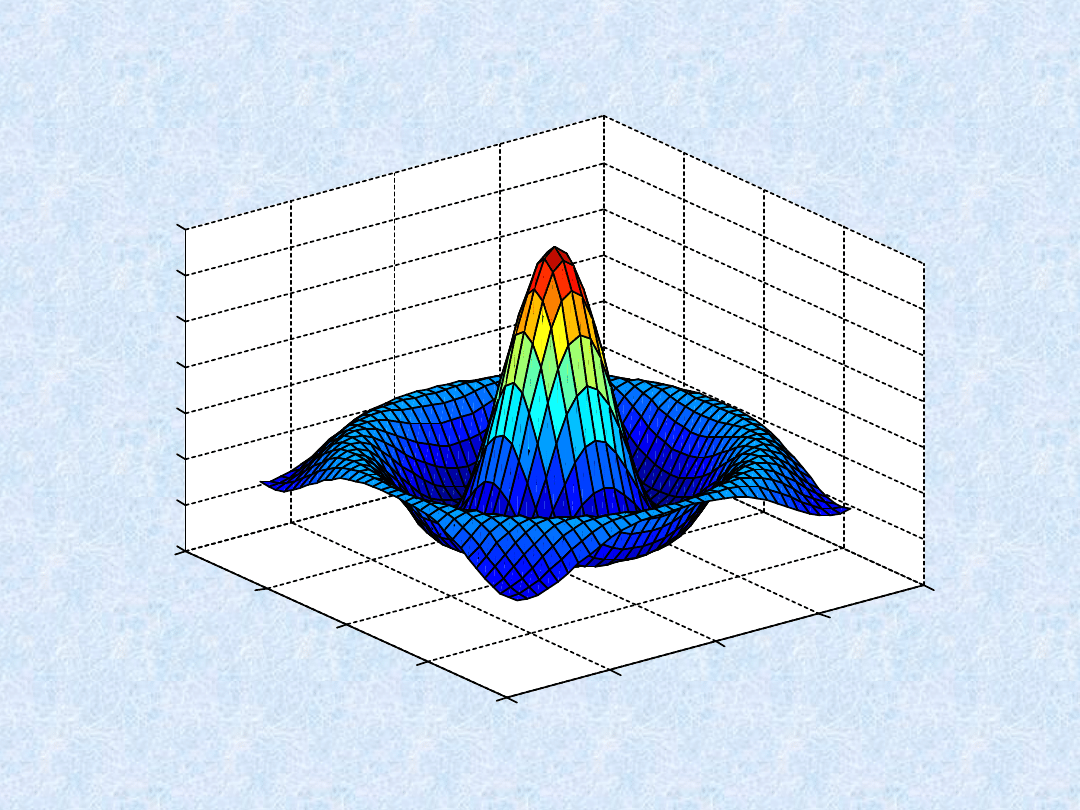
Wykresy 3D - przykłady

» surf(X,Y,Z)

PWSZ, 2006

7

-10

-5

0

5

10

-10

-5

0

5

10

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

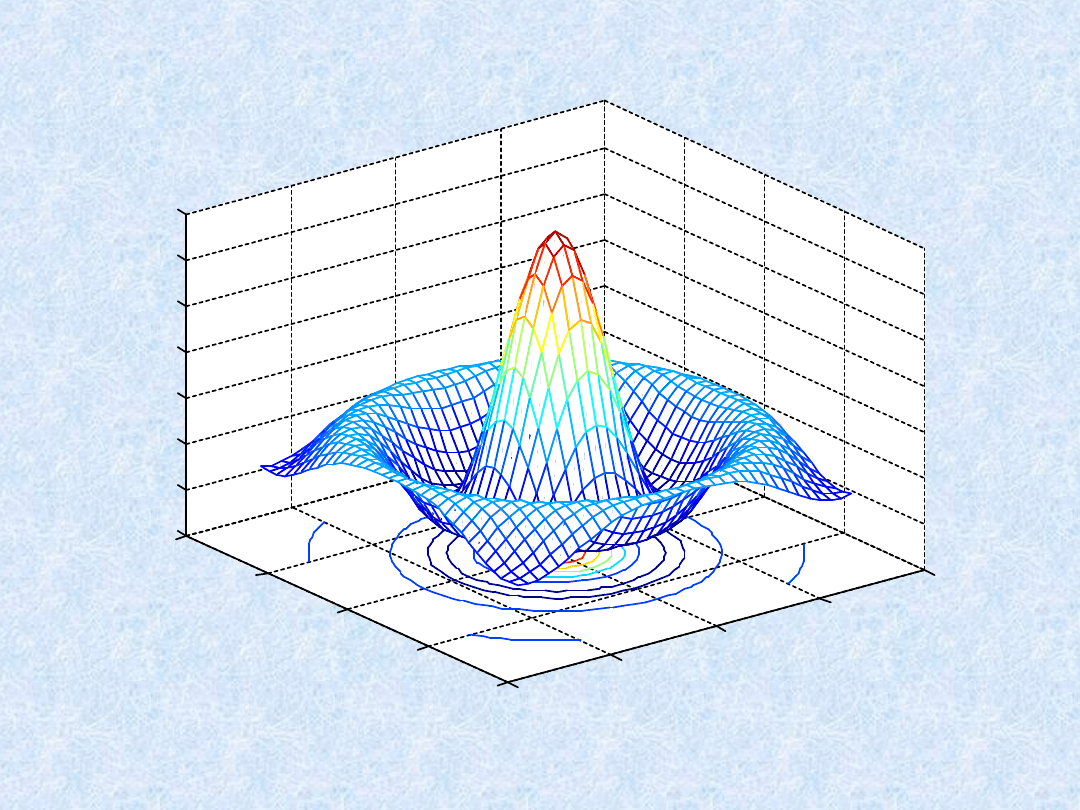
Wykresy 3D - przykłady

» meshc(X,Y,Z)

PWSZ, 2006

8

-10

-5

0

5

10

-10

-5

0

5

10

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

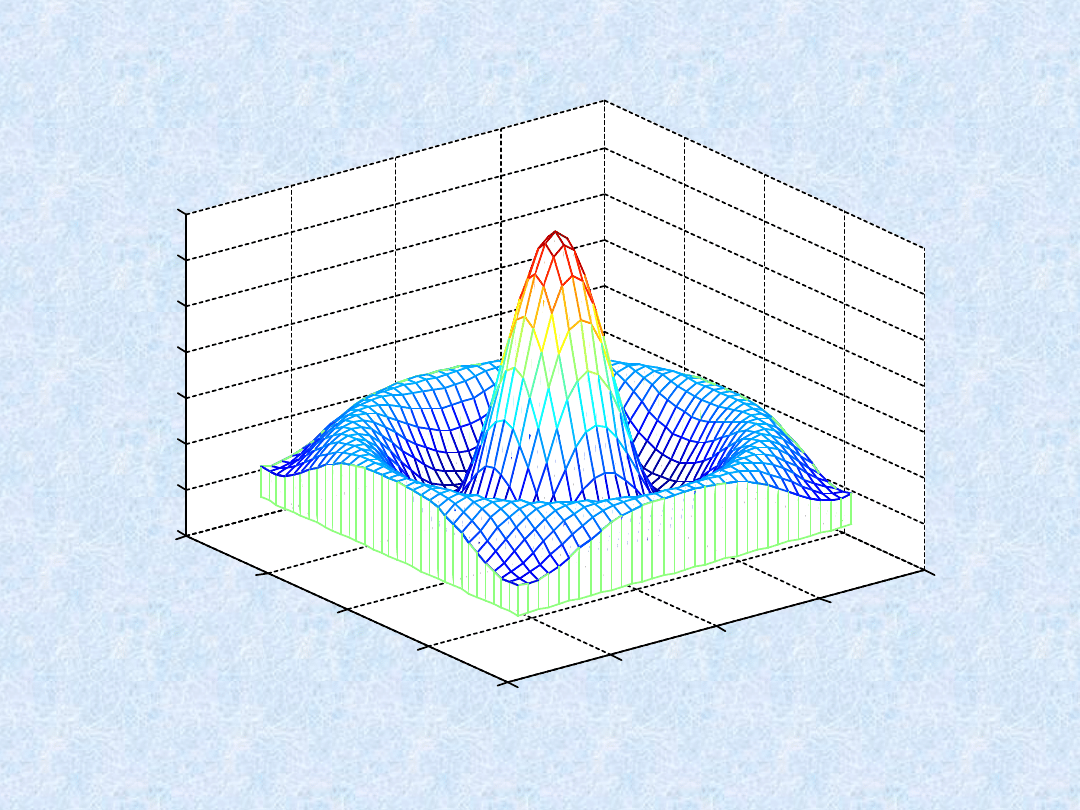
Wykresy 3D - przykłady

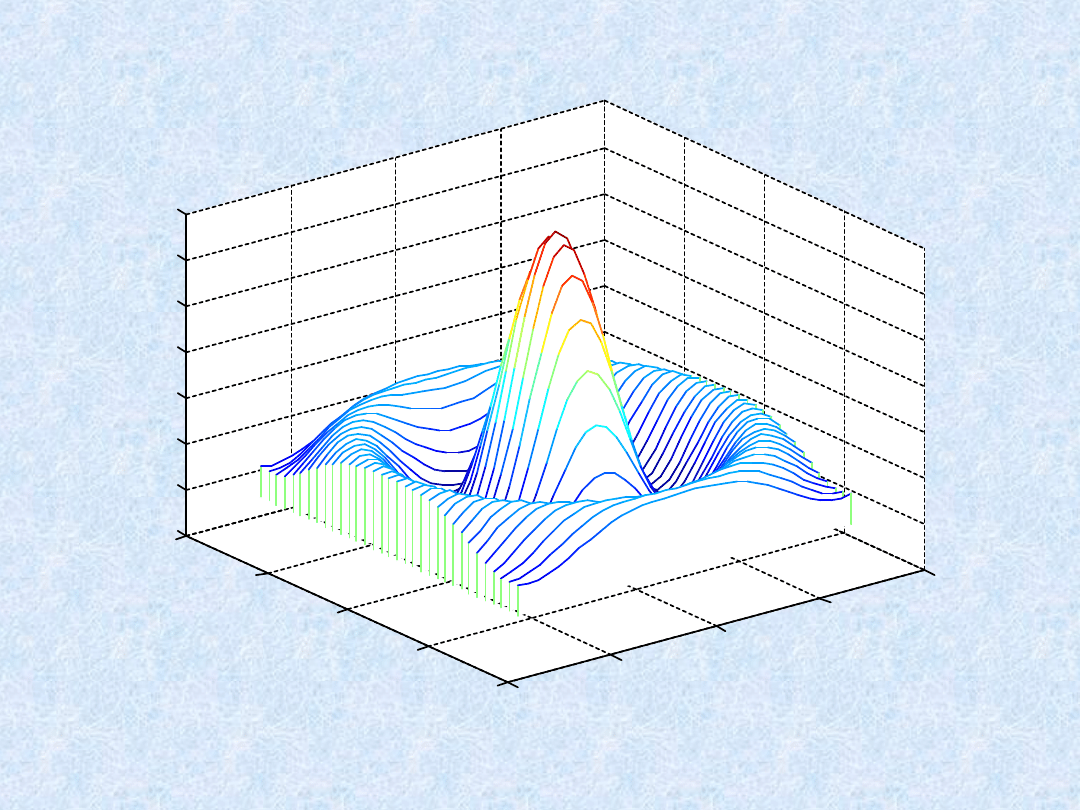
» meshz(X,Y,Z)

PWSZ, 2006

9

-10

-5

0

5

10

-10

-5

0

5

10

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

Wykresy 3D - przykłady

» waterfall(X,Y,Z)

PWSZ, 2006

10

-8

-6

-4

-2

0

2

4

6

8

-8

-6

-4

-2

0

2

4

6

8

Wykresy 3D - przykłady

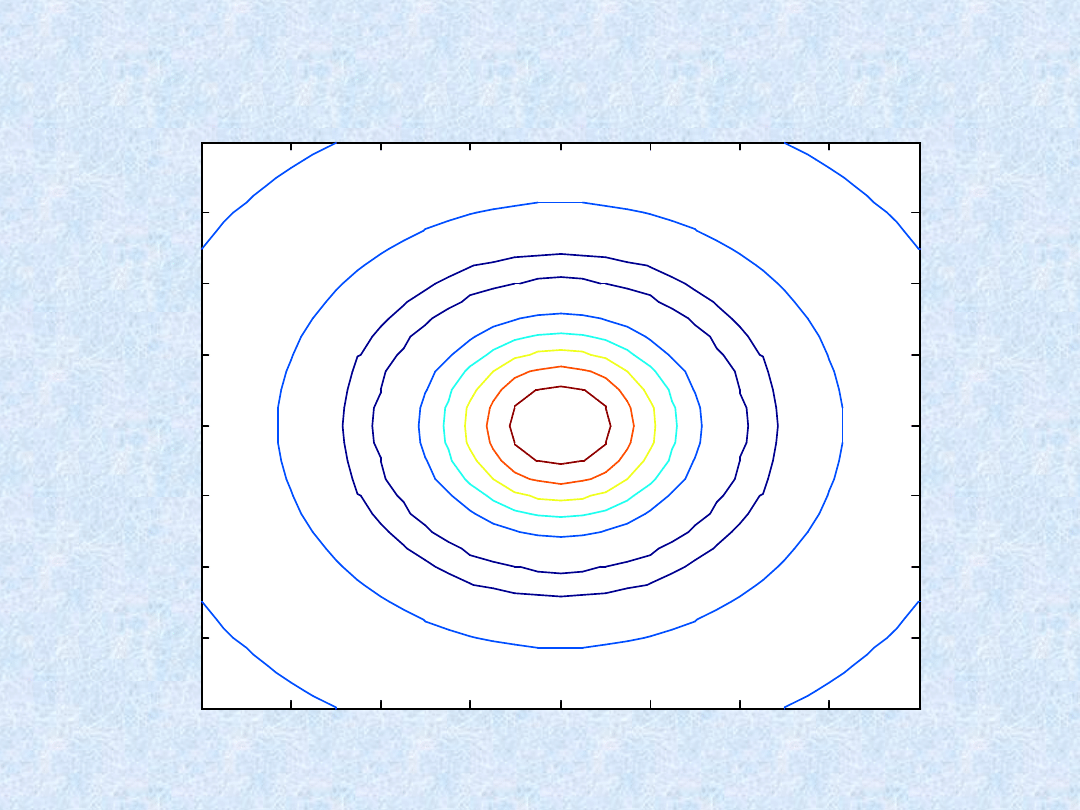
» contour(X,Y,Z)

PWSZ, 2006

11

Wykresy 3D - przykłady

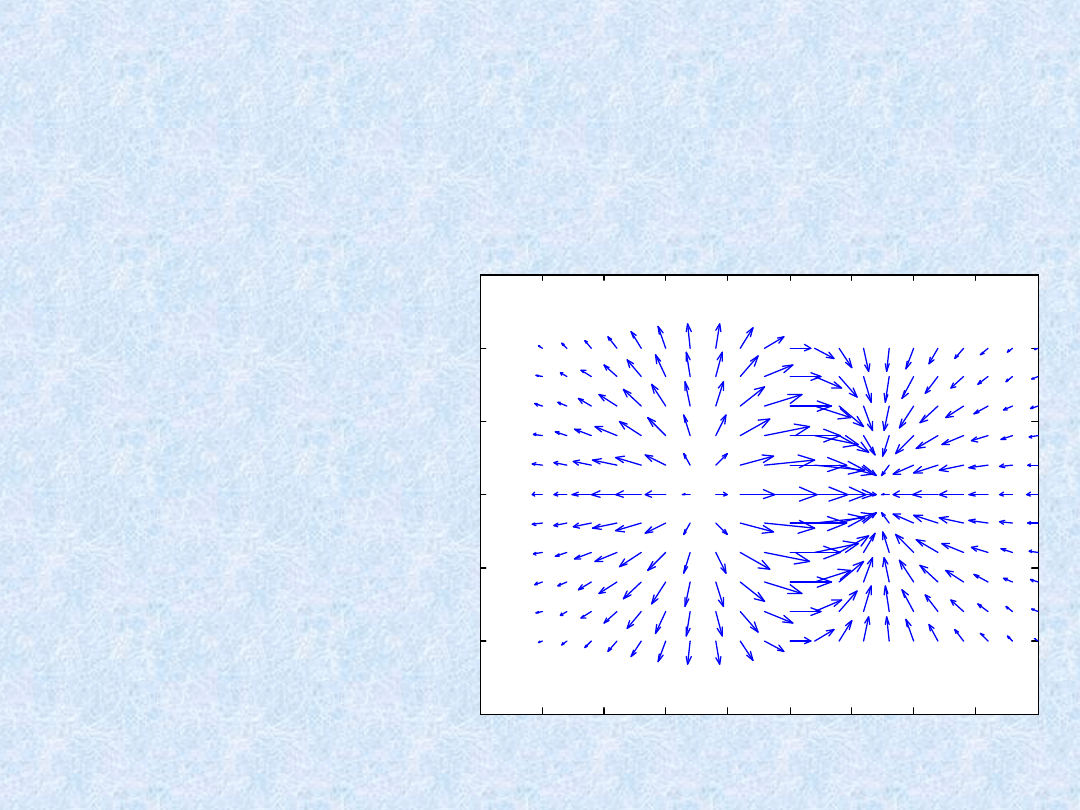
» x = -2:.2:2; y = -1:.2:1;
»[xx,yy] = meshgrid(x,y);
» zz = xx.*exp(-xx.^2-yy.^2);
»[px,py] = gradient(zz,.2,.2);
» quiver(x,y,px,py,2);

-2.5

-2

-1.5

-1

-0.5

0

0.5

1

1.5

2

-1.5

-1

-0.5

0

0.5

1

1.5

PWSZ, 2006

12

Wykresy 3D - ćwiczenie 1

Wyświetlenie funkcji dwóch zmiennych
Narysować wykres powierzchni opisanej równaniem:

dla:

 

2

2

y

x

e

)

y

x

)(

y

x

(

)

y

,

x

(

f

















5

,

5

y

,

x

PWSZ, 2006

13

Wykresy 3D - ćwiczenie 1

Wyświetlenie funkcji dwóch zmiennych
Narysować wykres powierzchni opisanej równaniem:

dla:

 

» [x,y] = meshgrid(-5:.5:5,-5:.5:5);

» z =(x-y).*(x+y)+exp(sqrt(x.^2+y.^2));
» mesh(x,y,z)
» mesh(z)

2

2

y

x

e

)

y

x

)(

y

x

(

)

y

,

x

(

f

















5

,

5

y

,

x

PWSZ, 2006

14

Wykresy 3D - ćwiczenie 2

Wyświetlenie funkcji dwóch zmiennych
Narysować wykres powierzchni opisanej równaniem:

dla:

)

y

cos(

)

x

sin(

)

y

,

x

(

f













,

y

,

x

PWSZ, 2006

15

Wykresy 3D - ćwiczenie 2

Wyświetlenie funkcji dwóch zmiennych
Narysować wykres powierzchni opisanej równaniem:

dla:

Funkcja rysowana została zdefiniowana w pliku fgr2.m:

function z=fgr2(x,y)
z=sin(x).*cos(y);

Skrypt realizujący zadanie:

close all

%zamknięcie wszystkich okien

X=(-1:0.1:2)*pi;
x,y] = meshgrid(X); z=fgr2(x,y);
mesh(x,y,z), title(‘Mesh’)
figure(2), meshc(x,y,z), title(‘Meshc’)
figure(3), meshz(x,y,z), title(‘Meshz’)

)

y

cos(

)

x

sin(

)

y

,

x

(

f













,

y

,

x

PWSZ, 2006

16

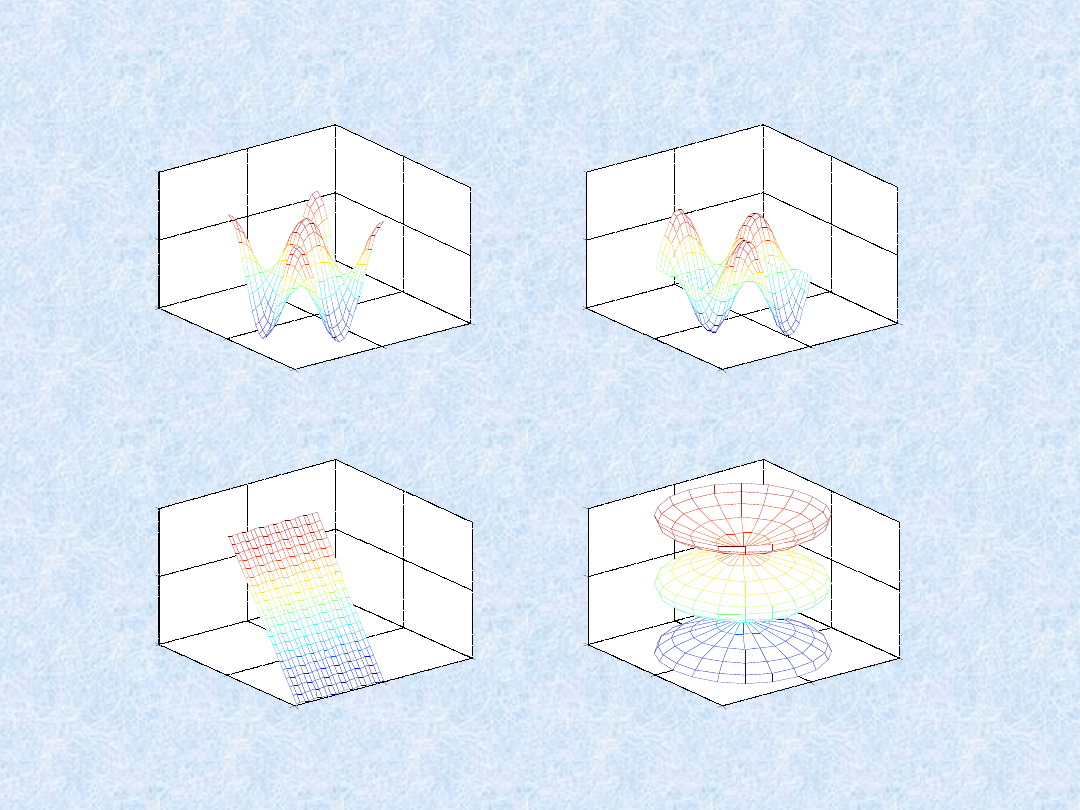
Macierze rysunkowe

Funkcja subplot umożliwia wyświetlenie kilku wykresów w tym samym
oknie rysunkowym. Polecenie:

subplot(m,n,p)

dzieli okno rysunkowe na macierz o wymiarach m-n, której elementami
są okna poszczególnych wykresów, parametr p wybiera p-te okno
wykresu jako bieżące. Wykresy są numerowane wierszami, począwszy od
pierwszego wiersza znajdującego się u góry okna rysunkowego. W celu
wyświetlenia wykresów w czterech odrębnych oknach wykresów należy:

t = 0:pi/10:2*pi;

[X,Y,Z] = cylinder(4*cos(t));
subplot(2,2,1)
mesh(X)
subplot(2,2,2); mesh(Y)
subplot(2,2,3); mesh(Z)
subplot(2,2,4); mesh(X,Y,Z)

PWSZ, 2006

17

Macierze rysunkowe

0

20

40

0

20

40

-5

0

5

0

20

40

0

20

40

-5

0

5

0

20

40

0

20

40

0

0.5

1

-5

0

5

-5

0

5

0

0.5

1

Dziękuję za uwagę