ZASTOSOWANIE SIECI 

NEURONOWYCH

W ROBOTYCE

 

 

Mózg

- 

ok. 100 mld neuronów połączonych w sieć, 

-  objętość 1400 cm

3.

-  powierzchnia 2000 cm

2.

-  liczba neuronów ok. 10

11

 (100 mld),

-  liczba połączeń między neuronami: 10

15,

-  średni dystans połączenia: 0,01 mm – 1 m,
-  impulsy: częstotliwość 1-100 Hz, czas trwania 1-2 ms,
-  szybkość pracy mózgu: 10

18

 operacji/s.

Charakterystyka:
•  proste jednostki przetwarzające – neurony podobne do siebie,
•  tworzą one układ rozproszony – sieć neuronową 
•  funkcjonowanie sieci: przetwarzanie sygnałów elektrochemicznych.۰
•  przetwarzanie informacji – obliczenia dokonywane w sposób równoległy 
(wiele neuronów   

pracuje równocześnie),

•  wiedza – zawarta niejawnie w strukturze połączeń między neuronami, 
•  o tym, jaka reprezentacja środowiska zewnętrznego jest zapisana 
decyduje:
  -  sposób połączeń (które jednostki są ze sobą połączone),
  -  siła połączeń (wagi).

Cechy mózgu ludzkiego pożądane w sztucznych systemach, które przysługują 
sieciom neuronowym:
۰ odporność na uszkodzenia, 
۰ elastyczność – „uczenie się”,
۰ zdolność radzenia sobie z informacją zaszumioną, losową lub niespójną,
۰ równoległość działania.

 

 

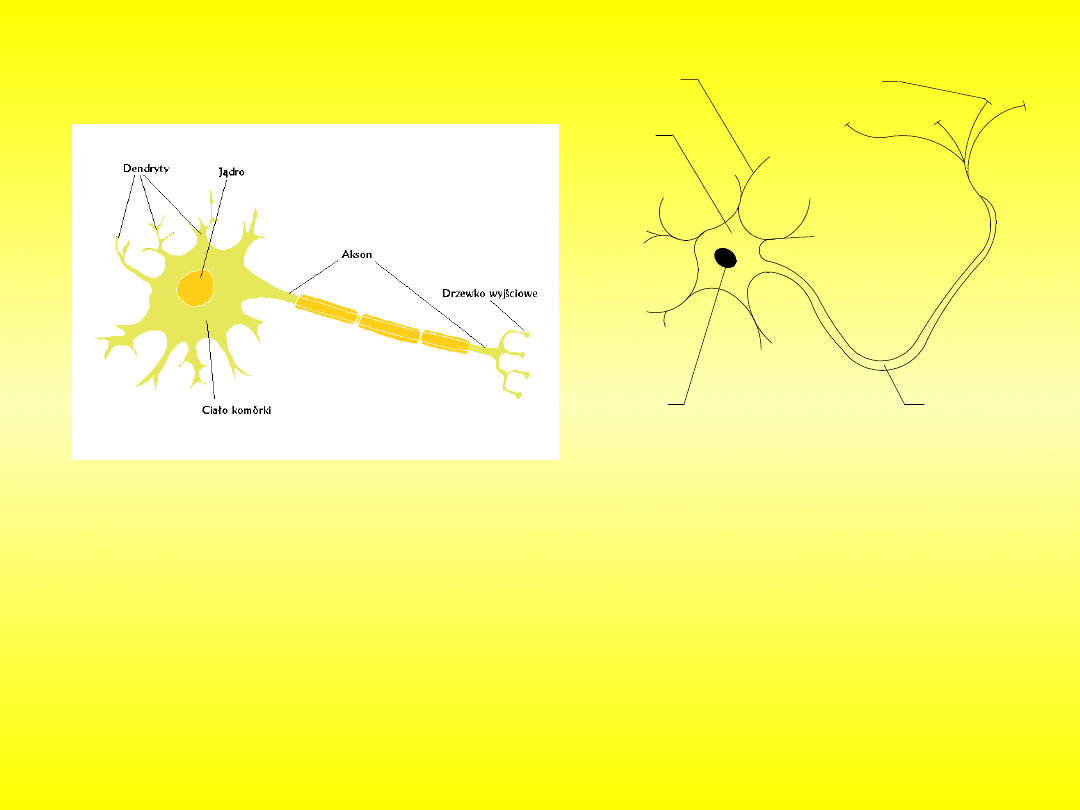
W  rzeczywistości  komórka  nerwowa  posiada  kilka  tysięcy 

dendrytów,  a  z  innymi  neuronami  kontaktuje  się  poprzez  miliony  połączeń. 
Powierzchnia neuronu nie jest zwykłą gładką błoną. Znajduje się na niej około 
miliona 

tzw. 

sodowo-potasowych 

pomp 

adenozyno-trójfosfatazowych, 

odpowiedzialnych za utrzymaniu na wewnętrznej stronie błony potencjału -70 
mV  względem  otoczenia.  Odbywa  się  to  poprzez  “wypompowywanie”  jonów 
sodu  z  wnętrza  komórki,  a  wpuszczanie  jonów  potasu.  Proces  ten  musi 
przebiegać  ciągle,  gdyż  błona  komórkowa  jest  nieszczelna  i  nie  zapobiega 
zjawisku 

odwrotnemu 

prowadzącemu 

do 

zniwelowania 

tej 

różnicy 

potencjałów. 

Naturalny neuron

2

3

1

4

5

Rys. Uproszczony schemat budowy 

neuronu: 1-cytoplazma komórki, 2-

jądro komórkowe,  3-akson, 4-dendryt, 

5-synapsa

 

 

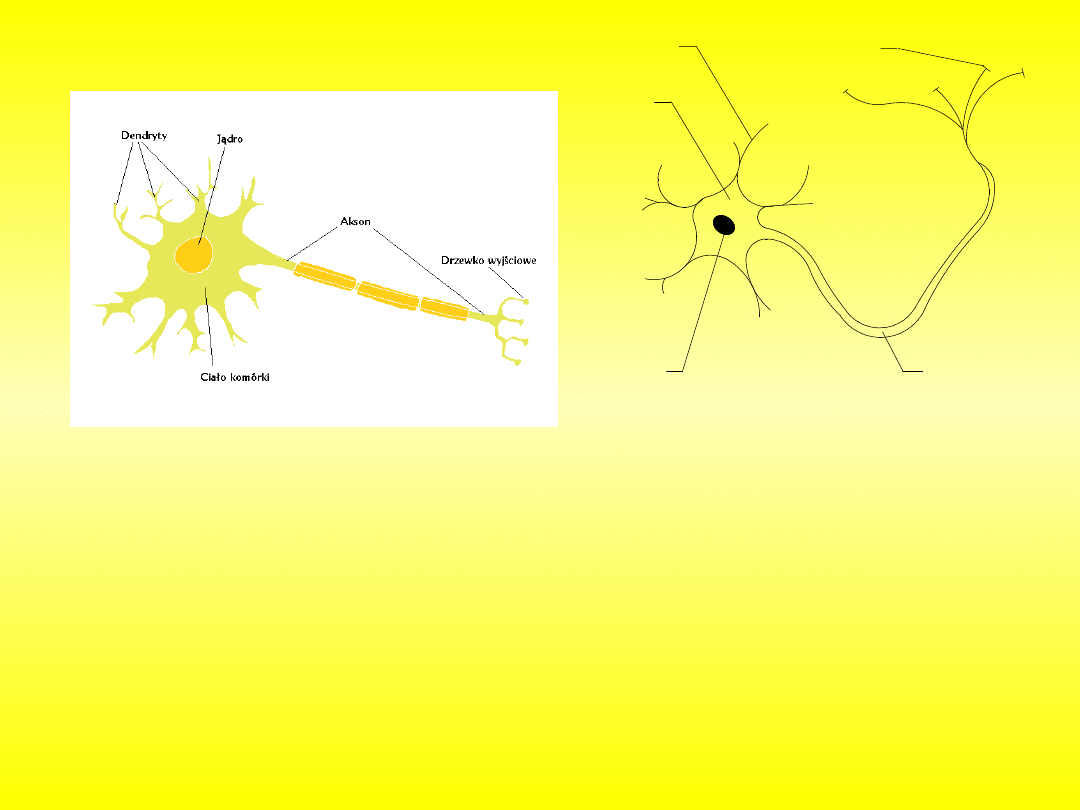
Bodziec  dostarczony  do  komórki  powoduje  zmianę  jej  stanu 

elektrycznego przebiegającą następnie wzdłuż aksonu. Dzieje się to jednak nie na 
drodze przewodnictwa elektrycznego, a poprzez ekspansję lokalnych zmian stanu 
elektrycznego  błony  komórkowej.  Zmiany  potencjału  błony  są  skutkiem  jej 
zmiennej  przepuszczalności  dla  jonów  sodowych  i  potasowych.  Po  przejściu 
impulsu  błona  powraca  do  normalnego  stanu.  Dojście  impulsu  do  synapsy 
(połączenia  akson-dendryt  lub  dendryt  z  inną  komórką)  powoduje  uwolnienie  z 
komórki  pobudzającej  neurotransmitera,  który  z  kolei  jest  przyczyną  pobudzenia 
komórki odbierającej impuls. Neurotransmiter to związek chemiczny przekazujący 
informację między neuronami. Pobudzenie neuronu odbierającego sygnał jest tym 
większe,  im  więcej  neurotransmitera  wydzieli  się  z  kolbki  synaptycznej  komórki 
pobudzającej.  Łączne  pobudzenie  komórki  nerwowej  jest  sumą  pobudzeń  na 
wszystkich połączeniach synaptycznych. Fakt ten ma bardzo duże znaczenie przy 
tworzeniu modelu neuronu, i jest podstawą teorii sztucznych sieci neuronowych. 

Naturalny neuron

2

3

1

4

5

Rys. Uproszczony schemat budowy 

neuronu: 1-cytoplazma komórki, 2-

jądro komórkowe,  3-akson, 4-dendryt, 

5-synapsa

 

 

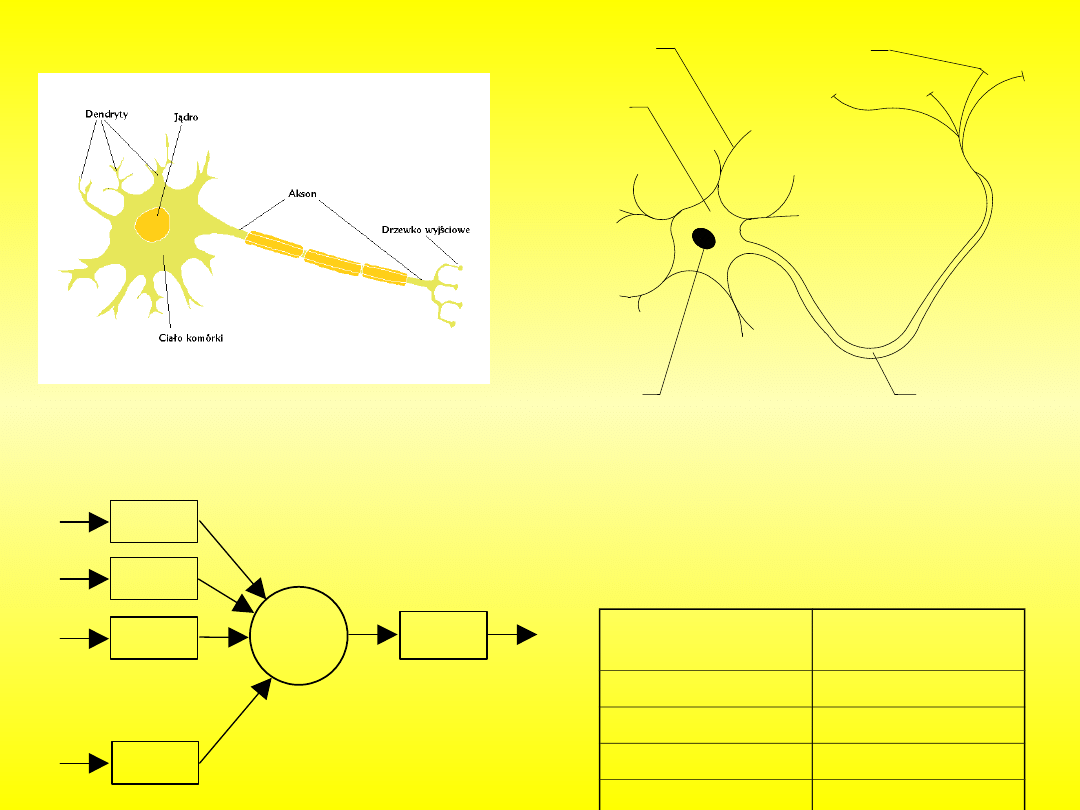
Naturalny neuron

2

3

1

4

5

Rys. Uproszczony schemat budowy 

neuronu: 1-cytoplazma komórki, 2-

jądro komórkowe,  3-akson, 4-dendryt, 

5-synapsa

Tab. Porównanie między elementami 

naturalnego  i modelu neuronu 

 

x

n

x

3

x

2

x

1

y





W

n

W

1

W

2

W

3

 ( )

Model neuronu

Naturalny 
neuron

Model neuronu

Dendryty

Wejścia

Synapsy

Wagi

Jądro

Blok sumujący

Akson

Blok aktywacji

 

 

x

n

x

3

x

2

x

1

y





W

n

W

1

W

2

W

3

 ( )

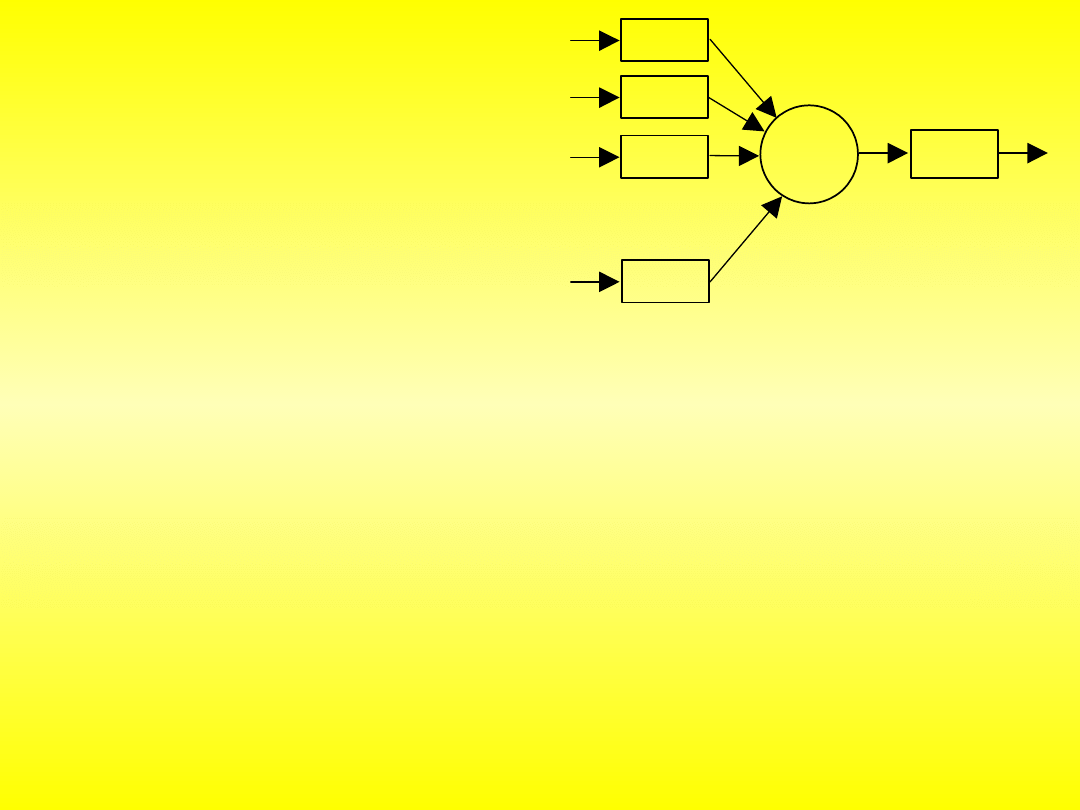
Na  wejścia  neuronu  (ich  liczba  jest  dowolna)  warstwa  wejściowa  lub 

inny neuron podaje się informacje. Są one mnożone przez wagi. Wartości wag są 
one ustalane przez uczenie się sieci neuronowej, i oznaczają to, jak ważna jest ta 
informacja.  Blok  sumowania,  jak  sama  nazwa  wskazuje,  sumuje  otrzymane 
iloczyny. W zależności od przeznaczenia sieci, stosuje się różne funkcje aktywacji. 
Informacja z wyjścia trafia na wejścia innych neuronów. Poszczególny neuron jest 
już siecią, ale do bardziej skomplikowanych operacji nie wystarczy. 

Wprowadzenie do sieci 
neuronowych







n

i

i

i

x

W

y

0

Sygnał wyjściowy sumatora:

Sieci  neuronowe  składają  się  ze  sztucznych  neuronów,  stworzonych  na  bazie 
neuronów w ludzkim mózgu. Mają bardzo podobne właściwości. Składają się z 
wejść, wag, bloku sumowania, bloku aktywacji i wyjścia.

 

 

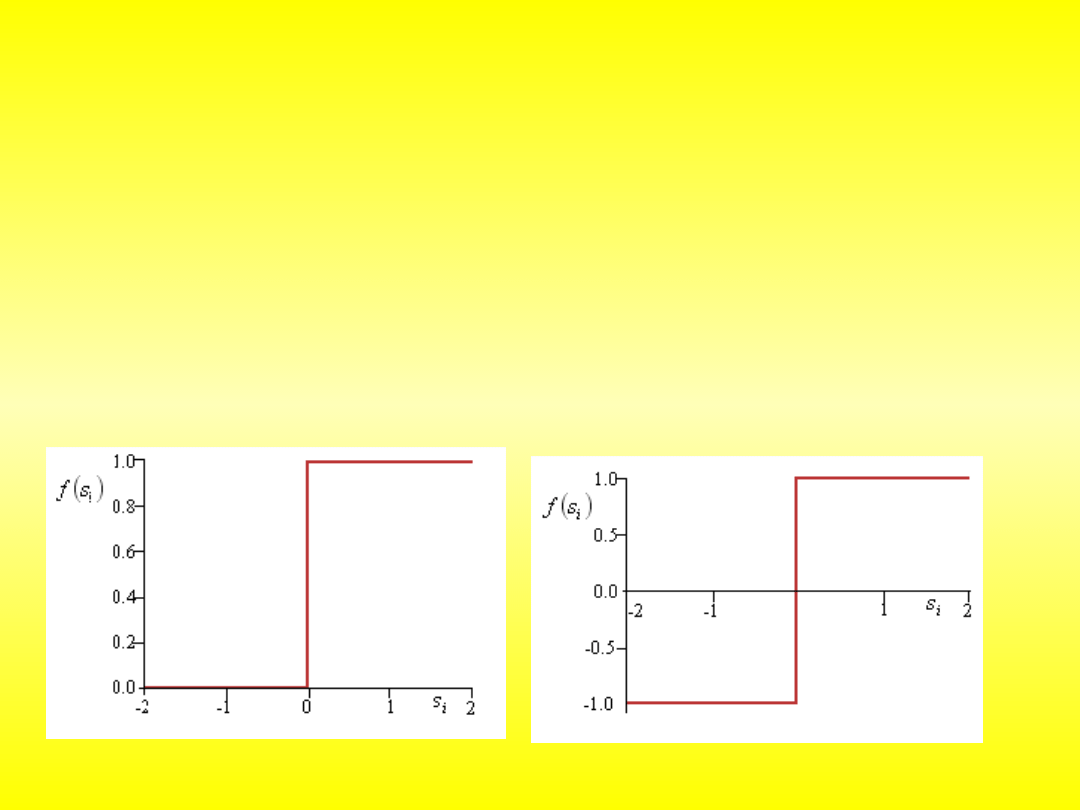
Podział neuronów ze względu na rodzaj funkcji aktywacji

 

 funkcja liniowa

 

 

i

i

s

s

f



 funkcje nieliniowe dyskretne – skokowe: 

 













0

0

0

1

i

i

i

s

dla

s

dla

s

f

 

 

















0

1

0

1

sgn

i

i

i

i

s

dla

s

dla

s

s

f

 

1

,

0



y





1

,

1





y

unipolarna:

 

bipolarna:

 

 

 

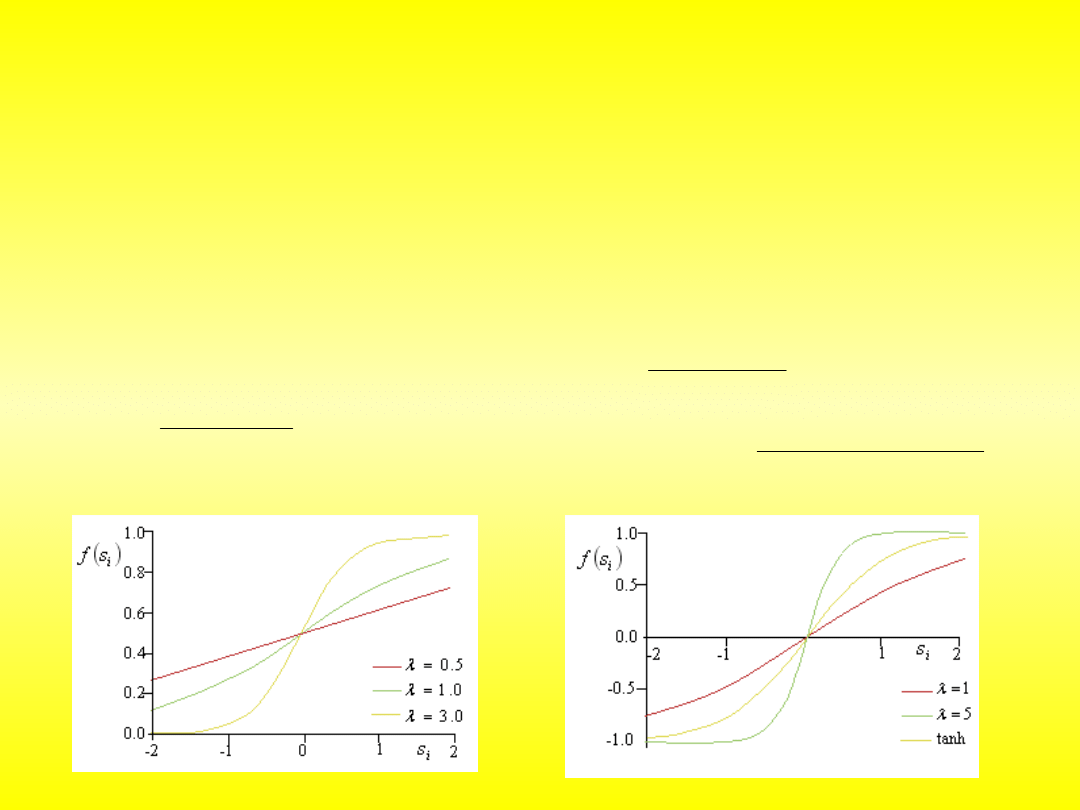
Funkcje nieliniowe ciągłe

 

 





i

i

s

s

f









exp

1

1

 





i

i

s

s

f









exp

1

2

 

1

,

0



y





1

,

1





y

 

 

 





 





i

i

i

i

i

i

s

s

s

s

s

s

f





















exp

exp

exp

exp

tanh

unipolarna:

 

bipolarna:

 

0





0





W  bardziej  zaawansowanych  rozwiązaniach  stosuje  się  funkcje 

przejścia.  Najpopularniejszą  klasę  funkcji  stosowanych  w  sieciach  neuronowych 
stanowią  funkcje  sigmoidalne,  np.  tangens  hiperboliczny.  Sieć  zbudowana  z 
neuronów wyposażonych w nieliniową funkcję przejścia ma zdolność nieliniowej 
separacji wzorców wejściowych. Jest więc uniwersalnym klasyfikatorem.

 

 

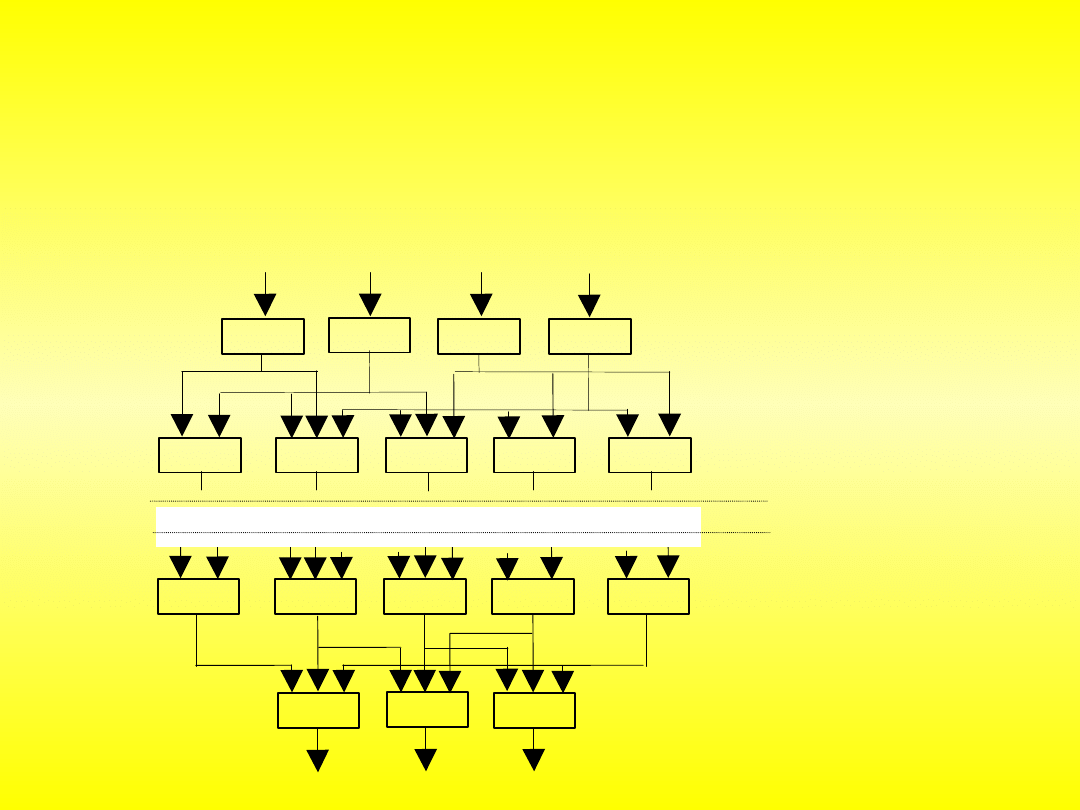
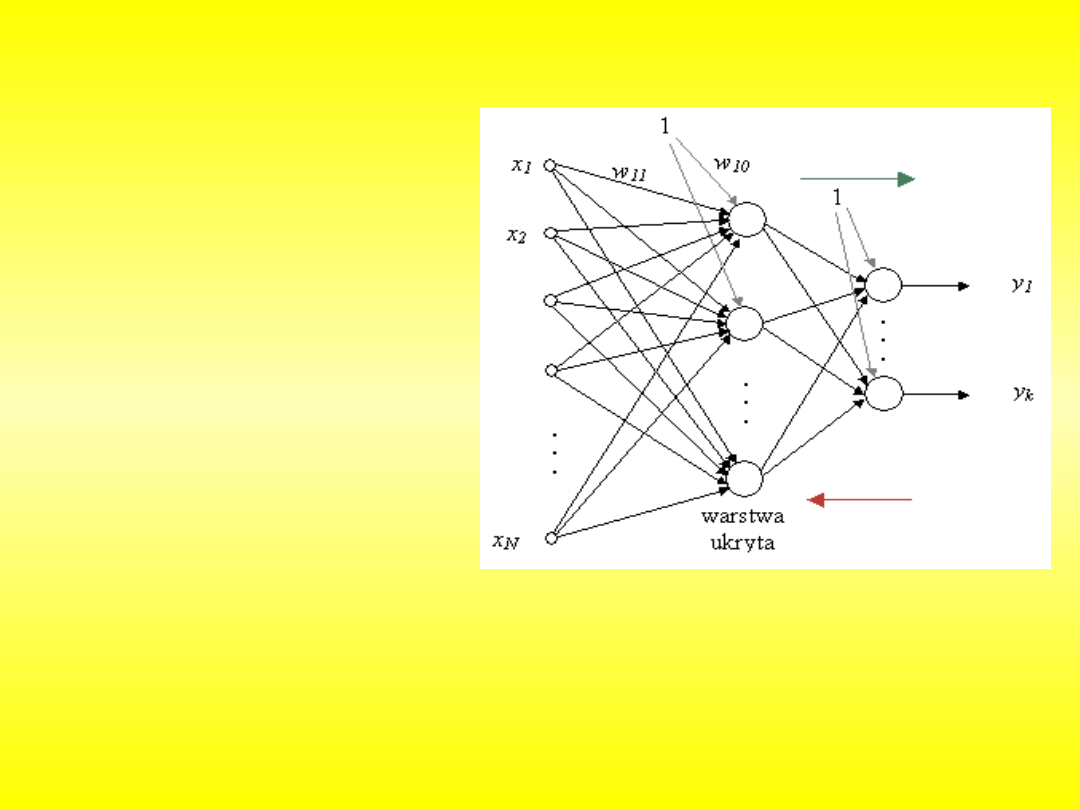
Rozbudowana sieć neuronowa składa się z warstw. Pierwszą warstwą to 

zawsze    warstwa  wejściowa.  Pobiera  ona  od  użytkownika  lub  innej  sieci 
neuronowej  dane,  które  są  przesyłane  dalej  do  sieci.  Następną  warstwą  składa 
się  już  ze  sztucznych  neuronów,  tak  zwana  warstwa  ukryta.  Neurony  w 
poszczególnych  warstwach  nie  są  ze  sobą  połączone,  ale  łączą  się  warstwami. 
Neuron  z  warstwy  pierwszej  jest  połączony  z  wszystkimi  neuronami  z  warstwy 
następnej.  W  praktyce  oznacza  to,  że  w  sieci  może  pracować  dowolna  liczba 
warstw.  Ostatnią  warstwą  jest  zawsze  warstwa  wyjściowa.  Przekazuje  ona 
informację czytelną dla użytkownika. 

Rys. Budowa sieci neuronowej

neuron

neuron

neuron

neuron

neuron

neuron

neuron

pierwsza

warstwa ukryta

n-ta warstwa

ukryta

warstwa wyjściowa

sygnały wyjściowe

sygnały wejściowe

warstwa wejściowa

neuron

neuron

neuron

neuron

neuron

neuron

neuron

neuron

neuron

neuron

 

 

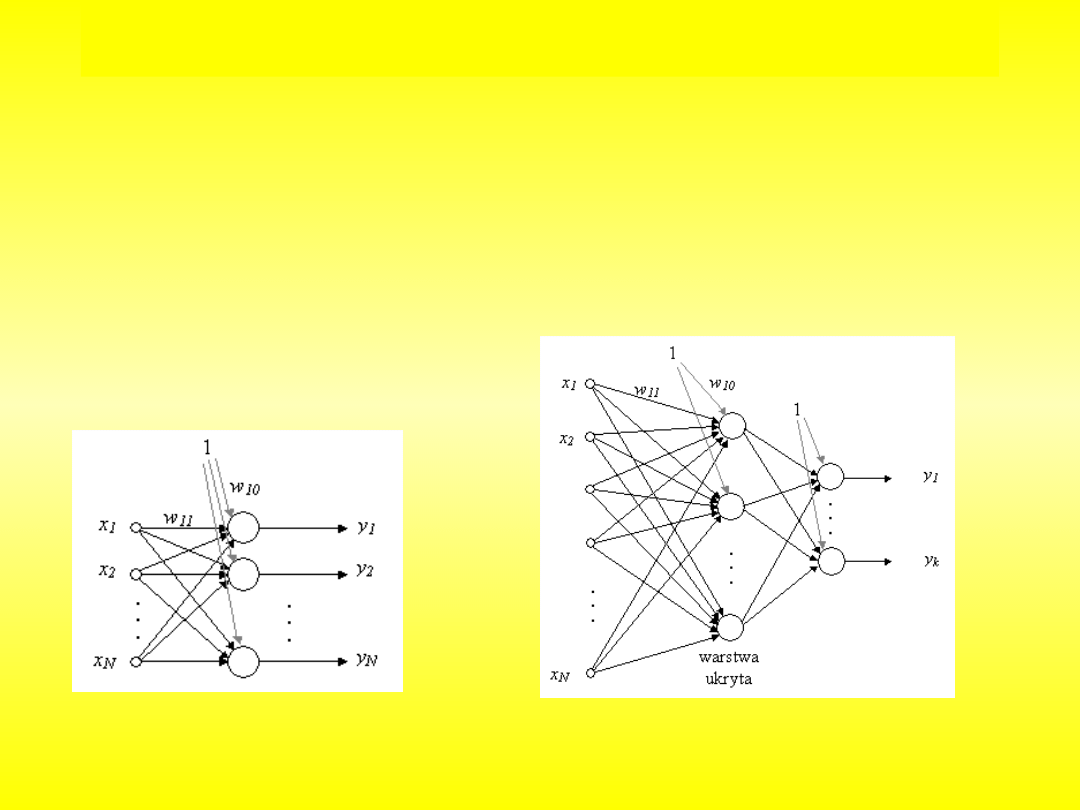
Podstawowe typy architektury sieci

 

 















































N

j

i

j

ij

N

j

i

j

ij

i

i

x

w

f

w

x

w

f

s

f

y

1

1

0











































H

h

N

j

h

j

hj

h

hk

k

k

w

x

w

f

w

w

f

y

1

1

0

0

0

jednowarstwowe

wielowarstwowe

Cechą  wspólną  wszystkich  sieci  neuronowych  jest  to,  że  na  ich 

strukturę  składają  się  neurony  połączone  ze  sobą  synapsami.  Z  synapsami 
związane  są  wagi,  czyli  wartości  liczbowe,  których  interpretacja  zależy  od 
modelu.

Sieci  jednokierunkowe

  to  sieci  neuronowe,  w  których  nie  występuje 

sprzężenie zwrotne

,  czyli  pojedynczy  wzorzec  lub  sygnał  przechodzi  przez 

każdy neuron dokładnie raz w swoim cyklu. Najprostszą siecią neuronową jest 
pojedynczy perceptron progowy, opracowany przez McCullocha i Pittsa w roku 
1943.

 

 

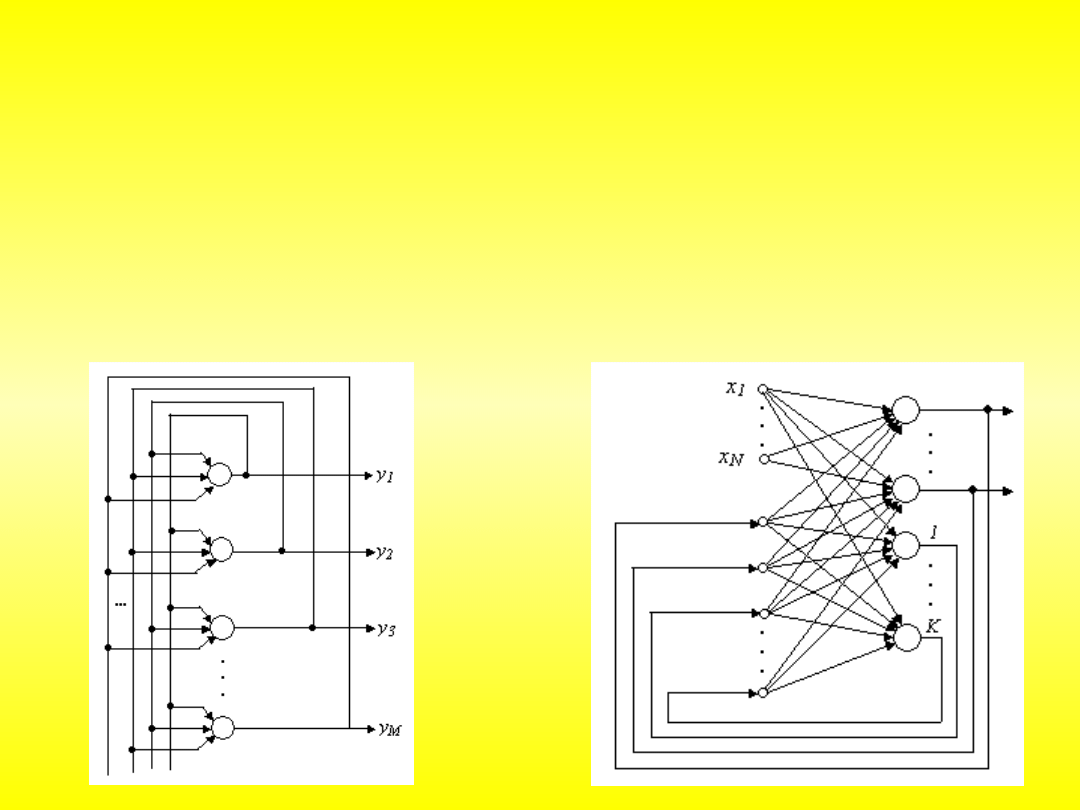
jednowarstwowe

wielowarstwowe 

Sieci rekurencyjne

 to sieci, w których połączenia między neuronami stanowią 

graf

 z cyklami. Wśród różnorodności modeli rekurencyjnych sztucznych sieci 

neuronowych wyróżnić można:

sieć Hopfielda

 – układ gęsto połączonych ze sobą neuronów (każdy z każdym, 

ale bez połączeń zwrotnych) realizującą dynamikę gwarantującą zbieżność do 
preferowanych wzorców 

maszyna Boltzmanna

 – opracowana przez 

Geoffa Hintona

 i 

Terry'ego Sejnowskiego

 

stochastyczna modyfikacja sieci Hopfielda; modyfikacja ta pozwoliła na uczenie 
neuronów ukrytych i likwidację wzorców pasożytniczych kosztem zwiększenia 
czasu symulacji. 
Sieci Hopfielda i maszyny Boltzmanna stosuje się jako pamięci adresowane 
kontekstowo, do 

rozpoznawania obrazów

, 

rozpoznawania mowy

, a także do 

rozwiązywania problemów minimalizacji (np. 

problemu komiwojażera

).

 

 

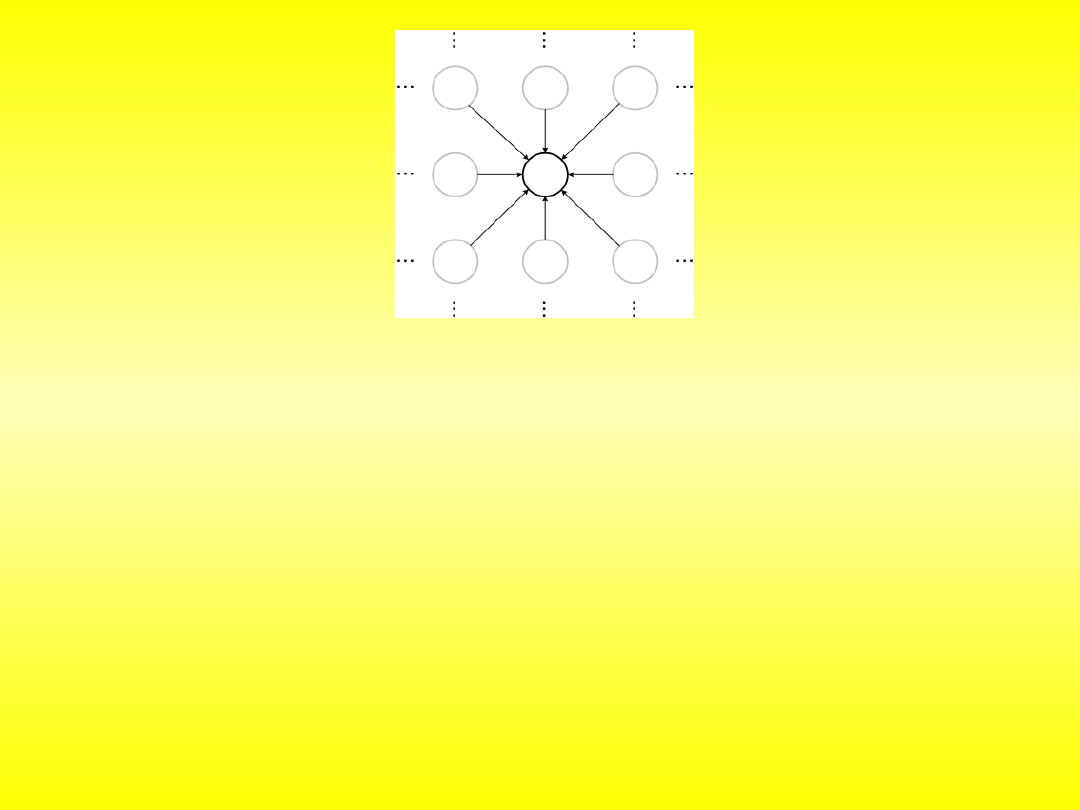
۰ podklasa sieci rekurencyjnych, która wyróżniana ze względu na swoją funkcję, 

۰ 

wzorowana na zasadach funkcjonowania mózgu ludzkiego 

۰ zdolność odtwarzania całości informacji na podstawie informacji niepełnej lub 
zniekształcone,j 

Sieci komórkowe

 

 

 

Sposoby uczenia sieci:

1. Nauka z nauczycielem

2. Nauka z krytykiem

3. Samodzielna nauka sieci

Nauczona sieć neuronowa może już służyć do tego, do czego została stworzona

.

Jedną  z  zalet  sieci  neuronowych  jest  to,  że  nie  trzeba  prawie  nic 

programować.  Sieć  neuronową  się  uczy.  Nauka  polega  na  “dostrajaniu”  wag  w 
ten sposób, aby sieć rozpoznawała dane poprawnie.

W  modelu  neuronu,  zmianę  wagi  synaptycznej  W

i

(j)

  neuronu  W

i

(j)

 

podczas  przejścia  z  chwili  j  do  j+1,  która  zależy  od  jego  stanu  y

(j)

  oraz  stanu 

wejścia x

i

(j)

, analizuje się wg wzoru:  

W

i

(j)

 =   y

(j)

 x

i

(j) 

                                                   (1)

Zmodyfikowana waga:

W

i

(j+1)

 = W

i

(j)

 + W

i

(j)  

                                                (2)

W

i

(j+1)

 = W

i

(j)

 +  y

(j)

 x

i

(j)              

                             

            (3)

 

 

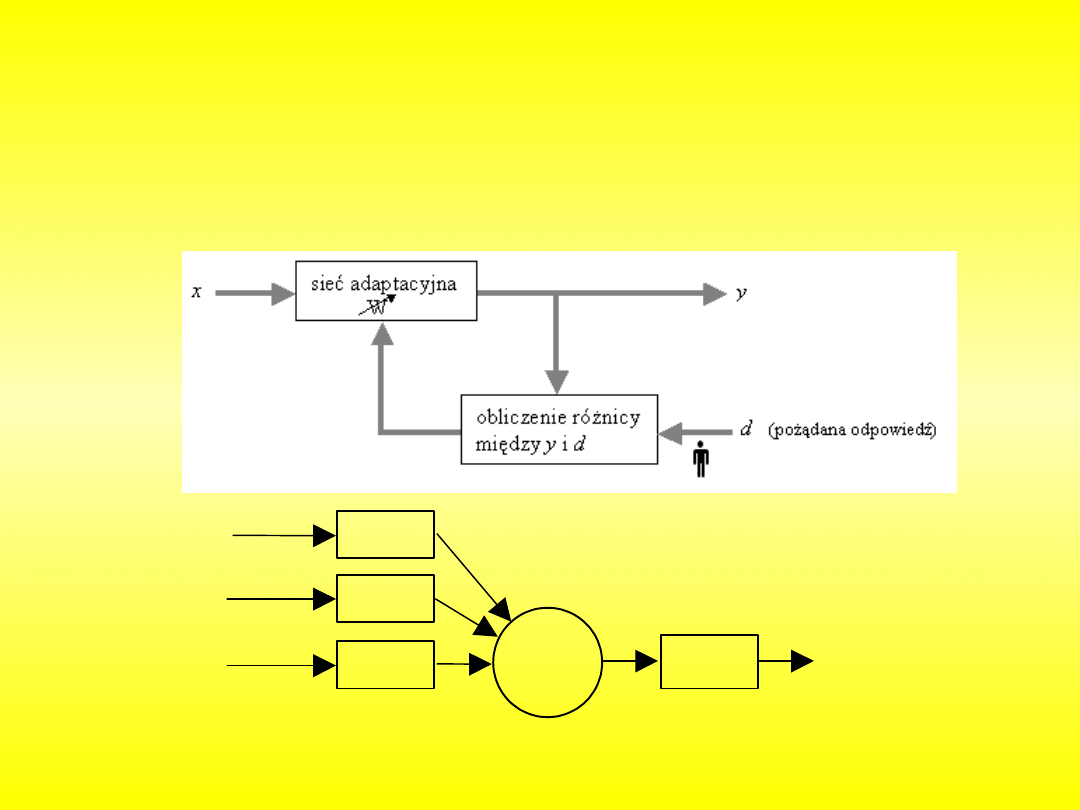
Nauka z nauczycielem

x

3 

= 4

x

2 

= 2

x

1 

= 3

Y = 16





W

1 

= 2

W

2 

= 3

W

3 

= 1

 ( )

W  tym  sposobie,  nauczyciel  samodzielnie  koryguje  wagi.  Przykładowo: 

nauczyciel podaje na wejście sieci dane. Następnie sprawdza poprawność danych 
na  wyjściu.  Jeśli  informacja  okaże  się  błędna,  nauczyciel  ręcznie  zmienia  wagi,  i 
uruchamia  sieć  z  tymi  samymi  danymi,  aż  do  skutku.  Jest  to  dość  pracochłonny 
sposób.

 

 

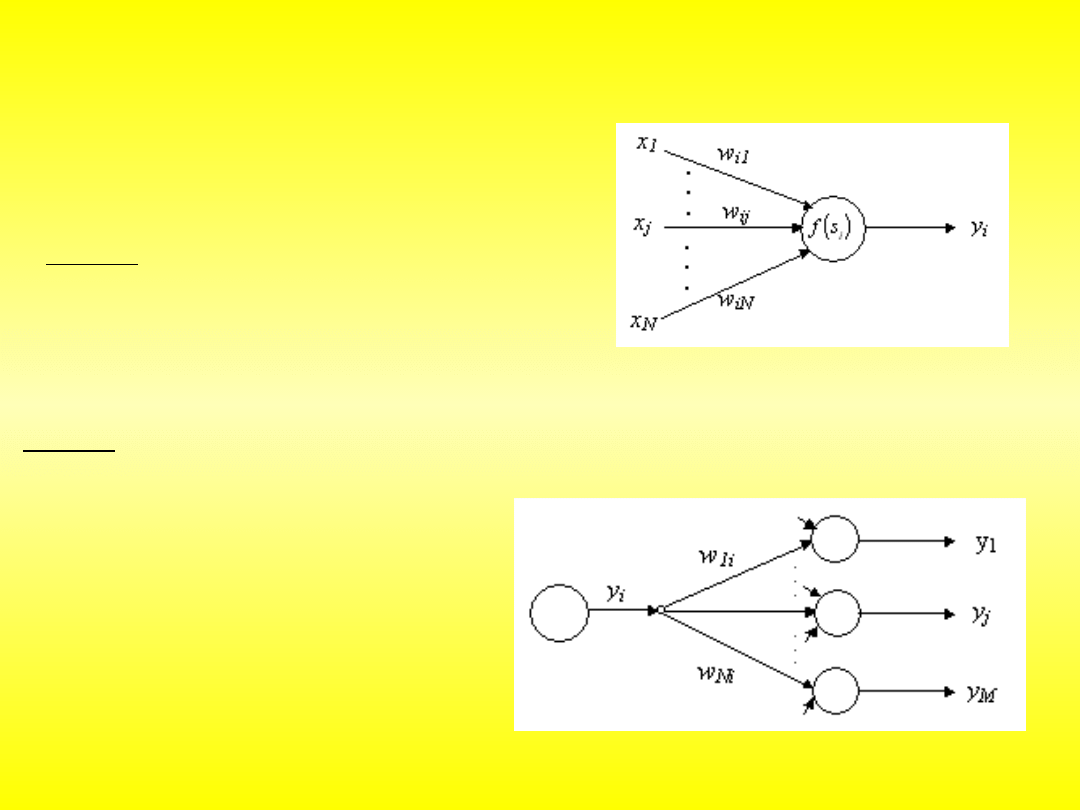
 Instar i Outstar 

۰ zdefiniowane przez S. Grossberga
۰ komplementarne

Instar: dopasowuje wagi do sygnałów wejściowych
zadanie: rozpoznanie wektora danego na wejście

Outstar: dopasowuje wagi wychodzące z neuronu do węzłów, 
dla których zadane są wartości sygnałów wyjściowych
zadanie: wygenerowanie w odpowiedzi na określony sygnał wejściowy 
wektora pożądanego przez inne neurony powiązane z danym neuronem

 

 

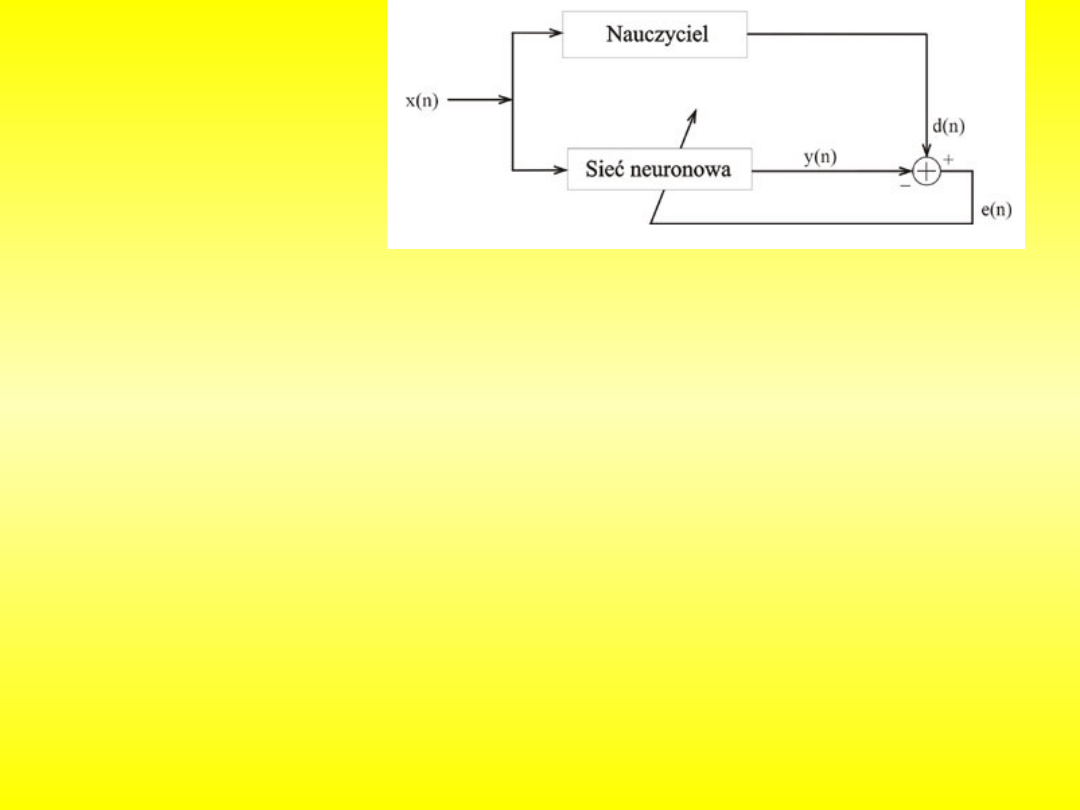
۰ cel: modyfikacja, aby dla wszystkich wektorów wejściowych

 

     

0

,





k

e

k

y

k

d

     

0

,





k

e

k

y

k

d

 osłabiamy wagi neuronu 

 wzmacniamy wagi neuronu 

۰ zasada działania: 

 

0



k

e

۰ działanie:  -  inicjalizacja wag w

ij

      -  podanie wektora uczącego na wejście x   
      - wyznaczenie wartość sygnału wyjściowego y 

                         - korekcja wektora wag wg wzoru: 





 

 

 

   

 

 

   

 

 

































1

;

1

1

;

1

1

k

d

k

y

gdy

k

x

k

w

k

d

k

y

gdy

k

x

k

w

k

d

k

y

gdy

k

w

k

w

i

i

i

i

Procedurę powtarza się dla wszystkich danych uczących, aż do uzyskania 
minimalizacji różnicy pomiędzy d i y 

۰ prezentacja nowego wektora uczącego i ponowna aktualizacja wag

 reguła perceptronowa 





i

i

d

x ,

– zbiór par wektorów (wzorców) uczących postaci:





T

M

d

d

d

...,

,

1



 

   

k

y

k

d

k

e





– funkcja błędu

  



1

,

1





k

y

Uczenie z 
nauczycielem jako 
system adaptacyjny

 

 

Nauka z krytykiem

 

Odmiana uczenia z nauczycielem.

 

Ucząc sieć w ten sposób, nie koryguje 

się  nic  ręcznie.  Sieć  sama  próbuje  korygować  wagi.  Krytyk  tylko 
informuje sieć o poprawności danych otrzymanych na wyjściu.

 

   nie korzysta się z informacji o pożądanych wartościach wyjściowych 
systemu, 
      korzysta  się  z  informacji,  czy  zmiana  wartości  wag,  która  została 
podjęta daje wyniki 
   pozytywne czy negatywne w sensie pożądanego zachowania systemu:
̶̶        pozytywne    wzmocnienie  tendencji  do  właściwego  zachowania  się 
systemu w     podobnych sytuacjach w przyszłości,
̶̶    negatywne  osłabienie tendencji takiego działania systemu,
   bardziej uniwersalne w zastosowaniu,
   realizacja praktyczna - bardziej skomplikowana. 

 

 

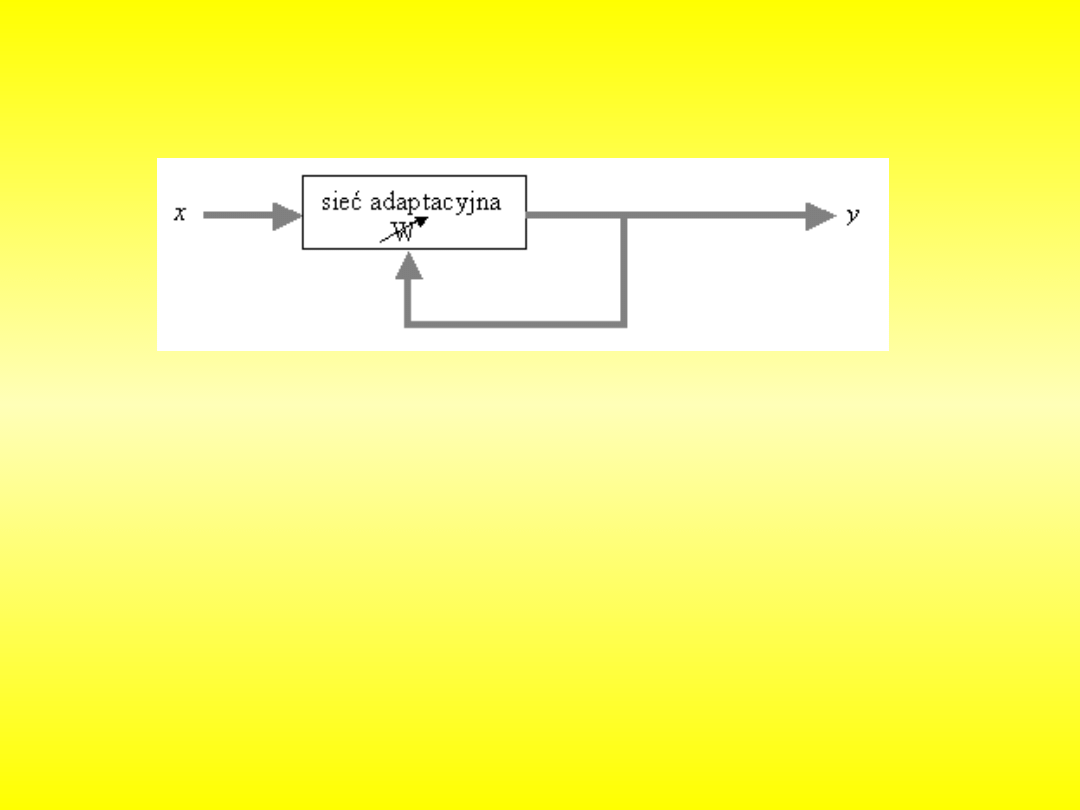
Uczenie bez 

nauczyciela

 

۰ 

algorytm uczenia typu korelacyjnego 

 reguła Hebba

۰ 

wykorzystuje wyniki obserwacji biologicznych:   waga powiązań między 

neuronami wzrasta przy jednoczesnym  pobudzeniu obu neuronów, w 
przeciwnym wypadku maleje:





 

 

k

w

k

w

k

w

ij

ij

ij







1

 

   

k

y

k

cx

k

w

i

j

ij





x

j

 – sygnał wejściowy (presynaptyczny)

y

i

 – sygnał wyjściowy (postsynaptyczny)

c – z (0,1),  współczynnik określający stopień w jakim sygnały uczące 
  w chwili k wpływają na dobór wag
w

ij

 – waga połączenia między sygnałem wejściowym x

j

 a węzłem sumacyjnym 

  i-tego neuronu o sygnale wyjściowym y

i

Sieci  neuronowe  potrafią  się  też  uczyć  same.  Działa  to  dzięki  takim 

zasadom  jak  “wygrywający  bierze  wszystko”.  Jednak  te  metody  nauki  nie 
zawsze są skuteczne.

 

 

Uczenie sieci wielowarstwowej

۰ 1969 – Minsky i Papert – Perceptrons: 
  - kilku elementarnych obliczeń nie można wykonać na jednowarstwowym 
  perceptronie (np. problem XOR) 
  - brak algorytmów uczenia dla sieci wielowarstwowych

۰ 1985 – algorytm wstecznej propagacji błędu: 
  - algorytm uczenia sieci wielowarstwowej 
  - możliwość rozwiązania wielu problemów, z którymi nie potrafiły 
  sobie poradzić sieci jednowarstwowe (np. XOR) 

 

 

Metoda wstecznej propagacji błędu (back propagation)

۰ podanie na wejście sygnału uczącego x 
  i wyliczenie aktualnych wyjść y 

۰ obliczenie błędów w warstwie ostatniej 
  (na podstawie porównania sygnałów 
  wyjściowych y i wzorcowych d) 

۰ obliczenie błędów dla neuronów we 
  wszystkich warstwach wcześniejszych po kolei 
  (zawsze jako pewnej funkcji błędu warstwy następnej, który jest już znany) 

۰ adaptacja wag:
od warstwy wejściowej do wyjściowej 

۰ sygnał błędu rozprzestrzenia się wstecz: od warstwy ostatniej do wejściowej

۰ powtarzamy procedurę do momentu kiedy sygnały wyjściowe sieci będą 
dostatecznie bliskie oczekiwanym 

algorytm:

 

 

Sieci Kohonena

Sieci  Kohonena  są  jednym  z  podstawowych  typów  sieci 

samoorganizujących  się.  Właśnie  dzięki  zdolności  samoorganizacji 
otwierają  się  zupełnie  nowe  możliwości  -  adaptacja  do  wcześniej 
nieznanych  danych  wejściowych,  o  których  bardzo  niewiele  wiadomo. 
Wydaje się to naturalnym sposobem uczenia, który jest używany chociażby 
w  naszych  mózgach,  którym  nikt  nie  definiuje  żadnych  wzorców,  tylko 
muszą  się  one  krystalizować  w  trakcie  procesu  uczenia,  połączonego  z 
normalnym  funkcjonowaniem.  Sieci  Kohonena  stanowią  synonim  całej 
grupy  sieci,  w  których  uczenie  odbywa  się  metodą  samoorganizującą  typu 
konkurencyjnego.  Polega  ona  na  podawaniu  na  wejścia  sieci  sygnałów,  a 
następnie  wybraniu  w  drodze  konkurencji  zwycięskiego  neuronu,  który 
najlepiej 

odpowiada 

wektorowi 

wejściowemu. 

Dokładny 

schemat 

konkurencji  i  późniejszej  modyfikacji  wag  synaptycznych  może  mieć  różną 
postać.  Wyróżnia  się  wiele  podtypów  sieci  opartych  na  konkurencji,  które 
różnią się dokładnym algorytmem samoorganizacji.

Najczęściej  stosuje  się  w  tego  typu  sieciach  architekturę 

jednokierunkową  jednowarstwową.  Jest  to  podyktowane  faktem,  że 
wszystkie neurony muszą uczestniczyć w konkurencji na równych prawach. 
Dlatego  każdy  z  nich  musi  mieć  tyle  wejść  ile  jest  wejść  całego  systemu. 
Jest  to  podyktowane  faktem,  że  wszystkie  neurony  muszą  uczestniczyć  w 
konkurencji na równych prawach. Dlatego każdy z nich musi mieć tyle wejść 
ile jest wejść całego systemu. 

 

 

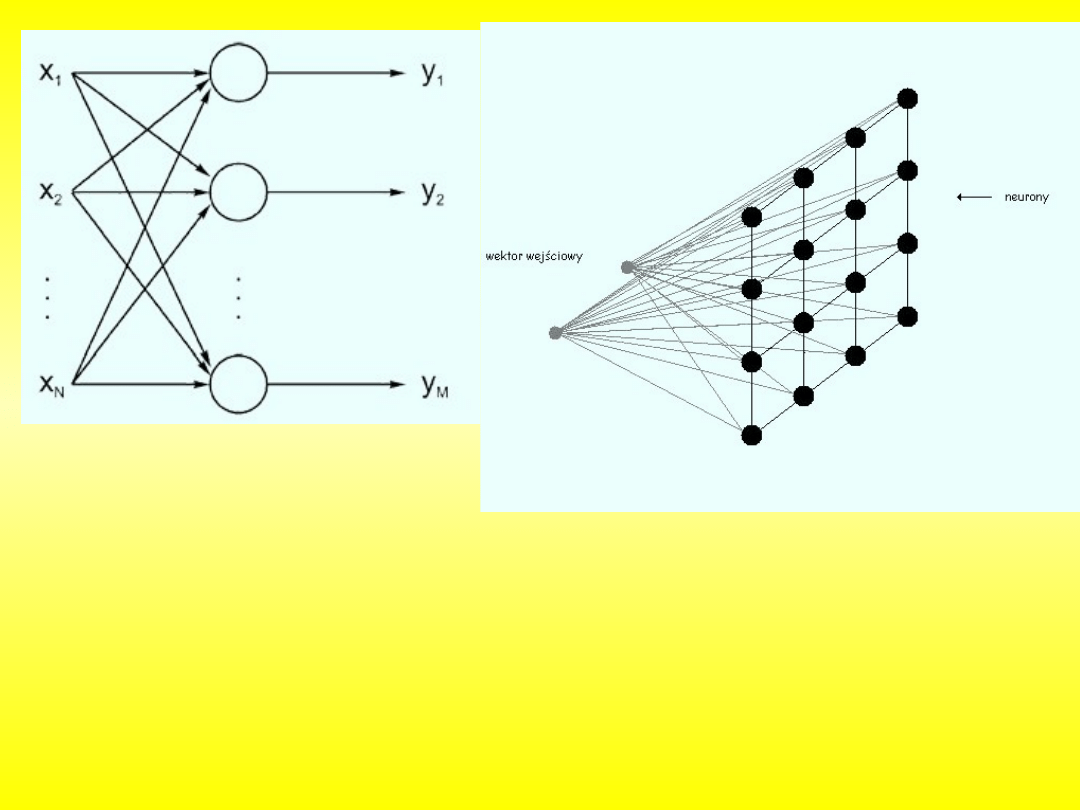
Schemat sieci jednowarstwowej 

jednokierunkowej

Dwuwymiarowa mapa neuronów

 

 

Etapy działania::

 

Funkcjonowanie samoorganizujących się sieci neuronowych odbywa się w 

trzech etapach: 

•  konstrukcja 
•  uczenie 
•  rozpoznawanie 

System, który miałby realizować funkcjonowanie sieci samoorganizującej 

powinien  składać  się  z  kilku  podstawowych  elementów.  Pierwszym  z  nich  jest 
macierz  neuronów  pobudzanych  przez  sygnały  wejściowe.  Sygnały  te  powinny 
opisywać  pewne  charakterystyczne  cechy zjawisk  zachodzących  w otoczeniu, tak, 
aby na ich podstawie sieć była w stanie je pogrupować. Informacja o zdarzeniach 
jest przekładana na bodźce pobudzające neurony. Zbiór sygnałów przekazywanych 
do  każdego  neuronu  nie  musi  być  identyczny,  nawet  ich  ilość  może  być  różna. 
Muszą one jednak spełniać pewien warunek, a mianowicie jednoznacznie określać 
dane zdarzenia.

Kolejną  częścią  składową  sieci  jest  mechanizm,  który  dla  każdego 

neuronu  określa  stopień  podobieństwa jego wag  do danego sygnału wejściowego 
oraz  wyznacza  jednostkę  z  największym  dopasowaniem  -  zwycięzcę.  Obliczenia 
zaczyna się dla wag równych małym liczbom losowym, przy czym ważne jest, aby 
nie zachodziła żadna symetria. W trakcie uczenia wagi te są modyfikowane w taki 
sposób,  aby  najlepiej  odzwierciedlać  wewnętrzną  strukturę  danych  wejściowych. 
Istnieje  jednak  niebezpieczeństwo,  że  zwiążą  się  one  z  pewnymi  wartościami 
zanim  jeszcze  grupy  zostaną  prawidłowo  rozpoznane  i  wtedy  trzeba  ponawiać 
uczenie z innymi wagami.

Wreszcie  konieczne  do  przeprowadzenia  samoorganizacji  jest,  aby  sieć 

była  wyposażona w  zdolność  do  adaptacji  wartości  wag  neuronu  zwycięzcy i  jego 
sąsiadów  w  zależności  od  siły,  z  jaką  odpowiedział  on na  dane  wejście.  Topologię 
sieci można w łatwy sposób określić poprzez zdefiniowanie sąsiadów dla każdego 
neuronu.  Załóżmy,  że  jednostkę,  której  odpowiedź  na  dane  pobudzenie  jest 
maksymalna,  będziemy  nazywali  "obrazem"  tego  pobudzenia.  Wtedy  możemy 
przyjąć,  że  sieć  jest  uporządkowana,  jeśli  topologiczne  relacje  między  sygnałami 
wejściowymi i ich obrazami są takie same.

 

 

Współcześnie nie ma wątpliwości, że sztuczne sieci neuronowe nie 

stanowią  dobrego  modelu  mózgu,  choć  różne  ich  postaci  wykazują  cechy 
charakterystyczne  dla  biologicznych  układów  neuronowych:  zdolność  do 
uogólniania  wiedzy,  uaktualniania  kosztem  wcześniej  poznanych  wzorców, 
dawanie  mylnych  odpowiedzi  po  przepełnieniu.  Mimo  uproszczonej  budowy 
sztuczne  sieci  neuronowe  stosuje  się  czasem  do  modelowania  schorzeń 
mózgu.

Sztuczne sieci neuronowe znajdują zastosowanie w rozpoznawaniu 

i  klasyfikacji  wzorców  (przydzielaniu  wzorcom  kategorii),  predykcji 
szeregów  czasowych,  analizie  danych  statystycznych,  odszumianiu  i 
kompresji  obrazu  i  dźwięku  oraz  w  zagadnieniach  sterowania  i 
automatyzacji.

 

 

Magazyn BYTE wymienia między innymi następujące zastosowania tych 

sieci:

•diagnostyka 

układów elektronicznych

 

•badania psychiatryczne 
•prognozy giełdowe 
•prognozowanie sprzedaży 
•poszukiwania 

ropy naftowej

 

•interpretacja badań biologicznych 
•prognozy cen 
•analiza badań medycznych 
•planowanie remontów maszyn 
•planowanie postępów w nauce 
•analiza problemów produkcyjnych 
•optymalizacja działalności handlowej 
•analiza 

spektralna

 

•optymalizacja utylizacji odpadów 
•dobór surowców 
•selekcja celów śledztwa w kryminalistyce 
•dobór pracowników 
•sterowanie procesów przemysłowych. 
Najpopularniejsze obecnie zastosowanie sieci neuronowych:
•w programach do rozpoznawania pisma, 
•na lotniskach do sprawdzania, czy prześwietlony bagaż zawiera 

niebezpieczne ładunki 

•do 

syntezy mowy

.

 

 

 

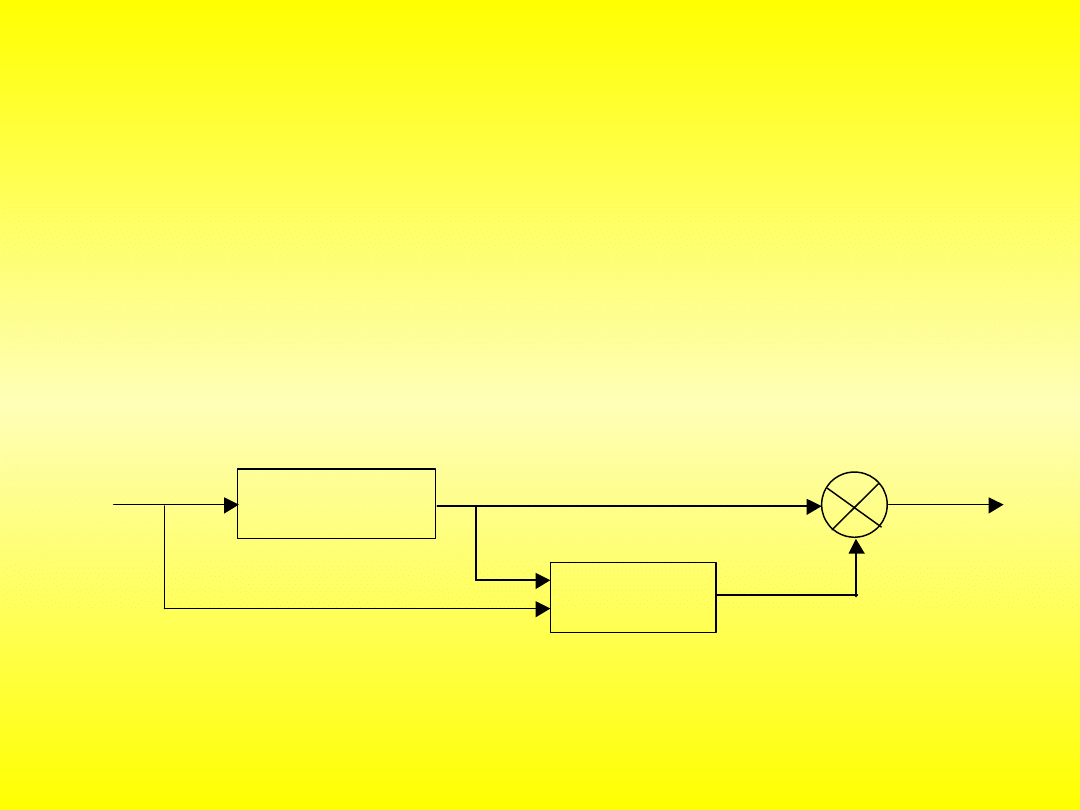
Rys. 9.5. Schemat blokowy układu uczącego się

 

Zastosowanie sieci neuronowych do sterowania ruchem 
robota

Rozważony  będzie  przykład  sterowania  ruchem  dwóch  członów 

wykonawczych  robota  przegubowego,  sterowania  opartego  o  zasady 
działania  układów  biologicznych  i  wykorzystującego  warstwowe  sieci 
neuronowe.  Zadaniem  układu  będzie  kompensacja  błędów  trajektorii  ruchu, 
które  mogą  być  spowodowane  wpływem  warunków  rzeczywistych,  poprzez 
“nauczenie się” niezbędnych poprawek, określonych różnicami

 



1

 = 

1

 - ’

1

    oraz    

2

 = 

2

 - ’

2

                                           (10.3)

gdzie: 1 ,2 - rzeczywiste wartości przemieszczeń kątowych, odpowiednio dla pierwszej, i 
drugiej pary kinematycznej, 1, 2, - teoretycznie obliczone wartości przemieszczeń

.

Sieć

neuronowa

Układ sterowania

robota



1

’    

2

’

x    y



1

    

2

 

1

    

2

 

 

Współrzędne  prostokątne  x,  y  punktu  końcowego  (docelowego) 

ruchu  są  wprowadzone  do  układu  sterowania  ruchem  robota,  a  jego 
zadaniem jest wygenerowanie takich wartości sygnałów, aby kąty ustawienia 
ramion  1  ,2  dokładnie  odpowiadały  punktowi  o  współrzędnych  x,  y. 
Przekształcenia 

obliczane 

przez 

sterownik 

robota 

określone 

są 

zależnościami: 





































c

 

-

 

l 

l

s

 

l

arctg

x

y

arctg

2

1

2

1



















c

s

arctg

2

2

1

2
2

2

1

2

2

2

l 

l 

2

l 

-

 

l 

-

 

 y

+

 

x

cos

s







2

sin

c





gdzie: l

1

, l

2

 - długości ramion.

 

Uczenie  sieci  polegało  na  ustaleniu  wag  połączeń  dla  zbioru 

punktów x, y w przestrzeni roboczej robota. Stwierdzono, że uczenie sieci 
nawet na jednym tylko punkcie powoduje poprawę dokładności o ok. 50%, 
natomiast  po  8  punktowej  serii  uczącej,  dokładność  pozycjonowania 
wzrastała  10  -  krotnie.  Bardzo  krótki  czas  uczenia  pozwala  na  szybkie 
dostosowanie  urządzenia  do  zmieniających  się  warunków  pracy  - 
przykładowo w przypadku niewielkich przesunięć podstawy robota. 

 

 

Zastosowanie sieci neuronowych do rozpoznawania 
obrazów

Obraz  z  kamery  jest  przetwarzany  na  mapę  bitową,  a  w  dalszym 

etapie  przy  pomocy  sieci  neuronowych  następuje  rozpoznanie  obiektu  na 
podstawie  jego  cech  charakterystycznych  i  sklasyfikowanie  do  odpowiedniego 
typu  obiektów.  Przy  układach  scalonych  sprawdza  się  też,  czy  został 
wmontowany  wcześniej  określony  typ  układu  oraz  czy  też  nie  został  on 
obrócony przy montażu o kąt 180

0

 .

Kamera  TV  która  zapisała  ten  obraz  znajdowała  się  w  stałej 

odległości  od  analizowanych  obiektów,  znajdujących  się  na  stanowisku 
oświetlanym  przez  lampę  halogenową.  Uzyskany  obraz  ma  256  poziomów 
jasności i wymiary 512 x 512 pikseli.

 

 

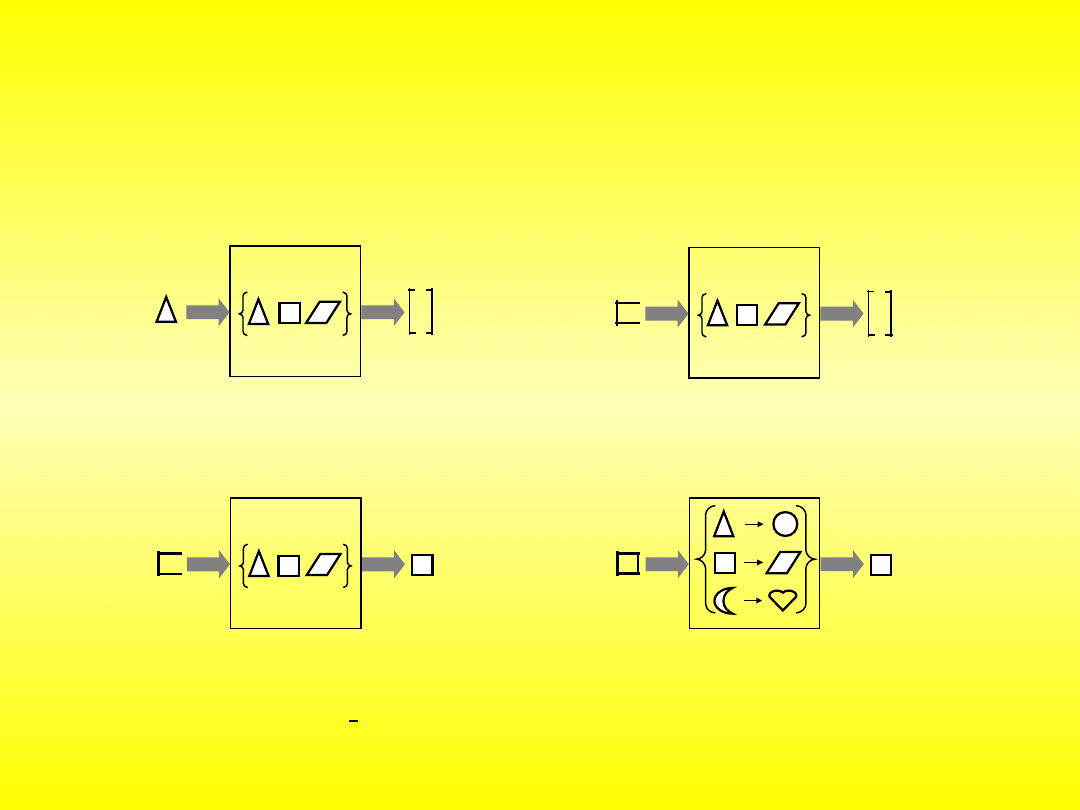
Zadania sieci neuronowej

 klasyfikacja i rozpoznawanie 

obraz 

wejściowy

numer 

klasy

0
1

obraz 

wejściowy

1
0

numer 

klasy

 asocjacja

autoasocjacja

heteroasocjacja

 wykrywanie grup 

 optymalizacja

obraz 

wejściowy

numer 

klasy

niekompletny 

kwadrat

kwadrat

obraz 

wejściowy

numer 

klasy

niekompletny 

kwadrat

kwadrat

 

 

W pierwszym etapie obraz zostaje poddany procesowi binaryzacji. 

Istotą  jest  przypisanie  każdemu  z  pikseli  obrazu,  jednego  z  dwóch 
poziomów  jasności.  W  tym  przypadku  w  grę  założono  poziomy  0  i  255 
odpowiadające  odpowiednio  barwom  czarnej  i  białej.  Aby  przypisać 
pikselom  odpowiedni  poziom  jasności  musi  być  zdefiniowana  uprzednio 
wartość  progowa. Od niej zależy to, czy na pozyskanym z kamery obrazie 
poziomy jasności pikseli będą znajdowały się poniżej czy powyżej wartości 
progowej.  Wynikiem  procesu  binaryzacji  jest  zawsze  znaczna  redukcja 
informacji zawartej w obrazie. Zatem odpowiedni dobór wartości progowej 
jest bardzo istotny, ponieważ bez niej mogłyby zostać utracone w obrazie 
informacje,  bez  których  rozpoznanie  obiektu  stałoby  się  niemożliwe  do 
zrealizowania.    Po  zdefiniowaniu  wartości  progowej  w  tym  przypadku 
wszystkie piksele staną się czarne lub białe – rys. 10.9.

Rys. 10.9. Obraz układu scalonego po binaryzacji

 

 

 

W 

drugim 

etapie 

wstępnego 

przetwarzania, 

obraz 

zbinaryzowany poddawany jest segmentacji. W tym przykładzie ma to na 
celu  wydzielenie  z  obrazu  fragmentu  przedstawiającego  oznaczenia  na 
obudowie układu scalonego. 

Analizując  osiem  typów  układów  scalonych,  przy  podziale 

fragmentu  obrazu  na  cztery  równe  części  o  wymiarach  50  x  75  pikseli, 
otrzymano wzorcowe wartości cech dla każdego z sektorów zestawione w 
tabeli 10.1.

Typ

piksele

UCY7453

SN7406

N

UCY740

4

SN7403N UCY7417 UCY7438

UCA6410

UL1201

 sek. 1

83

759

0

570

109

332

99

8

 sek. 2

707

779

568

526

666

619

458

689

 sek. 3

706

467

604

835

775

428

698

702

 sek. 4

555

474

439

627

251

274

357

240

Tablica 10.1. Wzorcowe wartości cech różnych typów układów 

scalonych 

Otrzymane  w  ten  sposób  liczby  stanowią  dane  wejściowe,  na 

podstawie  których  można  skonstruować  zbór  treningowy  do  nauczania 
sieci  neuronowej  prawidłowej  realizacji  zadania  rozpoznawania.  Po 
ukończeniu  procesu  treningu  i  po  podaniu  na  wejścia  liczby 
odpowiadające białym pikselom w poszczególnych sektorach obrazu, sieć 
powinna  wskazać  do  której  z  uprzednio  określonych  klas  przynależności 
ten układ należy.

 

 

Dalej  pokazano  wyniki  przy  pracy  na  nieliniowej  sieci  neuronowej 

Hopfielda  składającej  się  z  trzech  warstw.  Warstwy  wejściowe  i  ukryte 
składają się z trzech neuronów, a warstwa wyjściowa ma osiem neuronów, co 
odpowiada  liczbie  klas  przynależności  rozpoznawanych  układów  scalonych. 
Ten  z  neuronów,  który  wykazuje  największą  wartość  sygnału  na  swoim 
wyjściu, wskazuje na klasę przynależności aktualnie rozpoznawanego układu 
scalonego.  Po  treningu  sieci,  w  przypadku  podziału  obrazu  układu  na  trzy  i 
cztery równe sektory, otrzymano różne wyniki rozpoznawania. 

Przy podziale na cztery sektory wyniki stu eksperymentów wykazały 

bezbłędne wytypowanie właściwej klasy przynależności układu – tab. 10.2.

Wyniki

UCY7453 SN7406N UCY7404 SN7403N UCY7417 UCY7438

UCA6410

UL1201

Trafne    100

    100

    100

    100

    100

    100

    100

   100

Błędn

e

     0

      0

      0

      0

      0

      0

      0

      0

Tablica 10.2. Wyniki rozpoznawania obrazów układów scalonych (podział obrazu na 4 

sektory) dla sieci trójwarstwowej

Inaczej  było  przy  podziale  na  trzy  sektory.  W  przypadku 

trójwymiarowej  przestrzeni  cech  opisującej  obrazy  rozpoznawanych 
układów  scalonych  pojawiły  się  pierwsze  błędy  procesu  rozpoznawania. 
Łatwo  więc  stwierdzić,  że  nie  należy  zbyt  zmniejszać  ilości  informacji  o 
danym obiekcie bo efekty są odwrotne od oczekiwanych.

Wyniki

UCY7453 SN7406N UCY7404 SN7403N UCY7417 UCY743

8

UCA6410

UL1201

Trafne    100

     98

     99

    100

     96

     99

    100

    98

błędn

e

     0

      2

      1

      0

      4

      1

      0

      2

Tablica 10.3. Wyniki rozpoznawania obrazów układów scalonych (podział obrazu na 3 

sektory) dla sieci trójwarstwowej

 

 

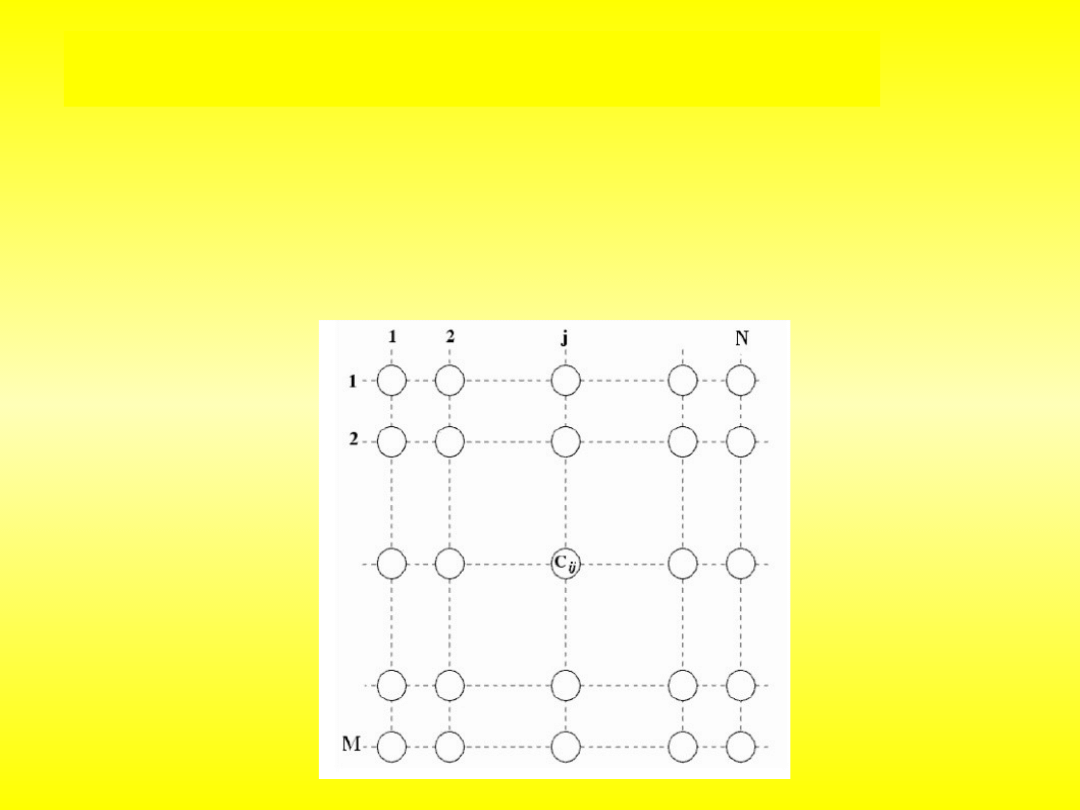
Jednym  z  narzędzi  automatycznego  planowania  trasy  przejazdu 

robota  mobilnego  są neuronowe  sieci  komórkowe  (ang.  CNN  -  Cellular 
neural  network)  z  wewnętrzną  strukturą  geometryczną  w  której 
neurony ułożone są w kształcie prostokąta. Położenie każdego neuronu 
w  sieci  opisane  jest  za  pomocą  dwóch  indeksów  (i,j),  które  określają 
numer wiersza i kolumny (rys.). 

Sieci komórkowe do planowania trasy dla robota 
mobilnego

 

 

W  sieciach  komórkowych  połączenia  synaptyczne  łączą  każdy  neuron 
jedynie z neuronami leżącymi w jego sąsiedztwie r: dla r = 1 każdy neuron 
ma  8  sąsiadów,  a  dla  r  =  2  –  24  sąsiadów  (rys.).  Podstawową  cechą  sieci 
komórkowych  jest  to,  że  układ  połączeń  synaptycznych  w  obrębie 
sąsiedztwa jest identyczny dla każdego neuronu.

 

 

W  metodzie  automatycznego  planowania  trasy  przejazdu  robota  mobilnego, 
zaproponowano następujący algorytm wykorzystujący sieć komórkową:
I.

Otoczenie robota dzielone jest na podobszary w kształcie kwadratu. 

Każdej  z komórek  przypisana  zostaje  odpowiednia  etykieta:  “wolna”  lub 
“zajęta”.
II.

Otoczenie  to  reprezentowane  jest  przez  sieć  komórkową,  w  której 

każda komórka odpowiada jednemu kwadratowi przestrzeni.
II.

Dwie  komórki  sieci  są  ze  sobą  połączone,  jeśli  odpowiadające  im 

obszary stykają się ze sobą, tzn. sąsiedztwo r = 1. 
IV.

Tworzona jest mapa dyfuzyjna:

a)   Inicjalizacja sieci – ustalenie wartości wag połączeń między sąsiadującymi 
komórkami sieci, zgodnie ze wzorem:

)

,

(

kl

ij

kl

ij

c

c

dist

a 

gdzie:,       to odpowiednie komórki mapy,       - waga łącząca komórkę       z        .

b)     Wagi połączeń między komórkami są proporcjonalne do odległości 
euklidesowej między środkami odpowiadających komórkom obszarów, tzn. 
wynoszą 1 lub      .
Ustalenie wartości sygnałów zewnętrznych        =

0  gdy komórka jest fragmentem przeszkody,
1  gdy komórka jest wolna.

c) Ustalenie początkowej wartości komórek =

T>>1, gdy komórka reprezentuje cel,
0, w przeciwnym przypadku

gdzie: T jest wartością początkową komórki reprezentującej cel.

ij

c

kl

ij

a

ij

c

kl

c

2

ij

u

 

 

d)    Proces dyfuzji – stan komórki w chwili  (t+1) obliczany jest zgodnie 
z zależnością: 





)

)

(

max(

),

(

max

)

(

)

1

(

ij

kl

kl

ij

ij

ij

a

t

x

t

x

t

u

t

x







Proces  dyfuzji  kontynuowany  jest,  aż  do  osiągnięcia  przez  sieć  stanu 
równowagi, gdy:

)

0

(

)

1

(







t

x

t

x

ij

ij

Postać  mapy  dyfuzyjnej  (rys.  6.15)  uzyskanej  przy  zastosowaniu 
powyższego  algorytmu  nie  zależy  od  położenia  robota,  a  jedynie  od 
położenia  celu  i  przeszkód.  W  sytuacji,  w  której  cel  lub  robot  jest 
otoczony  przez  przeszkody,  stan  komórki  zajętej  przez  robota  po 
uzyskaniu  przez  sieć  stanu  równowagi  wynosi  zero.  W  pozostałych 
przypadkach  optymalna  trasa,  którą  powinien  poruszać  się  robot  aby 
dojechać  do  celu,  składa  się  z  obszarów  uzyskanej  mapy  dyfuzyjnej  o 
rosnącej  wartości  odpowiadających  komórek,  tzn.  robot  powinien  w 
każdej  chwili  przemieszczać  się  do  sąsiedniego  obszaru  o  największej 
wartości.

 

 

Programy w wersjach bez instalatora i bibliotek

Nazwa programu

Nazwa pliku

Wielkość

Sieci neuronowe ART

SN_ART.exe

1.18 MB

Sieci neuronowe BAM

SN_BAM.exe

1.18 MB

Sieci 

neuronowe 

jednokierunkowe

BackPropagation + modyfikacje

SN_BP+.exe

1.23 MB

Sieci neuronowe CounterPropagation

SN_CP.exe

1.19 MB

Sieci neuronowe Hamminga

SN_HAM.exe

1.18 MB

Sieci neuronowe Hopfielda

SN_HOP.exe

1.18 MB

Sieci neuronowe RBF

SN_RBF.exe

1.29 MB

Sieci  neuronowe  jednokierunkowe  z  alg.
RLS

SN_RLS.exe

1.21 MB

Sieci neuronowe Kohonena - SOM

SN_SOM.exe

1.2 MB

 

 

Programy w wersjach instalacyjnych z bibliotekami

Nazwa programu

Nazwa pliku

Wielkość

Sieci neuronowe ART

setup_SN_ART.exe

5.82 MB

Sieci neuronowe BAM

setup_SN_BAM.exe

6.36 MB

Sieci 

neuronowe 

jednokierunkowe

BackPropagation + modyfikacje

setup_SN_BP+.exe

6.37 MB

Sieci neuronowe CounterPropagation

setup_SN_CP.exe

6.36 MB

Sieci neuronowe Hamminga

setup_SN_Hamming.exe

6.36 MB

Sieci neuronowe Hopfielda

setup_SN_Hopfield.exe

6.36 MB

Sieci neuronowe RBF

setup_SN_RBF.exe

6.42 MB

Sieci  neuronowe  jednokierunkowe  z  alg.
RLS

setup_SN_RLS.exe

6.37 MB

Sieci neuronowe Kohonena - SOM

setup_SN_SOM.exe

6.37 MB

 

 

Kody źródłowe programów

Nazwa programu

Nazwa pliku

Wielkość

Sieci neuronowe ART

SN_code_ART.zip

213 KB

Sieci neuronowe BAM

SN_code_BAM.zip

184 KB

Sieci 

neuronowe 

jednokierunkowe

BackPropagation + modyfikacje

SN_code_BP+.zip

225 KB

Sieci neuronowe CounterPropagation

SN_code_CP.zip

203 KB

Sieci neuronowe Hamminga

SN_code_HAM.zip

206 KB

Sieci neuronowe Hopfielda

SN_code_HOP.zip

216 KB

Sieci neuronowe RBF

SN_code_RBF.zip

220 KB

Sieci neuronowe jednokierunkowe z alg. RLS

SN_code_RLS.zip

219 KB

Sieci neuronowe Kohonena - SOM

SN_code_SOM.zip

217 KB

Źródła wszystkich programów

SN_paczka_code.zip

1.90 MB

 

 

Biblioteki i dane uczące

Nazwa programu

Nazwa pliku

Wielkość

Biblioteki Borland Delphi 7

SN_biblioteki.zip

1.86 MB

Dane uczące

SN_dane_uczace.zip

8 kB

Zestawy wszystkich programów

Nazwa programu

Nazwa pliku

Wielkość

Zestaw  wszystkich  programów  z
bibliotekami

SN_paczka_(z_bibliotekami).zip

6.41 MB

Zestaw wszystkich  programów  bez
bibliotek

SN_paczka_(bez_bibliotek).zip

4.55 MB

 

 

- na wejście neuronów konkurujących podajemy wektor x
- na podstawie sygnałów s

i

 wyłaniany jest zwycięzca neuron i*, dla którego 

wartość ta jest największa: 

۰ działanie:

- przyjmuje on stan 1, co umożliwia mu aktualizację dochodzących do niego wag 
- neurony przegrywające – stan 0, co uniemożliwia im aktualizację dochodzących 
do nich wag 
- aktualizacja wag zwycięzcy dokonuje się na podstawie reguły Kohonena: 





 

 





k

w

x

c

k

w

k

w

ij

j

ij

ij







1

- podajemy na wejście kolejny wektor uczący

 

 

 reguła gwiazdy wyjść (outstar) i gwiazdy wejść (intstar) 

۰ dopasowuje wagi neuronu do swoich sygnałów wejściowych 





 

 





k

w

x

cy

k

w

k

w

ij

j

i

ij

ij







1

۰ uczenie zgodnie z regułą Grossberga: 

c - stała uczenia, zazwyczaj z (0,1)
   -  gdy c=1   zapominanie wcześniej nauczonej wartości
  -  gdy c<1   wagi przyjmują uśrednione wartości dla wektorów uczących x





 

 





k

w

y

cy

k

w

k

w

ij

j

i

ij

ij







1

Instar 

Outstar

۰ uczenie: dobór wag, aby sygnały wyjściowe outstara były równe 
pożądanym przez neurony z nim współpracujące, czyli:

۰ tryb odtworzeniowy:   

x = w  y = 1

          

x prostopadły do w  y = 0

۰ tryb odtworzeniowy: aktywacja neuronu źródłowego powoduje 
wysłanie przez outstara pożądanego sygnału 

۰ Instar, Oustar: możliwe uczenie z nauczycielem i bez

 

 

 uczenie typu konkurencyjnego 

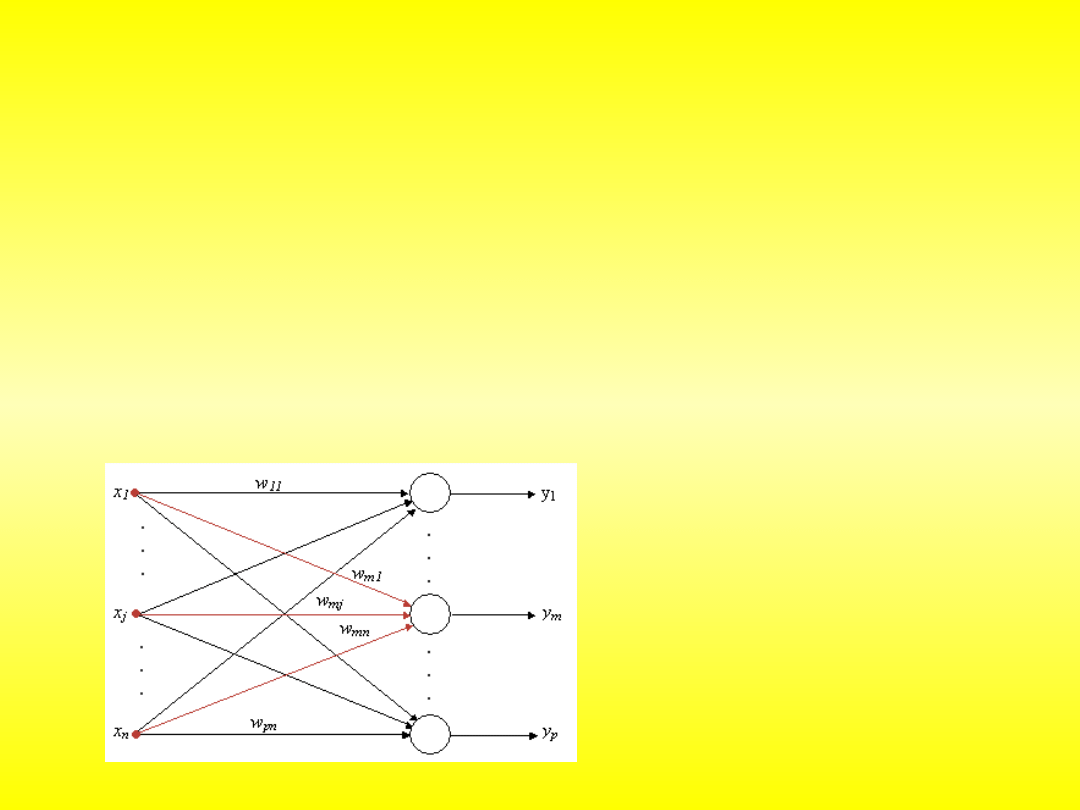
WTA – Winner Takes All: 
tylko jeden neuron może być aktywny, pozostałe – w spoczynku

۰ neurony współzawodniczą ze sobą, aby stać się aktywnymi

WTA 

۰ x

j

 – sygnały podawane na wejściu –  takie same dla wszystkich neuronów 

współzawodniczących
۰ zwycięzcą jest neuron, którego sygnał sumacyjny s

i

 jest najwyższy

۰ zwycięzca: y

i

 = 1, pozostałe neurony 0

WTM – Winner Takes Most: 
neuron wygrywający konkurencję uaktywnia się w sposób maksymalny 
i umożliwia częściowe uaktywnienie neuronów z nim sąsiadujących

 

 

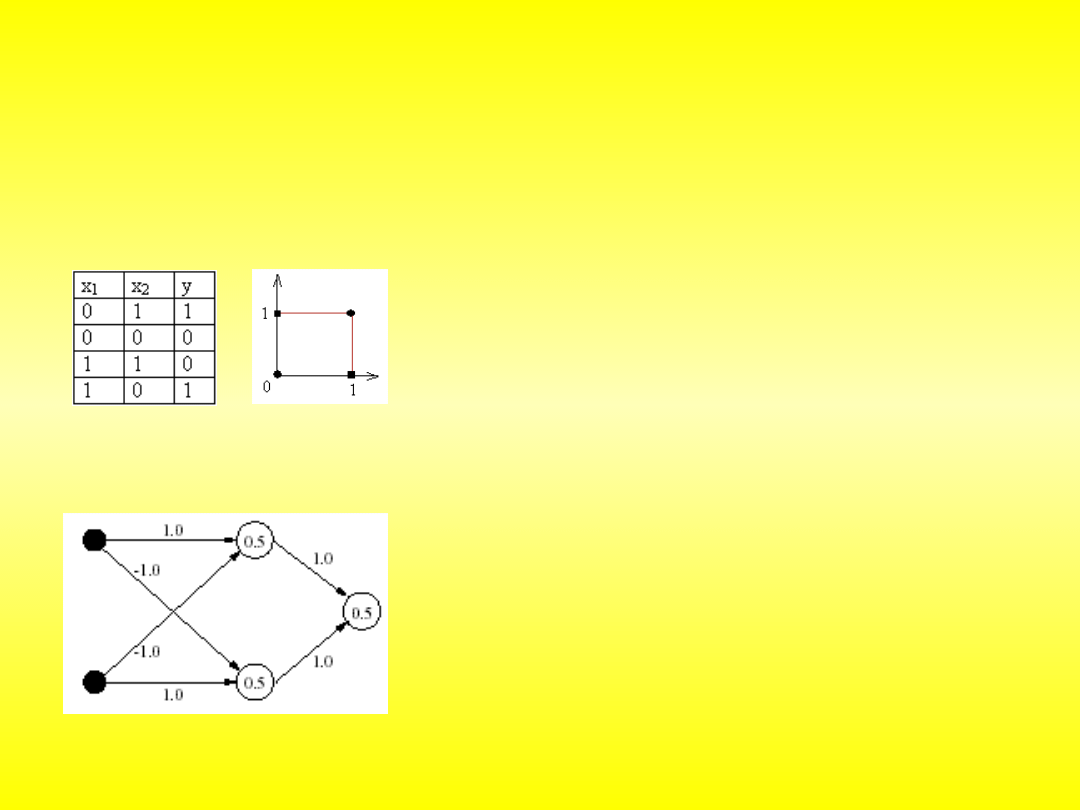
Problem XOR

۰ przykład odwzorowania, którego realizacji nie można przeprowadzić 
za pomocą jednowarstwowej sieci

۰ najmniej podobne do siebie konfiguracje powinny 
generować na wyjściu identyczne wartości

۰ problem rozwiązuje dodanie warstwy ukrytej:

- umożliwia ona tworzenie wewnętrznej 
reprezentacji wejściowych danych 

- podobieństwo stworzone przez neurony warstwy 
ukrytej stanowi wystarczające uzupełnienie, 
umożliwia właściwego przyporządkowanie

 

 

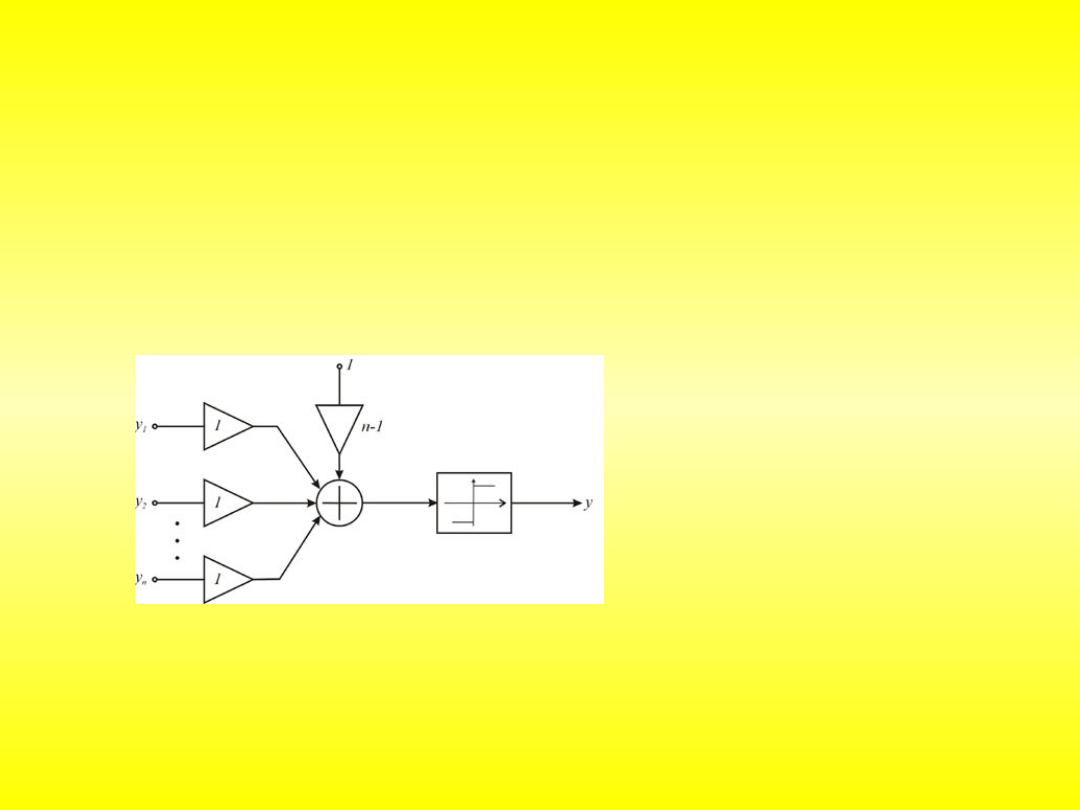
Najbardziej znane modele neuronów

 Perceptron 

 Sigmoidalny  
 Adaline  (ADAptive LInear NEuron) 

sieć typu or: n-1  y = 1, gdy choć jeden sygnał wejściowy y

i

 ma wartość 1

sieć typu and: 1-n  y = 1, gdy wszystkie sygnały wejściowe y

i

 mają wartość 1

sieć typu majority: 0  y = 1, gdy choć większość sygnałów wejściowych y

i

 ma wartość 1 

 Madaline  (Many ADAptive Linear NEuron) 

 

 

 ۰ uogólnienie - dla neuronów dyskretnych i ciągłych

 reguła Widrowa-Hoffa

  ۰ korekcja wag wg wzoru:





 

 

k

w

k

w

k

w

ij

ij

ij







1

 

   

 





k

y

k

d

k

x

k

w

i

i

j

ij







, gdzie

obie wymienione reguły: wykorzystują jedynie informację o aktualnej wartości 
sygnału wyjściowego neuronu oraz wartości zadanej tegoż sygnału

 reguła delta 





  

  

x

s

f

y

d

c

k

w

k

w

i

i

i

ij

ij

|

1









c – stała uczenia