Lech Pławecki, 1004.r.

1

Złożoność

obliczeniowa

Lech Pławecki, 1004.r.

2

Wstęp

Liczba elementarnych operacji, np.
porównań, dodawań, mnożeń, przestawień
elementów, wykonywanych przez algorytm,
podawana na ogół w zależności od długości
(ilości) danych. Na przykład liczba
porównań potrzebnych do znalezienia
najmniejszego (lub największego) elementu
w nieuporządkowanym ciągu jest o jeden
mniejsza od liczby elementów w tym ciągu.

Lech Pławecki, 1004.r.

3

Wstęp

Złożoność algorytmów jest określana jako liczba

wykonywanych porównań i zamian elementów,

wyrażona w zależności od liczby

porządkowanych elementów. Złożoność

najlepszych algorytmów sortowania jest

proporcjonalna do nlog

2

n, gdzie n jest liczbą

porządkowanych elementów.
Rzeczywisty czas działania algorytmu może być

podany dopiero dla konkretnych danych i

konkretnego komputera. Inną miarą jakości

algorytmu jest jego efektywność określana na

podstawie testowania szybkości jego działania

na przykładowych danych.

Lech Pławecki, 1004.r.

4

Rodzaje złożoności

• Złożoność pesymistyczna-

określa

złożoność w najgorszym przypadku.

• Złożoność oczekiwana.

czyli średnia

• Złożoność asymptotyczna

która

mówi o tym jak kształtuje się złożoność
dla dużych, granicznych rozmiarów
danych.

Lech Pławecki, 1004.r.

5

Notacje

Do określenia złożoności

asymptotycznej stosuje się
notacje O, Ω i Θ.Jeżeli złożoność
jest określona funkcją f(n) , to
notacje te określają pewną
funkcję g(n), zwaną „rzędem
złożoności”.

Lech Pławecki, 1004.r.

6

Notacja „Wielkie O”

Mówimy, że f jest co najwyżej rzędu g

gdy istnieją takie

stałe n

0>0

oraz c>0, że:

c*f(n)<=g(n)

n>n

o

Zapis f(n)=O(g(n))
Określenia „złożoność co najwyżej rzędu

O(f(n))” i „złożoność O(f(n))” ze sobą

równoznaczne

Lech Pławecki, 1004.r.

7

Notacja „Wielkie Omega”

Mówimy, że f jest co najmniej rzędu g
gdy istnieją takie

stałe n

0>0

oraz c>0, że:

c*f(n)>=g(n)

n>n

o

Zapis f(n)=(g(n))
Określenia „złożoność co najmniej rzędu
(f(n))” i „złożoność C ze sobą

równoznaczne

Lech Pławecki, 1004.r.

8

Notacja „Teta”

Mówimy, że f jest dokładnie rzędu g gdy istnieją takie

stałe

n

0>0

oraz c

1

>0 i c

2

=o, że:

c

1

*g(n)<=f(n)<C

2*g

(n)

n>n

o

Zapis f(n)=(g(n))
Można powiedzieć że f(n)=(g(n)) gdy f(n) jest jednocześnie

rzędu O(g(n)) i O(g(n))

Lech Pławecki, 1004.r.

9

Złożoność obliczeniowa i

jej ocena

•

proporcjonalna do liczby operacji

elementarnych

•

istotny składnik najszybciej rosnący ze

wzrostem rozmiaru problemu.

•

Stąd klasy złożoności obliczeniowej
algorytmów:

•

logarytmiczne — O(log

2

n)

•

liniowe — O(n)

•

wielomianowe — O(n

2

), O(n

3

), O(n

4

). . .

•

wykładnicze — O(2

n

),

•

inne — O(nlog2 n) , O(n!),

Lech Pławecki, 1004.r.

10

Złożoność obliczeniowa

i jej ocena

Lech Pławecki, 1004.r.

11

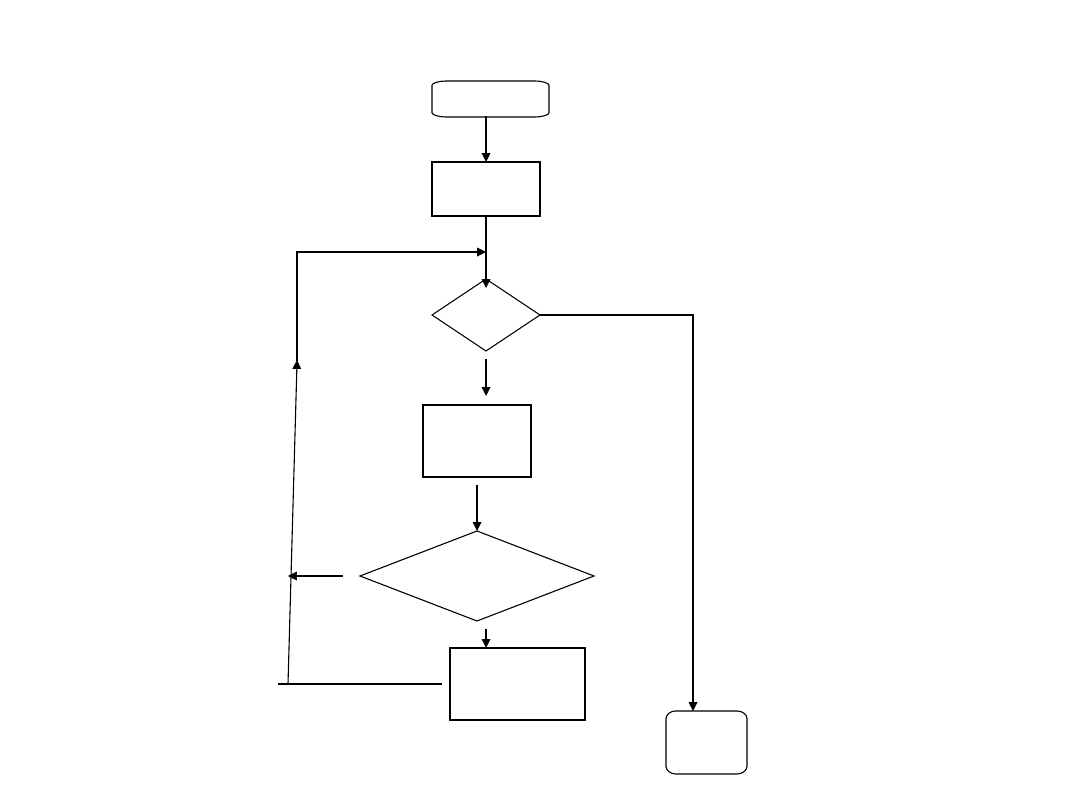
Przykład 1

Złożoność obliczeniowa algorytmu
poszukującego konkretnego elementu w
tablicy o n elementach.

i=0
WHILE i<n DO
BEGIN

i=i+1
IF x[i]=element THEN zwróć i

END

Lech Pławecki, 1004.r.

12

Przykład 1.

i=0

i<n?

x[i]=element

i=i+i

Zwróć i

tak

nie

nie

tak

stop

start

Lech Pławecki, 1004.r.

13

Przykład 1

Pętla wykonuje n obiegów, a w

każdym obiegu wykonuje się lub nie
wykonuje zwrócenie wartości i. A
więc złożoność będzie wynosić O(n).

Lech Pławecki, 1004.r.

14

Przykład 2

Złożoność obliczeniowa algo rymu wyświetlającego

elementy tablicy dwuwymiarowej.
for a:=1 to n do {pętla A}
for b:=1 to n do {pętla B}
Wypisz x(a,b);
Ile razy wykona się instrukcja Wypisz? Pętla A wykona

się n razy, a za każdym razem wykona ona pętlę B,

mającą również n przebiegów. Zatem Wypisz zostanie

wywołane n * n razy, czyli n

2

. Jeżeli wywołamy program

z liczbą 3 jako n, nasza procedura wywołana zostanie 9

razy, jeżeli n zwiększymy dwukrotnie - do 6, to liczba

wywołań wzrośnie czterokrotnie. Tak więc widzimy,że

algorytm ma większą złożoność obliczeniową niż

poprzedni algorytm - złożoność kwadratową O(n

2

).

Lech Pławecki, 1004.r.

15

Przykład 3

Złożoność obliczeniowa przeszukiwania dychotomicznego

(metoda bisekcji)

il:=pocz
ih:=kon
WHILE il<ih DO
BEGIN

ip:=część całkowita(il+ih)/2
IF x[ip]<szuk THEN il:=ip+1

ELSE IF x[ip]>szuk THEN ih:=ip-1
ELSE zwróć ip jako indeks szukanej wartości
END

Lech Pławecki, 1004.r.

16

Przykład 3

Twierdzenie: Złożoność obliczeniowa

algorytmu szukania dychotomicznego wynosi

O(log(n))
Dowód: niech il

i

i ih

i

będą wartościami tych

zmiennych w i-tym przebiegu pętli i niech
n

i

= il

i

– ih

i.

. Łatwo udowodnić,żę:

n

1

= n

n

i

=n

i-1

/ 2 czyli n

i

/ n

i-1

=1/2

tak więc postęp geometryczny o pierwszym

wyrazie n i ilorazie ½. Wobec tego :

n

i

=n*(1/2)

(i-1)

Lech Pławecki, 1004.r.

17

Przykład 3

Gdy n

i

osiągnie wartość 1 (koniec

szukania) mamy:

i –1 = log(n)

Widzimy więc, że ilość iteracji jest
proporcjonalna do logarytmu z ilości
elementów tablicy.

c.b.d.o.

Lech Pławecki, 1004.r.

18

Przykład funkcji silnia.

Definicja

rekurencyjna:

0!=1,
n!=n*(n-1)! gdzie

n>=0

Lech Pławecki, 1004.r.

19

Funkcja silnia

 silnia( n)
Begin
if (n=0) then return 1;
else

return n*silnia(n-1);

end

 

Lech Pławecki, 1004.r.

20

Przykład funkcji silnia.

Zakładamy, że najbardziej czasochłonną instrukcją

jest instrukcja porównania if. Przy takim
założeniu czas wykonania programu możemy
zapisać:

 

T(0)=t

c

T(n)=tc+T(n-1) , dla n>=1

Po rozpisaniu układu, dodaniu równań stronami i

redukcji składników otrzymujemy następującą
zależność:

T(n)=(n+1)*tc

Złożoność O(n)