TEORETYCZNE

PODSTAWY

INFORMATYKI

Prowadzący:

ppor. mgr inż. Mariusz

CHMIELEWSKI

e-mail:

[e-mail]

Temat 3:

Temat 3:

Analiza złożoności

Analiza złożoności

obliczeniowej algorytmów

obliczeniowej algorytmów

2

ppor. mgr inż. Mariusz CHMIELEWSKI

Przykłady praktyczne mierzenia

złożoności obliczeniowej

Przykład : Prosta pętla

for (i=sum=0; i<n; i++) sum+=a[i];

Powyższa pętla powtarza się n razy, podczas każdego jej przebiegu realizuje
dwa przypisania: aktualizujące zmienną „sum” i zmianę wartości zmiennej „i”.
Mamy zatem 2n przypisań podczas całego wykonania pętli; jej

asymptotyczna złożoność wynosi O(n).

asymptotyczna złożoność wynosi O(n).

3

ppor. mgr inż. Mariusz CHMIELEWSKI

Przykłady praktyczne mierzenia

złożoności obliczeniowej

Przykład : Pętla zagnieżdżona

for (i=0; i<n; i++) {

for (j=1, sum=a[0]; j<=i; j++)
sum+=a[j]; }

Na samym początku zmiennej „i” nadawana jest wartość początkowa.
Pętla zewnętrzna powtarza się n razy, a w każdej jej iteracji wykonuje
się wewnętrzna pętla oraz instrukcja przypisania wartości zmiennym „i”,
„ j”, „ sum”. Pętla wewnętrzna wykonuje się „i” razy dla każdego i e
{1,...,n-1}, a na każdą iteracje przypadają dwa przypisania:jedno dla
„sum”, jedno dla „j”. Mamy zatem
1 + 3n + 2(1+2+...+n-1) = 1 + 3n + n (n-1) = O(n) + O(n

2

) = O(n

2

)

przypisań wykonywanych w całym programie.
Jej

asymptotyczna złożoność wynosi O(n

asymptotyczna złożoność wynosi O(n

2

2

).

).

Pętle zagnieżdżone mają zwykle większą złożoność niż pojedyncze,

Pętle zagnieżdżone mają zwykle większą złożoność niż pojedyncze,

jednak nie musi tak być zawsze.

jednak nie musi tak być zawsze.

4

ppor. mgr inż. Mariusz CHMIELEWSKI

Przykłady praktyczne mierzenia

złożoności obliczeniowej

Analiza tych dwóch przypadków była stosunkowo prosta ponieważ
liczba iteracji nie zależała od wartości elementów tablicy.
Wyznaczenie złożoności asymptotycznej jest trudniejsze jeżeli
liczba iteracji nie jest zawsze jednakowa.

Przykład : Znajdź najdłuższą podtablicę zawierającą
liczby uporządkowane rosnąco.

for (i=0; len=1; i<n-1; i++) {

for (i1=i2=k=i; k<n-1 && a[k]<a[k+1]; k++,i2++);
if(len < i2-i1+1) len=i2-i1+1; }

=> Jeśli liczby w tablicy są uporządkowane malejąco, to pętla zewnętrzna
wykonuje się n-1 razy, a w każdym jej przebiegu pętla wewnętrzna
wykona się tylko raz. Złożoność algorytmu jest więc

O(n).

O(n).

5

ppor. mgr inż. Mariusz CHMIELEWSKI

Przykłady praktyczne mierzenia

złożoności obliczeniowej

Analiza tych dwóch przypadków była stosunkowo prosta ponieważ
liczba iteracji nie zależała od wartości elementów tablicy.
Wyznaczenie złożoności asymptotycznej jest trudniejsze jeżeli
liczba iteracji nie jest
zawsze jednakowa.

Przykład : Znajdź najdłuższą podtablicę zawierającą
liczby uporządkowane rosnąco.

for (i=0; len=1; i<n-1; i++) {

for (i1=i2=k=i; k<n-1 && a[k]<a[k+1]; k++,i2++);
if(len < i2-i1+1) len=i2-i1+1; }

Jeśli liczby w tablicy są uporządkowane rosnąco, to pętla zewnętrzna wykonuje się
n-1 razy, a w każdym jej przebiegu pętla wewnętrzna wykona się i razy dla i {1,...,n-1}.

Złożoność algorytmu jest więc

O(n

O(n

2

2

).

).

6

ppor. mgr inż. Mariusz CHMIELEWSKI

Przykłady praktyczne mierzenia

złożoności obliczeniowej

Analiza tych dwóch przypadków była stosunkowo prosta ponieważ
liczba iteracji nie zależała od wartości elementów tablicy.
Wyznaczenie złożoności asymptotycznej jest trudniejsze jeżeli
liczba iteracji nie jest
zawsze jednakowa.

Przykład : Znajdź najdłuższą podtablicę zawierającą
liczby uporządkowane rosnąco.

for (i=0; len=1; i<n-1; i++) {

for (i1=i2=k=i; k<n-1 && a[k]<a[k+1]; k++,i2++);
if(len < i2-i1+1) len=i2-i1+1; }

=> Z reguły dane nie są uporządkowane i ocena złożoności algorytmu jest
rzeczą niełatwą, ale bardzo istotną. Staramy się wyznaczy złożoność
w „przypadku optymistycznym”, „przypadku pesymistycznym” oraz
„przypadku średnim”.

7

ppor. mgr inż. Mariusz CHMIELEWSKI

Indukcja matematyczna



Podstawa indukcji –

dowód, że wyrażenie jest

prawdziwe dla n=1 (lub przyjętej wartości początkowej)



Hipoteza indukcji –

założenie, że wyrażenie jest

prawdziwe dla dowolnego n>=1 (lub innej wartości
początkowej)



Krok indukcyjny –

dowód, że jeżeli wyrażenie jest

prawdziwe dla n, to musi być prawdziwe dla n+1

1)

Na początku wykazujemy, że wyrażenie jest
prawdziwe dla n=1,

2)

Pokazujemy, że jeżeli jest ono prawdziwe dla
wybranej dodatniej liczby całkowitej n, musi być
prawdziwe dla n+1.

Przykład:

2

)

1

(

...

2

1











n

n

n

8

ppor. mgr inż. Mariusz CHMIELEWSKI

Sortowanie stabilne

Definicja:



Metoda sortowania jest stabilna, jeśli
zachowuje względną kolejność elementów o
jednakowych kluczach.

Oznaczenia : sortujemy tablicę:
ElemType a[n];
Definiujemy funkcję
replaceElements( x, y)
,która zamienia wartości dwóch elementów

9

ppor. mgr inż. Mariusz CHMIELEWSKI

Sortowanie bąbelkowe (bubblesort)

for (i = n-1; i>=1 ; i--)

for (j = 0 ; j<=i-1 ; j++)

if (a[j]>a[j+1])

replaceElements (a[j],a[j+1]);

Idea działania:
w i-tej iteracji, kolejne zamiany w zakresie a[0..i-1] powodują, że największy spośród elementów

w a[0..i-1] trafia na miejsce o indeksie "i-1"; iteracja jest powtarzana dla i=n-1,n-2,...,1.

Złożoność:

Operacjami dominującymi są porównania a[j]>a[j+1]. Jest ich:

(n-1) + (n-2) + . . . + 1 = n*(n-1) / 2

Zatem pesymistyczna złożoność czasowa wynosi
T(n) = 1/2 * n

2

– 1/2 * n

T(n) = 1/2 * n

2

+ O(1)

T(n) = O(n

2

)

Złożoność średnia: identyczna jak pesymistyczna.
Czyli: liczba porównań pesymistycznie i średnio ok. 1/2 n

2

.

Metoda jest stabilna.

10

ppor. mgr inż. Mariusz CHMIELEWSKI

Sortowanie przez wybieranie

for (i = 0; i< (n-1); i++){
min = i ;

for (j = i+1; j<=n-1; j++)
if (a[j] < a[min]) min := j;
replaceElements ( a[i], a[min] );

}

Idea:
w i-tym kroku znajdź najmniejszy element spośród a[i . .n-1] i zamień go z

elementem a[i]; powtarzaj ten krok dla i=0,...,n-2

 
Złożoność: identycznie jak dla metody bąbelkowej

T(n) = O(n

2

)

Czyli: zarówno w pesymistycznym, jak i średnim przypadku, liczba

porównań wynosi ok. 1/2 n

2

.

 Zalety:
Wykonuje tylko n-1 zamian (istotne dla długich rekordów) 
Sortowanie metodą selekcji nie jest stabilne.

11

ppor. mgr inż. Mariusz CHMIELEWSKI

Sortowanie przez wstawianie

for (i = 1; i< n; i++){

j = i-1;
tmp = a[i];
while ((j >= 0)&&(tmp < a[j])){
a[j+1]=a[j];

j=j-1;

}
a[j+1] = tmp;
}

Idea: W i-tym kroku wstaw element a[i] na właściwe miejsce w posortowanym fragmencie a[0 . . i-

1], wcześniej przesuwając wszystkie elementy większe od niego w tym fragmencie w prawo o

1; powstaje posortowany fragment a[0 . . i].

Złożoność pesymistyczna (ciąg posortowany malejąco na wejściu) identyczna jak dla poprzednich

przypadków.

Średnia dwukrotnie lepsza.

w przypadku pesymistycznym ok. 1/2 n

2

porównań

w przypadku średnim ok. 1/4 n

2

porównań.

Zalety:
1. Stabilność
2. Średnio dwukrotnie szybszy niż inne proste metody
3. Optymalny dla ciągów prawie posortowanych

12

ppor. mgr inż. Mariusz CHMIELEWSKI

Przykłady praktyczne mierzenia złożoności

obliczeniowej

Przykład :

Algorytm sortowania
Insertion-Sort(A)

1. for j:=2 to length[A]
2. do key:=A[j]
/* Wstaw A[i] w

posortowany

ciąg A[1..j-1].*/
3. i:= j-1
4. while i>0 i A[i] > key
5. do A[i+1] := A[i]
6. i:= i-1
7. A[i+1] := key

Przykład działania
algorytmu

5 2 4 6 1 3

2 5 4 6 1 3
2 4 5 6 1 3
2 4 5 6 1 3
1 2 4 5 6 3
1 2 3 4 5 6

13

ppor. mgr inż. Mariusz CHMIELEWSKI

Przykłady praktyczne mierzenia złożoności obliczeniowej

Przykłady praktyczne mierzenia złożoności obliczeniowej

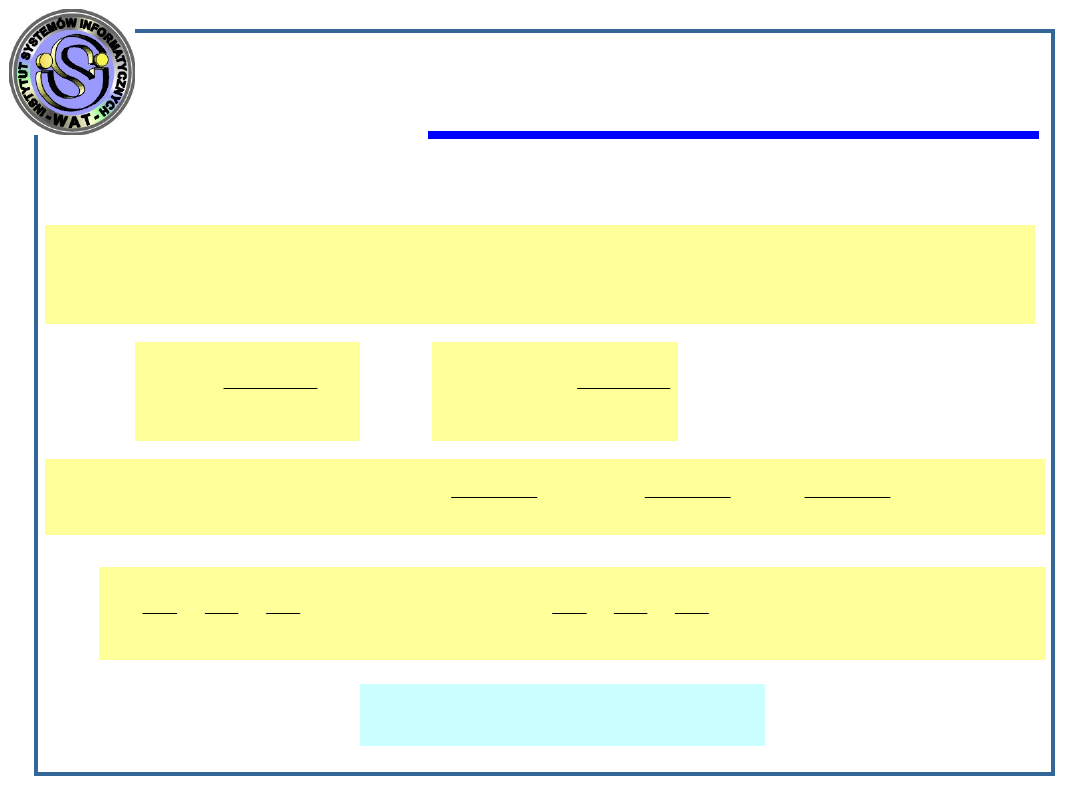
Insertion-Sort(A)

koszt

koszt

liczba wykonań

liczba wykonań

1.

for j:=2 to length[A]

c

1

n

2.

do key:=A[i]

c

2

n-1

3.

i:= j-1

c

3

n-1

4.

while i>0 i A[i] > key

c

4

5.

do A[i+1] := A[i]

c

5

6.

i:= i-1

c

6

7.

A[i+1] := key

c

7

n-1





n

j

j

t

2







n

j

j

t

2

)

1

(







n

j

j

t

2

)

1

(

14

ppor. mgr inż. Mariusz CHMIELEWSKI

Przykłady praktyczne mierzenia złożoności

obliczeniowej

)

1

(

)

1

(

)

1

(

)

1

(

)

1

(

)

(

7

2

6

2

5

2

4

3

2

1





































n

c

t

c

t

c

t

c

n

c

n

c

n

c

n

T

n

j

j

n

j

j

n

j

j

1

2

)

1

(

2











n

n

j

n

j

2

)

1

(

)

1

(

2











n

n

j

n

j



































































)

1

(

2

)

1

(

2

)

1

(

1

2

)

1

(

)

1

(

)

1

(

)

(

7

6

5

4

3

2

1

n

c

n

n

c

n

n

c

n

n

c

n

c

n

c

n

c

n

T

)

(

2

2

2

2

2

2

7

4

3

2

7

6

5

4

3

2

1

2

6

5

4

c

c

c

c

n

c

c

c

c

c

c

c

n

c

c

c





















































)

(

)

(

2

2

n

c

bn

an

n

T











15

ppor. mgr inż. Mariusz CHMIELEWSKI

Metoda „dziel i zwyciężaj”



Metoda polega na podziale realizacji problemu
na dwie lub większą liczbę mniejszych części (są
one realizacjami oryginalnego problemu).



Jeżeli potrafimy rozwiązać mniejsze realizacje to
poprzez scalanie możemy rozwiązać problem
główny – łączenie składowych rozwiązań.



Metoda „dziel i zwyciężaj” jest przykładem
podejścia zstępującego – rozwiązanie
głównego zadania uzyskiwane jest przez jego
rozkład na mniejsze elementy i szukania ich
rozwiązania.



Powiązanie metody „dziel i zwyciężaj” z rekurencją
(rekursją).

16

ppor. mgr inż. Mariusz CHMIELEWSKI

Wyszukiwanie binarne –

przykład zastosowania metody dziel i zwyciężaj



Opis werbalny algorytmu:

1.

Jeżeli x jest równy elementowi środkowemu to STOP

algorytmu, w przeciwnym przypadku:

2.

Dzielimy tablicę ba dwie podtablice o rozmiarze dwa

razy mniejszym od oryginalnej.

1.

Jeżeli x< od elementu środkowego to wybieramy

lewą podtablicę

2.

Jeżeli x> od elementu środkowego to wybieramy

prawą podtablicę

3.

Zwyciężamy (rozwiązujemy) podtablicę poprzez

określenie, czy x do niej należy. (W przypadku gdy

podtablica jest jeszcze za duża wykorzystujemy

rekurencję do jej dalszego podziału)

4.

Otrzymujemy rozwiązanie problemu tablicy na

podstawie rozwiązania podtablicy.

17

ppor. mgr inż. Mariusz CHMIELEWSKI

Wyszukiwanie binarne –

przykład zastosowania metody dziel i zwyciężaj



Formalny problem

Dane wejściowe: dodatnia liczba całkowita n, posortowana (niemalejąco) tablica

kluczy tab indeksowana 0,..,n-1, klucz x

Dane wyjściowe: położenie elementu x w tabeli tab

int seekBinary (int low, int high){
int mid;
if (low>high){
return 0;
}else {
mid = (low+high)/2;
if (x == tab[mid])
return mid;
else if (x<tab[mid])
return seekBinary(low,mid-1);
else if (x>tab[mid])
return seekBinary(mid+1,high);
}
}

18

ppor. mgr inż. Mariusz CHMIELEWSKI

Wyszukiwanie binarne –

przykład zastosowania metody dziel i zwyciężaj



Przykład:

10 13 15 20 31 43 56 67 87 100 120

10 13 15 20 31 43 56 67 87 100 120

tab

x =100

X>tab[mid]

Wybieramy prawą podtablicę

56 67 87 100 120

X>tab[mid]

Wybieramy prawą podtablicę

X==tab[mid]

Znaleziono klucz

100 120

19

ppor. mgr inż. Mariusz CHMIELEWSKI

Algorytm sortowania metodą scalania

Analizujemy pesymistyczną złożoność czasową – operacjami dominującymi są porównania wykonywane podczas

scalania.

Załóżmy najpierw, że n jest potęgą dwójki, n = 2

k

Analiza złożoności algorytmu "dziel i zwyciężaj" za pomocą równania rekurencyjnego na liczbę operacji

dominujących.

Tutaj:

T(n) = 0, jeśli n = 1

2 T(n/2) + n , jeśli n > 1 bo:



dwa podzadania wielkości n/2,



koszt podziału pomijalny (zero porównań) ,



koszt scalania to liczba porównań podczas scalania ciągów posortowanych, równa sumie ich

długości – tutaj n.

Rozwiązanie równania rekurencyjnego: na T(n) przez iterowanie tego równania i wywnioskowanie stąd jego

ogólnej postaci:
T(n) = 2 T(n/2) + n = 2 ( 2 T(n/4) + n/2) + n = 2 ( 2 ( 2 T(n/8) + n/4 ) + n/2 ) + n =

= 2 ( . . . . 2 ( 2 T(1) + 2 ) + 4 ) + . . . . . ) + n = n log n

Inna metoda: rozrysowując drzewo wywołań rekurencyjnych. Na każdym poziomie zagnieżdżenia rekurencji liczba

porównań wynosi n, a drzewo ma wysokość log n.

Dla dowolnego n (tzn. niekoniecznie będącego potęgą dwójki) wysokość drzewa wywołań nie przekracza log n + 1.
Liczba porównań w algorytmie sortowania przez scalanie wynosi zatem:

T(n) = n log n + O(n)

Wady metody:

potrzebuje pamięci roboczej rozmiaru O(n) (złożoność pamięciowa)
traci czas na przepisywanie elementów.

20

ppor. mgr inż. Mariusz CHMIELEWSKI

Mierzenie złożoności obliczeniowej

– przydatne funkcje

2

)

1

(

0









n

n

i

n

i

1

2

2

1

0











n

n

i

i

n

n

i

i

n

2

0



















1

1

1

0













x

x

x

n

n

i

i

3

)

1

)(

5

.

0

(

0

2











n

n

n

i

n

i

)

1

(

ln

1

1

O

n

i

n

i









21

ppor. mgr inż. Mariusz CHMIELEWSKI

Mierzenie złożoności obliczeniowej

– przydatne funkcje

 

O S Z A C O W A N I A :

J e ś li f () j e s t f u n k c j ą r o s n ą c ą , to :

















1

1

)

(

)

(

)

(

b

a

b

a

i

b

a

dx

x

f

i

f

dx

x

f

J e ś li f () j e s t f u n k c j ą m a le j ą c ą , to :

















b

a

b

a

i

b

a

dx

x

f

i

f

dx

x

f

1

1

)

(

)

(

)

(

22

ppor. mgr inż. Mariusz CHMIELEWSKI

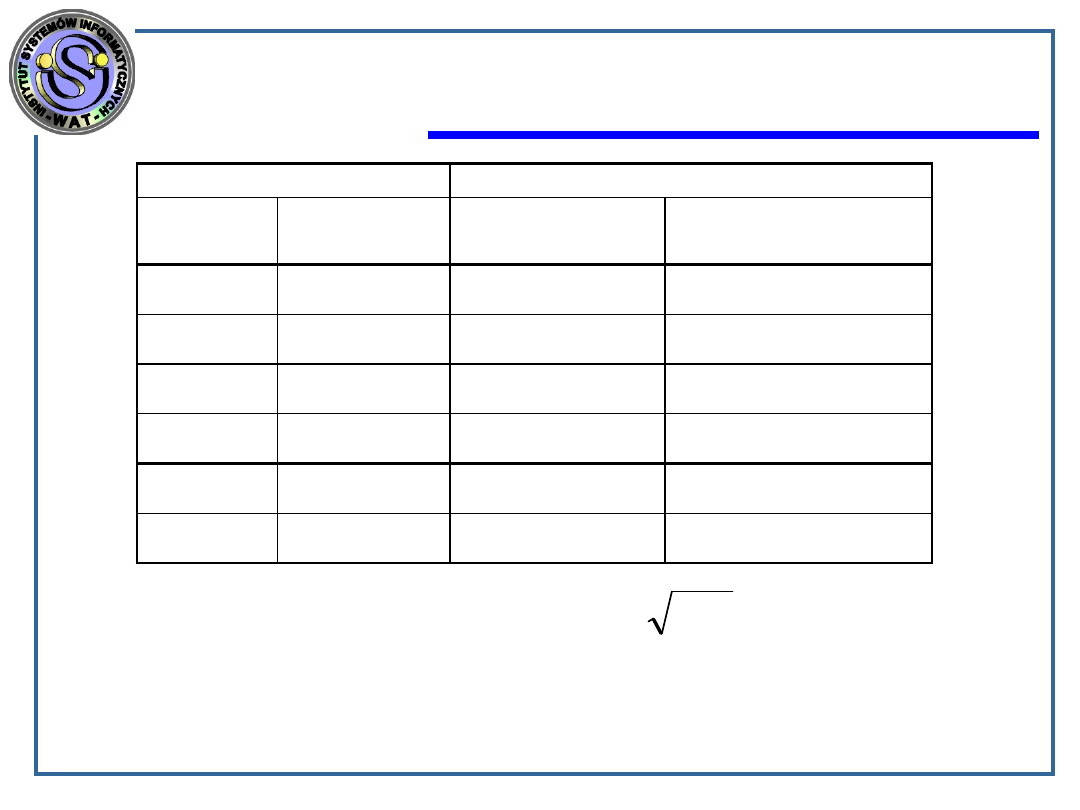
KLASY I TYPY FUNKCJI ZŁOŻONOŚCI

OBLICZENIOWEJ

Klasa funkcji

Typ funkcji

Przykłady

stała





n

e

n

2

sin





,

 

n

/

1



subliniowa

polilogarytmiczna





n

log

log



,





n

2

log



liniowa

 

n



,









n

n

n

/

1

1



quasi-liniowa





n

nlog



,





n

n

log

log



wielomianowa

kwadratowa

 

2

n



,



























2

n

superwielomianowa

 

n

n

lg



,

 

n

e



wykładnicza

 

n

2



,





n

n 3

2



niewielomianowa

superwykładnicza

 

n

n

2



,

 

n

n



23

ppor. mgr inż. Mariusz CHMIELEWSKI

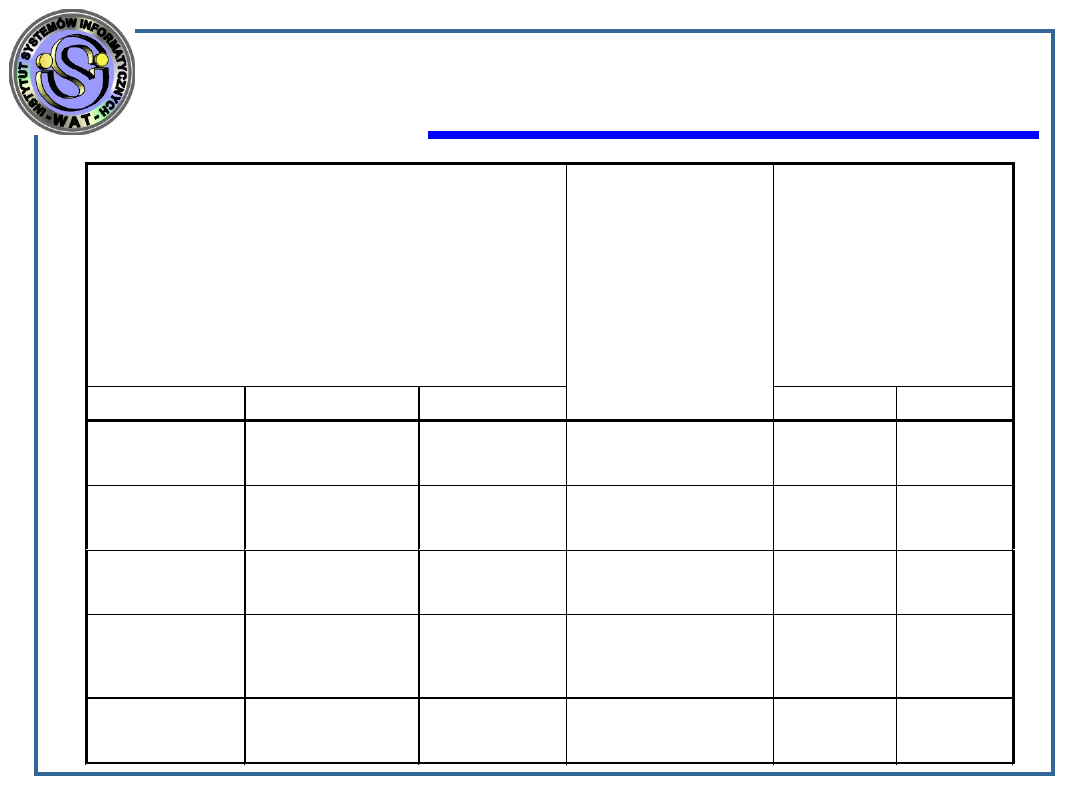
Wpływ wzrostu prędkości komputera na

maksymalny rozmiar zagadnienia, które można

rozwiązać w jednostce czasu

Algorytm

Maksymalny rozmiar zagadnienia

Symbol

Złożoność

przed wzrostem

prędkości

po 100-krotnym

wzroście prędkości

5

A

 

n



N

5

5

100N

4

A

 

2

n



N

4

10 N

4

3

A

 

3

n



N

3

4.64 N

3

2

A

 

5

n



N

2

3.5 N

2

1

A

 

n

2



N

1

6.64+N

1

0

A





n

nlog



N

0

0

100N dla

1

0



N

h

N 1

2

4

 ,





100

1

2

4

4



h

N

c



10

100

4





c

h

N

1

2

1



,

100

1

2

1

1







h

c

N



100

2

1



c

 c

1

=

lo

g

2

1

0

0

=

6

.6

4

24

ppor. mgr inż. Mariusz CHMIELEWSKI

Przykład postępu, jaki dokonał się w

dziedzinie projektowania algorytmów

badających planarność grafu

A lgo rytm

R o zm ia r

a na lizo w a neg o

gra fu

w przyp a dku

udo stęp nia nia

ko m putera na

o kres

Sym bo l

A uto r [ ro k] Z ło żo no ść

C za s o bliczeń

dla

ms

c

10



100



n

m inuty go dziny

1

A

K urato w sk i

[19 30]

6

cn

325 lat

4

8

2

A

G o ldstein

[19 63]

3

cn

2.8 go dz in

18

71

3

A

L em pel et al.

[19 67]

2

cn

100 sek und

77

6 0 00

4

A

H o pcro ft-

T arjan [197 1]

n

cn

2

log

7 sek und

643

24 6 73

5

A

H o pcro ft-

T arjan [197 4]

cn

1 sek unda

6 000

4

10

36 

25

ppor. mgr inż. Mariusz CHMIELEWSKI

Związek pomiędzy rzędem złożoności, stałą

proporcjonalności, rozmiarem danych i rzeczywistym

czasem obliczeń na minikomputerze i superkomputerze

n

C

r

a

y

-1

3

3

n [n

s

]

P

E

N

T

IU

M

IV

1

.6

G

H

z

1

9

5

0

0

0

n

[n

s

]

1

0

3

μ

s

3

0

0

μ

s

1

0

0

3

m

s

3

m

s

1

0

0

0

3

s

3

0

m

s

1

0

0

0

0

4

9

m

in

.

3

0

0

m

s

1

0

0

0

0

0

0

9

5

la

t

3

s

M

im

o

ż

e

a

lg

o

r

y

t

m

s

z

e

ś

c

ie

n

n

y

„

w

y

s

t

a

r

t

o

w

a

ł”

z

w

ię

k

s

z

y

m

im

p

e

t

e

m

,

d

r

u

g

i a

lg

o

r

y

t

m

(

lin

io

w

y

)

, m

a

ją

c

y

z

ło

ż

o

n

o

ś

ć

o

2

r

z

ę

d

y

n

iż

s

z

ą

(

O

(

n

)

w

s

t

o

s

u

n

k

u

d

o

O

(

n

3

)

)

,

„

d

o

g

o

n

ił g

o

”

i o

k

a

z

a

ł s

ię

s

z

y

b

s

z

y

d

la

100



n

.