Kwadrat łaciński
Kwadrat łaciński pozwala planować
doświadczenie na małej liczbie elementów
Analizę wariancji w układzie kwadratu
łacińskiego stosuje się często w
badaniach żywieniowych
Mamy t-obiektów czynnika
doświadczalnego (np. t-dawek
żywieniowych) i chcemy porównać jaki
wpływ wywiera ten czynnik na badaną
cechę (np. na przyrosty zwierząt)
Kwadrat łaciński
zwierzę
A
zwierzę
B
zwierzę
C
Okres 1
a
b
c
Okres 2
b
c
a
Okres 3
c
a
b
Kwadrat łaciński
Założenia:
- każdy z czynników: dawka, zwierzę i okres
musi mieć taką samą liczbę poziomów
- każdy poziom jednego czynnika musi
wystąpić dokładnie raz w każdym z
poziomów innego czynnika
zwierzę
A
zwierzę
B
zwierzę
C
Okres 1
a
b
c
Okres 2
b
c
a
Okres 3
c
a
b
Kwadrat łaciński
Czy zastosowany czynnik doświadczalny
(dawka) wpływa istotnie na badaną
cechę (przyrosty)?
Hipoteza zerowa:
H
0
: μ
1
= μ
2
= μ
3
= …. = μ
t
Hipoteza alternatywna:
H
A
: ~(μ
1
= μ
2
= μ
3
= …. = μ
t
)
Model liniowy dla układu
kwadratu łacińskiego
x
ij(k)
– obserwacja dla (k)-tego obiektu w
i-tym
wierszu oraz j-tej kolumnie
μ – średnia populacji
τ
(k)
– efekt czynnika doświadczalnego
α
i
– efekt wiersza
β
j
– efekt kolumny
e
ij(k)
– zmienność resztowa
)
(
)
(
)
(
ε
β
α
τ
μ
k
ij
j
i
k
k
ij
x
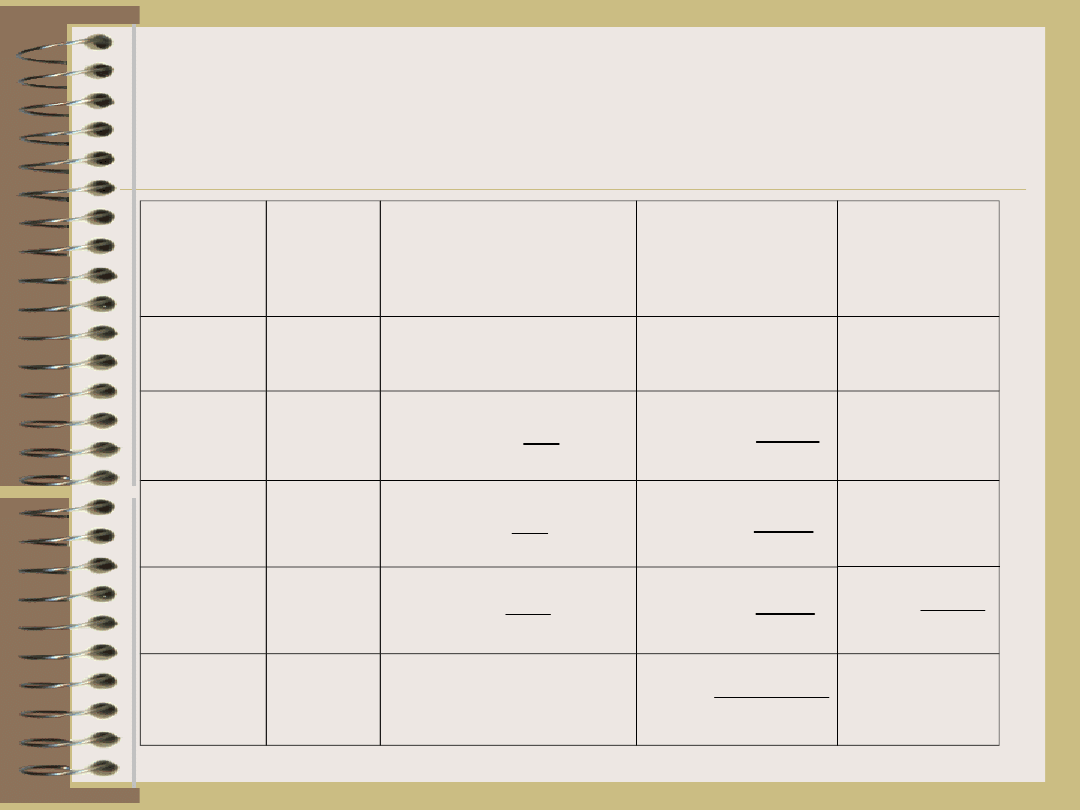
Tabela analizy wariancji
w
układzie kwadratu
łacińskiego
C
t
x
SS
j
K
2
C
x
SS
2
ij
T
C
t
x
SS
k
o
2
)
(
1
t
SS
MS
K
K
E
o
MS
MS
F
0
O
K
W
T
E
SS
SS
SS
SS
SS
)
2
)(
1
(
t
t
SS
MS
E
E
Źródło
zmiennoś
ci
df
stopnie
swobod
y
SS
suma kwadratów
MS
średni kwadrat
(wariancja)
F
0
statystyka
testowa
Ogólna
t
2
- 1
–
–
Między
wierszam
i
t - 1
Między
kolumna
mi
t - 1
Między
obiektam
i
t - 1
Resztowa
(t-1)(t-
2)
C
t
x
SS
i
W
2
1
t
SS
MS
W
W
1
t
SS
MS
o
o
)
(
)
(
)
(
ε
β
α
τ
μ
k
ij
j
i
k
k
ij
x
Analiza wariancji w układzie
kwadratu łacińskiego
Hipoteza zerowa weryfikowana jest za
pomocą testu F:
Jeśli F
0
> F
α
to odrzucamy H
0
Jeśli F
0
< F
α
to nie ma podstaw do
odrzucenia H
0
F
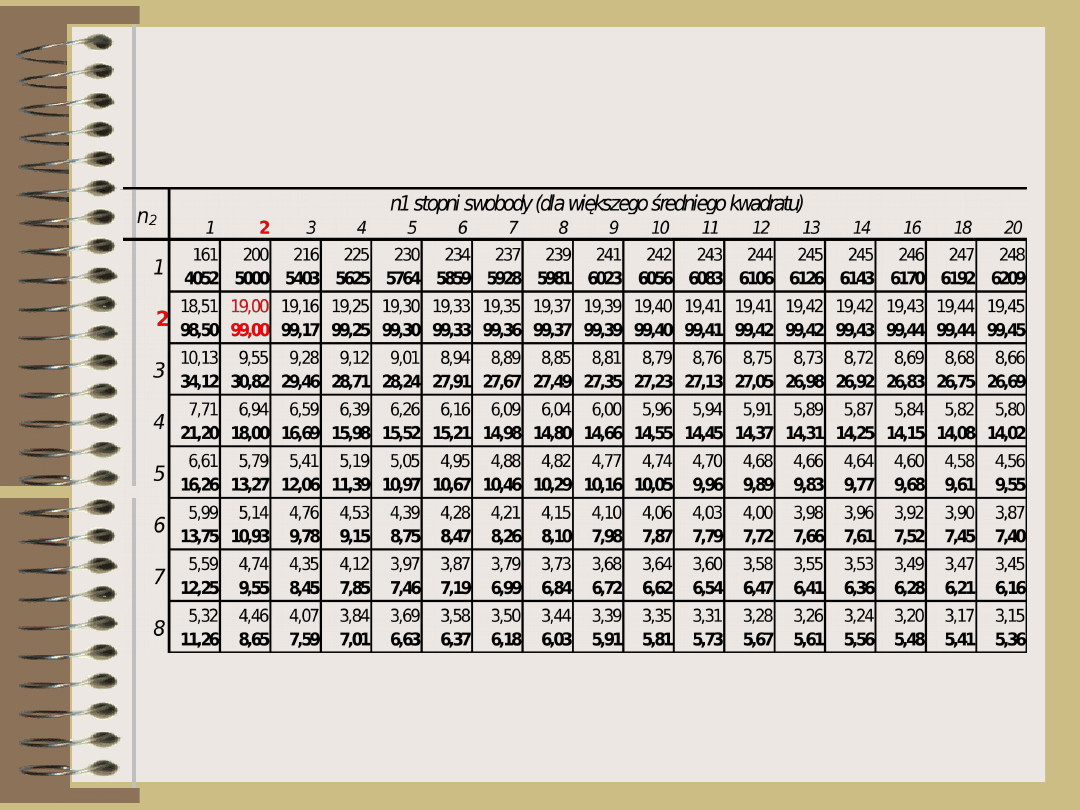
α
- tablicowa wartość testu F zależna od
poziomu istotności α oraz odpowiednich
stopni swobody:
df
o
= t-1 i df
E
= (t-1)(t-2)
E
o
MS
MS
F
0
Przykład
Badano przyrosty u tuczników żywionych
trzema różnymi dawkami pokarmowymi
(A, B, C). Doświadczenie przeprowadzono
w układzie kwadratu łacińskiego. Czy
rodzaj dawki pokarmowej ma istotny
wpływ na przyrosty u tuczników?
H
0
: μ
A
= μ
B
= μ
C
(tzn. tuczniki karmione każdą z trzech
dawek pokarmowych uzyskują średnio
takie same przyrosty)
H
A
: ~(μ
A
= μ
B
= μ
C
)
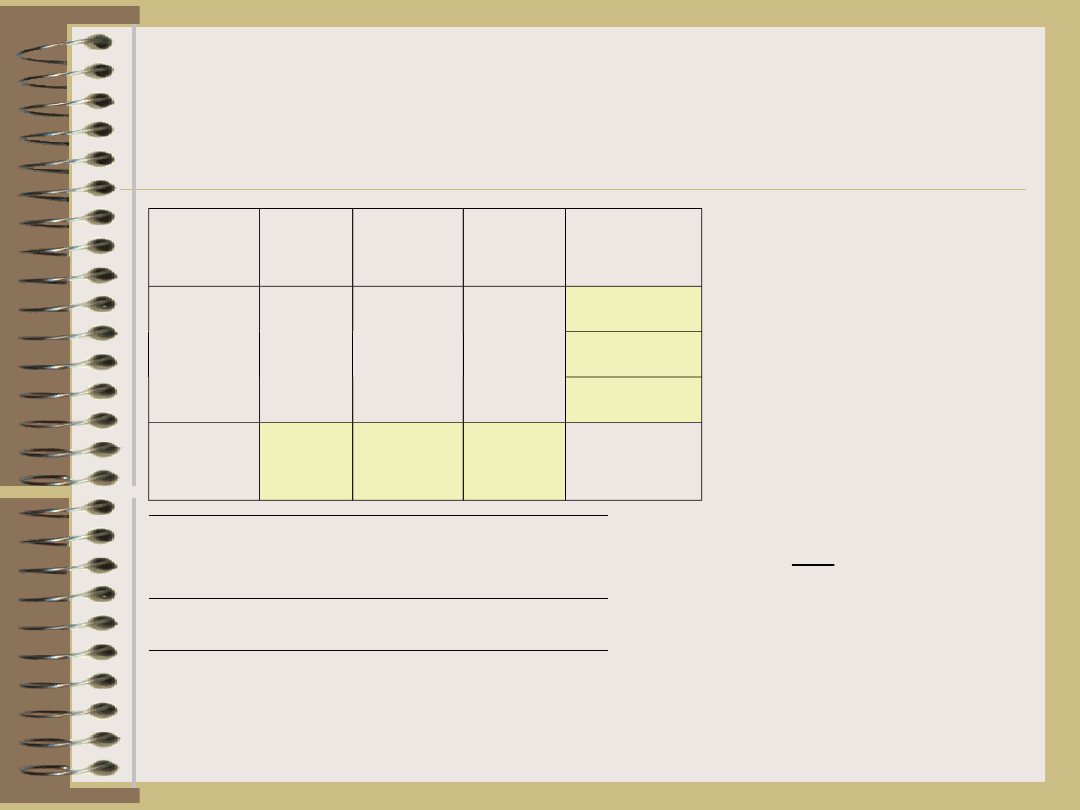
Przykład
0
,
27
ij
x
77
,
3
88
,
90
11
,
87
:
9
3
3
:
9
28
2
C
SS
C
poprawka
N
obserwacji
liczba
T
88
,
90
2
ij
x
1
2
3
Suma
(x
i
)
I
2,5
A
2,0
B
3,5
C
8,0
II
3,0
B
3,0
C
4,0
A
10,0
III
3,7
C
2,5
A
3,8
B
10,0
suma
(x
j
)
9,2
7,5
11,3 x
=28,0
zwierzę
okres
dawk
a
A
B
C
x
(k)
9,0
8,8
10,2
Przykład
08
,
0
69
,
3
77
,
3
)
38
,
0
42
,
2
89
,
0
(
77
,
3
38
,
0
11
,
87
49
,
87
3
48
,
262
3
2
,
10
8
,
8
0
,
9
42
,
2
11
,
87
53
,
89
3
58
,
268
3
3
,
11
5
,
7
2
,
9
89
,
0
11
,
87
88
3
264
3
0
,
10
0
,
10
0
,
8
2
2
2
2
2
2
2
2
2
E
o
K
W
SS
C
C
SS
C
C
SS
C
C
SS
okres
I
II
III
x
i
8,0
10,
0
10,
0
zwierz
ę
1
2
3
x
j
9,2
7,5
11,
3
dawka
A
B
C
x
(k)
9,0 8,8 10,
2
C=87,11
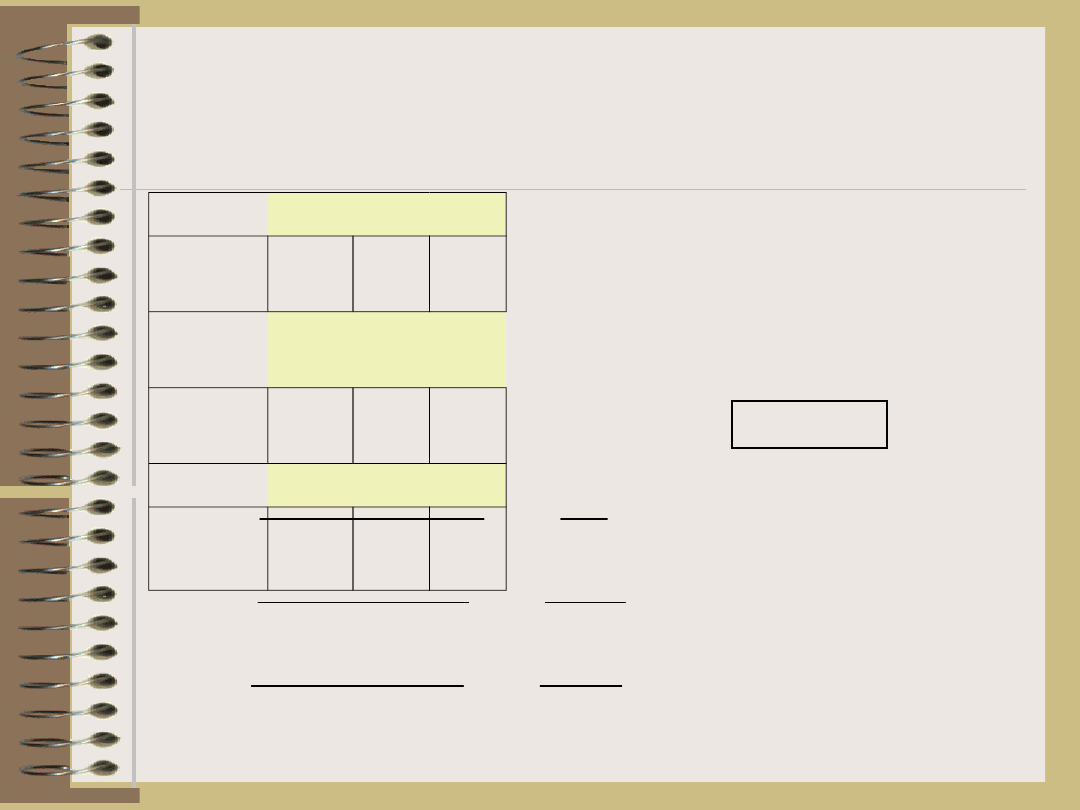
Tabela analizy wariancji
Źródło
zmiennoś
ci
df
stopnie
swobody
SS
suma kwadratów
MS
średni kwadrat
(wariancja)
F
0
statystyka
testowa
Ogólna
t
2
–
1=8
SS
T
=3,77
–
–
Między
wierszam
i
t – 1=2
SS
W
=0,89
MS
W
=0,445
Między
kolumna
mi
t – 1=2
SS
K
=2,42
MS
K
=1,21
Między
obiektami
t – 1=2
SS
o
=0,38
MS
o
=0,19
Resztowa
(t-1)(t-
2) = 2
SS
E
=0,08
MS
E
=0,04
75
,
4
04
,
0
19
,
0
0
F
Tablice F
Analiza wariancji
dawk
a
A
B
C
9,0
8,8
10,2
średnie
3,0
2,93
3,4
3,11
ij
x
i
x
x
F
0
< F
0,05
więc brak
podstaw
do odrzucenia H
0
Brak podstaw do odrzucenia H
0
na poziomie
istotności α=0,05 oznacza, że między średnimi
przyrostami zwierząt karmionych trzema
dawkami (porównywanymi obiektami czynnika
doświadczalnego) nie występują statystycznie
istotne różnice (średnio przyrosty są podobne,
niezależnie od zastosowanej dawki)
F
0
=4,75
F
0,05
=1
9,0