1

ELEKTROTECHNIKA II

WYKŁAD I

prof. dr hab. inż. T. Niedziela

2

Układy trójfazowe

3

Literatura

1.

Bolkowski S

.:

Elektrotechnika

. Wydawnictwo

Szkolne i Pedagogiczne Spółka Akcyjna, Warszawa

1993.
2.

Bolkowski S

.:

Elektrotechnika teoretyczna

, Tom 1,

Teoria obwodów elektrycznych. Wydawnictwo

Naukowo – Techniczne, Warszawa 1986.
3. Goźlińska E. Maszyny elektryczne. Wydawnictwo

Szkolne i Pedagogiczne Spółka Akcyjna, Warszawa

1995r.
4.

Lucyk C.

Zasady energoelektryki

. Oficyna

Wydawnicza Politechniki Warszawskiej, Warszawa

2000.
5.

Lucyk C

.

Elektrotechnika podstawowa

, Warszawa

2006. –

http://www.it.pw.edu.pl

/-clucyk

Wprowadzenie

Wielkości

charakteryzujące sygnały

okresowe

1.

Wartością chwilową sygnału

nazywamy

wartość, jaką przyjmuje sygnał w danej chwili
(np. f(t), i(t), u(t)).
2.

Wartością średnią całookresową

sygnału (i(t),

u(t)) okresowego o okresie T nazywamy średnią
arytmetyczną tego sygnału obliczoną dla
jednego okresu T.

3.

Wartością skuteczną

sygnału okresowego o

okresie T nazywamy pierwiastek kwadratowy z
wartości średniej kwadratu sygnału obliczonej
dla jednego okresu T.

4.

Wartością wyprostowaną

nazywamy średnią z

modułu sygnału.

 

 





T

dt

t

f

T

t

f

0

1

 

 

t

f

dt

t

f

T

F

T

2

0

2

1







 





T

dt

t

f

T

F

0

1

5.

Współczynnikiem szczytu

(k

sz

) sygnału

okresowego nazywamy stosunek wartości
maksymalnej (szczytowej) sygnału do jego
wartości skutecznej F.

np:

6.

Współczynnikiem kształtu

(k

k

) sygnału

okresowego nazywamy stosunek wartości
skutecznej sygnału F do jego wartości średniej .

np:

 

F

m

F

sz

k 

U

u

u

sz

k

I

i

i

sz

k

max

,

max

,





 

t

f

F

k

k 

)

(

,

t

i

I

i

k

k



Współczynniki szczytu oraz kształtu prądu

i napięcia sinusoidalnego

gdzie: 

i,



u,

- faza początkowa odpowiednio

prądu i napięcia.

Wartości skuteczne:
Wartości wyprostowane:

 Stąd:

Współczynniki szczytu, oraz współczynnik kształtu

)

sin(

)

(

)

sin(

2

)

sin(

)

(

u

t

m

U

t

u

i

t

I

i

t

m

I

t

i































2

,

2

m

U

U

m

I

I





m

U

U

m

I

śr

I

I





2

,

2







2

2

2

2

)

(sin

2

2

max

)

(sin





















m

I

m

I

I

I

k

k

m

I

m

I

I

i

sz

k

8

Wstęp



EEnergia elektryczna

przy napięciu i prądzie

zmiennym

lepiej nadaje się do przesyłania na

duże odległości niż energia elektryczna przy
napięciu i prądzie stałym.



ZZatem wytwarzanie, przesyłanie i rozdzielanie

energii elektrycznej

aktualnie jest dokonywane

przy użyciu urządzeń prądu zmiennego.



SZ pośród wszystkich stosowanych w
elektrotechnice przebiegów zmiennych
najbardziej rozpowszechnione są

przebiegi o

zmienności sinusoidalnej

w czasie.

9

9

9

Podstawowe pojęcia

Układ wielofazowy

to zbiór obwodów elektrycznych,

w których działają napięcia źródłowe sinusoidalnie
zmienne o jednakowej częstotliwości, przesunięte
względem

siebie

w

fazie

i

wytwarzane

(zamontowane) w jednym źródle energii zwanym

prądnicą

lub

generatorem wielofazowym.

Poszczególne

obwody

prądnicy

wielofazowej

nazywamy

obwodami fazowymi

-

fazami

(według

(według

normy PN-90/E-01242 oznaczeniami faz są

normy PN-90/E-01242 oznaczeniami faz są

L

1

, L

2

, L

2

i

N

)

)

.

.

Początki uzwojeń kolejnych faz prądnicy oznaczamy

U1, V1, W1

, a końce faz

U2, V2, W2

.

10

W prądnicy trójfazowej rozróżniamy

STATOR

(nazywany stojanem) – w którym są umieszczone
uzwojenia, oraz

ROTOR

(

wirnik

)

pełniący rolę

magneśnicy

i wirujący ze stałą prędkością kątową.

Zasada działania prądnicy

polega na przecinaniu

polega na przecinaniu

trzech, przesuniętych przestrzennie (o kąt 2π/3),

trzech, przesuniętych przestrzennie (o kąt 2π/3),

uzwojeń

przez

stały

strumień

magnetyczny

uzwojeń

przez

stały

strumień

magnetyczny

wytworzony w wirniku.

wytworzony w wirniku.

Do wytwarzania napięć źródłowych w układzie
trójfazowym

służą

prądnice

trójfazowe

(generatory) .

W każdym

uzwojeniu fazowym indukuje się

napięcie źródłowe e sinusoidalnie zmienne

, przy

czym ze względu na symetrię układu i
przesunięcie przestrzenne uzwojeń o ten sam
kąt, w fazach indukują się napięcia o
jednakowych

amplitudach,

o

tej

samej

częstotliwości i przesunięte względem siebie o
1/3 okresu.

Równania napięć chwilowych

źródłowych (e

A

, e

B

,

e

C

)

wytwarzanych w prądnicy

trójfazowej mają postać:

11

11

sin

A

m

e

E

t

w

=

2

sin

3

B

m

e

E

t

p

w

�

�

=

-

�

�

�

�

2

sin

3

C

m

e

E

t

p

w

�

�

=

+

�

�

�

�

Równania napięć źródłowych (napięć
fazowych)

wytwarzanych w prądnicy

trójfazowej, można przedstawić również

w

postaci zespolonej

Napięcie źródłowe fazy B

opóźnia się o kąt

2π/3 względem napięcia źródłowego fazy A,
natomiast

napięcie źródłowe fazy C

wyprzedza

o 2π/3 napięcie źródłowe fazy A

natomiast

opóźnia się o kąt 2π/3 względem napięcia
źródłowego fazy B.

12

A

E

E

=

2

3

j

B

E

Ee

p

-

=

2

3

j

C

E

Ee

p

=

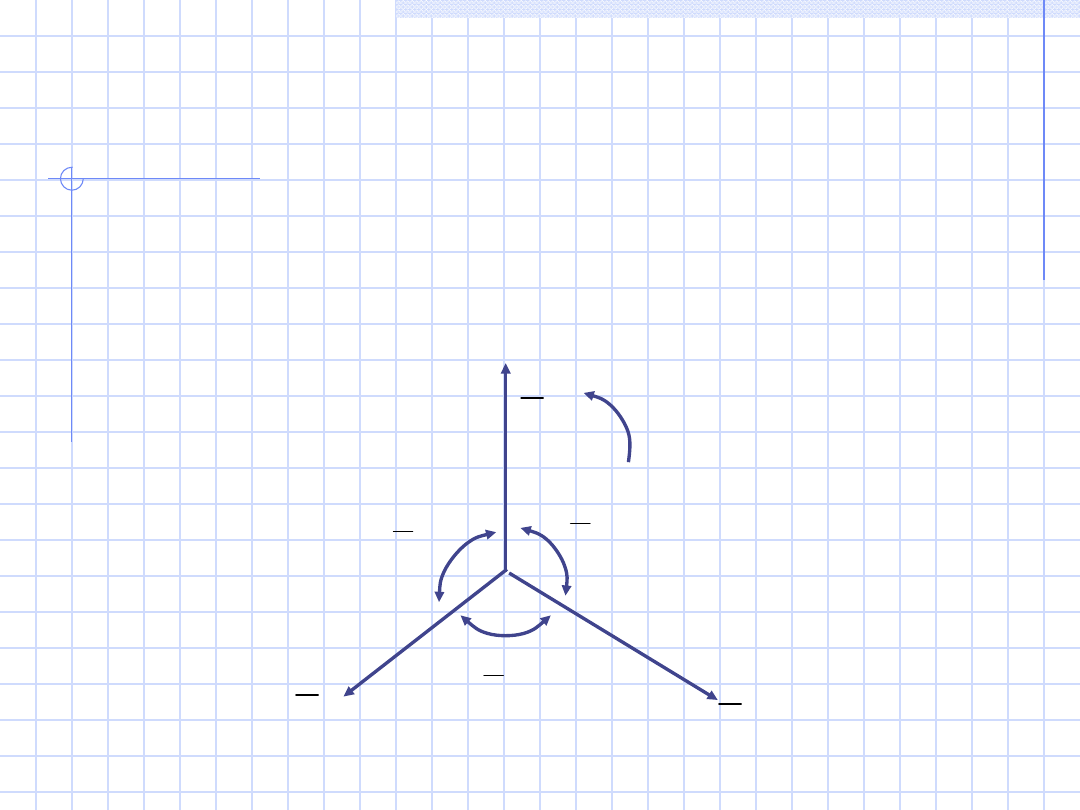
Układ napięć

będziemy nazywać

układem

symetrycznym zgodnym

(rys. 2a), gdy przy

(zaznaczonym na rys. 2a) dodatnim
kierunku wirowania, następstwo faz jest
zgodne, przez co rozumiemy następstwo A,
B, C.

13

л

3

2

л

л

A

E

C

E

B

E

Rys 2.

a



3

2

3

2

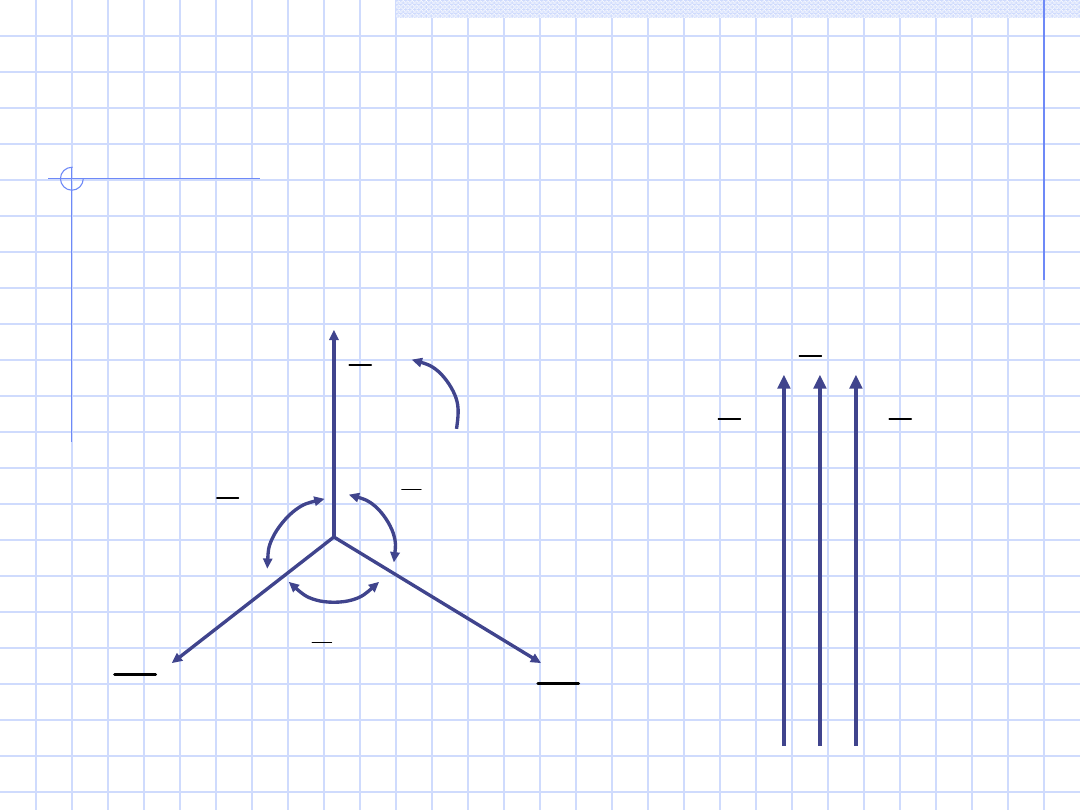
Układ napięć

nazywamy

układem

symetrycznym przeciwnym

, gdy przy

(zaznaczonym na rys. 2b) dodatnim kierunku
wirowania, następstwo faz jest przeciwne w
stosunku do przyjętego za zgodne, czyli A

,

C,

B.

Rys 2b

14

л

3

2

л

A

E

B

E

C

E

A

E

B

E

C

E

c)



3

2

3

2

Układ trójfazowy

został po raz pierwszy zastosowany

w 1889r.

Ważnym osiągnięciem

było wówczas

opracowanie

urządzeń

do

wytwarzania

i

przetwarzania energii prądu trójfazowego.

Zostały zbudowane, oprócz

prądnicy trójfazowej

,

transformator trójfazowy

oraz

silnik indukcyjny

trójfazowy

.

Silnik trójfazowy

okazał się najtańszym i bardzo

wygodnym przetwornikiem energii elektrycznej
w mechaniczną.

Również

przesyłanie energii elektrycznej

za pomocą

linii trójfazowych jest zarówno ze względów
technicznych jak i ekonomicznych aktualnie
niezastąpione.

15

Klasyfikacja układów

trójfazowych

Układ trójfazowy

Klasyfikacja układów
trójfazowych

Układ trójfazowy jest symetryczny

, jeśli prądnica trójfazowa

symetryczna jest połączona z odbiornikiem złożonym z

trzech identycznych impedancji zespolonych (Z)

.

Fazy prądnicy

oraz

impedancje odbiornika

można kojarzyć w

gwiazdę lub w trójkąt.

Prądnica

jest połączona w

gwiazdę

, jeśli końce uzwojeń (

U2,

V2, W2

)

trzech faz są ze sobą połączone we wspólny punkt

oznaczonym literą

N

, a początki uzwojeń (

U1, V1, W1

)

tworzą zaciski prądnicy.

18

Z punktu widzenia

sposobu połączenia źródła i odbiornika

można wyróżnić pięć różnych układów podstawowych:

-

układ trójfazowy

gwiazda - gwiazda trójprzewodowy

,

-

układ trójfazowy

gwiazda - gwiazda czteroprzewodowy

,

-

układ trójfazowy

trójkąt – trójkąt

,

-

układ trójfazowy

trójkąt –gwiazda

,

-

układ trójfazowy

gwiazda – trójkąt

.

19

Definicje podstawowe



Wspólny punkt trzech faz przy skojarzeniu w gwiazdę
nazywamy

punktem zerowym lub punktem neutralnym

.



Jeśli są połączone w gwiazdę fazy zarówno źródła, jak i
odbiornika, to ponadto mogą być ze sobą połączone punkty
zerowe.



PPrzewód łączący punkty zerowe źródła i odbiornika
nazywamy

przewodem zerowym lub przewodem

neutralnym

.



PPozostałe trzy przewody nazywamy

przewodami fazowymi

.

21

W układzie gwiazdowym napięcia

pomiędzy punktem

zerowym i końcem uzwojenia fazy

lub między

przewodem zerowym, a jednym z przewodów fazowych
nazywamy

napięciem fazowym

Napięcie

pomiędzy końcami faz

źródła lub odbiornika,

a

także napięcie pomiędzy przewodami fazowymi

nazywamy

napięciem międzyfazowym

Prąd płynący w przewodzie fazowym nazywamy

prądem przewodowym

22

W układzie

gwiazda—gwiazda

czteroprzewodowym

prąd płynący w

przewodzie zerowym (neutralnym)
nazywamy

prądem zerowym

lub

neutralnym i oznaczamy I

0

lub I

N

.

W układzie trójkątowym prąd płynący w
fazie źródła lub odbiornika nazywamy
prądem fazowym.

23

Układ trójfazowy gwiazda

– gwiazda

trójprzewodowy

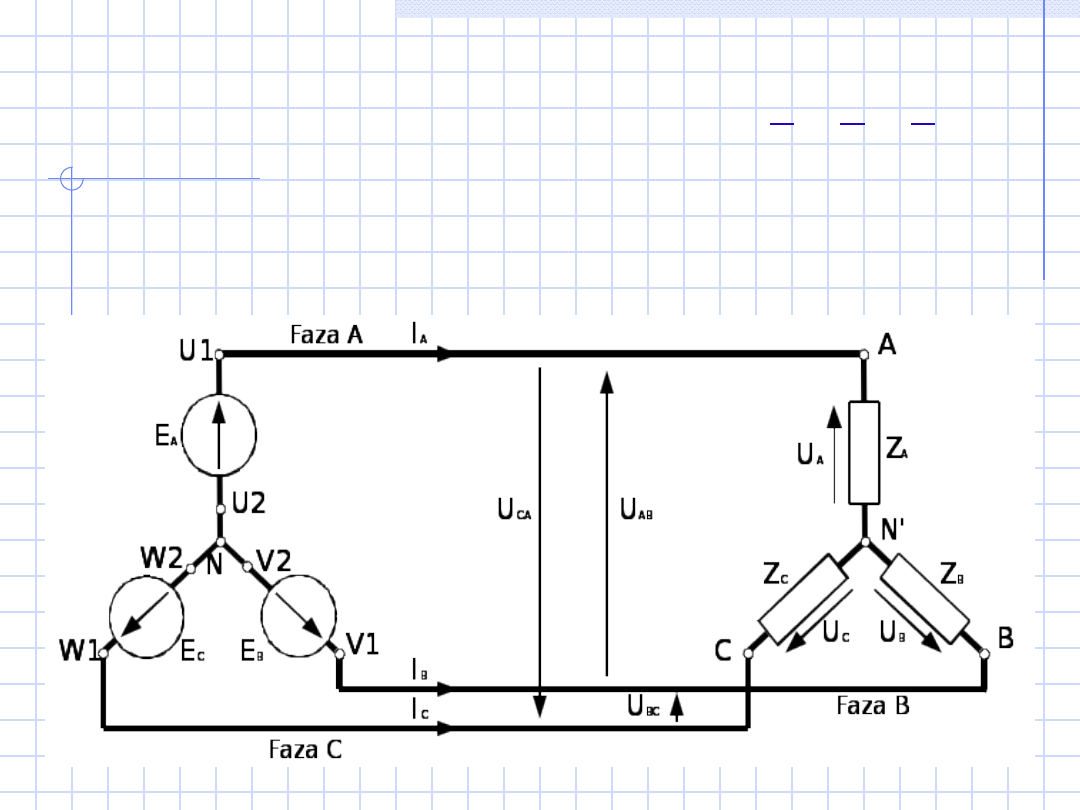
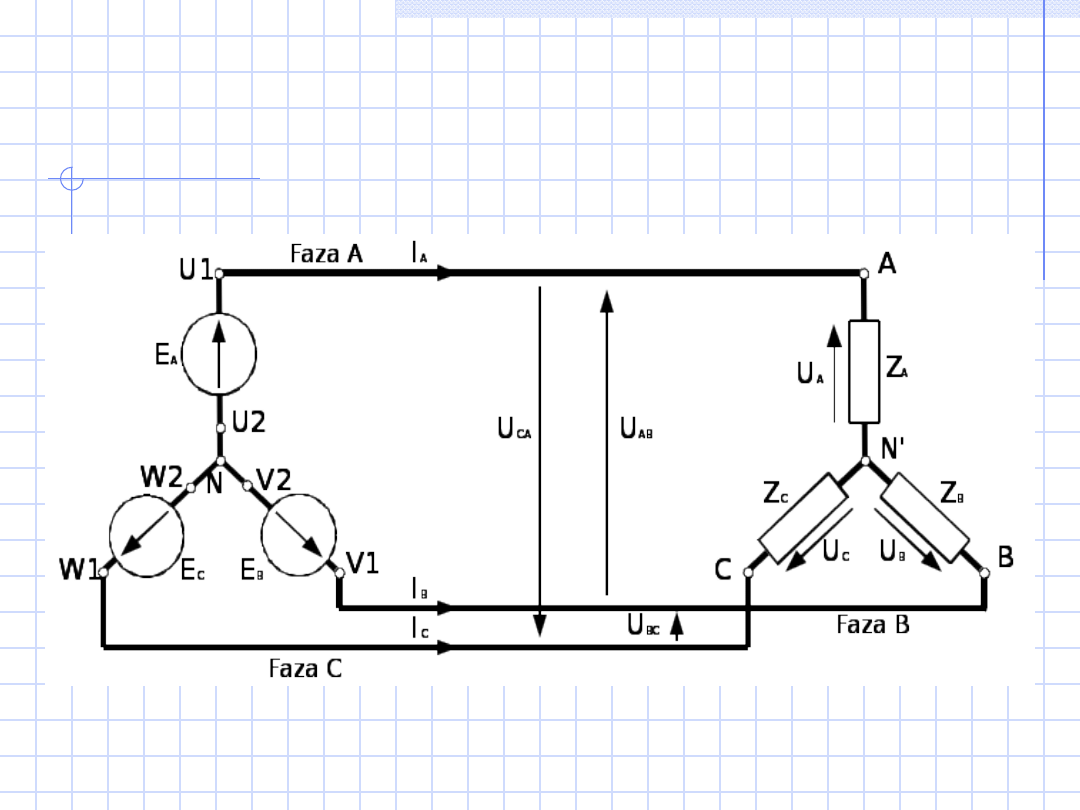
Odbiornik

można skojarzyć w gwiazdę łącząc jedne

(U2, V2, W2) końcówki impedancji (Z

A

, Z

B

, Z

C

) we

wspólny punkt, a trzy (U1, V1, W1) pozostałe
końcówki wyprowadzając na zewnątrz.

Układ trójfazowy gwiazda – gwiazda

trójprzewodowy

25

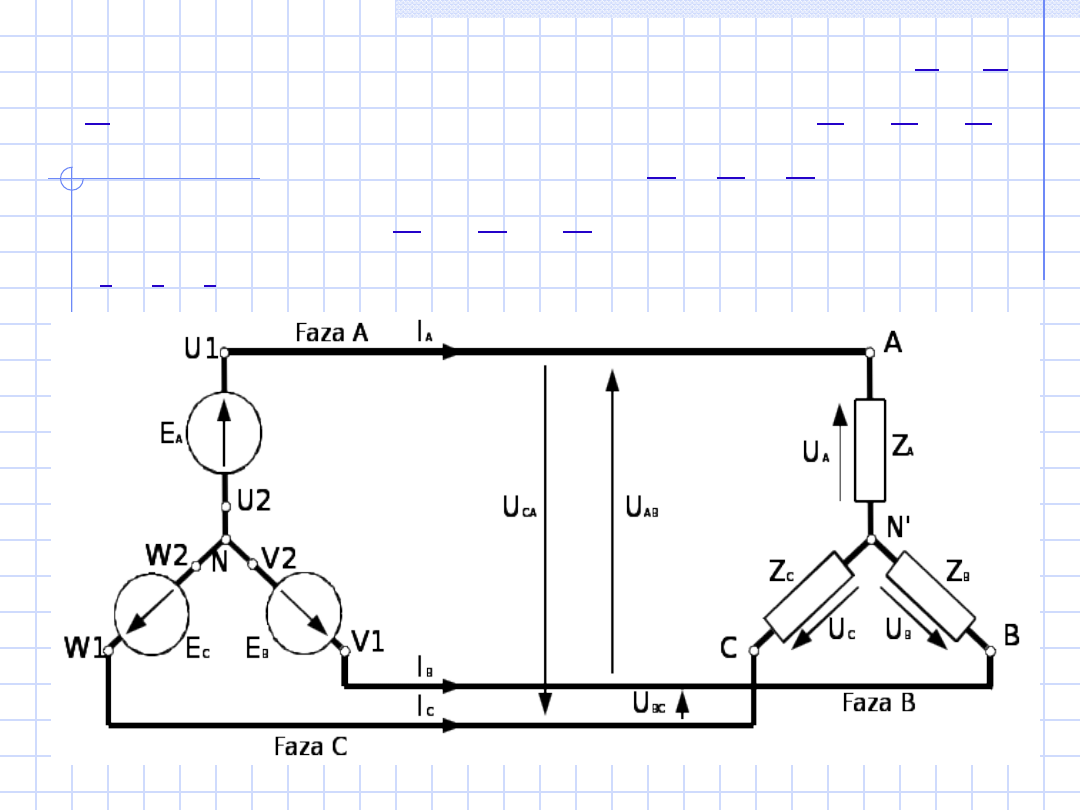
Napięcia fazowe źródła

oznacza się jako (E

A

, E

B

,

E

C

),

impedancje fazowe odbiornika

(Z

A

, Z

B

, Z

C

),

napięcia fazowe odbiornika

(U

A

, U

B

, U

C

),

napięcia

międzyfazowe

(U

AB

, U

BC

, U

CA

),

prądy przewodowe

(I

A

, I

B

, I

C

).

26

Układ trójfazowy gwiazda

– gwiazda

czteroprzewodowy

Jeśli połączymy bezimpedancyjnie lub przez
pewną impedancję (Z

NN

) punkty neutralne

źródła i odbiornika, to otrzymamy

układ

trójfazowy gwiazda – gwiazda
(niesymetryczny) czteroprzewodowy.

28

Układ trójfazowy gwiazda

– gwiazda (symetryczny)

czteroprzewodowy

30

Układ trójfazowy symetryczny (Z

A

= Z

B

= Z

C

= Z)

z odbiornikiem połączonym w gwiazdę z uziemionym

punktem neutralnym (

uproszczony schemat źródła

)

Układ trójfazowy

trójkąt – trójkąt

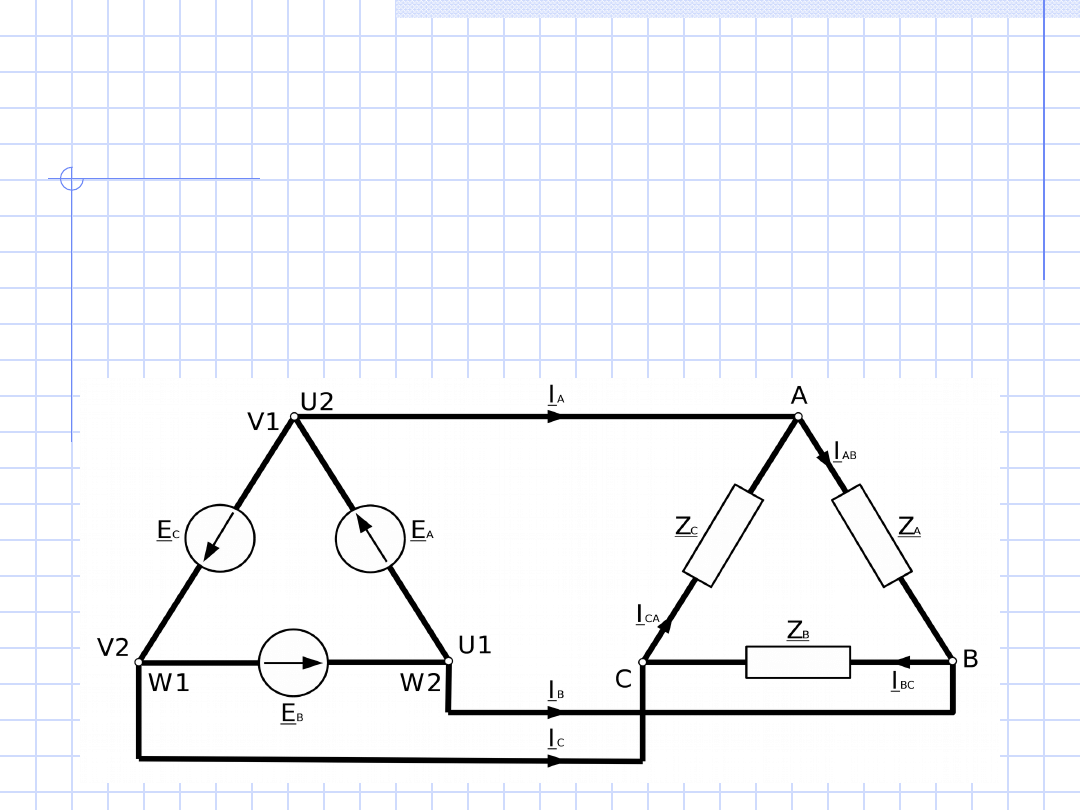
Jeżeli źródło jest połączone w trójkąt, a odbiornik
również w trójkąt, to mamy

układ trójfazowy trójkąt

– trójkąt.

Prądnica może być połączona w trójkąt

jeśli koniec

pierwszej fazy połączymy z początkiem drugiej (U2,
V1), koniec drugiej fazy z początkiem trzeciej, a
koniec trzeciej fazy z początkiem z początkiem
pierwszej.

Odbiornik też można połączyć w trójkąt

.

32

Układ trójfazowy

trójkąt – gwiazda

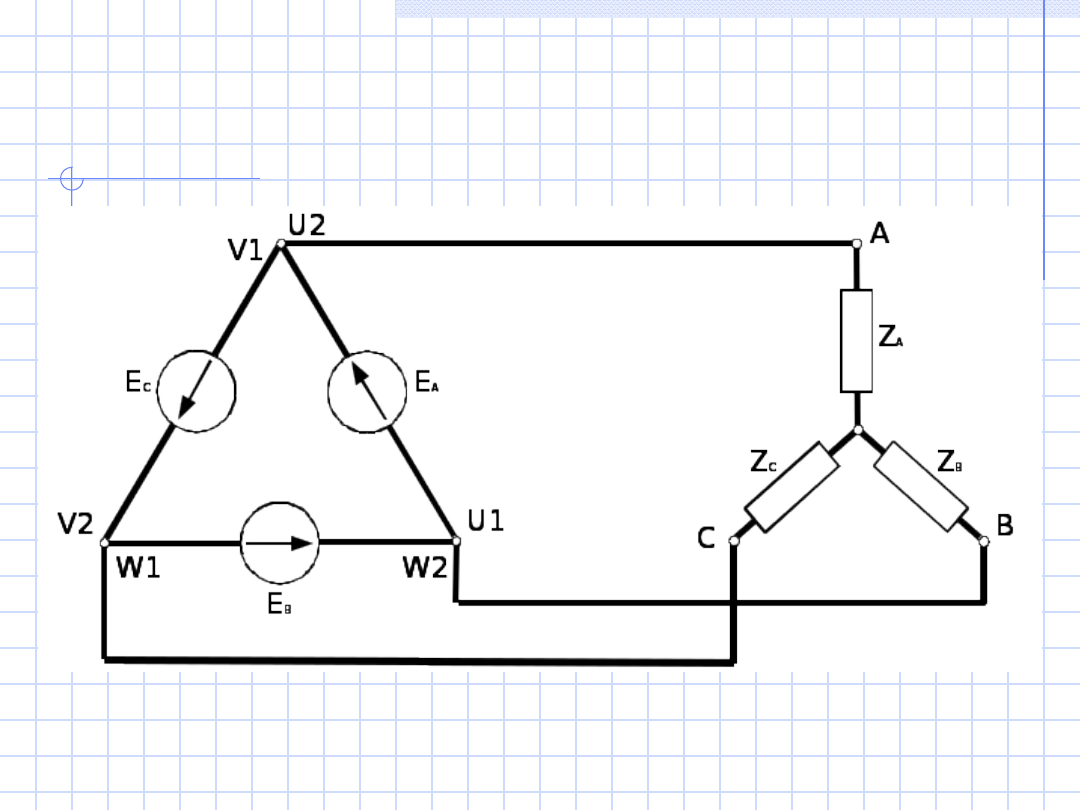
Jeżeli źródło jest połączone w trójkąt, a odbiornik w
gwiazdę, to mamy

układ trójfazowy trójkąt –

gwiazda.

34

Układ trójfazowy

gwiazda – trójkąt

Jeśli źródło jest połączone w gwiazdę, a odbiornik
w trójkąt, to mamy

układ trójfazowy gwiazda –

trójkąt.

36

Definicje podstawowe

W układzie gwiazdowym

napięcie występujące między punktem

neutralnym prądnicy i końcem uzwojenia fazy

nazywamy

napięciem fazowym źródła

(E

A

, E

B

, E

C

). Analogicznie dla

odbiornika określamy

napięcie fazowe odbiornika

(U

A

, U

B

, U

C

).

Napięcia międzyfazowe

(U

AB

, U

BC

, U

CA

) lub

liniowe

– napięcie

występujące między kolejnymi parami zacisków prądnicy lub
odbiornika, czyli

napięcia między przewodami fazowymi.

38

Prądy przewodowe

(I

A

, I

B

, I

C

) – prądy płynące w

przewodach fazowych.

Prądy fazowe

(I

AB

, I

BC

, I

CA

,) – prądy płynące w

fazach odbiornika trójkątowego.

39

DZIĘKUJĘ ZA UWAGĘ

WYKŁAD II

41

prof. dr hab. inż. T. Niedziela

ELEKTROTECHNIKA II

UKLADY TRÓJFAZOWE
SYMETRYCZNE

(Obliczenie układów)

42

A

.

Połączenie odbiornika w gwiazdę

Układ trójfazowy jest symetryczny,

jeśli prądnica trójfazowa symetryczna jest

połączona z odbiornikiem symetrycznym (tzn. złożonym z

trzech identycznych

impedancji zespolonych

(Z

A

= Z

B

= Z

C

).

Z punktu widzenia sposobu połączenia źródła i odbiornika (jak już powiedziano)
możemy wyróżnić

pięć różnych układów podstawowych.

Jednak dla obliczeń

zasadnicze znaczenie ma sposób połączenia odbiornika.

Podłączenie źródła jest tu mniej istotne, ponieważ przeważnie odbiorniki są

dołączone do sieci systemu, w którym punkt neutralny transformatora trójfazowego,

w zależności od sposobu jego połączenia, może być uziemiony lub izolowany.

43

Układ trójfazowy czteroprzewodowy, do
którego dołączono odbiornik połączony
w gwiazdę z uziemionym punktem
neutralnym

44

Ten sam układ (

układ trójfazowy symetryczny z

odbiornikiem połączonym w gwiazdę

) może być

przedstawiony następująco. Dorysowanie źródła
ułatwia zrozumienie zależności występujących w
tym układzie.

45 45

Obliczenie układu

polega na

wyznaczeniu

prądów przewodowych i fazowych odbiornika,
napięć fazowych odbiornika oraz mocy czynnej,
biernej i pozornej pobieranej przez odbiornik.

Dla uproszczenia załóżmy ze

faza początkowa

napięcia

źródłowego (fazy A) jest równa zeru.

Napięcia fazowe źródeł (E

A,

E

B

, E

C

)

przedstawimy

w postaci zespolonej:

46

A

E

E

=

2

3

1

3

2

2

j

B

A

A

E

E e

E

j

p

-

�

�

-

=

=

- -

�

�

�

�

�

�

2

3

1

3

2

2

j

C

A

A

E

E e

E

j

p

�

�

-

=

=

- +

�

�

�

�

�

�

gdyż:

47

2

2

3

3

1

3

1

3

;

2

2

2

2

j

j

e

j

e

j

p

p

-

=- -

=- +

Z powyższych zależności (po dodaniu stronami) wynika, że:

0

A

B

C

E

E

E

+

+

=

W układzie trójfazowym symetrycznym gwiazda - gwiazda

potencjał punktu neutralnego (N) źródła jest równy

potencjałowi punktu neutralnego odbiornika (N’).

W takim razie jeżeli

w układzie trójfazowym symetrycznym gwiazda-gwiazda

potencjał

punktu neutralnego źródła jest równy potencjałowi punktu neutralnego odbiornika , to

E

A

= U

A

E

B

= U

B

E

C

= U

C

zatem

stwierdzamy, że w układzie trójfazowym symetrycznym

przy połączeniu

odbiornika w gwiazdę:

Suma wartości skutecznych zespolonych napięć fazowych

odbiornika jest równa zeru.

48

0

A

B

C

U

U

U

+

+

=

Wobec

równości

potencjałów

punktów

neutralnych N i N’ można te punkty zewrzeć,

zatem prądy fazowe odbiornikowe:

49

0

A

B

C

U

U

U

+

+

=

A

A

A

B

B

B

C

C

C

E

U

I

Z

Z

E

U

I

Z

Z

E

U

I

Z

Z

=

=

=

=

=

=

Ponieważ impedancja każdej fazy odbiornika
wynosi:

zatem

prądy fazowe

:

50

j

Z Ze

R jX

j

=

= +

2

2

3

3

2

2

3

3

j

j

A

A

A

j

j

j

B

B

A

j

j

j

C

C

A

E

I

e

I e

Z

E

I

e

e

I e

Z

E

I

e e

I e

Z

j

j

p

p

j

j

p

p

j

j

-

-

�

�

-

+

-

�

�

-

�

�

�

�

+

�

�

-

�

�

=

=

=

=

=

=

a

moduły prądów przewodowych (I

A

, I

B

, I

C

) są

odpowiednio:

Wniosek. Moduły prądów we wszystkich
fazach są jednakowe

, ponadto wartości

skuteczne zespolone:

51

A

A

B

C

p

E

I

I

I

I

Z

= = =

=

2

3

1

3

2

2

j

B

A

A

I

I e

I

j

p

-

�

�

-

=

=

- -

�

�

�

�

�

�

2

3

1

3

2

2

j

C

A

A

I

I e

I

j

p

�

�

=

=

- +

�

�

�

�

�

�

Zatem:

Wniosek.

Suma

wartości

skutecznych

zespolonych

prądów

fazowych

(przewodowych) jest równa zeru.

Stąd wynika,

że w układzie symetrycznym

prąd w przewodzie

neutralnym jest równy zeru.

Napięcie międzyfazowe

jest różnicą napięć

fazowych,

przy

czym

działania

należy

przeprowadzać

na

wartościach

skutecznych

zespolonych.

52

0

A

B

C

I

I

I

+ + =

Zatem:

Moduły napięć międzyfazowych są
sobie równe:

a

suma wartości skutecznych zespolonych

napięć międzyfazowych jest równa zeru,

czyli:

53

AB

A

B

BC

B

C

CA

C

A

U

U

U

U

U

U

U

U

U

=

-

=

-

=

-

AB

BC

CA

p

U

U

U

U

=

=

=

0

AB

BC

CA

U

U

U

+

+

=

Na kolejnym rysunku zobrazujemy wyniki

naszych

obliczeń

w

postaci

wykresu

wektorowego napięć i prądów dla układu
trójfazowego symetrycznego przy podłączeniu
odbiornika w gwiazdę

54

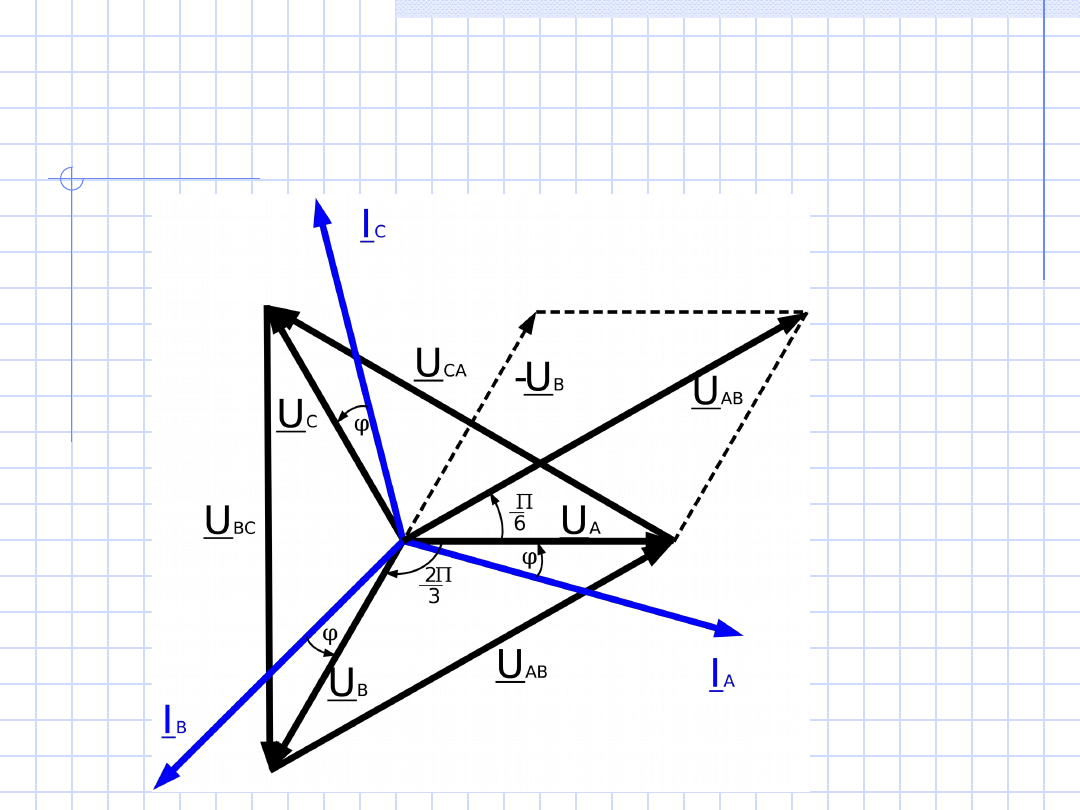
Wykres wektorowy napięć i prądów dla
układu trójfazowego symetrycznego
przy połączeniu odbiornika w gwiazdę

55

Na wykresie wektorowym przedstawiliśmy

napięcia

fazowe

(U

A

, U

B

, U

C

),

międzyfazowe

(U

AB

, U

BC

, U

CA

)

oraz

prądy przewodowe, które są równe prądom
fazowym odbiornika

(I

A

, I

B

, I

C

) przy połączeniu

impedancji fazowych w gwiazdę.

Ponieważ

trzy wektory napięć międzyfazowych

(U

AB

,

U

BC

, U

CA

)

tworzą trójkąt

, zatem ich suma jest równa

zeru.

56

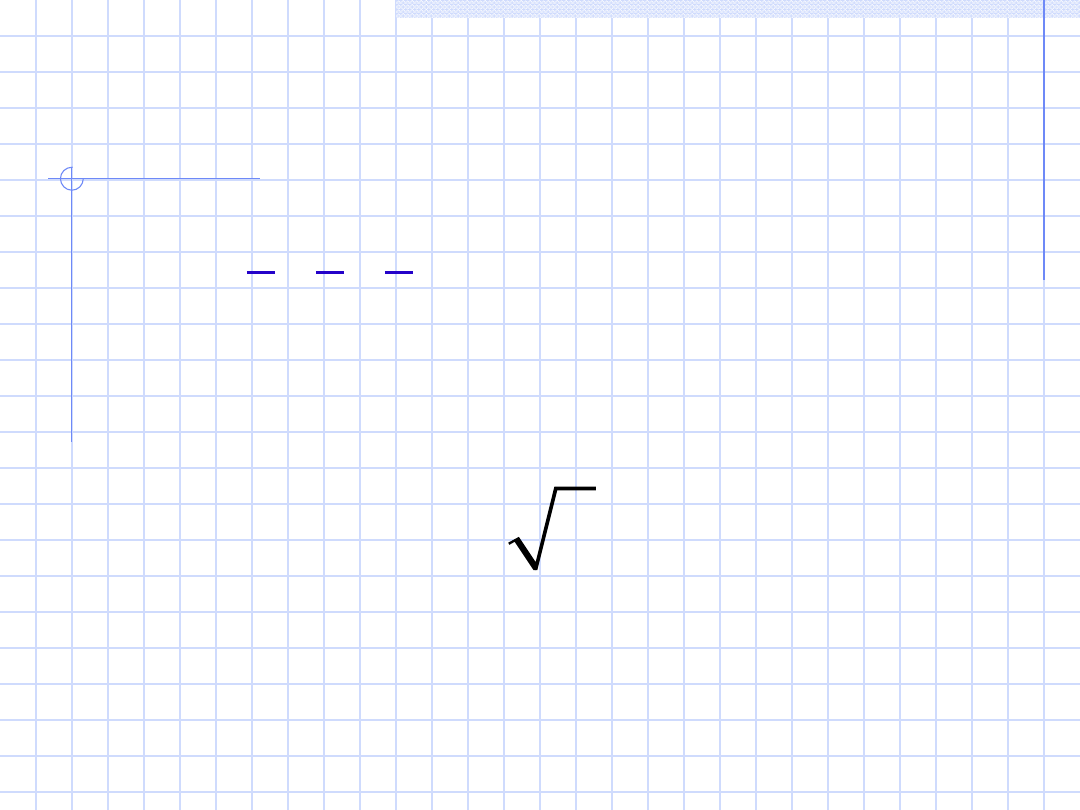
Z zależności dla trójkąta równoramiennego o
bokach U

A

, U

B

, U

AB

i o kątach 2π/3, π/6 i π/6

wynika że

moduł napięcia międzyfazowego

U

AB

= U

p

jest pierwiastek z 3 razy większy

od modułu napięcia fazowego U

f

,

czyli:

57

3

f

Up

U

=

Z zależności tej wynika, że w sieci o napięciu
fazowym U

f

= 220V, napięcie międzyfazowe:

Moc czynną P pobraną przez odbiornik
trójfazowy symetryczny

możemy obliczyć

jako potrójną wartość (3P

f

) mocy pobieranej

przez jedną fazę odbiornika:

przy czym R, jest rezystancją jednej fazy
odbiornika.

58

3 220 380

P

U

V

=

�

=

2

P

ff

ff

U I cos

RI

j

=

=

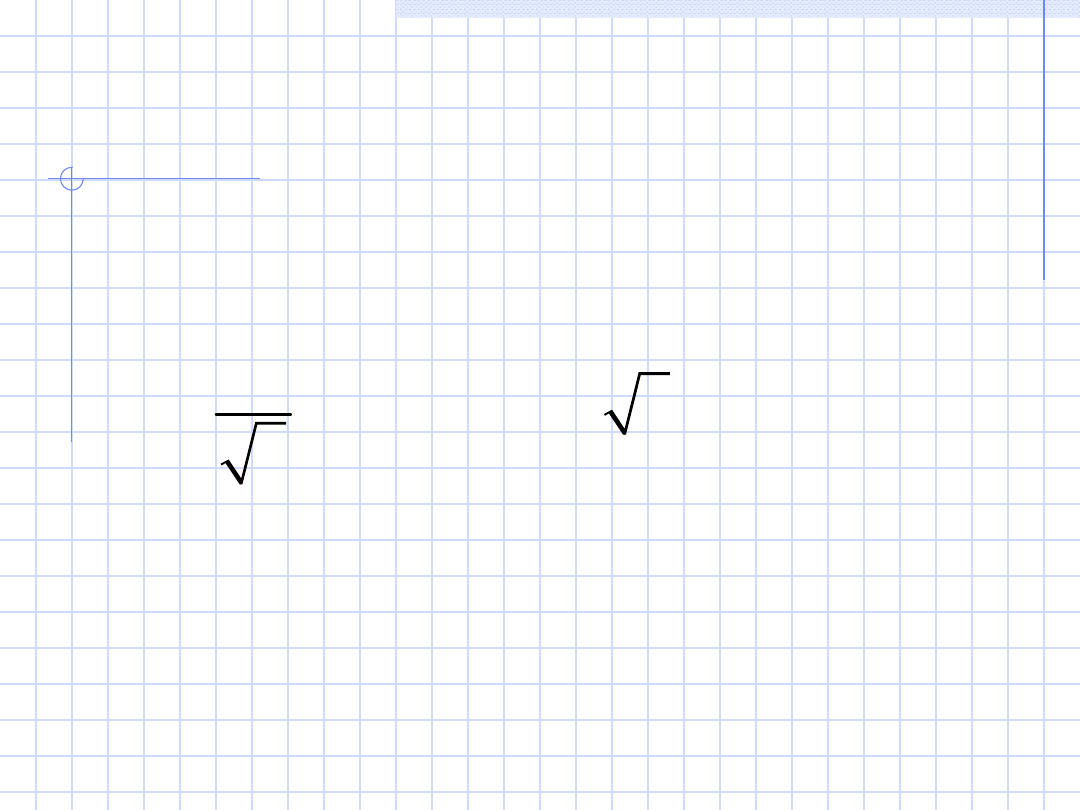
Zatem moc czynna

pobierana przez

odbiornik

trójfazowy symetryczny:

Po podstawieniu otrzymujemy ,

moc czynną P

jako:

Wzór ten jest najczęściej stosowany do
obliczania mocy czynnej P pobieranej przez
odbiornik trójfazowy symetryczny, gdyż
uzależnia moc od wartości związanych z
parametrami sieci zasilającej odbiornik (U

p

oraz

I

p

).

59

2

3P

3

ff

ff

P

U I cos

RI

j

=

=

=

3

cos

3

cos

3

p p

p p

P

U I

U I

j

j

=

=

Wykład II

60

B. Połączenie odbiornika w

trójkąt

Na kolejnym rysunku zilustrujemy

układ

trójfazowy symetryczny

, w którym

odbiornik

połączono w trójkąt,

natomiast źródło w

gwiazdę.

Punktem wyjścia do naszych obliczeń

prądów

fazowych, napięć fazowych oraz mocy

czynnej, biernej i pozornej odbiornika

są

napięcia międzyfazowe.

Gdyby źródło było połączone np. w trójkąt,

wówczas napięcia międzyfazowe są

jednocześnie napięciami fazowymi źródła

.

61

B. Połączenie odbiornika w

trójkąt

Układ trójfazowy symetryczny z
odbiornikiem

połączonym w

trójkąt

62

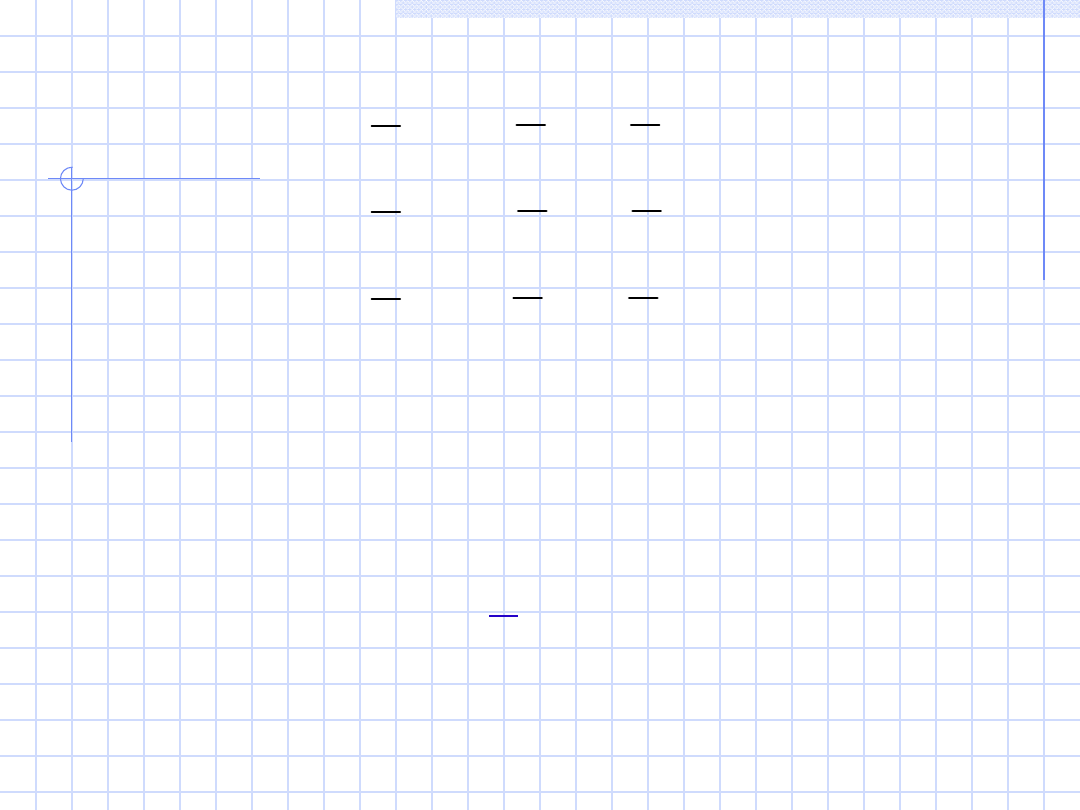
Wyznaczone za pomocą powyższych równań

napięcia międzyfazowe tworzą układ
trójfazowy symetryczny napięć

, przy czym

po założeniu

, że faza początkowa napięcia

międzyfazowego

U

AB

jest

równa

zeru

otrzymamy:

63

AB

A

B

BC

B

C

CA

C

A

U

E

E

U

E

E

U

E

E

=

-

=

-

=

-

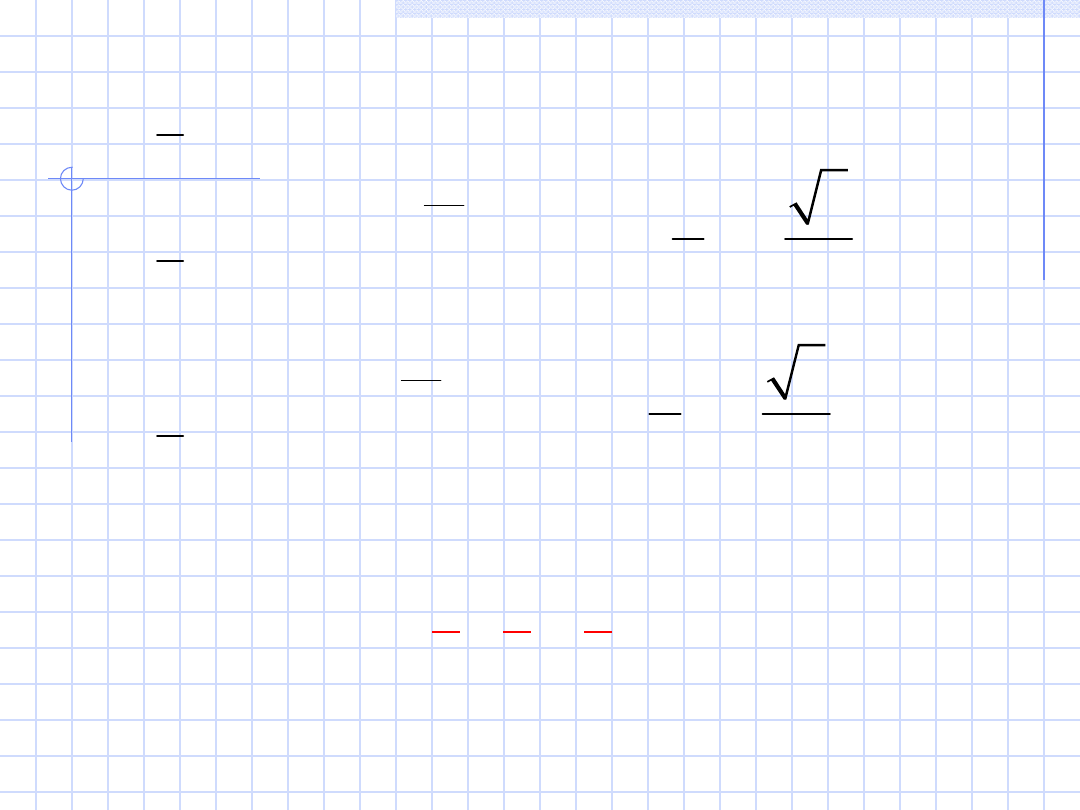
Z powyższych zależności wynika, że wektory

napięć fazowych (U

AB,

U

BC

, U

CA

) odbiornika tworzą

gwiazdę symetryczną gdzie ich suma jest równa
zero.

64

2

3

2

3

1

3

2

2

1

3

2

2

AB

AB

j

BC

AB

AB

j

CA

AB

AB

U

U

U

U e

U

j

U

U e

U

j

p

p

-

=

�

�

=

=

- -

�

�

�

�

�

�

�

�

=

=

- +

�

�

�

�

�

�

a moduły tych napięć (napięć

międzyfazowych) są jednakowe

(U

AB

= U

BC

= U

CA

= U

f

)

65

0

AB

BC

CA

U

U

U

+

+

=

Obliczone

napięcia międzyfazowe występują

na zaciskach odbiornika

, którego

impedancja każdej fazy

wynosi:

Prądy fazowe odbiornika (I

AB

, I

BC

, I

CA

)

możemy wyznaczyć z prawa Ohma dla
wartości skutecznych zespolonych:

66

j

Z Ze

R jX

j

=

= +

j

j

AB

AB

AB

AB

U

U

I

e

I e

Z

Z

j

j

-

-

=

=

=

Powyższe wyrażenia wskazują, że

wektory

prądów fazowych odbiornika tworzą gwiazdę
symetryczna ale opóźnioną o kąt

φ

w stosunku

do gwiazdy napięć fazowych.

67

2

2

3

3

2

2

3

3

j

j

j

BC

AB

BC

AB

j

j

j

CA

AB

CA

AB

U

U

I

e

e

I e

Z

Z

U

U

I

e e

I e

Z

Z

p

p

j

j

p

p

j

j

�

�

-

+

-

�

�

-

�

�

�

�

+

�

�

-

�

�

=

=

=

=

=

=

Przy czym:

Stwierdzamy więc, moduły prądów
fazowych płynących w gałęziach
odbiornika połączonego w trójkąt są
jednakowe i równe prądowi fazowemu I

f

.

68

AB

AB

BC

CA

f

U

I

I

I

I

Z

=

=

=

=

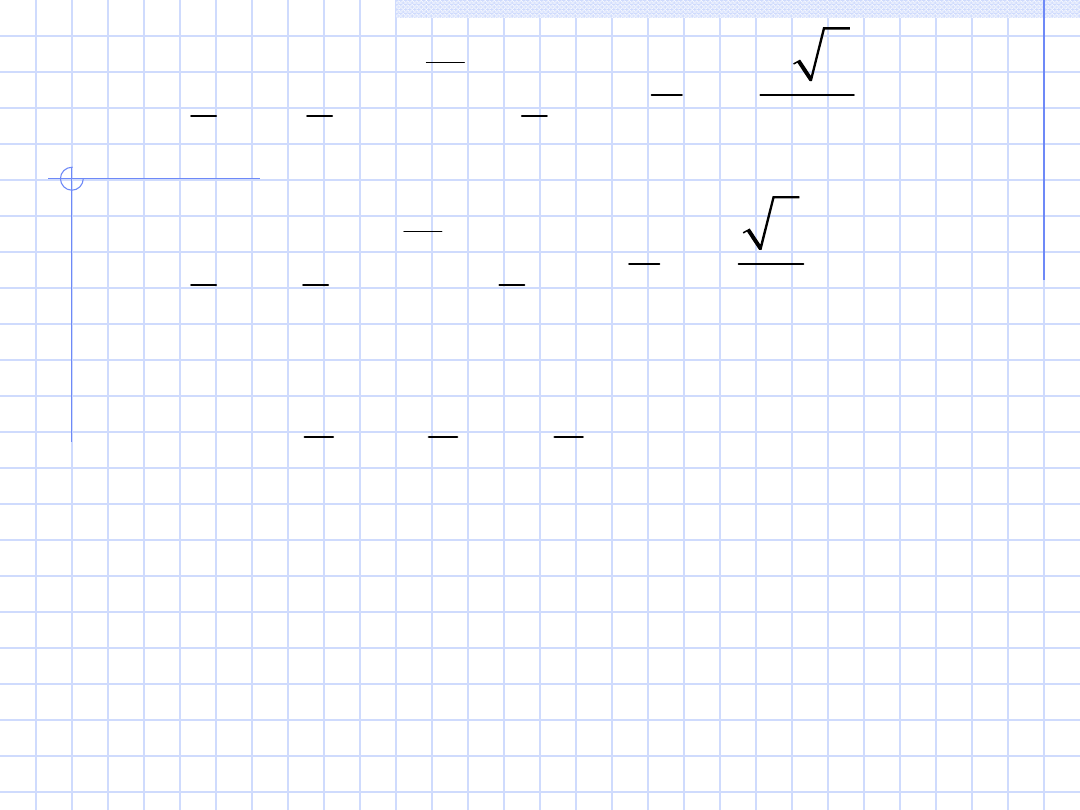
Zatem:

Wniosek.

Suma

wartości

skutecznych

zespolonych prądów fazowych jest równa zeru.

Prądy

przewodowe

obliczamy

jako

różnicę

odpowiednich

prądów fazowych

. Korzystając z

prawa Kirchhoffa dla kolejnych węzłów otrzymujemy:

69

2

3

2

3

1

3

2

2

1

3

2

2

j

BC

AB

AB

j

CA

AB

AB

I

I e

I

j

I

I e

I

j

p

p

-

�

�

-

=

=

- -

�

�

�

�

�

�

�

�

=

=

- +

�

�

�

�

�

�

0

AB

BC

CA

I

I

I

+

+

=

Moduły prądów przewodowych są sobie
równe,

tzn:

a

suma ich wartości skutecznych

zespolonych jest równa zeru,

czyli:

70

A

AB

CA

B

BC

AB

C

CA

BA

I

I

I

I

I

I

I

I

I

=

-

=

-

=

-

A

B

C

P

I

I

I

I

= = =

0

A

B

C

I

I

I

+ + =

Obliczenia przedstawimy na wykresie wektorowym.

Wykreślamy trzy

wektory napięć międzyfazowych

( faza początkowa U

AB

jest równa zeru).

Prąd fazowy

w każdej fazie jest opóźniony względem napięcia fazowego o

kąt φ.

Wektory prądów fazowych

( I

AB

, I

BC

, I

CA

) tworzą gwiazdę symetryczną.

Wektor prądu przewodowego

opóźnia się względem wektora prądu

fazowego o 30

0

.

71

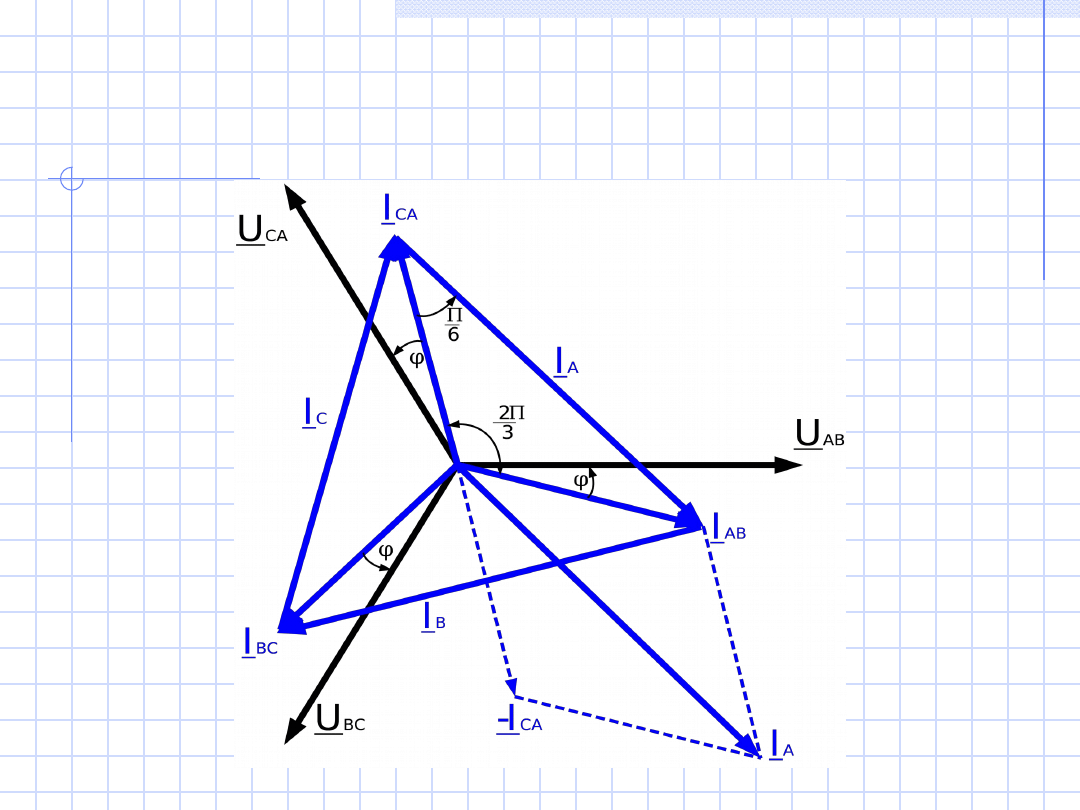
Wykres wektorowy prądów i napięć dla układu
trójfazowego symetrycznego przy połączeniu
odbiornika w trójkąt

72

Ponieważ trzy wektory prądów
przewodowych

(I

A

, I

B

, I

C

)

tworzą trójkąt,

zatem ich suma jest równa zeru

, co jest

zgodne z obliczeniami. Z zależności trójkąta
równoramiennego i kątów wynika, że

moduł

prądu przewodowego (I

A

=I

B

=I

C

=I

p

)

jest

pierwiastek z trzech razy większy od modułu
prądu fazowego

(I

AB

=I

BC

=I

CA

=I

f

) .

Dla odbiornika połączonego w trójkąt

, moc

pobieraną

przez

odbiornik

trójfazowy

symetryczny połączony w trójkąt obliczamy jako
potrójną wartość mocy pobieranej przez jedną
fazę a zatem

moc czynna P

:

73

3

f

Ip

I

=

2

3P

3

3

ff

ff

P

U I cos

RI

j

=

=

=

Przy czym R jest rezystancją jednej fazy
odbiornika.
Po podstawieniu I

f

=I

p

/3

1/2

oraz U

p

=U

f

moc

czynna P jest równa:

Podobnie

moc bierną Q

obliczymy jako potrójną

wartość mocy biernej, pobieranej przez jedną fazę.

Po uwzględnieniu zależności na I

f

oraz U

f

,

moc

pozorna S

:

74

3

cos

3

cos

3

p p

p p

P

U I

U I

j

j

=

=

2

3

sin

3

ff

f

Q

U I

XI

j

=

=

3

p p

S

U I

=

WNIOSKI:

1. Niezależnie od sposobu połączenia faz odbiornika

trójfazowego symetrycznego, odpowiednio moc czynną,
bierną i pozorną obliczamy z tych samych wzorów.

2. Do obliczania mocy odbiornika trójfazowego

symetrycznego połączonego w gwiazdę i trójkąt jest
potrzebna znajomość napięcia międzyfazowego, prądu
przewodowego i kata fazowego odbiornika.

3. Suma prądów fazowych i napięć fazowych odbiornika

trójfazowego symetrycznego połączonego zarówno w
gwiazdę i trójkąt jest równa zero.

75

DZIĘKUJĘ ZA UWAGĘ

76

Źródła:

„Elektrotechnika” – Bolkowski

Równania matematyczne napisano w

programie: MathType 5.0

Schematy układów elektrycznych w nakładce

programu MS Word.

77