
Podstawy kryptografii
Podstawy kryptografii
Copyright, 2003 © Maciej Miłostan
M
M
gr inż.
gr inż.
Maciej Miłostan
Maciej Miłostan
Po
Po
litechnika Poznańska
litechnika Poznańska
Inst
Inst
ytut Informatyki
ytut Informatyki
ul.Piotrowo 3a
ul.Piotrowo 3a
60-965 Poznań, Polska
60-965 Poznań, Polska
Email:
Email:
Maciej.Milostan@cs.put.poznan.pl
Maciej.Milostan@cs.put.poznan.pl
Ochrona danych i
Ochrona danych i
kryptografia
kryptografia

Maciej Miłostan, Kryptograf
ia
2
Agenda
Agenda
•
Terminologia
Terminologia
•
Systemy kryptograficzne
Systemy kryptograficzne
•
Szyfry z kluczem tajnym
Szyfry z kluczem tajnym
•
Asymetryczne systemy
Asymetryczne systemy
szyfrowania
szyfrowania
•
Znajdywanie liczb pierwszych
Znajdywanie liczb pierwszych
•
Funkcje skrótu
Funkcje skrótu

Maciej Miłostan, Kryptograf
ia
3
T
T
erminologia
erminologia
•
Computer
Computer
security
security
•
Network security
Network security
•
Internetwork
Internetwork
security
security
•
Security vs. safty
Security vs. safty
Maciej Miłostan, Kryptograf
ia
4
Przykłady ataków na
Przykłady ataków na
bezpieczeństwo
bezpieczeństwo
Przerwanie
Przechwycenie
Modyfikacja
Podrobienie

Maciej Miłostan, Kryptograf
ia
5
Usługi i mechanizmy
Usługi i mechanizmy
•
Klasyfikacja usług
Klasyfikacja usług
– Poufność (confidentiality)
– Uwierzytelnienie (authentication)
– Nienaruszalność (integrity)
– Niezaprzeczalność
(nonrepudiation)
– Kontrola dostępu (access control)
T=1/2 * Z * |A|
h
/ V
|A|=26, h=6[zn], z=20, v=9600[zn/s]
to T=30 dni.
|A|=95, T=194 lata
– Dyspozycyjność (availability)
•
Mechanizmy
Mechanizmy
– Element wspólny = techniki
kryptograficzne
P
Poznan,
13.10.2003
Ja Jan Kowalski,
chory na
umyśle i zdrowy
na ciele
oświadczam, co
nastepuje....
Ja Jan
Kowalski
...

Maciej Miłostan, Kryptograf
ia
6
Kryptografia
Kryptografia
•
Krypto grafos - grec. ukryte pismo
Krypto grafos - grec. ukryte pismo
•
Kryptografia – „Sztuka przekształcania
Kryptografia – „Sztuka przekształcania
tekstu pisanego, zrozumiałego dla
tekstu pisanego, zrozumiałego dla
wszystkich, w tekst zaszyfrowany
wszystkich, w tekst zaszyfrowany
zrozumiały tylko dla wtajemniczonych
zrozumiały tylko dla wtajemniczonych
znających dany szyfr;” Słownik J. pol. PWN.
znających dany szyfr;” Słownik J. pol. PWN.
•
Szyfr – „Rodzaj kodu, zapisu tekstu za
Szyfr – „Rodzaj kodu, zapisu tekstu za
pomocą systemu umownych znaków w
pomocą systemu umownych znaków w
celu zatajenia treści tekstu przed osobami
celu zatajenia treści tekstu przed osobami
niepowołanymi” Słownik J. pol. PWN.
niepowołanymi” Słownik J. pol. PWN.
Maciej Miłostan, Kryptograf
ia
7
Agenda
Agenda
• Terminologia
•
Systemy
Systemy
kryptograficzne
kryptograficzne
•
Szyfry z kluczem tajnym
Szyfry z kluczem tajnym
•
Asymetryczne systemy
Asymetryczne systemy
szyfrowania
szyfrowania
•
Znajdywanie liczb pierwszych
Znajdywanie liczb pierwszych
•
Funkcje skrótu
Funkcje skrótu
Maciej Miłostan, Kryptograf
ia
8
Systemy kryptograficzne
Systemy kryptograficzne
E
k
D
k
Klucz
Bezpieczny kanał
•
Symetryczny system
kryptograficzny (z kluczem tajnym,
klasyczny, konwencjonalny)
• As
ymetryczny system
kryptograficzny (z kluczem
publicznym, publiczny)
E
k
D
k
Klucz
Klucz
*
Klucz
*
Klucz
f

Maciej Miłostan, Kryptograf
ia
9
Bezpieczny system
Bezpieczny system
kryptograficzny
kryptograficzny
•
Bezwarunkowo
Bezwarunkowo
bezpieczny:
bezpieczny:
– Klucz stosowany
jednokrotnie
– Klucz musi mieć
długość co najmniej
taką jak wiadomość
– Klucz musi być
losowy tzn. nic nie
można powiedzieć o
kluczu na podstawie
kryptogramu
•
Obliczeniowo
Obliczeniowo
bezpieczny:
bezpieczny:
– Używamy funkcji
jednokierunkowej

Maciej Miłostan, Kryptograf
ia
10
Funkcja jednokierunkowa
Funkcja jednokierunkowa
•
F:X
F:X
Y
Y
– Dla każdego x X – wartość f(x) wyznacz się w
czasie wielomianowym
– Dla każdego y Y – wartość f
-1
(y) wyznacz się w
czasie wykładniczym, nawet jeżeli funkcja f jest
znana
•
Nie udowodniono, że istnieje chociaż jedna taka
Nie udowodniono, że istnieje chociaż jedna taka
funkcja
funkcja
•
Za jednokierunkowe uważa się:
Za jednokierunkowe uważa się:
– Rozkład liczby na czynniki pierwsze,
– y = x
2
mod n (liczby 100 cyfrowe)
– y = a
x
mod n (także liczby 100 cyfrowe)

Maciej Miłostan, Kryptograf
ia
11
Kryptoanaliza
Kryptoanaliza
•
Atak na tekst zaszyfrowany – dostępny
Atak na tekst zaszyfrowany – dostępny
tylko szyfrogram
tylko szyfrogram
•
Atak poprzez tekst częściowo znany –
Atak poprzez tekst częściowo znany –
istnieją słowa, których na pewno użyto
istnieją słowa, których na pewno użyto
•
Atak poprzez wybrany tekst jawny
Atak poprzez wybrany tekst jawny
•
Atak poprzez wybrany tekst
Atak poprzez wybrany tekst
zaszyfrowany
zaszyfrowany
•
Atak poprzez wybrany tekst
Atak poprzez wybrany tekst
Maciej Miłostan, Kryptograf
ia
12
Agenda
Agenda
• Terminologia
• Systemy kryptograficzne
•
Szyfry z kluczem
Szyfry z kluczem
tajnym
tajnym
•
Asymetryczne systemy
Asymetryczne systemy
szyfrowania
szyfrowania
•
Znajdywanie liczb pierwszych
Znajdywanie liczb pierwszych
•
Funkcje skrótu
Funkcje skrótu

Maciej Miłostan, Kryptograf
ia
13
Szyfry przestawieniowe
Szyfry przestawieniowe
•
Tekst jawny
Tekst jawny
figura geometryczna
figura geometryczna
tekst zaszyfrowany
tekst zaszyfrowany
np. JAUERASINTCAMH
np. JAUERASINTCAMH
lub JETRUSMIAACNHA
lub JETRUSMIAACNHA
J
J
E
E
S
S
T
T
M
M
A
A
R
R
I
I
C
C
H
H
U
U
A
A
N
N
A
A
*
*
E
E
S
S
T
T
M
M
J
J
A
A
R
R
I
I
C
C
H
H
U
U
A
A
N
N
A
A
*
*

Maciej Miłostan, Kryptograf
ia
14
Szyfry przestawieniowe (1)
Szyfry przestawieniowe (1)
•
k = Antonio
k = Antonio
M = Stoi na stacji lokomotywa ...
M = Stoi na stacji lokomotywa ...
Szyfrogram: STTCKTŻOAJOYKIIMWANLOAAOCSIĘ
Szyfrogram: STTCKTŻOAJOYKIIMWANLOAAOCSIĘ
A
A
N
N
T
T
O
O
N
N
I
I
O
O
1
1
3
3
7
7
5
5
4
4
2
2
6
6
1
1
S
S
2
2
T
T
O
O
I
I
N
N
A
A
S
S
3
3
T
T
A
A
4
4
C
C
J
J
I
I
L
L
O
O
5
5
K
K
O
O
M
M
O
O
6
6
T
T
Y
Y
W
W
A
A
C
C
I
I
Ę
Ę
7
7
Ż
Ż
K
K
A
A

Maciej Miłostan, Kryptograf
ia
15
Szyfry przestawieniowe (2)
Szyfry przestawieniowe (2)
1
1
S
S
2
2
T
T
3
3
O
O
4
4
I
I
13
13
N
N
9
9
A
A
5
5
S
S
1
1
T
T
5
5
A
A
6
6
C
C
7
7
J
J
8
8
I
I
14
14
L
L
10
10
O
O
6
6
K
K
2
2
O
O
9
9
M
M
10
10
O
O
11
11
T
T
12
12
Y
Y
15
15
W
W
11
11
A
A
7
7
C
C
3
3
I
I
13
13
Ę
Ę
14
14
Ż
Ż
15
15
K
K
16
16
O
O
16
16
G
G
12
12
R
R
8
8
O
O
4
4
M
M
4
4
N
N
8
8
A
A
12
12
I
I
16
16
P
P
16
16
O
O
15
15
T
T
14
14
Z
Z
13
13
N
N
3
3
I
I
7
7
E
E
11
11
J
J
15
15
S
S
12
12
P
P
11
11
Ł
Ł
10
10
Y
Y
9
9
W
W
2
2
A
A
6
6
T
T
10
10
L
L
14
14
U
U
8
8
S
S
7
7
T
T
6
6
A
A
5
5
O
O
1
1
L
L
5
5
I
I
9
9
W
W
13
13
A
A
4
4
U
U
3
3
F
F
2
2
F
F
1
1
*
*

Maciej Miłostan, Kryptograf
ia
16
Szyfry przestawieniowe (3)
Szyfry przestawieniowe (3)
1
1
S
S
2
2
T
T
3
3
O
O
4
4
I
I
13
13
N
N
9
9
A
A
5
5
S
S
1
1
T
T
5
5
A
A
6
6
C
C
7
7
J
J
8
8
I
I
14
14
L
L
10
10
O
O
6
6
K
K
2
2
O
O
9
9
M
M
10
10
O
O
11
11
T
T
12
12
Y
Y
15
15
W
W
11
11
A
A
7
7
C
C
3
3
I
I
13
13
Ę
Ę
14
14
Ż
Ż
15
15
K
K
16
16
O
O
16
16
G
G
12
12
R
R
8
8
O
O
4
4
M
M
4
4
N
N
8
8
A
A
12
12
I
I
16
16
P
P
16
16
O
O
15
15
T
T
14
14
Z
Z
13
13
N
N
3
3
I
I
7
7
E
E
11
11
J
J
15
15
S
S
12
12
P
P
11
11
Ł
Ł
10
10
Y
Y
9
9
W
W
2
2
A
A
6
6
T
T
10
10
L
L
14
14
U
U
8
8
S
S
7
7
T
T
6
6
A
A
5
5
O
O
1
1
L
L
5
5
I
I
9
9
W
W
13
13
A
A
4
4
U
U
3
3
F
F
2
2
F
F
1
1
*
*
TAONSAJSWOŁYNLSG*TIIOT
...

Maciej Miłostan, Kryptograf
ia
17
Szyfry podstawieniowe
Szyfry podstawieniowe
•
Klasa bogata w przykłady
Klasa bogata w przykłady
•
f:
f:
1:1
m = DADA BABE
m = DADA BABE
c = ELEL ALAR
c = ELEL ALAR
•
Szyfr Cezara:
Szyfr Cezara:
n – liczba liter w alfabecie (np.
26)
k – przesunięcie (np. 3)
c=(m+k) mod n
np. rondel i zupa= ?
A
A
B
B
C
C
D
D
E
E
...
...
Z
Z
L
L
A
A
M
M
E
E
R
R
Y
Y

Maciej Miłostan, Kryptograf
ia
18
Szyfry podstawieniowe (1)
Szyfry podstawieniowe (1)
•
c=(m*k) mod n
c=(m*k) mod n
np.: n = 27; k=3; m= 2 9 10 1
(2*3) mod 27 = 6
c= 6 0 3 3
– Dodatkowy warunek NWD(k,n)=1
np.: k=7; n=27
– m=(c*k
-1
) mod n
Artymetyka modularna: (a
-1
*a) mod n =1
np.: dla n=27
7
-1
= 4, bo (7*4) mod 27 =1;
5
-1
=11, bo (5*11) mod 27 =1;

Maciej Miłostan, Kryptograf
ia
19
Funkcja i Twierdzenie Eulera
Funkcja i Twierdzenie Eulera
•
Funkcja Eulera:
Funkcja Eulera:
(n) = ilość liczb mniejszych od n, względnie
pierwszych z n.
•
Własność funkcji Eulera:
Własność funkcji Eulera:
– Jeżeli p jest liczbą pierwszą to:
– (p) = p-1
– (p
a
) = p
a-1
(p-1)
– Jeżeli p i q są liczbami pierwszymi to:
(pq) = (p-1)(q-1)
– Jeżeli p
1
, p
2
,..., p
n
są względnie pierwsze, to:
(p
1*
p
2 *
...
*
p
n
) = (p
1
)
*
(p
2
)
* ...
*
(p
n
)
-
Twierdzenie Eulera: a
Twierdzenie Eulera: a
(n)
(n)
mod n = 1, dla a i n
mod n = 1, dla a i n
wzgl. pierwszych
wzgl. pierwszych

Maciej Miłostan, Kryptograf
ia
20
Szyfr podstawieniowy (2)
Szyfr podstawieniowy (2)
•
Z twierdzenia Eulera i własności
Z twierdzenia Eulera i własności
arytmetyki modularnej wynika, że dla a i
arytmetyki modularnej wynika, że dla a i
n wzgl. pierwszych:
n wzgl. pierwszych:
1. a
-1
a mod n = 1
2. a
(n)
mod n = 1
3. a*b mod n = a*c mod n, to b mod n = c mod n
•
Z 1., 2., 3. otrzymujemy równość:
Z 1., 2., 3. otrzymujemy równość:
a
-1
a mod n = a
(n)
mod n = (a*a
(n)-1
) mod n = 1
a
-1
mod n = a
(n)-1
mod n

Maciej Miłostan, Kryptograf
ia
21
Szyfry podstawieniowe (3)
Szyfry podstawieniowe (3)
•
Algorytm obliczania a
Algorytm obliczania a
t
t
mod n;
mod n;
a
a
{0,1,2,...,n-1}
{0,1,2,...,n-1}
t-liczba całkowita dodatnia
t-liczba całkowita dodatnia
1)
Zapisujemy t w postaci binarnej:
t=t
x
·2
x
+ t
x-1
·2
x-1
+...+
t
1
·2 +
t
0
2)
Zastosować algorytm:
result := 1
For i = x downto 0 do //x – liczb bitów reprezentacji
binarnej -1
begin
result : = result
2
mod n
if t
i
= 1 then result := (result *a) mod n
end
Writeln (result) //result = a
t
mod n

Maciej Miłostan, Kryptograf
ia
22
Szyfry podstawieniowe (4)
Szyfry podstawieniowe (4)
•
Przykład:
Przykład:
a
-1
mod n = a
(n)-1
mod n;
a=7; n=27;
(27)=(3
3
)= 3
2
· (3-1) = 18
t = 17 = 10001b
i = 4, w = 1, w = 1 · 7 mod 27 = 7
i = 3, w = 7
2
mod 27 = 22
i = 2, w = 22
2
mod 27 = 484 mod 27 = 25
i = 1, w = 25
2
mod 27 = 625 mod 27 = 4
i = 0, w = 4
2
mod 27 = 16, w = 16*7 mod 27 =
112 mod 27 =
4

Maciej Miłostan, Kryptograf
ia
23
Szyfry homofoniczne
Szyfry homofoniczne
•
Homonimy:
Homonimy:
morze może
morze może
Bóg Bug buk
Bóg Bug buk
Alfabet
Alfabet
jawny
jawny
Homofony
Homofony
A
A
X={d,@,
X={d,@,
%,1}
%,1}
B
B
Y={e,o,5,4}
Y={e,o,5,4}
C
C
Z={f,g,
Z={f,g,
$,i,7}
$,i,7}
X
X
Y=
Y=
Przykład:
Przykład:
m = BCABB =
m = BCABB =
= e$d5o =
= e$d5o =
= 4f@e5
= 4f@e5
Przestaje działać
Przestaje działać
analiza
analiza
częstotliwości
częstotliwości

Maciej Miłostan, Kryptograf
ia
24
Szyfry polialfabetyczne
Szyfry polialfabetyczne
•
Jeden alfabet wejściowy, wiele wyjściowych
Jeden alfabet wejściowy, wiele wyjściowych
•
Szyfr Vigen
Szyfr Vigen
é
é
re:
re:
c=(m+k
i
) mod 27 i={1,2,3,4,5}
Przykład: k = BARAN
m=ABERACJA
k =BARANBARAN
CCWSOEKS
– Łamanie: badanie okresu klucza, indeks
koincydencji

Maciej Miłostan, Kryptograf
ia
25
Szyfry polialfabetyczne (1)
Szyfry polialfabetyczne (1)
•
Szyfr Vernama (1917)
Szyfr Vernama (1917)
m XOR k = c;
m XOR k = c;
–
m i k binarne,
–
klucz generowany pseudolosowo przez
rejestr przesuwny, wykorzystywany
jednokrotnie,
–
długość klucza = długości wiadomości,
–
przy długim kluczu (np.: 10
100
) i
pseudolosowym kluczu, można ten szyfr
uznać za bezwarunkowo bezpieczny

Maciej Miłostan, Kryptograf
ia
26
Szyfry wieloliterowe
Szyfry wieloliterowe
•
Szyfr Playfaira’a
Szyfr Playfaira’a
– 25 znaków alfabetu,
– Klucz - układ znaków w tablicy
(wygenerowany losowo) = 25!
możliwości
Z
M A
P W
S
F
U
H
B
T
C
I
R
O
G
V
N
Y
D
X
Q
E
K
L

Maciej Miłostan, Kryptograf
ia
27
Szyfr Playfair
Szyfr Playfair
•
Każdą parę liter tekstu jawnego
Każdą parę liter tekstu jawnego
m
m
1
1
m
m
2
2
szyfruje się
szyfruje się
wg następujących reguł:
wg następujących reguł:
1.
m
1
i m
2
w tym samym wierszu, to c
1
i c
2
są znakami z
prawej strony m
1
i m
2
, (pierwsza kolumna położona na
prawo
od
ostatniej).
2.
m
1
i m
2
w tej samej kolumnie, to c
1
i c
2
są znakami
położonymi poniżej m
1
i m
2
, (pierwszy wiersz położony pod
ostatnim
wierszem).
3.
m
1
i m
2
znajdują się w różnych wierszach i kolumnach, to c
1
i c
2
brane z przeciwległych rogów prostokąta wyznaczonego
przez m
1
i m
2
, przy czym c
1
pochodzi z wiersza
zawierającego m
1
, c
2
zaś - z wiersza zawierającego m
2
4.
m
1
=m
2
, to do tekstu jawnego między te litery wstawia się
nieznaczącą literę (np. X), co eliminuje powtórzenia.
5.
Jeśli tekst jawny ma nieparzystą liczbę znaków, to na końcu
tekstu jawnego dopisuje się nieznaczącą literę.

Maciej Miłostan, Kryptograf
ia
28
Szyfr Playfair (przykład)
Szyfr Playfair (przykład)
•
Przykład:
Przykład:
m
m
=
=
U N
U N
I W
I W
E R
E R
S Y
S Y
T E
T E
T X
T X
T X
T X
X - znak pusty
X - znak pusty
c = I E O A
K I H G I X G Z G Z
Z
M A
P W
S
F
U
H
B
T
C
I
R
O
G
V
N
Y
D
X
Q
E
K
L

Maciej Miłostan, Kryptograf
ia
29
Szyfry wieloliterowe (1)
Szyfry wieloliterowe (1)
•
Szyfr
Szyfr
Hill
Hill
’a
’a
(
(
1929
1929
)
)
Przekształca tekst wejściowy o dł
Przekształca tekst wejściowy o dł
.
.
t
t
na ci
na ci
ą
ą
g wyjściowy o takiej samej długości.
g wyjściowy o takiej samej długości.
Ogólnie :
Ogólnie :
c
c
= (K *
= (K *
m
m
) mod n
) mod n
Przykład t = 2
Przykład t = 2
m
m
= m
= m
1
1
c
c
= c
= c
1
1
K = k
K = k
11
11
k
k
12
12
m
m
2
2
c
c
2
2
k
k
21
21
k
k
22
22
c
c
1
1
= ( k
= ( k
11
11
m
m
1
1
+ k
+ k
12
12
m
m
2
2
) mod n
) mod n
jeśli t = 3 to 3 równania itd...
jeśli t = 3 to 3 równania itd...
c
c
2
2
= ( k
= ( k
21
21
m
m
1
1
+ k
+ k
22
22
m
m
2
2
) mod n
) mod n
Łatwe do złamania, wystarczy przechwycić cztery pary (m,c).
Łatwe do złamania, wystarczy przechwycić cztery pary (m,c).
Wiedząc, że
Wiedząc, że
c
c
=K*
=K*
m
m
mod n można wyznaczyć K=
mod n można wyznaczyć K=
cm
cm
-1
-1
mod n.
mod n.
Deszyfracja następuje za pomocą macierzy odwrotnej K
Deszyfracja następuje za pomocą macierzy odwrotnej K
-1
-1
.
.
D
D
K
K
(c)=K
(c)=K
-1
-1
c
c
mod n=K
mod n=K
-1
-1
Km mod n=
Km mod n=
m,
m,
przy czym:
przy czym:
K
K
-1
-1
K mod n=I (macierz jednostkowa).
K mod n=I (macierz jednostkowa).

Maciej Miłostan, Kryptograf
ia
30
Szyfry produktowe
Szyfry produktowe
•
P
P
rodukt funkcji - złożenie funkcji
rodukt funkcji - złożenie funkcji
•
Szyfry produktowe = szyfry
Szyfry produktowe = szyfry
kaskadowe
kaskadowe
•
Przykłady:
Przykłady:
– Enigma
– Lucifer
– DES i Triple DES
– FEAL-N
– IDEA

Maciej Miłostan, Kryptograf
ia
31
Enigma
Enigma
•
Maszyna rotorowa
Maszyna rotorowa
(lata 20-te)
(lata 20-te)
– 1919 - maszyna szyfrująca do celów handlowych,
wycofana po pewnych zmianach do celów
wojskowych
– 1929 - kurs kryptologów w Poznaniu
– 1930 - Rajewski, Różycki, Zygalski – złamanie
Enigmy
– 5 do 8 walców (rotorów) każdy z nich permutował 26
elementów (na wejście walca wchodziło 26 cyfr i
wychodziło w zmienionym, przypadkowym porządku)
– Połączenie kilku walców = dużo kombinacji.
– Kluczem początkowe ustawienie rotorów.
– Błędy Niemców: Te same słowa na początku i końcu
komunikatów, klucz przesyłany tym samym kanałem,
co wiadomość.
Maciej Miłostan, Kryptograf
ia
32
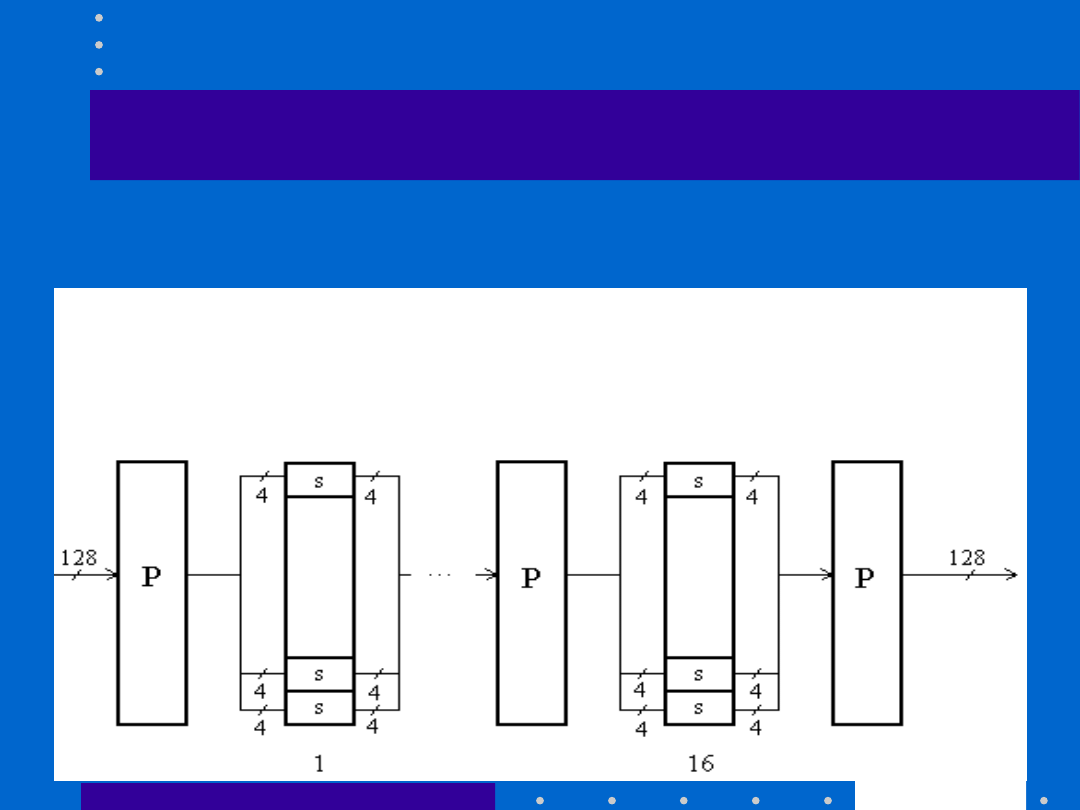
Lucifer
Lucifer
•
Algorytm opracowany przez IBM w
Algorytm opracowany przez IBM w
latach 70-tych (klucz 128 bitowy
latach 70-tych (klucz 128 bitowy
powielony do 512)
powielony do 512)
N a p r z e m i a n p o d s t a w i e n i a S
i
i p e r m u t a c j e P
i
.
K a ż d e p o d s t a w i e n i e S
i
j e s t f u n k c j ą k l u c z a K .
C
E
M
P
S
P
S
P
M
K
t
t
(
)
. . .
(
)
1
2
1
1
S-
skrzynka
P-
permutacj
a
Maciej Miłostan, Kryptograf
ia
33
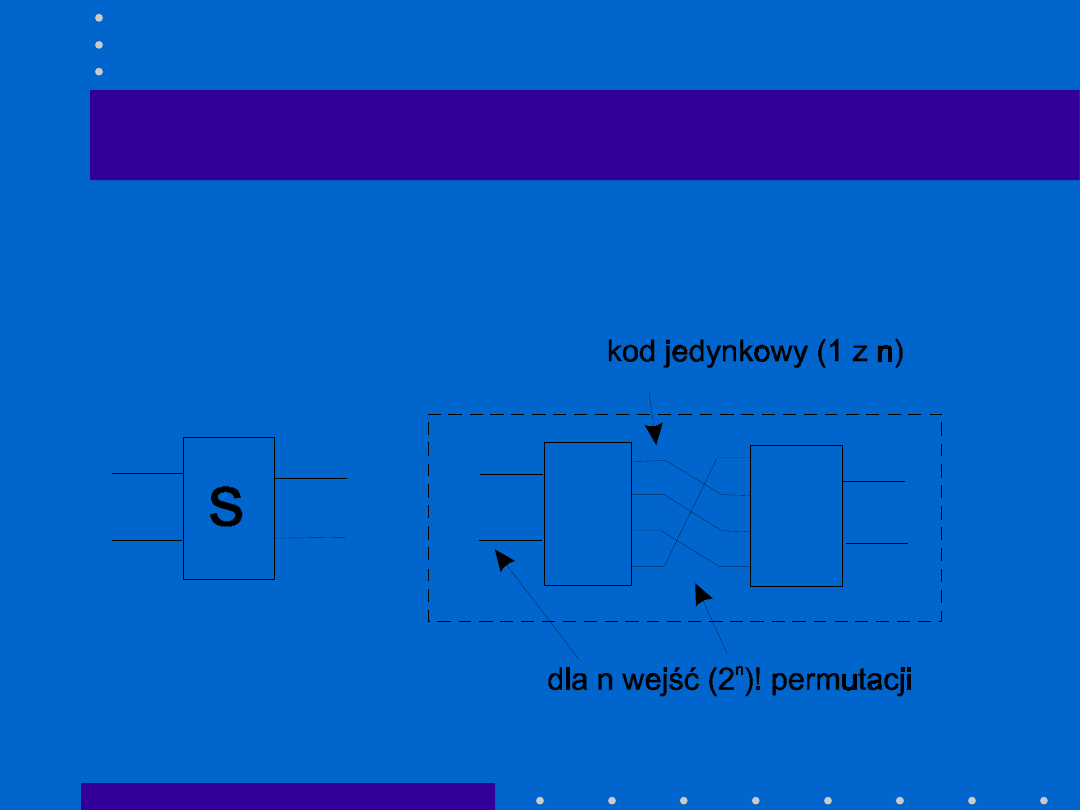
Lucifer (1)
Lucifer (1)
•
Budowa skrzynki s (schemat
Budowa skrzynki s (schemat
uproszczony)
uproszczony)

Maciej Miłostan, Kryptograf
ia
34
Lucifer (2)
Lucifer (2)
•
Żeby szyfr był dobry funkcje realizowane
Żeby szyfr był dobry funkcje realizowane
przez skrzynkę muszą być nieliniowe
przez skrzynkę muszą być nieliniowe
(muszą być n
(muszą być n
ieafiniczną funkcj
ieafiniczną funkcj
ą
ą
boolowską
boolowską
)
)
Dla skrzynek S :
Dla skrzynek S :
- 2 wejścia
- 2 wejścia
- wszystkie funkcje są liniowe
- wszystkie funkcje są liniowe
- 3 wejścia
- 3 wejścia
- 3% funkcji liniowych
- 3% funkcji liniowych
-
-
4 wejścia
4 wejścia
- wszystkie funkcje są nieliniowe
- wszystkie funkcje są nieliniowe
(skrzynki w Luciferze
(skrzynki w Luciferze
są
są
4-wejściowe).
4-wejściowe).

Maciej Miłostan, Kryptograf
ia
35
DES (Data Encryption
DES (Data Encryption
Standard)
Standard)
•
R
R
ozwinięcie Lucifera
ozwinięcie Lucifera
– NBS (dziś NIST - National Institution
of Standard and Technology) ogłosiła
konkurs na szyfr blokowy
– Wygrał IBM - DES uznany za
standard w USA (1977).

Maciej Miłostan, Kryptograf
ia
36
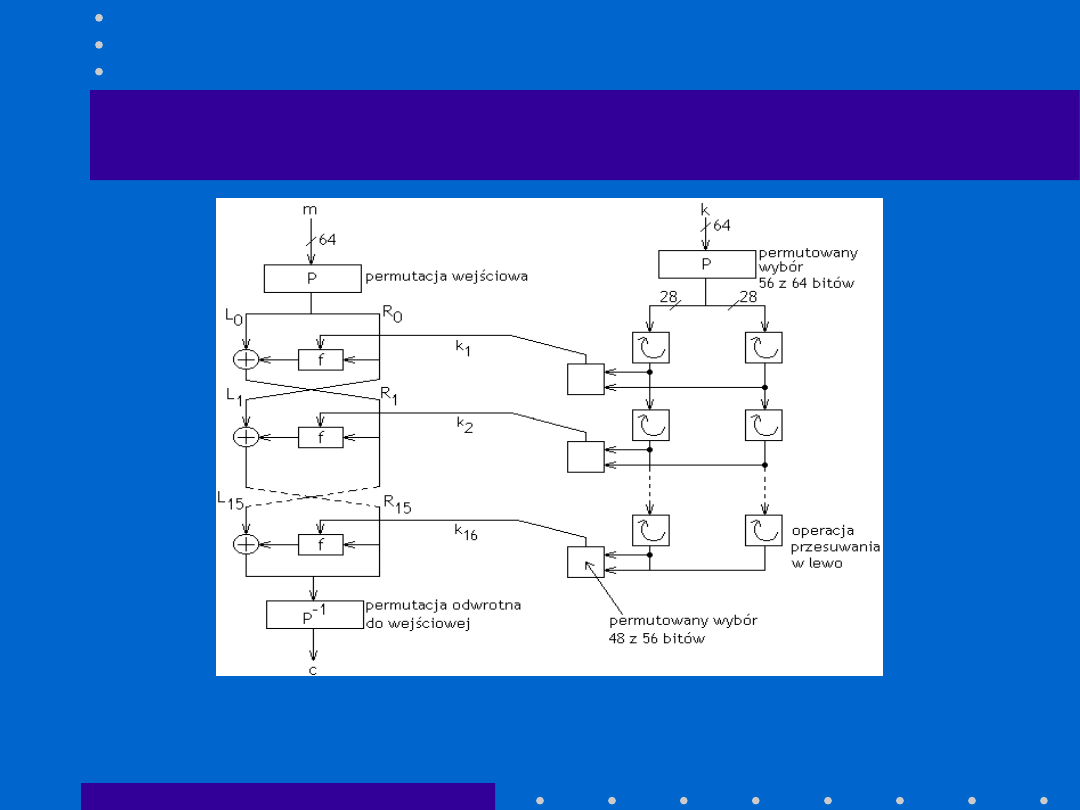
DES (1)
DES (1)
P
P
racuje na 64-bitowych blokach tekstu jawnego. Po początkowej permutacji blok
racuje na 64-bitowych blokach tekstu jawnego. Po początkowej permutacji blok
wejściowy jest dzielony na lewą i prawą połowę, każda o długości 32 bitów.
wejściowy jest dzielony na lewą i prawą połowę, każda o długości 32 bitów.
Następnie jest wykonywanych 16 cykli jednakowych operacji, nazywanych
Następnie jest wykonywanych 16 cykli jednakowych operacji, nazywanych
funkcjami
funkcjami
f
f
, w czasie których dane są łączone z kluczem. Po szesnastym cyklu
, w czasie których dane są łączone z kluczem. Po szesnastym cyklu
lewa i prawa połowa są łączone z kluczem. Następnie są one łączone i
lewa i prawa połowa są łączone z kluczem. Następnie są one łączone i
końcowa permutacja (będąca odwrotnością permutacji początkowej) kończy
końcowa permutacja (będąca odwrotnością permutacji początkowej) kończy
przebieg algorytmu.
przebieg algorytmu.
Klucz ma długość 56 bitów. (Zwykle klucz jest zapisany za pomocą 64 bitów, przy
Klucz ma długość 56 bitów. (Zwykle klucz jest zapisany za pomocą 64 bitów, przy
czym każdy co ósmy jest bitem parzystości, który jest pomijany). Kluczem
czym każdy co ósmy jest bitem parzystości, który jest pomijany). Kluczem
może być dowolna liczba o długości 56 bitów, która może być zmieniona w
może być dowolna liczba o długości 56 bitów, która może być zmieniona w
dowolnej chwili. Kilka z tych liczb jest uważane za klucze słabe, lecz mogą one
dowolnej chwili. Kilka z tych liczb jest uważane za klucze słabe, lecz mogą one
być pominięte. Całe bezpieczeństwo spoczywa na kluczu.
być pominięte. Całe bezpieczeństwo spoczywa na kluczu.
W każdym cyklu bity klucza są przesuwane, a następnie jest wybierane 48 bitów z
W każdym cyklu bity klucza są przesuwane, a następnie jest wybierane 48 bitów z
56 bitów klucza. Prawa połowa bloku danych jest rozszerzona do 48 bitów za
56 bitów klucza. Prawa połowa bloku danych jest rozszerzona do 48 bitów za
pomocą permutacji z rozszerzeniem, łączona za pomocą po
pomocą permutacji z rozszerzeniem, łączona za pomocą po
e
e
lementowej sumy
lementowej sumy
modulo 2 z 48 bitami przesuniętego i permutowanego klucza, jest dokonywane
modulo 2 z 48 bitami przesuniętego i permutowanego klucza, jest dokonywane
podstawienie bloku 32 nowych bitów za pomocą algorytmu podstawiania, a
podstawienie bloku 32 nowych bitów za pomocą algorytmu podstawiania, a
potem jeszcze raz jest dokonywana permutacja. Te cztery operacje tworzą
potem jeszcze raz jest dokonywana permutacja. Te cztery operacje tworzą
funkcje
funkcje
f
f
. Ciąg wyjściowy funkcji
. Ciąg wyjściowy funkcji
f
f
jest dalej łączony z lewą połową za pomocą
jest dalej łączony z lewą połową za pomocą
poelementowej sumy modulo 2. Wynikiem tych operacji jest nowa prawa
poelementowej sumy modulo 2. Wynikiem tych operacji jest nowa prawa
połowa bloku; stara prawa połowa staje się nową lewą.
połowa bloku; stara prawa połowa staje się nową lewą.
Maciej Miłostan, Kryptograf
ia
37
DES(2)
DES(2)
W przypadku deszyfracji klucze
podane w odwrotnej kolejności
Maciej Miłostan, Kryptograf
ia
38
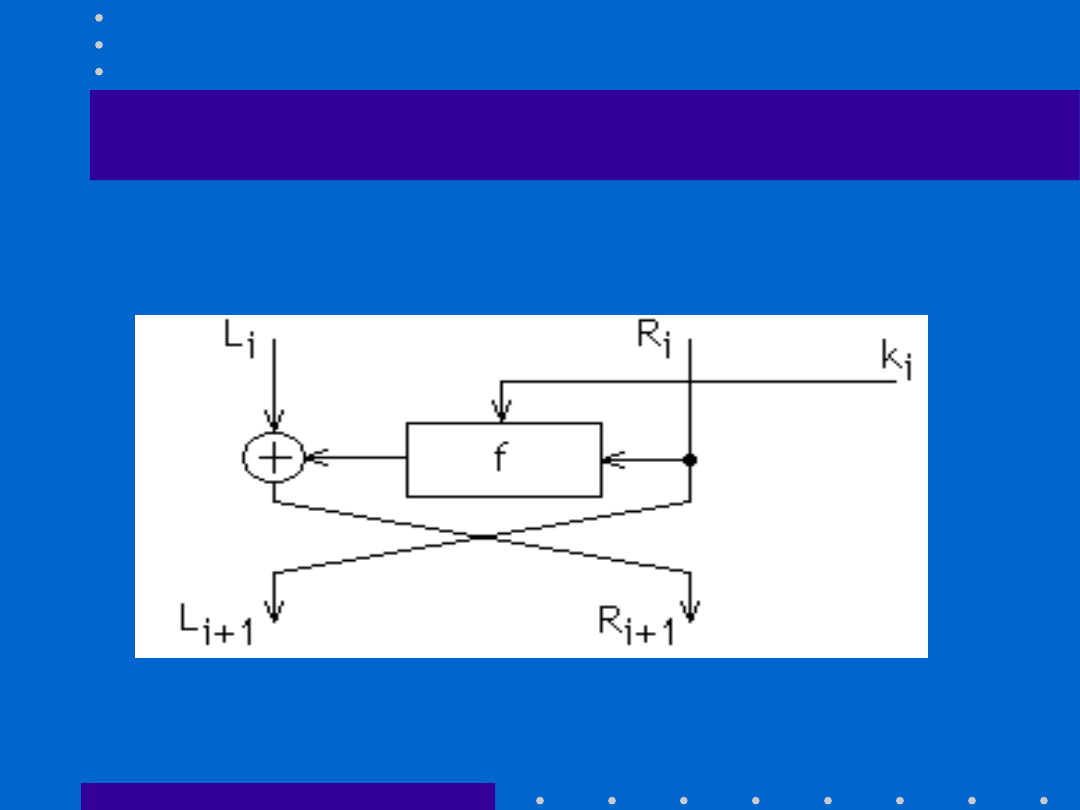
DES(3)
DES(3)
•
Pojedyncza iteracja (w uproszczeniu)
Pojedyncza iteracja (w uproszczeniu)
•
Funkcja f składa się z s-bloków o tajnej
Funkcja f składa się z s-bloków o tajnej
strukturze
strukturze

Maciej Miłostan, Kryptograf
ia
39
DES (4)
DES (4)
•
Łamanie:
Łamanie:
– Liczba możliwych kluczy to 2
56
.
– Średnia liczba bezpiecznych kluczy przy ataku brutalnym
(całościowe przeszukiwanie to 2
54
)
– Kryptoanaliza
różnicowa
(możliwość
wykonania
eksperymentu - przesłanie wiadomości jawnej i odczytania
zaszyfrowanej) zmniejsza przestrzeń bezpiecznych kluczy
do 2
47
. Dokonuje się jej przez wprowadzenie dwóch wejść
różniących się o ustaloną liczbę bitów i obserwuje wyjście.
– Analiza liniowa (również atak przez tekst jawny) pozwala
zmniejszyć przestrzeń bezpiecznych kluczy do 2
43
(można
złamać w kilka dni)
– Rozwiązaniem jest częste zmienianie kluczy.
– Gdyby klucz był 128 - bitowy (2
128
kluczy) - nie do złamania
Maciej Miłostan, Kryptograf
ia
40
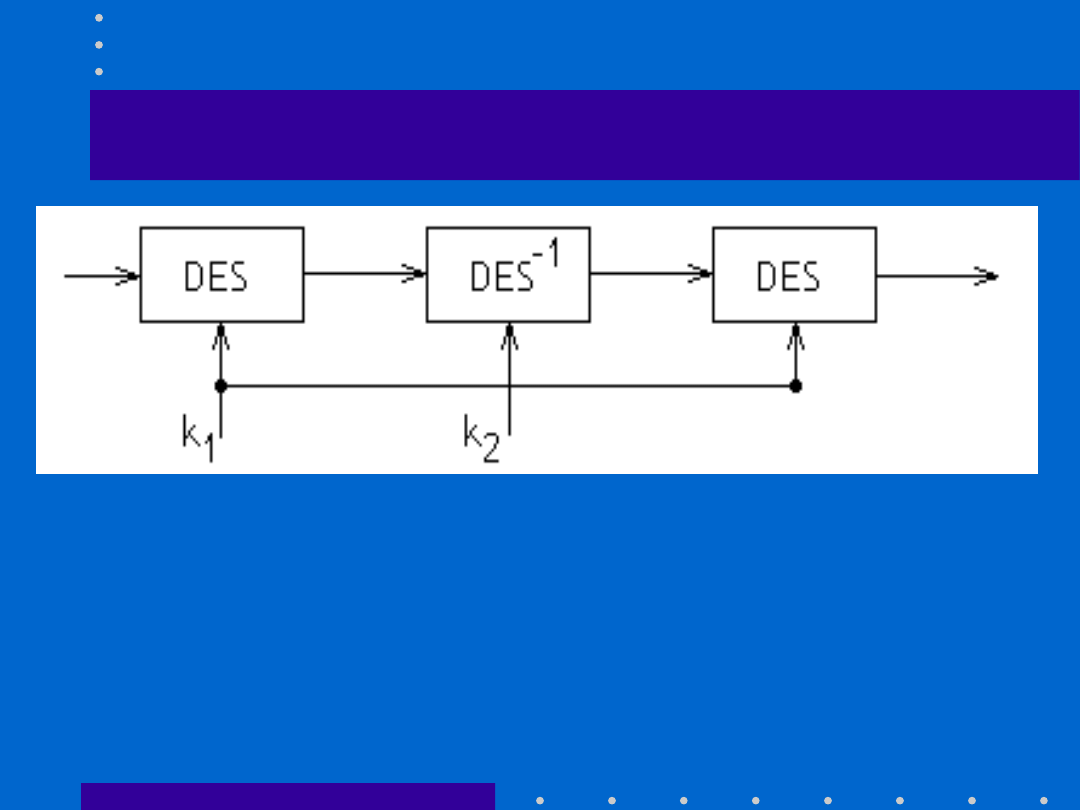
Potrójny DES
Potrójny DES
•Zaadaptowny w ramach standardu
ANS X9.17 i
ISO 8732, oraz w ramach PEM (privacy
enhanced mail)
•Metoda brutalna 2
112
(5x10
35
) kluczy,
kryptoanaliza różnicowa 10
52

Maciej Miłostan, Kryptograf
ia
41
Szyfry produktowe (cd.)
Szyfry produktowe (cd.)
•
Feal-N -
Feal-N -
wykorzystuje 64-bitowe
wykorzystuje 64-bitowe
bloki i 64 lub 128 - bitowy klucz.
bloki i 64 lub 128 - bitowy klucz.
Zamiarem
jego
twórców
było
Zamiarem
jego
twórców
było
opracowanie algorytmu podobnego
opracowanie algorytmu podobnego
do DES, lecz takie, żeby każdy cykl
do DES, lecz takie, żeby każdy cykl
był mocniejszy niż w DES. Algorytm
był mocniejszy niż w DES. Algorytm
taki, składający się z mniejszej
taki, składający się z mniejszej
liczby cykli, byłby szybszy.
liczby cykli, byłby szybszy.

Maciej Miłostan, Kryptograf
ia
42
IDEA
IDEA
•
IDEA - International Data (Encryption) Encipherment Algorithm
IDEA - International Data (Encryption) Encipherment Algorithm
•
S
S
zyfrem blokowy. Pracuje na 64-bitowych blokach tekstu jawnego. Klucz
zyfrem blokowy. Pracuje na 64-bitowych blokach tekstu jawnego. Klucz
ma długość 128 bitów. Ten sam algorytm jest stosowany do szyfrowania
ma długość 128 bitów. Ten sam algorytm jest stosowany do szyfrowania
i
i
deszyfrowania.
deszyfrowania.
•
IDEA wykorzystuje następujące operacje:
IDEA wykorzystuje następujące operacje:
- dodawanie modulo 2
16
(dodawanie z pominięciem przepełnienia)
- poelementowe dodawanie modulo 2
- mnożenie modulo 2
16
+1 (mnożenie z pominięciem przepełnienia)
•
Wszystkie te operacje (są to jedyne operacje w tym algorytmie) działaj
Wszystkie te operacje (są to jedyne operacje w tym algorytmie) działaj
ą
ą
na
na
16-bitowych podblokach.
16-bitowych podblokach.
•
Blok danych o długości 64 bitów dzielony na cztery 16-bitowe podbloki. Te
Blok danych o długości 64 bitów dzielony na cztery 16-bitowe podbloki. Te
cztery podbloki stanowi
cztery podbloki stanowi
ą
ą
wej
wej
ś
ś
cie do pierwszego cyklu algorytmu. W sumie
cie do pierwszego cyklu algorytmu. W sumie
jest 8 cykli. W ka
jest 8 cykli. W ka
ż
ż
dym cyklu te cztery podbloki są sumowane modulo 2,
dym cyklu te cztery podbloki są sumowane modulo 2,
dodawane i mno
dodawane i mno
ż
ż
one ze sob
one ze sob
ą
ą
oraz sze
oraz sze
ś
ś
cioma 16-bitowymi podblokami
cioma 16-bitowymi podblokami
klucza. Mi
klucza. Mi
ę
ę
dzy cyklami podblok drugi i trzeci s
dzy cyklami podblok drugi i trzeci s
ą
ą
zamieniane miejscami.
zamieniane miejscami.
Ostatecznie, otrzymane podbloki s
Ostatecznie, otrzymane podbloki s
ą
ą
ł
ł
ą
ą
czone w jeden blok szyfrogramu.
czone w jeden blok szyfrogramu.

Maciej Miłostan, Kryptograf
ia
43
IDEA (1)
IDEA (1)
•
Algorytm wykorzystuje w sumie 52 podbloki klucza - sześć dla
Algorytm wykorzystuje w sumie 52 podbloki klucza - sześć dla
każdego z ośmiu cykli i cztery w ko
każdego z ośmiu cykli i cztery w ko
ń
ń
cowym przekształceniu.
cowym przekształceniu.
•
Deszyfrowanie przebiega dokładnie tak samo, z wyj
Deszyfrowanie przebiega dokładnie tak samo, z wyj
ą
ą
tkiem
tkiem
tego, że podbloki klucza są odwracane i trochę zmienione
tego, że podbloki klucza są odwracane i trochę zmienione
(korzysta się przy tym z tabeli przekształcania). Podbloki
(korzysta się przy tym z tabeli przekształcania). Podbloki
klucza są zarówno addytywnymi, jak i multiplikatywnymi
klucza są zarówno addytywnymi, jak i multiplikatywnymi
odwrotnościami podbloków klucza użytego do szyfrowania.
odwrotnościami podbloków klucza użytego do szyfrowania.
Obliczenia z tym związane wymagają pewnego wysiłku, lecz
Obliczenia z tym związane wymagają pewnego wysiłku, lecz
wykonuje się je tylko raz dla każdego klucza deszyfrującego.
wykonuje się je tylko raz dla każdego klucza deszyfrującego.
•
Odporność na analityki kryptograficzne - nie jest znana
Odporność na analityki kryptograficzne - nie jest znana
metoda nawet ograniczenia przestrzeni kluczy w sposób
metoda nawet ograniczenia przestrzeni kluczy w sposób
istotny. Znana jest klasa kluczy słabych (w sensie, że jeżeli
istotny. Znana jest klasa kluczy słabych (w sensie, że jeżeli
zostaną użyte, to łatwo je zidentyfikować przy ataku
zostaną użyte, to łatwo je zidentyfikować przy ataku
wybranymi tekstami jawnymi).
wybranymi tekstami jawnymi).
Maciej Miłostan, Kryptograf
ia
44
Agenda
Agenda
• Terminologia
• Systemy kryptograficzne
• Szyfry z kluczem jawnym
•
Asymetryczne
Asymetryczne
systemy szyfrowania
systemy szyfrowania
•
Znajdywanie liczb pierwszych
Znajdywanie liczb pierwszych
•
Funkcje skrótu
Funkcje skrótu

Maciej Miłostan, Kryptograf
ia
45
Szyfry wykładnicze
Szyfry wykładnicze
•
K
K
lucz szyfrujący to para e, n
lucz szyfrujący to para e, n
:
:
m, c {0,1,...,n-1} e, d N
c = m
e
mod n k
e
= (e, n) - klucz szyfrujący
m = c
d
mod n k
d
= (d, n) - klucz deszyfrujący
•
Szyfrowanie
Szyfrowanie
jednym
kluczem,
jednym
kluczem,
deszyfrowanie drugim
deszyfrowanie drugim
•
W
W
arunki
arunki
, które para kluczy musi spełniać
, które para kluczy musi spełniać
:
:
– (m
e
mod n)
d
mod n = m — warunek oczywisty
potrzebny do deszyfracji
– (c
d
mod n)
e
mod n = c
•
Jakie warunki muszą spełniać e, d, n, aby
Jakie warunki muszą spełniać e, d, n, aby
przemienność m i c była możliwa?
przemienność m i c była możliwa?

Maciej Miłostan, Kryptograf
ia
46
Szyfry wykładnicze (1)
Szyfry wykładnicze (1)
•
Tw. Fermata
Tw. Fermata
Jeżeli
Jeżeli
m
m
i
i
n
n
są względnie pierwsze,
są względnie pierwsze,
to
to
m
m
(n)
(n)
mod n =1
mod n =1
•
Jeżeli
Jeżeli
1
1
e d mod
e d mod
(n) = 1, gdzie
(n) = 1, gdzie
jest funkcją
jest funkcją
Eulera
Eulera
2
2
m
m
[0, n-1], przy czym NWD(m, n)=1
[0, n-1], przy czym NWD(m, n)=1
to:
to:
1.
1.
(m
(m
e
e
mod n)
mod n)
d
d
mod n = m
mod n = m
2.
2.
(m
(m
d
d
mod n)
mod n)
e
e
mod n = m
mod n = m

Maciej Miłostan, Kryptograf
ia
47
Szyfry wykładnicze (2)
Szyfry wykładnicze (2)
•
Z 1
Z 1
wynika, że dla pewnej liczby całkowitej
wynika, że dla pewnej liczby całkowitej
r:
r:
e d
e d
=
=
r
r
(n) + 1
(n) + 1
•
Wobec powyższego w
Wobec powyższego w
ybór
ybór
d
d
i
i
e
e
przedstawia się następująco
przedstawia się następująco
:
:
Wybieramy
Wybieramy
d
d
z zadanego wcześniej przedziału (
z zadanego wcześniej przedziału (
d
d
musi być liczbą
musi być liczbą
względnie pierwszą z
względnie pierwszą z
(n)
(n)
). Wyznaczamy
). Wyznaczamy
e
e
jako odwrotność
jako odwrotność
d
d
, co
, co
oznaczamy
oznaczamy
e
e
=
=
inv(d,
inv(d,
(n))
(n))
na podstawie równania:
na podstawie równania:
ed
ed
mod
mod
(n)
(n)
=1
=1
w sposób następujący:
w sposób następujący:
e
e
=
=
d
d
(
(
(n))-1
(n))-1
mod
mod
(n)
(n)
.
.
Można oczywiście wybrać na początku
Można oczywiście wybrać na początku
e
e
i analogicznie wyliczyć
i analogicznie wyliczyć
d
d
.
.
•
Konstruując system kryptograficzny musimy mieć na uwadze
Konstruując system kryptograficzny musimy mieć na uwadze
warunki 1
warunki 1
i 2
i 2
.
.

Maciej Miłostan, Kryptograf
ia
48
S
S
zyfr Pohlinga — Hellmana
zyfr Pohlinga — Hellmana
•
Moc
Moc
algorytmu leży w złożoności — trudności
algorytmu leży w złożoności — trudności
w logarytmowaniu dyskretnym dla dużych
w logarytmowaniu dyskretnym dla dużych
p
p
p - duża liczba pierwsza
p - duża liczba pierwsza
c = m
e
mod p k
e
= (e, p) - klucz szyfrujący
m = c
d
mod p k
d
= (d, p) - klucz deszyfrujący
(p) = p -1
(p) = p -1
e d mod (p - 1) = 1
e d mod (p - 1) = 1
d = e
d = e
-1
-1
mod (p-1)= e
mod (p-1)= e
(p-
(p-
1) -1
1) -1
mod (p-1)
mod (p-1)
•
Klucze
do
szyfrowania
k
Klucze
do
szyfrowania
k
e
e
=(e,
p)
i
=(e,
p)
i
deszyfrowania k
deszyfrowania k
d
d
=(d, p)
=(d, p)

Maciej Miłostan, Kryptograf
ia
49
Szyfr RSA
Szyfr RSA
•
W szyfrze RSA (Rivesta-Shamira-Adlemana)
W szyfrze RSA (Rivesta-Shamira-Adlemana)
modułem prowadzonych obliczeń jest liczba n
modułem prowadzonych obliczeń jest liczba n
będąca iloczynem dwóch wielkich liczb
będąca iloczynem dwóch wielkich liczb
pierwszych p i q:
pierwszych p i q:
n=pq
n=pq
z czego wynika:
z czego wynika:
(
(
n
n
) =
) =
(p-1)(q-1)
(p-1)(q-1)
•
d
d
[max (p, q)+1, n-1] - jest „dowolną” liczbą
[max (p, q)+1, n-1] - jest „dowolną” liczbą
pierwszą
pierwszą
z tego przedziału, ale musi być
z tego przedziału, ale musi być
względnie pierwsza z
względnie pierwsza z
(p-1)(q-1).
(p-1)(q-1).
Jeśli po wyznaczeniu na podstawie
Jeśli po wyznaczeniu na podstawie
d
d
liczby
liczby
e=inv(d,
e=inv(d,
(n)) i e<log
(n)) i e<log
2
2
n
n
,
,
to trzeba wybrać inną
to trzeba wybrać inną
wartość
wartość
d
d
.
.

Maciej Miłostan, Kryptograf
ia
50
Szyfr RSA (1)
Szyfr RSA (1)
•
Można ujawnić klucz szyfrujący k
Można ujawnić klucz szyfrujący k
e
e
.
.
•
Z każdym użytkownikiem wiążemy parę (k
Z każdym użytkownikiem wiążemy parę (k
e
e
;
;
k
k
d
d
). Każdy może zaszyfrować, zdeszyfrować
). Każdy może zaszyfrować, zdeszyfrować
może ten kto ma klucz k
może ten kto ma klucz k
d
d
— (dokładnie ten,
— (dokładnie ten,
kto zna
kto zna
d
d
)
)
•
W tym przypadku są 2 możliwości ataku:
W tym przypadku są 2 możliwości ataku:
–
logarytmowanie dyskretne - znając parę m, c
można obliczyć e=log
m
c
–
rozkład modułu n na czynniki pierwsze dlatego
liczby p i q muszą być duże, losowe, nie mogą być
blisko siebie.

Maciej Miłostan, Kryptograf
ia
51
Szyfr RSA (2)
Szyfr RSA (2)
Przykład:
Przykład:
_
_
A
A
B
B
...
...
Z
Z
0
0
1
1
2
2
...
...
26
26
szyfrujemy BOAT
szyfrujemy BOAT
m =
m =
02
02
15
15
01
01
20
20
=
=
m
m
1
1
m
m
2
2
m
m
3
3
m
m
4
4
generujemy klucze p=7, q=79
generujemy klucze p=7, q=79
n=7*79=553
n=7*79=553
d
d
[max(7,79)+1,552]
[max(7,79)+1,552]
(p-1)(q-1)=6*78=468
(p-1)(q-1)=6*78=468
d=401
d=401
,
,
401*e mod 468 =1
401*e mod 468 =1
,
,
e=401
e=401
(468)-1
(468)-1
mod 468
mod 468
(468)=
(468)=
(2
(2
2
2
3
3
2
2
13)=144
13)=144
e=401
e=401
143
143
mod 468 =461
mod 468 =461
k
k
e
e
=(461, 553), k
=(461, 553), k
d
d
=(401, 553);
=(401, 553);

Maciej Miłostan, Kryptograf
ia
52
Szyfr RSA (3)
Szyfr RSA (3)
Przykaład:
Przykaład:
BOAT
BOAT
m=
m=
02
02
15
15
01
01
20 = m
20 = m
1
1
m
m
2
2
m
m
3
3
m
m
4
4
c
c
1
1
=
=
2
2
461
461
mod 553
mod 553
=
=
c
c
2
2
= 15
= 15
461
461
mod 553
mod 553
=
=
c
c
3
3
=
=
1
1
461
461
mod 553 =
mod 553 =
c
c
4
4
= 20
= 20
461
461
mod 553 =
mod 553 =
44
44
5
5
14
14
8
8
1
1
4
4
2
2
6
6
c =
c =
445
445
148
148
001
001
426
426
•
UWAGI:
UWAGI:
–Nie stosuje się RSA do szyfrowania - jest zbyt wolny.
–Używa się go do podpisu cyfrowego

Maciej Miłostan, Kryptograf
ia
53
Zastosowanie RSA
Zastosowanie RSA
•
Kontrola tożsamości nadawcy
Kontrola tożsamości nadawcy
•
Gra w pokera na odległość
Gra w pokera na odległość
•
Podpis cyfrowy (przykład)
Podpis cyfrowy (przykład)
•
Wymiana kluczy
Wymiana kluczy

Maciej Miłostan, Kryptograf
ia
54
S
S
zyfr Elgamal’a
zyfr Elgamal’a
S
S
zyfr Elgamal’a
zyfr Elgamal’a
{wystarczy 200 cyfr}
{wystarczy 200 cyfr}
g
g
{0,1, ..., q-1};
{0,1, ..., q-1};
q — liczba pierwsza
q — liczba pierwsza
Każdy użytkownik wybiera sobie losowo liczbę całkowitą a,
Każdy użytkownik wybiera sobie losowo liczbę całkowitą a,
gdzie a
gdzie a
{0,1,..., q-1}
{0,1,..., q-1}
k
k
d
d
= (a, q);
= (a, q);
k
k
e
e
= (g
= (g
a
a
, q)
, q)
m - wiadomości
m - wiadomości
r - całkowite, losowo wybrane
r - całkowite, losowo wybrane
przesyłamy (g
przesyłamy (g
r
r
mod q, m g
mod q, m g
ar
ar
mod q)
mod q)
odbiorca oblicza:
odbiorca oblicza:
(g
(g
r
r
)
)
a
a
mod q = g
mod q = g
ar
ar
mod q
mod q
(m g
(m g
ar
ar
mod q)( g
mod q)( g
ar
ar
)
)
-1
-1
mod q = m
mod q = m
Maciej Miłostan, Kryptograf
ia
55
Agenda
Agenda
• Terminologia
• Systemy kryptograficzne
• Szyfry z kluczem jawnym
• Asymetryczne systemy
szyfrowania
•
Znajdywanie liczb
Znajdywanie liczb
pierwszych
pierwszych
•
Funkcje skrótu
Funkcje skrótu

Maciej Miłostan, Kryptograf
ia
56
Znajdywanie liczby
Znajdywanie liczby
pierwszych
pierwszych
•
Sita
są
niefektywne
(np.
sito
Sita
są
niefektywne
(np.
sito
eratostenesa)
eratostenesa)
•
Przykładowe tw.
Przykładowe tw.
– Liczba n jest pierwsza istnieje x:
1 x
n-1
mod n =1
2 x
(n-1)/p.
mod n 1; dla każdego p/(n-1)
– Liczby Mersenne’a M
n
=2
n
-1. Znamy ich 29
(ostatnia n=132049), jeżeli M
n
liczbą
pierwszą, to n jest liczbą pierwszą

Maciej Miłostan, Kryptograf
ia
57
Funkcja skrótu
Funkcja skrótu
•
Bezpieczna – niewykonalne
Bezpieczna – niewykonalne
znalezienie dwóch wiadomości o
znalezienie dwóch wiadomości o
tym samym skrócie
tym samym skrócie
•
Szybkość – powinien bazować na
Szybkość – powinien bazować na
zbiorze prostych operacji bitowych
zbiorze prostych operacji bitowych
•
Prostota i zwartość
Prostota i zwartość
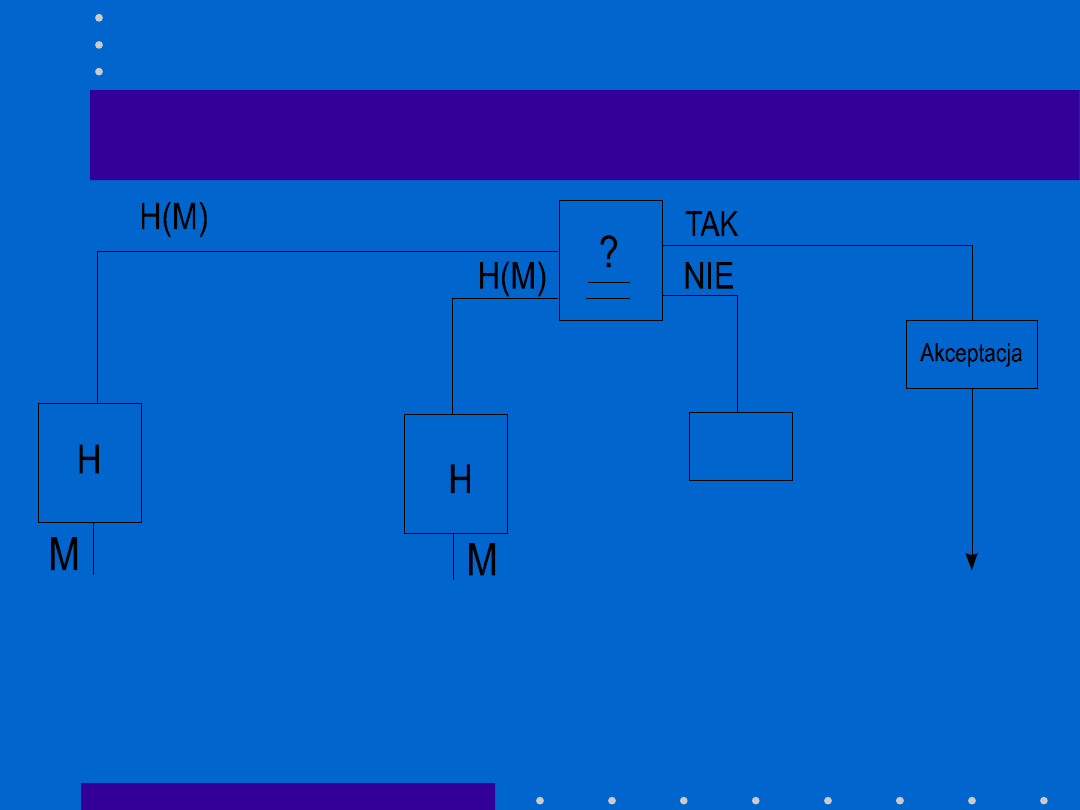
Maciej Miłostan, Kryptograf
ia
58
Funkcja skrótu
Funkcja skrótu
•Jednokierunkowa funkcja skrótu zależna od klucza jest często
oznaczana jako MAC (Message Authentication Code - ciąg
uwierzytelniania wiadomości).
Tylko osoba mająca identyczny klucz może zweryfikować skrót. Są
one bardzo użyteczne w zabezpieczaniu autentyczności bez
wprowadzania tajności.
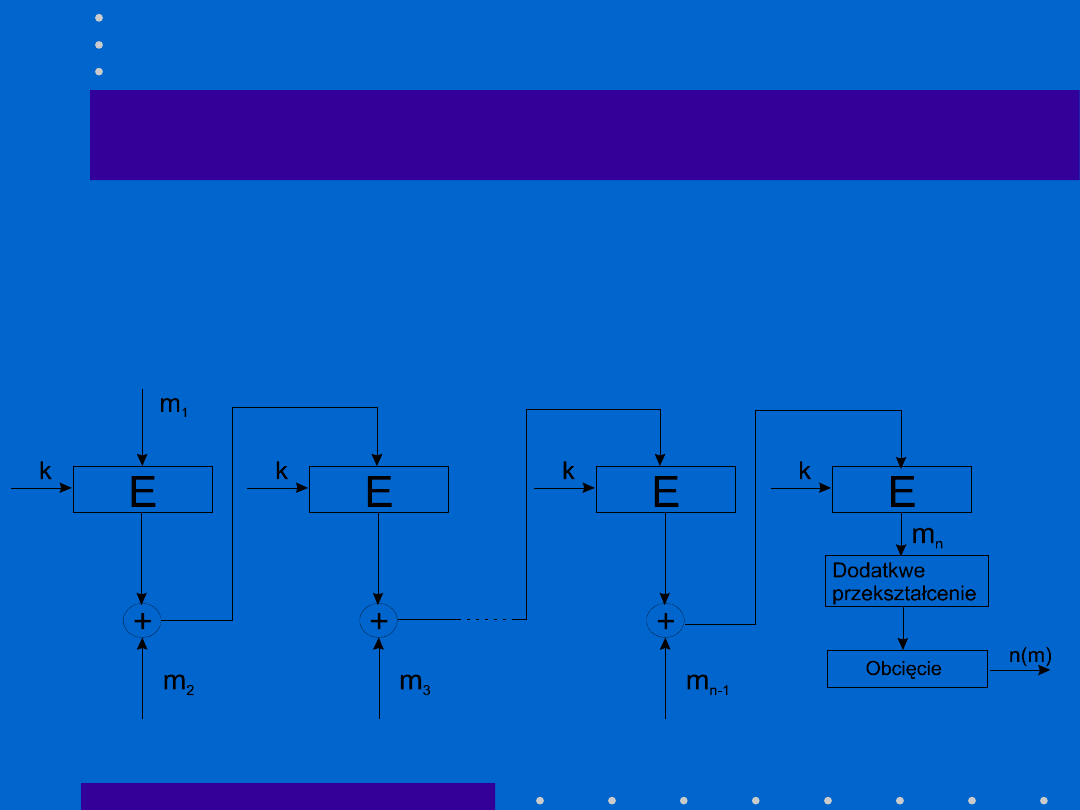
Maciej Miłostan, Kryptograf
ia
59
Funkcja skrótu (1)
Funkcja skrótu (1)
m = m
1
m
2
m
3
...m
n-1
Jednokierunkowa funkcja skrótu z kluczem.
H = H
n
= h(m)
H
i
=p(H
i-1
, m
i
)

Maciej Miłostan, Kryptograf
ia
60
Funkcja skrótu (2)
Funkcja skrótu (2)
•
MAC na bazie szyfru blokowego
MAC na bazie szyfru blokowego
– Najprostszym sposobem utworzenia jednokierunkowej funkcji
skrótu zależnej od klucza jest szyfrowanie wiadomości za
pomocą algorytmu blokowego w trybie szyfrowego sprzężenia
zwrotnego (CFB) (ANSI X9.9, ISO9797). Funkcja RIPE-MAC
bazuje na normie ISO9797 i korzysta z algorytmu DES jako
blokowej funkcji szyfrującej. Istnieją dwie odmiany funkcji RIPE-
MAC: jedna wykorzystująca zwykły algorytm DES (RIPE-MAC1),
druga wykorzystująca trzykrotne szyfrowanie algorytmem DES
w celu uzyskania jeszcze większego bezpieczeństwa (RIPE-
MAC3).
– Algorytm składa się z trzech części. Najpierw wiadomość jest
poszerzana do długości będącej wielokrotnością 64 bitów.
Następnie poszerzona wiadomość jest dzielona na 64-bitowe
bloki. Do skracania tych bloków używa się funkcji kompensującej
z kluczem, sterowanej przez klucz tajny, która daje pojedynczy
blok 64 bitów. W tym bloku można użyć alg. DES, jednorazowo
lub trzykrotnie. Ostatecznie ciąg wyjściowy jest poddawany
szyfrowaniu na bazie alg. DES z innym kluczem, otrzymanym z
klucza wykorzystywanego w procesie kompensacji.

Maciej Miłostan, Kryptograf
ia
61
Funkcje skrótu (3)
Funkcje skrótu (3)
Funkcj
a
Wejście
Wyjście (długość
skrótu)
N-Hash
128-bitowe bloki wiadomości
128-bitów
MD2
128-bitów
MD4
128-bitów
MD5
tekst rozszerza się do
wielokrotności 512 bitów
zmniejszonej o 64 bity (na nich
zapisujemy długość wiadomości
przed rozpoczęciem operacji
rozszerzania)
128-bitów
SHA
jak wyżej
160-bitów

Maciej Miłostan, Kryptograf
ia
62
Podpis cyfrowy
Podpis cyfrowy
•
sign(m) = D
sign(m) = D
k
k
*
*
(m)
(m)
•
podpis jest związany z kluczem i podpisującym
podpis jest związany z kluczem i podpisującym
•
Podpisuje się skrót wiadomości
Podpisuje się skrót wiadomości
•
Problem w wygenerowaniu par kluczy (k, k
Problem w wygenerowaniu par kluczy (k, k
*
*
) dla
) dla
każdego użytkownika.
każdego użytkownika.

Maciej Miłostan, Kryptograf
ia
63
Głosowanie w sieci
Głosowanie w sieci
Udział bierze trzech uczestników. Oddają oni głosy: A
Udział bierze trzech uczestników. Oddają oni głosy: A
V
V
A
A
, B
, B
V
V
B
B
, C
, C
V
V
C
C
.
.
Głosowanie powinno być uczciwe, tajne, każdy oddaje dokładnie jeden głos.
Głosowanie powinno być uczciwe, tajne, każdy oddaje dokładnie jeden głos.
Wykorzystujemy system asymetryczny.
Wykorzystujemy system asymetryczny.
Zapis X
Zapis X
Y:
Y:
message
message
oznacza:
oznacza:
X
X
wysyła do
wysyła do
Y
Y
wiadomość
wiadomość
message
message
.
.
•
Kolejne kroki :
Kolejne kroki :
1.
1.
A
A
A: E
A: E
A
A
E
E
B
B
E
E
C
C
(V
(V
A
A
)
)
BA: E
A
E
B
E
C
(V
B
)
CA: E
A
E
B
E
C
(V
C
)
2.
2.
Realizowane przez A
Realizowane przez A
D
D
A
A
E
E
A
A
E
E
B
B
E
E
C
C
(V
(V
B
B
)=E
)=E
B
B
E
E
C
C
(V
(V
B
B
), bo D
), bo D
A
A
E
E
A
A
jest przekształceniem identycznościowym
jest przekształceniem identycznościowym
D
D
A
A
E
E
A
A
E
E
B
B
E
E
C
C
(V
(V
C
C
)=E
)=E
B
B
E
E
C
C
(V
(V
C
C
)
)
3.
3.
A
A
B: E
B: E
B
B
E
E
C
C
(V
(V
A
A
)
)
E
E
B
B
E
E
C
C
(V
(V
B
B
)
)
E
E
B
B
E
E
C
C
(V
(V
C
C
)
)
K
K
omunikaty wysyłamy w losowej(przypadkowej) kolejności.
omunikaty wysyłamy w losowej(przypadkowej) kolejności.
•
4.
4.
Realizowane przez B
Realizowane przez B
D
D
B
B
E
E
B
B
E
E
C
C
(V
(V
A
A
)=E
)=E
C
C
(V
(V
A
A
)
)
D
D
B
B
E
E
B
B
E
E
C
C
(V
(V
B
B
)=E
)=E
C
C
(V
(V
B
B
)
)
D
D
B
B
E
E
B
B
E
E
C
C
(V
(V
C
C
)=E
)=E
C
C
(V
(V
C
C
)
)

Maciej Miłostan, Kryptograf
ia
64
Głosowanie w sieci (1)
Głosowanie w sieci (1)
5.
5.
B
B
C:
C:
E
E
C
C
(V
(V
A
A
)
)
E
E
C
C
(V
(V
B
B
)
)
E
E
C
C
(V
(V
C
C
)
)
Wysyłamy w losowej kolejności
Wysyłamy w losowej kolejności
6.
6.
Realizowane przez C
Realizowane przez C
D
C
E
C
(V
A
)=V
A
D
D
C
C
E
E
C
C
(V
(V
B
B
)=V
)=V
B
B
D
D
C
C
E
E
C
C
(V
(V
C
C
)=V
)=V
C
C
C zna już wynik głosowania i powinien ten wynik ogłosić.
C zna już wynik głosowania i powinien ten wynik ogłosić.
7.
7.
C
C
B:
B:
D
D
C
C
(V
(V
A
A
)
)
D
D
C
C
(V
(V
B
B
)
)
D
D
C
C
(V
(V
C
C
)
)
8.
8.
Realizowane przez B
Realizowane przez B
E
E
C
C
D
D
C
C
(V
(V
A
A
)=V
)=V
A
A
E
E
C
C
D
D
C
C
(V
(V
B
B
)=V
)=V
B
B
E
E
C
C
D
D
C
C
(V
(V
C
C
)=V
)=V
C
C
B zna wynik, ale by go sprawdzić zaszyfrowuje go za pomocą E
B zna wynik, ale by go sprawdzić zaszyfrowuje go za pomocą E
C
C
i sprawdza, czy jest to zgodne z wersją
i sprawdza, czy jest to zgodne z wersją
zaszyfrowaną, jaką posiadał poprzednio.
zaszyfrowaną, jaką posiadał poprzednio.
W kolejnych krokach B wysyła wynik do A podpisując go za
W kolejnych krokach B wysyła wynik do A podpisując go za
pomocą D
pomocą D
B
B
. A odbiera to, deszyfruje za pomocą E
. A odbiera to, deszyfruje za pomocą E
B
B
i sprawdza zgodność (przez zaszyfrowanie
i sprawdza zgodność (przez zaszyfrowanie
odpowiednimi kluczami i porównanie jak wyżej).W tym przypadku klucze E
odpowiednimi kluczami i porównanie jak wyżej).W tym przypadku klucze E
A
A
, E
, E
B
B
i E
i E
C
C
są oczywiście
są oczywiście
ogólnie znane. Tajne są jedynie przekształcenia D
ogólnie znane. Tajne są jedynie przekształcenia D
A
A
, D
, D
B
B
, D
, D
C
C
, które służą do podpisywania.
, które służą do podpisywania.
•
Protokół ten jest niewygodny dla dużej liczby głosujących.
Protokół ten jest niewygodny dla dużej liczby głosujących.

Maciej Miłostan, Kryptograf
ia
65
Koniec
Koniec
Dziękuję za uwagę
Dziękuję za uwagę
!
!
... i zapraszam po przerwie
... i zapraszam po przerwie
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
Wyszukiwarka
Podobne podstrony:
Podstawy kryptografii
SII 08 Podstawy kryptologii
w13 Podstawy kryptografii
Podstawy kryptografii
Podstawy kryptografii Wydanie II
Podstawy kryptografii
Podstawy kryptografii
Podstawy kryptografii 2
Podstawy kryptografii pokryp
Podstawy kryptografii pokryp
Podstawy kryptografii
PODSTAWY MATEMATYCZNE, MECHANIZMY KRYPTOGRAFICZNE - WYKŁADY
więcej podobnych podstron