Wykład z Fizyki Ogólnej

Dr Anna Hajdusianek

Instytut Fizyki

•

Pok. 231 A1

•

tel. [phone]

•

[e-mail]

•

godziny konsultacji:

–

pn. 12

00

-13

00

–

śr. 10

00

-13

00

EGZAMIN

•

I termin egzaminu

–

16 czerwiec 2003- (pn) godz.12

00

•

II termin egzaminu

–

26 czerwiec 2003- (cz.) godz. 18

00

•

Warunkiem przystąpienia do egzaminu

jest zaliczenie ćwiczeń oraz laboratorium

z fizyki na ocenę pozytywną

Terminy wykładów z

fizyki

•

Środa godz. 13

15

sala 314

•

Środa godz. 17

05

sala 322

Plan wykładu:

•

Wstęp

•

Kinematyka

•

Dynamika

•

Praca i energia

•

Prawa
zachowania

•

Grawitacja

•

Mechanika bryły
sztywnej

•

Mechanika płynów

•

Drgania

•

Fale sprężyste

•

Termodynamika

•

Kinetyczna teoria
gazów

Literatura:

•

I.W. Sawieliew „Wykłady z fizyki „ tom1

•

D.Halliday, R.Resnick „Fizyka” tom1

•

Cz. Bobrowski „Fizyka - krótki kurs”

•

H.Young, R.Freedman ”University
Physics”

•

J. Orear „Fizyka”

•

K.Jezierski, B.Kołodka, K.Sierański
„Wzory i prawa z objaśnieniami”

Wektory

•

Charakterystyka wektora

–

wartość

–

kierunek

–

zwrot

•

Składowe wektora

•

Współrzędne wektora

•

Wersor - wektor jednostkowy

r



r



)

,

,

(

k

j

i

r









1



r

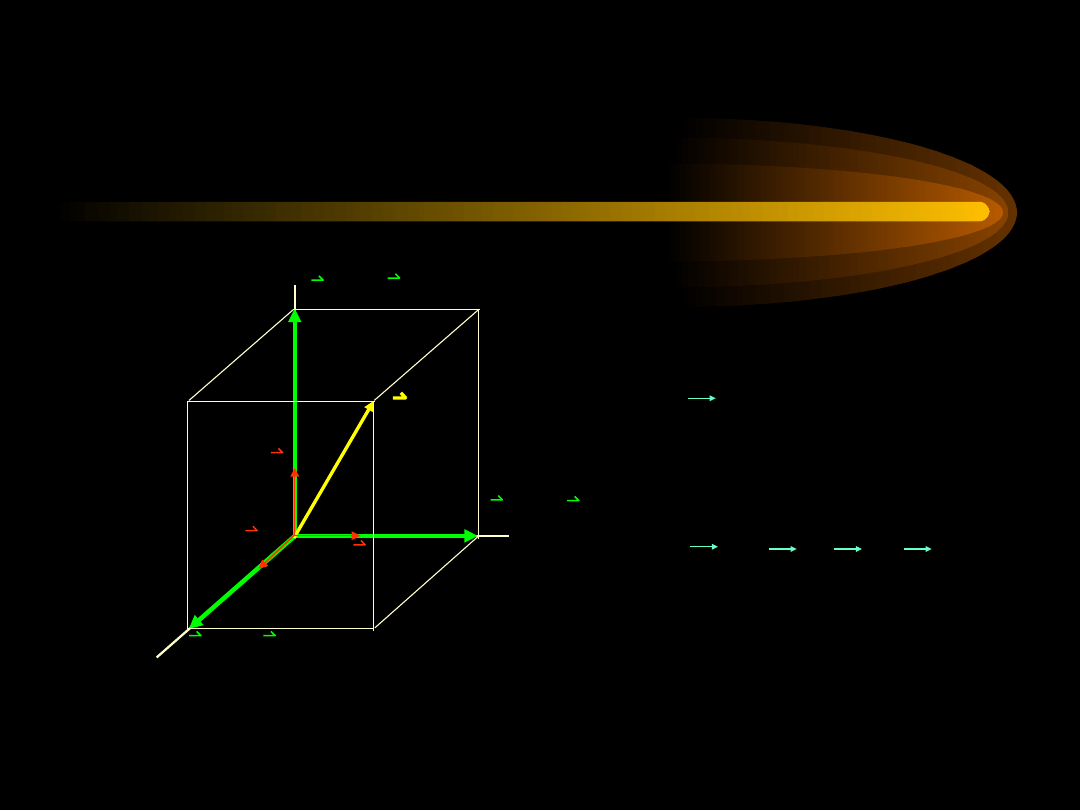
Kartezjański układ

współrzędnych

A

i

j

k

x

y

z

A

x

= A

x



i

A

y

= A

y



j

A

z

= A

z



k

A=[A

x

,A

y

,A

z

]

A=A

x

i+A

y

j+A

z

k

Wartość (długość) wektora

2

2

2

z

y

x

a

a

a

a









a



Wektor przeciwny

a



a



Działania na wektorach

•

Dodawanie i odejmowanie
wektorów

•

mnożenie wektora przez liczbę

•

iloczyn skalarny

•

iloczyn wektorowy

Dodawanie wektorów

B

C

A+B=C

A=[A

x

,A

y

,A

z

]

B=[B

x

,B

y

,B

z

]

C=[A

x

+ B

x

, A

y

+B

y

,

A

z

+B

z

]

A

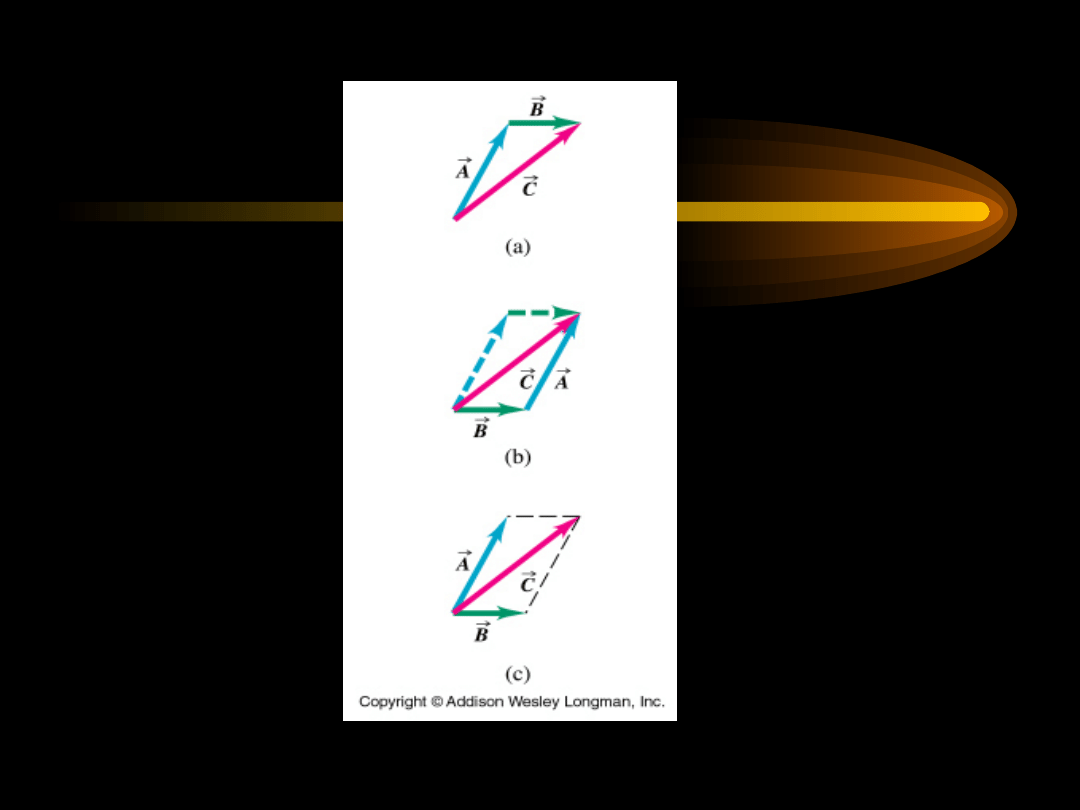
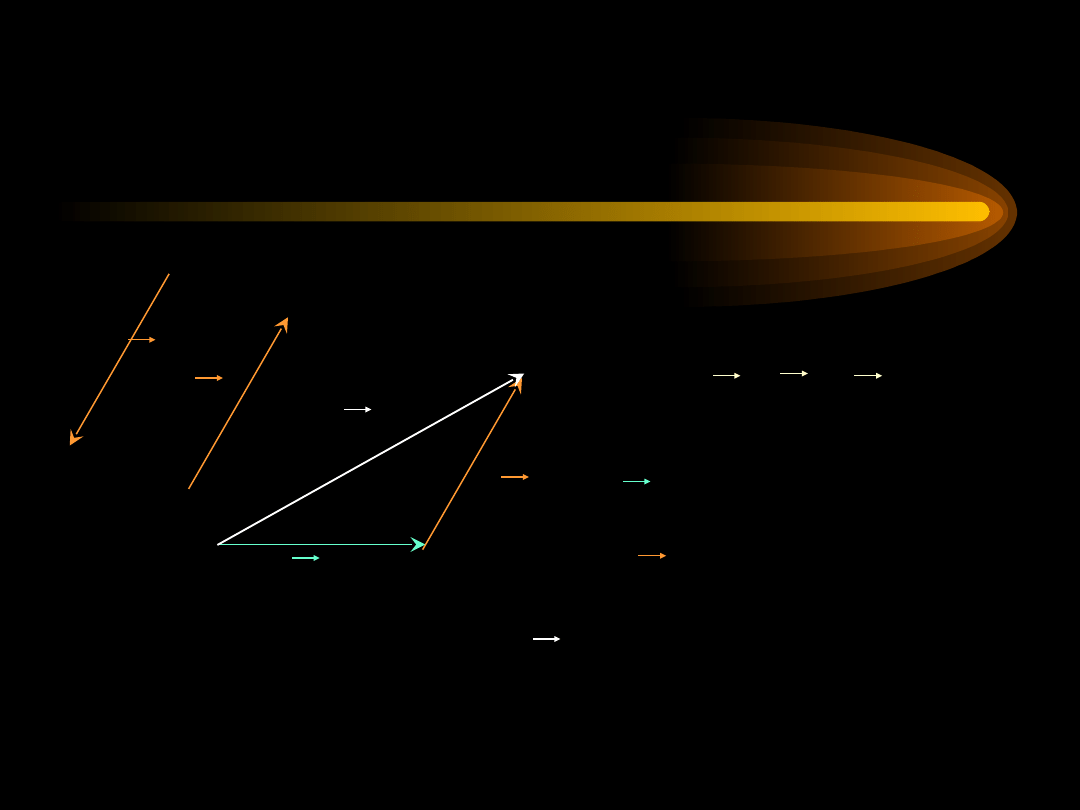
Odejmowanie wektorów

A+(-B) =C

A=[A

x

,A

y

,A

z

]

B=[-B

x

,-B

y

,-B

z

]

C=[A

x

-B

x

, A

y

-B

y

, A

z

-B

z

]

-B

C

A

B

-B

Mnożenie wektora przez

liczbę

A

A

A=[A

x

,A

y

,A

z

]

A=[A

x

, A

y

, A

z

]

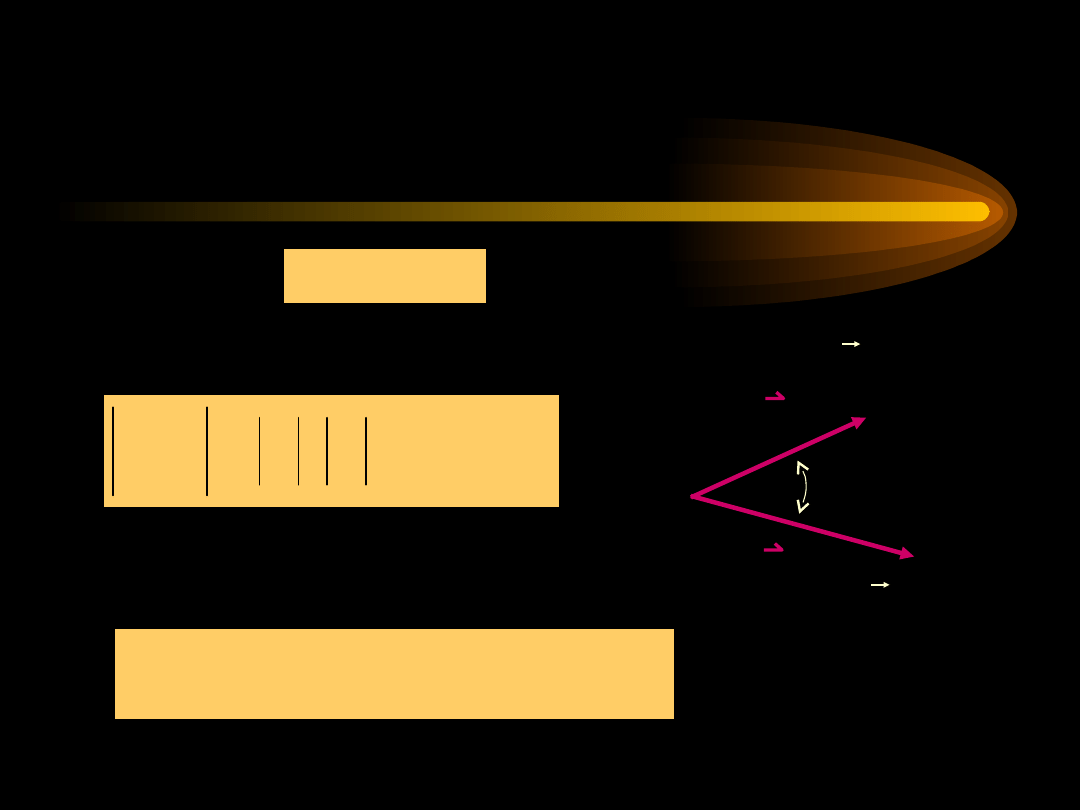
Iloczyn skalarny

C

B

A









)

,

cos( B

A

B

A

B

A















A

B



z

z

y

y

x

x

B

A

B

A

B

A

C







C jest liczbą !!!

A=[A

x

,A

y

,A

z

]

B=[B

x

,B

y

,B

z

]

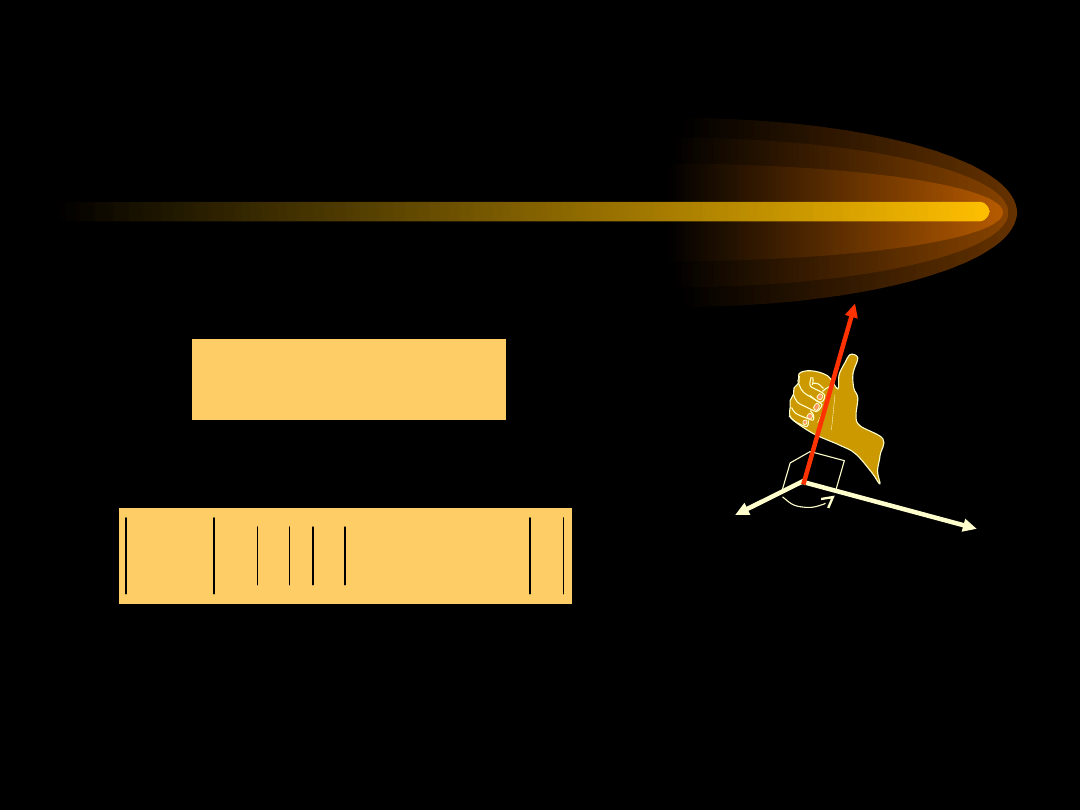
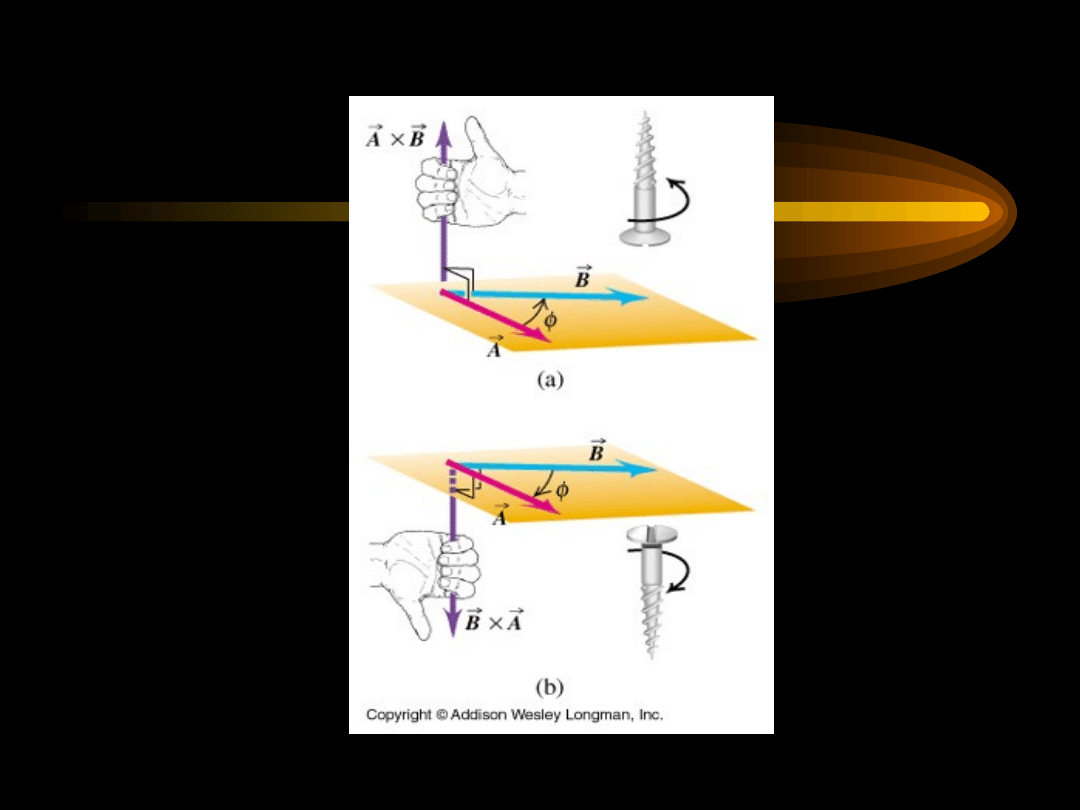
Iloczyn wektorowy

C

B

A

B

A

B

A



















)

,

sin(

C

B

A











A

B



Zwrot wektora C określa reguła prawej dłoni
(śruby prawoskrętnej)

Iloczyn wektorowy

B



A

C

 

  

A B

i

j k

  A A A

B B B

x

y

z

x

y

z

k

B

A

B

A

j

B

A

B

A

i

B

A

B

A

x

y

y

x

z

x

x

z

y

z

z

y











)

(

)

(

)

(













B

A





x

y

y

x

z

x

x

z

y

z

z

y

B

A

B

A

B

A

B

A

B

A

B

A











,

,

B

A